Consider the discrete composite interval time-delay system S which is described as an interconnection of N subsystems
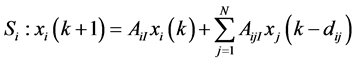 ,
,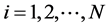 (1)
(1)
where
Define matrices Ui, Vi, Eij, and Fij, respectively, as
In fact, system (1) can also be represented as follows.
 ,
,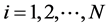 (5)
(5)
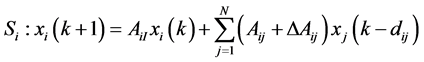 ,
,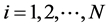 (6)
(6)
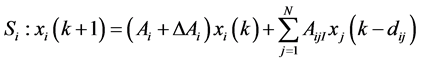 ,
,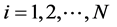 (7)
(7)
where Ai and Aij, respectively, is defined by
Here, ΔAi and ΔAij denote the parametric uncertainties with the following properties:
where Ri and Sij are defined as
Then, we derive the following criteria.
Theorem 1. For
then the composite uncertain time-delay system (1) or (5) is robustly stable
Proof. The condition (11) infers
which can further implies
Therefore, we obtain


Here, we choose Qi as
where
Then, from the Lyapunov Equation (14), we have
Due to the fact that
Then, utilizing these inequalities, we obtain
Substituting this inequality into (16), it is seen that if the condition (12) is satisfied then the right-hand side of (16) is a negative definite matrix. This means that the solution Pi of the Lyapunov Equation (16) has the upper bound
Here, we construct a Lyapunov function as follows.
Taking the forward difference for the Lyapunov function (19) results in
where (15) and the following relation are used.
Therefore, obviously the condition (11) can infer ΔV < 0 and hence the composite uncertain time-delay system (5) is robustly stable. Thus, this completes the proof.
Following the same approach that proposed in the proof of Theorem 1, we have the following results.
Theorem 2. The composite uncertain system (6) or (1) is robustly stable if the following condition is satisfied for
Proof. Using the Lyapunov Equation (7) with
Then, let
It is easy to obtain the stability condition (23). Details of the proof are omitted.
Theorem 3. If the following condition holds for
then the composite uncertain system (7) or (1) is robustly stable.
Proof. From (14), if we choose
and
then the condition (26) can assure the stability of the large-scale system (7) or (1). We also omit the remaining proof.
Remark 1. In [
where Ni denotes the number of
It is obvious that the condition (28) involves an inverse matrix and how to determine the positive constant βi such that (28) is satisfied is an open problem. Furthermore, it is assumed that all eigenvalues of Ai are distinct. The conditions (11), (23), and (26) do not involve any inverse matrix and free variable. It is also not necessary to assume all eigenvalues of Ai are distinct. Therefore, they are less restrictive than (28). Besides, we have found that the tightness of the obtained results cannot be compared.