Journal of Biophysical Chemistry
Vol.2 No.2(2011), Article ID:5134,17 pages DOI:10.4236/jbpc.2011.22011
Analytical consideration of the selectivity of oligonucleotide hybridization
Institute of Chemical Biology and Fundamental Medicine SB RAS, Novosibirsk, Russia; *Corresponding Author: kabilov@niboch.nsc.ru
Received 7 February 2010; revised 1 May 2010; accepted 27 December 2010.
Keywords: Allele Specific Hybridization; Duplex Stability; Oligonucleotide Probes; SNP Discrimination; Specificity; Thermodynamics
ABSTRACT
Systematic analysis of factors determining efficiency in discrimination of a point substitution (SNP) within specific DNA sequences was carried out in the context of hybridization approach. There are two types of selectivity that are critical for the rational design of highly specific oligonucleotides probes. The first type is the real selectivity of hybridization (fa) that is the ratio of association degrees of targets with an oligonucleotide probe upon the perfect and imperfect complex formation. This type of selectivity reflects the level of discrimination between matched and mismatched signals, which is determined both by experimental conditions and the thermodynamics of oligonucleotide hybridization. The second parameter characterizeing the efficiency of SNP discrimination is the limit selectivity of hybridization, which determines the utmost value of fa at a given temperature. This value can be calculated as the ratio of corresponding equilibrium association constants of perfect and imperfect complex formation determined purely by thermodynamics. We have shown that the fa function is the most reliable characteristic describing the hybridization selectivity. For the analytical system designed to reveal any type of perturbation in DNA (e.g. SNP or modification), there is usually a temperature at which fa has its maximum value. The dependency of the fa maximum on different experimental parameters as well as the structural characteristics of a probe are described in details. The results allowed us to postulate points of principle to rationally design the most selective probes on the basis of oligonucleotides or their derivatives.
1. INTRODUCTION
The method of molecular hybridization of oligonucleotide probes with nucleic acids in order to reveal specific sequences has been widely utilized in molecular biology [1,2]. The hybridization allows for discrimination of minimal perturbations in the nucleic acid structure e.g., SNP, deletion, insertion (allele-specific hybridization). The high selectivity of interactions between nucleic acids and oligonucleotides or their analogs and derivatives is important for physico-chemical biology and, in particular, for DNA diagnostics [3-6]. To date, there are several strategies for enhancing selectivity of hybridization between oligonucleotides and nucleic acids (NA), including variation of hybridization conditions (temperature, the probe concentration, and the buffer composition) [7-9] and competitive inhibition through the use of stringency clamping [10] or molecular beacons [11,12]. Selectivity is also affected by the difference in kinetics of complex formation for complementary and mismatched duplexes [13-16]. Additionally, changing the probe length [17] or using tandem short probes [18-21] has been shown to influence selectivity. Another strategy involves the use of nanoparticles bearing immobilized oligonucleotide probes [22-24]. The use of modified oligonucleotides is the promising method for the enhancement of hybridization selectivity. Moreover oligonucleotide derivatives have unique properties, e.g., greater resistance to nuclease digestion and stronger affinity for NA. Modifications can be conventionally divided in two groups: (1) those that increase the thermostability of the DNA-probe complex (PNA [25]; LNA [4]; cyclic, cross-linked, and bicyclic oligo-nucleotides [26,27]; 3’-minor groove binder-DNA probes [28]; HNA and ANA [29], etc.) and (2) those that decrease the thermostability of the DNA-probe complex due to an artificial mismatch [30,31], a non-nucleotide insert [32,33] and others.
The main parameter currently used for comparison of the probe selectivity is the difference between melting temperatures (DTm) of complementary and mismatched complexes [12,28,30,31,34-37]. Other parameters used include the ratio of equilibrium association constants for the perfect (N) and mismatched (M) complexes KN /KM [25], the change of Gibbs energy DDGO [10,26-38, 38-41], and the difference aN – aM [12,42] or the ratio  [43,44] of the association degrees.
[43,44] of the association degrees.
To date, however, there is no generally accepted parameter for the quantitative evaluation of the hybridization selectivity. There are, furthermore, no analytical expressions for the influence of different parameters on the selectivity. The relationship between these parameters and the experimental ratio of the specific and nonspecific signals is still questionable. Some of these parameters, e.g., KN /KM and , do not depend on certain experimental conditions like the concentrations of interacting components and buffer content, that do affect the real selectivity of hybridization.
, do not depend on certain experimental conditions like the concentrations of interacting components and buffer content, that do affect the real selectivity of hybridization.
In this work, we used the methodology of allelespecific hybridization to perform a systematic analysis of the factors determining efficiency of discrimination of a point substitution in specific DNA sequences. A number of the being theses such as “the shorter the probe, the higher its selectivity”, “the rise of DTm means the increase of selectivity”, “molecular beacons are more selective than linear probes” etc., were revised. The results allowed us to reveal points of principle for the rational design of the most selective probes based on oligonu-cleotides or their derivatives.
2. MODELS AND METHODS
2.1. Model for Evaluation of Selectivity
Consider the variant of hybridization of an oligonucleotide probe (p) with the mixture of two templates, one of which is completely complementary (tN) to the probe, and the other contains a single nucleotide substitution or any other modification of the primary structure (tM), which leads to the decreased efficiency of complex formation:
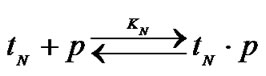 and
and 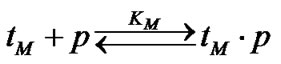
The probe has, obviously, the maximal discrimination ability when the equilibrium concentration of the perfect complex [tN ×p] maximally differs from that of the imperfect complex [tM ×p]. The selectivity function fa is the ratio of the concentrations of perfect and imperfect complexes:

where aN and aM are the association degrees of the perfect and imperfect complexes, respectively, and cN and cM are the initial concentrations of the corresponding DNA templates. Association degree is the ratio of the duplex concentration [tN,M ×p] in the equilibrium system to the total concentration of interacting components, e.g. [tN,M]0. If cN is equal to cM, selectivity function fa is represented as:
 (1)
(1)
Thus, fa indicates the ratio of the degrees of complex formation for perfect and mismatched complexes. Conditions providing the maximum fa value are, apparently, the same for the maximal selectivity of interaction of the probe with the template.
The association degrees of the corresponding complexes can be expressed in terms of the equilibrium constants of association of the probe with the templates. When concentration of the probe (cp) sufficiently exceeds that of the templates (ct) (that is usual for DNA analysis), the association degrees are simplified to:
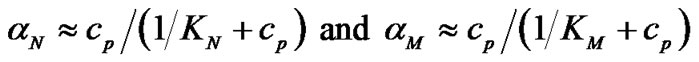 (2)
(2)
Eq.2 shows that the association degree depends on the probe concentration and does not depend on the template concentration. In this case, when a high excess of the probe is used, templates do not compete for binding to the probe. It does not matter, therefore, if either one or two templates are to be analyzed. Starting from (2), fa can be presented as:
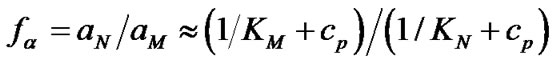 (3)
(3)
where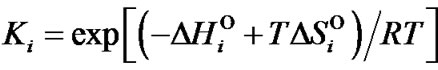 ,
, 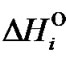 and
and 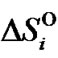
are enthalpy and entropy of complex formation, respectively, i = N or M, R is the gas constant (1.987 cal/K∙mol).
2.2. Calculation of Thermodynamic Parameters for DNA Complexes
Thermodynamic characteristics 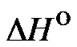 and
and  for complementary and single mismatched complexes were calculated under standard conditions (1 M NaCl, pH 7) using unified nearest neighbor parameters [45-50]. The parameters
for complementary and single mismatched complexes were calculated under standard conditions (1 M NaCl, pH 7) using unified nearest neighbor parameters [45-50]. The parameters 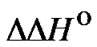 and
and  were calculated as the difference between the corresponding characteristics:
were calculated as the difference between the corresponding characteristics:
 and
and 
Thermodynamic parameters of complex formation for averaged oligomer of the (lp + 1) length were calculated using the following equations:
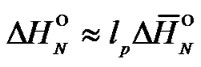 (4)
(4)
 (5)
(5)
where  k·cal/mol and
k·cal/mol and 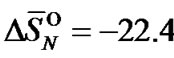 cal/(mol∙K) are enthalpy and entropy, respectively, for the formation of an averaged dinucleotide of the DNA helix, calculated by averaging of the nearest neighbors parameters. For simplicity, the terminal effects and initiation penalty were not taken into account in these calculations.
cal/(mol∙K) are enthalpy and entropy, respectively, for the formation of an averaged dinucleotide of the DNA helix, calculated by averaging of the nearest neighbors parameters. For simplicity, the terminal effects and initiation penalty were not taken into account in these calculations.
The 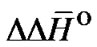 and
and  values for each X/Y mismatch averaged over all possible combinations of nearest neighbors were calculated according to:
values for each X/Y mismatch averaged over all possible combinations of nearest neighbors were calculated according to:
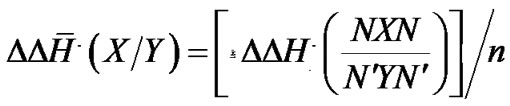
and

where N/N’ is complementary bp. The average statistical effect of a single internal mismatch in the duplex is characterized by values 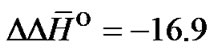 kcal/mol and
kcal/mol and  cal/(mol∙K). The ratio of the averaged enthalpy values for complex formation and destabilization requires, therefore, a value of approximately 2:
cal/(mol∙K). The ratio of the averaged enthalpy values for complex formation and destabilization requires, therefore, a value of approximately 2:
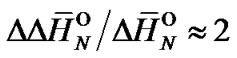 (6)
(6)
2.3. Oligonucleotide System
The main thermodynamic data were obtained for DNA probes and the corresponding perfect and imperfect duplexes are listed in Table 1" target="_self">Table 1. Thermodynamic parameters were calculated in accordance with [45-50].
3. RESULTS
At first, the terminology for the following analytical consideration should be stated. According to IUPAC, “selectivity” is the extent, to which a particular method can be used to determine analytes under given conditions in the presence of other components of the similar behavior. Unlike, “specificity” is considered as an absolute term, and thus cannot be graded [51]. Therefore, it is necessary to use “selectivity” as the obligatory term if we consider the quantitative parameters characterizing the ability of an oligonucleotide probe to distinguish one sequence from the other one. It should be kept in mind, however, that there are different levels of the contextual usage of both terms, specificity and selectivity [52]. We considered the variant implying that the analyzed site was unique, i.e., occurred once in both native and mutated form of the analyzed target. We used the term “se
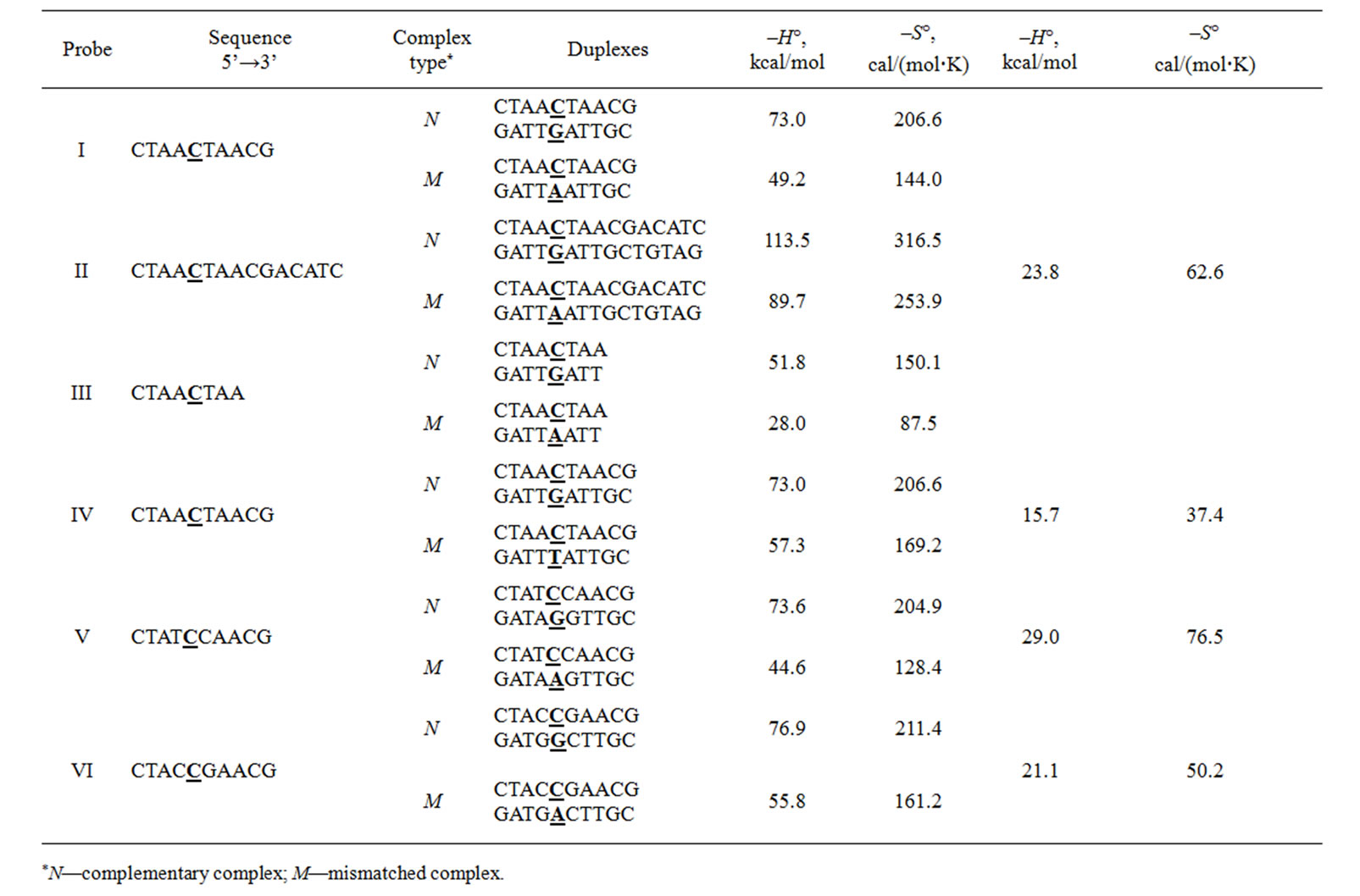
Table 1" target="_self">Table 1. Thermodynamic parameters for complex formation of probes with perfect and mismatched (С/А) templates.
lectivity” as the parameter characterizing the quantitative level of discrimination between the perfect and imperfect (containing point substitution) nucleic acid analytes upon its hybridization with the sequence specific probe having the unique binding site within the DNA template.
3.1. Analysis of the Selectivity Function
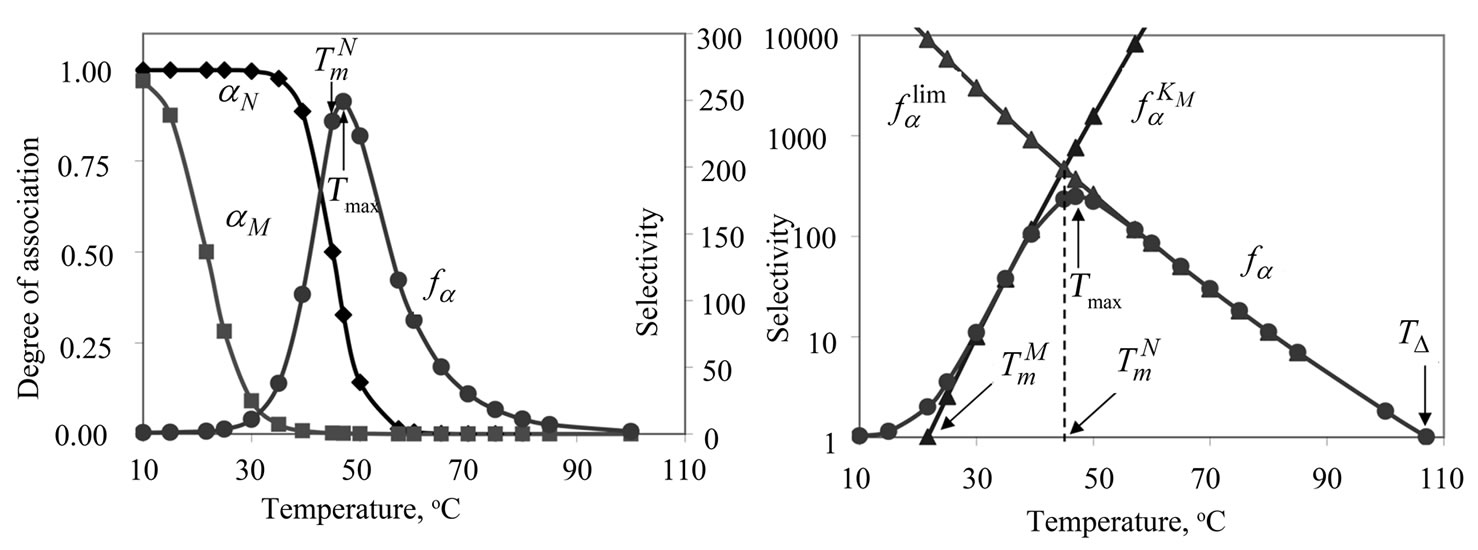
One of the main experimental parameters often used upon optimization is the temperature of hybridization. Consider the dependence of the function fa (3) on temperature using the example of probe I, which is used for discrimination of the substitution of A for G (Table 1" target="_self">Table 1). Figure 1(a) demonstrates the temperature dependence of function fa and the association degrees of the complementary (aN) and mismatched (aM) complexes. The temperature dependence of function fa is the bell-shaped curve. The temperature providing the maximum value of fa is designated as Tmax.
The selectivity function is described by simple expressions within the defined temperature regions (Table 2" target="_self">Table 2).
1) When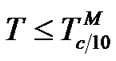 , fa ® 1 because the degree of association of the probe with either of the two templates is approximated to 1 (Table 2" target="_self">Table 2, p. 1) (S1.1).
, fa ® 1 because the degree of association of the probe with either of the two templates is approximated to 1 (Table 2" target="_self">Table 2, p. 1) (S1.1).
2) When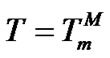 , fa ® 2, provided that expression
, fa ® 2, provided that expression 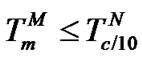 is true (Table 2" target="_self">Table 2, p. 2) (S1.2).
is true (Table 2" target="_self">Table 2, p. 2) (S1.2).
3) Function  tends to
tends to 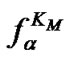 in the range of temperatures
in the range of temperatures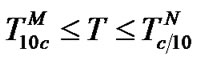 , where
, where
 (7)
(7)
Indeed, fa at these temperatures corresponds to the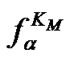 , which is pseudolinear in log chart (S1.3) (Figure 1(b)). The
, which is pseudolinear in log chart (S1.3) (Figure 1(b)). The 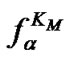 values depend on the hybridization properties of the mismatch complex and probe concentration cp (Table 2" target="_self">Table 2, p. 3).
values depend on the hybridization properties of the mismatch complex and probe concentration cp (Table 2" target="_self">Table 2, p. 3).
4) In the range of high temperatures ,
,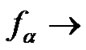
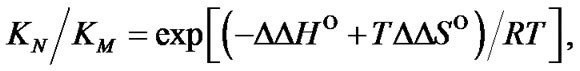 i.e. function fa is determined by the ratio of equilibrium association constants of complementary and imperfect duplexes (S1.4). At these temperatures the fa values fall into the “linear” region (log chart) and are described by a new function (Figure 1(b)) designated as the function of the high limit selectivity (Table 2" target="_self">Table 2, p. 5):
i.e. function fa is determined by the ratio of equilibrium association constants of complementary and imperfect duplexes (S1.4). At these temperatures the fa values fall into the “linear” region (log chart) and are described by a new function (Figure 1(b)) designated as the function of the high limit selectivity (Table 2" target="_self">Table 2, p. 5):
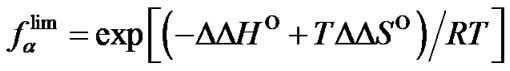 (8)
(8)
Function 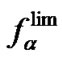 depends only on temperature and the type of mismatch (
depends only on temperature and the type of mismatch ( and
and ); it shows the upper limit value of fa at the given temperature.
); it shows the upper limit value of fa at the given temperature.
5) When T ≥ TD, where TD = DDH°/DDS° is the temperature of inversion of selectivity, fa £ 1. It should be taken into account that TD is the characteristic value for the given pair of match/mismatch. In these temperatures the values of association degrees aN and aM are extremely low for commonly used values of probe concentration. In the case of probe I, as an example, complex formation is extremely low (aN < 10–7) at TD > 100˚C.
6) The most important temperature for any hybridization analysis is Tmax, corresponding to the real maxima of the selectivity function fa. It is not feasible to solve the differential equation  in a strong analytical way and, thus, to find a rigorous solution for the calculation of Tmax. The Tmax value was, therefore, found numerically using the given probe concentration and
in a strong analytical way and, thus, to find a rigorous solution for the calculation of Tmax. The Tmax value was, therefore, found numerically using the given probe concentration and
 (a) (b)
(a) (b)
Figure 1. (a) Temperature dependence of the association degrees of the perfect (aN) and imperfect (aM) complexes (left axis) and of the selectivity function fa (right axis) for probe I at cp=10–5 M. (b) Temperature dependence of fa ,  and
and  (log scale). Tmax is the temperature of the selectivity maximum,
(log scale). Tmax is the temperature of the selectivity maximum,  and
and  are melting temperatures of the perfect and mismatched complexes respectively, TD is temperature of inversion of selectivity.
are melting temperatures of the perfect and mismatched complexes respectively, TD is temperature of inversion of selectivity.

Table 2" target="_self">Table 2. The selectivity function for probe I upon revealing C/A mismatch at different temperatures. Indexes N and M correspond to the complementary and imperfect complexes, respectively. See derivation of formula in supplementary material (S1.1 - S1.5).
thermodynamic parameters of hybridization. Aside from numerical calculation, the approximate evaluation of Tmax is shown to be also possible. For this purpose, one should pay attention to the fact that functions 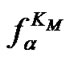 (7) and
(7) and  (8) are pseudo linear in the log chart (Figure 1(b)), confining fa at its left and right, and describing it well within certain temperature regions. The temperature where
(8) are pseudo linear in the log chart (Figure 1(b)), confining fa at its left and right, and describing it well within certain temperature regions. The temperature where 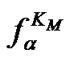 and
and 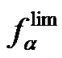 intersect is the melting temperature of the complementary complex
intersect is the melting temperature of the complementary complex , which is close to Tmax (S1.4). At the same time, these functions intersect the abscissa axis at temperatures
, which is close to Tmax (S1.4). At the same time, these functions intersect the abscissa axis at temperatures 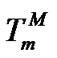 and TD. One can expect that the
and TD. One can expect that the 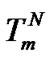 values are as close to Tmax as possible when
values are as close to Tmax as possible when ,
, 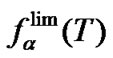 , and the abscissa axis form an isosceles triangle, i.e.
, and the abscissa axis form an isosceles triangle, i.e. . For probe I, these values are
. For probe I, these values are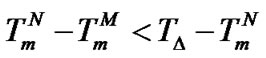 , which results in a shifting of Tmax to higher temperatures.
, which results in a shifting of Tmax to higher temperatures.
Numerical calculations showed that the Tmax values are close to , i.e. to the melting temperature of the perfect complex for all probes (Tables 3-5). The difference (
, i.e. to the melting temperature of the perfect complex for all probes (Tables 3-5). The difference ( ) in these examples is always positive and varies in the range from 0.6˚C to 4.9˚C although theoretically it should be negative in some cases when destabilization of the mismatched duplex is very high (unpublished data). This difference decreases for short probes. So, we can expect in most cases:
) in these examples is always positive and varies in the range from 0.6˚C to 4.9˚C although theoretically it should be negative in some cases when destabilization of the mismatched duplex is very high (unpublished data). This difference decreases for short probes. So, we can expect in most cases:
 (9)
(9)
It was shown using (9) that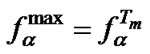 , where
, where 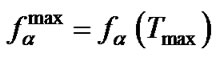 and
and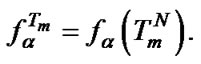 Comparison of these two parameters for all probes under investigation was carried out. We determined that
Comparison of these two parameters for all probes under investigation was carried out. We determined that  was 11% less on average than
was 11% less on average than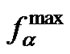 , and deviation of
, and deviation of  from
from 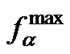 was in the range of 0.3% - 23.4% (Tables 3-5). On the other hand, the selectivity function at melting temperature
was in the range of 0.3% - 23.4% (Tables 3-5). On the other hand, the selectivity function at melting temperature 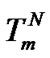 is equal to the half of the limit selectivity function (S1.5).
is equal to the half of the limit selectivity function (S1.5).
 (10)
(10)
The use of this equation simplifies the quantitative evaluation of the probe selectivity sufficiently upon revealing point mutations, because it is necessary to know only melting temperature of the perfect complex 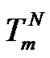 and the influence of the mismatch on thermodynamic parameters, i.e.,
and the influence of the mismatch on thermodynamic parameters, i.e., 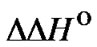 and
and . Substitution of the
. Substitution of the  value into (10) gives (11) and allows one to determine parameters that influence the selectivity function close to its maximum.
value into (10) gives (11) and allows one to determine parameters that influence the selectivity function close to its maximum.
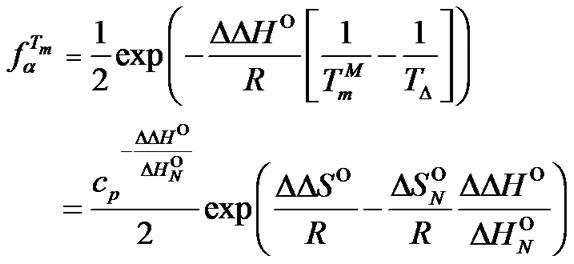 (11)
(11)
These parameters are the length and the structure of the probe ( and
and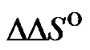 ). Below we will consider in detail the influence of each parameter on the maximum of the selectivity function.
). Below we will consider in detail the influence of each parameter on the maximum of the selectivity function.
3.2. Influence of the Probe Concentration on the Selectivity Function
The influence of probe I concentration on the selectivity function fa is presented in Figure 2 and Table 3" target="_self">Table 3. The

Table 3" target="_self">Table 3. Dependence of melting temperature and selectivity for probe I on its concentration upon revealing C/A mismatch.

Table 4" target="_self">Table 4. Thermodynamic and selectivity data characterizing the discrimination of the С/А mismatch using probes I-III of different length either at the same concentration or the same Tmax values.

Table 5. Pairs of “complementary” mismatches in order decreasing of limit selectivity. Mismatch X/Y, where X and Y are nucleotides in template and in probe, respectively.
decrease of the typical probe concentration leads to an increase of the maximal value of fa (T), and to its shift to lower temperatures, with the function values tending to 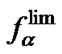 at temperatures higher than Tmax. This demonstrates the well known fact that a probe has higher discriminating ability when it is used at lower concentrations [7-9].
at temperatures higher than Tmax. This demonstrates the well known fact that a probe has higher discriminating ability when it is used at lower concentrations [7-9].
Dependence of  (10) on temperature in logarithmic scale is the “straight” line, which passes the fa curves obtained for different concentrations of probe I at the temperatures corresponding to
(10) on temperature in logarithmic scale is the “straight” line, which passes the fa curves obtained for different concentrations of probe I at the temperatures corresponding to  values. The straight line intersects the curves of the selectivity functions of probe I close to their maxima (Figure 2). Thus the
values. The straight line intersects the curves of the selectivity functions of probe I close to their maxima (Figure 2). Thus the  function allows for the accurate evaluation of the
function allows for the accurate evaluation of the 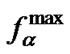 value at the known melting temperature of the perfect complex.
value at the known melting temperature of the perfect complex.
Using (11), we can evaluate the dependence of the maximal value of the selectivity function  upon varying probe concentration. Assume that probe concentration is changed by a factor of x. The change of the maximal probe selectivity (gc) can be determined from the ratio
upon varying probe concentration. Assume that probe concentration is changed by a factor of x. The change of the maximal probe selectivity (gc) can be determined from the ratio  to
to  (S2):
(S2):
 (12)
(12)
The behaviour of change in 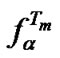 is exponential and depends not only on the concentration change (x) but also on the relative enthalpic contribution of mismatch (perturbation)
is exponential and depends not only on the concentration change (x) but also on the relative enthalpic contribution of mismatch (perturbation)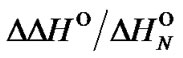 .
.
The simplest way to demonstrate the behavior of gc is the use of an averaged probe (4) upon revealing an av-

Figure 2. Temperature dependence of the selectivity functions for probe I upon revealing C/A mismatch when varying its concentration from 10–8 to 10–5 M.
eraged mismatch (6). Equation (12) can be simplified and presented as the dependence of the change of selectivity on the length of a statistically averaged oligonucleotide probe.
 (13)
(13)
The equation shows that the greater the length of the probe, the less impact its concentration has on its selectivity.
Using (13), we now evaluate the change of selectivity for an averaged probe of 10 nt length (lp + 1) when its concentration is changed by one order of magnitude. Calculations show the increase of the maximum of the selectivity function  for a statistically average probe and an average statistical mismatch by a factor of two (gc ≈ 0.1–2/9 ≈ 1.7) when the probe concentration decreases by one order of magnitude (x = 0.1), and the decrease of this function by a factor of 1.5 (gc ≈ 10–2/9 ≈ 0.6) when concentration increases by one order of magnitude (x = 10).
for a statistically average probe and an average statistical mismatch by a factor of two (gc ≈ 0.1–2/9 ≈ 1.7) when the probe concentration decreases by one order of magnitude (x = 0.1), and the decrease of this function by a factor of 1.5 (gc ≈ 10–2/9 ≈ 0.6) when concentration increases by one order of magnitude (x = 10).
3.3. The Change of Selectivity upon Variation of the Probe Structure
Here we consider changes in the probe structure, which do not influence the thermodynamic characteristics of mismatch discrimination (
 ). One can hypothesize that such a situation is possible when a change of any type is located far from the mismatch in the duplex, and there is virtually no cross-interaction between these elements.
). One can hypothesize that such a situation is possible when a change of any type is located far from the mismatch in the duplex, and there is virtually no cross-interaction between these elements.
Let us consider one particular variation in the probe structure, namely, the change of its length. Using (11), one can demonstrate that in this case, the gl value characterizes the change of  and depends on the melting temperatures of complementary complexes of probes of different lengths (S3).
and depends on the melting temperatures of complementary complexes of probes of different lengths (S3).
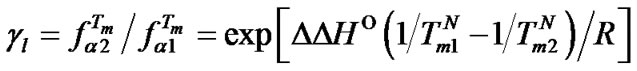 (14)
(14)
When the probe is long enough, the terminal effects can be neglected [53], and (4) and (5) can be used for calculation of hybridization properties of an average probe. In this case gl can be expressed in terms of the probe lengths l1 + 1 and l2 +1 (S3):
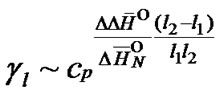 (15)
(15)
In case of discrimination of an averaged mismatch (6), this equation is transformed to:
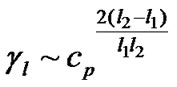 (16)
(16)
Thus, the dependence of the maximum of the selectivity function on the probe length is a rough approximation described by the power function at the given concentration. The longer the probe, the weaker the dependence of selectivity on the change of its length.
Let us evaluate the change of selectivity of a statistically average probe with a length of l1 + 1 = 10 at a concentration cp=10–5 M using (16). The shortening (l1 + 1 = 6) or lengthening (l2 + 1 = 14) of the probe by four nucleotides results in the increase of  approximately by a factor of 7.7 (by one order of magnitude), or a decrease by a factor of 2, respectively.
approximately by a factor of 7.7 (by one order of magnitude), or a decrease by a factor of 2, respectively.
The detailed analysis of the behavior of the selectivity function upon discrimination of the same mismatch С/А, using the probes of different lengths, is represented in Table 4" target="_self">Table 4. Figure 3(a) shows the dependence of fa on temperature for probes I-III, with the lengths of 8, 10, and 15 nucleotides (Table 4" target="_self">Table 4) at 10–5 M concentration of each probe. As expected, the shortening of an oligonucleotide results in the shift of Tmax to lower temperatures and in the increase of the  values.
values.
Interesting results were obtained when considering the behavior of fa(T) in the case of a set of the probes of different length, but with the same Tmax. For this purpose, concentrations for the probes with lengths of 8 and 15 nucleotides were numerically found using (3) (Table 4" target="_self">Table 4). The behavior of fa for these two probes differs markedly from each other (Figure 3(b)). The maximal selectivity value  increases with the increase of the probe length. An elongated probe at temperatures T < Tmax flattens the function fa, as compared to shorter probes, while at a temperature close to Tmax this function increases more dramatically for the longer probe. At temperatures T ≥ Tmax, the function fa tends to
increases with the increase of the probe length. An elongated probe at temperatures T < Tmax flattens the function fa, as compared to shorter probes, while at a temperature close to Tmax this function increases more dramatically for the longer probe. At temperatures T ≥ Tmax, the function fa tends to  for all probes, with fa for the longer probe tending to
for all probes, with fa for the longer probe tending to  at lower temperatures. This can be expressed as
at lower temperatures. This can be expressed as  (Figure 3(b)). Thus, one can hypothesize that fa→1 at T < Tmax and fa →
(Figure 3(b)). Thus, one can hypothesize that fa→1 at T < Tmax and fa → at T ≥ Tmax when the lengthening of the probe is pronounced.
at T ≥ Tmax when the lengthening of the probe is pronounced.
These results open a question about what criteria should be used for evaluating the discrimination ability of the probe at a definite temperature, or at some range of temperatures. We should still consider the temperature
 (a) (b)
(a) (b)
Figure 3. (a) Temperature dependence of the selectivity functions for probes with the length of 15(II), 10 (I), and 8 (III) nt (cp = 10–5 M). (b) Temperature dependence of the selectivity functions for probes with the length of 15 (II), 10 (I) and 8 (III) nt having the same Tmax at concentrations 2.3∙10–3, 1∙10–5, and 1.3∙10–9 M, respectively.
range in which  is found, taking into account that the precision calculation of Tmax is restricted by the accuracy of thermodynamic parameters. Then the integral value of fa within the given temperature range determines the probe selectivity. Consider probes I-III (Table 4" target="_self">Table 4) under conditions where their Tmax are the same (Figure 3(b)), provided that the accuracy of Tmax is ±5˚C, and find the values
is found, taking into account that the precision calculation of Tmax is restricted by the accuracy of thermodynamic parameters. Then the integral value of fa within the given temperature range determines the probe selectivity. Consider probes I-III (Table 4" target="_self">Table 4) under conditions where their Tmax are the same (Figure 3(b)), provided that the accuracy of Tmax is ±5˚C, and find the values . The results show the higher integral selectivity of probe II (15-mer) within this temperature range as compared to the shorter oligonucleotides. On the contrary, short probe III has the highest integral selectivity within the whole experimental temperature range chosen from 20˚C to 80˚C. Nevertheless, there is no evident preference of one probe over another because of the slight dependence of the integral selectivity on the probe length (Table 4" target="_self">Table 4).
. The results show the higher integral selectivity of probe II (15-mer) within this temperature range as compared to the shorter oligonucleotides. On the contrary, short probe III has the highest integral selectivity within the whole experimental temperature range chosen from 20˚C to 80˚C. Nevertheless, there is no evident preference of one probe over another because of the slight dependence of the integral selectivity on the probe length (Table 4" target="_self">Table 4).
Let T–1/2 and T+1/2 are temperatures where selectivity function faTm is reduced by half.
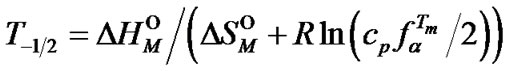 (17)
(17)
 (18)
(18)
Although the  values for the probes differ insignificantly from each other at the same Tmax, the T+1/2 values are 57.1˚C for all probes and the T–1/2 values are 41.5˚C, 39.4˚C and 36.6˚C for the 15-mer, 10-mer, and 8-mer, respectively (Table 4" target="_self">Table 4). Thus T–1/2 and T+1/2 characterize the temperature range where selectivity function fa has significantly high values.
values for the probes differ insignificantly from each other at the same Tmax, the T+1/2 values are 57.1˚C for all probes and the T–1/2 values are 41.5˚C, 39.4˚C and 36.6˚C for the 15-mer, 10-mer, and 8-mer, respectively (Table 4" target="_self">Table 4). Thus T–1/2 and T+1/2 characterize the temperature range where selectivity function fa has significantly high values.
3.4. The Influence of the Mismatch Type on Hybridization Selectivity
The efficiency of mismatch discrimination for a probe depends on the value of its destabilization effect in the probe/template complex. The change of selectivity examined above while varying concentration and length of the probe do not involve the parameters 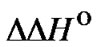 and
and , which determine the
, which determine the  values (8). One way to change the limit selectivity is to vary the type of mismatch.
values (8). One way to change the limit selectivity is to vary the type of mismatch.
For example, let us consider the situation when the same probe is used for revealing two different mismatches C/A and C/T (Table 1" target="_self">Table 1, I and IV). In this case, the difference in the efficiency of discrimination results only from the variation of the  and
and 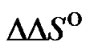 values due to the nature of the imperfect base pair. Temperature dependence of functions fa and
values due to the nature of the imperfect base pair. Temperature dependence of functions fa and 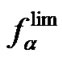 for the same probe (cp = 10–5 M and 10–8 M,
for the same probe (cp = 10–5 M and 10–8 M,  and
and  are constants) are depicted in Figure 4. The coincidence of the maxima of functions fa (C/A) and fa (C/T) charac-
are constants) are depicted in Figure 4. The coincidence of the maxima of functions fa (C/A) and fa (C/T) charac-

Figure 4. Temperature dependence of the selectivity functions when revealing two different mismatches C/A (I) and C/T (IV) using the same probe at 10–5 M and 10–8 М concentrations.
terizing the discrimination of these mismatches at Tmax ≈ 45˚C (cp = 10–5M) can be seen. The decrease of probe concentration (cp = 10–8M) leads to the lowering of Tmax to 30˚C and to the difference between the 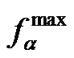 values by a factor of more than three. The efficiency of discrimination of mismatches can thus sufficiently change when varying the Tmax values. So, mismatches with the same selectivity at a definite temperature become markedly distinguishable at some other temperature.
values by a factor of more than three. The efficiency of discrimination of mismatches can thus sufficiently change when varying the Tmax values. So, mismatches with the same selectivity at a definite temperature become markedly distinguishable at some other temperature.
The range of the changes of 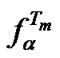 upon variation of a mismatch type and, consequently
upon variation of a mismatch type and, consequently  and
and 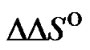 parameters, was calculated using (10). If the
parameters, was calculated using (10). If the  and
and  values change by h and s, respectively, the change of the selectivity function (gpert) near its maximum becomes the following (S4):
values change by h and s, respectively, the change of the selectivity function (gpert) near its maximum becomes the following (S4):
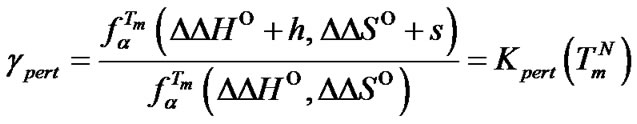 (19)
(19)
where Kpert(T) = exp[(–h + Ts)/RT] is the “perturbation” constant. The change of the maximal selectivity function eventually depends on parameters h and s. The expression gpert > 1 is true when the ratio h/s is higher than the melting temperature of the complementary complex (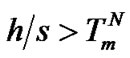 ).
).
There is no need to determine the dependence of fa on temperature for each particular case in order to evaluate the maximal probe selectivity. Instead, the expression  (T)/2 can be used, allowing preliminary evaluation of
(T)/2 can be used, allowing preliminary evaluation of  at a given hybridization temperature according to (10).
at a given hybridization temperature according to (10).
We compared the efficiency of discrimination of all types of internal single mismatches in DNA/DNA duplexes using the thermodynamic parameters 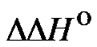 and
and  [53]. There are 12 types of internal mismatches as a result of orientational asymmetry. For example, mismatches A/G and G/A are not equivalent because they correspond to A/T and G/C complementary pairs in a perfect complex, respectively. The values of
[53]. There are 12 types of internal mismatches as a result of orientational asymmetry. For example, mismatches A/G and G/A are not equivalent because they correspond to A/T and G/C complementary pairs in a perfect complex, respectively. The values of 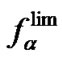 (T) for 12 types of mismatches averaged over nearest neighbors are presented in Table 5. The maximal discrimination ability of probes is shown for the imperfect pairs C/C, A/C, and T/C. The efficiency of discrimination of all other mismatches is sufficiently lower and depends significantly on the chosen temperature conditions.
(T) for 12 types of mismatches averaged over nearest neighbors are presented in Table 5. The maximal discrimination ability of probes is shown for the imperfect pairs C/C, A/C, and T/C. The efficiency of discrimination of all other mismatches is sufficiently lower and depends significantly on the chosen temperature conditions.
A mutation can be revealed in either of two strands of dsDNA that allows one to say about “complementary” related mismatches. The selectivity of revealing mismatches follows the trend: C/C > G/G, A/C > T/G, T/C > A/G, C/A > G/T, C/T > G/A at any temperatures over the range of 20˚C to 80˚C. In the case of the pair of “complementary” mismatches A/A and T/T the former is better discriminated at temperatures < 45˚C and the latter at temperatures > 45˚C.
Using the dependence  (T)/2, we can choose the type of a mismatch, temperature, and oligonucleotide probe that provide the maximal efficiency of discrimination, and therefore, the highest selectivity for revealing point mutations.
(T)/2, we can choose the type of a mismatch, temperature, and oligonucleotide probe that provide the maximal efficiency of discrimination, and therefore, the highest selectivity for revealing point mutations.
3.5. The Change of Selectivity Conferred by Using Modified Probes
Most often, there is a necessity to determine how modification of a native probe influences its selectivity. To date, there is no systematic information about thermodynamic characteristics describing in detail the imperfect complexes formed by modified oligonucleotides, e.g., PNA, LNA, etc.
When the same type of a mismatch has to be discriminated, variation of the nearest neighbors of the polymorphic site can be a model of the modification resulting in the change of 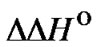 and
and 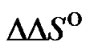 Let us examine the identification of a C/A mismatch using probes I, V, and VI (Table 1" target="_self">Table 1), which are distinguished from each other only by the nucleotide sequences around the mismatch. Figure 5 demonstrates the temperature
Let us examine the identification of a C/A mismatch using probes I, V, and VI (Table 1" target="_self">Table 1), which are distinguished from each other only by the nucleotide sequences around the mismatch. Figure 5 demonstrates the temperature

Figure 5. Temperature dependence of the selectivity functions when revealing С/А mismatch using 10–5 M probes I, V, or VI.
dependence of the selectivity function and limit selectivity function for these probes. At the defined concentration, the temperature of the selectivity maxima varies in its dependence on hybridization properties of the probes. The selectivity of each probe is always higher at the melting temperature of its complementary complex ( ,
,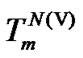 or
or ) than at the other temperature (Table 6). However, the straight lines
) than at the other temperature (Table 6). However, the straight lines  (T) are not intersected in the range from 30 to 80˚C; we can therefore say that the attainable selectivity of the probes increases in a row I < V < VI (Figure 5). The same ratio is true for the selectivity maxima of these probes
(T) are not intersected in the range from 30 to 80˚C; we can therefore say that the attainable selectivity of the probes increases in a row I < V < VI (Figure 5). The same ratio is true for the selectivity maxima of these probes 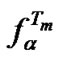 at a definite temperature.
at a definite temperature.
One of interesting question that can be asked while searching the new types of modification (perturbation) of the probe, is what values of the DDH° and DDS° can provide the high level of limit selectivity. As can be seen from (8), the function ln  (T) is a hyperbola, and can be fitted with a high accuracy (R2 > 0.98) by the linear dependence in the temperature range from 0˚C to 100˚C:
(T) is a hyperbola, and can be fitted with a high accuracy (R2 > 0.98) by the linear dependence in the temperature range from 0˚C to 100˚C:
 (20)
(20)
where c1 and c2 are positive constants (S5). Thus, the slope of the function depends only on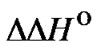 , while the constant term is determined by both types of thermody
, while the constant term is determined by both types of thermody

Table 6. Thermodynamic and selectivity data obtained upon discrimination of C/A mismatch using 10–5 M probes I, V, or VI (Table 1" target="_self">Table 1), which differ from each other by neighbors nearest to the mutation site.
namic characteristics.
The discrimination of mismatches is characterized by the decrease of selectivity upon increasing the temperature if unmodified probes are used. One can expect, in general, that some modifications of the probe structure can change such a relationship. There are three possible cases when falim(T) >1 in the temperature range from 0 to 100˚C:
1) 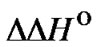 < 0 and TD > 0˚C:,
< 0 and TD > 0˚C:,  (T) decreases with temperature increase;
(T) decreases with temperature increase;
2)  = 0 and
= 0 and  > 0,
> 0,  (T) is independent on temperature and the perfect complex is more favorable in entropy than the mismatched one
(T) is independent on temperature and the perfect complex is more favorable in entropy than the mismatched one ;
;
3) 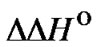 > 0 and TD < 0˚C:,
> 0 and TD < 0˚C:,  (T) increases with temperature increase.
(T) increases with temperature increase.
The first case (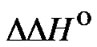 < 0) is the main subject of the analysis in this work. The other cases are obviously uncharacteristic for the obtained thermodynamic effects caused by mismatches in duplexes formed by unmodified oligonucleotides. The third case, when
< 0) is the main subject of the analysis in this work. The other cases are obviously uncharacteristic for the obtained thermodynamic effects caused by mismatches in duplexes formed by unmodified oligonucleotides. The third case, when 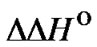 > 0, however, is very attractive for the application of allele specific hybridization at high temperatures. Function fa(T) increases with the temperature rise without reaching a maximum. The hypothetical situation corresponding to this condition is depicted in Figure 6. In this case, the lengthening of the probe, the increase of its concentration, and the increase of hybridization temperature are favorable for the selectivity of the interaction. It would be promising if a type of modification that results in a positive change in enthalpy was found.
> 0, however, is very attractive for the application of allele specific hybridization at high temperatures. Function fa(T) increases with the temperature rise without reaching a maximum. The hypothetical situation corresponding to this condition is depicted in Figure 6. In this case, the lengthening of the probe, the increase of its concentration, and the increase of hybridization temperature are favorable for the selectivity of the interaction. It would be promising if a type of modification that results in a positive change in enthalpy was found.

Figure 6. Temperature dependence of the association degrees of the perfect (aN) and imperfect (aM) complexes (left axis) and of the selectivity functions fa, 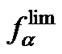 and
and 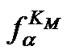 (right axis, log scale) for some modified probe at cp = 10–5 M.
(right axis, log scale) for some modified probe at cp = 10–5 M.  is melting temperature of the perfect complex. The values DHO = 73, DDHO = 23.8 kcal/mol, DSO = –206.6, DDSO = –95 cal/(mol∙K) are calculated for the hypothetic case.
is melting temperature of the perfect complex. The values DHO = 73, DDHO = 23.8 kcal/mol, DSO = –206.6, DDSO = –95 cal/(mol∙K) are calculated for the hypothetic case.
4. DISCUSSION
4.1. Parameters of Selectivity Used in the Literature
The identification of point mutations in nucleic acids using the allele-specific hybridization method implies, as a rule, that nucleotide sequences of NA, and the type and location of a probable nucleotide substitution are known. The aim of the analysis of the polymorphic site is to distinguish mutated and normal states with the highest reliability. The selectivity of the analysis is determined by the prevalence of perfect complex formation of a probe in comparison with imperfect one.
There are several approaches in the literature to the evaluation of hybridization selectivity based on the comparison of the association degrees of the perfect and mismatched complexes. Some authors have used the difference between them aN – aM [12,42]. We suppose that the use of the ratio of these parameters is more correct since, according to IUPAC, selectivity in analytical chemistry is the ratio of specific and nonspecific signals [51]. Here, we used the selectivity function fa, which is the ratio aN/aM, for the evaluation of the ability of probes to discriminate point mutations.
One of the first attempts in quantitative evaluation of selectivity of hybridization between an extended oligonucleotide probe and genomic DNA was performed in the work of Hearst J.E., who proposed the function lg(fa) [43]. In this case, the selectivity was calculated using the empirical formula: lg[fa(Tm)] = (3.8 – lgcp)Dl/l, where l + 1 is the probe length, Dl is the length of the non-complementary region of the probe-DNA complex, and cp is the probe concentration. Graphic analysis of this function showed that the maximal selectivity of interaction between a probe and a template is achieved at a melting temperature of the perfect complex. This formula was not, however, widely adopted in practice. Function fa was also used as one of the criteria for the choice of “structure-free” oligonucleotides as elements of combinatorial DNA word sets [44]. The ratio of specific to nonspecific signals, that is, in general, fa, is used in hybridization analysis for the evaluation of the selectivity of a given probe [17,54]. The detailed analysis of the influence of different parameters on this function was not, however, carried out.
Evaluations of selectivity are more often based on other parameters such as KN/KM [25], 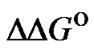 [10, 26-28,38-41], and DTm [12,28,30,31,34-37]. The ratio of equilibrium constants of perfect and imperfect complex formation
[10, 26-28,38-41], and DTm [12,28,30,31,34-37]. The ratio of equilibrium constants of perfect and imperfect complex formation  is equal to
is equal to 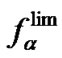 (8) per se. This ratio can be used for evaluation of real hybridization selectivity in two cases: when hybridization temperature is more or equal to
(8) per se. This ratio can be used for evaluation of real hybridization selectivity in two cases: when hybridization temperature is more or equal to , i.e., when fa ®
, i.e., when fa ®  (Table 2" target="_self">Table 2, p.5) and at the melting temperature of complementary complex where
(Table 2" target="_self">Table 2, p.5) and at the melting temperature of complementary complex where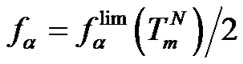 . So, the ratio KN /KM describes the limit selectivity values; it corresponds to the real selectivity fa in particular cases. This argumentation is fully applicable to the characteristic of selectivity
. So, the ratio KN /KM describes the limit selectivity values; it corresponds to the real selectivity fa in particular cases. This argumentation is fully applicable to the characteristic of selectivity 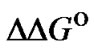 since
since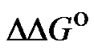 = –RTln(
= –RTln( ). In contrast to the ratio of KN/KM, the
). In contrast to the ratio of KN/KM, the 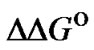 does not directly describe the reachable ratio of specific to nonspecific signals because this parameter is the logarithm of
does not directly describe the reachable ratio of specific to nonspecific signals because this parameter is the logarithm of  normalized by RT value, which is monotonously increased with temperature rising. This can lead to the erroneous interpretation about the selectivity criterion based on
normalized by RT value, which is monotonously increased with temperature rising. This can lead to the erroneous interpretation about the selectivity criterion based on  upon increasing the hybridization temperature. For example, in the hypothetic case, when the function
upon increasing the hybridization temperature. For example, in the hypothetic case, when the function  (T) seems to be constant (
(T) seems to be constant (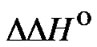 ® 0), the selectivity criterion referred to
® 0), the selectivity criterion referred to 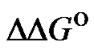 changes shows a slight improvement of the mismatch discrimination. But
changes shows a slight improvement of the mismatch discrimination. But 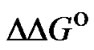 is, nevertheless, a useful criterion, which can be used for the comparison of the general selectivity of a set of probes at a given temperature.
is, nevertheless, a useful criterion, which can be used for the comparison of the general selectivity of a set of probes at a given temperature.
To date, one of the most utilizing parameters for comparison of probe selectivity is . Conclusions concerning the enhancement of hybridization selectivity caused by the modification of a probe are often based upon increasing the DTm value. As it can be seen from the expression
. Conclusions concerning the enhancement of hybridization selectivity caused by the modification of a probe are often based upon increasing the DTm value. As it can be seen from the expression 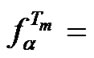
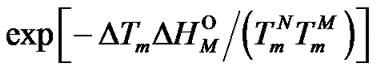 , there is no direct relation between
, there is no direct relation between  and DTm, so it is difficult to evaluate the hybridization selectivity just from the DTm value.
and DTm, so it is difficult to evaluate the hybridization selectivity just from the DTm value.
The additional analysis allows us to estimate how the change of DTm affects the maximal hybridization selectivity. It was shown above that 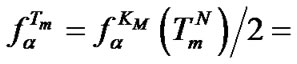
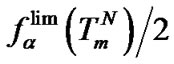 (10). Using the approximation
(10). Using the approximation 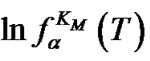
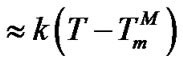 , where k is proportional to
, where k is proportional to 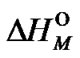 (analogous to (20)), we can express
(analogous to (20)), we can express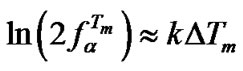 . The following equation can be used to analyze the change of
. The following equation can be used to analyze the change of 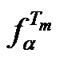 caused by variation of any parameters affecting the relative thermostabilities of complexes:
caused by variation of any parameters affecting the relative thermostabilities of complexes: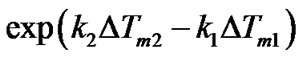
 .
.
Thus, the comparison of DTm values can be used as a certain characteristic of the selectivity change only when k1 = k2. This is true when . If the
. If the  values are not equal and unknown, the difference DTm1 – DTm2 cannot show changes of hybridization selectivity upon the variation of the system parameters (length and modification of a probe, type of a mismatch, and buffer composition).
values are not equal and unknown, the difference DTm1 – DTm2 cannot show changes of hybridization selectivity upon the variation of the system parameters (length and modification of a probe, type of a mismatch, and buffer composition).
4.2. Selectivity of Hybridization
The maximal selectivity of hybridization can be provided by changing the thermodynamics of duplex formation (e.g. the structure of a probe), probe concentration, and hybridization temperature. It should be noted that all of these parameters influence the hybridization efficiency of the probe and, consequently, are included in the analyzed selectivity function fa.
When examining the discrimination ability of two different probes intended to reveal the same substitution in an analyzed template, it is necessary to clearly distinguish the notions of the probe selectivity fa (3) for the specific hybridization conditions and the limit probe selectivity 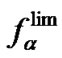 as a general parameter (8). Thus, to determine what probe has the maximal selectivity, it is necessary to know the dependence of the
as a general parameter (8). Thus, to determine what probe has the maximal selectivity, it is necessary to know the dependence of the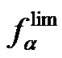 values on temperature. A given probe is, in general, more selective than another probe if the corresponding functions
values on temperature. A given probe is, in general, more selective than another probe if the corresponding functions  (T) are greater in the range of used hybridization temperatures.
(T) are greater in the range of used hybridization temperatures.
The results allow us to conclude that the thesis “affinity and specificity are anticorrelated” [55] become rather questionable. Actually, the increase in affinity (equilibrium binding constant) of a probe due, for example, to its lengthening or changing temperature, can both decrease and increase the real selectivity fa. There are condition ranges where these functions are correlated (for example, in temperature range Tmax – TD), anticorrelated (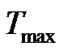
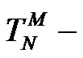 ) or practically independent on each other (
) or practically independent on each other ( ). In general, in case of hybridization native oligonucleotide probes, the sign and the value of DDH° results in correlation of the limit selectivity function
). In general, in case of hybridization native oligonucleotide probes, the sign and the value of DDH° results in correlation of the limit selectivity function 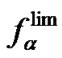 (T) with affinities of a probe (KN (T) or KM (T)).
(T) with affinities of a probe (KN (T) or KM (T)).
The 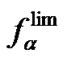 value reflects the potentially attainable selectivity; for native oligonucleotide probes, it usually increases with the decrease of hybridization temperature. One of the approaches to varying the limit probe selectivity when revealing a certain mismatch is, therefore, the modification of the probe structure, which leads to the change of the
value reflects the potentially attainable selectivity; for native oligonucleotide probes, it usually increases with the decrease of hybridization temperature. One of the approaches to varying the limit probe selectivity when revealing a certain mismatch is, therefore, the modification of the probe structure, which leads to the change of the 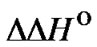 and
and  parameters. In this context, it is very important to determine the thermodynamic characteristics of new oligonucleotide probes designed from their derivatives or analogues in detail. The absence of the appropriate information in most cases makes the understanding of the real effect of modification on changes of hybridization selectivity difficult. Only a few examples of well-grounded statements concerning the enhancement of selectivity of modified probes in comparison with native ones are described in the literature. Oligonucleotides containing a number of C5-propynyl-modified pyrimidines displayed enhanced specificity due to the long-range cooperativity of interaction between modified bases [56]. Many derivatives of natural oligonucleotides and their analogues are proposed for enhancing the selectivity of nucleic acid recognition. The most promising compounds are PNA [25]; LNA [4], cyclic, cross-linked, and bicyclic oligonucleotides [26,27], oligonucleotides bearing minor groove binders [28], and probes containing analogues of nitrogen bases [30,57].
parameters. In this context, it is very important to determine the thermodynamic characteristics of new oligonucleotide probes designed from their derivatives or analogues in detail. The absence of the appropriate information in most cases makes the understanding of the real effect of modification on changes of hybridization selectivity difficult. Only a few examples of well-grounded statements concerning the enhancement of selectivity of modified probes in comparison with native ones are described in the literature. Oligonucleotides containing a number of C5-propynyl-modified pyrimidines displayed enhanced specificity due to the long-range cooperativity of interaction between modified bases [56]. Many derivatives of natural oligonucleotides and their analogues are proposed for enhancing the selectivity of nucleic acid recognition. The most promising compounds are PNA [25]; LNA [4], cyclic, cross-linked, and bicyclic oligonucleotides [26,27], oligonucleotides bearing minor groove binders [28], and probes containing analogues of nitrogen bases [30,57].
The selectivity function was shown to reach two upper values, which were determined by the distinctive behavior of this function in two cases: temperature was varied, or it was not. If temperature is the variable parameter, the unique case is fulfilled with a maximum of the selectivity function. This is the most probable case for SNP identification systems when unmodified oligonucleotides with  < 0 are used. In this case, there is the temperature (Tmax) close to the melting temperature of the perfect complex (
< 0 are used. In this case, there is the temperature (Tmax) close to the melting temperature of the perfect complex (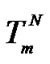 ) where the selectivity reaches maximum. For systems with
) where the selectivity reaches maximum. For systems with  > 0, fa is a monotonically increasing function independently of all possible types of experimentally controlled variables. In this case, the maximal selectivity at any given temperature is the limit selectivity
> 0, fa is a monotonically increasing function independently of all possible types of experimentally controlled variables. In this case, the maximal selectivity at any given temperature is the limit selectivity  (T). However, this leads to the necessity of decreasing efficiency of formation of the perfect duplex as much as possible for reliable detection at the given sensitivity of the method. This is the general rule to reach the maximal selectivity of hybridization independently of the thermodynamic features of the system, i.e., for any
(T). However, this leads to the necessity of decreasing efficiency of formation of the perfect duplex as much as possible for reliable detection at the given sensitivity of the method. This is the general rule to reach the maximal selectivity of hybridization independently of the thermodynamic features of the system, i.e., for any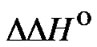 . Therefore, it is necessary to find a compromise between the observable selectivity level and the recorded signal to noise ratio. In this way, the highest level of selectivity can be achieved when the efficiency of hybridization is extremely low. Therefore, the corresponding experimental conditions should be used only when the sensitivity of detection of the hybridization signal is high enough.
. Therefore, it is necessary to find a compromise between the observable selectivity level and the recorded signal to noise ratio. In this way, the highest level of selectivity can be achieved when the efficiency of hybridization is extremely low. Therefore, the corresponding experimental conditions should be used only when the sensitivity of detection of the hybridization signal is high enough.
The comparative analysis of the dependence of hybridization selectivity on the length of a native oligonucleotide revealed a quite unexpected fact (Figure 3). The longer the oligonucleotide probe, the higher the maximum value of selectivity observed at the same Tmax. The differences are, however, not sufficient: for example, the value of the maximal selectivity at a given temperature for an 8-mer is 1.5 times lower than for a 15-mer probe (Table 4" target="_self">Table 4). Therefore, the choice of probe length should be determined by other parameters. The minimal length of the probe is determined by probe concentration and the unique binding site in the DNA to be analyzed. The upper limit of the probe length is conditioned by a possibility of obtaining the detectable hybridization signal at low probe concentration under a given experimental condition. In our example, to maintain the same Tmax for a 10-mer and a 15-mer, the concentration of the longer oligonucleotide should be decreased by four orders of magnitude in comparison with the shorter one (Table 4" target="_self">Table 4). Thus, the choice of the probe length for a given temperature is a complex problem concerned with the sensitivity of detection, the sequence specificity of the probe, and, to a lesser degree, with the maximal selectivity of hybridization.
Identical conclusions can be reached when no changes of probe structure influence the  and
and  values. One example of this is the variation of the mismatch position in a probe binding site, which can change the GC content of the probe. Another example is some modification of the probe, which does not affect the duplex structure close to the mismatched base pair.
values. One example of this is the variation of the mismatch position in a probe binding site, which can change the GC content of the probe. Another example is some modification of the probe, which does not affect the duplex structure close to the mismatched base pair.
These conclusions allow us to suppose that molecular beacons are not more selective than linear probes [11]. Because of the formation of hairpin, the concentration of non-structured form of molecular beacon interacting with a target reduces that can increase fa. Since the  and
and  values do not change, the same selectivity can be reached when concentration of the ordinary linear probe is reduced. Advantage of molecular beacons consists in their ability to generate the specific signal but not in enhancing the hybridization selectivity.
values do not change, the same selectivity can be reached when concentration of the ordinary linear probe is reduced. Advantage of molecular beacons consists in their ability to generate the specific signal but not in enhancing the hybridization selectivity.
The most readily available way to increase the probe selectivity is modifications of the probe structure, which resulted in the change of 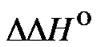 and
and 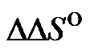 parameters. The increase or decrease of the thermostability of the probe complexes, and the commonly used DTm parameter do not reflect a change of selectivity. Only the knowledge of thermodynamics of complexation allows one to describe a change of attainable selectivity. Unfortunately, it is rather difficult to predict the exact effects of any modification on entropy and enthalpy of the probe complexation. Therefore, to choose a suitable modification it is necessary to screen a large number of variants. This is a difficult task because many of the detailed thermodynamic data should be obtained and analyzed in accordance with analytical considerations represented here.
parameters. The increase or decrease of the thermostability of the probe complexes, and the commonly used DTm parameter do not reflect a change of selectivity. Only the knowledge of thermodynamics of complexation allows one to describe a change of attainable selectivity. Unfortunately, it is rather difficult to predict the exact effects of any modification on entropy and enthalpy of the probe complexation. Therefore, to choose a suitable modification it is necessary to screen a large number of variants. This is a difficult task because many of the detailed thermodynamic data should be obtained and analyzed in accordance with analytical considerations represented here.
4.3. Conclusions
There are two principal ways of increasing the hybridization selectivity. The first way is to search modified oligonucleotide probes for those that provide an enhanced level of discrimination of any perturbation in the specific sequence in comparison with native oligonucleotides. The second way is the optimization of hybridization conditions and minor variations in probe structure (for example, the length change). In both cases a successful result can be obtained if there is an accurate thermodynamic description of the analyzed system.
To evaluate the real effect caused by modification of the probe on the selectivity, it is necessary to analyze the changes of the  (T) values. For this purpose, the corresponding thermodynamic characteristics
(T) values. For this purpose, the corresponding thermodynamic characteristics 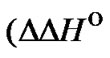 and
and  should be determined. These thermodynamic parameters should depend not only on the modification of the probe, but also on buffer conditions (pH, ion composition, ionic strength, and, in some cases, on organic or inorganic additions having the preferable affinity either to matched or mismatched complexes). As a result, the enhancement of
should be determined. These thermodynamic parameters should depend not only on the modification of the probe, but also on buffer conditions (pH, ion composition, ionic strength, and, in some cases, on organic or inorganic additions having the preferable affinity either to matched or mismatched complexes). As a result, the enhancement of  (T) by itself does not guarantee the maximal selectivity of hybridization while using a given probe at given conditions. The choice of the optimal probe in any particular case is a multiparametric task that implies the optimization of the probe structure, its concentration and hybridization temperature on the basis of the analysis fa function.
(T) by itself does not guarantee the maximal selectivity of hybridization while using a given probe at given conditions. The choice of the optimal probe in any particular case is a multiparametric task that implies the optimization of the probe structure, its concentration and hybridization temperature on the basis of the analysis fa function.
In this work, we considered the theoretical aspects of hybridization selectivity while using the oligonucleotide probe for revealing any perturbation in an analyzed NA duplex. The proposed analytical description allows one to evaluate the efficiency of discrimination of such a perturbation and can provide the basis for software for the rational design of the optimal probe structure.
5. ACKNOWLEDGEMENTS
We are grateful to Asya Levina for reading this manuscript and helpful suggestions. This work was supported by grant of RFBR 10-04-01492, by programs of the Presidium of the RAS “Molecular and Cellular Biology”, by interdisciplinary grant of the SB RAS 76 and by MES RF (GC P1073).
REFERENCES
- Southern, E.M. (1975) Detection of specific sequences among DNA fragments separated by gel electrophoresis. Journal of Molecular Biology, 98, 503-517.doi:10.1016/S0022-2836(75)80083-0
- Wetmur, J.G. (1991) DNA probes: Applications of the principles of nucleic acid hybridization. Critical Reviews in Biochemistry and Molecular Biology, 26, 227-259.doi:10.3109/10409239109114069
- Knorre, D.G. and Vlassov, V.V. (1991) Reactive oligonucleotide derivatives as gene-targeted biologically active compounds and affinity probes. Genetica, 85, 53-63. doi:10.1007/BF00056106
- Mouritzen, P., Nielsen, A.T., Pfundheller, H.M., Choleva, Y., Kongsbak, L. and Moller, S. (2003) Single nucleotide polymorphism genotyping using locked nucleic acid (LNA). Expert Review of Molecular Diagnostics, 3, 27-38. doi:10.1586/14737159.3.1.27
- Kofiadi, I.A. and Rebrikov, D.V. (2006) Methods for detecting single nucleotide polymorphisms: Allele-specific PCR and hybridization with oligonucleotide probe. Genetika, 42, 22-32.
- Marras, S.A., Tyagi, S. and Kramer, F.R. (2006) Real-time assays with molecular beacons and other fluorescent nucleic acid hybridization probes. Clinical Chimica Acta, 363, 48-60. doi:10.1016/j.cccn.2005.04.037
- Maskos, U. and Southern, E.M. (1992) Parallel analysis of oligodeoxyribonucleotide (oligonucleotide) interactions. I. Analysis of factors influencing oligonucleotide duplex formation. Nucleic Acids Research, 20, 1675-1678. doi:10.1093/nar/20.7.1675
- Relogio, A., Schwager, C., Richter, A., Ansorge, W. and Valcarcel, J. (2002) Optimization of oligonucleotide-based DNA microarrays. Nucleic Acids Research, 30, e51. doi:10.1093/nar/30.11.e51
- Sorokin, N.V., Chechetkin, V.R., Livshits, M.A., Pankov, S.V., Donnikov, M.Y., Gryadunov, D.A., Lapa, S.A. and Zasedatelev, A.S. (2005) Discrimination between perfect and mismatched duplexes with oligonucleotide gel microchips: Role of thermodynamic and kinetic effects during hybridization. Journal of Biomolecular Structure and Dynamics, 22, 725-734.
- Roberts, R.W. and Crothers, D.M. (1991) Specificity and stringency in DNA triplex formation. Proceedings of the National Academy of Sciences of the USA, 88, 9397-9401.
- Bonnet, G., Tyagi, S., Libchaber, A. and Kramer, F.R. (1999) Thermodynamic basis of the enhanced specificity of structured DNA probes. Proceedings of the National Academy of Sciences of the USA, 96, 6171-6176.doi:10.1073/pnas.96.11.6171
- Tsourkas, A., Behlke, M.A., Rose, S.D. and Bao, G. (2003) Hybridization kinetics and thermodynamics of molecular beacons. Nucleic Acids Research, 31, 1319-1330. doi:10.1093/nar/gkg212
- Livshits, M.A., Ivanov, I.B., Mirzabekov, A.D. and Florent’ev, V.L. (1992) DNA sequencing by hybridization with an oligonucleotide matrix (SHOM). The theory of DNA elution after hybridization. Molekuliarnaia Biologiia (Moskva), 26, 1298-1313.
- Dai, H., Meyer, M., Stepaniants, S., Ziman, M. and Stoughton, R. (2002) Use of hybridization kinetics for differentiating specific from non-specific binding to oligonucleotide microarrays. Nucleic Acids Research, 30, e86. doi:10.1093/nar/gnf085
- Bishop, J., Blair, S. and Chagovetz, A.M. (2006) A competitive kinetic model of nucleic acid surface hybridization in the presence of point mutants. Biophysical Journal, 90, 831-840. doi:10.1529/biophysj.105.072314
- Bishop, J., Chagovetz, A.M. and Blair, S. (2008) Kinetics of multiplex hybridization: Mechanisms and implications. Biophysical Journal, 94, 1726-1734.doi:10.1529/biophysj.107.121459
- Lucarelli, F., Marrazza, G. and Mascini, M. (2007) Design of an optimal allele-specific oligonucleotide probe for the efficient discrimination of a thermodynamically stable (G x T) mismatch. Analitica Chimica Acta, 603, 82-86. doi:10.1016/j.aca.2007.09.047
- Parinov, S., Barsky, V., Yershov, G., Kirillov, E., Timofeev, E., Belgovskiy, A. and Mirzabekov, A. (1996) DNA sequencing by hybridization to microchip octa and decanucleotides extended by stacked pentanucleotides. Nucleic Acids Research, 24, 2998-3004. doi:10.1093/nar/24.15.2998
- Pyshnyi, D.V., Lokhov, S.G., Podyminogin, M.A., Ivanova, E.M. and Zarytova, V.F. (2000) A new strategy of discrimination of a point mutation by tandem of short oligonucleotides. Nucleosides Nucleotides Nucleic Acids, 19, 1931-1941. doi:10.1080/15257770008045469
- Maldonado-Rodriguez, R. and Beattie, K.L. (2001) Analysis of nucleic acids by tandem hybridization on oligonucleotide microarrays. Methods in Molecular Biology, 170, 157-171.
- Pyshnyi, D.V., Goldberg, E.L. and Ivanova, E.M. (2003) Efficiency of coaxial stacking depends on the DNA duplex structure. Journal of Biomolecular Structure and Dynamics, 21, 459-468.
- Storhoff, J.J., Elghanian, R., Mucic, R.C., Mirkin, C.A. and Letsinger, R.L. (1998) One-pot colorimetric differentiation of polynucleotides with single base imperfections using gold nanoparticle probes. Journal of the American Chemical Society, 120, 1959-1964.doi:10.1021/ja972332i
- Dubertret, B., Calame, M. and Libchaber, A.J. (2001) Single-mismatch detection using gold-quenched fluorescent oligonucleotides. Nature Biotechnology, 19, 365-370. doi:10.1038/86762
- Harris, N.C. and Kiang, C.H. (2006) Defects can increase the melting temperature of DNA-nanoparticle assemblies. The Journal of Physical Chemistry B, 110, 16393-16396. doi:10.1021/jp062287d
- Ratilainen, T., Holmen, A., Tuite, E., Nielsen, P.E. and Norden, B. (2000) Thermodynamics of sequence-specific binding of PNA to DNA. Biochemistry, 39, 7781-7791. doi:10.1021/bi000039g
- Narayan, C.C. and Eric, T.K. (1995) Very high affinity DNA recognition by bicyclic and cross-linked oligonucleotides. Journal of the American Chemical Society, 117, 10434-10442. doi:10.1021/ja00147a004
- Wang, S., Friedman, A.E. and Kool, E.T. (1995) Origins of high sequence selectivity: A stopped-flow kinetics study of DNA/RNA hybridization by duplexand triplex-forming oligonucleotides. Biochemistry, 34, 9774-9784. doi:10.1021/bi00030a015
- Kutyavin, I.V., Afonina, I.A., Mills, A., Gorn, V.V., Lukhtanov, E.A., Belousov, E.S., Singer, M.J., Walburger, D.K., Lokhov, S.G., Gall, A.A., Dempcy, R., Reed, M.W., Meyer, R.B. and Hedgpeth, J. (2000) 3’-minor groove binder-DNA probes increase sequence specificity at PCR extension temperatures. Nucleic Acids Research, 28, 655-661. doi:10.1093/nar/28.2.655
- Abramov, M., Schepers, G., Van Aerschot, A., Van Hummelen, P. and Herdewijn, P. (2008) HNA and ANA high-affinity arrays for detections of DNA and RNA single-base mismatches. Biosensors and Bioelectronics, 23, 1728-1732. doi:10.1016/j.bios.2008.01.033
- Guo, Z., Liu, Q. and Smith, L.M. (1997) Enhanced discrimination of single nucleotide polymorphisms by artificial mismatch hybridization. Nature Biotechnology, 15, 331-335. doi:10.1038/nbt0497-331
- Burgner, D., D’Amato, M., Kwiatkowski, D.P. and Loakes, D. (2004) Improved allelic differentiation using sequence-specific oligonucleotide hybridization incorporating an additional base-analogue mismatch. Nucleosides Nucleotides Nucleic Acids, 23, 755-765. doi:10.1081/NCN-120039216
- Pyshnaya, I.A., Pyshnyi, D.V., Lomzov, A.A., Zarytova, V.F. and Ivanova, E.M. (2004) The influence of the non-nucleotide insert on the hybridization properties of oligonucleotides. Nucleosides Nucleotides Nucleic Acids, 23, 1065-1071. doi:10.1081/NCN-200026073
- Pyshnyi, D.V., Lomzov, A.A., Pyshnaya, I.A. and Ivanova, E.M. (2006) Hybridization of the bridged oligonucleotides with DNA: Thermodynamic and kinetic studies. Journal of Biomolecular Structure and Dynamics, 23, 567-580.
- Jacobsen, N., Bentzen, J., Meldgaard, M., Jakobsen, M.H., Fenger, M., Kauppinen, S. and Skouv, J. (2002) LNA-enhanced detection of single nucleotide polymorphisms in the apolipoprotein E. Nucleic Acids Research, 30, e100. doi:10.1093/nar/gnf099
- Jacobsen, N., Fenger, M., Bentzen, J., Rasmussen, S.L., Jakobsen, M.H., Fenstholt, J. and Skouv, J. (2002) Genotyping of the apolipoprotein B R3500Q mutation using immobilized locked nucleic acid capture probes. Clinical Chemistry, 48, 657-660.
- Seela, F., Peng, X. and Li, H. (2005) Base-pairing, tautomerism, and mismatch discrimination of 7-halogenated 7-deaza-2’-deoxyisoguanosine: Oligonucleotide duplexes with parallel and antiparallel chain orientation. Journal of the American Chemical Society, 127, 7739-7751. doi:10.1021/ja0425785
- You, Y., Moreira, B.G., Behlke, M.A. and Owczarzy, R. (2006) Design of LNA probes that improve mismatch discrimination. Nucleic Acids Research, 34, e60.doi:10.1093/nar/gkl175
- Lai, J.S. and Kool, E.T. (2004) Selective pairing of polyfluorinated DNA bases. Journal of the American Chemical Society, 126, 3040-3041. doi:10.1021/ja039571s
- Gao, J., Liu, H. and Kool, E.T. (2004) Expanded-size bases in naturally sized DNA: Evaluation of steric effects in Watson-Crick pairing. Journal of the American Chemical Society, 126, 11826-11831.doi:10.1021/ja048499a
- Liu, H., Gao, J. and Kool, E.T. (2005) Helix-forming properties of size-expanded DNA, an alternative four-base genetic form. Journal of the American Chemical Society, 127, 1396-1402. doi:10.1021/ja046305l
- Gong, J. and Sturla, S.J. (2007) A synthetic nucleoside probe that discerns a DNA adduct from unmodified DNA. Journal of the American Chemical Society, 129, 4882-4883. doi:10.1021/ja070688g
- Monia, B.P., Johnston, J.F., Ecker, D.J., Zounes, M.A., Lima, W.F. and Freier, S.M. (1992) Selective inhibition of mutant Ha-ras mRNA expression by antisense oligonucleotides. The Journal of Biological Chemistry, 267, 19954-19962.
- Hearst, J.E. (1988) A photochemical investigation of the dynamics of oligonucleotide hybridization. Annual Review of Physical Chemistry, 39, 291-315.doi:10.1146/annurev.pc.39.100188.001451
- Shortreed, M.R., Chang, S.B., Hong, D., Phillips, M., Campion, B., Tulpan, D.C., Andronescu, M., Condon, A., Hoos, H.H. and Smith, L.M. (2005) A thermodynamic approach to designing structure-free combinatorial DNA word sets. Nucleic Acids Research, 33, 4965-4977.doi:10.10Xar/gki812
- SantaLucia, J. Jr (1998) A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proceedings of the National Academy of Sciences of the USA, 95, 1460-1465.doi:10.1073/pnas.95.4.1460
- Allawi, H.T. and SantaLucia, J. Jr (1997) Thermodynamics and NMR of internal G.T mismatches in DNA. Biochemistry, 36, 10581-10594.doi:10.1021/bi962590c
- Allawi, H.T. and SantaLucia, J. Jr (1998) Nearest-neighbor thermodynamics of internal A.C mismatches in DNA: Sequence dependence and pH effects. Biochemistry, 37, 9435-9444. doi:10.1021/bi9803729
- Allawi, H.T. and SantaLucia, J. Jr (1998) Thermodynamics of internal C.T mismatches in DNA. Nucleic Acids Reseach, 26, 2694-2701. doi:10.1093/nar/26.11.2694
- Allawi, H.T. and SantaLucia, J. Jr (1998) Nearest neighbor thermodynamic parameters for internal G.A mismatches in DNA. Biochemistry, 37, 2170-2179.doi:10.1021/bi9724873
- Peyret, N., Seneviratne, P.A., Allawi, H.T. and SantaLucia, J. Jr (1999) Nearest-neighbor thermodynamics and NMR of DNA sequences with internal A.A, C.C, G.G, and T.T mismatches. Biochemistry, 38, 3468-3477. doi:10.1021/bi9825091
- Vessman, J., Stefan, R.I., Van Staden, J.F., Danzer, K., Lindner, W., Burns, D.T., Fajgelj, A. and Muller, H. (2001) Selectivity in analytical chemistry. Pure and Applied Chemistry, 73, 1381-1386.doi:10.1351/pac200173081381
- Von Hippel, P.H. and Berg, O.G. (1986) On the specificity of DNA-protein interactions. Proceedings of the National Academy of Sciences of the USA, 83, 1608-1612.doi:10.1073/pnas.83.6.1608
- SantaLucia, J. Jr and Hicks, D. (2004) The thermodynamics of DNA structural motifs. Annual Review of Biophysics and Biomolecular Structure, 33, 415-440.doi:10.1146/annurev.biophys.32.110601.141800
- Urakawa, H., El, F.S., Smidt, H., Smoot, J.C., Tribou, E.H., Kelly, J.J., Noble, P.A. and Stahl, D.A. (2003) Optimization of single-base-pair mismatch discrimination in oligonucleotide microarrays. Applied and Environmental Microbiology, 69, 2848-2856.doi:10.1128/AEM.69.5.2848-2856.2003
- Demidov, V.V. and Frank-Kamenetskii, M.D. (2004) Two sides of the coin: Affinity and specificity of nucleic acid interactions. Trends in Biochemical Sciences, 29, 62-71. doi:10.1016/j.tibs.2003.12.007
- Barnes, T.W. III and Turner, D.H. (2001) C5-(1-propynyl)-2’-deoxy-pyrimidines enhance mismatch penalties of DNA:RNA duplex formation. Biochemistry, 40, 12738-12745. doi:10.1021/bi011033+
- Peng, X., Li, H. and Seela, F. (2006) pH-Dependent mismatch discrimination of oligonucleotide duplexes containing 2’-deoxytubercidin and 2- or 7-substituted derivatives: Protonated base pairs formed between 7-deazapurines and cytosine. Nucleic Acids Research, 34, 5987-6000.
APPENDIX
S1. Analysis of the Selectivity Function
S1.1. Function 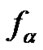 tends to 1 in the range of temperatures
tends to 1 in the range of temperatures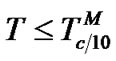 :
: 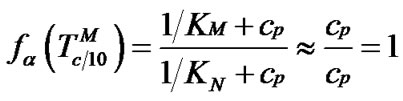
This is true if 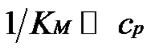 and
and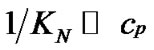 , since
, since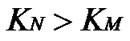 , one can consider only
, one can consider only 
 , then
, then

S1.2. Function 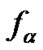 tends to 2 when
tends to 2 when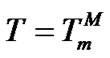 :
:
 due to
due to 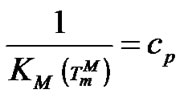
This is true if , that is observed if
, that is observed if 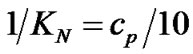 and corresponds to temperature
and corresponds to temperature 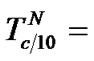
 .Thus, if
.Thus, if , inequality is fulfilled.
, inequality is fulfilled.
S1.3. Function 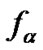 tends to
tends to 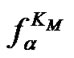 in the range of temperatures
in the range of temperatures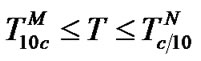 :
:
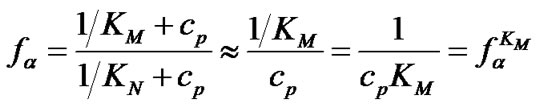
This is true if 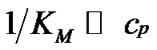 and
and , that corresponds to the range
, that corresponds to the range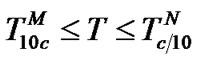 .
.
Thus, if

inequality is fulfilled.
S1.4. Function  tends to
tends to 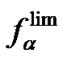 in the range of high temperatures
in the range of high temperatures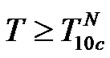 :
:

This is true if  and
and , since
, since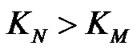 , one can consider only
, one can consider only , Let
, Let , then
, then 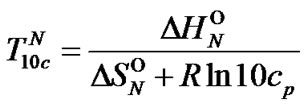
S1.5. Quantitative evaluation of maximum selectivity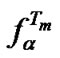 :
:
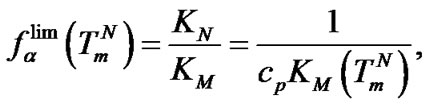

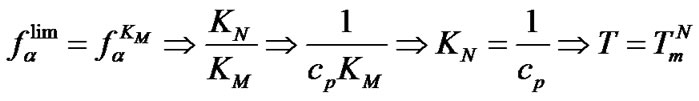
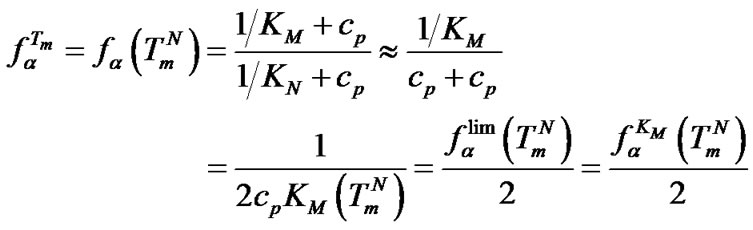

S2. Dependence of the Maximum of the Selectivity Function on the Probe Concentration

S3. Dependence of the Maximum of the Selectivity Function on the Probe Length

S4. Dependence of the Maximum of the Selectivity Function on the Type of a Mismatch

S5. Linear Dependence Logarithm of Limit Selectivity Function
Within temperature range from 0˚C to 100˚C the function 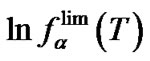 can be described by linear dependence with good accuracy. So we can propose:
can be described by linear dependence with good accuracy. So we can propose:

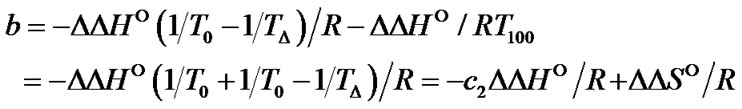
In
where 

