Open Journal of Statistics
Vol.1 No.1(2011), Article ID:4697,14 pages DOI:10.4236/ojs.2011.11001
Modified Cp Criterion for Optimizing Ridge and Smooth Parameters in the MGR Estimator for the Nonparametric GMANOVA Model
Department of Mathematics, Graduate School of Science, Hiroshima University
1-3-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8626, Japan
E-mail: d093481@hiroshima-u.ac.jp
Shrinkage estimator, Varying coefficient model
Received March 18, 2011; revised April 2, 2011; accepted April 12, 2011
Keywords: Generalized ridge regression, GMANOVA model, Mallows'  statistic, Non-iterative estimator,
statistic, Non-iterative estimator,
Abstract
Longitudinal trends of observations can be estimated using the generalized multivariate analysis of variance (GMANOVA) model proposed by [10]. In the present paper, we consider estimating the trends nonparametrically using known basis functions. Then, as in nonparametric regression, an overfitting problem occurs. [13] showed that the GMANOVA model is equivalent to the varying coefficient model with non-longitudinal covariates. Hence, as in the case of the ordinary linear regression model, when the number of covariates becomes large, the estimator of the varying coefficient becomes unstable. In the present paper, we avoid the overfitting problem and the instability problem by applying the concept behind penalized smoothing spline regression and multivariate generalized ridge regression. In addition, we propose two criteria to optimize hyper parameters, namely, a smoothing parameter and ridge parameters. Finally, we compare the ordinary least square estimator and the new estimator.
1. Introduction
We consider the generalized multivariate analysis of variance (GMANOVA) model with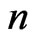 observations of
observations of 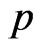 -dimensional vectors of response variables. This model was proposed by [10]. Let
-dimensional vectors of response variables. This model was proposed by [10]. Let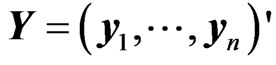 ,
, 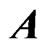 ,
, 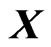 and
and 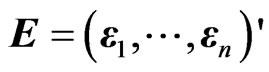 be an
be an 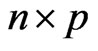 matrix of response variables, an
matrix of response variables, an 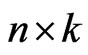 matrix of non-stochastic centerized between-individual explanatory variables (i.e.,
matrix of non-stochastic centerized between-individual explanatory variables (i.e.,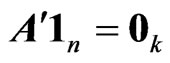 )
)
of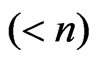
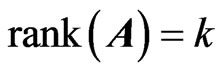 , a
, a 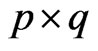 matrix of non-stochastic within-individual explanatory variables of
matrix of non-stochastic within-individual explanatory variables of 
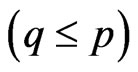 , and an
, and an 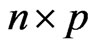 matrix of error variables, respectively, where
matrix of error variables, respectively, where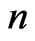 is the sample size,
is the sample size, 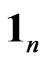 is an
is an 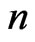 -dimensional vector of ones and
-dimensional vector of ones and 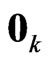 is a
is a  -dimensional vector of zeros. Then, the GMANOVA model is expressed as
-dimensional vector of zeros. Then, the GMANOVA model is expressed as

where 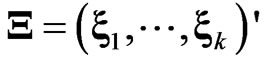 is a
is a 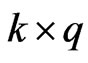 unknown regression coefficient matrix an
unknown regression coefficient matrix an  is
is 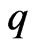 -dimensional unknown vector. We assume that
-dimensional unknown vector. We assume that 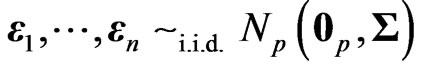 where
where  is a
is a 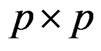 unknown covariance matrix of
unknown covariance matrix of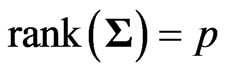 . Then we can express the GMANOVA model as
. Then we can express the GMANOVA model as
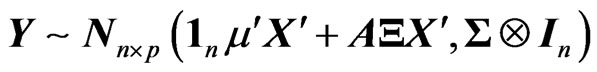
Let 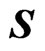 be an unbiased estimator of the unknown covariance matrix
be an unbiased estimator of the unknown covariance matrix 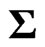 that is given by
that is given by
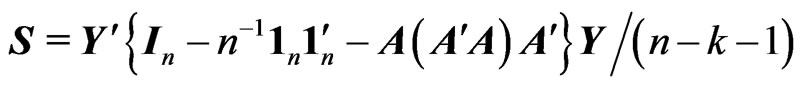
Then, the maximum likelihood (ML) estimators of 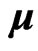 and
and are given by
are given by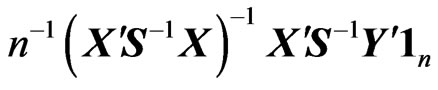 and
and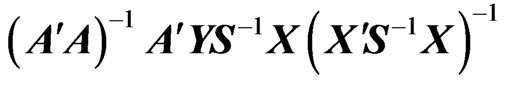 , respectively. The ML estimators are the unbiased and asymptotically efficiency estimators of
, respectively. The ML estimators are the unbiased and asymptotically efficiency estimators of 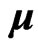 and
and .
.
In the GMANOVA model, 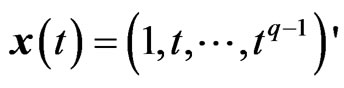 ,
, 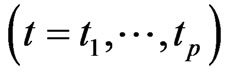 is often used as the
is often used as the 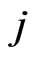 th row vector of
th row vector of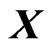 . Then, we estimate the longitudinal trends of
. Then, we estimate the longitudinal trends of  using
using 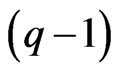 -polynomial curves. However, occasionally, the polynomial curve cannot thoroughly express flexible longitudinal trends. Hence, we consider estimating the longitudinal trends nonparametrically in the same manner as [11] and [5], i.e., we use the known basis function as
-polynomial curves. However, occasionally, the polynomial curve cannot thoroughly express flexible longitudinal trends. Hence, we consider estimating the longitudinal trends nonparametrically in the same manner as [11] and [5], i.e., we use the known basis function as  and assume that
and assume that 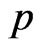 is large. In the present paper, we refer to the GMANOVA model with
is large. In the present paper, we refer to the GMANOVA model with 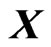 obtained from the basis function as the nonparametric GMANOVA model. In the nonparametric GMANOVA model, it is well known that the ML estimators become unstable because
obtained from the basis function as the nonparametric GMANOVA model. In the nonparametric GMANOVA model, it is well known that the ML estimators become unstable because 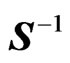 becomes unstable when
becomes unstable when 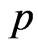 is large. Thus, we deal with the least square (LS) estimators of
is large. Thus, we deal with the least square (LS) estimators of 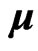 and
and , which are obtained by minimizing
, which are obtained by minimizing 
 . Then, the LS estimators of
. Then, the LS estimators of 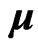 and
and  are obtained by
are obtained by  and
and
 respectively. Note that
respectively. Note that 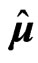 does not depend on
does not depend on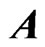 . The LS estimators are simple and unbiased estimators of
. The LS estimators are simple and unbiased estimators of 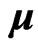 and
and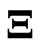 . However, as well as ordinary nonparametric regression model, the LS estimators cause an overfitting problem when we use basis functions to estimate the longitudinal trends nonparametrically. In order to avoid the overfitting problem, we use
. However, as well as ordinary nonparametric regression model, the LS estimators cause an overfitting problem when we use basis functions to estimate the longitudinal trends nonparametrically. In order to avoid the overfitting problem, we use 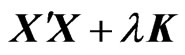 instead of
instead of 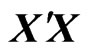 as the penalized smoothing spline regression (see, e.g., [2]), where
as the penalized smoothing spline regression (see, e.g., [2]), where 
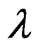 is a smoothing parameter and
is a smoothing parameter and  is a
is a 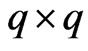 known penalty matrix.
known penalty matrix.
Let , and let
, and let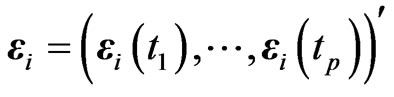 . Then, the GMANOVA model can be expressed as
. Then, the GMANOVA model can be expressed as
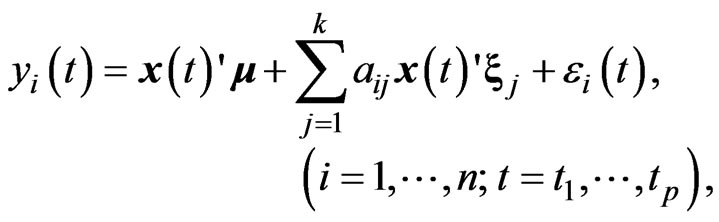
where 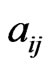 is the
is the 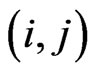 th element of
th element of . This expression indicates that the GMANOVA model is equivalent to the varying coefficient model with non-longitudinal covariates [13], i.e.,
. This expression indicates that the GMANOVA model is equivalent to the varying coefficient model with non-longitudinal covariates [13], i.e.,
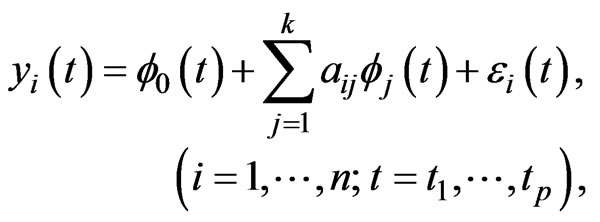 (4)
(4)
where  and
and ,
,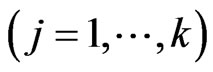 . Hence, estimating the longitudinal trends in the GMANOVA model nonparametrically is equivalent to estimating the varying coefficients
. Hence, estimating the longitudinal trends in the GMANOVA model nonparametrically is equivalent to estimating the varying coefficients ,
, 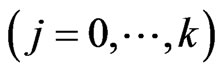 nonparametrically. However, when multicollinearity occurs in
nonparametrically. However, when multicollinearity occurs in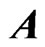 , the estimate of
, the estimate of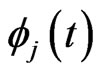 ,
, 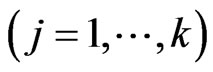 becomes unstable, as does the ordinary LS estimator of regression coefficient, because the variance of an estimator of
becomes unstable, as does the ordinary LS estimator of regression coefficient, because the variance of an estimator of 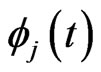 becomes large. Hence, we avoid the multicollinearity problem in
becomes large. Hence, we avoid the multicollinearity problem in 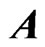 by the ridge regression.
by the ridge regression.
When 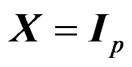 and
and 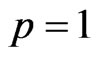 in the model (1), [4] proposed a ridge regression. This estimator is generally defined by adding
in the model (1), [4] proposed a ridge regression. This estimator is generally defined by adding 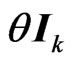 to
to  in (3), where
in (3), where  is referred to as a ridge parameter. Since the ridge estimator changes with
is referred to as a ridge parameter. Since the ridge estimator changes with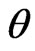 , optimization of
, optimization of 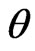 is very important. One method for optimizing
is very important. One method for optimizing 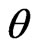 is minimizing the
is minimizing the  criterion proposed by [7,8] in the univariate linear regression model (for multivariate case, see e.g., [15]). For the case in which
criterion proposed by [7,8] in the univariate linear regression model (for multivariate case, see e.g., [15]). For the case in which 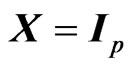 and
and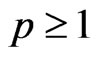 , [17] proposed the
, [17] proposed the 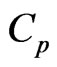 and its bias-corrected
and its bias-corrected  (modified
(modified ;
;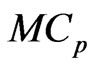 ) criteria for optimizing the ridge parameter. However, an optimal
) criteria for optimizing the ridge parameter. However, an optimal 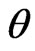 cannot be obtained without an iterative computational algorithm because an optimal
cannot be obtained without an iterative computational algorithm because an optimal 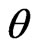 cannot be obtained in closed form.
cannot be obtained in closed form.
On the other hand, [4] also proposed a generalized ridge (GR) regression in the univariate linear regression model, i.e., the model (1) with 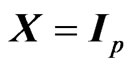 and
and , simultaneously with the ridge regression. The GR estimator is defined not by a single ridge parameter, but rather by multiple ridge parameters
, simultaneously with the ridge regression. The GR estimator is defined not by a single ridge parameter, but rather by multiple ridge parameters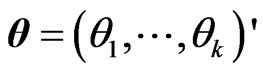 ,
,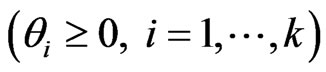 . Then, several authors proposed a non-iterative GR estimator (see, e.g., [6]). [18] proposed a GR regression in the multivariate linear regression model, i.e., the model (1) with
. Then, several authors proposed a non-iterative GR estimator (see, e.g., [6]). [18] proposed a GR regression in the multivariate linear regression model, i.e., the model (1) with 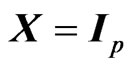 and
and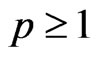 . We call this generalized ridge regression the multivariate GR (MGR) regression. They also proposed the
. We call this generalized ridge regression the multivariate GR (MGR) regression. They also proposed the 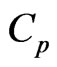 and
and 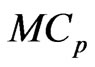 criteria for optimizing ridge parameters
criteria for optimizing ridge parameters 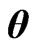 in the MGR regression. They showed that the optimized
in the MGR regression. They showed that the optimized 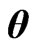 by minimizing two criteria are obtained in closed form. [9] proposed non-iterative MGR estimators by extending non-iterative GR estimators. Several computational tasks are required in estimating
by minimizing two criteria are obtained in closed form. [9] proposed non-iterative MGR estimators by extending non-iterative GR estimators. Several computational tasks are required in estimating 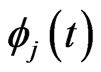 nonparametrically because we determine the optimal
nonparametrically because we determine the optimal  and the number of basis functions simultaneously. Fortunately, [18] reported that the performance of the MGR regression is the almost same as that of the multivariate ridge regression. Hence, we use the MGR regression in order to avoid the multicollinearity problem that occurs in
and the number of basis functions simultaneously. Fortunately, [18] reported that the performance of the MGR regression is the almost same as that of the multivariate ridge regression. Hence, we use the MGR regression in order to avoid the multicollinearity problem that occurs in 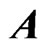 in order to reduce the number of computational tasks.
in order to reduce the number of computational tasks.
The remainder of the present paper is organized as follows: In Section 2, we propose new estimators using the concept of the penalized smoothing spline regression and the MGR regression. In Section 3, we show the target mean squared error (MSE) of a predicted value of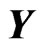 . We then propose the
. We then propose the  and
and 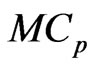 criteria to optimize ridge parameters and smoothing parameter in the new estimator. Using these criteria, we show that the optimized ridge parameters are obtained in closed form under the fixed
criteria to optimize ridge parameters and smoothing parameter in the new estimator. Using these criteria, we show that the optimized ridge parameters are obtained in closed form under the fixed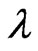 . We also show the magnitude relationship between the optimized ridge parameters. In Section 4, we compare the LS estimator in (3) with the proposed estimator through numerical studies. In Section 5, we present our conclusions.
. We also show the magnitude relationship between the optimized ridge parameters. In Section 4, we compare the LS estimator in (3) with the proposed estimator through numerical studies. In Section 5, we present our conclusions.
2. The New Estimators
In the model (1), we consider estimating the longitudinal trends nonparametrically by using basis functions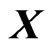 . Then, we consider the following estimators in order to avoid the overfitting problem in the nonparametric GMANOVA model,
. Then, we consider the following estimators in order to avoid the overfitting problem in the nonparametric GMANOVA model, 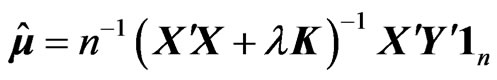 and
and
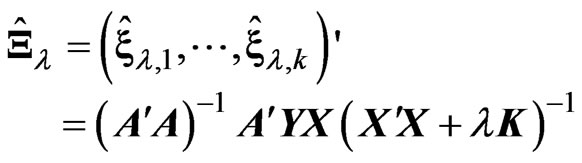 (5)
(5)
where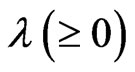 is a smoothing parameter and
is a smoothing parameter and  is a
is a 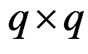 known penalty matrix. In this estimator, we must determine
known penalty matrix. In this estimator, we must determine 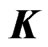 before using this estimator. Since
before using this estimator. Since 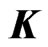 is usually set as some nonnegative definite matrix, we assume that
is usually set as some nonnegative definite matrix, we assume that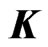 is a nonnegative definite matrix. If
is a nonnegative definite matrix. If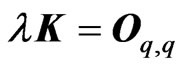 , where
, where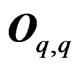 is a
is a 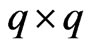 matrix of zeros, then this estimator corresponds to the LS estimators
matrix of zeros, then this estimator corresponds to the LS estimators 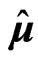 and
and 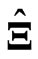 in (1). Note that this estimator controls the smoothness of each estimated curve
in (1). Note that this estimator controls the smoothness of each estimated curve 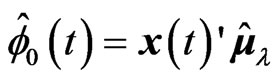 and
and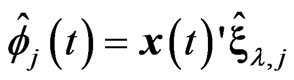 ,
,  through only one parameter
through only one parameter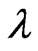 . When we use this estimator, we need to optimize the parameter
. When we use this estimator, we need to optimize the parameter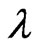 because this estimator changes with
because this estimator changes with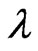 .
.
If multicollinearity occurs in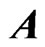 , then the LS estimator
, then the LS estimator 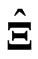 in (1) and the proposed estimator
in (1) and the proposed estimator 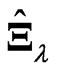 in (5) are not good estimators in the sense of having large variance. Note that neither the LS estimator
in (5) are not good estimators in the sense of having large variance. Note that neither the LS estimator 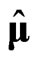 nor the proposed estimator
nor the proposed estimator 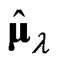 depend on
depend on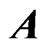 . Hence, we avoid the multicollinearity problem for estimating
. Hence, we avoid the multicollinearity problem for estimating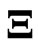 . Multicollinearity often occurs when
. Multicollinearity often occurs when 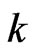 becomes large. Using the following estimator, the multicollinearity problem in
becomes large. Using the following estimator, the multicollinearity problem in 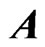 can be avoided,
can be avoided,
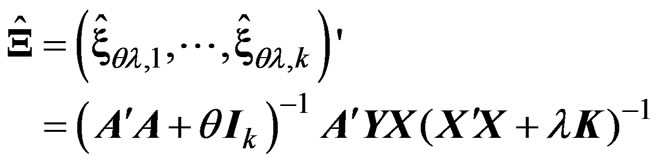 (6)
(6)
where 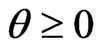 is a ridge parameter. This estimator with
is a ridge parameter. This estimator with 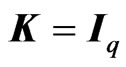 corresponds to the estimator of [16]. If
corresponds to the estimator of [16]. If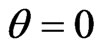 , then this estimator corresponds to the estimator in (5). Note that
, then this estimator corresponds to the estimator in (5). Note that 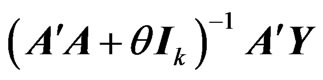 in this estimator corresponds to the ridge estimator for a multivariate linear model [17]. In this estimator, we need to optimize
in this estimator corresponds to the ridge estimator for a multivariate linear model [17]. In this estimator, we need to optimize 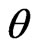 and
and 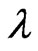 because this estimator changes with these parameters. However, we cannot obtain the optimized
because this estimator changes with these parameters. However, we cannot obtain the optimized 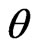 and
and  in closed form. Thus, we need to use an iterative computational algorithm to optimize two parameters. From another point of view, this estimator controls the smoothness of each estimated curve
in closed form. Thus, we need to use an iterative computational algorithm to optimize two parameters. From another point of view, this estimator controls the smoothness of each estimated curve ,
,  through only one parameter
through only one parameter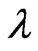 . Hence, this estimator is not a well fitting curve when the smoothnesses of the true curves differ.
. Hence, this estimator is not a well fitting curve when the smoothnesses of the true curves differ.
Hence, we apply the concept of the MGR estimator [18] to  in order to obtain the optimized ridge parameter in closed form. Here, we derive the MGR estimator for the nonparametric GMANOVA model as follows:
in order to obtain the optimized ridge parameter in closed form. Here, we derive the MGR estimator for the nonparametric GMANOVA model as follows:
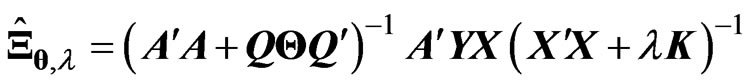 (7)
(7)
where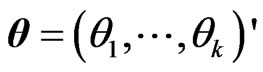 ,
,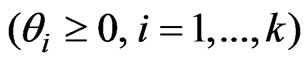 is also a ridge parameter,
is also a ridge parameter, 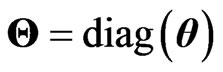 , and
, and 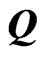 is the
is the 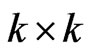 orthogonal matrix that diagonalizes
orthogonal matrix that diagonalizes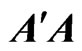 , i.e.,
, i.e., 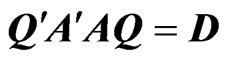 where
where 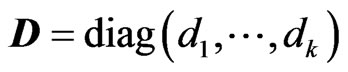 and
and 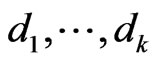
![]()
![]() are eigenvalues of
are eigenvalues of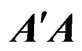 . It is clearly that
. It is clearly that ,
,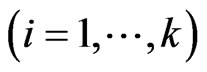 . In this estimator, since
. In this estimator, since 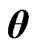 shrinks the estimators of
shrinks the estimators of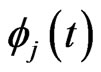 ,
, 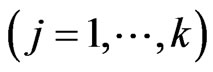 to 0, we can regard
to 0, we can regard 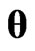 as controlling the smoothness of
as controlling the smoothness of . Therefore, in this estimator, rough smoothness of the estimated curves is controlled by
. Therefore, in this estimator, rough smoothness of the estimated curves is controlled by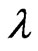 , and each smoothness of
, and each smoothness of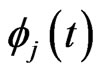 ,
, 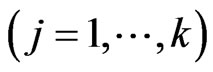 is controlled by
is controlled by .
.
Clearly, 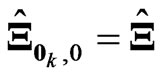 and
and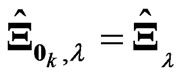 . The
. The  with
with 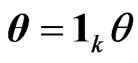 for some
for some 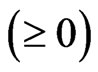
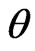 corresponds to
corresponds to 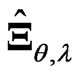 in (6). Thus, the estimator
in (6). Thus, the estimator 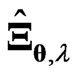 includes these estimators. The estimator
includes these estimators. The estimator 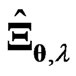 is more flexible than these estimators
is more flexible than these estimators 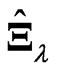 and
and 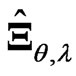 because
because 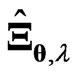 has
has 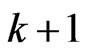 parameters and
parameters and 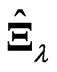 or
or 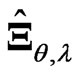 has only one or two parameters. Hence, we consider
has only one or two parameters. Hence, we consider 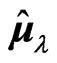 and
and  in estimating the longitudinal trends or the varying coefficient curve, while avoiding the overfitting and multicollinearity problems in the nonparametric GMANOVA model. When
in estimating the longitudinal trends or the varying coefficient curve, while avoiding the overfitting and multicollinearity problems in the nonparametric GMANOVA model. When 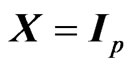 and
and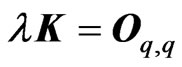 ,
, 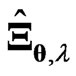 corresponds to the MGR estimator in [18].
corresponds to the MGR estimator in [18].
3. Main Results
3.1. Target MSE
In order to define the MSE of the predicted value of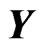 , we prepare the following discrepancy function for measuring the distance between
, we prepare the following discrepancy function for measuring the distance between 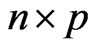 matrices
matrices  and
and
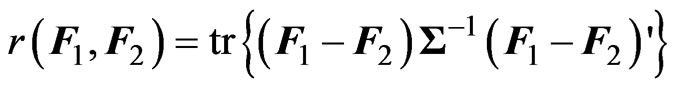 :
:
Since 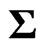 is an unknown covariance matrix, we use the unbiased estimator
is an unknown covariance matrix, we use the unbiased estimator 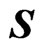 in (2) instead of
in (2) instead of 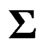 to estimate
to estimate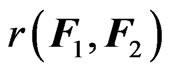 . Hence, we estimate
. Hence, we estimate 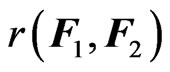 using the following sample discrepancy function:
using the following sample discrepancy function:
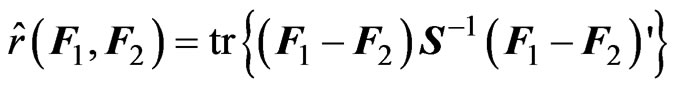 (8)
(8)
These two functions, 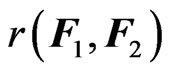 and
and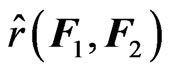 , correspond to the summation of the Mahalanobis distance and the sample Mahalanobis distance between the rows of
, correspond to the summation of the Mahalanobis distance and the sample Mahalanobis distance between the rows of 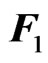 and
and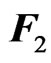 , respectively. Clearly,
, respectively. Clearly, 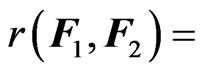
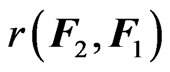 and
and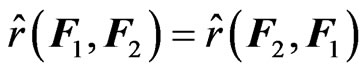 . Through simple calculation, we obtain the following properties:
. Through simple calculation, we obtain the following properties:
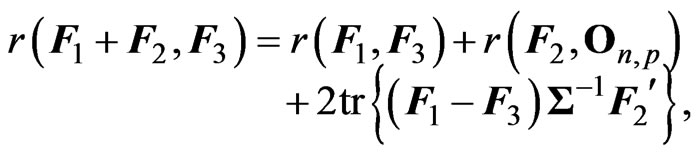

for any  matrices
matrices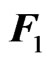 ,
, 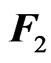 and
and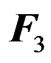 , Using the discrepancy function
, Using the discrepancy function , the MSE of the predicted value of
, the MSE of the predicted value of 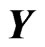 is defined as
is defined as
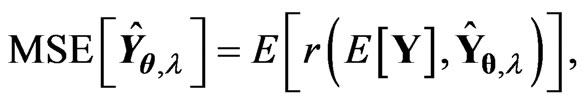 (9)
(9)
where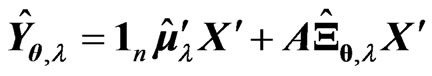 , which is the predicted value of
, which is the predicted value of 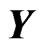 when we use
when we use 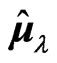 and
and  in (7). In the present paper, we regard
in (7). In the present paper, we regard  and
and 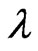 making the MSE the smallest as the principle optimum. However, we cannot use the MSE in (9) in actual application because this MSE includes unknown parameters. Hence, we must estimate (9) in order to estimate the optimum
making the MSE the smallest as the principle optimum. However, we cannot use the MSE in (9) in actual application because this MSE includes unknown parameters. Hence, we must estimate (9) in order to estimate the optimum 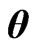 and
and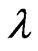 .
.
3.2. The 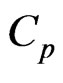 and
and 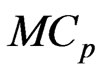 Criteria
Criteria
Let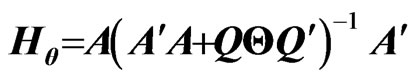 and
and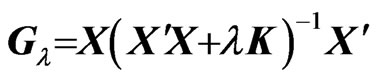 . Note that
. Note that . Hence, we obtain
. Hence, we obtain
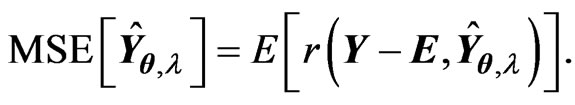
From the properties of the function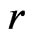 and using
and using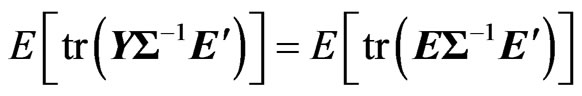 , since
, since  is a nonstochastic variable and
is a nonstochastic variable and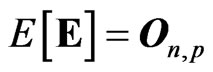 , and
, and 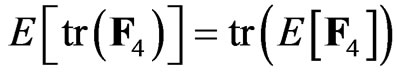 for any square matrix
for any square matrix , we obtain
, we obtain

Note that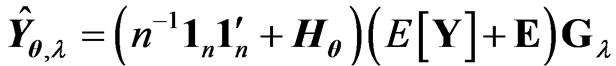 .Thus, we can calculate
.Thus, we can calculate 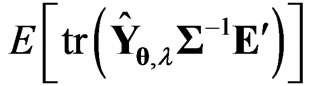 as follows:
as follows:
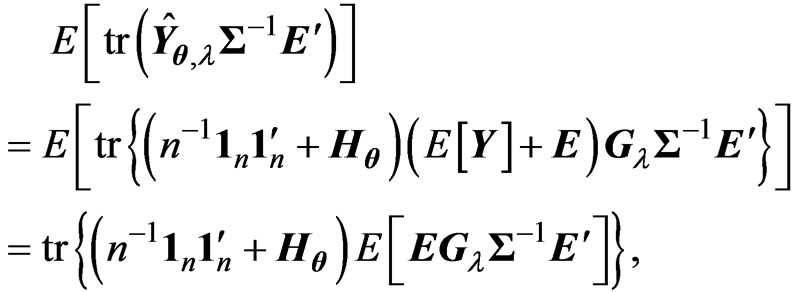
because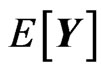 ,
, 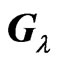 and
and 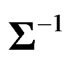 are non-stochastic variables. For calculating the expectations in the MSE, we prove the following lemma.
are non-stochastic variables. For calculating the expectations in the MSE, we prove the following lemma.
Lemma 3.1. For any 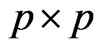 non-stochastic matrix
non-stochastic matrix , we obtain
, we obtain .
.
proof. Since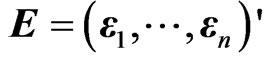 , we obtain the
, we obtain the 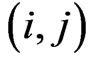 th element of
th element of  as
as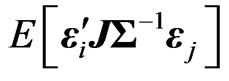 ,
, 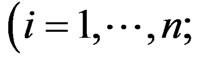
 . We obtain
. We obtain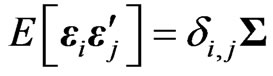 because
because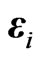
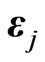 for any
for any 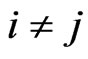 and
and 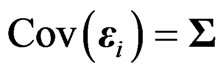 for any
for any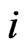 , where
, where 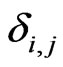 is defined as
is defined as 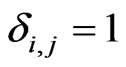 if
if 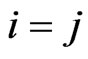 and
and 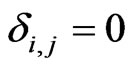 if
if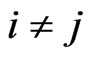 . Hence we obtain
. Hence we obtain 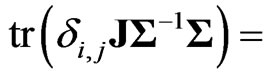
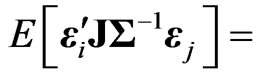
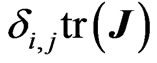 . This result means that
. This result means that 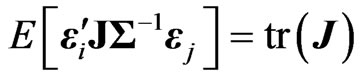 if
if 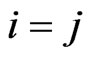 and
and  if
if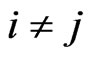 . Thus, the lemma is proven.
. Thus, the lemma is proven.
Using this lemma, we obtain 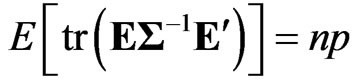 and
and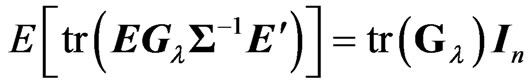 . Hence, we obtain
. Hence, we obtain
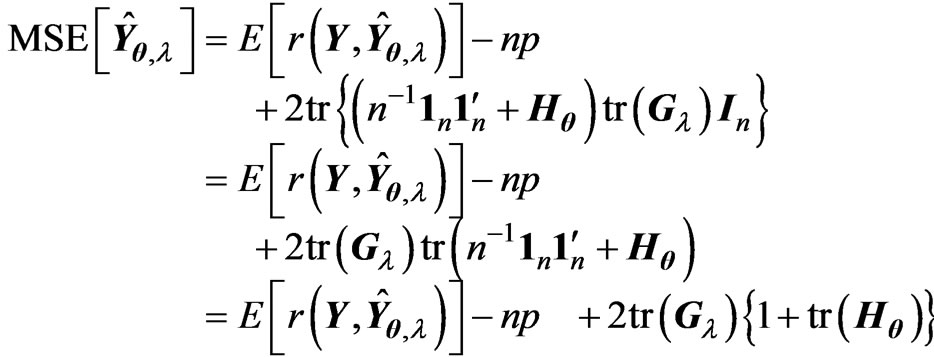
By replacing 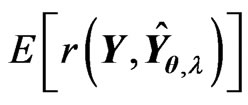 with
with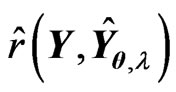 , we can propose the instinctive estimator of MSE, referred to as the
, we can propose the instinctive estimator of MSE, referred to as the 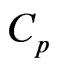 criterion, as follows:
criterion, as follows:
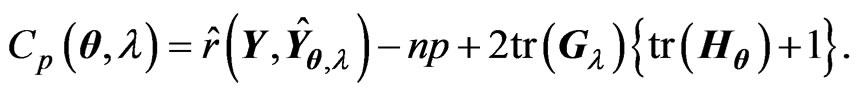 (10)
(10)
When we use this criterion, we optimize the ridge parameter  and the smoothing parameter
and the smoothing parameter 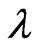 by the following algorithm:
by the following algorithm:
1) We obtain , where
, where 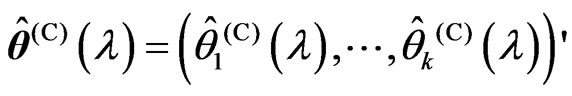
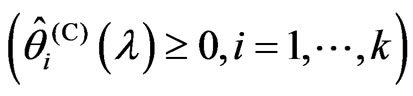 if
if 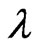 is given.
is given.
2) We obtain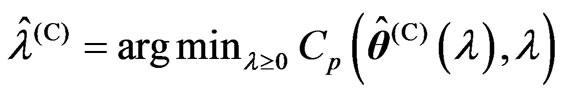 .
.
3) We obtain , where
, where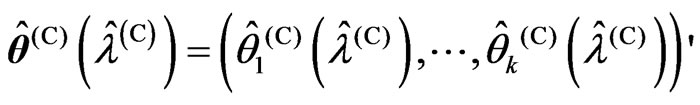 ,
,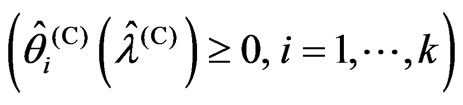 under fixed
under fixed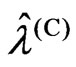 .
.
4) We optimize the ridge parameter and the smoothing parameter as 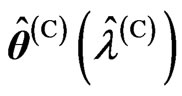 and
and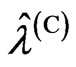 , respectively.
, respectively.
Note that this  criterion corresponds to that in [18] when
criterion corresponds to that in [18] when 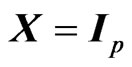 and
and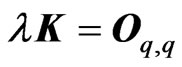 .
.
There is some bias between the MSE in (9) and the 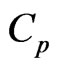 criterion in (10) because the
criterion in (10) because the 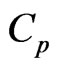 criterion is obtained by replacing
criterion is obtained by replacing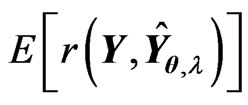 in the MSE with
in the MSE with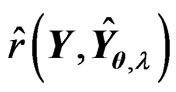 . Generally, when the sample size
. Generally, when the sample size 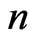 is small or the number of explanatory variables
is small or the number of explanatory variables 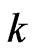 is large, this bias becomes large. Then, we cannot obtain the higher-accuracy estimation of the optimum parameters because we cannot obtain the higher-accuracy estimation of MSE of
is large, this bias becomes large. Then, we cannot obtain the higher-accuracy estimation of the optimum parameters because we cannot obtain the higher-accuracy estimation of MSE of 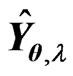 in (9). Hence, we correct the bias between
in (9). Hence, we correct the bias between  and the
and the 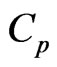 criterion. To correct the bias, we assume
criterion. To correct the bias, we assume .
.
Let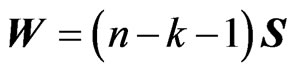 and
and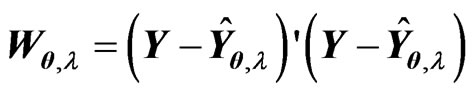 .
.
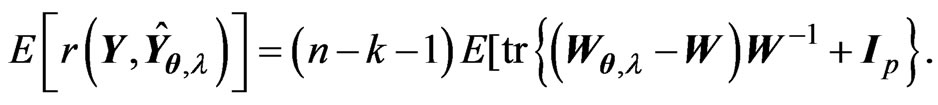
Note that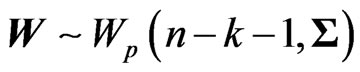 and
and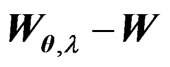
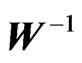 because
because  and
and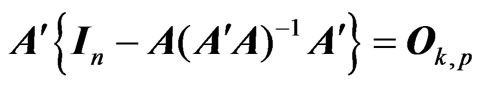 . Then, we obtain Since
. Then, we obtain Since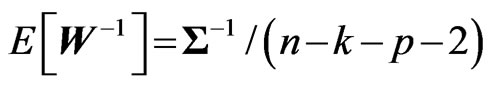 ,
,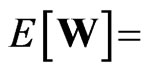
 (see, e.g., [14]) and
(see, e.g., [14]) and 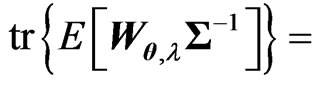
 , we obtain
, we obtain
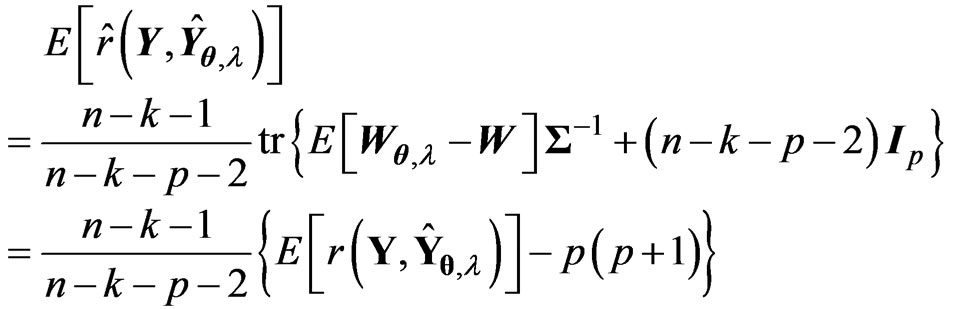
Therefore, we obtain the unbiased estimator for 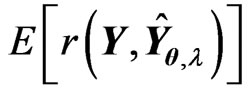 as
as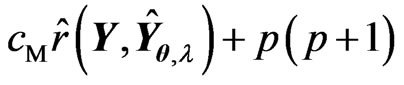 , where
, where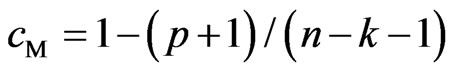 . This implies that the bias corrected
. This implies that the bias corrected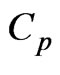 criterion, denoted as
criterion, denoted as 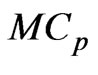 (modified
(modified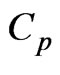 ) criterion, is obtained by
) criterion, is obtained by
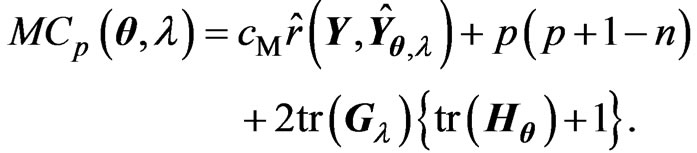 (11)
(11)
As in the case of using the , we optimize
, we optimize  and
and 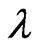 using this criterion as follows:
using this criterion as follows:
1) We obtain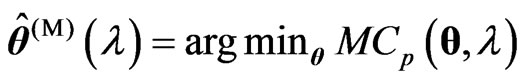 , where
, where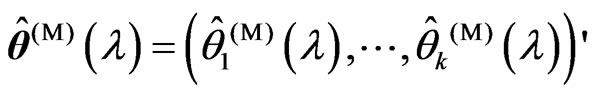 ,
,
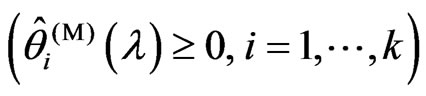 if
if 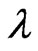 is given.
is given.
2) We obtain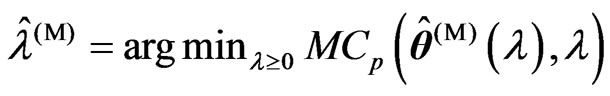 .
.
3) We obtain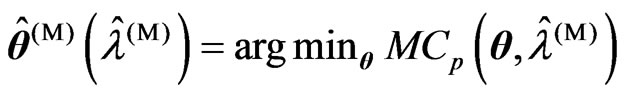 , where
, where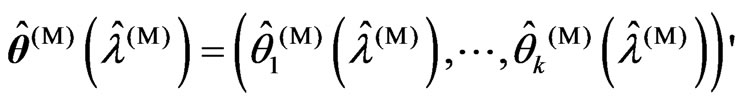 ,
, 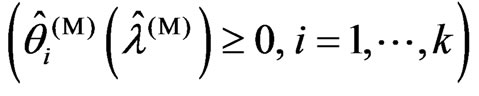 under fixed
under fixed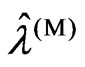 .
.
4) We optimize the ridge parameter and the smoothing parameter as 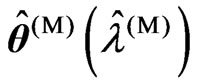 and
and 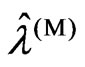 , respectively.
, respectively.
Note that the 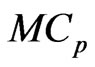 criterion corresponds to that in [18] when
criterion corresponds to that in [18] when 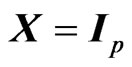 and
and . The
. The  criterion completely omits the bias between the MSE of
criterion completely omits the bias between the MSE of 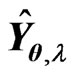 in (9) and the
in (9) and the  criterion in (10) by using a number of constant terms
criterion in (10) by using a number of constant terms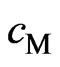 and
and . If
. If 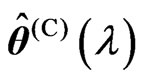 and
and 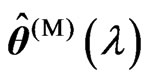 can be expressed in closed form for any fixed
can be expressed in closed form for any fixed , we do not need the above iterative computational algorithm.
, we do not need the above iterative computational algorithm.
3.3. Optimizations using the 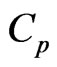 and
and Criteria
Criteria
Using the generalized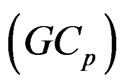
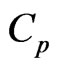 criterion, which is given in (14), we can express the
criterion, which is given in (14), we can express the  and
and 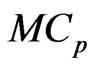 criteria as follows:
criteria as follows:
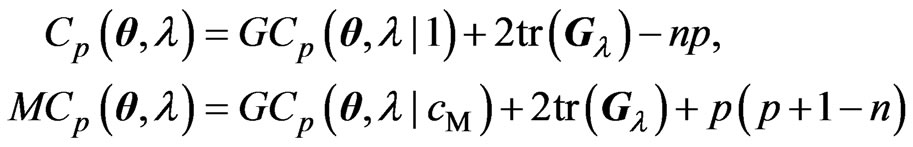
Note that the terms with respect to 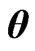 in the
in the 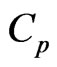 and
and  criteria correspond to
criteria correspond to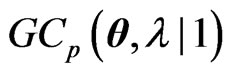 and
and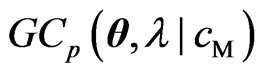 , respectively. Hence, we consider obtaining the optimum
, respectively. Hence, we consider obtaining the optimum 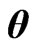 by minimizing the
by minimizing the 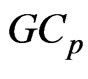 criterion. From Theorem A, the optimum
criterion. From Theorem A, the optimum 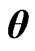 is obtained in closed form as (15). Using the closed form in (15), we obtain
is obtained in closed form as (15). Using the closed form in (15), we obtain 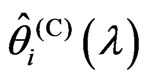 and
and 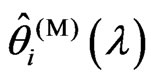 for each
for each 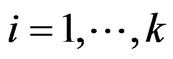 and any fixed
and any fixed 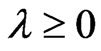 as follows:
as follows:
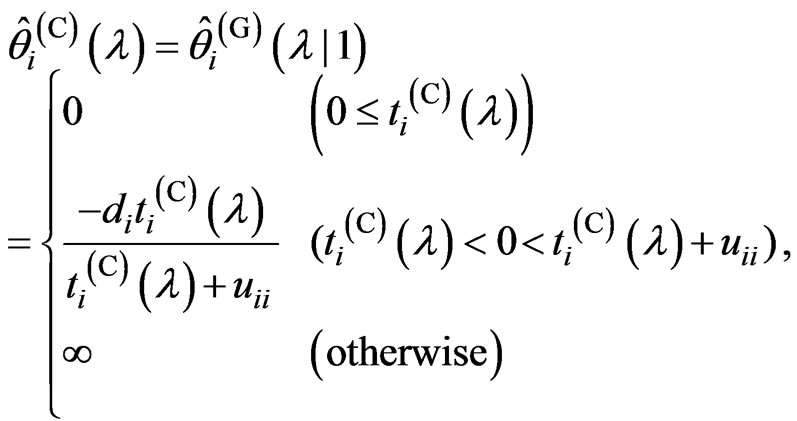 (12)
(12)
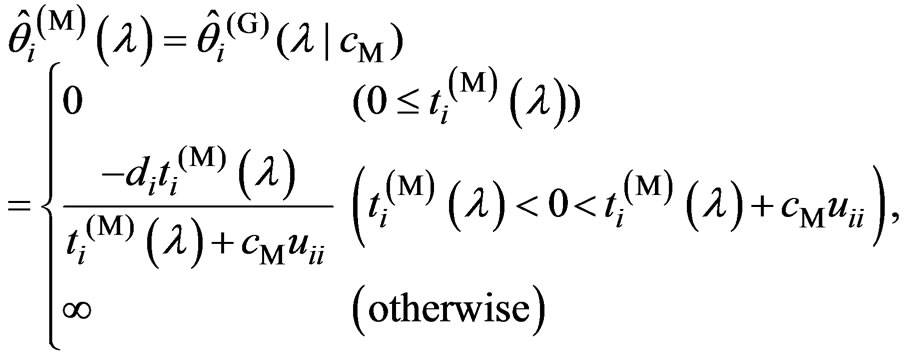 (13)
(13)
where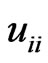 and
and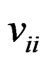 are the
are the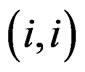 th elements of
th elements of![]() and
and![]() ,respectively,
,respectively,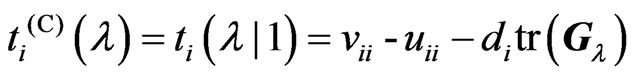 and
and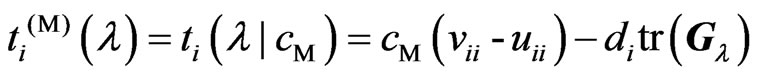 . Note that
. Note that  and
and 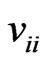 vary with
vary with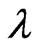 . Since
. Since  and
and 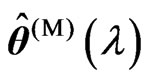 are regarded as a function of
are regarded as a function of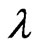 , we can regard the
, we can regard the 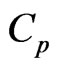 and
and 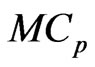 criteria for optimizing
criteria for optimizing 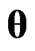 and
and 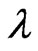 in (10) and (11) as a function of
in (10) and (11) as a function of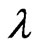 . This means that we can use these criteria to optimize
. This means that we can use these criteria to optimize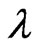 .
.
Then, we can rewrite the optimization algorithms to optimize the ridge parameter 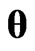 and the smoothing parameter
and the smoothing parameter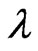 by minimizing the
by minimizing the 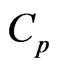 and
and 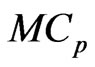 criteria in (10) and (11) as follows:
criteria in (10) and (11) as follows:
1) We obtain and
and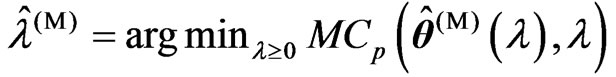 .
.
2) We optimize the ridge parameter and the smoothing parameter as  and
and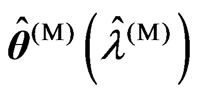 , respectively, by using
, respectively, by using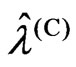 ,
, 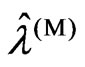 and the closed forms in (12) and (13).
and the closed forms in (12) and (13).
This means that we can reduce the processing time to optimize the parameters, and we need to use the optimization algorithm for only one parameter, 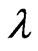 , for any
, for any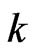 .
.
3.4. Magnitude Relationships between
Optimized Ridge Parameters
In this subsection, we prove the magnitude relationships between  and
and ,
, .
.
Lemma 3.2. For any , we obtain
, we obtain .
.
proof. Since we assume 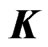 as a nonnegative definite matrix, there exists
as a nonnegative definite matrix, there exists 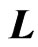 that satisfies
that satisfies 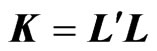 (see, e.g., [3]). Then, since
(see, e.g., [3]). Then, since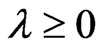 , we have
, we have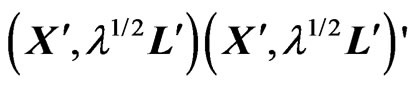
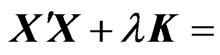 . Hence,
. Hence, 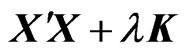 is a nonnegative definite matrix. This means that all of the eigenvalues of
is a nonnegative definite matrix. This means that all of the eigenvalues of 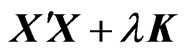 are nonnegative. Hence, all of the eigenvalues of
are nonnegative. Hence, all of the eigenvalues of 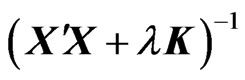 are nonnegative. Thus,
are nonnegative. Thus, 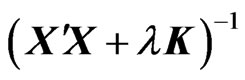 is also a nonnegative definite matrix for any
is also a nonnegative definite matrix for any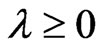 . Since
. Since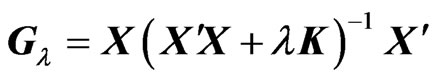 , we obtain
, we obtain 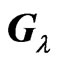 as a nonnegative definite matrix for any
as a nonnegative definite matrix for any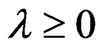 . Thus, the lemma is proven.
. Thus, the lemma is proven.
Using the same idea, we have 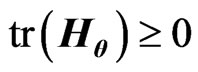 for any
for any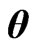 ,
,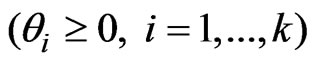 . Therefore, the final terms of the
. Therefore, the final terms of the 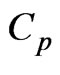 and
and 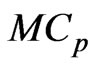 criteria in (10) and (11) are always greater than
criteria in (10) and (11) are always greater than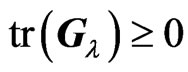 . In order to prove the magnitude relationship between
. In order to prove the magnitude relationship between 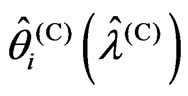 and
and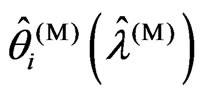 , we consider two situations in which
, we consider two situations in which 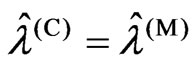 is satisfied and
is satisfied and 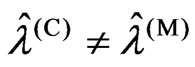 is satisfied.
is satisfied.
First, we consider 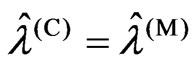 to be satisfied. Let
to be satisfied. Let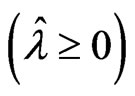
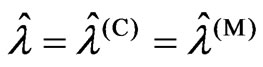 . Using
. Using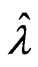 , we obtain the following corollary:
, we obtain the following corollary:
Corollary 3.1. For any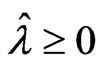 , we obtain
, we obtain 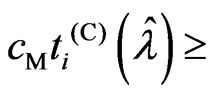
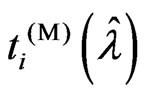 .
.
proof. Through simple calculation, we obtain
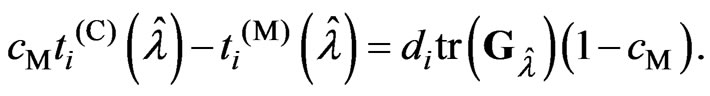
Since ,
, 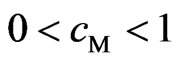 and
and  from lemma 3.1, the corollary is proven.
from lemma 3.1, the corollary is proven.
This corollary indicates that 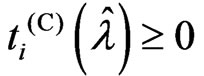 is satisfied when
is satisfied when  is satisfied because
is satisfied because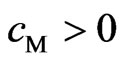 , and
, and 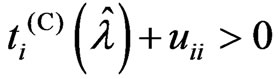 is satisfied when
is satisfied when 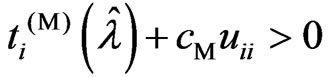 is satisfied because
is satisfied because 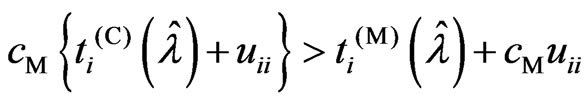 and
and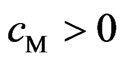 . Using these relationships, we obtain the following theorem.
. Using these relationships, we obtain the following theorem.
Theorem 3.1. For any , we obtain
, we obtain 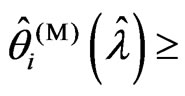
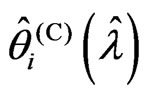 .
.
proof. We consider the following situations:
1) 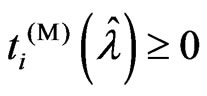 is satisfied
is satisfied
2) 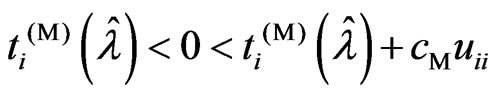 is satisfied
is satisfied
3) 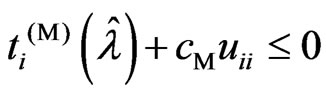 is satisfied.
is satisfied.
In (1), 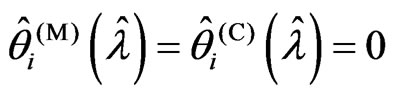 , because
, because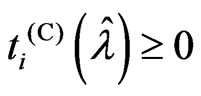 . In (3),
. In (3), 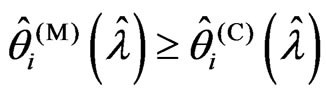 , because
, because 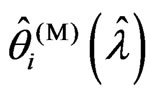 becomes
becomes . Hence, we only consider situation (2). Note that
. Hence, we only consider situation (2). Note that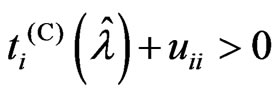 , because
, because  and
and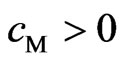 . This means that
. This means that  does not become
does not become . This theorem holds when
. This theorem holds when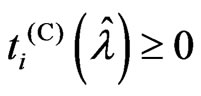 , because, in this case,
, because, in this case,  and
and . We also consider
. We also consider 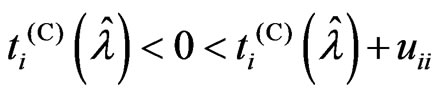 to be satisfied. Then, we obtain
to be satisfied. Then, we obtain
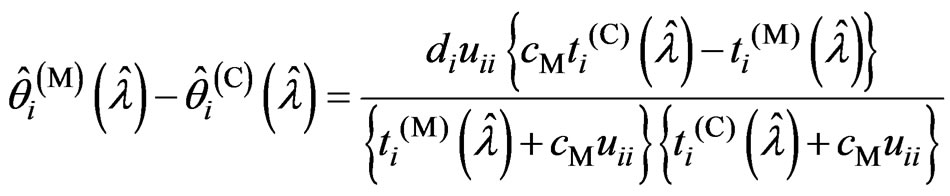
Since 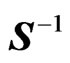 is a positive definite matrix,
is a positive definite matrix, 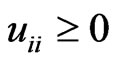 for any
for any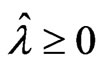 . From corollary 3.1, we have
. From corollary 3.1, we have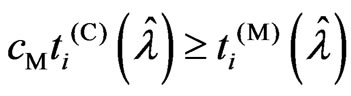 for any
for any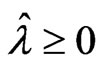 . Hence we obtain
. Hence we obtain 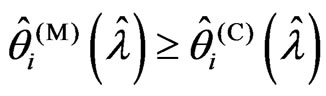 for any
for any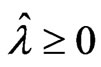 since
since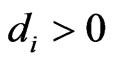 ,
, 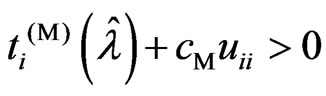 and
and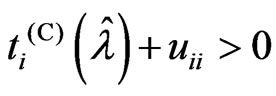 . Thus, this theorem is proven.
. Thus, this theorem is proven.
This theorem corresponds to that in [9] when 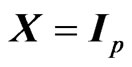 and
and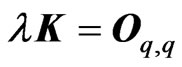 .
.
From Theorem 3.1, we obtained the relationships between 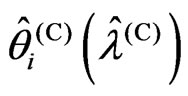 and
and 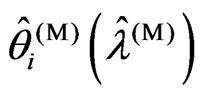 for the case in which the optimized smoothing parameters
for the case in which the optimized smoothing parameters  and
and 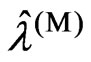 are the same. However,
are the same. However, 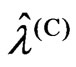 and
and 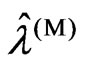 are optimized by minimizing the
are optimized by minimizing the 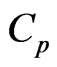 and
and 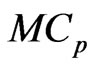 criteria in (10) and (11). Hence,
criteria in (10) and (11). Hence, 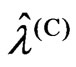 and
and 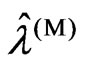 are generally different. Thus, we consider the relationship between
are generally different. Thus, we consider the relationship between and
and 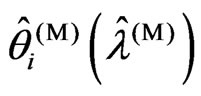 when
when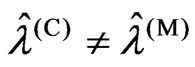 . Since
. Since 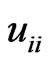 is regarded as a function of
is regarded as a function of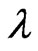 , we write
, we write  as
as  and
and 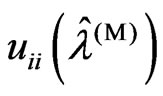 for each optimized smoothing parameter.
for each optimized smoothing parameter.
Theorem 3.2. We consider the following situations:
1) 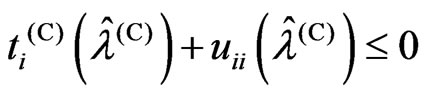 or
or  is satisfied
is satisfied
2) and
and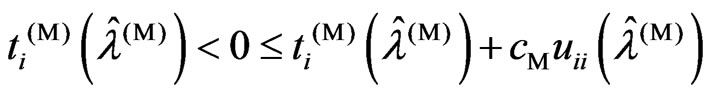 are satisfied
are satisfied
3) 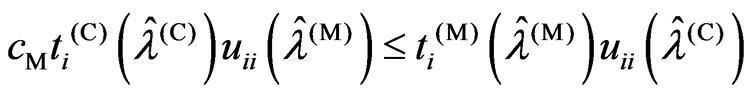 is satisfied
is satisfied
4)  is satisfied
is satisfied
5) 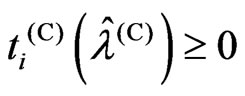 or
or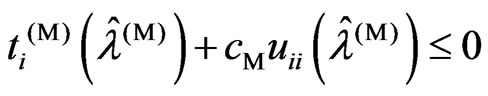 is satisfied.
is satisfied.
For any 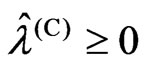 and
and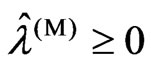 , we obtain the following relationships based on the above situations:
, we obtain the following relationships based on the above situations:
1) If (1), then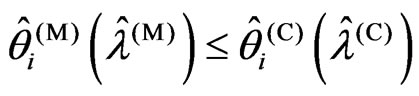
2) If (2) and (3), then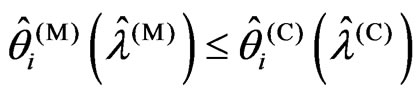
3) If (2) and (4), then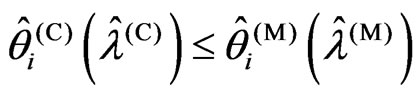
4) If (5), then .
.
proof. In (1) and (5), the relationships (i) and (iv) are true. Hence we need only prove relationships (ii) and (iii). Then we obtain 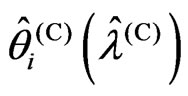 and
and 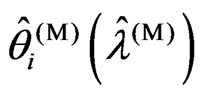 using the closed forms of (12) and (13). Through simple calculation, we obtain Since
using the closed forms of (12) and (13). Through simple calculation, we obtain Since 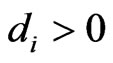 and the denominator is positive, the sign of
and the denominator is positive, the sign of 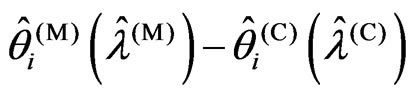 is the same as the sign of
is the same as the sign of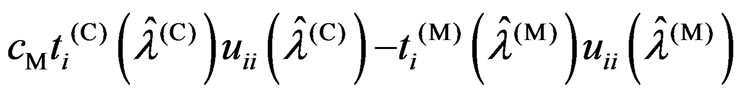 . Hence we obtain relationships (ii) and (iii). Thus, the theorem is proven.
. Hence we obtain relationships (ii) and (iii). Thus, the theorem is proven.
4. Numerical Studies
In this section, we compare the LS estimator 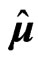 and
and  in (3) with the proposed estimator
in (3) with the proposed estimator 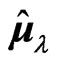 and
and 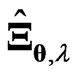 in (7) through a numerical study. Let
in (7) through a numerical study. Let , and let
, and let 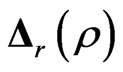 be an
be an 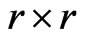 matrix as follows:
matrix as follows:
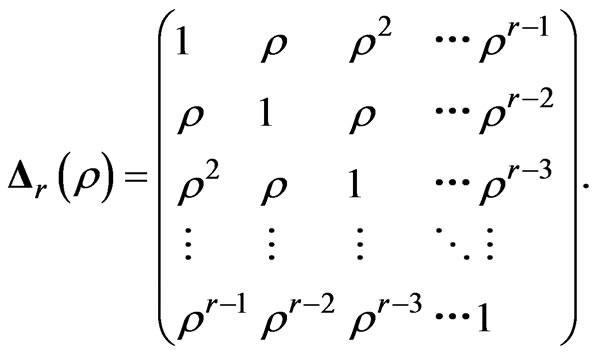
The explanatory matrix 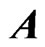 is given by
is given by  where
where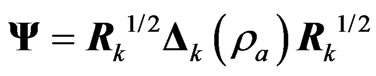 ,
, 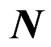 is an
is an 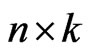 matrix and each row vector of
matrix and each row vector of 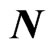 is generated from the independent
is generated from the independent 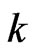 -dimensional normal distribution with mean
-dimensional normal distribution with mean 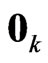 and covariance matrix
and covariance matrix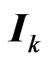 . Let
. Let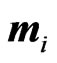 ,
, 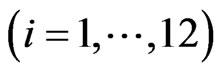 be a
be a 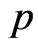 -dimensional vector. We set each
-dimensional vector. We set each  as follows:
as follows:

where 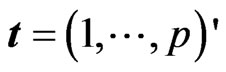 and the
and the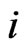 th element of
th element of 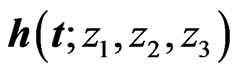 is
is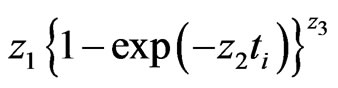 . Each element of
. Each element of 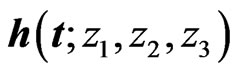 is Richard's growth curve model [12]. We set the longitudinal trends using these
is Richard's growth curve model [12]. We set the longitudinal trends using these  as
as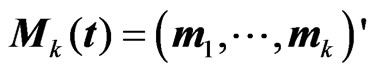 . Note that
. Note that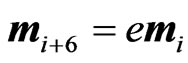 ,
, , which indicates that the last six rows of
, which indicates that the last six rows of are obtained by changing the scale of
are obtained by changing the scale of . The response matrix
. The response matrix 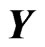 is generated by
is generated by 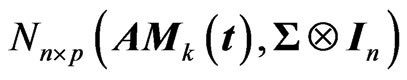 where
where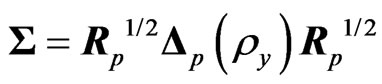 . Then, we standardized
. Then, we standardized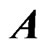 . Let
. Let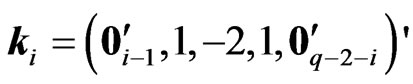 ,
,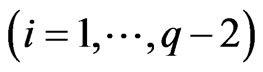 and
and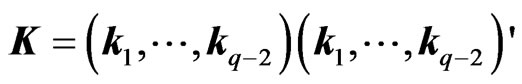 . We set each element of
. We set each element of 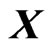 as a cubic
as a cubic  -spline basis function. Since
-spline basis function. Since  is set using the cubic
is set using the cubic  -spline, we note that
-spline, we note that . Additional details concerning
. Additional details concerning 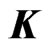 and
and  are reported in [2]. We simulate
are reported in [2]. We simulate 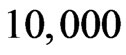 repetitions for each
repetitions for each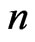 ,
, 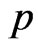 ,
, 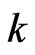 ,
, 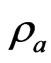 and
and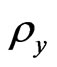 . In each repetition, we fixed
. In each repetition, we fixed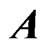 , but
, but 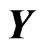 varies. We search
varies. We search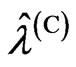 and
and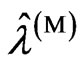 using fminsearch, which is a program in the software Matlab used to search for a minimum value, because
using fminsearch, which is a program in the software Matlab used to search for a minimum value, because 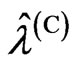 and
and 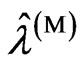 cannot be obtained in closed form. In searching
cannot be obtained in closed form. In searching 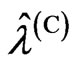 and
and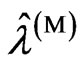 , we transform
, we transform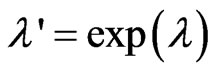 and search optimized
and search optimized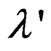 by each criterion because
by each criterion because and
and . In the search algorithm, the starting point for the search is set as
. In the search algorithm, the starting point for the search is set as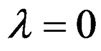 . Then, we obtain the optimized ridge parameters
. Then, we obtain the optimized ridge parameters  and
and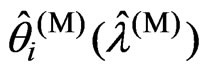 using the closed forms of (12) and (13) in each repetition. In each repetition, we need to optimize
using the closed forms of (12) and (13) in each repetition. In each repetition, we need to optimize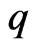 because
because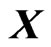 and
and vary with
vary with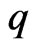 . We calculate
. We calculate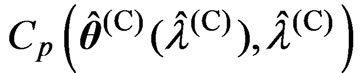 and
and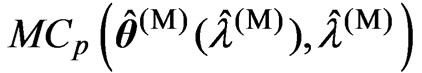 for each
for each  in each repetition. Then, we adopt the optimized
in each repetition. Then, we adopt the optimized  by minimizing each criterion in each repetition. After that, we calculate for
by minimizing each criterion in each repetition. After that, we calculate for each criterion, where
each criterion, where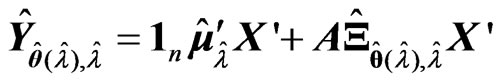 , which is obtained using
, which is obtained using 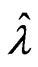 and
and 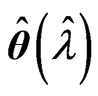 for each criterion and the optimized
for each criterion and the optimized 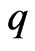 in each repetition. The average of
in each repetition. The average of 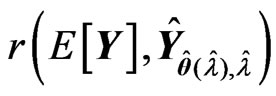 over
over  repetitions is regarded as the MSE of
repetitions is regarded as the MSE of . We compare the values predictedusing the estimators
. We compare the values predictedusing the estimators 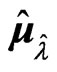 and
and 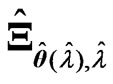 with those using the LS estimators
with those using the LS estimators  and
and , and the estimators
, and the estimators 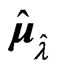 and
and 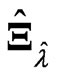 in (5). When we use
in (5). When we use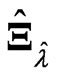 , we obtain
, we obtain 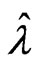 by minimizing
by minimizing 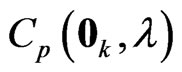 and
and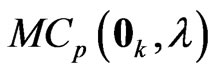 . As in the case of using
. As in the case of using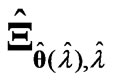 , we adopt
, we adopt  by using each criterion in each repetition for
by using each criterion in each repetition for 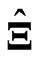 and
and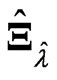 . Some of the results are shown in Tables 1 and 2. The values in the tables are obtained by
. Some of the results are shown in Tables 1 and 2. The values in the tables are obtained by ,
,
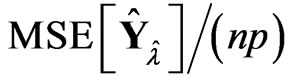 where
where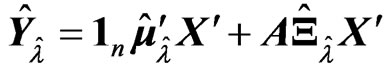 ,and
,and
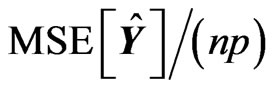 where
where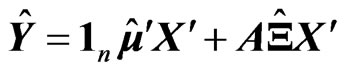 .
.
Each estimator optimized by using the 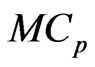 criterion for
criterion for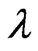 ,
, 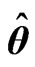 , and
, and  is more improve than that by using the
is more improve than that by using the 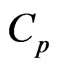 criterion for each estimator in almost all situations. This indicates that the
criterion for each estimator in almost all situations. This indicates that the 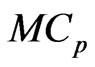 criterion is a better estimator of the MSE of each predicted value of
criterion is a better estimator of the MSE of each predicted value of 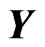 than the
than the 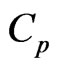 criterion. The reasons for this are that the
criterion. The reasons for this are that the 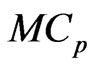 criterion is an unbiased estimator of MSE
criterion is an unbiased estimator of MSE
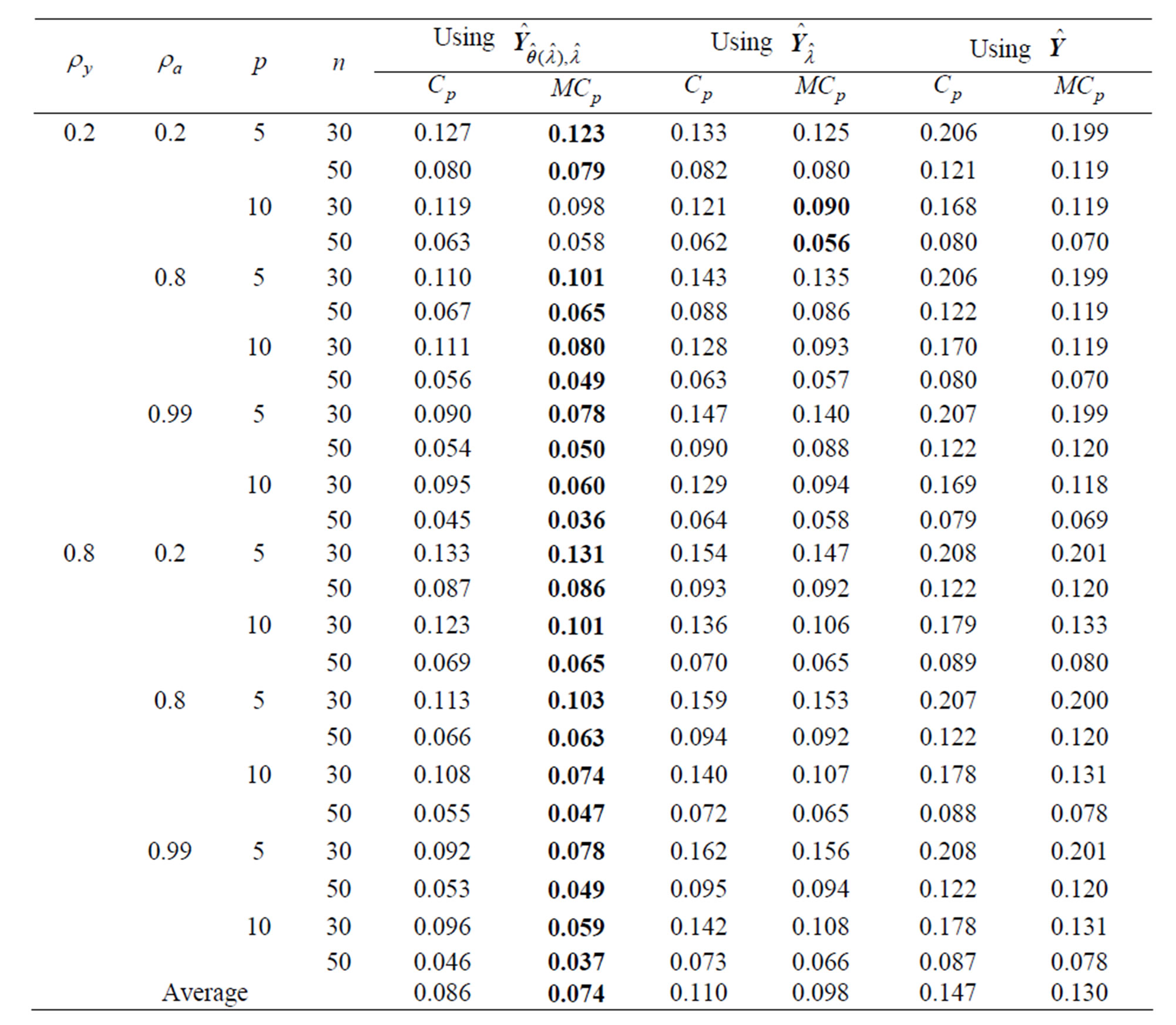
Table 1. MSE when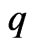 is selected using each criterion for each method in each repetition
is selected using each criterion for each method in each repetition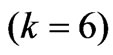 .
.
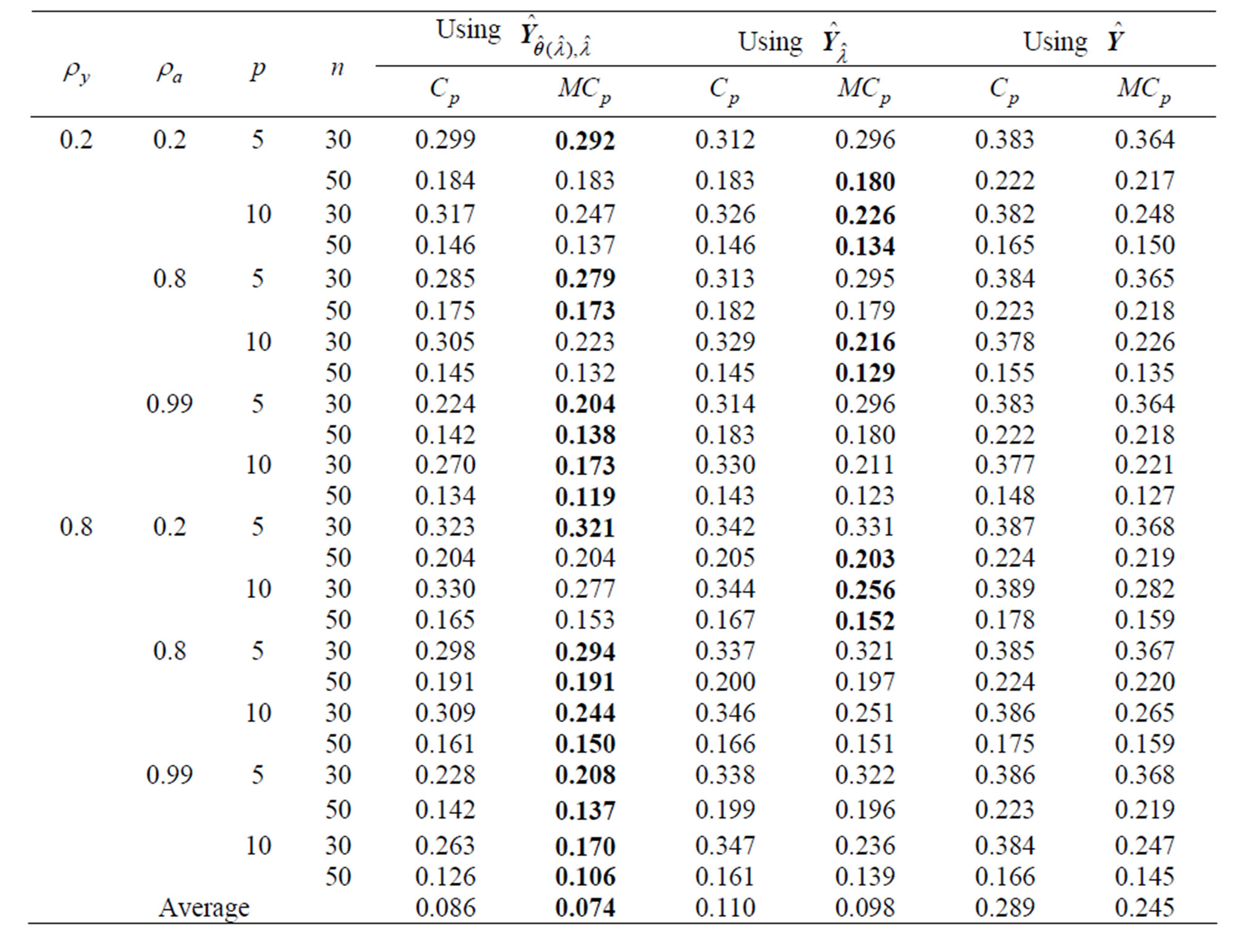
Table 2. MSE when is selected using each criterion for each method in each repetition
is selected using each criterion for each method in each repetition .
.
and each of the parameters in each estimator is optimized by minimizing the  criterion. When
criterion. When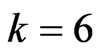 ,
, 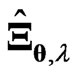 provides a greater improvement than either
provides a greater improvement than either  or
or  in all situations. The estimator
in all situations. The estimator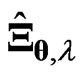 , which is optimized using the
, which is optimized using the 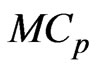 criterion, has the smallest MSE among these estimators for almost situations when
criterion, has the smallest MSE among these estimators for almost situations when . Here,
. Here,  provides a greater improvement than
provides a greater improvement than 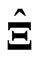 when
when 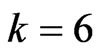 in all situations. When
in all situations. When  is large, the estimator
is large, the estimator 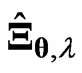 provides a greater improvement than
provides a greater improvement than  in most situations when
in most situations when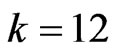 . On the other hand,
. On the other hand,  provides a greater improvement than
provides a greater improvement than 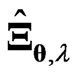 in most situations when
in most situations when 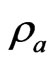 is small,
is small, 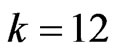 and
and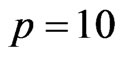 . If
. If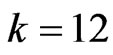 , then
, then 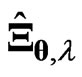 and
and  improve the LS estimator. Comparing the results for
improve the LS estimator. Comparing the results for 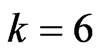 with the results for
with the results for 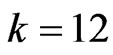 reveals that these estimators become poor esti mators when
reveals that these estimators become poor esti mators when 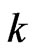 becomes large. The reasons for this are thought to be that
becomes large. The reasons for this are thought to be that  and
and 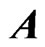 become unstable and the
become unstable and the 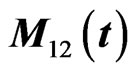 has some curves that are in a different scale. Each MSE using each method and the
has some curves that are in a different scale. Each MSE using each method and the 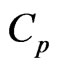 criterion is similar to that using the
criterion is similar to that using the 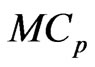 criterion if
criterion if 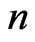 becomes large because
becomes large because  is close to 1. When
is close to 1. When 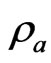 becomes large,
becomes large, 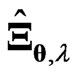 improves the LS estimator more than when
improves the LS estimator more than when 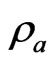 is small. Since
is small. Since 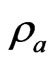 controls the correlation in
controls the correlation in , the multicollinearity in
, the multicollinearity in 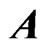 becomes large when
becomes large when  becomes large. Then,
becomes large. Then,  is not a good estimator because
is not a good estimator because 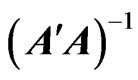 is unstable. Hence, we can avoid the multicollinearity problem in
is unstable. Hence, we can avoid the multicollinearity problem in 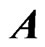 by using
by using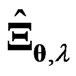 , which is one of the purposes of the present study. In all situations, the new estimators improve the LS estimator
, which is one of the purposes of the present study. In all situations, the new estimators improve the LS estimator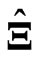 . In addition,
. In addition, 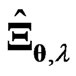 is better than
is better than 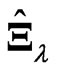 in most situations, especially when
in most situations, especially when 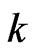 is small or
is small or 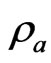 is large. In general,
is large. In general, 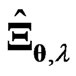 optimized using
optimized using  is the best method.
is the best method.
5. Conclusions
In the present paper, we estimate the longitudinal trends nonparametrically by using the nonparametric GMANOVA model in (1), which is defined using basis functions as 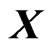 in the GMANOVA model. When we use basis functions as
in the GMANOVA model. When we use basis functions as , the LS estimators
, the LS estimators 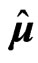 and
and 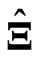 incur overfitting. In order to avoid this problem, we proposed
incur overfitting. In order to avoid this problem, we proposed  and
and 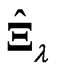 in (5) using the smoothing parameter
in (5) using the smoothing parameter 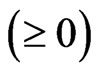
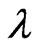 and the
and the 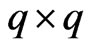 known penalty non-negative definite matrix
known penalty non-negative definite matrix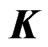 . However, if multicollinearity occurs in
. However, if multicollinearity occurs in ,
, 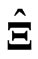 and
and 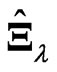 are not good estimators due to large variance. In the present paper, we also proposed
are not good estimators due to large variance. In the present paper, we also proposed 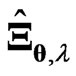 in (7) in order to avoid the multicollinearity problem that occurs in
in (7) in order to avoid the multicollinearity problem that occurs in 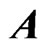 and the overfitting problem by using basis functions as
and the overfitting problem by using basis functions as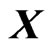 . The estimator
. The estimator 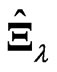 controls the smoothness of each estimated longitudinal curve using only one parameter
controls the smoothness of each estimated longitudinal curve using only one parameter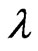 . On the other hand, in the estimator
. On the other hand, in the estimator , the rough smoothness of estimated longitudinal curves is controlled using
, the rough smoothness of estimated longitudinal curves is controlled using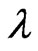 , and each smoothness of
, and each smoothness of 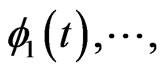
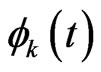 in the varying coefficient model (4) is controlled by
in the varying coefficient model (4) is controlled by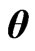 .
.
We also proposed the  and
and 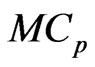 criteria in (10) and (11) for optimizing the ridge parameter
criteria in (10) and (11) for optimizing the ridge parameter 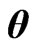 and the smoothing parameter
and the smoothing parameter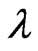 . Then, using the
. Then, using the 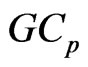 criterion in (14) and minimizing this criterion in Theorem A, we obtain the optimized
criterion in (14) and minimizing this criterion in Theorem A, we obtain the optimized 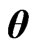 using the
using the 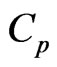 and
and 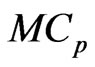 criteria in closed form as (12) and (13) for any
criteria in closed form as (12) and (13) for any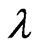 . Thus, we can regard the
. Thus, we can regard the 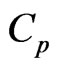 and
and 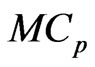 criteria as a function of
criteria as a function of .
.
Hence, we need to optimize only one parameter 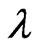 in order to optimize
in order to optimize 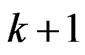 parameters in
parameters in 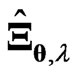 using these criteria. On the other hand, we must optimize two parameters when we use
using these criteria. On the other hand, we must optimize two parameters when we use 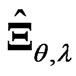 in (6). This optimization is difficult and requires a complicated program and a long processing time for simulation or analysis of real data because the optimized
in (6). This optimization is difficult and requires a complicated program and a long processing time for simulation or analysis of real data because the optimized  cannot be obtained in closed form even if
cannot be obtained in closed form even if  is fixed. This is the advantage of using
is fixed. This is the advantage of using . This advantage does not appear to be important because of the high calculation power of CPUs. However, this advantage is made clear when we use
. This advantage does not appear to be important because of the high calculation power of CPUs. However, this advantage is made clear when we use 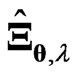 together with variable selection. Even if
together with variable selection. Even if  becomes large, then this advantage remains when
becomes large, then this advantage remains when  is used because the optimized
is used because the optimized  obtained using each criterion is always obtained as (12) and (13) for any
obtained using each criterion is always obtained as (12) and (13) for any . Furthermore, we must optimize
. Furthermore, we must optimize 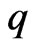 if we use model (1) to estimate the longitudinal trends. This means that we optimize the parameters in the estimators and calculate the valuation of the estimator for each
if we use model (1) to estimate the longitudinal trends. This means that we optimize the parameters in the estimators and calculate the valuation of the estimator for each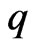 , and then we compare these values in order to optimize
, and then we compare these values in order to optimize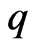 . Since this optimization requires an iterative computational algorithm, we must reduce the processing time for estimating the parameters in the estimator. Hence, the advantage of using
. Since this optimization requires an iterative computational algorithm, we must reduce the processing time for estimating the parameters in the estimator. Hence, the advantage of using 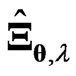 is very important. This optimized ridge parameter in (12) and (13) corresponds to that in [18] when
is very important. This optimized ridge parameter in (12) and (13) corresponds to that in [18] when 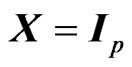 and
and
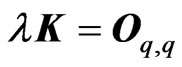 .
.
Using some matrix properties, we showed that 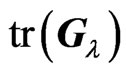 and
and  in the
in the  and
and 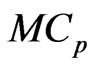 criteria are always nonnegative. From
criteria are always nonnegative. From 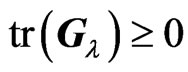 for any
for any 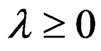 in lemma 3.1, we also established the relationship between
in lemma 3.1, we also established the relationship between 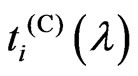 and
and 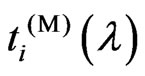 for any
for any 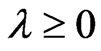 in corollary 3.1. Then, in Theorem 3.1, we established the relationship between
in corollary 3.1. Then, in Theorem 3.1, we established the relationship between 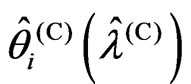 and
and  if
if 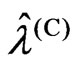 and
and 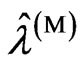 are the same, where
are the same, where 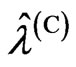 and
and 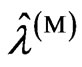 are obtained by minimizing the
are obtained by minimizing the 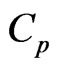 and
and 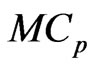 criteria. Note that this relationship corresponds to that in [9] when
criteria. Note that this relationship corresponds to that in [9] when  and
and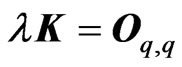 . In Theorem 3.2, we also established the relationships between
. In Theorem 3.2, we also established the relationships between 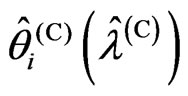 and
and  for the more general case, in which
for the more general case, in which 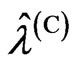 and
and 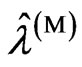 are different. The reason of the relationship in Theorem 3.2 is occurred is that
are different. The reason of the relationship in Theorem 3.2 is occurred is that  and
and 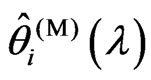 for each
for each 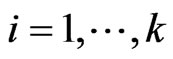 can be regarded as a function of
can be regarded as a function of .
.
The numerical results reveal that 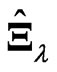 and
and  have some following properties. These estimation methods
have some following properties. These estimation methods 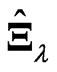 and
and 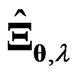 improve the LS estimator in all situations, especially when
improve the LS estimator in all situations, especially when 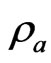 is large. This indicates that the proposed estimators are better than the LS estimator. Even if
is large. This indicates that the proposed estimators are better than the LS estimator. Even if 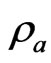 becomes large, we note that
becomes large, we note that 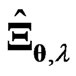 is stable because we add the ridge parameter to
is stable because we add the ridge parameter to 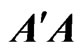 in the LS estimator. This result indicates that the multicollinearity problem in
in the LS estimator. This result indicates that the multicollinearity problem in  can be avoided by using the estimator in (7). These estimators can be used to estimate the true longitudinal trends nonparametrically using basis functions as
can be avoided by using the estimator in (7). These estimators can be used to estimate the true longitudinal trends nonparametrically using basis functions as 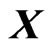 without overfitting. The LS estimator and the proposed estimators
without overfitting. The LS estimator and the proposed estimators 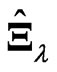 and
and 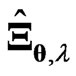 optimized using the
optimized using the 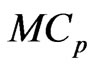 criterion provide a greater improvement than the estimators optimized using the
criterion provide a greater improvement than the estimators optimized using the  criterion in most situations. The reason for this is that the
criterion in most situations. The reason for this is that the  criterion is the unbiased estimator of MSE of the predicted value of
criterion is the unbiased estimator of MSE of the predicted value of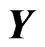 . Based on the present numerical study,
. Based on the present numerical study, 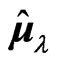 and
and 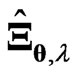 can be used to estimate the longitudinal trends in most situations. In addition, the
can be used to estimate the longitudinal trends in most situations. In addition, the 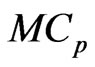 can be used to optimize the smoothing parameter
can be used to optimize the smoothing parameter 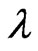 and the number of basis functions
and the number of basis functions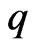 . Hence, we can use
. Hence, we can use 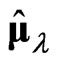 and
and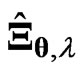 , the parameters
, the parameters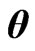 ,
, 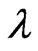 , and
, and 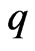 of which are optimized by the
of which are optimized by the 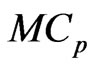 criterion for estimating the longitudinal trends.
criterion for estimating the longitudinal trends.
6. Acknowledgments
I would like to express my deepest gratitude to Dr. Hirokazu Yanagihara of Hiroshima University for his valuable ideas and useful discussions. In addition, I would like to thank Prof. Yasunori Fujikoshi, Prof. Hirofumi Wakaki, Dr. Kenichi Satoh and Dr. Kengo Kato of Hiroshima University for their useful suggestions and comments. Finally, I would like to thank Dr. Tomoyuki Akita of Hiroshima University for his advice with regard to programming.
7. Appendix
7.1. Minimization of the  Criterion
Criterion
In this appendix, we show that the optimizations using the 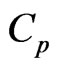 and
and 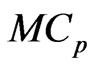 criteria in (10) and (11) are obtained in closed form as (12) and (13) for any
criteria in (10) and (11) are obtained in closed form as (12) and (13) for any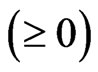
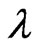 . [9] proposed the generalized
. [9] proposed the generalized 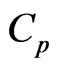
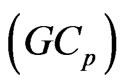 criterion for the MGR regression (originally the
criterion for the MGR regression (originally the 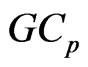 criterion for selection variables in the univariate regression was proposed by [1]). Similar to their idea, we proposed the
criterion for selection variables in the univariate regression was proposed by [1]). Similar to their idea, we proposed the 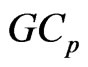 criterion for the nonparametric GMANOVA model.
criterion for the nonparametric GMANOVA model.
By omitting constant terms and some terms with respect to 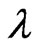 in the
in the 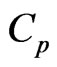 and
and 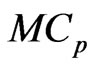 criteria in (10) and (11), these criteria are included in a class of criteria specified by
criteria in (10) and (11), these criteria are included in a class of criteria specified by
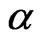 . This class is expressed by the
. This class is expressed by the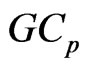 criterion as
criterion as
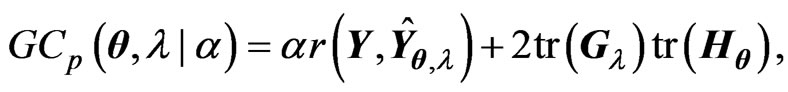 (14)
(14)
where the function 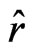 is given by (8). Note that
is given by (8). Note that  and
and 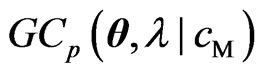 correspond to the terms with respect to
correspond to the terms with respect to 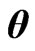 in the
in the 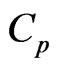 and
and 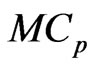 criteria. Using this
criteria. Using this 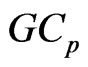 criterion, we can deal systematically with the
criterion, we can deal systematically with the  and
and  criteria for optimizing
criteria for optimizing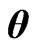 . Let
. Let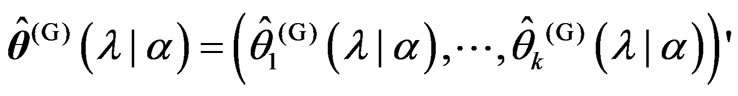 ,
,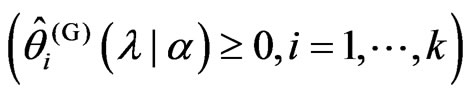 which minimize the
which minimize the  criterion for any
criterion for any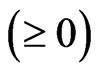
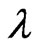 . Then,
. Then, 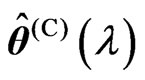 and
and 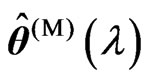 are obtained as
are obtained as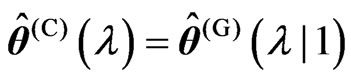 and
and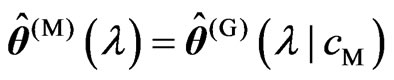 , respectively. Thus, we can deal systematically with the optimizations of
, respectively. Thus, we can deal systematically with the optimizations of  when we use the
when we use the 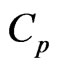 and
and 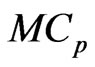 criteria. This means that we need only obtain
criteria. This means that we need only obtain 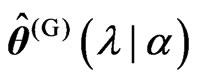 in order to obtain
in order to obtain  and
and 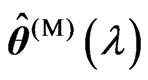 for any
for any and some
and some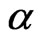 . If
. If 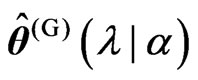 is obtained in closed form for any fixed
is obtained in closed form for any fixed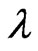 , we do not need to use the iterative computational algorithm for optimizing the ridge parameter
, we do not need to use the iterative computational algorithm for optimizing the ridge parameter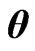 . In order to obtain
. In order to obtain , we obtain
, we obtain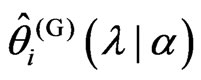 ,
, 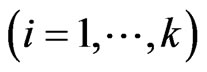 in closed form, as shown in the following theorem.
in closed form, as shown in the following theorem.
Theorem A. For any  and
and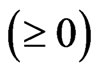
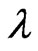 ,
,  is obtained as
is obtained as
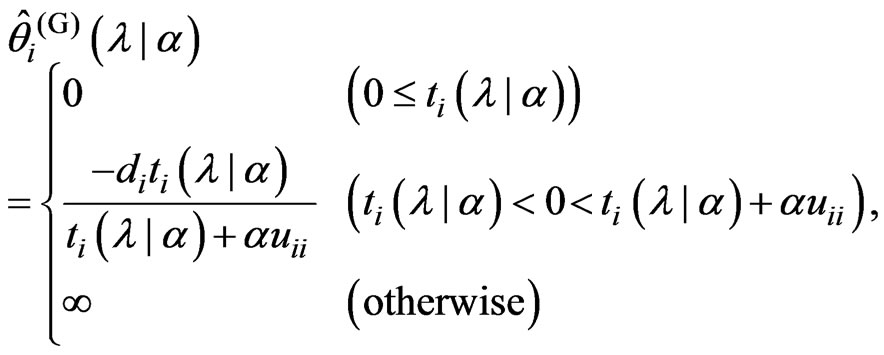 (15)
(15)
where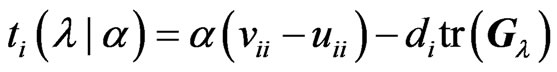 .
.
proof. Since 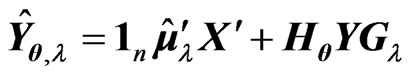 and we use the
and we use the
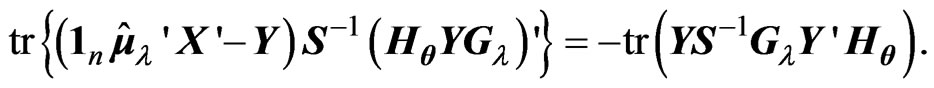
properties of the function  in Section 3.1, we can calculate
in Section 3.1, we can calculate  in the
in the 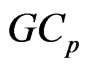 criterion in (14) as follows:
criterion in (14) as follows:

Since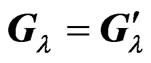 for any
for any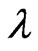 ,
, 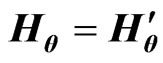 and
and 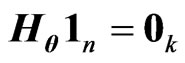 for any
for any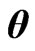 , the second term in the right-hand side of the above equation can be calculated as Note that
, the second term in the right-hand side of the above equation can be calculated as Note that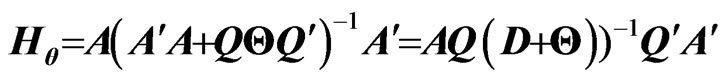 because
because 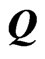 is an orthogonal matrix and
is an orthogonal matrix and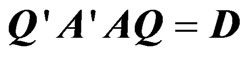 . Hence, we obtain the following results:
. Hence, we obtain the following results:
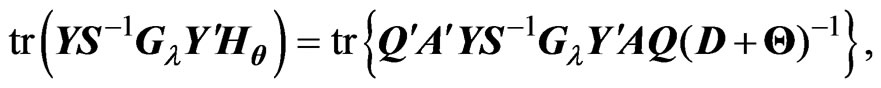
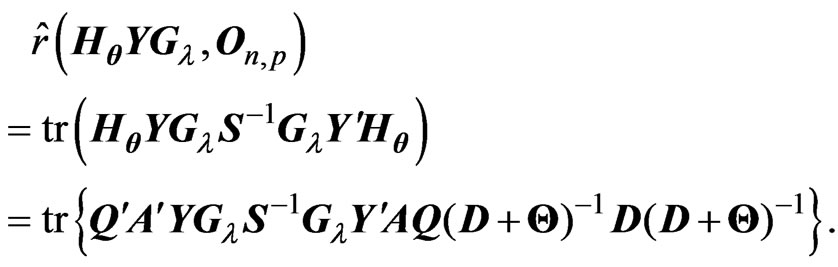
Since  and
and 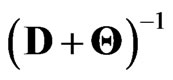 are diagonal matrices, we obtain
are diagonal matrices, we obtain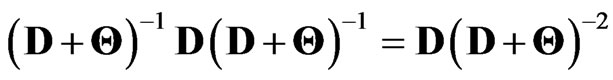 . Hence
. Hence  is calculated as
is calculated as
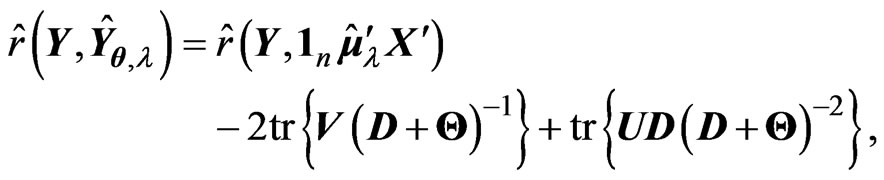
where and
and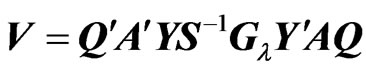 . Clearly,
. Clearly,  and
and  change with
change with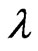 . Based on this result and
. Based on this result and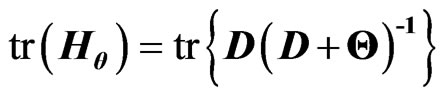 , we can calculate the
, we can calculate the 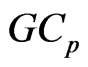 criterion in (14) as follows:
criterion in (14) as follows:

Then, we calculate the second and third terms in the right-hand side of the above equation as follows:
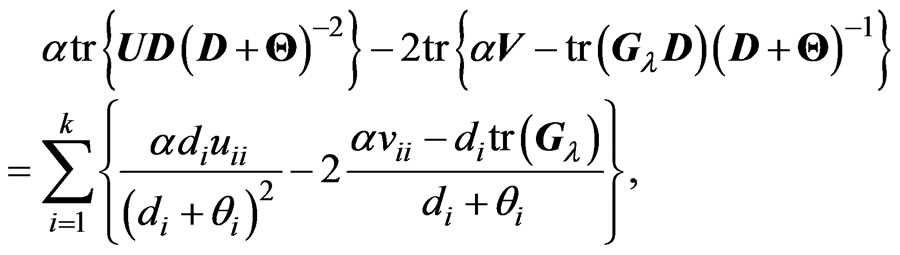
where  and
and 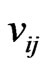 are the
are the 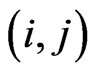 th element of
th element of 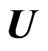 and
and , respectively. Clearly,
, respectively. Clearly, 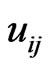 and
and 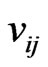 also vary with
also vary with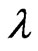 . Note that
. Note that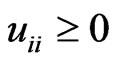 ,
,  for any
for any 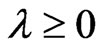 because
because 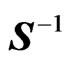 is a positive definite matrix (see, e.g., [3]). Let
is a positive definite matrix (see, e.g., [3]). Let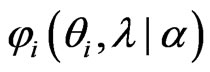 ,
, 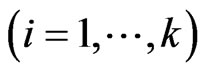 be as follows:
be as follows:
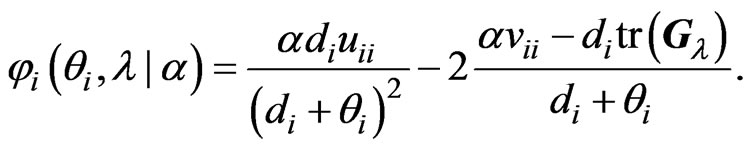 (16)
(16)
Using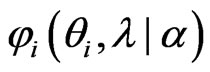 , we can express
, we can express
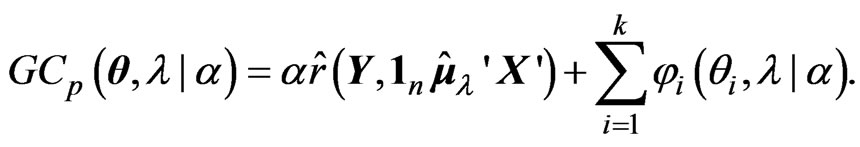
Since 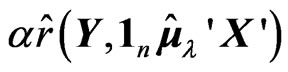 does not depend on
does not depend on , we can obtain
, we can obtain 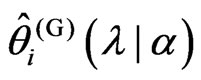 by minimizing
by minimizing  for each
for each  and any
and any 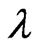
 . In order to obtain
. In order to obtain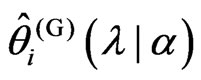 , we consider the following function for
, we consider the following function for :
:
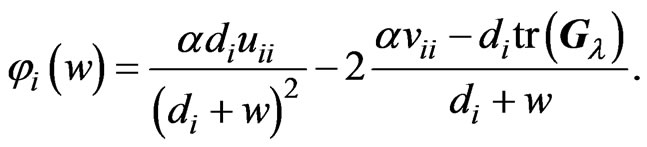 (17)
(17)
If we restrict  to be greater than or equal to 0, then this function is equivalent to the function
to be greater than or equal to 0, then this function is equivalent to the function 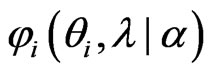 in (16), which must be minimized. Note that
in (16), which must be minimized. Note that 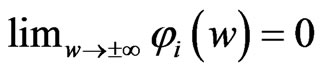 and
and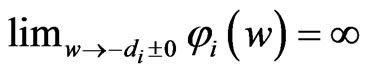 . Letting
. Letting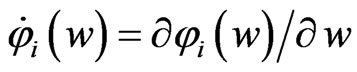 , we obtain
, we obtain
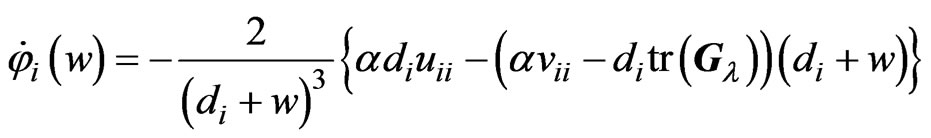
Let 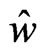 satisfy
satisfy 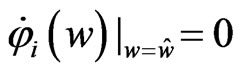 and
and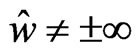 , then
, then 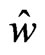 is obtained by
is obtained by

where . Note that
. Note that 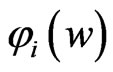 in (17) has a minimum value at
in (17) has a minimum value at , which is
, which is 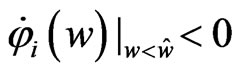 and
and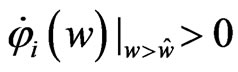 . Note that the sign of
. Note that the sign of  is the same as the sign of
is the same as the sign of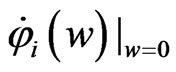 . In order to obtain
. In order to obtain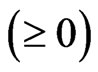
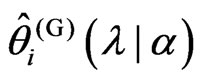 , we consider the following situations:
, we consider the following situations:
1) 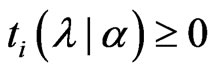 is satisfied
is satisfied
2) 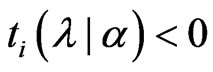 and
and  are satisfied
are satisfied
3) 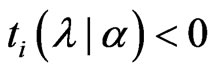 and
and 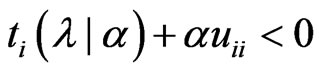 are satisfied.
are satisfied.
In (1),  , because
, because 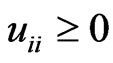 and
and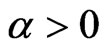 . In addition,
. In addition, 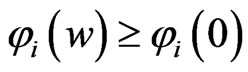 for any
for any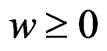 , because
, because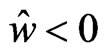 , and
, and 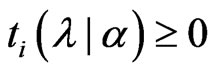 indicates that the sign of
indicates that the sign of 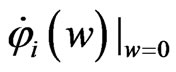 is nonnegative. This means that the minimum value of
is nonnegative. This means that the minimum value of  in
in 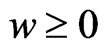 is obtained when
is obtained when 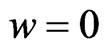 in situation (1). In (2),
in situation (1). In (2), 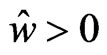 , and then the minimum value of
, and then the minimum value of 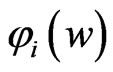 in
in 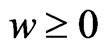 is obtained when
is obtained when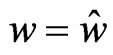 . In (3), since
. In (3), since 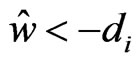 and
and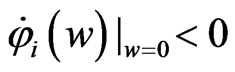 , we obtain
, we obtain 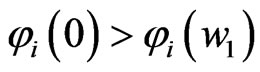
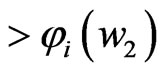 for any
for any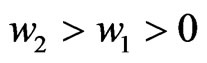 . Hence,
. Hence, 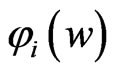 is minimized when
is minimized when 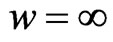 in
in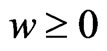 . From the above results, we obtain
. From the above results, we obtain 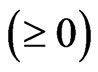
 as follows:
as follows:
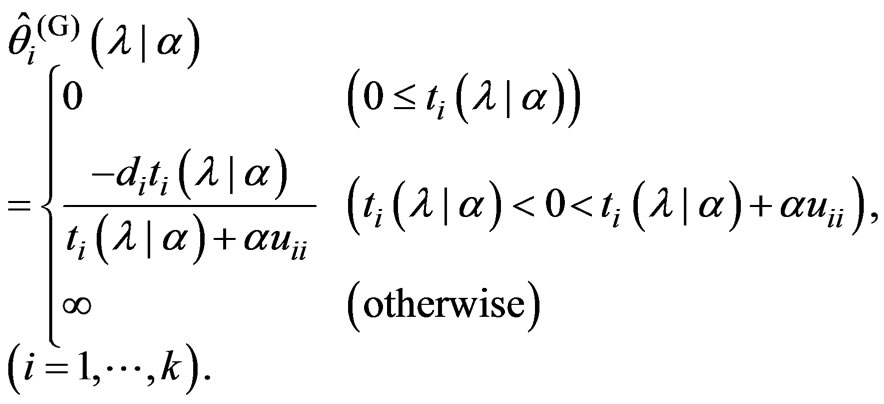
Thus, the theorem is proven.
Note that  corresponds to that in [9] when
corresponds to that in [9] when 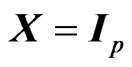 and
and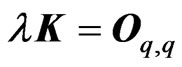 . Since we obtain
. Since we obtain 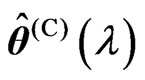 and
and 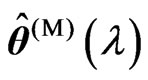 in closed form as (15) for any
in closed form as (15) for any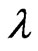 , we must optimize only one parameter
, we must optimize only one parameter 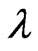 in order to optimize
in order to optimize  parameters. The use of
parameters. The use of 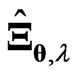 is advantageous because only an iterative computational algorithm is required for optimizing only one parameter
is advantageous because only an iterative computational algorithm is required for optimizing only one parameter 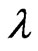 for any
for any . This means that we can reduce the processing time required to optimize the parameters in the estimator
. This means that we can reduce the processing time required to optimize the parameters in the estimator 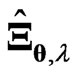 which is defined by (7). When we use
which is defined by (7). When we use  in (5), we also need the same iterative computational algorithm to optimize only one parameter
in (5), we also need the same iterative computational algorithm to optimize only one parameter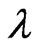 .
.
On the other hand, when we use 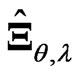 in (6), the
in (6), the 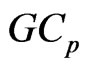 criterion for optimizing
criterion for optimizing  for any fixed
for any fixed  is obtained as
is obtained as
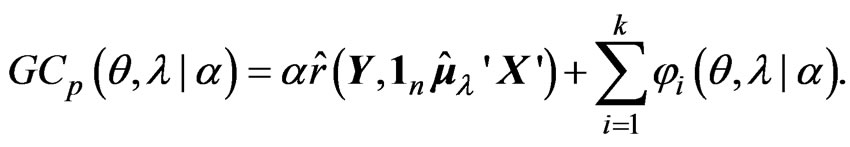
Since we need to minimize 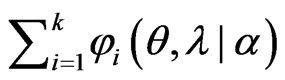 in order to optimize
in order to optimize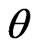 , we cannot obtain
, we cannot obtain 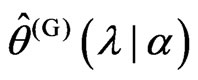 that minimizes this
that minimizes this 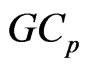 criterion for
criterion for 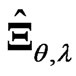 in closed form, even if
in closed form, even if 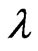 is fixed. Thus, we use an iterative computational algorithm to optimize the parameters
is fixed. Thus, we use an iterative computational algorithm to optimize the parameters  and
and 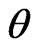 simultaneously. This iterative computational algorithm for optimizing two parameters is difficult and requires a longer processing time than the optimization of a single parameter
simultaneously. This iterative computational algorithm for optimizing two parameters is difficult and requires a longer processing time than the optimization of a single parameter
8. References
[1] A. C. Atkinson, “A note on the generalized information criterion for choice of a model,” Biometrika, vol. 67, no. 2, March 1980, pp. 413-418., pp. 291-293.
[2] P. J. Green and B. W. Silverman, “Nonparametric Regression and Generalized Linear Models,” Chapman & Hall/CRC, 1994.
[3] D. A. Harville, “Matrix Algebra from a Statistician’s Perspective,” New York Springer, 1997.
[4] A. E. Hoerl and R. W. Kennard, “Ridge regression: biased estimation for nonorthogonal problems,” Technometrics, vol. 12, No. 1, February 1970, pp. 55-67.
[5] A. M. Kshirsagar and W. B. Smith, “Growth Curves,” Marcel Dekker, 1995.
[6] J. F. Lawless, “Mean squared error properties of generalized ridge regression,” Journal of the American Statistical Association, vol. 76, no. 374, 1981, pp. 462-466.
[7] C. L. Mallows, “Some comments on Cp,” Technometrics, vol. 15, no. 1, November 1973, pp. 661-675.
[8] C. L. Mallows, “More comments on Cp,” Technometrics, vol. 37, no. 4, November 1995, pp. 362-372.
[9] I. Nagai, H. Yangihara and K. Satoh, “Optimization of Ridge Parameters in Multivariate Generalized Ridge Regression by Plug-in Methods,” TR 10-03, Statistical Research Group, Hiroshima University, 2010.
[10] R. F. Potthoff and S. N. Roy, “A generalized multivariate analysis of variance model useful especially for growth curve problems,” Biometrika, vol. 51, no. 3–4, December 1964, pp. 313-326.
[11] K. S. Riedel and K. Imre, “Smoothing spline growth curves with covariates,” Communications in Statistics – Theory and Methods, vol. 22, no. 7, 1993, pp. 1795-1818.
[12] F. J. Richard, “A flexible growth function for empirical use,” Journal of Experimental Botany, vol. 10, no. 2, 1959, pp. 290–301.
[13] K. Satoh and H. Yanagihara, “Estimation of varying coefficients for a growth curve model,” American Journal of Mathematical and Management Sciences, 2010 (in press).
[14] M. Siotani, T. Hayakawa and Y. Fujikoshi, “Modern Multivariate Statistical Analysis: A Graduate Course and Handbook,” American Sciences Press, Columbus, Ohio, 1985.
[15] R. S. Sparks, D. Coutsourides and L. Troskie, “The multivariate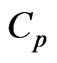 ,” Communications in Statistics - Theory and Methods, vol. 12, no. 15, 1983, pp. 1775-1793.
,” Communications in Statistics - Theory and Methods, vol. 12, no. 15, 1983, pp. 1775-1793.
[16] Y. Takane, K. Jung and H. Hwang, “Regularized reduced rank growth curve models,” Computational Statistics and Data Analysis, vol. 55, no. 2, February 2011, pp. 1041-1052.
[17] H. Yanagihara and K. Satoh, “An unbiased Cp criterion for multivariate ridge regression,” Journal of Multivariate Analysis, vol. 101, no. 5, May 2010, pp. 1226-1238.
[18] H. Yanagihara, I. Nagai and K. Satoh, “A bias-corrected Cp criterion for optimizing ridge parameters in multivariate generalized ridge regression,” Japanese Journal of Applied Statistics, vol. 38, no. 3, October 2009, pp. 151-172 (in Japanese).

