Journal of Biophysical Chemistry
Vol.2 No.2(2011), Article ID:5153,6 pages DOI:10.4236/jbpc.2011.22019
A model study on the stacking interaction of phenanthroline ligand with nucleic acid base pairs: an ab initio, MP2 and DFT studies
Chemistry Department, Gauhati University, P.O Gauhati University, Guwahati, India;
*Corresponding Author: Email: chitrani@sify.com
Received 21 January 2011; revised 9 March 2011; accepted 28 March 2011.
Keywords: Intercalation; Stacking Interaction; Phenanthroline Ligand; Ab initio; Basis set
ABSTRACT
The stacking of phenanthroline(phen) ligand within base pair sequences is one of the important factors for the stabilization of metalphen complex within DNA. The stacking ability of this ligand has been assessed to deduce the base pair selectivity as well as to identify the favored region of intercalation. Different level of theories have been used to predict the favorable regions for stacking interaction of phen ligand with base pair, but the results of MP2/6-31 + G(d,p) is found to be reasonably good for monitoring such interactions.
1. INTRODUCTION
The interaction between aromatic ligand and base pair of DNA is one of the important characteristics of certain potential anticancer agents, and then the sequence specificity of ligand in DNA binding has been the major concern in many literatures [1-7]. There are wide ranges of drugs, such as acridine derivatives, Amsa and Daunomycin etc., that intercalate within sequences of DNA [8-10]. The tris phenanthroline(phen) metal complexes have been known as important compounds for their antitumour activity. Most phen metal complexes bind with DNA either through non-covalent interaction within base pairs or within major and minor grooves (Figure 1). The charge transfer band from metal to ligand of some complexes as found in experimental studies is an important characteristic of ligand intercalation [11-17]. Such non covalent interactions also partly contribute to the stabilization of metal complex within DNA. It has been evidenced that some complexes can bind better with d(CGCGCG)2 oligonucleotide than d(GTGCAC)2, and the proton NMR chemical shift of drug-DNA adduct of these oligonucleotides may be taken as indirect implication of phen ligand intercalation within d(CGCGCG)2, but there is no concrete evidence to distinguish the groove binding or intercalation within these oligonucleotides [4-16]. Although the structural disposition of intercalated drug and conformational changes of double helical DNA can be analyzed by experimental methods like, 1H NMR and X-Ray diffraction studies, it may be necessary to understand insight into the energetic of weak interaction between phen ligand and base pair. As we know that 1H NMR chemical shift can only infer the structural information of metal complex-oligonucleotide adduct [17-20]. Nevertheless, it is likely that this ligand may also intercalate within GC sequences of d(CGCGCG)2 unlike the minor groove binding with d(GTGCAC)2. Also the drug may not easily access within AT containing oligonucleotide for intercalation, and hence the drug is found stabilized within the groove of DNA. However in certain crystal structure, the phen ligand is found partially intercalated within two thymine nucleobases [18]. As we know that the stacking interaction depends on the charge transfer capability of phen ligand and base pair. The stability of intercalated metalphen complex within base pair sequences may be either due to the stacking interaction with base pairs or perhaps depend on the conformational accessibility of ligand towards minor groove. In view of this, it is noteworthy to compare the stacking interaction between phen ligand and base pairs of DNA. In the sense that the extent of stacking interaction of phen ligand with AT and GC base pairs may be different, thereby produces AT or GC specificity during ligand intercalation.
Ab initio methods have been found useful for computing weak non-bonded interactions. In most cases the accurate ab initio methods are recommended for studying such type of interactions, where inclusion of large basis set and electron correlation is always necessary
Figure 1. Intercalation of phenanthroline with base pair.
[21-27]. The stacking interaction of aromatic molecules can be estimated from the extent of dispersion forces, short range exchange repulsion and electrostatic interactions, while the extent of intermolecular electron correlation between aromatic rings is the core factor for calculating the dispersion forces. However, it is often found that the less accurate force field methods, and even density functional method have been successfully applied to large molecules [24,25]. The DFT method is not a valuable tool for studying stacking interactions because of its failure to estimate dispersion energies of stacked molecules. Moreover the ab initio calculations with the inclusion of correlation effect at least at the MP2/6-31G* level have been found successful in some cases. The applications of correlated ab initio methods are limited for small molecules, and the Moller-plesset perturbation theory (MP2) can be used for medium size molecules. As we know that the ab initio methods like CCSD(T) is not so popular for large molecules, and in some cases the DFT method may describe the p-p stacking of large molecules[23-28]. Although the DFT method cannot be used for calculating the dispersion energies required for the stabilization of stacked structures, the additional empirical terms included in this method for computing some dispersion forces may sometimes useful. In this context, there are many other concerns over the limitations of high level ab initio methods for studying non-bonded interactions particularly for large molecules [22-28]. Hence, systematic analysis of various stacked models is always necessary because certain configurations might produce strong repulsion, which is not suitable for calculating weak stacking interactions. On the other hand the stacking pattern of charged drugs with base pair may again hamper in describing the nonbonded p-p interactions, since some intercalators bear charges [22]. For such molecules, comparison of results obtained from different level of theories may not particularly explain the stacking interactions perfectly. To rationalize such issues, the phen ligand, which is used in many potential metal-based anticancer drugs, has been taken up for assessing the stacking interaction with base pairs.
2. METHODOLOGY
The completely optimized geometries (HF/6-31G**) of base pairs and phen ligand were taken for constructing the stacked models. The optimum structures of stacked phen ligand with base pair were identified from various stacked structures by translating the phen ligand over AT and GC, and stacking energies were computed with different methods. All models are constructed at the intermolecular separation of 3.6 Å, since the available crystal structure of metal-phen complex and most aromatic ligands intercalate with base pairs approximately at this distance [10-12,18]. We have used rigid geometries of the stacked molecules i.e., the relaxation of the geometries of drug and base pair after interaction is not considered and single point calculations have been carried out on the interacted systems.
In order to visualize the nature of the structural characteristic of phen ligand and base pair interaction, we have analysed the different model structures, and the structure so obtained is compared with the available crystal structure. The stacking energies for mutual orientations (both horizontal and axial shifting) of phen ligand have been carefully analyzed by constructing several stacked models with the help of self developed programme package (JoinMolecule) [29]. Accountable error in the stacking energies might occur due to small deviation of certain parameter from the uniformity in the model construction. JoinMolecule has been developed for constructing desired models accurately.
The stacking energies are calculated from the following equationE = EST – EB – EPHEST , EB and EPH are the energies of stacked structure, base pair and phen ligand respectively. It is extremely important to choose appropriate basis set in the ab initio calculations [28]. In the present study, different types of basis set, which are tested in several calculations, have been used. The stacking energies and optimum stacked structures of phen ligand and base pairs obtained from various calculations have been compared.
3. RESULT AND DISCUSSION
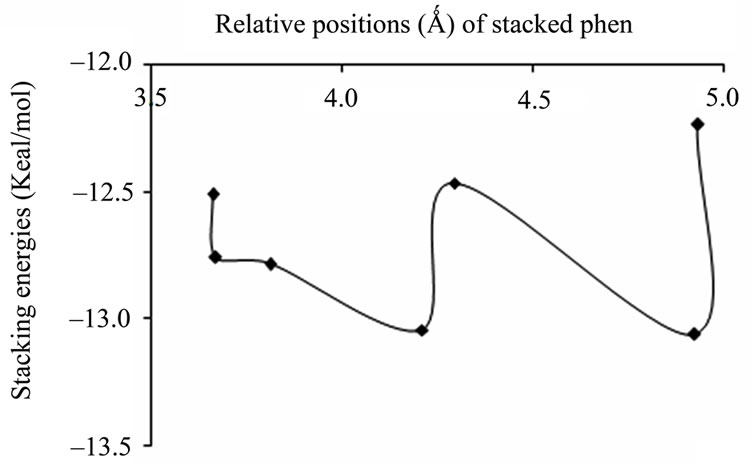
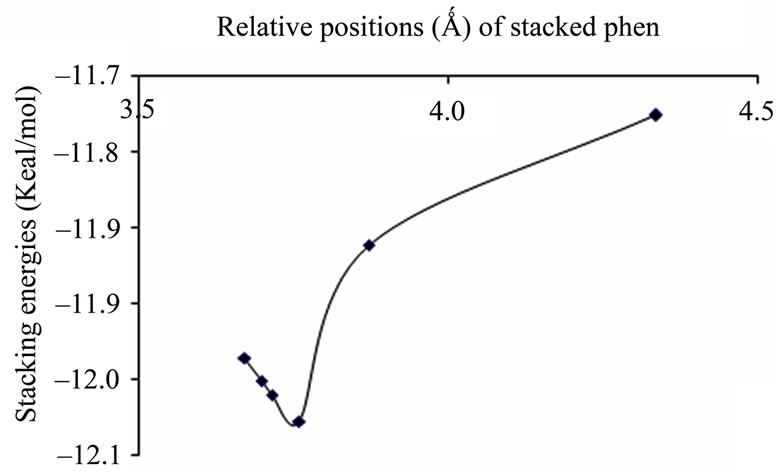
The variation of stacking energies calculated with MP2/6-31 + G(d,p) for some arbitrarily chosen stacked structures of phen ligand with GC and AT are shown in Figures 2 and 3. The optimum structures are identified from the energy minima in the plots (Figure 4), and the corresponding stacking energies are given in Table 1. Similarly the variation of stacking energies with different basis set in the DFT calculations is also analyzed. The stacking energies of most stable structures are given in Table 2, where the values of SVP, LANL2DZ, and cc-PVDZ are too small for the analysis of stacked phen with base pair. The plots in Figures 2 and 3 may be used for illustrating the relative change of stacking energies with the position of stacked phen within AT and GC. The stacking energies with the diffused function [6-31 + G(d,p) basis set] in the MP2 calculation are found better than the 6-31G** basis set with the improved stacking energies of ~10kcal/mol, and the dispersion interaction included in the calculation may be useful for analyzing the stabilization of stacked structures. The method has been found useful for analyzing similar type of chemical issues [20-24].
Although different level of theories and basis set have been taken up in the study, the results of MP2/6-31 + G(d,p) are mainly used for demonstrating base pair specificity of phen ligand. In fact, inclusion of diffused function and the electron correlation in this method may be appropriate for analyzing the stacking interactions. It has been known from similar investigations on weak interactions that the inclusion of diffused function such as 6-31 + G(d,p) in the MP2 calculation lead to the cancellation of errors in combination with the MP2 methods [20-21]. The HF calculations have been carried out for several stacked structures, and the variation of stacking energies are slightly basis set dependent (Table 1). The stacking energies obtained from HF calculations are all positive, which clearly demonstrates the weakness of the level of theory for studying stacking of molecules.
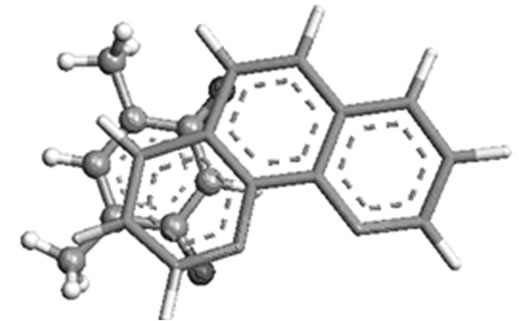
The most favorable position of phen ligand in stacked AT and GC can be analysed from the plots of MP2/6-31 + G(d,p) calculations. The optimum structures are shown in Figures 4(a) and (b), where the phen ligand is found
 (a)
(a)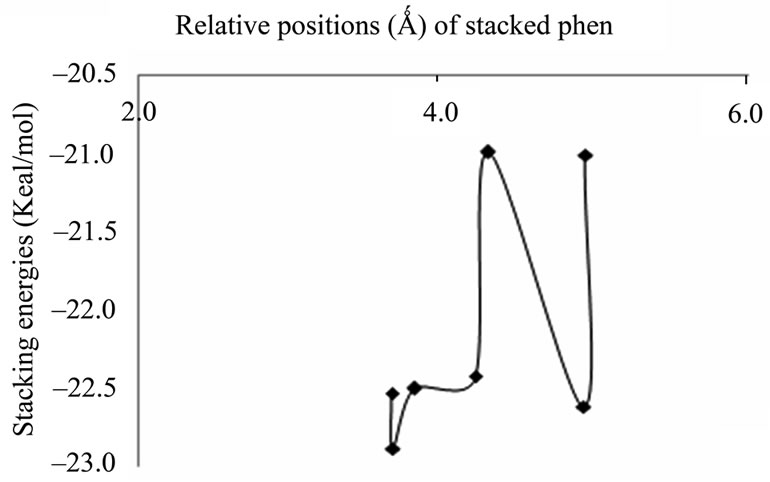 (b)
(b)
Figure 2. Plots of stacking energies (kcal/mol) vs distances (Ǻ) of GC sequence for MP2 method with different basis sets (a) 6-31 + G(d,p); (b) 6-31G**.
 (a)
(a)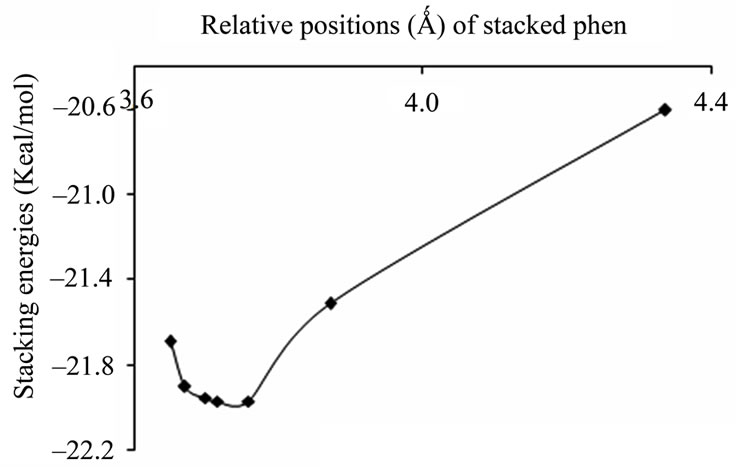 (b)
(b)
Figure 3. Plots of stacking energies (kcal/mol) vs distances (Ǻ) of AT sequence for MP2 method with different basis sets (a) 6-31 + G(d,p); (b) 6-31G**.
 (a)
(a)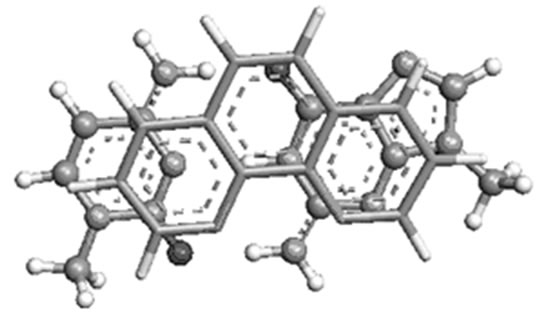 (b)
(b)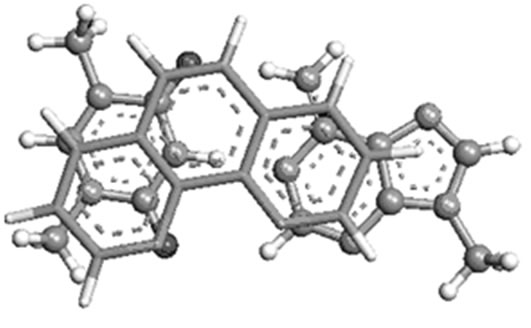 (c)
(c)
Figure 4. Most stable structures of stacked phen with (a) AT; (b) GC and (c) T( crystal structure).
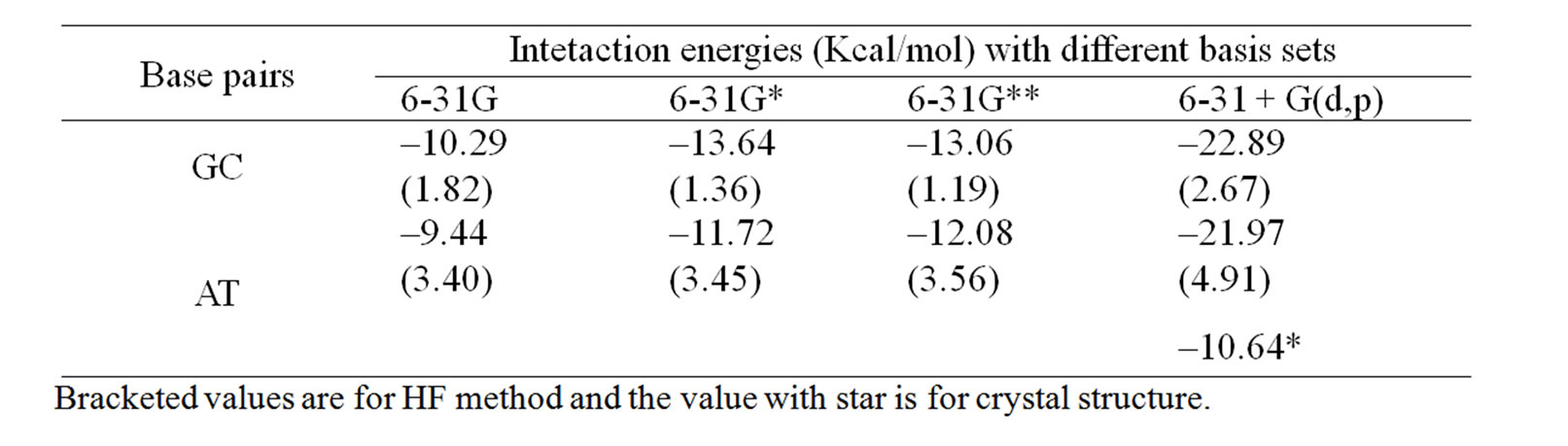
Table 1. The computed stacking energies (Kcal/mol) of stacked phen with base pairs with HF and MP2 methods.

Table 2. The computed stacking energies (Kcal/mol) of stacked phen with base pairs with DFT methods.
preferably towards T of AT, and C of GC. The theoretically predicted structure of phen-AT is found complementary to the reported crystal structure of phen coordinated metal complexes shown in Figure 4(c) [18]. In this case, the two oxygen atoms in thymine could result better stacking interaction with phen ligand, whereas the hydrogen bonded region in AT is found not preferable region for ligand stacking. Tables 1 and 2 present the stacking energies of the most stable structures obtained from different level of theories and basis set. The stacking energies obtained from correlated method, such as MP2 may be compared with that of DFT and HF methods, where the MP2/6-31 + G(d,p) energies are within the range of –23 to –21 kcal/mol. Although high level calculations may be required for such systems, the MP2/6-31 + G(d,p) may still be used for understanding stacking interaction. In order to check the effect of diffused function in the basis set of MP2 calculation, we have taken various basis set in the calculations. The stacking energies are found consistently more negative than the other methods. Moreover the limitation of DFT method for computing dispersion interaction is distinctly shown, in spite of its applicability for some larger molecules as reported in literatures [24-27]. We have also carried out extensive calculations of various stacked models with HF and DFT methods for comparison with MP2 method, but the stacking energies are uniformly positive (detail results are supplied in supplementary materials). Tables 1 and 2 demonstrate the trend of stacking energies of MP2, HF and DFT for some chosen basis set. Hence the electron correlation effect included in the MP2/6-31 + G(d,p) may be sufficient for explaining the stabilization of stacked phen with base pairs, but the ordering of HF and MP2 energies is not very drastically contradictory (Table 1). Comparison of the MP2/6-31 + G(d,p) results with that of more accurate ab inito method is rather difficult for such large system. But the different sets of calculations with HF, DFT and MP2 may gain some information on the stacking stabilization of phen ligand and base pair.
However the optimum structures obtained from different methods are not exactly similar but it is highly basis set dependent. The stacking energies of most favorable structure with MP2/6-31 + G(d,p) calculation is found to be approximately –23 kcal/mol compared to –9 kcal/mol with MP2/6-31G calculation. There are no other reported ab initio calculations on stacked phen with base pair, and some calculations on the stacking interaction of small molecules are available [20,21,28]. Moreover the position of phen predicted by MP2/6-31 + G(d,p) agrees well with that of crystal structure, but the stacking energies of experimentally reported stacked geometry is higher by 10 kcal/mol (Figure 4(c) and Table 1) [18]. The molecular geometry of crystal structure is not equal to optimized geometry and it may be due to other factors like crystal packing and additional effect from accompanied solvent molecules as well as ions in the crystal. The stacking energy of phen ligand with GC is found more negative compared to that of AT, and it shows that there is still possibility of phen ligand intercalation within GC rich oligonucleotide as evidenced in some studies [4].
4. CONCLUSIONS
The stacking interaction of phen ligand with base pair is clearly explained in this work. Both AT and GC base pairs may stabilize phen ligand, but with preference for GC base pair. The predicted stacked structure of phen ligand with AT base pair is found complementary to the available crystal structure. The study demonstrates that the stacking energies of MP2/6-31 + G(d,p) may be useful for studying such systems, although accurate ab initio method is necessary. The DFT calculation cannot be used to demonstrate the energetic of aromatic ring stacking in spite of the inclusion of diffused function in the basis set. Even the stacking energies of MP2 method with smaller basis set are reasonably good for application to large molecules where the calculation with accurate ab initio method is not possible.
5. ACKNOWLEDGEMENTS
The authors thank Department of Science and technology and Council of Scientific Research, New Delhi for financial assistant.
REFERENCES
- Denny, W.A., Baguley, B., Neidle, S. and Waring, M. (1994) Molecular aspects of anti-cancer drug-DNA interaction. British Journal of Clinical Pharmacology, 37, 103.
- Mukherjee, A., Lavery, R., Bagchi, B. and Hynes, J.T. (2008) On the molecular mechanism of drug intercalation into DNA: A simulation study of the intercalation pathway, free energy, and DNA structural changes. Journal of the American Chemical Society, 130, 9747-9755.doi:10.1021/ja8001666
- Rehmann, J.P. and Barton, J.K. (1990) H NMR studies of tris (phenanthroline) metal complexes bound to oligonucleotides: Characterization of binding modest. Biochemistry, 29, 1701-1709. doi:10.1021/bi00459a006
- Coggan, D.Z.M., Haworth, I.S., Bates, P.J., Robinson, A. and Rodger, A. (1999) DNA binding of ruthenium tris(1, 10-phenanthroline): Evidence for the dependence of binding mode on metal complex concentration. Inorganic Chemistry, 38, 4486-4497. doi:10.1021/ic990654c
- Barton, J.K., Basile, L.A., Danishefsky, A. and Alexandrescu, A. (1984) Chiral probes for the handedness of DNA helices: Enantiomers of tris(4,7 diphenylphenanthroline) ruthenium (II). Proceedings of National Acadamy of Sciences of USA, 81, 1961-1965. doi:10.1073/pnas.81.7.1961
- Haworth, I.S., Elcock, A.H., Freeman, J., Rodger, A. and Richards, W.G. (1991) Sequence selective binding to the DNA major groove: tris(1,10-phenanthroline) metal complexes binding to poly(dG-dC) and poly(dA-dT). Journal of Biomolecular Structure and Dynamics, 9, 23-44.
- Satyanarayana, S., Dabrowiak, J.C. and Chaires, J.B. (1992) Neither DELTAnor LAMBDA-tris(phenanthroline) ruthenium (II) binds to DNA by classical intercalation. Biochemistry, 31, 9319-9324.doi:10.1021/bi00154a001
- Eriksson, M., Leijon, M., Hiort, C, Nordén, B. and Graslund, A. (1994) Binding of DELTAand LAMBDA- [Ru(phen)3]2+ to [d(CGCGATCGCG)]2 Studied by NMR. Biochemistry, 33, 5031-5040.doi:10.1021/bi00183a005
- Lyng, R., Rodger, A. and Nordén, B. (1991) The circular dichroism of drug-DNA systems. Poly(dG-dC) B-DNA. Biopolymers, 31, 1709-1720.
- Lyng, R., Rodger, A. and Nordén, B. (1992) The circular dichroism of drug-DNA systems poly(dA-dT) B-DNA. Biopolymers, 32, 1201-1214. doi:10.1002/bip.360320910
- Lincoln, P. and Nordén, B. (1998) DNA Binding Geometries of Ruthenium (II) Complexes with 1,10-phenanthroline and 2,2’-bipyridyl ligands studied with linear dichroism spectra. Borderline cases of intercalation. Journal of Physical Chemistry, 102, 9583-9594. doi:10.1021/jp9824914
- Cho, C.B., Cho, T.S., Kim, S.K., Kim, B.J., Han, S.W. and Jung, M.J. (2000) Binding mode of [Ruthenium (II) (1, 10-Phenanthroline)2L]2+ to poly(dG)·poly(dC)·poly (dC)+ triplex DNA. Korean Chemical Society, 21, 995-999.
- Coury, J.E., Anderson, J.R., McFail-Isom, L., Williams, L.D. and Bottomley, L.A. (1997) Scanning force microscopy of small ligand-nucleic acid complexes: tris(o-phenanthroline)ruthenium (II) as a test for a new assay. Journal of the American Chemical Society, 119, 3792-3796. doi:10.1021/ja9623774
- Hiort, C., Nordén, B., Rodger, A. (1990) Enantiopreferential DNA binding of [ruthenium (II) (1,10-phenanthroline)3]2+ studied with linear and circular dichroism. Journal of the American Chemical Society, 112, 1971-1982. doi:10.1021/ja00161a050
- Kumar, C.V., Barton, J.K. and Turro, N.J. (1985) Photophysics of ruthenium complexes bound to double helical DNA. Journal of the American Chemical Society, 107, 5518-5523. doi:10.1021/ja00305a032
- Patel, D. and Shapiro, L. (1985) Molecular recognition in noncovalent antitumor agent-DNA complexes: NMR studies of the base and sequence dependent recognition of the DNA minor groove by netropsin. Biochiemie, 67, 887-915. doi:10.1016/S0300-9084(85)80181-4
- Pyle, A.M., Rehman, R.M., Kumar, C.V., Turro, N.J. and Barton, J.K. (1989) Mixed-ligand complexes of ruthenium (11): Factors governing binding to DNA. Journal of the American Chemical Society, 111, 3051-3058. doi:10.1021/ja00190a046
- Kumar, S.V., Sakore, T.D. and Sobell, H.M. (1984) Structure of a novel drug-nucleic acid crystalline complex: 1,10-phenanthroline-platinum (II) ethylenediamine-5’-phosphoryl-thymidylyl (3’-5’) deoxyadenosine. Journal of Biomolecular Structure and Dynamics, 2, 333-344.
- Barton, J.K., Goldberg, J., Kumar, C.V. and Turro, N.J. (1986) Binding modes and base specificity of tris(phenanthroline)ruthenium(II) enantiomers with nucleic acids: Tuning the stereoselectivity. Journal of the American Chemical Society, 108, 2081-2088.doi:10.1021/ja00268a057
- Kirshenbaum, M.R., Tribolet, R. and Barton, J.K. (1988). Rh(DIP)3(3+) a shape-selective metal complex which targets cruciforms. Nucleic Acid Research, 16, 7943-7960. doi:10.1093/nar/16.16.7943
- Hill, J.G. and Platts, J.A. (2009) Local electron correlation descriptions of the intermolecular stacking interactions between aromatic intercalators and nucleic acids. Chemical Physical Letter, 479, 279-283.doi:10.1016/j.cplett.2009.08.021
- Riley, K.E. and Hobza, P. (2007) Assessment of the MP2 method, along with several basis sets, for the computation of interaction energies of biologically relevant hydrogen bonded and dispersion bound complexes. Journal of Physical Chemistry A, 111, 8257-8263.doi:10.1021/jp073358r
- Grimme, S. (2003) Improved second-order Møller-Plesset perturbation theory by separate scaling of paralleland antiparallel-spin pair correlation energies. Journal of Chemical Physics, 118, 9095-9102.doi:10.1063/1.1569242
- Janet, E. and Bene, D. (1988) Ab initio molecular orbital study of the structures and energies of neutral and charged bimolecular complexes of water with the hydrides AHn (A = nitrogen, oxygen, fluorine, phosphorus, sulfur, and chlorine). Journal of Physical Chemistry A, 92, 2874-2880.
- McDonald, D.Q. and Still, W.C. (1994) Conformational free energies from simulation: Stochastic dynamics/monte carlo simulations of a homologous series of Gellman’s diamides. Journal of the American Chemical Society, 116, 11550-11553. doi:10.1021/ja00104a039
- Hobza, P. and Zahradnik, R. (1988) Intermolecular interactions between medium-sized systems. Nonempirical and empirical calculations of interaction energies. Successes and failures. Chemical Review, 88, 871-897.doi:10.1021/cr00088a004
- Hobza, P., Sponer, J. and Leszczynski, J. (1997) Comment on electron-correlated calculations of electric properties of nucleic acid bases. Journal of Physical Chemistry B, 101, 8038-8039. doi:10.1021/jp970622f
- Frisch, M.J., Trucks, G.W., Schlegel, H.B., Gill, P.M.W., Johnson, B.G., Robb, M.A., Cheeseman, J.R., Keith, T., Petersson, G.A., Montgomery, J.A., Raghavachari, K., Al-Laham, M.A., Zakrzewaki, V.G., Ortiz, J.V., Foresmann, J.B., Ciolowski, J., Stefanov, B.B., Namayakkara, A., Challacombe, M., Peng, C.Y., Ayala, P.Y., Chen, W., Wong, M.W., Andres, J.L., Replogle, E.S., Gomperts, R., Martin, R.L., Fox, D.J., Binkley, J.S., Defrees, D.J., Baker, J., Stewart, J.P., Head-Gordon, M., Gonzalez, C. and Pople, J.A., Gaussian 03, Gaussian Inc, Pittsburgh PA.
- Medhi, C. and Kalita, R. (2008) Join Molecule, Department of Chemistry, Gauhati University, Gauhati.

