Journal of Computer and Communications
Vol. 1 No. 1 (2013) , Article ID: 27708 , 5 pages DOI:10.4236/jcc.2013.11001
Numerical Methods for Solving Turbulent Flows by Using Parallel Technologies
![]()
Department Mechanics and Mathematics, al-Farabi Kazakh National University, Almaty, Kazakhstan
Email: aliisahov@mail.ru
Received 2013
Keywords: Domain Decomposition; Parallel Computations; Dynamic Smagorinsky Model; LES Approach
ABSTRACT
Parallel implementation of algorithm of numerical solution of Navier-Stokes equations for large eddy simulation (LES) of turbulence is presented in this research. The Dynamic Smagorinsky model is applied for sub-grid simulation of turbulence. The numerical algorithm was worked out using a scheme of splitting on physical parameters. At the first stage it is supposed that carrying over movement amount takes place only due to convection and diffusion. Intermediate field of velocity is determined by method of fractional steps by using Thomas algorithm (tridiaginal matrix algorithm). At the second stage found intermediate field of velocity is used for determination of the field of pressure. Three dimensional Poisson equation for the field of pressure is solved using upper relaxation method. Moreover various ways of geometrical decomposition for parallel numerical solution of three dimensional Poisson equations are investigated.
1. Introduction
Most flows occurring in nature and in engineering applications are turbulent. Turbulent flow is a fluid motion that possesses complex and seemingly random structure at some macroscopic scale of dynamical importance. The most important physical consequence of turbulence is the enhancement of transport processes. In turbulent flow, momentum, energy and particle transport rates greatly exceed the corresponding molecular transport rates. Turbulent flow exhibit much more small-scale structure than their non-turbulent counterparts. In fact, this small-scale structure is correlated with enhanced turbulent transport phenomena. Small-scale structure itself is evidence of enhanced transport in the sense that small scale develop from the degradation of large-scale excitations and are maintained by energy transport from one scale to another. Another important characteristic of turbulent flows is their apparent randomness and instability to small perturbations. Currently, there are three basic and commonly used approaches for simulation of turbulent flows. First approach is direct numerical simulation (DNS) which applies to solve Navier – Stokes equations, resolving all the scales of motion, with initial and boundary conditions appropriate to the considered flow. Each simulation produces a single realization of the flow. The DNS approach was infeasible until the 1970s when computers of sufficient power became available. In DNS whole range of spatial and temporal scales of the turbulence must be resolved. All the spatial scales of the turbulence must be resolved in the computational mesh, from the smallest dissipative scales (Kolmogorov microscales), up to the integral scale L, associated with the motions containing most of the kinetic energy. Second approach is large eddy simulation (LES), the larger three – dimensional unsteady turbulent motions are directly represented, whereas the effects of the smaller-scale motions are modelled. In computational expense, LES lies between Reynolds-stress models and DNS. Because the large-scale unsteady motions are represented explicitly, LES can be expected to be more accurate and reliable than Reynolds-stress models for flows in which largescale unsteadiness is significant – such as the flow over bluff bodies, which involves unsteady separation and vortex shedding. The computational cost of DNS is high, and it increases as the cube of the Reynolds number, so that DNS is inapplicable to high Reynolds number flows. Nearly all of the computational effort in DNS is expended on the smallest, dissipative motions, whereas the energy and anisotropy are contained predominantly in the larger scales of motion. In LES, the dynamics of the large-scale motions are computed explicitly, the influence of the smaller scales being represented by simple models. Third approach is the Reynolds-averaged Navier–Stokes equations (or RANS equations) are time-averaged equations of motion for fluid flow. The idea behind the equations is Reynolds decomposition, whereby an instantaneous quantity is decomposed into its time-averaged and fluctuating quantities, an idea was first proposed by Osborne Reynolds. The RANS equations are primarily used to describe turbulent flows. These equations can be used with approximations based on knowledge of the properties of flow turbulence to give approximate time-averaged solutions to the Navier–Stokes equations.
2. Mathematical Model
Under the assumption of incompressible flow, the dimensionless governing equations are as follows [1,2,7]:
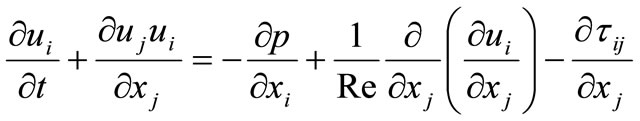 (1)
(1)
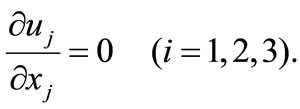 (2)
(2)
where 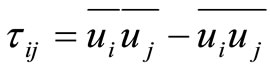
The solution of spread of flow in three dimensional areas were considered in this work. 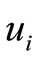 velocity, p represents the total pressure. The Reynolds number is defined as
velocity, p represents the total pressure. The Reynolds number is defined as 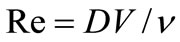 (
(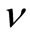 dynamic viscosity). Furthermore Cartesian coordinate system is employed, in which z is stream wise direction, x, y are in the lateral directions.
dynamic viscosity). Furthermore Cartesian coordinate system is employed, in which z is stream wise direction, x, y are in the lateral directions.
As for constructing model of turbulence we used dynamic model of Smagorinsky, the following is the underlying principle of the dynamic model for extracting information concerning a given eddy-viscosity model via a double filtering in physical space. It is worth to admit that the most of the historical developments have been done with Smagorinsky’s model [6,9]
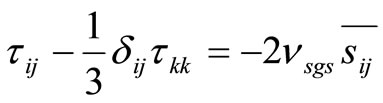 (3)
(3)
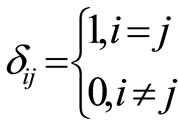 Kroneker symbol where
Kroneker symbol where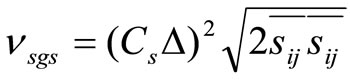 ,
,
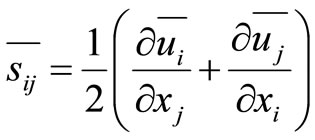 ,
, 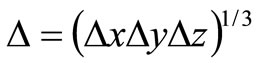 (4)
(4)
 ,
, 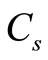 =0.18 for a Kolmogorov constant of 1,4.
=0.18 for a Kolmogorov constant of 1,4.
But the dynamic procedure applies in fact to the types of eddy viscosities such as those used in the structure-function model.
We start with regular LES corresponding to a “bar-filter” of width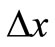 , an operator associating an function
, an operator associating an function . Then we define a second “test filter” tilde of large width
. Then we define a second “test filter” tilde of large width 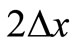 associating
associating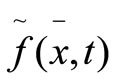 . So let us first apply this filter product to the Navier-Stokes equation. The subgrid-scale tensor of the field
. So let us first apply this filter product to the Navier-Stokes equation. The subgrid-scale tensor of the field 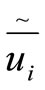 is obtained from equation (4) with the replacement of the filter bar by the double filter and tilde filter:
is obtained from equation (4) with the replacement of the filter bar by the double filter and tilde filter:
 (5)
(5)
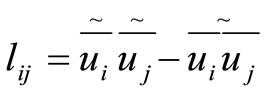 (6)
(6)
Now we apply the tilde filter to equation (4), which leads to
 (7)
(7)
Adding equations (6) and (7) and using equation (5), we obtain
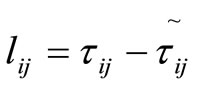
Further we use Smagorinsky’s model expression for the subgrid stresses related to the bar filter and tilde-filter to get
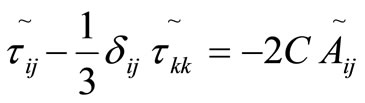
where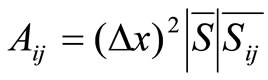 (8)
(8)
We have to determine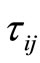 , the stress resulting from the filter product. This is again obtained using the Smagorinsky model, which yields
, the stress resulting from the filter product. This is again obtained using the Smagorinsky model, which yields
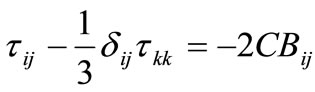 where
where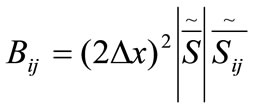 (9)
(9)
Subtracting (8) from (9) with the aid of Germano’s identity we get the following
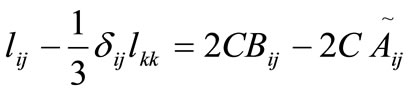
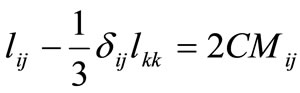
where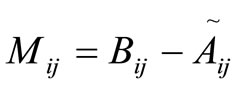 (10)
(10)
All the terms of equation (10) may now be determined by means of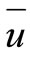 . Unfortunately, there are five independent equations for only one variable C, and thus the problem is over determined. The first solution was proposed by Germano to multiply (10) tensorially by
. Unfortunately, there are five independent equations for only one variable C, and thus the problem is over determined. The first solution was proposed by Germano to multiply (10) tensorially by 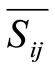 to get 1.
to get 1. 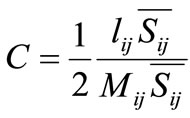
3. Numerical Simulation
The numerical solution of system is built on the staggered grid with the usage of the compact scheme for convective terms and scheme against a stream of the second type [5].
The scheme of splitting on physical parameters is used for the solution of turbulence problem [9-12,14]:
I. 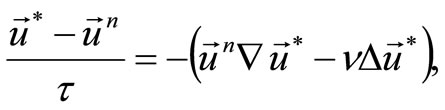
II. 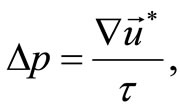
III. 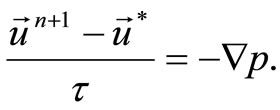
The first stage is solved by fractional step method in combination of Thomas algorithm (tridiaginal matrix algorithm) [8, 11,13].
Three dimensional Poisson equation for pressure field using an over - relaxation method is handled at the second stage. Three dimensional Poisson equation is parallelized by using various geometrical decomposition (1D, 2D and 3D). Geometric decomposition of the grid area is selected as the basic approach of parallelization. In this case, there are three different ways of sharing the values of the grid function on the compute nodes one-dimensional, two-dimensional and three-dimensional of the grid computing nodes [3,4].
After a stage of decomposition, when performed on separate data blocks for the construction of a parallel algorithm, we proceed to relation between the blocks, the calculations which will be run parallel. Because of we used an explicit difference scheme for computing the next approximation in the border nodes of each subdomain is necessary to know the value of the grid function with bordering neighboring processor elements. To accomplish this, in each compute node a fake edge for storing data from a neighboring computational node and arranged shipment of these boundary values needed to ensure the homogeneity of the calculations by explicit formulas. Sending data is done using the procedures library MPI. Let us turn to a preliminary theoretical analysis of the effectiveness of various methods of decomposition of the computational domain for this case. We will estimate the time of the parallel program as the time of consistent program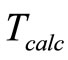 , divided by the number of processors used, plus the time shipments
, divided by the number of processors used, plus the time shipments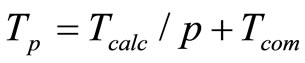 . While shipments to different ways of decomposition can be approximately expressed in terms of the amount of bandwidth:
. While shipments to different ways of decomposition can be approximately expressed in terms of the amount of bandwidth:
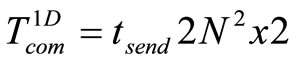
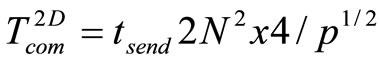 (11)
(11)
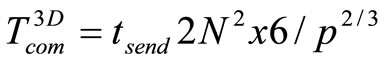
where  - dimension of finite-difference problems, p – number of computing nodes,
- dimension of finite-difference problems, p – number of computing nodes, 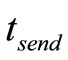 - shipping time of one number.
- shipping time of one number.
Calculations were performed on a cluster system URSA KazNU after al-Farabi on grids of 128 × 128 × 128 and 256 × 256 × 256 by using up to 64 processors. Results of computational experiment showed the presence of a good speed in solving problems of this class. They are mainly focused on over-time shipments and time calculations for various methods of decomposition.
In the first stage we used one overall program, the size of arrays from run to run have not changed, each processor element numbering of the array elements starting from scratch. Despite the fact that, in accordance with the theoretical analysis of the 3D decomposition is the best option for parallelization (Figure 1), computational experiments have shown that better results can be achieved using 2D decomposition when the number of processes from 25 to 144 (Figure 2)
On the basis of preliminary theoretical analysis of the graphs it must have the following pattern. Computation time without interprocessor communication costs at different ways of decomposition should be approximately the same for the same number of processors and shrink as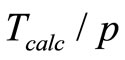 . In reality, the calculated data (Figure 4) indicate that the use of 2D decomposition on different grids gives the minimum cost for computation and payment schedules depending on the computation time on the number of processors which placed much higher than
. In reality, the calculated data (Figure 4) indicate that the use of 2D decomposition on different grids gives the minimum cost for computation and payment schedules depending on the computation time on the number of processors which placed much higher than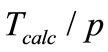 .
.
To explain these results there is a need to pay attention to the assumptions that were made during the preliminary theoretical analysis of the problem.
Firstly, it was assumed that regardless of how the distribution of data on a single processor element executed the same amount of computational work, which should lead to identical time-consuming. Secondly, we assumed that the time spent on interprocessor shipping any order of the same amount of data that does not depend on their selection from memory. To understand what happens in reality, the next set of test calculations was held. To assess the consistency of first admission was considered when the program is run in a single-processor version, and thus simulates different ways of geometric data decomposition for the same amount of computation performed by each processor.
Thus, for explicit difference methods for solving three dimensional Poisson equation can be applied one-dimensional, two and three-dimensional decomposition, but the results of testing programs have shown that the 3D decomposition does not gain in time compared with the
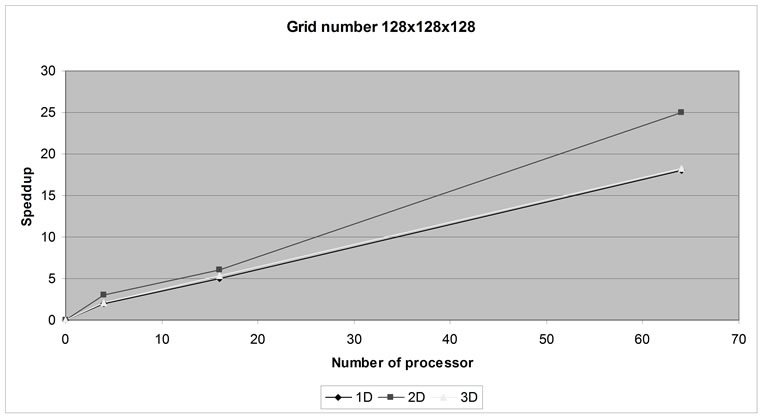
Figure 1 Speed up for different ways to decompose the computational domain
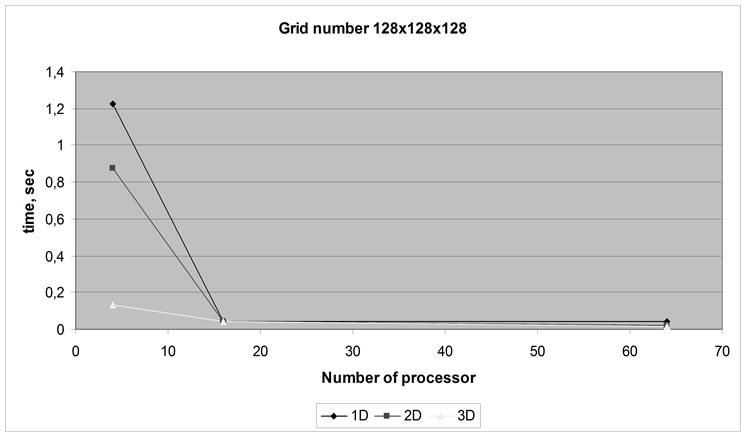
Figure 2 Computation time without considering the cost of data transfer for various methods of decomposition
2D decomposition, at least for the number of processors does not exceed 250, and the 3D decomposition has a more time-consuming software implementation and the use of 2D decomposition is sufficient for the scale of the problem at the present number of compute nodes.
4. Testing results of the numerical method
Consideration of a turbulent flow, which is located in the channel (Figure 1). Computations were performed for the Reynolds number 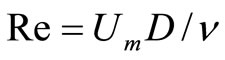 equal to 8000 defined based on the jet axis velocity. Also the following grid
equal to 8000 defined based on the jet axis velocity. Also the following grid  is taken in the calculations.
is taken in the calculations.
The spread of flow in three dimensional areas is described in numerical solution. Figure 6 shows isosurface of spread flow in three dimensional areas at different time scale.

5. Conclusions
The results of numerical experiments showed that the constructed mathematical model of turbulence is able to reproduce the characteristic features of turbulent flow. The usage of dynamic Smagorinsky model allowed us to obtain good data for the study area. Application in the calculation of 2D decomposition gives 65% efficiency in the use of 25 compute nodes. With further increase in the number of compute nodes and 100 for the chosen mesh size, a characteristic was obtained for problems of this class efficiency value is around 45%.
REFERENCES
- J.D. Jr. Anderson, “Computational Fluid Dynamics”, New York: McGraw-Hill. 1995.
- C.A. Fletcher, “Computational Techniques for Fluid Dynaimics,” Vol 2: Special Techniques for Differential Flow Categories, Berlin: Springer-Verlag. 1988.
- G. E. Karniadakis, “Parallel Scientific Computing in C++ and MPI.” 2000
- P. Pacheco. “Parallel Programming with MPI,” Morgan Kaufmann. 1996.
- S.K. Lely. “Compact finite difference scheme with spectral-like resolution,” J. Comp. Phys., 183, 1992, pp. 16-42.
- M. Lesieur, O. Metais, P. Comte, “Large-eddy simulations of turbulence,” Cambridge university press. 2005.
- R. Peyret, D. Th. Taylor, “Computational Methods for Fluid Flow,” New York: Berlin: Springer-Verlag. 1983.
- N.N. Yanenko, “The Method of Fractional Steps,” New York: Springer-Verlag. In J.B.Bunch and D.J. Rose (eds.), Space Matrix Computations, New York: Academics Press. 1979.
- A. Issakhov, “Large eddy simulation of turbulent mixing by using 3D decomposition method,” J. Phys.: Conf. Ser. 318(4), 042051, 2011. doi: 10.1088/1742-6596/318/4/ 042051
- B. Zhumagulov, A. Issakhov, “Parallel implementation of numerical methods for solving turbulent flows,” Vestnik NEA RK. 1(43), 2012, pp. 12–24
- A. Issakhov, “Parallel algorithm for numerical solution of three-dimensional Poisson equation,” Proceedings of world academy of science, engineering and technology 64, 2012, pp. 692–694.
- A. Issakhov, “Mathematical modeling of the influence of hydrothermal processes in the water reservoir,” Proceedings of world academy of science, engineering and technology 69, 2012, pp. 632–635.
- A. Issakhov, “Mathematical modelling of the influence of thermal power plant to the aquatic environment by using parallel technologies,” AIP Conf. Proc. 1499, 2012, pp. 15-18. doi: http://dx.doi.org /10.1063/ 1.4768963
- A. Issakhov, “Development of parallel algorithm for numerical solution of three-dimensional Poisson equation,” Journal of Communication and Computer. Volume 9, Number 9, 2012, pp. 977-980.

