Open Access Library Journal
Vol.06 No.08(2019), Article ID:94147,9 pages
10.4236/oalib.1105537
On the Implication of Tai Chi Diagram and Its Value in Physics
Zixuan Wang1, Yanbing Zhang1, Chengjun Wu2
1School of Information Science and Technology, East China University of Science and Technology, Shanghai, China
2School of Foreign Languages, East China University of Science and Technology, Shanghai, China

Copyright © 2019 by author(s) and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 12, 2019; Accepted: August 3, 2019; Published: August 6, 2019
ABSTRACT
As a symbol of Chinese Yin-Yang theory, the implication of Tai Chi diagram has been widely acknowledged in Natural Sciences and Philosophy in both east and west. Taking three well-known principles in physics for example, “the principle of complementarity”, “dissipative structure theory” and “Wheeler’s principle of austerity”, this paper interprets the symbolic representation of Tai Chi diagram and explores the compatibility between these three modern physical principles and Taoist philosophy. Through the combination of modern physics in the horizon of Tai Chi wisdom, this paper hopes to arouse the continuous attention and reflection of this issue in academic circles.
Subject Areas:
Education, Modern Physics, Sociology
Keywords:
Tai Chi Diagram, Modern Physics, The Principle of Complementarity, Dissipative Structure, Wheeler’s Principle of Austerity

1. 引言
太极图是中国古代先民概括阴阳易理、探讨宇宙人生变化发展规律的图式。千百年来,它以博大精深的内涵、千古永辉的义理,激励着一代又一代的研究者对其寻根溯源,探赜索隐。
后世所绘太极图种类有很多:如天地自然河图、唐朝的太极先天图、北宋周敦颐的周氏太极图、明朝来知德的来氏太极图、明朝左辅制作的景岳太极图与左辅太极图,清朝胡煦所制的循环太极图等。但一般认为,真正的太极图应当是以阴阳鱼相互涵容交感的圆形图案为主,外套八卦或六十四卦的环形图案。今日所见太极图为纯粹的阴阳鱼图,并无外套的八卦,实为时代发展要求图形日趋简明的结果 [1] 。
在漫漫历史长河的流传与演变中,太极图这一古老的形象成为了诠释阴阳学说、一分为二和对立统一思想的完美图形,从古至今为社会科学与自然科学领域所重视。作为中国古人的伟大创举,“太极图实际上体现了有、无的关系,这种关系,西方古代属于存在与非存在的关系,今天看来则是物质与空间的关系” [2] 。
丹麦量子物理学大师玻尔(N. H. D. Bohr, 1885~1962)在1937年访问中国之后,说中国的治学传统使他产生了灵感,随后太极阴阳图被玻尔用来作为并协性的象征;美国科学院院士、物理学家和思想家惠勒(John A. Wheeler, 1911~2008)教授1981年应邀来中国演讲时说“物理学的基础结构注定要坍塌,并将重建在一个新的基础之上”。在其演讲集的第一讲“不可思议的量子行业”的第一页上,出现了中国文化源头的太极图,太极图与现代物理学重建之间的关系是什么?这一问题引人思考;比利时物理学家、诺贝尔化学奖获得者、非平衡态统计物理与耗散结构理论奠基人普利高津(Ilya Prigogine, 1917~2003)认为中国传统科学的自然观是一种“自发的自组织世界”的观点(陈红兵,2006),而他的耗散结构理论“对自然界的描述非常接近中国关于自然界中的自组织与和谐的传统观点” [3] 。
当代科学史学科的重要奠基者之一萨顿(George Sarton, 1884~1956)早在1930年就在他的演讲《东方和西方》中指出:“新的启示可能会,并且一定会来自东方”。越来越多的西方哲学家、科学家开始渐渐将目光转向了被忘却已久的东方神秘世界。他们发现归纳、综合的思维方式和灵感、顿悟的认知模式并非是“保守”、“愚昧”、“落后”的同义词。恰恰相反,它们是东方世界认识客观世界、发展科学的强大利器,是道家提供的最深刻并且最完美的生态智慧 [4] 。
太极图就这样鬼使神差地成了沟通中西方文化的中介,并被东西方的自然科学与哲学家进行着各式各样的文化破译与解读。在这一人类文化符号中所蕴含的中国太极文化的巨大科学价值,早已为东西方人类所共认。当代科学所探讨的重心逐渐从“存在”走向“生成”,从“实体”转向“关系”,转向“信息”与“时间”,太极图令人惊异地成了这一当代科学发展潮流与趋势的象征。耗散结构理论创始人、化学诺贝尔奖获得者普利高津认为,西方经典科学注重的是“实休”,中国传统哲学注重的是“关系”,现代人类真正的科学精神与科学革命必须将二者综合,把注重实验、分析、还原与定量公式描述的西方科学传统同注重“自发的有组织的世界”的中国传统哲学结合起来,这必将“导致新的自然哲学和自然观” [5] 。
中国传统文化以《易》学为主轴、核心太极图与《易》学密切联系,可认为太极图是《易》学哲理的一个“全息元”。《易》中包含着许多朴素辩证法,太极图正是对如对立统一等基本规律的一个形象描述。如太极图形象概括表示了“阴阳对立”、“阴阳互根”、“阴阳消长”、“阴阳合一”等朴素辩证法。太极图又与道家、道教有极深渊源,为丹家秘宝,与人体、大脑、生命等有深刻联系。从太极图简洁顺滑流畅、黑白对称、旋转运动和阴阳相合的图形中,人们猜测它定是一幅内蕴天地自然之妙、深藏哲理的宇宙自然模式图。确实,华夏先哲有着直觉体悟的特殊思维方式和取象比类的特殊科学方法,他们对宇宙万事万物的直觉体悟与天才猜察获得了独到认知,太极图正是他们探索宇宙自然的智慧结晶。
本文以物理学中著名的“并协原理”、“耗散结构”和“质朴性原理”为例,阐述了太极图与现代物理学的包容、共通和现实化具体体现的关系。我们认为对太极智慧的发掘研究,不是寻求其本义,而是着眼于现代科学的发展,从中索求智慧启迪 [6] 。
2. 玻尔的并协原理与八卦太极图
1928年玻尔提出并协原理(the principle of complementarity)。他认为波?粒二象性是任何辐射与物质都具有的内在的和根本的性质。这两种形象是互相排斥的,但同时又都是确定存在的。波动性和粒子性两种描述中任何单独一方都是不充分的,尽管它们彼此不相容,但为了说明所有可能的实验,它们又都是必要的 [7] 。
李仕?在其“玻尔‘并协原理’与《八卦太极图》”中说:“<太极图>并非古人的随意用画,它的形成是古人‘仰则观像于天,俯则观法于地,近取诸身,远取诸物’总结大量客观运动规律得出的”,这种规律的重要体现就是“四季阴、阳的消长规律”。由于影响“自然万物周期性变化的首要因素”是“太阳光照度的四季节律变化”,因此自然万物周期性的阴、阳消长规律在太极图中的最佳表示如图1所示 [8] 。
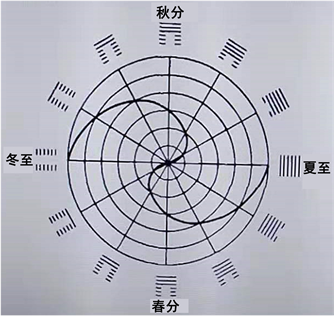
图1. 四季的阴、阳无限等分变化图
以圆心为极点,以极点到夏至的方向为极轴的正方向建立极坐标系,则阴、阳的大小β与时间θ之间数据变化关系满足如下关系式:
显然,这是两条阿基米德螺线 [9] 。
那么太极图和更为实际的物理概念是否还有关联呢?答案是肯定的。如果我们把阴和阳二者中的一个看作是物质的波动性,而另一种看作是物质的粒子性,会发现这与玻尔对波?粒二像性的补充说明以及德布罗意对于普遍性的粒子应具有波?粒二像性的假说十分相似,更精确地说,是与玻尔所述并协原理十分相似。这个原理首先来自于玻尔对波粒二象性的看法。波和粒子在同一时刻是互斥的,即类似我们说的波粒二象性,但它们在更高层次上统一。如物质的粒子性和波动性是严格分离的,但在解释实验时二者又是相互补充的,这些就是玻尔“并协原理”中“对立者相互补充”的真实写照,也是太极图所蕴含哲学思想的一部分精髓所在。举个例子,光速c = 3 × 108 m/s是当今人类能观察到的最高速度。若以人行速度v1 = 5 km/h = 1.4 m/s;火车速度v2 = 12 km/h = 33.3 m/s;宇宙飞船脱离地球的速度v3 = 11.8 km/s;地球在轨道中的运行速度v = 29.78 km/s;飞船脱离太阳系的速度v = 617.5 km/s相比,如果我们把光速c看成太极图中“正南纯阳”的动极点,而又让阳鱼代表运动(或波动性)、阴鱼代表静止(粒子性)的话,可见,上述物体的运动度(波动性) ≤0.00206,而静止度(粒子性)占99.8%以上。虽然它们相对光速而言属于“粒子”性,但它们周围伴随着波动,只是频率极低、波长极长罢了 [10] 。可见,我们以阳鱼代表粒子性,阴鱼代表粒子性的简单模型,已经可以在一定程度上很好地诠释并协原理了。这个通过太极图衍生的模型具有“波?粒二象性”,即与“并协原理”的内核相匹配。
如上所述,我们可以推测当玻尔在探寻微观粒子内在结构的秘密时,的确深受我国古代的阴阳八卦学说以及老子思想的启发。事实也是如此,1958年3月26日在给斯文・雨果于尔根森的一封信中,玻尔提到自己早在年轻时就读过中国老子的《道德经》:“我通过思斯特・缪勒的《老大师》一书而对它(《道德经》)有了一种美好的印象”。“老大师”便是老子,玻尔年轻时读的这本书,就是思斯特・缪勒的《基督以前的老大师和他的著作“道德经”》,这部书的正文为《道德经》译文。根据玻尔后来的叙述,老子《道德经》留给他深深的“美好印象”的,正是道家太极哲学的两个基本思想:一是阴阳对立统一的有机辩证观,万事万物都包含着排斥对立而又互补共存的两个方面;二是我道合一、主客一体的有机整体观。而“太极图”正是对道家太极哲学这两个基本思想的描述 [11] 。
同样,在玻尔的量子力学论文中,他不仅引用了《老子》的名句“道可道,非常道;名可名,非常名”,他对“太极图”的钟爱也表现得淋漓尽致。在1937年玻尔应时任清华大学校长吴有训之邀访问中国之前五年,玻尔就得出结论:量子论的中心思想是并协性。这一观念在西方似乎是革命性的,最著名的事件就是玻尔与爱因斯坦长达28年的辩论,爱因斯坦最初认为“量子论是何等的自相矛盾啊!”,而玻尔却坚信“完全没有矛盾” [12] 。正如玻尔自己所说,中国的治学传统使他产生了灵感,他认识到“在东方,并协观念乃是一种自然的思想方法” [13] ,而太极图正是这样一种能体现出宇宙万物对立统一运动的形象模式的代表。
1947年,玻尔因其在科学上的杰出成就以及对丹麦文化的重要贡献,被丹麦国王破格授予荣誉勋章。玻尔选定“太极图”作为自己礼仪罩袍的图案,借以表达自己对中国古代文明智慧与现代科技之间和谐一致性的认同。如图2所示,太极图上的丹麦文CONTRARIA SUNT COMPLEMENTA含义为“互斥即互补”,或被译为“对立者是相互补充的”。

图2. 玻尔礼仪罩袍图案
3. 耗散结构原理与太极图
比利时物理学家普利高津(Ilya Prigogine, 1917~2003)是耗散结构理论(dissipative structural theory)的创立者。这是一种关于非平衡系统的自组织理论 [14] 。该理论认为:一个远离平衡的开放系统(力学的、物理的、化学的、生物的、社会的经济的系统),通过不断地与外界交换物质和能量,在外界条件的变化达到一定的阙值时,可能从原有的混沌无序的混乱状态,转变为一种在时间上、空间上或功能上的有序状态 [15] 。而太极图所传递的“道生万物”和“道法自然”的思想与“耗散结构”的理论有着诸多相似之处。
从道生万物的角度来看,因为耗散结构原理研究的是开放系统,而宇宙中包括生命、时空在内的各种系统均为开放系统,力学的、物理的、化学的和生物的系统都是一样,这和道生一,一生二,二生三,三生万物的范畴是同样广泛的。老子说万物是从“道”开始的,要看世界的初始就要认识“道”;从道法自然的规律性来看,耗散结构原理指出一个开放体系在达到远离平衡态的非线性区域时,一旦体系的某一个参量达到一定的阙值,通过涨落,体系便可发生突变,即非平衡相变,这样就会由原来无序的混沌状态,变成时间、空间或功能有序的状态。这和老子所说的“人法地,地法天,天法道,道法自然”(第25章)有异曲同工之妙。耗散结构原理将“系统的演化过程看作一个自组织过程,其中‘自组织’的‘自’也包含‘自然’的内涵” [16] 。
具体来说,耗散结构原理和太极图的关联性如何呢?我们以人地关系系统演进的太极图图式(如图3)与耗散结构原理的关系加以说明。
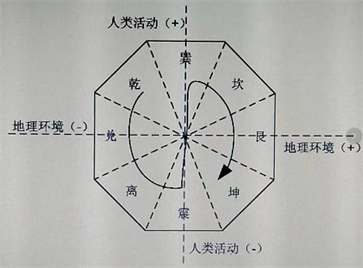
图3. 人地关系系统演进的太极图图式
人地关系中的“人”是指从事各种生产活动或社会活动的人;“地”是指与人类活动相关的地理环境 [17] ,人地关系是人类社会经济活动与地理环境之间的关系,人地系统可视为阴阳动态系统,人属于阳性,具有社会性和能动性,地属于阴性,具有被动型和承载性 [18] 。人地关系是开放的巨系统,与耗散结构在系统特性、系统层次、熵变规律、自组织现象、涨落之间等方面都表现出一定的共性 [19] 。
图3中将以地理环境熵流为横坐标、人类活动熵流为纵坐标,建立直角坐标系,人地系统状态基本上对应于图中直角坐标系的四个坐标轴、原点以及四个象限(王圣云,2013)。其中第三象限属于理想的类型,即人类系统和地理系统均向有序性增强方向发展;第一象限为即不理想类型,即人地冲突类型,人类系统和地理系统均向无序性增强方向发展,这是人地冲突的最终状态 [20] 。第四象限和第二象限分别属于地理环境与人类活动变化的过渡区。从图1可以看出,从“乾?兑?离?震”到“巽?坎?艮?坤”连结而成的S曲线,可反映人地系统演变。若将此太极S曲线按阴阳消长顺序按时间横轴展开,便可得到太极S曲线,对应于图3人地关系演进路径 [21] ,“S”曲线说明的正是“一阴一阳,互为进退”(张介宾《类经》)、“重阴必阳重阳必阴”《黄帝内经》)、“一动一静,互为其根”(周敦颐《太极图说》) [22] 的太极原理。
4. 惠勒质朴性原理与太极图
老子的“有生于无”的思想是约翰・阿奇博尔德・惠勒所倡导的“质朴性原理”(Wheeler’s principle of austerity)的哲学先驱。同玻尔1937年的中国之行使他发现“阴阳”图是并协原理的一个最好标志一样,1981年10月在来访中国期间,惠勒观赏了根据《封神演义》中的故事改编的舞剧《凤鸣岐山》,当他知道姜子牙手中指挥一切的“无”字旗上的含义是“NOTHING”时,极其兴奋,因为在中国古代思想中他找到了自己所倡导的“质朴性原理”的前驱,即物理学是从几乎一无所有达到几乎所有一切 [23] 。
老子认为“道”才是宇宙间最质朴者,它是不可名状的、混沌的始基。“道常无名、朴。虽小,天下莫能臣”。这里老子用“朴”形容“道”的原始无名的质朴状态。“朴”即无名之譬,勉强名之为“道”的宇宙始基就是浑然一体的“无”或“朴”。
作为道家的代表意象,太极图被用来体现“道”的质朴性也是极为贴切的。在《老子》第十四章对道的性质和状态做了具体的描述:“视之不见,名曰夷;听之不闻,名曰希;搏之不得,名曰微。此三者不可致诘,故混而为一。其上不敢,其下不昧,绳绳兮不可名,复归于无物。是谓无状之状,无物之象;是谓惚恍。迎之不见其首,随之不见其后”。老子所说的道是一种无色、无声、无形之物,有点像空气,混沌初始。这个概念和庄子在《应帝王》中讲到的“浑沌之死”中浑沌所代表的状态是一致的,是处于事物南北两极中间的中间状态、具有明确存在的“有”和无法精确甄别的“无”的属性的。
天地生两仪,两仪生四象,进而转向八卦图,太极八卦图其所具有的风水预测、运筹帷幄的功能性,也正是老子“道”即解释事物运行规律这一意蕴的真实写照,这也表明八卦图以“道”的潜在性和实用性来说明“道”之“有”,即非现实的“无”,即并非空无所有。这里的“无”和“有”是就超现象界、本体界而言的。
惠勒试图从他关于质朴性的哲学观点出发,即从“一无所有”导出整个物理学:“在过去的几个世纪里,物理学已经从很少几条原理导出了如此多的结论,从几乎一无所有中导出每一件事情。物理学曾是科学中最质朴者,它应当更加质朴”。也即是说物理学将终结于“没有定律的定律”这句质朴性的至理名言 [24] 。当代三个最伟大的场论体系(电动力学、几何动力学和色动力学)和质朴性之间的矛盾是最为激烈,通常很难想象这三个理论中所有的论证会源于混沌。对于这个问题的解答惠勒借用了“边界的边界为零”这一代数几何中并不显眼的恒等式来表达: 。因为在上述三个物理场论每个都要两次用到这个原理。惠勒用了一个立方体来阐述这个问题(如图4) [25] :立方体的“其中一个面的一维边界是由四个定向的线段构成的。立体方的二维边界则为六个面之和。把这六个面所有边棱都加起来,则其总和为零,因为立体方的每个棱边都用了两次,而方向想法,故成对地抵消了。这样,
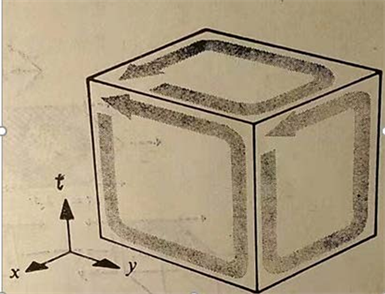
图4. 三维立体方的二维边界的一维边界是零
三维梯立体方的二维边界的一维边界是零, ”。据此,惠勒认为借助 这一边界之边界等于零的恒等式,我们可以说从一无所有中得到了应有尽有,因为这个等式包容了“今日的场物理学的整个广度和深度” [26] 。
尽管惠勒与老子这两位伟人在时空上相差太远,两者立论的基础和认识的深度也大不相同,但是惠勒的“质朴性原理”可以说是暗合老子的混沌之道。老子说道是“绳绳不可名”呈“惚恍”之状,“非无非有者”是庄子中浑沌形态。惠勒在“边界的边界――物理学的统一原理”一文中,惠勒借助热力学的第二定律,来说明物理定律说到底是“具有混沌的特征,是基于盲目的偶然性的”。在中国古汉字中,“倏”字和“忽”字都是“极快”的意思,与时间有关。倏为南帝,忽为北帝,混沌中间之帝,这儿的南、北、中显然是代表空间。庄子用“混沌”来描述处于事物南北两极中间的中间状态,是因为这个状态的特征就是不确定性,它具有明确存在的“有”和无法精确甄别的“无”的属性,七日之后,混沌开窍而死去,宇宙是否就从混沌中诞生了?这和惠勒说物理学的定律本身必定是在大爆炸时才出现的具有神奇的相似性。
也就是说,惠勒关于物理定律从无到有的思想,简直就是太极图之道的幽灵在现代物理学中的复现。将惠勒质朴性原理同太极图联系起来,我们会惊人的发现,以阴阳转换为基础的时空观,是时空物一体、无限循环的时空观,就此确立了阴质阳力,不可分离的质力关系。苗族文化解释阴阳时,不但解释出了质与力,还解释出了结构。质力与结构,为一分为三、合三为一的统一体。有生于无,无中生有;阴阳自动恒动,相互作用;阴阳永不重合,永不分离;阴阳圆周循环,对称平衡 [27] 。太极图中所蕴涵的“天下万物生于有,有生于无”当然也包括物理定律的创生过程。惠勒的物理学质朴性原理与太极图的意蕴惊人的一致,这绝不是偶然的巧合或者仅仅是不谋而合,而是一种古今贯通,东西文化的契合,这种契合的体现就是萨顿所说:“光明从东方来,法则从西方来” [28] 。
5. 结论
总的来说,太极图是玻尔“并协原理”的抽象化表现,是普利高津“耗散原理”物理内涵的哲学体现,也是“质朴性原理”、“有生于无”的真实写照,无论是玻尔族徽上的太极图样还是惠勒访华演讲时多次露面的太极卦图,这些,无一不说明中国的太极图所蕴含的“有生于无”、“从无序到有序”等的极深意蕴,正在成为那些东西方科学家启迪的源泉。正如创立介子场理论,被誉为现代“爱因斯坦”的汤川秀树在关于亚核粒子物理学的研究生涯中深感庄子的语言具有魅力,这里可以引用汤川秀树先生说过的一句话作为结语,“看来现代物理学在许多方面带来了古代哲学的回声。事实上,我们有时确实发现,古代世界的某一个学者思想中的一次灵感闪光,会在很晚以后的一个发现上渲染一种惊人明亮的光辉” [29] 。
参考文献
[1] “太极图”世界哲学的起源[J]. 科学大观园, 2009(9): 66-67.
[2] 李庆喜, 徐勤乐. 论物质范畴的内涵及两种存在的区别[J]. 安徽农学通报, 2007, 13(11): 203-204.
[3] 普利高津. 从存在到演化[M]. 曾庆宏, 等, 译. 上海: 上海科技出版社, 1986.
[4] 吴东好. 初探道家哲学与现代物理学[J]. 黑龙江科技信息, 2008(31): 200.
[5] 束景南. 太极图――人类文化之谜的破译[J]. 苏州大学学报, 1992(2): 1-10.
[6] 李以渝. 太极图意蕴与现代科学的平行与启迪[J]. 科学技术与辩证法, 1994, 11(5): 48-54.
[7] 李增智, 胡艳艳, 孟湛祥, 吴亚非. 玻尔的并协原理与我国古代阴阳学说[J]. 物理与工程, 2003, 13(2): 58-62.
[8] 王永炎, 张启明, 赵宜军. 太极图反映了自然界最基本的周期运动――简谐振动[J]. 自然杂志, 2009, 31(2): 71-72.
[9] 王永炎, 张启明, 赵宜军. 太极图反映了自然界最基本的周期运动――简谐振动[J]. 自然杂志, 2009, 31(2): 72.
[10] 李仕?. 玻尔“并协原理”与《八卦太极图》[J]. 周易研究, 1994(4): 74-75.
[11] 束景南. 太极图: 东方太极科技之光[J]. 寻根, 1996(3): 4-8.
[12] Wheeler, J.A. 惠勒演讲集: 物理学和质朴性[M]. 合肥: 安徽科学技术出版社, 1982: 5.
[13] Wheeler, J.A. 惠勒演讲集: 物理学和质朴性[M]. 合肥: 安徽科学技术出版社, 1982: 1.
[14] 汪霞. 耗散结构理论与后现代课程范式[J]. 全球教育展望, 2002, 31(7): 61-65.
[15] 伍进. 现代系统科学方法论及应用――优化方法与探索复杂性[M]. 成都: 成都电子科技大学出版社, 2005.
[16] 陈红兵. 试论中国传统科学范式与复杂性科学的相应[J]. 学术论坛, 2006(7): 18-21.
[17] 吴传钧. 论地理学的研究核心: 人地关系地域系统[J]. 经济地理, 1991, 11(3): 1-6.
[18] 王圣云. 人地系统演进的太极图式与模型构建[J]. 系统科学学报, 2013(3): 78.
[19] 王圣云. 人地系统演进的太极图式与模型构建[J]. 系统科学学报, 2013(3): 79.
[20] 潘玉君. 人地关系系统协调共生与区域可持续发展理论研究[J]. 齐齐哈尔大学学报(哲学社会科学版), 2000(1): 16-20.
[21] 王圣云. 人地系统演进的太极图式与模型构建[J]. 系统科学学报, 2013(3): 80.
[22] 吴攀升, 贾文毓. 人地耦合论: 一种新的人地关系理论[J]. 海南师范学院学报(自然科学版), 2002, 15(4): 50-53.
[23] Wheeler, J.A. 惠勒演讲集: 物理学和质朴性[M]. 合肥: 安徽科学技术出版社, 1982: 1-2.
[24] Wheeler, J.A. 惠勒演讲集: 物理学和质朴性[M]. 合肥: 安徽科学技术出版社, 1982: 45.
[25] Wheeler, J.A. 惠勒演讲集: 物理学和质朴性[M]. 合肥: 安徽科学技术出版社, 1982: 51.
[26] Wheeler, J.A. 惠勒演讲集: 物理学和质朴性[M]. 合肥: 安徽科学技术出版社, 1982: 57.
[27] 刘明武. 太极智慧: 物理学重建的理论基础[J]. 中州学刊, 2010(4): 143-146.
[28] 乔治・萨顿. 东方和西方的科学[EB/OL]. http://ishare.iask.sina.com.cn/f/19s1YTELNsd.html, 2019.
[29] 罗发海, 程民治. “道”与现代物理学[M]. 合肥: 安徽大学出版社, 2006.

