Journal of Applied Mathematics and Physics
Vol.07 No.07(2019), Article ID:93574,11 pages
10.4236/jamp.2019.77096
Oscillation for a Class of Fractional Differential Equation
Qian Feng, Anping Liu
School of Mathematics and Physics, China University of Geosciences, Wuhan, China




Received: May 25, 2019; Accepted: July 3, 2019; Published: July 10, 2019
ABSTRACT
We consider the oscillation of a class fractional differential equation with Robin and Dirichlet boundary conditions. By generalized Riccati transformation technique and the differential inequality method, oscillation criteria for a class of nonlinear fractional differential equation are obtained.
Keywords:
Oscillation, Fractional Derivative, Fractional Partial Differential Equation

1. Introduction
The fractional differential equations are used to describe mathematical models of numerous real processes and phenomena studied in many areas of science and engineering such as population dynamics, neural networks, industrial robotics, electric circuits, optimal control, biotechnology, economics and many other branches of science. Furthermore, the fractional calculus can also provide an excellent instrument for the description of memory and hereditary properties of various materials and processes due to the existence of a “memory” term in the model.
The oscillation theory as a part of the qualitative theory of differential equations has been developed rapidly in the last decades, and there has been a great deal of works on the oscillatory behavior of integer order differential equations [1] [2] [3]. As a new cross-cutting area, recently some attention has been paid to oscillations of fractional differential equations [4] [5] [6] [7]. Some new developments in the oscillatory behavior of solutions of fractional differential equations with damping terms [8] [9] [10] [11] have been reported by authors.
In this paper, we consider the oscillatory behavior of solutions of the following fractional differential equation:
(1.1)
where , is the Laplacian in , is a bounded domain in with a piecewise smooth boundary . is a real number and is the Riemann-Liouville left-sided fractional derivative of order of for .
We shall consider Robin and Dirichlet boundary conditions
(1.2)
and
(1.3)
where is continuous function, is the unit out normal vector to .
The following conditions are assumed to hold:
(H1) are convex in and is a monotone increasing function with for , there exist positive constants , such that for . And , , , , , , , .
(H2) and are positive continuous functions on for a certain , and is a nonpositive continuous function on for a certain . There exists a constant , for . And
, , .
(H3) is continuous function with for , there exists positive constant such that for , and for .
(H4) , and .
By a solution of (1.1), (1.2) and (1.3), it mean a nontrivial function
with ,
satisfies (1.1) for on and the boundary conditions (1.2) and (1.3).
A solution of (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative, otherwise it is nonoscillatory. Equation (1.1) is said to be oscillatory if all its solutions are oscillatory.
2. Preliminaries
In this section, there are several kinds of definitions of fractional derivatives and integrals and some lemmas which are useful throughout this paper.
Definition 2.1 [12] The Liouville left-sided fractional integral of order of a function on the half-axis is given by
provided that the left side is pointwise defined on , where is the gamma function.
Definition 2.2 [12] The Riemann-Liouville fractional partial derivative of order with respect to t of a function is given by
Lemma 2.3 [12] Let
Then
Lemma 2.4 [4] If and are nonnegative, then
where the equality holds if and only if .
3. Oscillation of (1.1) and (1.2)
For the sake of convenience, we set
Theorem 3.1 Suppose that (H1)?(H5) hold and if the fractional differential inequality
(3.1)
has no eventually positive solution and the fractional differential inequality
(3.2)
has no eventually negative solution, every solution of (1.1) and (1.2) is oscillatory in .
Proof Suppose that is a nonoscillatory solution of (1.1) and (1.2), it is either eventually positive or eventually negative. Without loss of generality, we may assume that is an eventually positive solution of (1.1) and (1.2) in . Integrating (1.1) with respect to over , we obtain
(3.3)
Using Green’s formula and boundary condition (1.2), it is obvious that
(3.4)
(3.5)
By using Jensen’s inequality and (H1), (H4), we get
(3.6)
Combining (3.3)?(3.6), we obtain
(3.7)
Therefore, is an eventually positive solution of (3.1), this contradicts the hypothesis.
Secondly, if is an eventually negative solution of the problem (1.1) and (1.2), then using above procedure, we can easily show that
is an eventually negative solution of the Equation (3.2).
This completes the proof.
Theorem 3.2 Suppose that (H1)?(H4) and
(3.8)
hold. if there exists a positive function such that
(3.9)
where , are defined as in (H1), then every solution of (3.1) and (3.2) is oscillatory.
Proof Suppose that is a nonoscillatory solution of (3.1). Without loss of generality, we may assume that is an eventually positive solution of (3.1). Then there exists , where is defined as in Lemma 2.3.
It follows from (3.7) that
(3.10)
Thus, is strictly decreasing on . Since for and (H1), we see that is eventually of one sign. We claim that
(3.11)
If not, there exists such that . Since is strictly decreasing on and it is clear that , where is a constant for . Therefore, we have
(3.12)
Due to and , we get
(3.13)
Integrating the above inequality from to , from Lemma 2.3, we have
(3.14)
which yields
(3.15)
By (H2) and (3.8), letting , we get . This contradicts the fact that . Hence, (3.11) holds.
From Lemma 2.3
(3.16)
therefore,
(3.17)
Define the function by the generalized Riccati substitution
(3.18)
Then we have for , and from (3.18), it follows that
(3.19)
Taking
(3.20)
from Lemma 2.4 and (3.19), we get
(3.21)
Integrating both sides of the inequality (3.21) from to , and taking the limit supremum of both sides of the above inequality as , we get
(3.22)
Which contradicts (3.9). The proof is complete.
Secondly, if is an eventually negative solution of the fractional differential inequality (3.2) and there exists . When (3.2) is oscillatory is similar to that of above procedure, and hence is omitted.
Theorem 3.3 Assume that (H1) - (H4) and (3.8) hold. Furthermore, suppose that there exist a positive function and a function , where , such that
where and has a nonpositive continuous partial derivative with respect to the second variable and satisfies
(3.23)
where , and are defined as in Theorem 3.2. Then all solutions of (3.1) and (3.2) are oscillatory.
Proof Suppose that is a nonoscillatory solution of (3.1). Without loss of generality, we may assume that is an eventually positive solution of (3.1). We proceed as in the proof of Theorem 3.2 to get (3.21), Multiplying (3.21) by and integrating from to , for , we derive
(3.24)
Therefore,
(3.25)
which is a contradiction to (3.23). The proof is complete.
Secondly, if is an eventually negative solution of the fractional differential inequality (3.2). The proof when (3.2) is oscillatory is similar to that of above procedure, and hence is omitted.
Next, we consider the case
(3.26)
which is different from (3.8). In this case, we have the following results.
Theorem 3.4 Assume that (H1)?(H4) and (3.26) hold, and that there exist a positive function such that (3.9) holds. If for every constant , such that
(3.27)
Then every solutions of (3.1) and (3.2) are oscillatory or satisfies or , where is defined as Lemma 2.3.
Proof Suppose that is a nonoscillatory solution of (3.1). We may assume that is an eventually positive solution of (3.1), proceeding as in the proof of Theorem 3.2 to get (3.10). Then there are two cases for the sign of .
When is eventually positive is similar to that of Theorem 3.2, we get that every solution of (3.1) is oscillatory.
If 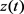 is eventually negative, there exists
is eventually negative, there exists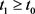 , such that
, such that 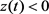 for
for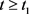 . From (3.16), therefore,
. From (3.16), therefore,
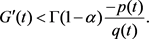 (3.28)
(3.28)
Since 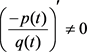 and
and 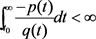 holds, then we obtain
holds, then we obtain
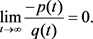 (3.29)
(3.29)
Letting 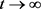 in (3.28), we have
in (3.28), we have
 (3.30)
(3.30)
If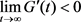 , then there exists
, then there exists 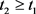 such that
such that 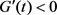 for
for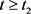 . Thus, we get
. Thus, we get 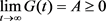 and
and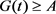 ,
,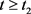 . Now we claim that
. Now we claim that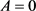 . If not, that is
. If not, that is

Integrating both sides of (3.31) from 


where

Integrating both sides of (3.33) from 


using 





Secondly, if 
Theorem 3.5 Assume that (H1) - (H4) and (3.26) hold, Let 






Proof Suppose that 


When 

4. Oscillation of (1.1) and (1.3)
In the next we establish sufficient conditions for the oscillation of all solutions of (1.1), (1.3). For this we need the following:
The smallest eigenvalue 

is positive and the corresponding eigenfunction 

Theorem 4.1 Let all the conditions of Theorem 3.2 and 3.3 be hold. Then every solution of (1.1) and (1.3) oscillates in
Proof Suppose that 








Using Green's formula and boundary condition (1.3), it is obvious that


By using Jensen's inequality and (H1) and (H4), we get

Set
Combining (4.2)-(4.5), we obtain

The rest of the proof is similar to that of Theorems 3.2 and 3.3, and hence the details are omitted.
Theorem 4.1 Let the conditions of Theorem 3.4 hold. Then every solution 



Theorem 4.2 Let the conditions of Theorem 3.5 hold; Then every solution 



The proofs of Theorem 4.1 and 4.2 are similar to that of Theorems 3.2-3.5 and hence the details are omitted.
5. Applications
Example 1 Consider the fractional differential equation

Here, 





Taking







Then, we get
It is clear that conditions (H1) - (H4) and (3.1) hold. Furthermore, taking

which satisfies condition (3.10). For every constant

Which shows that (3.27) holds. Therefore, by Theorem 3.4 every solution of (5.5) is oscillatory or satisfies 

Acknowledgements
This research was partially supported by grants from the National Basic Research Program of China, No. 41630643 and by the Science Foundation for The Excellent Youth Scholars of Ministry of Education of China, No. 11801530.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Feng, Q. and Liu, A.P. (2019) Oscillation for a Class of Fractional Differential Equation. Journal of Applied Mathematics and Physics, 7, 1429- 1439. https://doi.org/10.4236/jamp.2019.77096
References
- 1. Yang J., Liu, A. and Liu, G. (2013) Oscillation of Solutions to Neutral Nonlinear Impulsive Hyperbolic Equations with Several Delays. Electronic Journal of Differential Equations, 2013, 207-211.
- 2. Liu, A., Ma, Q. and He, M. (2010) Oscillation of Nonlinear Impulsive Parabolic Equations of Neutral Type. Rocky Mountain Journal of Mathematics, 36, 1011-1026. https://doi.org/10.1216/rmjm/1181069442
- 3. Liu, A., Xiao, L., Liu, T. and Zou, M. (2007) Oscillation of Nonlinear Impulsive Hyperbolic Equation with Several Delays. Rocky Mountain Journal of Mathematics, 37, 1669-1684. https://doi.org/10.1216/rmjm/1194275940
- 4. Xiang, S., Han, Z., Zhao, P. and Sun, Y. (2014) Oscillation Behavior for a Class of Differential Equation with Fractional-Order Derivatives. Abstract and Applied Analysis, 2014, Article ID: 419597. https://doi.org/10.1155/2014/419597
- 5. Grace, S.R., Agarwal, R.P., Wong, P.J.Y. and Zafer, A. (2012) On the Oscillation of Fractional Differential Equations. Fractional Calculus and Applied Analysis, 15, 222-231. https://doi.org/10.2478/s13540-012-0016-1
- 6. Han, Z., Zhao, Y., Sun, Y. and Zhang, C. (2013) Oscillation Theorem for a Kind of Fractional Differential Equations. Discrete Dynamics in Nature and Society, 2013, 216-219. https://doi.org/10.1155/2013/390282
- 7. Wang, Y., Han, Z., Zhao, P. and Sun, S. (2014) On the Oscillation and Asymptotic Behavior for a Kind of Fractional Differential Equations. Advances in Difference Equations, 2014, 50. https://doi.org/10.1186/1687-1847-2014-50
- 8. Yang, J., Liu, A. and Liu, T. (2015) Forced Oscillation of Nonlinear Fractional Differential Equations with Dampingterm. Advances in Difference Equations, 2015, 1. https://doi.org/10.1186/s13662-014-0331-4
- 9. Qi, C. and Huang, S. (2013) Interval Oscillation Criteria for a Class of Fractional Differential Equations with Damping Term. Mathematical Problems in Engineering, 2013, Article ID: 301085. https://doi.org/10.1155/2013/301085
- 10. Zheng, B. (2013) Oscillation for a Class of Nonlinear Fractional Differential Equations with Damping Term. Journal of Advanced Mathematical Studies, 6, 107-115. https://doi.org/10.1155/2013/912072
- 11. Prakash, P., Harikrishnan, S. and Benchohra, M. (2015) Oscillation of Certain Nonlinear Fractional Partial Differential Equation with Damping Term. Applied Mathematics Letters, 43, 72-79. https://doi.org/10.1016/j.aml.2014.11.018
- 12. Kilbas, A.A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractinal Differential Equations. North-Holland Mathematics Studies, 204.







