Energy and Power Engineering, 2009, 85-89
doi:10.4236/epe.2009.12013 Published Online November 2009 (http://www.scirp.org/journal/epe)
Heat Transfer by Natural Convection from a
Vertical and Horizontal Surfaces Using
Vertical Fins
H. R GOSHAYESHI1, F. AMPOFO2
1Department of Mechanical Engineering, Azad University of Mashhad (IAUM), Mashhad, Iran
2Department of Mechanical Engineering, School of Engineering System and Design, London South Bank
University, London, UK
Abstract: Natural convective heat transfer from a heated horizontal and vertical surfaces directly exposed
into air which vertical fins, attached to a surface, project vertically downwards has been numerically studied.
It has been assumed that the fins are everywhere at the temperature of the surface. The governing equations,
written in dimensionless form, have been solved using the finite element procedure. The results show that
vertical plate with vertical fins gives the best performance for natural cooling.
Keywords: natural convection, horizontal and vertical plate, fins, Nusselt number
1. Introduction
The vertical and horizontal plate configurations are the
most common geometry for a naturally cooled heat sink.
The configuration has been studied by number of re-
searchers. The most commonly used predictive equation
for convection was derived by Barcohen, S. & Rohsenow
W [1] and Kruaus, A. D & Bar-Dohen [2]. This situation
has been considered for free convective heat transfer
from a heated horizontal and vertical surface directly
exposed to air with a free surface to vertical fins attached
to surface that project vertically downward into the air
has been studied by Smith, H. [3] and Magyaro, L and
pep, H [4]. Unlike the well-study vertical/vertical con-
figuration very few research papers have been written on
the horizontal/up configuration. The most comprehensive
experimental interrogation was performed by Fuji, V. &
Magata, B, [5] but they did not derive an accurate equa-
tion which matched the full range of their experimental
data. This work compares horizontal plate heat sinks
with vertical plate heat sink for natural cooling applica-
tion. As shown in Figure 1, three different configurations
will be discussed: 1) vertical plate with vertical fins 2)
horizontal plate with fins facing up 3) vertical pate with
horizontal fins. Figure 1 gives some quick guideline on
the merits of the different configurations.
2 Governing Equations and Solution
Procedures
It has been assumed that flow is steady, laminar and
two-dimensional and that the air properties are constant
except for the density change with temperature which
gives rise to the buoyancy forces, this being treated using
the goussinesq approach. The following dimensionless
variables have then been defined:
2
/,/,/ ,/ ,()/()
H
C
H
xxHyyHTTTc TT  

  

(1)
where T is the temperature.
H
T is the temperature of
the hot wall and is the temperature of the fin. The
prime ( ' ) denotes a dimensional quality .
C
T
In terms of these dimensionless variables, the govern-
ing equations are:
22
22
xy




 (2)
x
T
Ra
yx
yxxy 

























2
2
2
2
Pr

(3)
22
22
0
TTTT
yx xyxy

  



 


(4)
Here Ra is the Rayleigh number based on the height,
3
()
HC
g
TTH
Ra


 
 (5)
The above dimensionless equations, subject to the
boundary conditions, have been solved using the fin
element procedure. The mean heat transfer rate across

H. R. GOSHAYESHI ET AL.
86
the enclosure has here been expressed in terms of a mean
Nusselt number, Nu, based on the height,
H

m
q
()
, the mean
heat transfer rate from the lower surface, and on and
the overall temperature difference,
H
igh
TLow T

.
3. Results and Discussion
The computer program shows that h convection for horizon-
tal backplane fin channel is lower than h convection for ver-
tical/vertical fin channels. For a given heat sink volume,
there exits an optimal fin spacing. The optimum value
occurs when two trends are balanced.
If the fins are closely spaced, the heat transfer coeffi-
cient (h) is lower because mixing of the boundary layer
occurs (the fills up with warm air). The graph if Figure 3
clearly shows that the heat transfer coefficient decreases
as the gap between fins decreases. However, if the fins
are closely spaced, there is also more dissipating surface
area (more fins for a given volume). The additional sur-
face area can counteract the reduced heat transfer coeffi-
cient. This can be seen by examining the graph of total
wattage dissipated in Figure 4. For the 150 mm X 150
mm vertical/vertical heat sink shown in the graph, the
spacing of 7.5 mm provided the optimal combination of
heat transfer coefficient and dissipating surface area.
Figure 4, presented above, shows the wattage dissi-
pated for an entire 150 mm X 150 mm heat sink, includ-
ing end fins and radiation (emissivity = 0.1, typical of a
bare extruded surface). When a horizontal baseplate heat
sink is sinks in not square, there will be two possible
orientations for the fin channel. As shown in Figure 5,
the fins should be oriented to provide the shortest chan-
nel depth. For a baseplate which 100 mm X 50 mm, the
proper channel orientation will provide 15% better per-
formance.
Figure 1. Fin configurations for natural (Free) cooling
Figure 2. Primary air flow pattern for the vertical/vertical configuration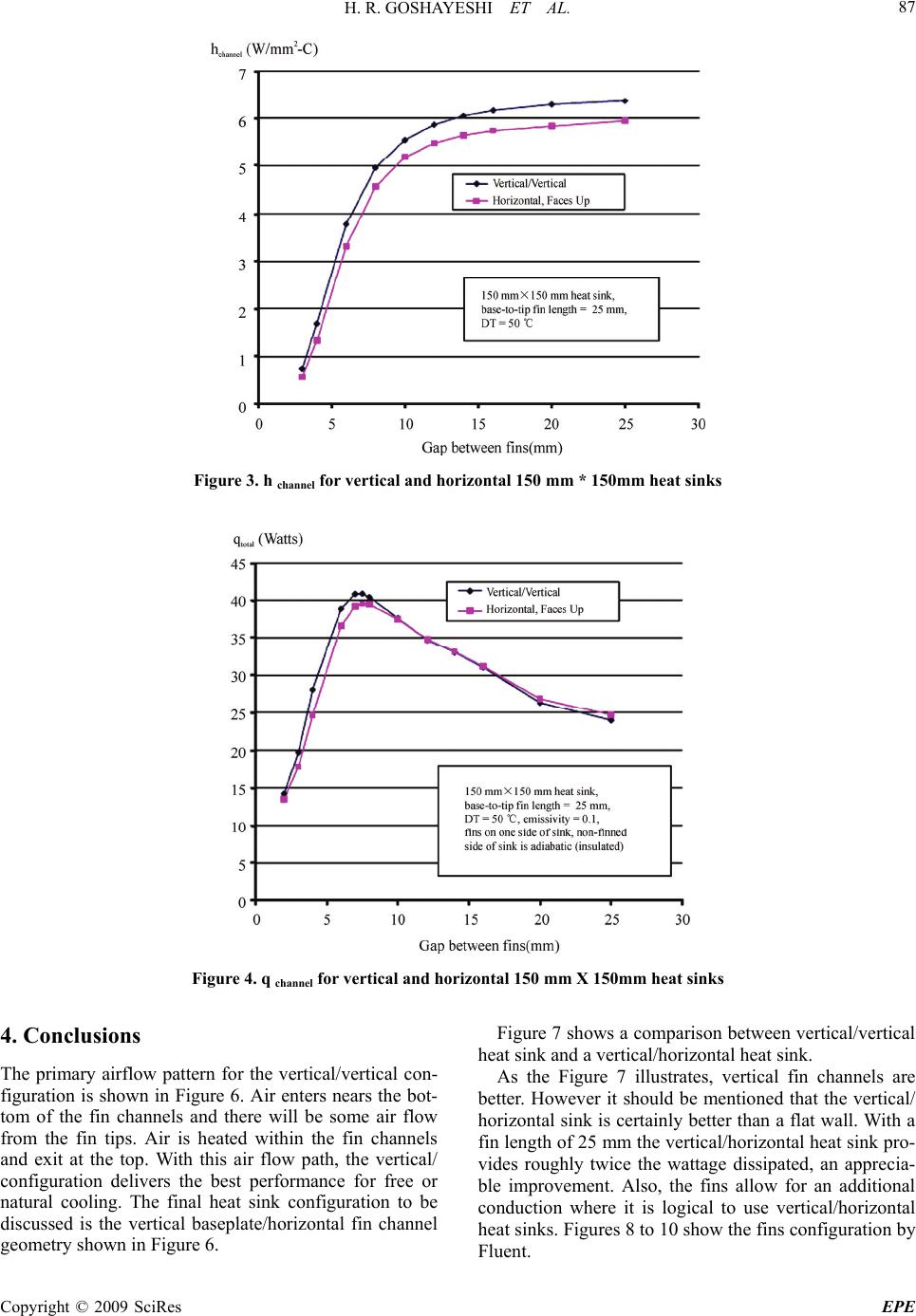

H. R. GOSHAYESHI ET AL. 87
Figure 3. h channel for vertical and horizontal 150 mm * 150mm heat sinks
Figure 4. q channel for vertical and horizontal 150 mm X 150mm heat sinks
4. Conclusions
The primary airflow pattern for the vertical/vertical con-
figuration is shown in Figure 6. Air enters nears the bot-
tom of the fin channels and there will be some air flow
from the fin tips. Air is heated within the fin channels
and exit at the top. With this air flow path, the vertical/
configuration delivers the best performance for free or
natural cooling. The final heat sink configuration to be
discussed is the vertical baseplate/horizontal fin channel
geometry shown in Figure 6.
Figure 7 shows a comparison between vertical/vertical
heat sink and a vertical/horizontal heat sink.
As the Figure 7 illustrates, vertical fin channels are
better. However it should be mentioned that the vertical/
horizontal sink is certainly better than a flat wall. With a
fin length of 25 mm the vertical/horizontal heat sink pro-
vides roughly twice the wattage dissipated, an apprecia-
ble improvement. Also, the fins allow for an additional
conduction where it is logical to use vertical/horizontal
heat sinks. Figures 8 to 10 show the fins configuration by
Fluent.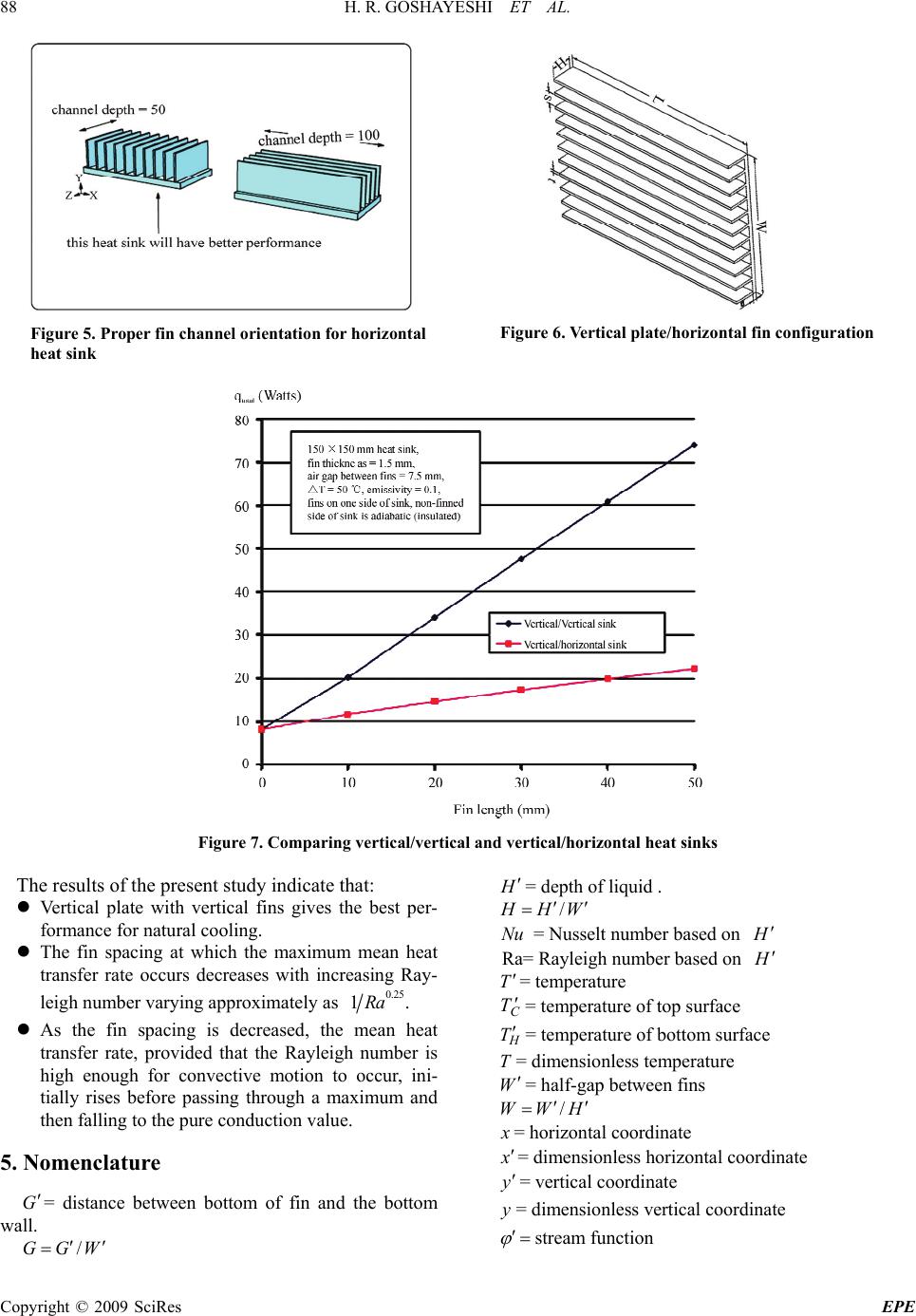

H. R. GOSHAYESHI ET AL.
88
Figure 5. Proper fin channel orientation for horizontal
heat sink
Figure 6. Vertical plate/horizontal fin configuration
Figure 7. Comparing vertical/vertical and vertical/horizontal heat sinks
The results of the present study indicate that:
 Vertical plate with vertical fins gives the best per-
formance for natural cooling.
 The fin spacing at which the maximum mean heat
transfer rate occurs decreases with increasing Ray-
leigh number varying approximately as 0.25
1Ra .
 As the fin spacing is decreased, the mean heat
transfer rate, provided that the Rayleigh number is
high enough for convective motion to occur, ini-
tially rises before passing through a maximum and
then falling to the pure conduction value.
5. Nomenclature
G= distance between bottom of fin and the bottom
wall.
WGG  /
H

= depth of liquid .
WHH



/
Nu = Nusselt number based on
H

Ra= Rayleigh number based on
H

T

= temperature
C
T

= temperature of top surface
H
T

= temperature of bottom surface
T= dimensionless temperature
W

= half-gap between fins
HWW



/
x
= horizontal coordinate
x

= dimensionless horizontal coordinate
y

= vertical coordinate
y= dimensionless vertical coordinate



stream function

H. R. GOSHAYESHI ET AL. 89
Figure 8: Fin configurations for vertical pate with horizontal fins by Fluent
Figure 9: Fin configurations for horizontal plate with fins facing up by Fluent
Figure 10: Fin configurations for vertical pate with horizontal fins by Fluent

= dimensionless stream function

or u= Velocity

= dimensionless velocity
REFERENCES
[1] S. Barcohen and W. Rohsenow, “Thermal optimum spa-
cing of vertical natural convection cooled parallel plates,”
Journal of Heat Treansfer, Vol. 106, pp. 116–123, 1984.
[
2] A. D. Kruaus and Bar-Dohen, “A design and analysis of heat
sink,” John Wiley and Sons, New York, pp. 305–320, 1995.
[3] H. Smith, “Combined heat and mass transfer effect in free
convection,” Electricity Research Laboratories, Leather-
head, Surrey, February 2006.
[4] L. Magyaro and H. Pep, “Free convection flow pass an
infinte vertical plate,” ASME Modelling B, Vol. 72, No.
3, 2007
[5] V. Fuji and B. Magata, “MHD unsteady free convection
flow through a prous media, Energy Research, Vol. 7, pp.
89–109, 2004.