Vol.1, No.3, 211-219 (2009)
doi:10.4236/health.2009.13036
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/
Health
Openly accessible at
Modelling of the relationship between systolic blood
pressure and glucose with the magnesium ion present
in the blood plasma: an approach using artificial neural
networks
Júlio C. D. Conway1,2, Stefânia N. Lavorato1, Vinícius F. Cunha1, Jadson C. Belchior1
1Departmento de Química-ICEx, Universidade Federal de Minas Gerais, Av. Antônio Carlos 6627, Pampulha, (31.270-901) Belo
Horizonte, Minas Gerais, Brazil; [e-mail], [e-mail], [e-mail], [e-mail]
2Pontifícia Universidade Católica de Minas Gerais, Av. Dom José Gaspar 500, Coração Eucarístico, (30.535-901) Belo Horizonte,
Minas Gerais, Brazil.
Received 20 August 2009; revised 9 September 2009; accepted 10 September 2009.
ABSTRACT
Artificial neural networks became an attractive
alternative for modeling and simulation of com-
plex biological systems. In the present work, a
blood plasma model based on artificial neural
networks was proposed in order to evaluate the
relationship between the magnesium ion pre-
sent in the blood plasma and systolic blood
pressure and glucose. Experimental and simu-
lated data were used to construct and validate
the model. It performed the analysis consider-
ing the systolic blood pressure and glucose as
a function of magnesium ion concentration at a
fixed temperature (37oC). Predictions of these
relationships through the proposed model
produced errors, on average, below 1% com-
pared against experimental data not presented
in the training step. The proposed methodology
revealed quantitative results and correctly pre-
dicted behaviors and trends towards the asso-
ciation between magnesium concentrations
and systolic blood pressure, and glucose in far
agreement with experimental results from lit-
erature. These results indicated that artificial
neural networks can successfully learn the
complexity of the relationships among bio-
logical parameters of distinct groups and can
be used as a complementary tool to assist
studies in which the role of magnesium in
systolic blood pressure and glucose are con-
sidered.
Keywords: Artificial Neural Networks; Blood
Plasma; Magnesium; Systolic Blood Pressure
1. INTRODUCTION
Magnesium plays an important role in cardiac and vas-
cular functions and participates in glucose metabolism [1].
The measurements of diabetic patients have shown that
plasma magnesium concentrations are inversely related to
plasma glucose values [2]. Some studies [3,4] have shown
that magnesium deficiency can be associated with coro-
nary diseases such as atherosclerosis and cardiac ar-
rhythmia. Magnesium is an essential element in cardiac
and vascular functions and is fundamental in the regula-
tion of blood pressure, as it regulates the rate of calcium,
sodium, potassium and the pH inside the cell [5]. These
elements are important in the process of contraction and
relaxation of the vascular smooth muscle. Consequently,
the reduction in magnesium levels can generate an in-
crease in the muscular tonus which, in turn, can produce
an increase in blood pressure [5].
Other factors can affect the blood pressure, such as
biochemical factors, age, sex and race [6]. In general,
magnesium can be found in three different forms in the
blood plasma: ionic form, complex form and connected to
plasma proteins. The free ionic form of magnesium
([Mg2+]free) has the main biological activity, however,
assaying the total ionic concentration ([Mg2+]total) is easier
and less expensive [7].
Studies based on the regulatory function of magnesium
have been developed across the years [8-10]. In the latter
works, low magnesium levels were found in patients with
hypertension and cardiovascular disease (CVD), mainly
among black individuals [8]. It found lower rates of mag-
nesium in the ionic form in hypertensive patients rather
than in those considered normotensives [9] and it verified a
significant inverse relation between plasma magnesium
and systolic blood pressure (SBP) [10]. However, the blood
plasma is a complex system, in which metal ions interact,
for example, in competition for ligands. Therefore, the

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/
212
Openly accessible at
development of methodologies capable of efficiently simu-
lating the relationships between plasma magnesium and
SBP as well as between plasma magnesium and glucose
can be a valuable tool for helping studies concerning this
metal and SBP and glucose.
Efficient computational methodologies have been ap-
plied in order to model the interaction between metal ions
presenting in blood plasma [11,12]. A model was pro-
posed [13], using multiple regression techniques to evaluate
the metal ion complexation in blood plasma. This method
proved to be efficient in simulating ion-ligands formation
and had been used to simulate experimental data [14,15].
Alternatively, artificial neural networks (ANNs) have already
been used to predict the behavior of metal ions and their
ligands in blood plasma [16]. Many researchers also pointed
out the use of ANNs in biomedicine [17-22] and more
specific in diagnosis [23,24]. Hence, ANNs are consid-
ered to be an efficient and reliable tool in simulation and
prediction of biological parameters [25,26]. A previous
work from our group demonstrated the use of ANNs to
analyze the temperature and pH effects on the complexa-
tion of magnesium and calcium in a blood plasma model.
It also analyzed the competition between these metals for
ligands. As pointed out, ANNs are suitable when simul-
taneously analyzing a great number of data, for example,
in studies with many individuals [27].
The present work focused on the applicability of the
ANN’s as a reliable tool for simulating and analyzing the
relationship between blood plasma magnesium concen-
trations and SBP and glucose. In view of this, the ex-
perimental data of SBP, glucose and [Mg2+]total from four
different groups of individuals (black man, black women,
white men, white women) were selected from previous
investigation [8] to build a model based on an ANN. This
model was then used to examine the relation between
SBP versus [Mg2+] and glucose versus [Mg2+], thus evi-
dencing the ability of ANNs in mapping complex non-
linear relationship. As these relationships are learned by
the ANN, this model can be applied as a different ap-
proach to determine the role of magnesium in SBP or
glucose, without the need of a large data set.
2. MATERIALS AND METHODS
2.1. Methods
A computational method was used to investigate the
relationships between [Mg2+]total and SBP. The artificial
neural network was trained with experimental and simu-
lated data. This approach is inspired by biological nerv-
ous systems, such as the brain, process information. It is
composed of a large number of highly interconnected
processing elements called neurons. These neurons work
together to solve specific problems, and then ANNs learn
from examples [28]. This knowledge is stored in the conne-
xions between neurons, through numbers, also known as
Figure 1. Basic multilayer perception structure.
synaptic weights. And learning involves adjustments to
these synaptic weights. The general structure of a multi-
layer perceptron ANN (see Figure 1) can be configured for
a specific application, such as pattern recognition or data
classification, through learning processes. ANNs have a
remarkable ability to derive meaning from complicated or
imprecise data, and can be used to extract patterns and
detect trends that are too complex to be noticed by either
humans or other computer techniques, such as numerical
mathematical methods. In addition, an ANN has the ad-
vantage of real time operation, since ANN computations
may be carried out in parallel, so special hardware devices
can be designed and manufactured to take advantage of the
real time operation capability [29].
The ANN structure used in this work is a multilayer
perception feed-forward network. Signals travel one way
only, from inputs to outputs. There is no feedback loops,
i.e. the output of any layer does not affect the previous
layers. In this work it used the backpropagation learning
algorithm. This algorithm consists of an interactive proc-
ess where the weights of each neuron are adjusted in such
way that the error between the desired output and the
actual output is reduced. According to Levenberg-
Marquardt method [30], these weights (W) can be up-
dated as
)()(])()([ 1
1n
l
n
T
nnn
T
nn WWJIWJWJWW


 (1)
The variable β is a parameter with initial value β = 0.01
and changes according to the minimization error. J is the
Jacobian matrix and I is the identity matrix. The error
between the desired output and the actual output is cal-
culated by the parameter ε, as given by
2
1)(
 n
j
l
jj
louty
 (2)
The parameter is the actual output value of layer l
and the parameter is the desired output value of layer
l. Thus, Eq.2 evaluates the quadratic error of each layer l.
The structure of an ANN can be defined as (in, ni, nj, out),
where in represents the number of input neurons, ni
represents the number of neurons of first hidden layer, nj
represents the number of neurons of the second hidden
l
j
out
j
y

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/
213
213
Openly accessible at
layer and out represents the number of neurons in the
output layer. This structure was used to construct the
models implemented in the present work.
2.2. Data
The proposed model aimed to evaluate the relationship
between SBP and glucose with the [Mg2+] presenting in the
blood plasma. Consequently, it was necessary to find ex-
periments in order to correlate these data. The experimen-
tal data relating SBP, glucose and [Mg2+]total which is a-
vailable to train and validate the proposed model were the
measurements of Ma et al. [8]. They examined the rela-
tionships between [Mg2+]total with cardiovascular disease,
hypertension, diabetes mellitus, insulin and glucose, of
four groups of individuals, participants of the ARIC
(Atherosclerosis Risk in Communities) Study [31]. About
15,000 participants took part in this study, male and female,
black and white, aging from 45 to 64 years old.
In the work of Ma et al. [8], it evaluated the relation-
ship between [Mg2+]total and SBP, and between [Mg2+]total
and glucose, among others. However, [Mg2+]free was not
considered. Thus, in order to extend the applicability of
the proposed model, [Mg2+]free was included in our model,
for a fixed pH value of 7.4. To simulate [Mg2+]free from
the experimental samples of [Mg2+]total, it used the blood
plasma model [13] which had been mentioned before.
This approach allowed us to generate approximately 3500
different simulated values for the relation between SBP
and [Mg2+]total and [Mg2+]free, and also approximately
3500 different simulated values for the relation between
glucose and [Mg2+]total and [Mg2+]free, for each group of
individuals (black man, black woman, white man and
white woman).
The success of the ANN method depends on the effi-
ciency of the ANN training and validation. It is desirable
that the ANN is trained with an experimental data set and
validated with a complete different set of data. However, in
lack of a different set of experimental data related [Mg2+]
to glucose and SBP, the experimental data used before [8]
was split into two sets: the first data set was used to train
and test the ANN; and the second was used to validate the
ANN. In this way, the ANN was validated with data which
did not take part in the training step.
2.3. ANN Training and Validation
The methodology used to obtain the ANN configuration
with the smallest training error consists of changing the
number of intermediate layers, as well as the number of
neurons in each layer of the ANN under construction. A
computer code evaluated each ANN configuration with 1
and 2 hidden layers, and with 3 to 10 neurons in each
layer, posteriorly indicating the best ANN configuration.
The ANN mean square error was calculated according to
Eq.2. The ANN activation functions used were hyper-
bolic tangent in the hidden layers and a linear function in
Figure 2. ANN minimization error.
the output layer. The initial weights were randomly se-
lected.
In order to perform the training and test of the ANN,
the first sight could be used as a hold-out procedure, for
example a random split of the data, with 2/3 for training
and the rest 1/3 for testing. However, this procedure has
two inconveniences. First, only 2/3 of the data are used
for training and only 1/3 of the data are used for testing,
reducing the amount of data available for training and
testing. Moreover, the classification accuracy is based on
a single random split of the data, which is not very sig-
nificant from a statistical point of view [32]. Therefore, to
avoid these drawbacks, a k-fold cross-validation proce-
dure was used. In this procedure, the data set of size N is
divided in k mutually exclusive subsets (folds) of ap-
proximately equal size (1 < k ≤ N). The training and test
are performed k times, using k-1 subsets for training and
the remainder for testing. Besides, the training of ANNs
is prone to local minimum, i.e., the final result depends on
the initial weights. Also, the random splitting (using holdout
or K-fold) is dependent of the type of split performed. To
overcome these dependencies, it performed multiple runs
and the results were presented as the average of these runs.
Consequently, for each configuration to be tested, a total
of 20 runs of 10-fold cross-validation procedure were used
to examine which ANN configuration would present the
smallest training error. The error minimization process
during the learn phase of the ANN is shown in Figure 2.
The training was performed until 5000 epochs. In this
convergence region, the mean square error was ap-
proximately 10-15, evidencing a correct mapping of the
input-output relationship. After the training step, the
ANN was ready to be used as a predictor, and the pre-
diction error was calculated according to
100


ex
prex
pr v
vv
Error (3)
in which Errorpr is the prediction error, vex is the expected
value and vpr is the value predicted by the ANN.
The normal range for [Mg2+]total in human blood plasma
is 0,65-1,25 mM [33]. As the experimental data for [Mg2+ ]total
from [8] was ranging from 0,7 to 0,9 mM, it was possible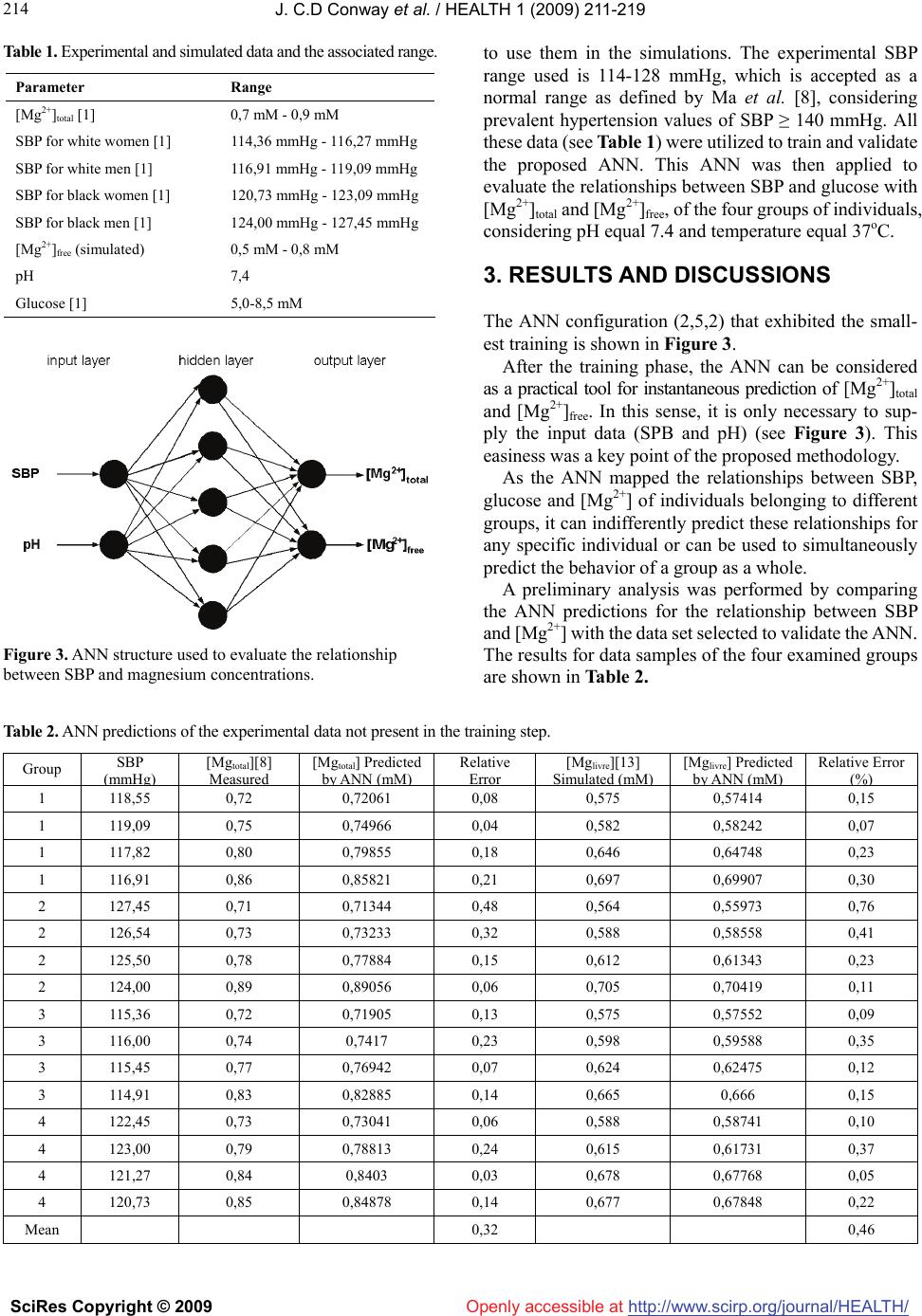

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/
214
Table 1. Experimental and simulated data and the associated range. to use them in the simulations. The experimental SBP
range used is 114-128 mmHg, which is accepted as a
normal range as defined by Ma et al. [8], considering
prevalent hypertension values of SBP ≥ 140 mmHg. All
these data (see Table 1) were utilized to train and validate
the proposed ANN. This ANN was then applied to
evaluate the relationships between SBP and glucose with
[Mg2+]total and [Mg2+]free, of the four groups of individuals,
considering pH equal 7.4 and temperature equal 37oC.
Parameter Range
[Mg2+]total [1] 0,7 mM - 0,9 mM
SBP for white women [1] 114,36 mmHg - 116,27 mmHg
SBP for white men [1] 116,91 mmHg - 119,09 mmHg
SBP for black women [1] 120,73 mmHg - 123,09 mmHg
SBP for black men [1] 124,00 mmHg - 127,45 mmHg
[Mg2+]free (simulated) 0,5 mM - 0,8 mM
pH 7,4
Glucose [1] 5,0-8,5 mM
3. RESULTS AND DISCUSSIONS
The ANN configuration (2,5,2) that exhibited the small-
est training is shown in Figure 3.
After the training phase, the ANN can be considered
as a practical tool for instantaneous prediction of [Mg2+]total
and [Mg2+]free. In this sense, it is only necessary to sup-
ply the input data (SPB and pH) (see Figure 3). This
easiness was a key point of the proposed methodology.
As the ANN mapped the relationships between SBP,
glucose and [Mg2+] of individuals belonging to different
groups, it can indifferently predict these relationships for
any specific individual or can be used to simultaneously
predict the behavior of a group as a whole.
A preliminary analysis was performed by comparing
the ANN predictions for the relationship between SBP
and [Mg2+] with the data set selected to validate the ANN.
The results for data samples of the four examined groups
are shown in Table 2.
Figure 3. ANN structure used to evaluate the relationship
between SBP and magnesium concentrations.
Table 2. ANN predictions of the experimental data not present in the training step.
Group SBP
(
mmH
g)
[Mgtotal][8]
M
easu
r
ed
[Mgtotal] Predicted
by
A
NN
(
mM
)
Relative
Err
or
[Mglivre][13]
S
im
u
l
a
t
ed
(
mM
)
[Mglivre] Predicted
by
A
NN
(
mM
)
Relative Error
(%)
1 118,55 0,72 0,72061 0,08 0,575 0,57414 0,15
1 119,09 0,75 0,74966 0,04 0,582 0,58242 0,07
1 117,82 0,80 0,79855 0,18 0,646 0,64748 0,23
1 116,91 0,86 0,85821 0,21 0,697 0,69907 0,30
2 127,45 0,71 0,71344 0,48 0,564 0,55973 0,76
2 126,54 0,73 0,73233 0,32 0,588 0,58558 0,41
2 125,50 0,78 0,77884 0,15 0,612 0,61343 0,23
2 124,00 0,89 0,89056 0,06 0,705 0,70419 0,11
3 115,36 0,72 0,71905 0,13 0,575 0,57552 0,09
3 116,00 0,74 0,7417 0,23 0,598 0,59588 0,35
3 115,45 0,77 0,76942 0,07 0,624 0,62475 0,12
3 114,91 0,83 0,82885 0,14 0,665 0,666 0,15
4 122,45 0,73 0,73041 0,06 0,588 0,58741 0,10
4 123,00 0,79 0,78813 0,24 0,615 0,61731 0,37
4 121,27 0,84 0,8403 0,03 0,678 0,67768 0,05
4 120,73 0,85 0,84878 0,14 0,677 0,67848 0,22
Mean 0,32 0,46
Openly accessible at

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/Openly accessible at
215
It is important to emphasize that these data were not
taken into account in the training step. It selected four
individuals of each group, and their SBP and pH (7.4) data
were submitted to the ANN. The results obtained with the
ANN were compared with the experimental data. The aver-
age prediction error is below 1% for both [Mg2+]total and
[Mg2+]free, indicating that the ANN correctly mapped the
relationship between the input and output data space. More-
over, although a mix of experimental and simulated data
were used to train and validate the ANN, the simulated
data were generated by an efficient and well established
blood plasma model [13], and therefore, it was appropri-
ate to demonstrate the validity of the proposed model.
Based on this preliminary analysis, further assessments
were performed to evaluate the effectiveness and accu-
racy of the proposed model. From the data set used to
validate de ANN, it selected only 10 samples for each
group of individuals to illustrate clearly the ANN predic-
tion capability. A simultaneous comparison for each group
of individuals between the experimental data and the
ANN predictions for SBP as a function of [Mg2+]total (see
Figure 4a) and SBP as a function of [Mg2+]free (see Fig-
ure 4b) are presented. Although the experimental data for
each group exhibit different shapes, the ANN accurately
classified each individual in its respective group.
As mentioned before, it is instructive to point out that
after the training step, it was only necessary to feed the
ANN with the values of SBP and pH, and the ANN in-
stantaneously produced the response, i.e., the values of
[Mg2+]total and [Mg2+]free for the race and sex corresponding
to the input values.
The model was also applied to perform a quantitative
analysis in order to demonstrate the efficiency of the pro-
posed methodology in determining the relationship be-
tween SBP and magnesium concentration. For example,
considering the white women group, simulating an in-
crease in the value of SBP, from 114,18 mmHg to 116,27
mmHg (a variation of about 2%), the ANN predicted a
decrease of the [Mg2+]total from 0,80 mM to 0,75 mM
(~6%), and a decrease of [Mg2+]free from 0,64 mM to
0,58 mM (~10%). In the same way, considering the
white men group, simulating an increase in SBP from
116,91 mmHg to 119,09 mmHg (~2%), the ANN pre-
dicted a decrease of [Mg2+]total from 0,86 mM to 0,75
mM (~13%), and a decrease of [Mg2+]free from 0,69 mM
to 0,58 mM (~16%). It was possible to observe that for
approximately the same variation of SBP (about 2%), the
variation of magnesium concentrations for white men
(~13% for [Mg2+]total and ~16% for [Mg2+]free) was
greater than those values for white women (~6% for
[Mg2+]total and ~10% for [Mg2+]free).
The quantitative relationship between SBP and mag-
nesium concentration of black individuals was also in-
vestigated. For example, considering the black women
group, when simulating an increasing in SBP from 120,73
mmHg to 123,00 mmHg (~2%), the ANN predicted a
decrease of [Mg2+]total from 0,85 mM to 0,79 mM (~7%),
and a decrease of [Mg2+]free from 0,67 mM to 0,61 mM
(~9%). Similarly, for the black men group, when in-
creasing SBP from 124,00 mmHg to 126,36 mmHg
(~2%), the ANN predicted a decrease of [Mg2+]total from
0,89 mM to 0,74 mM (16%), and a decrease of [Mg2+]free
from 0,70 mM to 0,59 mM (16%). Therefore, for an in-
crease of approximately 2% in SBP, the ANN predicted a
decrease in magnesium concentrations of approximately
16% for black men and about 8% for black women.
These results allowed extracting two important fea-
tures of the studied groups. First, the predictions sug-
gested that men have greater average SBP than women
(the predicted values for black men (BM) and white men
(WM) were greater than the predicted values for black
women (BW) and white women (WW), respectively.
These observations were in agreement with the work of
Eison et al. [34], who verified that women, in general,
have lower average SBP than men. Second, the SBP
predicted values for black men (BM) and black women
(BW) were greater than the SBP predicted values for
white men (WM) and white women (WW), and this
suggested that black individuals have average SBP val-
ues higher than white individuals. The same behavior
was verified in the experimental work of Agyemang et al.
[35] who showed that the higher prevalence of hyperten-
sion in blacks was due to the less effective control of
blood pressure than in whites. Also, the work of Li et al.
[36] showed that the hypertension and hypertensive
complications were more frequent in black people, due
to their lower socioeconomic level, and consequently,
for their minor access to medical assistance. Fauvel and
Laville [37] also showed that hypertension and salt sen-
sitivity were more intense in individuals of black race
than other racial groups. In addition, the proposed ap-
proach identified the groups as black or white individu-
als, and classified them by sex. Moreover, the proposed
methodology correctly allowed evaluating the relation-
ship between SBP, glucose and [Mg2+]free. In the experi-
mental data used, there were not measurements relating
those parameters. However, as an advantage of the pro-
posed approach the model was able to quantitatively
predict [Mg2+]free (see Figure 4b). It is interesting to say
that all these classifications and analyses were simulta-
neously performed.
3.1. Analysis of Glucose as a Function of
Magnesium Concentrations
As mentioned before [2], magnesium concentrations are
inversely related to plasma glucose in diabetes patients.
Also, several works [38,39,40] have shown that glucose
is related to the magnesium levels in blood plasma. For
example, the measurements of McNair et al. [38] for glucose
as a function of serum magnesium, in patients with car-
diovascular disease, showed that the blood plasma glu-
cose levels diminished when the serum magnesium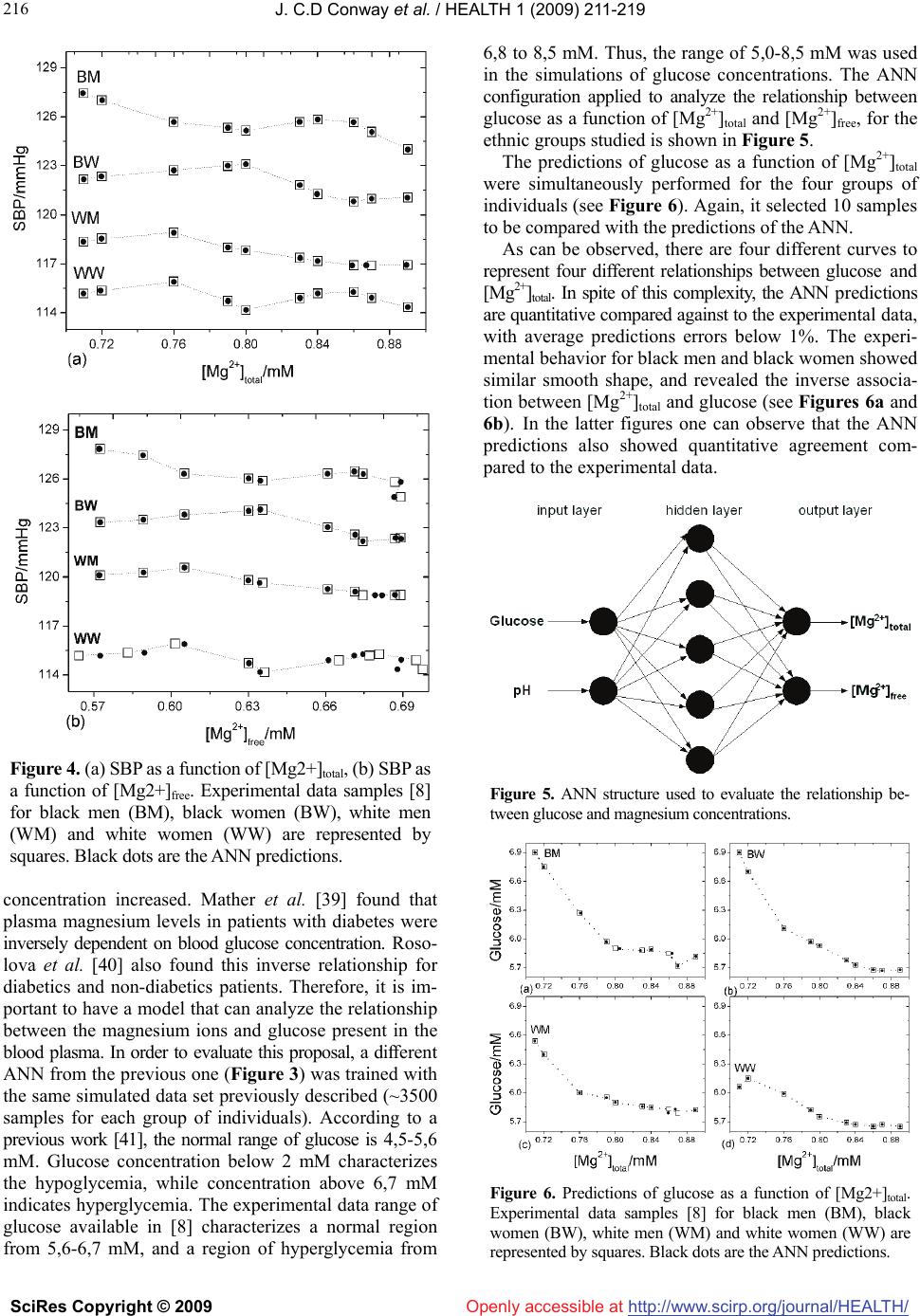

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/
216
Openly accessible at
Figure 4. (a) SBP as a function of [Mg2+]total, (b) SBP as
a function of [Mg2+]free. Experimental data samples [8]
for black men (BM), black women (BW), white men
(WM) and white women (WW) are represented by
squares. Black dots are the ANN predictions.
concentration increased. Mather et al. [39] found that
plasma magnesium levels in patients with diabetes were
inversely dependent on blood glucose concentration. Roso-
lova et al. [40] also found this inverse relationship for
diabetics and non-diabetics patients. Therefore, it is im-
portant to have a model that can analyze the relationship
between the magnesium ions and glucose present in the
blood plasma. In order to evaluate this proposal, a different
ANN from the previous one (Figure 3) was trained with
the same simulated data set previously described (~3500
samples for each group of individuals). According to a
previous work [41], the normal range of glucose is 4,5-5,6
mM. Glucose concentration below 2 mM characterizes
the hypoglycemia, while concentration above 6,7 mM
indicates hyperglycemia. The experimental data range of
glucose available in [8] characterizes a normal region
from 5,6-6,7 mM, and a region of hyperglycemia from
6,8 to 8,5 mM. Thus, the range of 5,0-8,5 mM was used
in the simulations of glucose concentrations. The ANN
configuration applied to analyze the relationship between
glucose as a function of [Mg2+]total and [Mg2+]free, for the
ethnic groups studied is shown in Figure 5.
The predictions of glucose as a function of [Mg2+]total
were simultaneously performed for the four groups of
individuals (see Figure 6). Again, it selected 10 samples
to be compared with the predictions of the ANN.
As can be observed, there are four different curves to
represent four different relationships between glucose and
[Mg2+]total. In spite of this complexity, the ANN predictions
are quantitative compared against to the experimental data,
with average predictions errors below 1%. The experi-
mental behavior for black men and black women showed
similar smooth shape, and revealed the inverse associa-
tion between [Mg2+]total and glucose (see Figures 6a and
6b). In the latter figures one can observe that the ANN
predictions also showed quantitative agreement com-
pared to the experimental data.
Figure 5. ANN structure used to evaluate the relationship be-
tween glucose and magnesium concentrations.
Figure 6. Predictions of glucose as a function of [Mg2+]total.
Experimental data samples [8] for black men (BM), black
women (BW), white men (WM) and white women (WW) are
represented by squares. Black dots are the ANN predictions.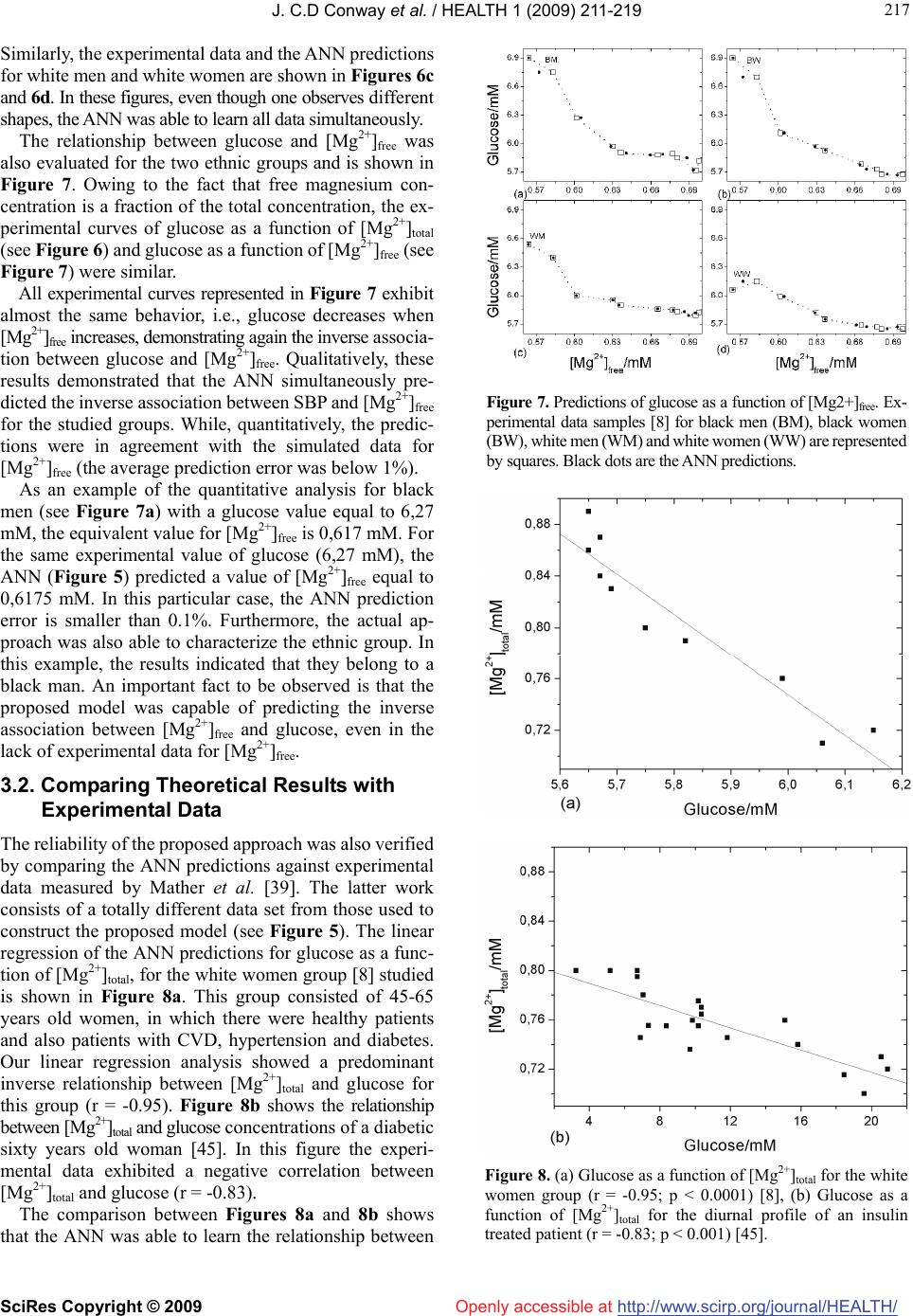

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/
217
217
Openly accessible at
Similarly, the experimental data and the ANN predictions
for white men and white women are shown in Figures 6c
and 6d. In these figures, even though one observes different
shapes, the ANN was able to learn all data simultaneously.
The relationship between glucose and [Mg2+]free was
also evaluated for the two ethnic groups and is shown in
Figure 7. Owing to the fact that free magnesium con-
centration is a fraction of the total concentration, the ex-
perimental curves of glucose as a function of [Mg2+]total
(see Figure 6) and glucose as a function of [Mg2+]free (see
Figure 7) were similar.
All experimental curves represented in Figure 7 exhibit
almost the same behavior, i.e., glucose decreases when
[Mg2+]free increases, demonstrating again the inverse associa-
tion between glucose and [Mg2+]free. Qualitatively, these
results demonstrated that the ANN simultaneously pre-
dicted the inverse association between SBP and [Mg2+]free
for the studied groups. While, quantitatively, the predic-
tions were in agreement with the simulated data for
[Mg2+]free (the average prediction error was below 1%).
As an example of the quantitative analysis for black
men (see Figure 7a) with a glucose value equal to 6,27
mM, the equivalent value for [Mg2+]free is 0,617 mM. For
the same experimental value of glucose (6,27 mM), the
ANN (Figure 5) predicted a value of [Mg2+]free equal to
0,6175 mM. In this particular case, the ANN prediction
error is smaller than 0.1%. Furthermore, the actual ap-
proach was also able to characterize the ethnic group. In
this example, the results indicated that they belong to a
black man. An important fact to be observed is that the
proposed model was capable of predicting the inverse
association between [Mg2+]free and glucose, even in the
lack of experimental data for [Mg2+]free.
3.2. Comparing Theoretical Results with
Experimental Data
The reliability of the proposed approach was also verified
by comparing the ANN predictions against experimental
data measured by Mather et al. [39]. The latter work
consists of a totally different data set from those used to
construct the proposed model (see Figure 5). The linear
regression of the ANN predictions for glucose as a func-
tion of [Mg2+]total, for the white women group [8] studied
is shown in Figure 8a. This group consisted of 45-65
years old women, in which there were healthy patients
and also patients with CVD, hypertension and diabetes.
Our linear regression analysis showed a predominant
inverse relationship between [Mg2+]total and glucose for
this group (r = -0.95). Figure 8b shows the relationship
between [Mg2+]total and glucose concentrations of a diabetic
sixty years old woman [45]. In this figure the experi-
mental data exhibited a negative correlation between
[Mg2+]total and glucose (r = -0.83).
The comparison between Figures 8a and 8b shows
that the ANN was able to learn the relationship between
Figure 7. Predictions of glucose as a function of [Mg2+]free. Ex-
perimental data samples [8] for black men (BM), black women
(BW), white men (WM) and white women (WW) are represented
by squares. Black dots are the ANN predictions.
Figure 8. (a) Glucose as a function of [Mg2+]total for the white
women group (r = -0.95; p < 0.0001) [8], (b) Glucose as a
function of [Mg2+]total for the diurnal profile of an insulin
treated patient (r = -0.83; p < 0.001) [45].

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/
218
Openly accessible at
glucose and [Mg2+]total of the white women group. As can
be seen, our theoretical results were in accordance with
the experimental data from different data set, obtained at
different times. The difference between the correlation
factors (r), approximately 12%, can be attributed to the
different biological conditions of the patients, i.e., the
first data (see Figure 8a) expressed medium values of
glucose concentrations of a heterogeneous group (range =
5,65–6,15 mM), while the second one (see Figure 8b)
expressed the conditions of a diabetic patient with high
glucose concentration (range = 3-22 mM). In spite of
these differences, the two curves clearly demonstrate the
inverse relationship between plasma glucose and [Mg2+]total.
These analysis showed that the ANN can predict the same
trend exhibited in the experimental data. It seems that the
use of about 3500 samples to train the proposed ANN was
enough to extract the behavior of the relationship between
[Mg2+]total and glucose.
4. CONCLUSIONS
This work has dealt with an alternative methodology in
order to study the relationships between the magnesium
ion present in blood plasma and systolic blood pressure
and glucose, through ANNs. The average prediction errors
for the relationship between SBP and serum magnesium
as well as between glucose and serum magnesium were
below 1%. All simulations showed that SBP and glucose
diminished with the increase of magnesium concentration.
The simulations also demonstrated that, in general, black
individuals have average SBP values higher than white
individuals and men’s average SBP values are generally
higher than women’s average SBP values. These results are
in fair agreement with the results reported elsewhere
[34,35,36,37,38,39,40].
A comparison between experimental data of a patient
and the ANN predictions for a different group of patients
showed that the ANN correctly predicted the inverse
association between glucose and [Mg2+]total and revealsed
the effectiveness of the proposed model in mapping the
relationship between [Mg2+]total and glucose concentrations.
Our main results indicate that the proposed approach
can be an efficient tool for analyzing the role of magne-
sium in hypertension and diabetes, and can be used to
obtain quantitative results which can contribute to the
improvement of diagnostic quality. Finally, the present
ANN model can be also applied to support researches
related to the role of magnesium in human blood plasma.
5. ACKNOWLEDGEMENTS
We thank Conselho Nacional de Desenvolvimento Científico e
Tecnológico (CNPq) and Fundação de Amparo à Pesquisa do Estado de
Minas Gerais (FAPEMIG) for financial support. J.C.D.C. also thanks
the Pontifícia Universidade Católica de Minas Gerais for financial
support during his doctoral period.
REFERENCES
[1] P. Laurant and R. M. Touyz, (2000) Physiological and
pathophysiological role of magnesium in the cardiovascular
system: implications in hypertension. J. Hypertens., 18,
1177-1191.
[2] C. S. Yajnik, R. F. Smith, T. D. R. Hockaday, and N. I. Ward,
(1984) Fasting plasma magnesium concentrations and
glucose disposal in diabetes. Br. Med. J., 288, 1032-1034.
[3] J. A. M. Maier, (2003) Low magnesium and atherosclerosis:
an evidence-based link. Mol. Aspects Med., 24, 137-146.
[4] S. Sasaki, T. Oshima, H. Matsuura, R. Ozono, Y. Higashi, N.
Sasaki, et al., (2000) Abnormal magnesium status in patients
with cardiovascular diseases. Clin. Sci., 98, 175-181.
[5] B. Sontia and R. M. Touyz, (2007) Role of magnesium in
hypertension. Arch. Biochem. Biophys., 458, 33-39.
[6] N. E. Saris, E. Mervaala, H. Darppanen, J. A. Khawaja
and A. Lewenstam, (2000) Magnesium: an update on
physiological, clinical and analytical aspects. Clin. Chim.
Acta, 294, 1-26.
[7] M. Speich, B. Bousquet and G. Nicolas, (1981) Reference
values for ionized, complexed, and protein-bound plasma
magnesium in men and women. Clin. Chem., 27, 246-248.
[8] J. Ma, A. R. Folson, S. L. Melnick, J. H. Eckfeldt, A. R.
Sharrett, A. A. Nabulsi, et al., (1995) Associations of serum
and dietary magnesium with cardiovascular disease, hyper-
tension, diabetes, insulin, and carotid arterial wall thickness:
The ARIC Study. J. Clin. Epidemiol., 48, 927-940.
[9] L. M. Resnick, O. Bardice, B. T. Altura, M. H. Alderman
and B. M. Altura, (1997) Serum ionized magnesium-relation
to blood pressure and racial factors. Amer. J. Hypert., 10,
1420-1424.
[10] R. M. Touyz, F. J. Milne, H. C. Seftel, and K. S. Reinach,
(1987) Magnesium, calcium, sodium and potassium status
in normotensive and hypertensive Johannesburg residents.
S. Afr. Med. J.,72, 377-381.
[11] D. D. Perrin, (1965) Multiple equilibria in assemblages of
metal ions and complexing species: a model for biological
systems. Nature, 206, 170-178.
[12] D. D. Perrin and I. G. Sayce, (1967) Computer calculation
of equilibrium concentrations in mixtures of metal ions
and complexing species. Talanta, 14, 833-842.
[13] P. M. May, P. W. Linder, and D. R. Williams, (1977)
Computer simulation of metal-ion equilibria in biofluids:
models for the low-molecular-weight complex distribution
of calcium(II), magnesium(II), manganese(II), iron(III),
copper(II), zinc(II), and lead(II) ions in human blood
plasma. J. Chem. Soc. Dalton, 6, 588-595.
[14] L. S. Nikolaeva and V. V. Chirkov, (2004) Computer
modeling of the influence of ethylenediamine-N, N’-bis
(methylenephosphonic acid) on metal-ion equilibria in
blood plasma. Russ. J. Inorg. Chem., 49, 1547-1552.
[15] J. P. Wang, H. Y. Zhang, K. Y. Yang, and C. J. Niu, (2004)
Computer simulation of Gd(III) speciation in human in-
terstitial fluid. Biometals, 17, 599-603.
[16] A. Liparini, S. Carvalho, and J. C. Belchior, (2005)
Analysis of the applicability of artificial neural networks
for studying blood plasma: determination of magnesium
ion concentration as a case study. Clin. Chem. Lab. Med.,
43, 939-946.
[17] S. R. Bhatikara, C. Degroffb, and R. L. Mahajana, (2005)
A classifier based on the artificial neural network ap-

J. C.D Conway et al. / HEALTH 1 (2009) 211-219
SciRes Copyright © 2009 http://www.scirp.org/journal/HEALTH/Openly accessible at
219
219
proach for cardiologic auscultation in pediatrics. Artif.
Intell. Med., 33, 251-260.
[18] I. Inza, M. Merin, N. P. Larra, J. Quiroga, B. Sierra, and M.
Girala, (2001) Feature subset selection by genetic algo-
rithms–a case study in the survival of cirrhotic patients
treated with tips. Artif. Intell. Med., 23, 187-205.
[19] D. Itchhaporia, P. B. Snow, R. J. Almassy, and W. J. Oet-
gen, (1996) Artificial neural networks: Current status in
cardiovascular medicine. J. Am. Coll. Cardiol., 28, 515-521.
[20] J. D. Martin, E. Soria, G. Campos, A. J. Serrano, J. R.
Sepulveda, and V. Gimenez, (2004) Neural networks as
effective techniques in clinical management of patients:
some case studies. Trans. Inst. Measur. Control, 26,
169-183.
[21] C. Thang, E. W. Cooper, Y. Hoshino, and K. Kamei, (2005)
A decision support system for rheumatic evaluation and
treatment in oriental medicine using fuzzy logic and
neural network. Lect. Note Artif. Intell., 3558, 399-409.
[22] J. Trujillano, J. March, and A. Sorribas, (2004) Methodo-
logical approach to the use of artificial neural networks for
predicting results in medicine. Med. Clin., 122, 59-67.
[23] R. Poli, S. Cagnoni, R. Livi, G. Coppini, and G. Valli, (1991)
A neural network expert system for diagnosing and
treating hypertension. Computer, 24, 64-71.
[24] A. M. Zhai, B. Q. Sun, Y. J. Feng, and H. Q. Wang, (2003)
A study on diagnosis of hypertension by intelligent
medical diagnostic system. Dyn. Cont. Discr. Imp. Syst.
Ser. B, Suppl.S, 478-480.
[25] M. Beksac, M. S. Beksac, V. B. Tipi, H. A. Duru, M. U.
Karakas, and A. N. Cakar, (1997), An artificial intelligent
diagnostic system on differential recognition of hemato-
poietic cells from microscopic images. Cytometric, 30,
145-150.
[26] F. Viazzi, G. Leoncini, G. Sacchi, D. Parodi, E. Ratto, V.
Falqui, et al., (2006) Predicting cardiovascular risk using
creatinine clearance and an artificial neural network in
primary hypertension. J. Hypertens., 24, 1281-1286.
[27] J. C. D. Conway, A. Liparini, J. R. Oliveira Júnior, and J.
C. Belchior, (2007) Analyses of the temperature and pH
effects on the complexation of the magnesium and cal-
cium in human blood plasma: an approach using artificial
neural networks. Anal. Bioanal. Chem., 30, 1585-1594.
[28] W. S. McCulloc and W. Pitts, (1943) A logical calculus of
the ideas immanent in nervous activity. Bull. Math. Bio-
phys., 5, 115-133.
[29] S. Haykin, (1999) Neural networks: A comprehensive
foundation. Prentice Hall.
[30] D. W. Marquardt, (1963) An algorithm for least-squares
estimation of nonlinear parameters. J. Soc. Indust. Appl.
Math., 11, 431-441.
[31] O. D. Williams, (1989) The atherosclerosis risk in commu-
nities (ARIC) study: design and objectives. Amer. J.
Epidemiol., 129, 687-702.
[32] A. A. Freitas, (2002) Data mining and knowledge dis-
covery with evolutionary algorithms. Springer.
[33] H. J. Milionis, G. E. Alexandrides, E. N. Liberopoulos, E.
T. Bairaktari, J. Goudevenos, and M. S. Elisaf, (2002)
Hypomagnesemia and concurrent acid-base and electro-
lyte abnormalities in patients with congestive heart failure.
Eur. J. Heart Fail., 4, 167-173.
[34] H. Eison, R. A. Phillips, M. Ardeljan and L. R. Krakoff,
(1990) Differences in ambulatory blood pressure between
men and women with mild hypertension, J. Hum. Hy-
pertens., 4, 400-404.
[35] C. Agyemang, N. Bindraban, G. Mairuhu, G. Van Montfrans,
R. Koopmans, and K. Stronks, (2005) Prevalence, awareness,
treatment, and control of hypertension among black suri-
namese, south Asian surinamese and white dutch in am-
sterdam, the netherlands: the sunset study. J. Hypertens.,
23, 1971 1977.
[36] J. L. Li, R. M. Canham, W. Vongpatanasin, D. Leonard, R.
J. Auchus, and R. G. Victor, (2006) Do allelic variantes in
alpha(2A) and alpha(2C) adrenergic receptors predispose
to hypertension in blacks?. Hypertension, 47, 1140-1146.
[37] J. P. Fauvel and M. Laville, (2006) Hypertension in blacks.
Press. Med., 35, 1067-1071.
[38] P. McNair, M. S. Christensen, and C. Christiansen, (1982)
Renal hypomagnesemia in human diabetes mellitus: its re-
lation to glucose homeostasis. Eur. J. Clin. Invest., 12, 81-85.
[39] H. M. Mather, G. E. Levin, J. A. Nisbet, L. A. A. Hadley
LAA, N. W. Oakley, and T. R. E. Pilkington, (1982) Di-
urnal profiles of plasma magnesium and blood glucose in
diabetes. Diabetologia, 22, 180-183.
[40] H. Rosolova, O. Mayer, and G. Reaven, (1997) Effect of
variations in plasma magnesium concentration on resis-
tance to insulin-mediated glucose disposal in nondiabetic
subjects. J. Clin. Endocrinol. Metab., 82, 3783-3785.
[41] P. E. Paulev, (1999) Textbook in medical physiology and
pathophysiology, essentials and clinical problems. Co-
penhagen Medical Plubishers.