Paper Menu >>
Journal Menu >>
 Open Journal of Fl ui d Dyn a mi cs, 20 1 1, 1, 1-11 doi:10.4236/ojfd.2011.11001 Published Online December 2011 (http://www.SciRP.org/journal/ojfd) Copyright © 2011 SciRes. OJFD 1 Radiation Ef f ect on Natu ral Convecti o n near a Vertical Plate Embedded in Porous Medium with Ramped Wall Temperature Sanatan Das, Mrinal Jana, Rabindra Nath Jana Department of Ap pl i e d M athematics, Vidyasagar University, Midnapore, India E-mail: jana261171@yahoo.co.in Received November 16, 2011; revised December 7, 2011; accepted De cember 20, 2011 Abstract Radiation effect on the natural convection flow of an optically thin viscous incompressible fluid near a ver- tical plate with ramped wall temperature in a porous medium has been studied. The exact solution of mo- mentum and energy equations is obtained by the use of Laplace transform technique. The variations in fluid velocity and temperature are shown graphically whereas the numerical values of shear stress and the rate of heat transfer at the wall are presented in tabular form for various values of flow parameters. The results show that the fluid velocity increases with increase in Grashof number, Darcy number and time parameters whereas the fluid velocity decreases with increase in the radiation parameter and Prandtl number for ramped temperature as well as isothermal wall temperature. It is found that an increase in radiation parameter leads to rise the temperature for both ramped wall temperature as well as isothermal wall temperature. Further, it is found that an increase in Prandtl number leads to fall the temperature for both ramped wall temperature as well as isothermal wall temperature. The shear stress at the wall decreases with increases in either Prandtl number or porosity parameter while the result shows reverse in the case of radiation parameter. Finally, the rate of heat transfer is increased with increase in the radiation parameter for both ramped wall temperature as well as isothermal wall temperature. Keywords: Natural Convection, Darcy Number, Radiation Parameter, Prandtl Number, Porous Medium, Ramped Wall Temperature and Isothermal Wall Temperature 1. Introduction The phenomenon of natural convection arises in fluids when temperature changes cause density variations lead- ing to buoyancy forces acting on the fluid particles. Such flows which are driven by temperature differences abound in nature and have been studied extensively because of its applications in engineering, geophysical and astro- physical environments. Comprehensive literature on va- rious aspects of free convection flows and its applica- tions could be found in Ghoshdastidar [1], Nield and Bejan [2]. Ghoshdastidar gave various areas of applica- tions of free convection flow such as those found in heat transfer from pipes and transmission lines as well as from electronic devices, heat dissipation from the coil of a refrigerator unit to the surrounding air, heat transfer from a heater to room air, heat transfer in nuclear fuel rods to the surrounding coolant, heated and cooled en- closures, quenching, wire-drawing and extrusion, at- mospheric and oceanic circulation. Unsteady free con- vection flows in a porous medium have received much attention in recent time due to its wide applications in geothermal and oil reservoir engineering as well as other geophysical and astrophysical studies. Moreover, con- siderable interest has been shown in radiation interaction with convection for heat and mass transfer in fluids. This is due to the significant role of thermal radiation in the surface heat transfer when convection heat transfer is small, particularly in free convection problems involving absorbing-emitting fluids. The unsteady fluid flow past a moving plate in the presence of free convection and ra- diation were studied by Mansure [3], Raptis and Perdikis [4], Das et al. [5], Grief et al. [6], Ganeasan and Loga- nathan [7], Mbeledogu et al. [8], Makinde [9] and Ab- dus-Sattar and Hamid Kalim [10]. All these studies have been confined to unsteady flow in a non-porous medium.  S. DAS ET AL. 2 Israel-Cookey et al. [11] have studied the influence of viscous dissipation and radiation on unsteady MHD free- convection flow past an infinite heated vertical plate in a porous medium with time-dependent suction. Radiative and free convective effects of a MHD flow through a porous medium between infinite parallel plates with time dependent suction have been investigated by Alagoa et al. [12]. Israel-Cookey et al. [13] have made an analysis on MHD oscillatory Couette flow of a radiating viscous fluid in a porous medium with periodic wall temperature. Sattar and Maleque [14,15] have studied the unsteady MHD Natural convection flow and mass transfer along an accelerated porous plate in a porous medium. Thermal radiation interaction with unsteady MHD flow past a vertical porous plate immersed in a porous medium has been analyzed by Samad and Rahman [16]. Mahanti and Gaur [17] have studied the effects of varying viscosity and thermal conductivity on steady free convective flow and heat transfer along an isothermal vertical plate in the presence of heat sink. Transient free convection past a semi-infinite vertical plate with variable surface tem- perature has been investigated by Takhar et al. [18]. In this present paper, we investigate the effects of ra- diation on the free convection flow of an optically thin incompressible viscous fluid past an infinite vertical plate with ramped wall temperature in porous medium. The fluid considered is a gray, radiation, absorbing, emitting but non-scattering medium and the Rosseland approximation is used to describe the radiative heat transfer in the energy equation. It is seen that the velocity 1 decreases for both ramped wall temperature as well as isothermal wall temperature with an increase in either radiation parameter or Prandtl number . It is also seen that the velocity 1 increases for both ramped wall temperature as well as isothermal wall temperature with an increase in either Grashof number or time u Ra Pr Gr u . It is found that an increase in radiation parameter leads to rise the temperature Ra for both ramped wall temperature as well as isothermal wall temperature. Further, it is found that an increase in Prandtl number leads to fall the temperature for ramped temperature as well as isothermal case. 2. Formulation of the Problem and Its Solutions Consider the unsteady free convection flow of an opti- cally thin viscous incompressible fluid past an moving infinite vertical plate coinciding with plane 0y , where the flow is confined to in a porous me- dium. Choose a cartesian co-ordinates system with x-axis along the wall in a vertically upward direction and y-axis is normal to it into the fluid (see Figure 1). At 0y 0t , the Figure 1. Geometry of the problem. plate and the surrounding fluid are at the same constant temperature T . At time , the temperature of the 0t wall is raised or lowered to 0 wt TTT t when 0 0tt l and the constant temperature w T is main- tained at 0. Since the plate is infinite along x-direc- tion, all the physical variables are the function of y an t ony. The flow is considered optically thin gray gas with natural convection and radiation. The radiative heat flux in the x-direction is considered negligible in com- parison to y-direction. tt d The Boussinesq approximation is assumed to hold and for the evaluation of the gravitational body force, the density is assumed to depend on the temperature accord- ing to the equation of reference state 01TT , (1) where is the fluid temperature, T the fluid density, the coefficient of thermal expansion and T and 0 being the reference temperature and the density re- spectively. Using Boussinesq Approximation (1), the momentum equation in a porous medium along x-axis is 2 2 uu g TT u tyk , (2) where , u g , , , and are respectively, fluid velocity, acceleration due to gravity, coefficient of thermal expansion, kinematic viscosity, fluid density and permeability of a porous media. k The energy equation is 2 2 1r pp q TkT tc cy y , (3) where is the thermal conductivity, k p c the specific heat at constant pressure and the radiative heat flux. r The initial and boundary conditions are q 0u , TT for and , 0y0t 0 Uu at for t, 0y0 Copyright © 2011 SciRes. OJFD  3 S. DAS ET AL. 0 0 0 at 0 for 0 at 0 for 0,as for 0 w w t TTT Tytt t TTy tt uTTy t (4) It has been shown by Cogley et al. [19] that in the op- tically thin limit for a non-gray gas near equilibrium, the following relation holds 0 0 0 4d h re qTT K yT , (5) where K is the absorption coefficient, is the wave length, h e is the Plank’s function and subscript 0 ` indicates that all quantities have been evaluated at the temperature which is the temperature of the wall at time . Thus our study will be limited to small dif- ference of wall temperature to the fluid temperature. T 0t On the use of (5), Equation (3) becomes 2 2 4 pp TkT TTI tc c y , (6) where 0 0 0 d h e IKT . (7) Introducing dimensionless variables 00 y Ut , 0 t t , 1 0 u uU , w TT TT , (8) Equations (2) and (6) become 2 11 1 2 1 uuuGr , (9) 2 2 1 Pr Ra , (10) where 3 0 w g TT Gr U is Grashof number, Pr p c k the Prandtl number, 2 0 4 p I Ra cU the ra- diation parameter, 2 0 2 kU M aDa the porosity parameter and the Darcy number. Da The characteristic time is defined as 0 t 02 0 tU . (11) The corresponding initial and boundary conditions for and 1 u are 10,0for 0 and 0,u 11at 0 for 0, at 0 for 01, u (12) 1 at 0 for 1 , , 10u 0 as for 0 . Taking Laplace transformation of the Equations (9) and (10), we get 2 1 1 2 d1 d u s uGr MaDa , (13) 2 2 dPr 0 dsRa , (14) where 11 0 0 ,, ,, s s us ue se d, d. (15) The corresponding boundary conditions for 1 u and are 12 1 11 ,1 at 0,0 as . s ue ss u 0, (16) The solution of the Equations (14) and (13) subject to the boundary conditions (16) can be easily obtained and are given by Pr 2 1 , s s Ra e se s , (17) 1 1 1 Pr 2 1 , 1 () sMaDa sssRa MaDa us e s eee ss (18) where 1Pr Gr and 1 Pr 1Pr Ra M aDa . (19) Taking the inverse Laplace transform of Equations (17) and (18), the solution for the fluid temperature , and fluid velocity 1,u are obtained and are given by 11 ,,,1H 1 , (20) 1 1 , erfc 22 erfc2 MaDa MaDa ue M aDa e M aDa Copyright © 2011 SciRes. OJFD  S. DAS ET AL. 4 , (21) where 11 ,,11H Pr 1 Pr 1Pr ,22 Pr erfc2 Pr Pr erfc, 22 Ra Ra e Ra Ra e Ra R a (22) 1 12 1 Pr Pr 1 ,2 1 erfc2 1 erfc2 Pr erfc2 Pr erfc2 MaDa MaDa Ra Ra ee MaDa eMaDa eRa eRa Pr 11 2 erfc2 11 2 11 Pr erfc2 2 Pr1 1Pr erfc22 MaDa MaDa R a MaDa e MaDa MaDa e e MaDa Ra Ra Ra Pr Pr , 2 Ra eerfc Ra (23) where erfc x 1 is the complementary error function and is the unit step function. 2.1. Solution in Case of Unit Prandtl Number Prandtl number is a measure of the relative stren the viscosity and thermal conductivity of the fluid. So the H gth of case Pr 1 us a order t solutio co visconess are of the ameof magnitude. Setting in Equation the xacn for the fluid temp rresponds to those fluids for which both nd thermal boundary layer thick sPr 1 erature (14) and following the same procedure as before, e , and fluid velocity 1,u is obtained and is expressed in the following form 22 ,,,11H , (24) 1 1 , erfc 22 MaDa Ma ue MaDa e 22 erfc 2 ,,11, Da MaDa H (25) where 2 1 ,erfc 222 erfc, 22 Ra Ra eR Ra eR Ra a a (26) 2 1 ,erfc 222 erfc 22 erfc 22 erfc, 22 Ra Ra MaDa MaDa eRa Ra eRa Ra MaDa eMaDa MaDa eMaDa and 1 Gr Ra M aDa . 2.2. Solution for Isothermal Case In order to highlight the effects of the ramped tempera- ture distribution near a vertical plate, it may be important mpare the effects of thal temperature dis- tribution for the fluid flow. The temperature and the ve- city for the fluid flow near an isothermal plate can be to coe isotherm lo expressed as Pr Pr 1Pr , erfc 22 Pr erfc, 2 Ra Ra eRa eRa (27) Copyright © 2011 SciRes. OJFD  5 S. DAS ET AL. 1 11 12 1 , erfc 22 erfc2 ,,, MaDa MaDa ue M aDa e M aDa uu (28) where 1 11 1 1 ,2 1 erfc2 1 erfc2 erfc2 erfc2 MaDa MaDa MaDa MaDa uee MaDa eMaDa eMaDa e Pr 12 Pr Pr 1 ,2 Pr erfc2 Pr erfc2 Pr erfc2 Ra Ra Ra MaDa uee Ra e eRa R a Pr Pr erfc. 2 Ra eRa (29) When , the Solutions (27) and (28) become Pr 1 1 ,erfc 22 erfc, 2 Ra Ra eR eR a a (30) 113 1314 , ,,uuu u , , (31) where 13 1 ,erfc 22 MaDa ue M aDa erfc , 2 MaDa eMaDa (32) 14 1 ,erfc 22 erfc. 2 Ra Ra ue eR Ra a (33) 3. Results and Discussion We have plotted the non-dimensional velocity and tem- perature for several values of radiation para Prandtl number , Grashof number , Darcy ber and tim meter Ra , Pr e Gr num- Da in Figures 2-9 2-6 resen e ve against . Figures rep- t thlocity 1 u foral valu and r sevees of Ra , Pr , Gr , Da . a ram mp creases mb Figure rameter p eratu for er Pr ow n pads hperat re 3 dis e ramped eratur tl nuysically, th 2 sh le tem Figur th mp in t am s that an to fall in in th at n enh crease in th e velo well as iso the in luid. a e radi rmal wall te ty u buo u atio for bot in Ra ed wall e. bo . Ph r city 1 u the veloci crease in Prand nt i l ure as plays wall e with is is the th 1 temperature as well as isothermal wall te d a true because the increase in the Prandtl number is due to increase in the viscosity of the fluid which makes fluid thick and hence causes a decrease he velocity of the f It is observed from Figure 4 that an increase in Gr , leads to a rise the values of velocity 1 u due to ncemen yancy force. Figure 5 reveals that the velocity 1 u increases for both ped wall tem- perature as wel as isothermal wall temperature with an increase in Darcy number Da. It is seen from Figure 6 that the velocity 1 increases for both ramped wall temperature as well as isothermal wall temperature with an increase in time . It is observed from Figure 7 that the temperature decreases as the radiation parameter Ra increases for both ramped wall temperature as well as isothermal wall temperature. This result qualitatively agrees with expectations, since the effect of radiation is ecrease the rate of energy transport to the fluid, thereby decreasing the temperature of the fluid. It is seen from Figure that the temperature to d 8 decreases for both ramped wall temperature as well as isothermal wall temperature with an increas in Prandtl number Pr. This implies that anncrease in Prandtl number leads to fall the thermal boundary layer flow for ramped tem- perature as well as isothermal wall temperature. The ef- fect of the Prandnumber is very important in the tem- ture field. A fall in temperature occurs due to an in- creasing value of the Prandtl number. This is in agree- ment with the physical fact that the thermal boundary e i tl decrease pera layer thicknesssFigure with increase in Pr . 9 Copyright © 2011 SciRes. OJFD  S. DAS ET AL. Copyright © 2011 SciRes. OJFD 6 and 0.04Da . R a when Pr0.71 , 25Gr , 0.1 Figure 2. Velocity profiles for variations in Figure 3. Velocity profiles for variations in when Pr 0.04Da , 25Gr , 0.1 and shows that the temperature 2Ra . increases for both ramped wall temperature as well as isothermal wall temperature with an increase in time . From the physical point of view, it is necessary to know the shear stress and the rate of heat transfer (or the Nusselt number) at the wall 0 . We have presen ted the expression for the rate heat transfer and shear stress of Nu 0 at the wall 0 emp erature in the following form for both themped wall terature and isothermal wall temp For the ramed wall temp ra erature. p , 33 , 0 11Nu H , (34) 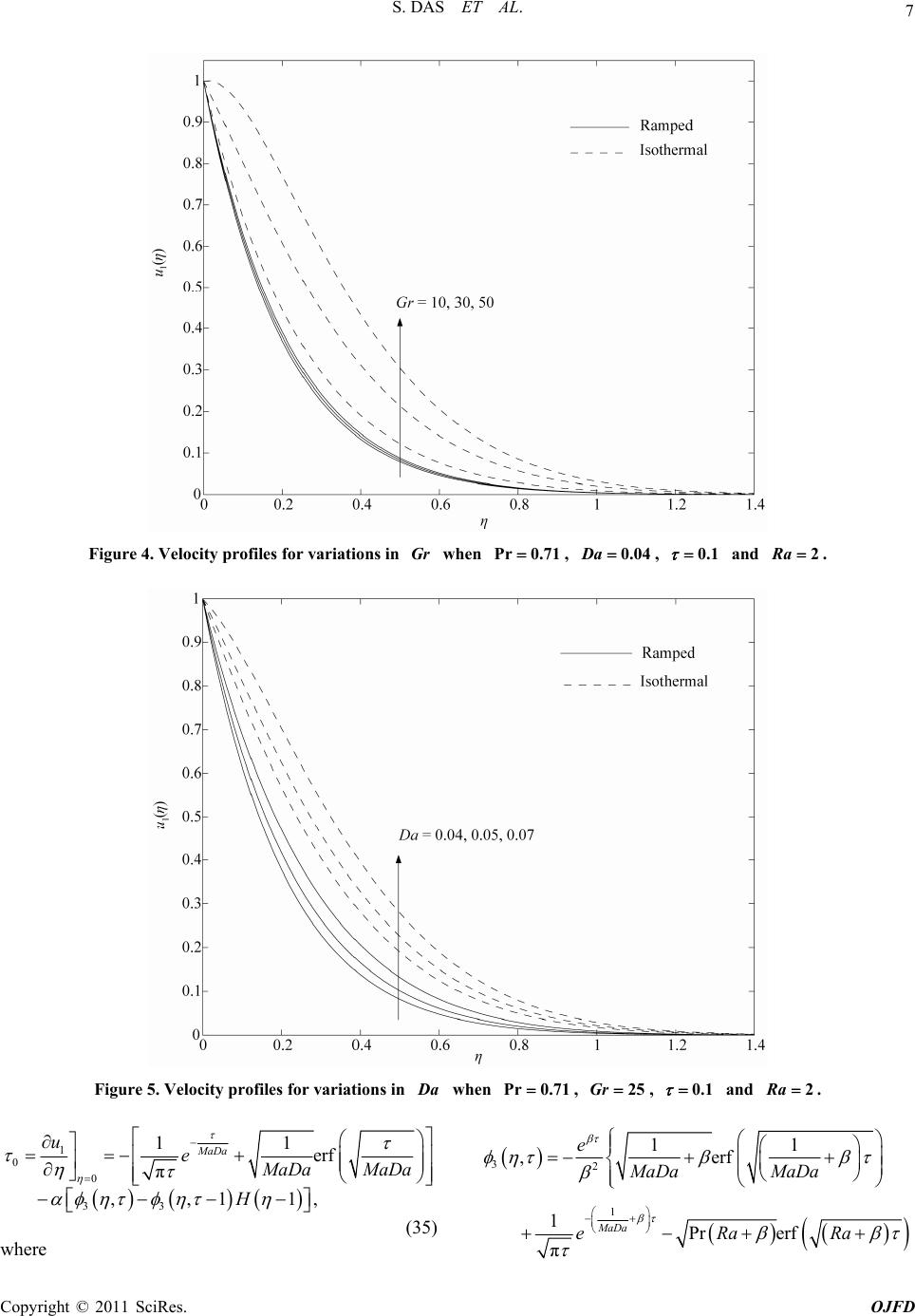 S. DAS ET AL. 7 Figure 4. Velocity profiles for variations in when GrPr 0.71 , 0.04Da , 0.1 and 2Ra . D a when Pr0.71 , 25Gr , 0.1 and 2Ra . Figure 5. Velocity profiles for variations in 1 0 0 33 11 erf π ,,11, MaDa ue M aDa MaDa H (35) 32 1 11 ,erf 1 Prerf π MaDa e MaDa MaDa eRaRa where Copyright © 2011 SciRes. OJFD 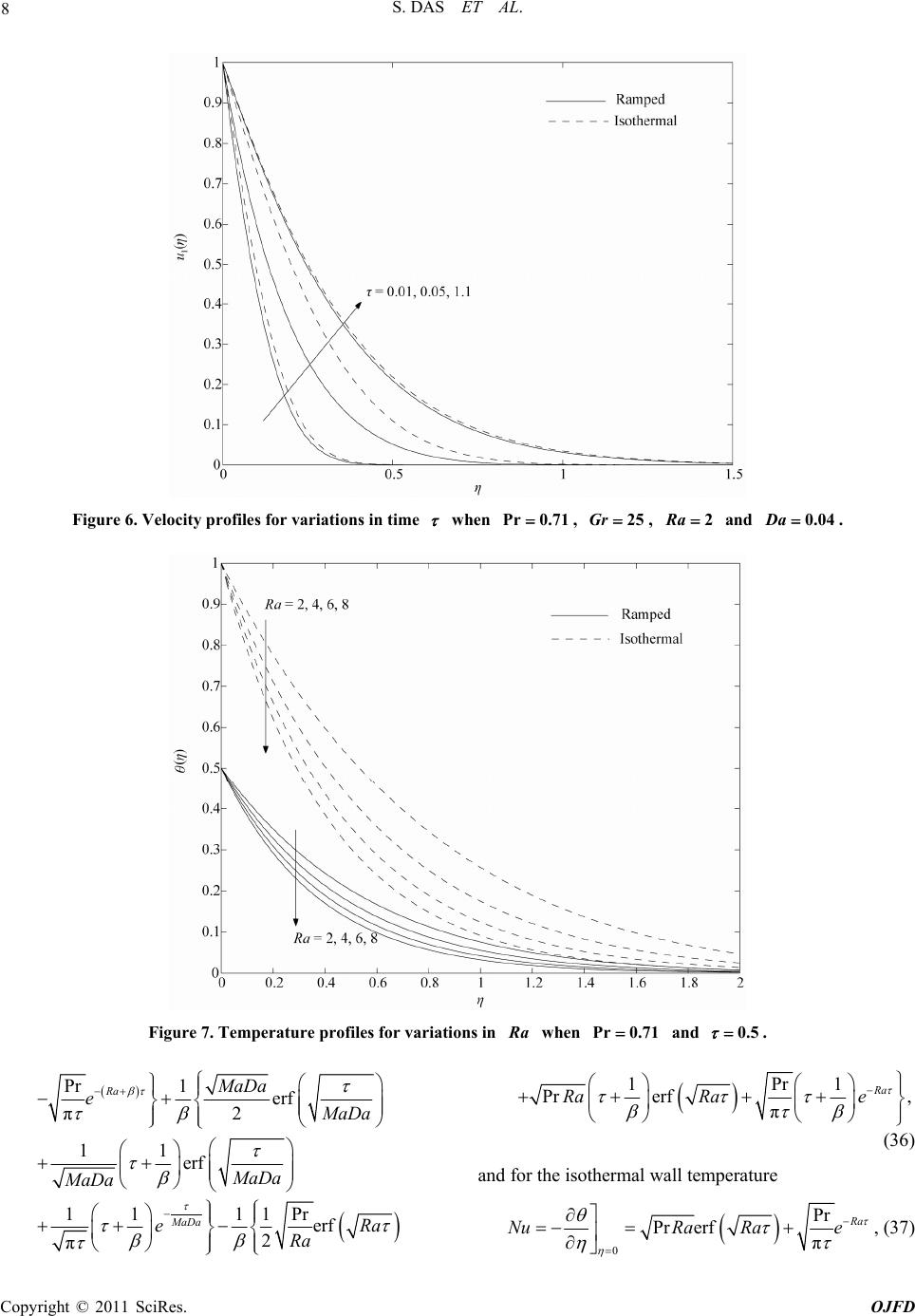 S. DAS ET AL. 8 Figure 6. Velocity profiles for variations in time when Pr0.71 , 25Gr , 2Ra and 0.04a. D R aFigure 7. Temperature profiles for variations in when Pr0.71 and 0.5 . Pr1 erf π2 11 erf 11 11Pr erf 2 π Ra MaDa MaDa eMaDa MaDa MaDa eR Ra a 1Pr1 Pr erf, π Ra Ra Rae (36) and for the isothermal wall temperature 0 Pr Pr erfπ R a NuRa Rae , (37) Copyright © 2011 SciRes. OJFD  S. DAS ET AL. 9 Figure 8. Temperature profiles for variations in whenPr 2Ra and 0.5 . and 2Ra . Figure 9. Temperature profiles for variations in time when Pr0.71 1 0 0 1 1erf 1 Prerf π MaDa u MaDa MaDa eeRa Ra 11 erf Pr erf. eMaDa MaDa Ra Ra (38) Copyright © 2011 SciRes. OJFD 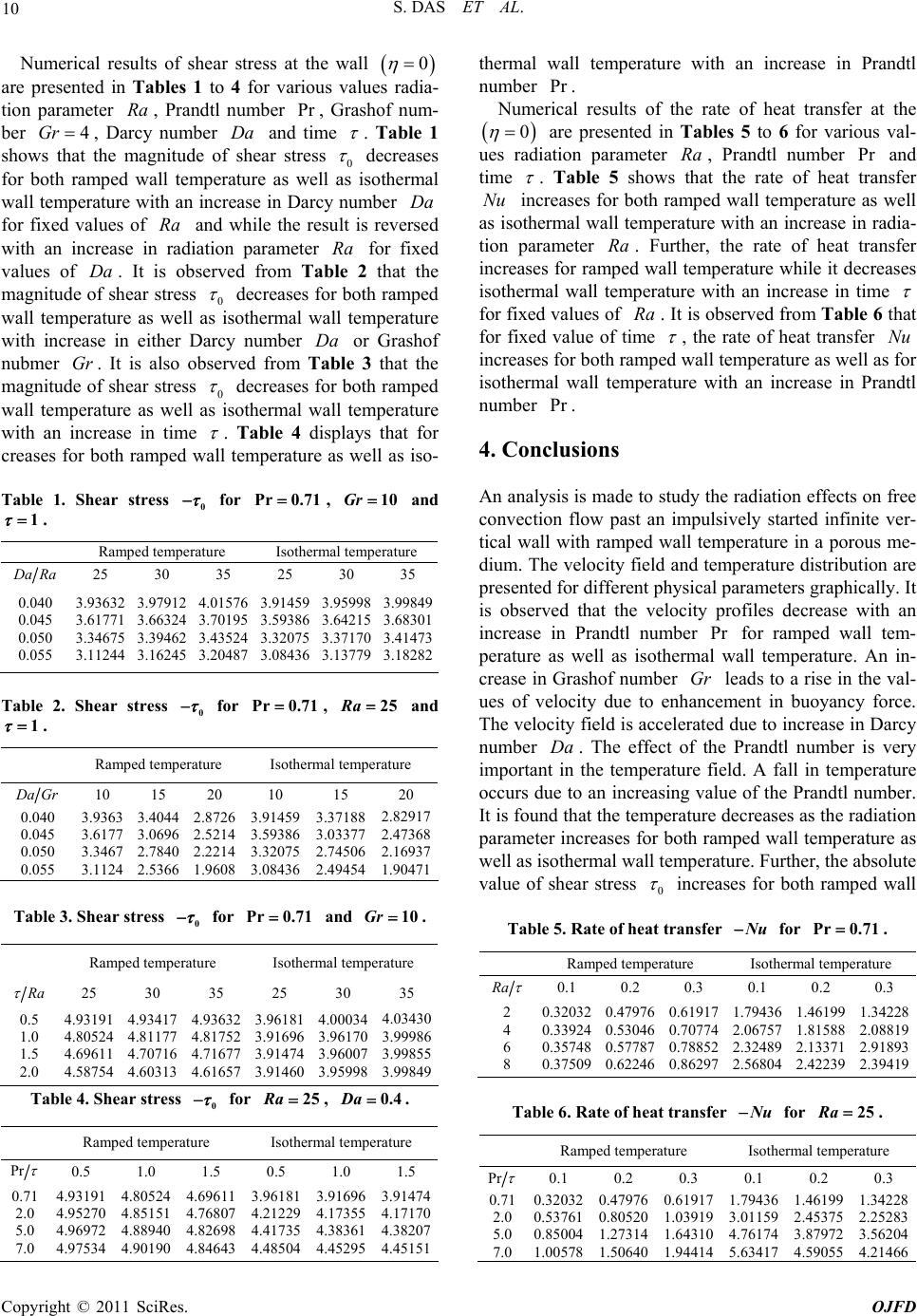 S. DAS ET AL. 10 Numerical results of shear stress at the wall 0 es radia- of num- thermal wall temperature with an increase in Prandtl number Numerical results of the rate of heat transfer at the are presented in Tables 1 to 4 for various valu tion parameter , Prandtl number , Grash ber , Dnumber and time Ra arcy Pr 4GrDa . 0 Table 1 shows thegnitude that ma of shear stress decreases thermal ber Da is reversed r fixed that the for bop temp erature with an in fo ande th with i ram fo valuserom mas th ram wall temp r fixed value an in es of gnitude of ed wall s of crease in . It i hear st erature crease in whil ation pa ved fr as well as Darcy e resu eter Ta iso num lt Ra ble 2 Ra rad s ob res Da s0 y num d decreases wall term with iDab nu from mas er Ta for both ram m or ble 3 ped perature Grashof that the mp ncreas bmer Gr gnitude of erature as well as isothe r . It is also observe res al wall te Da e s in eithe hear st rc 0 decreases wall term withe for both ram m ped perature mp an in erature as well as isothe tim al wall te crease in . Table 4 creases for both ramped wall temperature as well as iso- Table 1. Shear stress displays that for 0 for Pr0.71, 10Gr and 1 . Ramped temrature peratue Isothermal temper DaRa 25 30 35 25 30 35 0.040 0.045 0.050 0.055 3.93632 3.61771 3.34675 3.11244 3.97912 3.66324 3.39462 3.16245 4.01576 3.70195 3.43524 3.20487 3.91459 3.59386 3.32075 3.08436 3.95998 3.64215 3.37170 3.13779 3.99849 3.68301 3.41473 3.18282 Table 2. Shear stress 0 for Pr0.71, 25Ra and 1 . Ramped temature perature Isothermal temper Da Gr 10 15 20 10 15 20 0.040 0.045 0.050 0.055 3.9363 3.6177 3.3467 3.1124 3.4044 3.0696 2.7840 2.5366 2.8726 2.5214 2.2214 1.9608 3.91459 3.59386 3.32075 3.08436 3.37188 3.03377 2.74506 2.49454 2.82917 2.47368 2.16937 1.90471 Table 3. Shear stress 0 for and Pr 0.7110Gr . Ramped temperature Isothermal temperature R a 25 30 35 25 30 35 0.5 1.0 1.5 2.0 4.93191 4.80524 4.69611 4.58754 4.93417 4.81177 4.70716 4.60313 4.93632 4.81752 4.71677 4.61657 3.96181 3.91696 3.91474 3.91460 4.00034 3.96170 3.96007 3.95998 4.03430 3.99986 3.99855 3.99849 Table 4. Shear stress 0 for 25Ra , 0.4Da . Ramped temperature Isothermal temperature Pr Pr . 0 are presented in Tables 5 to 6 for various val- ation parameter , Prandtl number and ues radi time Ra Pr . Nu inc as isot tion pa increases isotherm Table 5 shows at the rate of heat fer reases for both ramed wall temperature as well hermal wall tempwith an increase in radia- rameter . Further, the rate of heatr for raed wall teperature while it decreases al wallwith an increase in time th p erature m erature trans transfe Ra mp temp at for fixe for fixed d valuesbserved from Ta th value of of tim Ra . e It is oble 6 , th ed wa w e rate of heat tran for ll temperature al wallith an increase in Pran 4. Conclusions An analysis is made to study the radiation effects on free convection flow past an impulsively started infinite ver- tical wall with ramped wall temperature in a porous me- dium. The velocity field and temperature distribution are ntental parameters graphically. It is observed that the velocity profiles decrease with an increase in Prandtl number for ramped wall tem- perature as well as isotherm wall temperature. An in- crease in Grashof number ads to a rise in the val- ues of velocity due to enhent in buoyancy force. The velocity field is accelerated due to increase in Darcy number . The effect Prandtl number is very importan in the temperatu. A fall in temperature occurs due to an increasing of the Prandtl number. It is fouat the temperature decreases as the radiation parameter increases for boted wall temperature as well as isormal wall temre. Further, the absolute value of ear stress sfer as well as for Nu dtl increases isotherm number both ram temp p erature Pr . prese d for differe physic Pr al le cem he field value ramp eratu Gr an of t re h p Da t nd th the sh 0 increases for both ramped wall Table 5. Rate of heat transfer for NuPr 0.71 . Ramped temperature Isothermal temperature R a 0.1 0.2 0.3 0.1 0.2 0.3 2 4 6 8 0.32032 0.33924 0.35748 0.37509 0.47976 0.53046 0.57787 0.62246 0.61917 0.70774 0.78852 0.86297 1.79436 2.06757 2.32489 2.56804 1.46199 1.81588 2.13371 2.42239 1.34228 2.08819 2.91893 2.39419 Tale 6. Rateransfer fb of heat t orNu 25Ra . Ramped temperature Isothermal temperature 0.5 1.0 1.5 0.5 1.0 1.5 Pr 0.1 0.2 0.3 0.1 0.2 0.3 0.71 2.0 5.0 7.0 4.93191 4.95270 4.96972 4.97534 4.80524 4.85151 4.88940 4.90190 4.69611 4.76807 4.82698 4.84643 3.96181 4.21229 4.41735 4.48504 3.91696 4.17355 4.38361 4.45295 3.91474 4.17170 4.38207 4.45151 0.71 2.0 5.0 7.0 0.32032 0.53761 0.85004 1.00578 0.47976 0.80520 1.27314 1.50640 0.61917 1.03919 1.64310 1.94414 1.79436 3.01159 4.76174 5.63417 1.46199 2.45375 3.87972 4.59055 1.34228 2.25283 3.56204 4.21466 Copyright © 2011 SciRes. OJFD  S. DAS ET AL. Copyright © 2011 SciRes. OJFD 11 temperature as well as isothermal wall temperature with an increase in Darcy number for fixed values of and while the result is rev with an increase in ion parameter for fivalues of. The heat transfer increases for both raed wall erature as well as isothermal wall tempe with rease in radiation rameter 5. References [1] P. S. Ghoshdastidar, “Heat Transfer,” Oxford Press, Oxford, 2004. [2] D. A. Nield and A. Bejan, “Convection in Porous Me- dia,” Springer, New York, 2006, pp. 94-97. [3] Effects ce S 275. 98 Da ersed xed Ra Ra radiat rate of temp an inc Ra Nu pa Da mp eratur . University M. A. Mansour, “Radiation and Free Convection on the Oscillating Flow past a Vertical Plate,” Astrophys- ics and Spacience, Vol. 166, No. 2, 1990, pp. 269- doi:10.1007/BF010948 F ka id [4] A. Raptis and C. Perdikis, “Radiation andree Convec- tion Flow past a Moving Plate,” Applied Mechanics and Engineering, Vol. 4, No. 4, 1999, pp. 817-821. [5] U. N. Das, R. De and V. M. Soundalgekar, “Radiation Effect on Flow past an Impulsively Started Vertical Plate: An Exact Solutions,” Journal of Applied Mathematics and FluMechanics, Vol. 1, No. 2, 1966, pp. 111-115. [6] R. Grief, I. S. Habib and J. C. Lin, “Laminar Convection of Radiating Gas in a Vertical Channel,” Journal of Fluid Mechanics, Vol. 46, 1991, pp. 513-520. doi:10.1017/S0022112071000673 [7] P. Ganesan and P. Lonathan, “Radiation and Mass Transfer Effects on Flow of an Incompressible Viscous Fluid past a Moving Vertical Cylinder,” International Journal of Heat and Mass Transfer, Vol. 45, No. 21, 2002, pp. 4281-4288. ga doi:10.1016/S0017-9310(02)00140-0 lu, “Un- ady MHD Free Convection Flow of a Compressible al Plata- diaveransfer,” Inatioournf Hend -331. :1 [8] I. U. Mbeledogu, A. R. C. Amakiri and A. Ogu ste Fluid pst a Moving Verticae in the Presence of R ti Heat Tnternal Jal oat a Mass Transfer, Vol. 50, No. 9-10, 2007, pp. 326 doi 0.1016/j.ijheatmasstransfer.2006.10.032 [9 D d r rous Plate,” International Communications in Heat and 32, No. 10, 2005, pp411-141 asstransfer.2005.07 05 ] O.. Makinde, “Free-Convection Flow with Thermal Raiation and Mass Transfer past a Moving Ve tical Po- Mass Transfer, Vol. . 19. doi:10.1016/j.icheatm .0 [10] M. D. Abdus-Sattar and M. D. Hamid Kalim, “Unsteady ree-Co with a Boundarea Jona MaatiPhysVol.96, pp. 25-37. [11] C. Israel-Cookey, A. Ogulu and V. B. Omubo-Pepple, “Influence of Viscous Dissipation- steadHD e-Cotion Flow past an Infinite lat aum im nct nV3 . n and Radiation on U y MFrenvec Heated T Vert e-Depe ical P dent Su e in tion,” Int Porous ernationa Medi l Journa with l of Hea ad Mass Transfer, ol. 46, No. 13, 2003, pp. 205-2311 doi:10.1016/S0017-9310(02)00544-6 [12] an. Abbey cts HD Flow through a Po- rous Medium Infinite Time,” Astro ci- ence l. 2699, p5-46 doi:10.1016 9 K. D. Alagoa, G. Tayd T. M, “Radiative and Free Convective Effeof a M between -Dependent Suction Parallel Plates with physics and Space S , Vo0, 19p. 458. /S0017- 310(02)00544-6 [1 C C O s a Porous Medium with Periodic Wall Temp 1,. 2, 2010, pp. 326-331. 3] . Israel-ookey, E. Amos and C. Nwaigwe, “MHD scillatory Couette Flow of a Radiating Viscou Fluid in erature,” American Journal of Scientific and Industrial Research, Vol. No doi:10.5251/ajsir.2010.1.2.326.331 . A. Sattar and M. A. Maleque, “Unsteady MHD Natu- ral Convection Flow along an Accelerated Porous Plate with Hall Current and Mass Transfer in a Rotating Porous Medium,” Journal of Energy, Heat and Mass Transfer, Vol. 22, 2000, pp. 67-72. [15] M. A. Sattar, M. M. Rahman and M. M. Alam, “Free Convection Flow and Heat Transfer through a Porous Vertical Flat Plate Immersed in a Porous Medium,” Journal of Energy Research, Vol. 22, No. 1, 2000, p. 17-21. [16] M. D. Abdus Samad and M. Mansur Rahman, “Thermal Radiation Interaction with Unsteady MHD Flow past a Vertical Porous Plate Immersed in a Porous Medium,” Jourl o Vol. 3 [14] M p naf Naval Architecture and Marine Engineering, , No. 1, 2006, pp. 7-14. “The Effects of Varying Vis- Conductivity on Steady Free Convec- [17] N. C. Mahanti and P. Gaur, cosity and Thermal tive Flow and Heat Transfer along an Isothermal Vertical Plate in the Presence of Heat Sink,” Journal of Applied Fluid Mechanics, Vol. 2, No. 1, 2009, pp. 23-28. [18] H. S. Takhar, P. Ganesan, K. Ekambavanan and V. M. Soundalgekar, “Transient Free Convection past a Semi Infinite Vertical Plate with Variable Surface Tempera- ture,” International Journal of Numerical Methods for Heat and Fluid Flo w, Vol. 7, No. 4, 1997, pp. 280-296. doi:10.1108/09615539710165804 [19] A. C. L. Cogley, W. G.ncenti and E. S. Gilles, “Dif- ferential Approximation for Radiative Heat Transfer in a Non Grey Gas near Equilibrium,” American Institute of Aeronautics and Astronautics, Vol. 6, No. 3, 1968, pp. 551-553. F nvection Intraction Thermal Radiation in y Lay l ofr Flow past them Vertical Porous Plate,” ics, urcal 30, 19 Vi |

