EEGcorco: a computer program to simultaneously calculate and statistically analyze EEG coherence and correlation

doi:10.4236/jbise.2011.412096

Paper Menu >>

Journal Menu >>

J. Biomedical Science and Engineering, 2011, 4, 774-787

doi:10.4236/jbise.2011.412096 Published Online December 2011 (http://www.SciRP.org/journal/jbise/

JBiSE

Published Online December 2011 in SciRes. http://www.scirp.org/journal/JBiSE

EEGcorco: a computer program to simultaneously calculate

and statistically analyze EEG coherence and correlation

Miguel Angel Guevara, Marisela Hernández-González*, Araceli Sanz-Martin, Claudia Amezcua

Instituto de Neurociencias, CUCBA, Universidad de Guadalajara, Guadalajara, México.

E-mail: mguevara@cencar.udg.mx, *mariselh@cencar.udg.mx, aracelisanz@yahoo.com, camezcu@cencar.udg.mx

Received 30 September 2011; revised 7 November 2011; accepted 26 November 2011.

ABSTRACT

EEGcorco is a computer program designed to ana-

lyze the degree of synchronization between two elec-

troencephalographic signals (EEG) by mean the

analysis of correlation and coherence index. The cor-

relation and coherence values permit the quantitative

determination of the similarity among EEG signals

from homologous areas of the cerebral hemispheres

(interhemispheric), and among localized areas within

one cerebral hemisphere (intrahemispheric). EEG

coherence is a function of frequency; thus it is com-

monly presented in a spectral manner (coherence

values in every frequency of the spectrum), in con-

trast, the correlation function has been employed

mainly to search periodic components of bioelectrical

signals, and normally appears as punctual values

defined in time, hence it is not common calculate

correlation spectra. EEGcorco offers an easy and

novel way to calculate correlation spectra by mean

the application of the Fast Fourier Transformation

(FFT) to digitized EEG signals. Both, correlation and

coherence spectra are obtained in both independent

frequencies and frequencies grouped in wide bands.

Moreover, the program applies parametric statistical

analyses to those coherence and correlation spectra

also, for each individual frequency and for the fre-

quencies grouped in bands. The program functions

on any PC-compatible computer equipped with a

Pentium or superior processor and a minimum of 512

Mb of RAM memory (though the higher the capacity

the better). The space required on the hard disk de-

pends on the signals to be analyzed, as the output

takes the form of files in text format that occupy very

little space. The program has been elaborated com-

pletely in the Delphi environment for the Windows

operating system. The efficacy and versatility of

EEGcorco allow it to be easily adapted to different

experimental and clinical needs.

Keywords: EEG; EEG Coherence; EEG Correlation

1. INTRODUCTION

The electroencephalogram (EEG) is defined as a mixture

of rhythmic sinusoidal-like fluctuations in voltage gen-

erated by the brain that, it has been suggested, represent

the global activity of the pyramidal cells of the cortex

and the activity of the neurons in the subcortical struc-

tures [1]. It has been used for many years as a sensitive

tool that makes it possible to examine brain functionality

with no invasive intervention under many physiological

conditions, during hormonal and pharmacological ma-

nipulations, and while subjects are resolving different

tasks [2,3]. This technique has an excellent temporal

resolution that allows the researcher to obtain recordings

of brain electrical activity from milliseconds to hours,

days and even months; hence, it is probably due to this

advantage that the EEG is still used in numerous labora-

tories around the world.

Although qualitative EEG analysis is still used in

medicine, quantitative analysis of EEGs has become

even more common due to the advances offered by per-

sonal computers. Such computerized analyses require

digitized EEG signals (discreet in amplitude and time)

and can be based on two techniques: coherence, in the

frequency domain; and correlation, in the time domain.

Coherence and correlation are two mathematical in-

dexes that allow the determination of the degree of simi-

larity between two electroencephalographic signals and

the establishment of a possible functional relation among

different regions of the brain. Though the two methods

are frequently considered equivalent, there are some

important differences in the procedures used to calculate

them and in the results they provide. Coherence is cal-

culated by dividing the numerical square of the cross-

spectrum by the product of the autospectra. Therefore, it

is sensitive to changes in power as well as to alterations

in phase relationships. Consequently, if either power or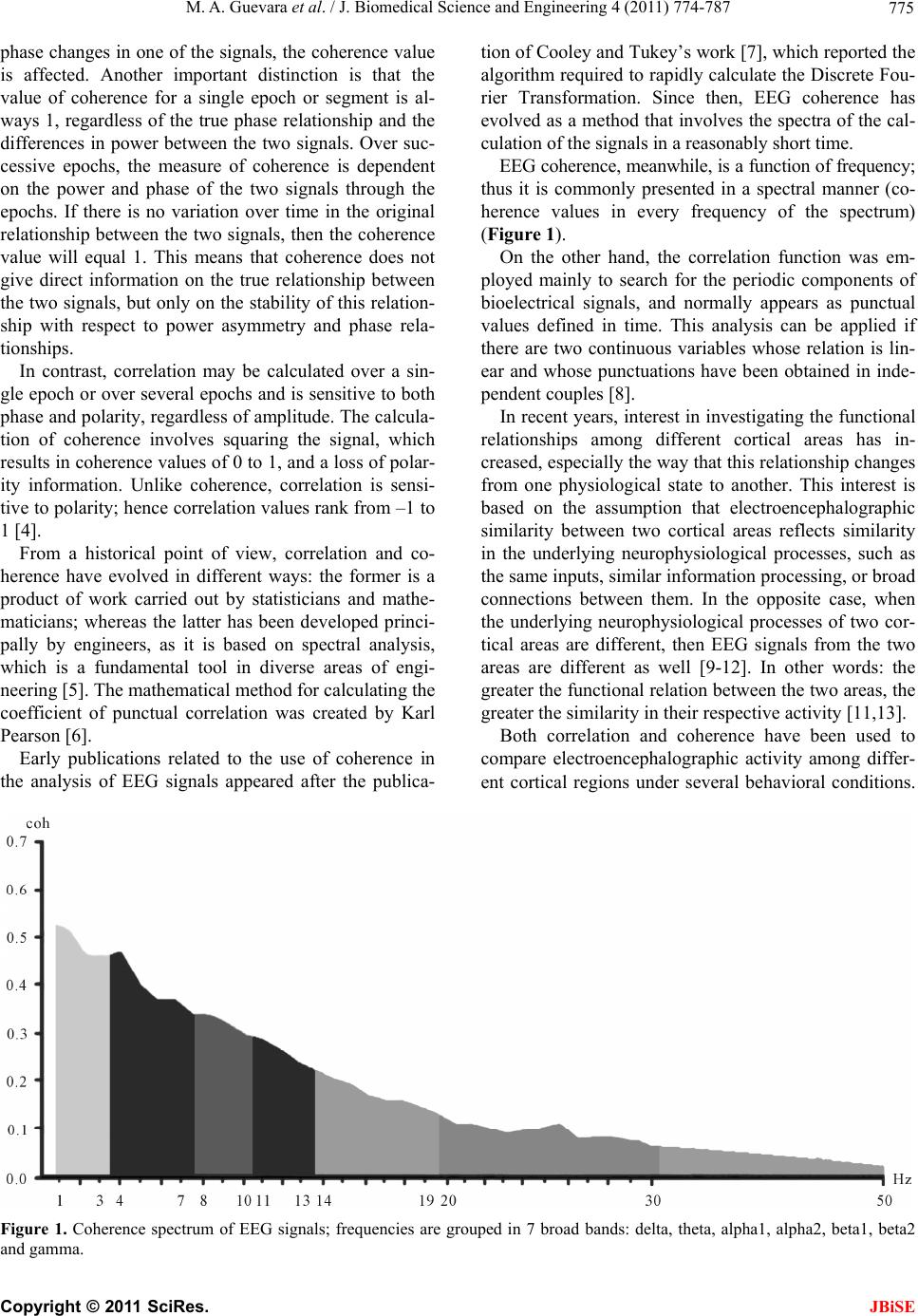

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787 775

phase changes in one of the signals, the coherence value

is affected. Another important distinction is that the

value of coherence for a single epoch or segment is al-

ways 1, regardless of the true phase relationship and the

differences in power between the two signals. Over suc-

cessive epochs, the measure of coherence is dependent

on the power and phase of the two signals through the

epochs. If there is no variation over time in the original

relationship between the two signals, then the coherence

value will equal 1. This means that coherence does not

give direct information on the true relationship between

the two signals, but only on the stability of this relation-

ship with respect to power asymmetry and phase rela-

tionships.

In contrast, correlation may be calculated over a sin-

gle epoch or over several epochs and is sensitive to both

phase and polarity, regardless of amplitude. The calcula-

tion of coherence involves squaring the signal, which

results in coherence values of 0 to 1, and a loss of polar-

ity information. Unlike coherence, correlation is sensi-

tive to polarity; hence correlation values rank from –1 to

1 [4].

From a historical point of view, correlation and co-

herence have evolved in different ways: the former is a

product of work carried out by statisticians and mathe-

maticians; whereas the latter has been developed princi-

pally by engineers, as it is based on spectral analysis,

which is a fundamental tool in diverse areas of engi-

neering [5]. The mathematical method for calculating the

coefficient of punctual correlation was created by Karl

Pearson [6].

Early publications related to the use of coherence in

the analysis of EEG signals appeared after the publica-

tion of Cooley and Tukey’s work [7], which reported the

algorithm required to rapidly calculate the Discrete Fou-

rier Transformation. Since then, EEG coherence has

evolved as a method that involves the spectra of the cal-

culation of the signals in a reasonably short time.

EEG coherence, meanwhile, is a function of frequency;

thus it is commonly presented in a spectral manner (co-

herence values in every frequency of the spectrum)

(Figure 1).

On the other hand, the correlation function was em-

ployed mainly to search for the periodic components of

bioelectrical signals, and normally appears as punctual

values defined in time. This analysis can be applied if

there are two continuous variables whose relation is lin-

ear and whose punctuations have been obtained in inde-

pendent couples [8].

In recent years, interest in investigating the functional

relationships among different cortical areas has in-

creased, especially the way that this relationship changes

from one physiological state to another. This interest is

based on the assumption that electroencephalographic

similarity between two cortical areas reflects similarity

in the underlying neurophysiological processes, such as

the same inputs, similar information processing, or broad

connections between them. In the opposite case, when

the underlying neurophysiological processes of two cor-

tical areas are different, then EEG signals from the two

areas are different as well [9-12]. In other words: the

greater the functional relation between the two areas, the

greater the similarity in their respective activity [11,13].

Both correlation and coherence have been used to

compare electroencephalographic activity among differ-

ent cortical regions under several behavioral conditions.

Figure 1. Coherence spectrum of EEG signals; frequencies are grouped in 7 broad bands: delta, theta, alpha1, alpha2, beta1, beta2

nd gamma. a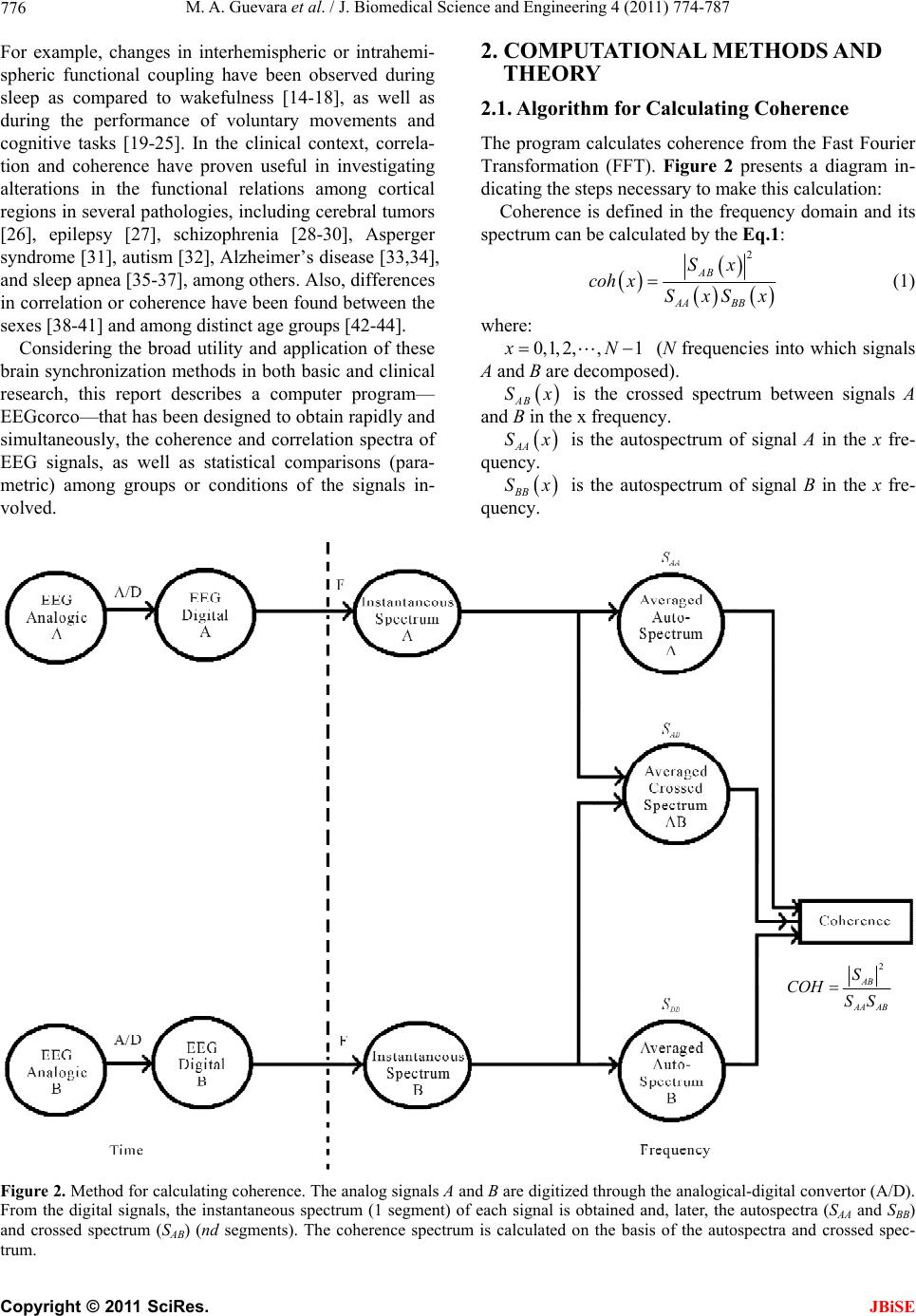

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787

776

For example, changes in interhemispheric or intrahemi-

spheric functional coupling have been observed during

sleep as compared to wakefulness [14-18], as well as

during the performance of voluntary movements and

cognitive tasks [19-25]. In the clinical context, correla-

tion and coherence have proven useful in investigating

alterations in the functional relations among cortical

regions in several pathologies, including cerebral tumors

[26], epilepsy [27], schizophrenia [28-30], Asperger

syndrome [31], autism [32], Alzheimer’s disease [33,34],

and sleep apnea [35-37], among others. Also, differences

in correlation or coherence have been found between the

sexes [38-41] and among distinct age groups [42-44].

Considering the broad utility and application of these

brain synchronization methods in both basic and clinical

research, this report describes a computer program—

EEGcorco—that has been designed to obtain rapidly and

simultaneously, the coherence and correlation spectra of

EEG signals, as well as statistical comparisons (para-

metric) among groups or conditions of the signals in-

volved.

2. COMPUTATIONAL METHODS AND

THEORY

2.1. Algorithm for Calculating Coherence

The program calculates coherence from the Fast Fourier

Transformation (FFT). Figure 2 presents a diagram in-

dicating the steps necessary to make this calculation:

Coherence is defined in the frequency domain and its

spectrum can be calculated by the Eq.1:

 

AA BB

coh xSxSx

 (1)

where:

0,1, 2,,1xN



 (N frequencies into which signals

A and B are decomposed).





Sx is the crossed spectrum between signals A

and B in the x frequency.





Sx is the autospectrum of signal A in the x fre-

quency.





Sx is the autospectrum of signal B in the x fre-

quency.

AA AB

COH SS



Figure 2. Method for calculating coherence. The analog signals A and B are digitized through the analogical-digital convertor (A/D).

From the digital signals, the instantaneous spectrum (1 segment) of each signal is obtained and, later, the autospectra (SAA and SBB)

and crossed spectrum (SAB) (nd segments). The coherence spectrum is calculated on the basis of the autospectra and crossed spec-

rum. t

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787 777

2.2. Algorithm for Calculating Correlation

Having ascertained each of the components (frequencies)

of the bioelectrical signals in the time domain, the Pear-

son product-moment coefficient of punctual correlation

for each frequency can be calculated using the following

Eq.2:

 

cov

var var

AA BB

 (2)

where:

0,1, 2,,1

xN

(

N frequencies into which signals

A and B are decomposed).



covAB

is the covariance between signals A and B,

in the x frequency.



varAA

is the variance of signal A in the x fre-

quency.



varBB

is the variance of signal B in the x fre-

quency.

The correlation coefficient can also be calculated fol-

lowing a method similar to that used in the coherence

calculation. It involves the use of the spectra amplitudes

of the signals, and is illustrated in Figure 3, and ex-

plained following steps 1 to 4:

1) Discrete Direct Fourier Transformation: Eq.3 indi-

cates how, from Eqs.4 and 5, it is possible to obtain the

instantaneous spectrum of a digitized sign.

 

Instantaneus spectrum2

re Fim (3)

 

2π

cos

Fre xfnN















(4)

 

2π

Fimxfn senN







 







(5)

where:





rex ,





imx : 0,1,2,,1xN



 (N frequencies

into which the signals are decomposed)





n: 0,1, 2,1,Nn





 (N samples that compose

signals in time)

Due to the properties of Discrete Fourier Transforma-

tion, we know that the number of frequencies into which



















 

AAreal

AA AB

SxSx



Correlation

Figure 3. Method for calculating Pearson’s punctual correlation in each x frequency. Analog signals A and B are digitized through an

analogical-digital convertor (A/D). From those digital signals, the instantaneous (1 segment) autospectra (SAA and SBB) and crossed

spectrum (SAB) are calculated. Correlation in each x frequency is calculated on the basis of the autospectra and real part crossed spec-

rum for this x frequency. t

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787

778

it is possible to separate the elements to a digital signal is

N/2 plus an element that represents the average level of

data (known as the level of direct current, or “DC” level);

the remaining N/2 – 1 frequencies are an image of the first

ones.

2) Discrete Inverse Fourier transformation: Eq.6 makes

it possible to return to a digitized signal from the fre-

quency domain to the time domain.

 

12π2π

cos

nx nx

fnFre xFim x sen







 





 

 



N

(6)

where:



rex ,





imx : (N frequencies

into which the signals are decomposed)

0,1,2,,1xN





n: (N samples that compose

to signals in time)

0,1,2,1,Nn 

3) The autospectra and crossed spectrum equations for

digitized signs are (Eqs.7-1 6):

Signal A Autospectrum:



 

lim nd

AAndi i



 







xAx (7)

 



 





lim nd

AA ndiiii

SFreA xFimA xFreA xFimA x

 















(8)







lim nd

AA ndii

SFreAxF

 









2

imAx (9)

Signal B Autospectrum:

 

lim nd

BBndi i



 







xBx (10)

 



 





lim nd

BB ndiiii

SFreB xFimB xFreB xFimB x

 















(11)







lim nd

BB ndii

SFreBxF

 









2

imBx (12)

Crossed spectrum between signals A and B:

 

lim limnd

ABi i

nd nd





 







AxBx (13)

 



 





lim nd

AB ndiiii

SFreAxFimAxFreB xFimB x

 















(14)

 



 





lim nd

ABre ndiiii

SFreAxFreB xFimAxFimBx

 













(15)

 



 





lim nd

ABim ndiiii

SFreAxFimBx FimAxFreBx

 













(16)

where:

nd = number of segments



x, i = instantaneous spectra of signals A

and B in the x frequency



,





i = conjugates from the instantaneous

spectra of signals A and B in the x frequency (the conju-

gate of a complex number is obtained by reversing the

sign of the imaginary part)



4) By applying the Fourier Inverse Transformation to

the crossed spectrum of a signal the crossed correlation

function is obtained; as expressed in the following Eq.17:

 



12π

cos

2π

rn Frex

Fim x senN



























(17)

with respect to this correlation function, the only ele-

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787 779

ment is the correlation at time zero for each x frequency;

thus n will always be zero. In other words, the only fac-

tor of interest is the first place (correlation at time zero)

of the correlation function. Thus, the equation is as fol-

lows (Eq.18):

 





rex (18)

This simplification was made possible due to n = 0, so:



2π

coscos 01.0









 

2π00.0

Fim x senFim x sen









It is clear that calculating the first place of the correla-

tion function does not require the use of the imaginary

part of the crossed spectrum. Moreover, if it is supposed

that for each x frequency all others are zero (as in an

ideal filter, where the signals contain only one fre-

quency), then for each x frequency, the correlation func-

tion at time zero will be calculated by Eq.19 :

 

rx Frex

 (19)

where:

1, 2,,2



 (2N frequencies into which the

signals are decomposed)

(x initiates at one because the “DC” component is not

considered)

As we know that in the previous equation





re x is

equal to the real part of the crossed spectrum, Eq.20:

 



 





lim nd

ABre ndiiii



rexSFreA xFreBxFimA xFimBx

 



 





 (20)

Upon considering a single segment (nd = 1, which is

possible for the correlation), Eqs.21 and 22 are obtained:



ABre

rx S

 (21)

  



rxFreA x FreBxFimA xFimBx





(22)

with these correlation values for each one of the N/2

frequencies, it becomes possible to calculate the correla-

tion spectrum for the two signals involved. However,

their values are not between –1 and +1, which is the best

way of seeing them. To obtain values in the aforemen-

tioned range, the values of every must be divided

by the square root of the product of place zero of the

inverse transformation of the autospectra signals for the

same x frequency; i.e., the autocorrelation at time zero of

each one of the A and B signals [FacA and facB ]), as

indicated in Eq.23 :



 

ABre

acA xfacBx

 (23)

where facA and facB are defined by Eqs.2 4 and 25:

 

12π2π

cos

nx nx

facAFreA xFimAx sen







 





 

 



N

(24)

 

12π2π

cos

nx nx

facBFreB xFimB x sen







 





 

 



N

(25)

However, considering that the only point of interest is

the place zero of the Inverse Transformation (n = 0),

then Eqs .2 6 and 27 are developed:



acAFreA x





 (26)



acBFreB x





 (27)

Since the autospectra do not contain an imaginary part,

and considering a value of zero for all the different fre-

quencies of X, then





reAx and



reBx are equiva-

lent to the autospectra of the A and B signals, respect-

tively (Eqs.28 and 29):









lim

ndi i

FreA xS

FreA xFimA x

 













(28)









lim

ndi i

FreB xS

FreB xFimB x

 













(29)

Therefore, for one segment (nd = 1), Eqs.30 and 31

re developed: a

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787

780

 



acAFreAxFreAx FimAxFimAx







 (30)

 



acBFreBxFreBx FimBxFimBx







 (31)

Upon substituting Eqs.20, 30 and 31 in number 32, we obtain:



















 



 



FreAxFreBx FimAxFimBx

reAx FreAxFimAxFimAxFreB xFreB xFimB xFimB x





(32)

In this way, it is possible to calculate the correlation

spectrum (correlation values for every frequency into

which the signal is decomposed) between two cerebral

areas.

3. DESCRIPTION OF THE PROGRAM

EEGcorco is a flexible program since it works with EEG

signals transformed to ASCII format. The most com-

mercial computer programs designed to acquire EEG

signals (i.e. Neuroscan Scan IV, Grass Technology

PolyVIEW or Medicit Track Waker) allow exporting

their data to ASCII format.

Use of the EEGcorco program is very simple. It re-

quires a text file (“file of names”) which contains the

name of the data files in every line (also in text format).

Each data file contains only one datum per line. All sig-

nals provided to the program must first be examined in

order to eliminate all segments contaminated with arti-

facts.

Parametric Statistical Tests

Before executing the program, it is necessary to know

precisely which statistical design is suitable for the data

that is to be analyzed. EEGcorco compares the correla-

tion or coherence values among groups using the next

parametrical statistical test: correlated and uncorrelated

Student’s t, correlated and uncorrelated ANOVA of one

and two factors, and Split-plot ANOVA of two factors).

Besides, when ANOVAs tests are realized, the program

calculates automatically Duncan and Tukey’s post hoc

test. In Figure 4 , different designs in which the data can

be arranged are represented graphically; in each design

Figure 4. Schematic representation of different statistical designs that can be applied by means of the EEGcorco program. In each

esign is indicated the statistical test used. d

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787 781

is presented the parametrical statistical test used.

It is important to clarify that in all those designs it is

indispensable that the number of subjects in every cell

be the same (i.e., no mismatches are allowed). As Fig-

ure 4 shows, cells are numbered in sequential order from

left-to-right and from top-down. Each signal (registered

channel) must be in an individual file (in text format,

with a specific name). The names of the individual files

will then be arranged in a main file in ASCII format,

which we call the “file of names”. In this file, the indi-

vidual files will be arranged following the order of the

cells.

Figure 5 exemplifies a “file of names” that contains

data from a two-factor mixed design (2 × 2). First, the

names of the files that constitute the first cell (group 1 in

the first condition) appear, followed by cell 2 (group 1 in

the second condition), cell 3 (group 2 in the first condition)

and, finally, cell 4 (group 2 in the second condition).

It is important to clarify that EEGcorco does not func-

tion if any files are missing; that is, it is necessary to

have all the files for all subjects (and all must appear in

the “file of names”).

EEGcorco transforms the coherence and correlation

data to Z of Fisher values for the purpose of bringing

them over, as far as possible, to a normal distribution (a

requirement to permit the application of parametric sta-

tistics) [45].

When the program is executed, an initial screen ap-

pears in which the user must provide the parameters for

program execution. Figure 6 shows an initial screen in

which those parameters have been filled in. The user

must indicate if there are 2 or 4 channels (in other words,

if 2 or 4 derivations will be analyzed); the level number

of the factors to be considered (for the statistics); if sam-

pling was done at 256, 512 or 1024 Hz (the only sam-

pling rates allowed); if the point number for each seg-

ment is 256, 512 or 1024 (the only segment durations

allowed by the program); and must always respect the

condition that each segment have a duration of at least

one second. By default, the program determines the lim-

its of the EEG bands to: band 1, from 1 to 3 Hz; band 2,

from 4 to 7 Hz; band 3, from 8 to 10 Hz; band 4, from

11 to 13 Hz; band 5, from 14 to 19 Hz; band 6, from 20

to 30 Hz; and, band 7, from 31 to 50 Hz. Nevertheless,

in the initial screen the user can modify the limits of the

first six bands of analysis (but the limits of band 7 can-

not be modified). If the user works with correlated or

mixed designs, it is possible to choose to subtract the

first cell from the other ones, since it is considered to be

the baseline.

4. PROGRAM PERFORMANCE

When the user presses the “Start the analysis” button, the

Figure 5. The order in which the file

names must be arranged in the “file of

names” assigned to the EEGcorco pro-

gram. Subjects 01, 21, 22 and 24 belong

to the first group, while subjects 09, 10,

12 and 14 belong to the second one.

Each group was recorded in 2 condi-

tions, HABA and HAHA (hence, there

are 4 cells). Also, each subject was re-

corded in 4 regions (derivations): F3,

F4, P3 and P4. The extension of the

files is N10 (but can be of any length).

program initiates calculations and then the result files of

Table 1 are obtained. All these files are in text format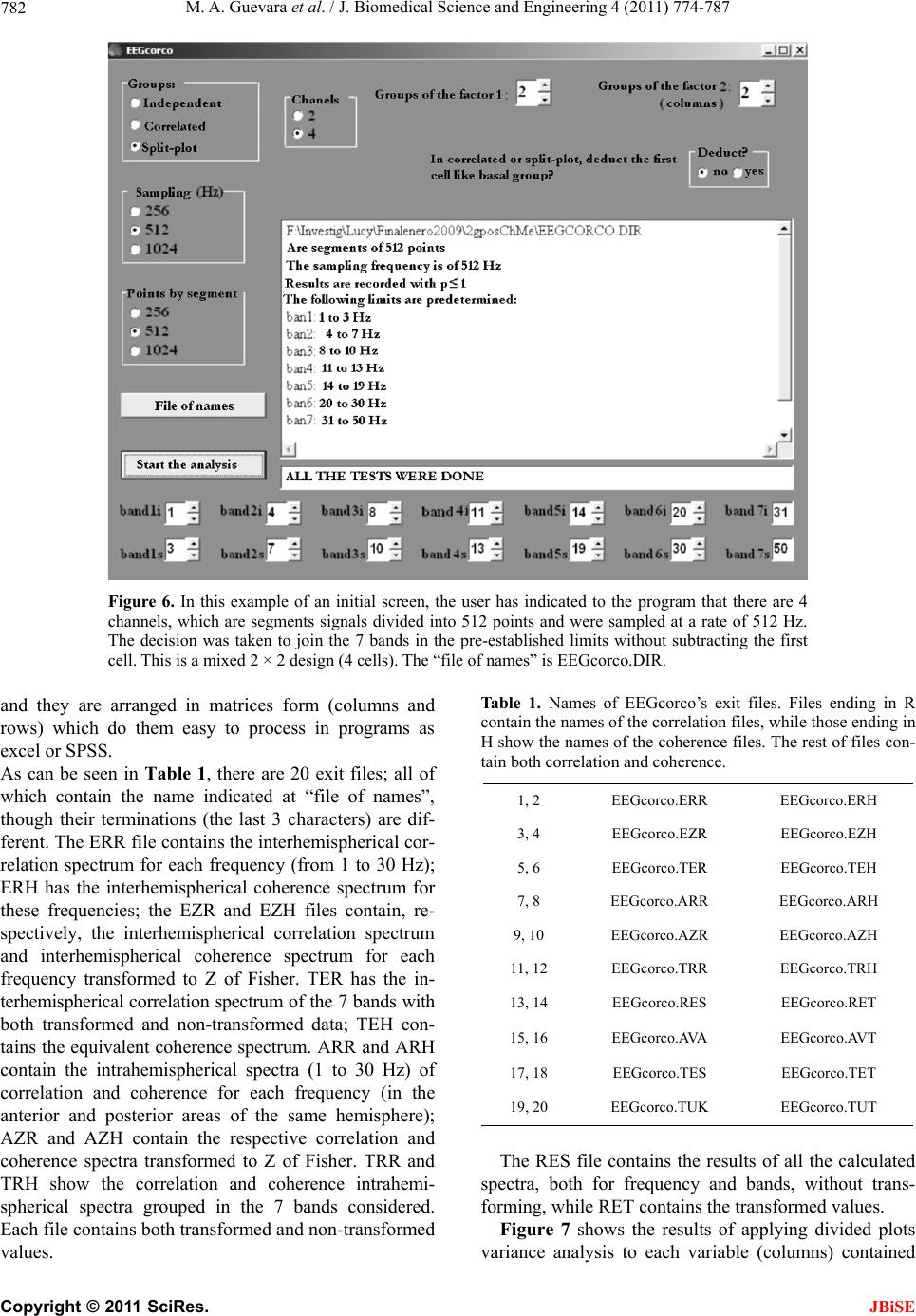

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787

782

Figure 6. In this example of an initial screen, the user has indicated to the program that there are 4

channels, which are segments signals divided into 512 points and were sampled at a rate of 512 Hz.

The decision was taken to join the 7 bands in the pre-established limits without subtracting the first

cell. This is a mixed 2 × 2 design (4 cells). The “file of names” is EEGcorco.DIR.

and they are arranged in matrices form (columns and

rows) which do them easy to process in programs as

excel or SPSS.

As can be seen in Table 1, there are 20 exit files; all of

which contain the name indicated at “file of names”,

though their terminations (the last 3 characters) are dif-

ferent. The ERR file contains the interhemispherical cor-

relation spectrum for each frequency (from 1 to 30 Hz);

ERH has the interhemispherical coherence spectrum for

these frequencies; the EZR and EZH files contain, re-

spectively, the interhemispherical correlation spectrum

and interhemispherical coherence spectrum for each

frequency transformed to Z of Fisher. TER has the in-

terhemispherical correlation spectrum of the 7 bands with

both transformed and non-transformed data; TEH con-

tains the equivalent coherence spectrum. ARR and ARH

contain the intrahemispherical spectra (1 to 30 Hz) of

correlation and coherence for each frequency (in the

anterior and posterior areas of the same hemisphere);

AZR and AZH contain the respective correlation and

coherence spectra transformed to Z of Fisher. TRR and

TRH show the correlation and coherence intrahemi-

spherical spectra grouped in the 7 bands considered.

Each file contains both transformed and non-transformed

values.

Table 1. Names of EEGcorco’s exit files. Files ending in R

contain the names of the correlation files, while those ending in

H show the names of the coherence files. The rest of files con-

tain both correlation and coherence.

1, 2 EEGcorco.ERR EEGcorco.ERH

3, 4 EEGcorco.EZR EEGcorco.EZH

5, 6 EEGcorco.TER EEGcorco.TEH

7, 8 EEGcorco.ARR EEGcorco.ARH

9, 10 EEGcorco.AZR EEGcorco.AZH

11, 12 EEGcorco.TRR EEGcorco.TRH

13, 14 EEGcorco.RES EEGcorco.RET

15, 16 EEGcorco.AVA EEGcorco.AVT

17, 18 EEGcorco.TES EEGcorco.TET

19, 20 EEGcorco.TUK EEGcorco.TUT

The RES file contains the results of all the calculated

spectra, both for frequency and bands, without trans-

forming, while RET contains the transformed values.

Figure 7 shows the results of applying divided plots

variance analysis to each variable (columns) contained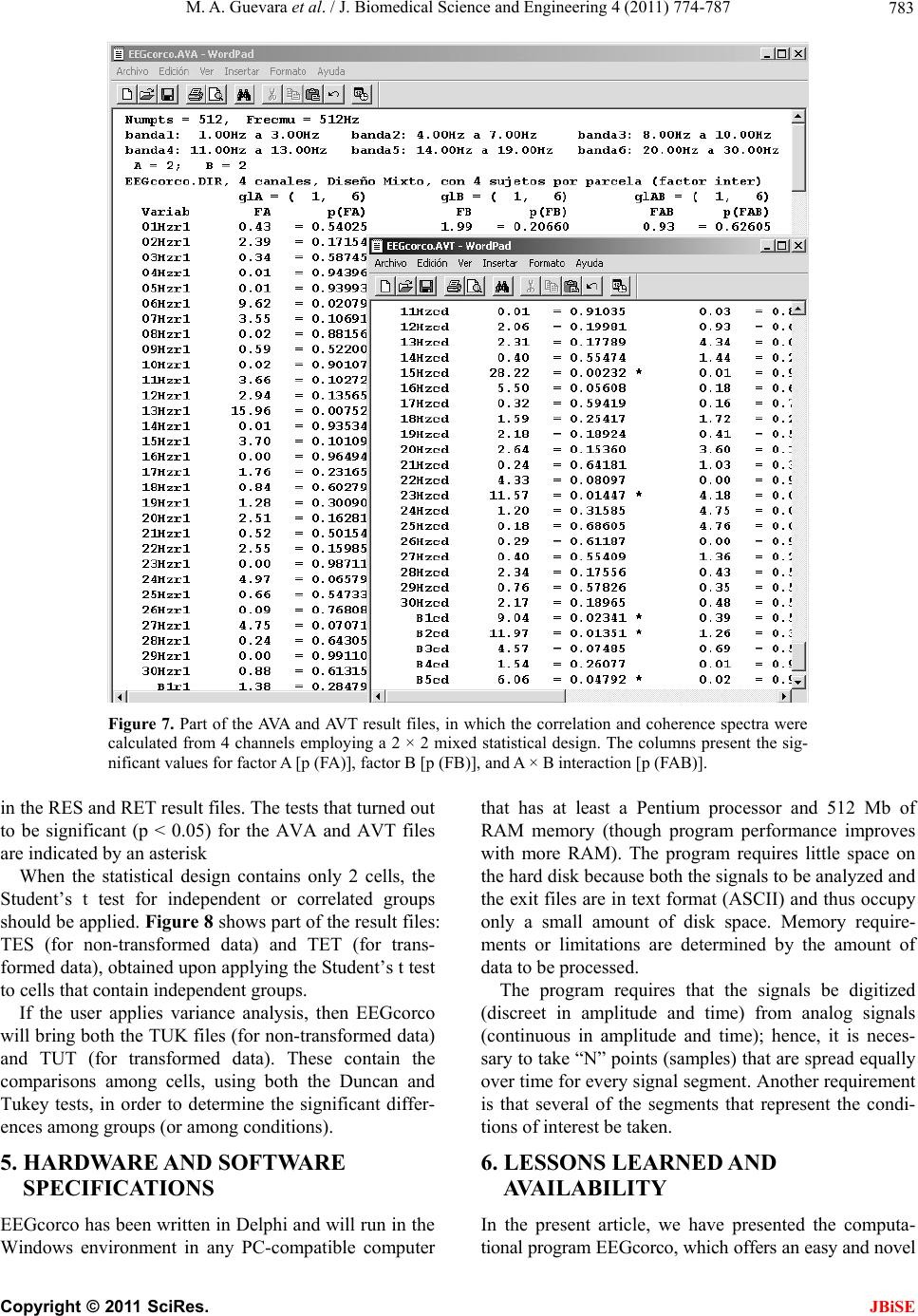

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787 783

Figure 7. Part of the AVA and AVT result files, in which the correlation and coherence spectra were

calculated from 4 channels employing a 2 × 2 mixed statistical design. The columns present the sig-

nificant values for factor A [p (FA)], factor B [p (FB)], and A × B interaction [p (FAB)].

in the RES and RET result files. The tests that turned out

to be significant (p < 0.05) for the AVA and AVT files

are indicated by an asterisk

When the statistical design contains only 2 cells, the

Student’s t test for independent or correlated groups

should be applied. Figure 8 shows part of the result files:

TES (for non-transformed data) and TET (for trans-

formed data), obtained upon applying the Student’s t test

to cells that contain independent groups.

If the user applies variance analysis, then EEGcorco

will bring both the TUK files (for non-transformed data)

and TUT (for transformed data). These contain the

comparisons among cells, using both the Duncan and

Tukey tests, in order to determine the significant differ-

ences among groups (or among conditions).

5. HARDWARE AND SOFTWARE

SPECIFICATIONS

EEGcorco has been written in Delphi and will run in the

Windows environment in any PC-compatible computer

that has at least a Pentium processor and 512 Mb of

RAM memory (though program performance improves

with more RAM). The program requires little space on

the hard disk because both the signals to be analyzed and

the exit files are in text format (ASCII) and thus occupy

only a small amount of disk space. Memory require-

ments or limitations are determined by the amount of

data to be processed.

The program requires that the signals be digitized

(discreet in amplitude and time) from analog signals

(continuous in amplitude and time); hence, it is neces-

sary to take “N” points (samples) that are spread equally

over time for every signal segment. Another requirement

is that several of the segments that represent the condi-

tions of interest be taken.

6. LESSONS LEARNED AND

AVAILABILITY

In the present article, we have presented the computa-

ional program EEGcorco, which offers an easy and novel t

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787

784

Figure 8. Parts of both the TES and TET results files. A comparison has been made among the cells

where the Student’s t test was applied for independent groups.

way to obtain complex quantitative analyses of EEG

synchronization. This program allows one to calculate,

in a fast and simultaneous manner, the correlation and

coherence spectra of EEG signals, as well as their re-

spective statistical parametric analyses. The calculation

of correlation and coherence spectra can be obtained for

both narrow and broad bands in a very short time by

applying several parametric statistical tests.

Dissimilarly to the most commercial programs de-

signed to analyze the EEG, EEGcorco allows extracts

the coherence and correlation. This last analysis has

many advantages on coherence, since it is sensitive to

both phase and polarity, regardless of amplitude. The

coherence not provide direct information as to the true

relationship between two signals and it only reflects the

stability of this relationship with respect to power

asymmetry and the phase relationship, For these reasons,

when interest focuses on waveform and time coupling

between two brain regions, correlation is a better choice

than coherence.

The main contribution of EEGcorco is that it allows

simultaneous inter- and intrahemispheric correlation and

coherence spectra calculations, and the application of

adequate parametric statistical analyses for which, to our

knowledge, there are no commercially available pro-

grams.

EEGcorco offers numerous advantages: it runs on any

PC, requires no complex equipment, and its output files

take up little memory space on the hard disk. The versa-

tility and flexibility of this program make it easily

adaptable to diverse experimental and clinical needs.

Moreover, the fact that EEGcorco can also be easily

adapted to portable computers means that it can solve

the problems that may arise when analyzing signals in

locations outside the laboratory; for example, in hospi-

tals or schools.

EEGcorco has been used for our work group as well

as for other researchers in both, basical and clinical

studies. For example, in a previous study we demon-

strate that the functional coupling between the prefrontal

and parietal cortices shows a characteristic pattern, spe-

cific to each age group (male children, teenagers and

young adults) during performance of the Hanoi task,

which is neuropsychological test widely used to evaluate

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787 785

executive functions as planning [46]. In other studies, we

found that alcohol decreases the correlation between

frontal and parietal areas in humans, and between sub-

cortical structures in rats [47,48]. Although in those in-

vestigations only the correlation analysis was used, in

futures studies we will use and compare both correlation

and coherence analysis in clinical populations, particu-

larly female adolescents with posttraumatic stress disor-

der and children abused. Finally, we believed that the

analysis exposed in the present paper could be useful in

clinical practice since the coupling between cortical ar-

eas could predict the cognitive functioning in neurode-

generative states as Alzheimer disease [49,50].

Although EEGcorco offers several advantages, it has

some limitations. One very important condition is that

the data of the different derivations and conditions of

each subject must be very well organized in their respec-

tive files; but, if this condition is followed adequately,

the program will run the statistical test (s) required with

no problem. Another limitation of this program is the

impossibility of analyzing more than four derivations

simultaneously. Nevertheless, for studies that require

more than four derivations, the program can be run sev-

eral times, until all the comparisons of interest have been

carried out. This program was created in order to answer

specific questions about functional similitude among two

or four brain regions.

EEGcorco is available upon request.

REFERENCES

[1] Lopes Da Silva, F.H. and Van Rotterdam, A. (1999) Bio-

physical aspects of EEG and Megnetoencephalogram

generation. In: Niedermeyer, E. and Lopes Da Silva, F.H.

Eds., Electroencephalography: Basic principles, clinical

applications and related fields, Lippicott Williams &

Wlikins, Baltimore, 93-109.

[2] Andreassi, J.L. (2000) Psychophysiology: Human beha-

vior & physiological response. 4th Editon, Lawrence Erl-

baum Associates Publishers, Mahwah.

[3] Fernández-Harmony, T. and González-Garrido, A. (2001)

EEG y cognición. In: Alcaraz-Romero, V. M. and Gumá-

Díaz, E. Eds., Texto de Neurociencias Cognitivas, Ma-

nual Moderno, Mexico City, 351-369.

[4] Guevara, M.A. and Corsi-Cabrera, M. (1996) EEG co-

herence or EEG correlation? International Journal of Psy-

chophysiology, 23, 145-153.

doi:10.1016/S0167-8760(96)00038-4

[5] Bendat, J.S. (1989) Engineering Applications of Correla-

tion and Spectral Analysis. John Wiley & Sons, USA.

[6] Pearson, K. and Lee, A. (1903) On the laws of inheri-

tance in man: I. Inheritance of physical characters. Bio-

metrika, 2, 357-462.

[7] Cooley, J.W. and Tukey J. W. (1965) An algorithm for the

machine calculation of complex fourier series. Mathe-

matics of Computation, 19, 297-301.

doi:10.1090/S0025-5718-1965-0178586-1

[8] Guilford, J.P. and Fruchter, B. (1984) Estadística aplicada

a la Psicología y la educación. McGraw-Hill, Mexico City.

[9] Brazier, M.A. and Casby, J.U. (1952) Cross-correlation and

autocorrelation studies of electroencephalographic poten-

tials. Electroencephalography and Clinical Neurophysio-

logy, 4, 201-211. doi:10.1016/0013-4694(52)90010-2

[10] French, C.C. and Beaumont, J.G. (1984) A critical review

of EEG coherence studies of hemisphere function. Inter-

national Journal of Psychophysiology, 1, 241-254.

doi:10.1016/0167-8760(84)90044-8

[11] Grindel, O.M. (1965) The significance of correlation

analysis for evaluation of the EEG in man Mathematical

analysis of the electrical activity of the brain. Harvard

University Press, Cambridge.

[12] Thatcher, R.W. and Walker, R.A. (1980) EEG coherence

and intelligence in children. Electroencephalography &

Clinical Neurophysiology, 49, S161.

[13] Shaw, J.C. (1981) An introduction to the coherence func-

tion and its use in EEG signal analysis. Journal of Medi-

cal Engineering & Technology, 6, 279-288.

doi:10.3109/03091908109009362

[14] Corsi-Cabrera, M., Guevara, M.A., Arce, C. and Ramos,

J. (1996) Inter and intrahemispheric EEG correlation as a

function of sleep cycles. Progress in Neuropsychophar-

macology and Biological Psychiatry, 20, 387-405.

doi:10.1016/0278-5846(96)00004-8

[15] Corsi-Cabrera, M., Munoz-Torres, Z., del Rio-Portilla, Y.

and Guevara, M.A. (2006) Power and coherent oscilla-

tions distinguish REM sleep, stage 1 and wakefulness.

International Journal of Psychophysiology, 60, 59-66.

doi:10.1016/j.ijpsycho.2005.05.004

[16] Kobayashi, T., Madokoro, S., Misaki, K., Murayama, J.,

Nakagawa, H. and Wada, Y. (2002) Interhemispheric dif-

ferences of the correlation dimension in a human sleep

electroencephalogram. Psychiatry and Clinical Neurosci-

ences, 56, 265-266.

doi:10.1046/j.1440-1819.2002.01020.x

[17] Perez-Garci, E., del-Rio-Portilla, Y., Guevara, M.A., Arce,

C. and Corsi-Cabrera, M. (2001) Paradoxical sleep is cha-

racterized by uncoupled gamma activity between fron-

tal and perceptual cortical regions. Sleep, 24, 118-126.

[18] Ramanand, P., Bruce, M.C. and Bruce, E.N. (2010) Mu-

tual information analysis of EEG signals indicates age-

related changes in cortical interdependence during sleep

in middle-aged versus elderly women. Journal of Clini-

cal Neurophysiology, 27, 274-284.

doi:10.1097/WNP.0b013e3181eaa9f5

[19] Corsi-Cabrera, M., Arce, C., Ramos, J., and Guevara,

M.A. (1997) Effect of spatial ability and sex on inter- and

intrahemispheric correlation of EEG activity. Electroen-

cephalography and Clinical Neurophysiology, 102, 5-11.

doi:10.1016/S0013-4694(96)96091-5

[20] Corsi-Cabrera, M., Gutiérrez, S., Ramos, J. and Arce, C.

(1988) Interhemispheric correlation of EEG activity dur-

ing successful and unsuccessful cognitive performance.

International Journal of Neuroscience, 39, 253-259.

doi:10.3109/00207458808985712

[21] Portella, C.E., Silva, J.G., Machado, S., Velasques, B., Bas-

tos, V.H., Ferreira-Vorkapic, C., Terra, P., Lopes, V., Cagy,

M., Carvalho, E., Orsini, M., Basile, L., Piedade, R. and

Ribeiro, P. (2007) EEG spectral coherence inter- and in-

trahemispheric during catching object fall task. Arquivos

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787

786

de Neuro-psiquiatria, 65, 63-67.

doi:10.1590/S0004-282X2007000100014

[22] Ramos, J., Corsi-Cabrera, M., Guevara, M.A. and Arce,

C. (1993) EEG activity during cognitive performance in

women. International Journal of Neuroscience, 69, 185-

195. doi:10.3109/00207459309003329

[23] Razumnikova, O.M. and Larina, E.N. (2005) Hemi-

spheric interactions during a search of original verbal

associations: EEG coherence in creative men and women.

Zhurnal Vyssheĭ Nervoĭ Deiatelnosti Imeni I P Pavlova,

55, 777-787.

[24] Serrien, D.J. (2008) Coordination constraints during bi-

manual versus unimanual performance conditions. Neuro-

psychologia, 46, 419-425.

doi:10.1016/j.neuropsychologia.2007.08.011

[25] Serrien, D.J. (2009) Verbal-manual interactions during

dual task performance: An EEG study. Neuropsychologia,

47, 139-144.

doi:10.1016/j.neuropsychologia.2008.08.004

[26] Grindel, O.M., Koptelov, M., Masherov, Iu, E. L. and

Pronin, I.N. (1998) Foci of pathological activity in the

human brain and their influence on the spatial-temporal

relationships of the EEG. Zhurnal Vyssheĭ Nervoĭ Dei-

atelnosti Imeni I P Pavlova, 48, 671-686.

[27] Cespedes-Garcia, Y., González-Hernández, J.A., García-Fi-

dalgo, J., Begueria-Santos, R.A. and Figueredo-Rodríguez.

P. (2003) Interictal EEG coherence in patients with par-

tial temporal lobe epilepsy. Revista de Neurología, 37,

1107-1111.

[28] Cerdan, L.F., Guevara, M.A., Sanz, A., Amezcua, C. and

Ramos-Loyo, J. (2005) Brain electrical activity changes

in treatment refractory schizophrenics after olanzapine

treatment. International Journal of Psychophysiology, 56,

237-247. doi:10.1016/j.ijpsycho.2004.12.008

[29] Higashima, M., Takeda, T., Kikuchi, M., Nagasawa, T.

and Koshino, Y. (2006) Functional connectivity between

hemispheres and schizophrenic symptoms: a longitudinal

study of interhemispheric EEG coherence in patients

with acute exacerbations of schizophrenia. Clinical EEG

and Neurosciences, 37, 10-15.

[30] Wada, Y., Nanbu, Z., Jiang, Y., Koshino, Y. and Hashi-

moto, T. (1998) Interhemispheric EEG coherence in ne-

ver-medicated patients with paranoid schizophrenia: Ana-

lysis at rest and during photic stimulation. Clinical EEG

(Electroencephalography), 29, 170-176.

[31] Lazar, A. S., Lazar, Z. I., Biro, A., Gyori, M., Tarnok, Z.,

Prekop, C., Keszei, A, Stefanik, K., Gadoros, J., Halasz,

P. and Bodizs, R. (2010) Reduced fronto-cortical brain

connectivity during NREM sleep in Asperger syndrome:

An EEG spectral and phase coherence study. Clinical Neu-

rophysiology, 121, 1844-1854.

doi:10.1016/j.clinph.2010.03.054

[32] Leveille, C., Barbeau, E.B., Bolduc, C., Limoges, E., Ber-

thiaume, C., Chevrier, E., Mottron, L. and Godbout, R.

(2010) Enhanced connectivity between visual cortex and

other regions of the brain in autism: A REM sleep EEG

coherence study. Autism Research, 3, 280-285.

doi:10.1002/aur.155

[33] Adler, G., Brassen, S. and Jajcevic, A. (2003) EEG co-

herence in Alzheimer’s dementia. Journal of Neural Tran-

smission, 110, 1051-1058.

doi:10.1007/s00702-003-0024-8

[34] Pogarell, O., Teipel, S. J., Juckel, G., Gootjes, L., Moller,

T., Burger, K., Leinsinger, G., Moller, H.J., Hegerl, U.

and Hampel, H. (2005) EEG coherence reflects regional

corpus callosum area in Alzheimer’s disease. Journal of

Neurology, Neurosurgery and Psychiatry, 76, 109-111.

doi:10.1136/jnnp.2004.036566

[35] Abdullah, H., Maddage, N.C., Cosic, I. and Cvetkovic, D.

(2010) Cross-correlation of EEG frequency bands and

heart rate variability for sleep apnoea classification. Me-

dical and Biological Engineering and Computing, 48, 1261-

1269. doi:10.1007/s11517-010-0696-9

[36] Abeyratne, U.R., Swarnkar, V., Rathnayake, S.I. and Hu-

kins, C. (2007) Sleep-stage and event dependency of

brain asynchrony as manifested through surface EEG.

Conference Proceedings: Annual International Confer-

ence of the IEEE Engineering in Medicine and Biology

Society, Lyon, 22-26 August 2007, 709-712.

[37] Aksahin, M., Aydin, S., Firat, H., and Erogul, O. (2010).

Artificial apnea classification with quantitative sleep EEG

synchronization. Journal of Medical Systems, 1-6.

[38] Bryzgalov, A.O. and Vol’f, N.V. (2006) Gender-related

differences in EEG coherence in Stroop task. Zhurnal Vy-

ssheĭ Nervoĭ Deiatelnosti Imeni I P Pavlova, 56, 464-471.

[39] Corsi-Cabrera, M., Ramos, J., Guevara, M.A., Arce, C.

and Gutierrez, S. (1993) Gender differences in the EEG

during cognitive activity. International Journal of Neu-

roscience, 72, 257-264.

doi:10.3109/00207459309024114

[40] Razumnikova, O.M. (2004) Gender differences in hemi-

spheric organization during divergent thinking: an EEG

investigation in human subjects. Neuroscience Letters,

362, 193-195. doi:10.1016/j.neulet.2004.02.066

[41] Vol’f, N.V., and Razumnikova, O.M. (2001) Dynamics of

interhemispheric asymmetry during perception of verbal

information in men and women: EEG analysis. Zhurnal

Vyssheĭ Nervoĭ Deiatelnosti Imeni I P Pavlova, 51, 310-

314.

[42] Grieve, P.G., Emerson, R.G., Fifer, W.P., Isler, J.R. and

Stark, R.I. (2003) Spatial correlation of the infant and

adult electroencephalogram. Clinical Neurophysiology, 114,

1594-1608. doi:10.1016/S1388-2457(03)00122-6

[43] Maurits, N.M., Scheeringa, R., van der Hoeven, J.H. and

de Jong, R. (2006) EEG coherence obtained from an

auditory oddball task increases with age. Journal of Cli-

nical Neurophysiology, 23, 395-403.

doi:10.1097/01.wnp.0000219410.97922.4e

[44] Tarokh, L., Carskadon, M.A. and Achermann, P. (2010)

Developmental changes in brain connectivity assessed

using the sleep EEG. Neuroscience, 171, 622-634.

doi:10.1016/j.neuroscience.2010.08.071

[45] Sánchez-Bruno, A., Borges del Rosal, A. (2005) Trans-

formación Z de Fisher para la determinación de in-

tervalos de confianza del coeficiente de correlación de

pearson. Psic othema, 17, 148-153.

[46] Guevara, M. A., Rizo-Martínez, L. E., Robles-Aguirre, F.

A., Hernández-González, M. (in press) Prefrontal-parie-

tal correlation during performance of the towers of Hanoi

task in male children, adolescents and young adults. De-

velopmental Cognitive Neuroscience.

[47] Sanz-Martin, A., Guevara, M. A., Amezcua, C., Santana,

G. and Hernández-González, M. (2011) Effects of red

wine on the electrical activity and functional coupling

M. A. Guevara et al. / J. Biomedical Science and Engineering 4 (2011) 774-787

787

JBiSE

between the prefrontal-parietal cortices in young men.

Appetite, 57, 84-93. doi:10.1016/j.appet.2011.04.004

[48] Hernández-González, M., Martínez-Pelayo, M., Arteaga-

Silva, M., Bonilla-Jaime, H., Guevara, M. A. (2008) Eth-

anol changes the electroencephalographic correlation of

the ventral tegmental area and nucleus accumbens, com-

ponents of the mesoaccumbens system in rats. Pharma-

cology, Biochemistry and Behavior, 92, 124-130.

[49] Besthorn, C., Förstl, H., Geiger-Kabisch, C., Sattel, H.,

Gasser, T. and Schreiter-Gasser, U. (1994) EEG coher-

ence in Alzheimer disease. Electroencephalography and

Clinical Neurophysiology, 90, 242-245.

doi:10.1016/0013-4694(94)90095-7

[50] Locatelli, T., Cursi, M., Liberati, D., Franceschi, M., Comi,

G. (1998) EEG coherence in Alzheimer´s disease. Elec-

troencephalography and Clinical Neurophysiology, 106,

229-237. doi:10.1016/S0013-4694(97)00129-6