Technology and Investment
Vol.3 No.3(2012), Article ID:22082,6 pages DOI:10.4236/ti.2012.33025
Genetic Algorithm for Arbitrage with More than Three Currencies
1Department of Quantitative Methods, University of Las Palmas de Gran Canaria, Las Palmas de Gran Canaria, Spain
2Department of Quantitative Methods, Complutense University of Madrid, Madrid, Spain
Email: adrian.fernandez102@alu.ulpgc.es, ffernandez@dmc.ulpgc.es, sosvilla@ccee.ucm.es
Received June 19, 2012; revised July 20, 2012; accepted July 27, 2012
Keywords: Arbitrage; Foreign Exchange Market; Genetic Algorithm
ABSTRACT
We develop a genetic algorithm that is able to find the optimal sequence of exchange rates that maximizes arbitrage profits with more than three currencies, being both the triangular arbitrage and the direct exchange rate two special cases of the proposed algorithm. Applying the algorithm to the most traded currencies, we find average profits ranking from 4.5083% to 0.3162% for changing 1 USD for EUR with respect to the direct exchange rate, for different transaction costs, during the period October 2000-April 2012. Our results also suggest that the arbitrage profits increased just after the subprime crisis in summer of 2007 and that they are higher when the market is less liquid.
1. Introduction
Triangular arbitrage is a widely used tool in foreign exchange (FX) markets. It is based on exploiting an arbitrage opportunity resulting from a pricing discrepancy among three currencies. FX traders with many years of experience are able to find triangular arbitrage opportunities at a glance, by comparing the prices of three currencies simultaneously. However, it is very unlikely that, at first glance, they could be able to find arbitrage opportunities when they come into play more than three currencies. Moreover, even if they are able to find triangular arbitrage opportunities at any given time, the profits from triangular arbitrage based on only three currencies could be lower than those obtained from arbitrating with more than three currencies.
We develop a fast genetic algorithm (GA) that is able to find the optimal sequence of exchange rates that maximizes arbitrage profits with more than three currencies, being both the triangular arbitrage and the direct exchange rate two special cases of the proposed algorithm.
2. A GA for Arbitrage with More than Three Currencies
GAs are a class of adaptive search and optimization technique based on the principles of natural evolution, initially developed in Reference [1]. In our strategy, we follow the methodology developed in Reference [2] for automatic selection.
The GA starts with a large number of randomly generated chromosomes designed to encode potential solutions to the problem. Suppose that we begin by considering a sequence of exchange rates taken at random with a maximum of 5 currencies{x1, x2, x3, x4, x5}, encoding the sequence by means of vectors formed by natural numbers between 0 and 6, where 0 means no currency and where 1 = Australian Dollar (AUD), 2 = Euro (EUR), 3 = Swiss Franc (CHF), 4 = Japanese Yen (JPY), 5= United States Dollar (USD), and 6 = Pound Sterling (GBP). Since the EUR/USD is the most traded rate, we seek for a sequence that allows us to exchange 1 USD for EUR. For instance, vector {x1, x2, x3, x4, x5} = {3, 6, 2, 5, 4} means the following sequence of currencies {CHF, GBP, EUR, USD, JPY}, or the following sequence of exchange rates (assuming that we exchange USD to EUR): {CHF/USD, GBP/CHF, EUR/GBP, USD/EUR, JPY/USD, EUR/JPY}.
Next, the following objective function evaluates each potential solution, assigning each chromosome a fitness value, ranking chromosomes from best to worst:
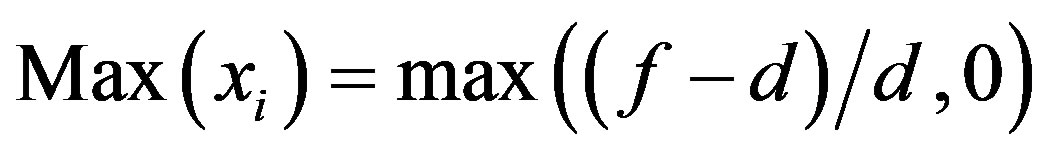
where f is the final amount of EUR that we obtain using the sequence suggested by chromosome {x1, x2, x3, x4, x5} and d is the amount of EUR that we obtain using the direct EUR/USD exchange rate. To keep our analysis realistic, every time we use an exchange rate, we apply a transaction cost k·0.05%, k = {1, 5, 10, 15}1, where the parameter k represents a penalty used to correct for possible data errors that could lead us to misleading profits2.
In order to carry out our arbitrage algorithm, we proceed as follows. We obtain an initial set of N sequences randomly selected currencies. Then, we select 50%·N of chromosomes better fitted as for the objective function. These chromosomes, the parents of the next generation, undergo a recombination process to produce descendants. Offspring are created combining information from two parent chromosomes to form a child that has the potential to outperform its parents. For instance, if we have the parent chromosomes {x1, x2, x3, x4, x5} = {3, 6, 2, 5, 4} and {x1, x2, x3, x4, x5} = {1, 3, 6, 5, 3}, for recombination we first randomly choose a cut off point within each chromosome (let us say the second position) and then the information is exchanged as outlined below:
![]()
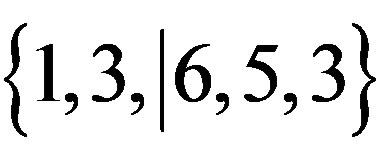 corresponding with the sequence (3, 6, 6, 5, 3)
corresponding with the sequence (3, 6, 6, 5, 3)
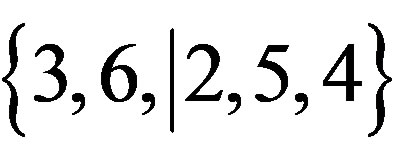 corresponding with the sequence (1, 3, 2, 5, 4)
corresponding with the sequence (1, 3, 2, 5, 4)
Finally, in order to avoid reaching local optima instead of global optima, all the chromosomes, except those best fitted as for the objective function, are candidates to be transformed by a mutation operator, which is essentially a mechanism by which information encoded along the chromosome is randomly altered. For example, if we select at random the penultimate element of the chromosome {3, 6, 2, 5, 4}, a mutation would be changing currency 5 by a random integer value between 0 and 6, as we proceeded when creating the initial population, namely:
{3, 6, 2, 5, 4} → {3, 6, 2, 1, 4}
The purpose of mutation is to recover lost genetic information that may not be present in the initial population and is not obtainable by recombination alone. In our case, the mutation rate is very small (5%).
After recombination and mutation, we obtained a second generation of chromosomes to which we apply again the same steps as before, the process ending when a convergence criterion is reached: either when the best of chromosomes remains stable during a given number of successive generations or when we reach a predetermined number of generations, this number being fixed beforehand.
To shorten the computation time and to reduce the number of currencies in the final optimal sequence (with a consequent reduction in transaction costs), we make some adjustments. First, given that our initial currency is 5 and the final currency is 2, we sequence, we remove of the sequence all the currencies located from this position, e.g. the chromosome {3, 6, 2, 1, 4} becomes {3, 6, 0, 0, 0}. Similarly, if the initial currency is located within the sequence before the final currency, we would remove from the sequence all the currencies located before the initial currency, e.g. the chromosome {3, 6, 5, 4, 1} is transformed into {0, 0, 0, 4, 1}. Finally, if the sequence is such that the same currency is selected in two or more positions, we remove all repetitions, keeping only the first one, e.g. the chromosome {3, 6, 1, 3, 4} converts into {3, 6, 1, 0, 4}.
3. Empirical Results
We have applied the GA arbitrage for changing 1 USD for EUR to daily data of closing cross rates from 01 October 2000 to 30 April 2012 taken from Thomson Reuters Datastream. We have employed the cross FX for the following most traded currencies in the market: US dollar, Australian dollar, Canadian dollar, Euro, Hong Kong dollar, Indian rupee, Japanese yen, Mexican peso, New Zeland dollar, Norwegian krone, Singapore dollar, Swedish krona, Swiss franc and Streling pound Table 1 reports the average GA arbitrage profit with respect to direct exchange rate and the average number of exchange rates, as well as their standard deviation and median, for the entire sample and for two subsamples (before and after the subprime crisis in August 2007).
As can be seen, GA always renders more EUR from 1 USD than those from the direct exchange rate, diminishing with higher values of k, suggesting the existence of arbitrage opportunities in the major FX even when we allow for high transaction costs. These profits with respect to the direct exchange rate rank from 4.5083% for k = 1, to 0.3162% for k = 15. Besides, the number of exchange rates in the optimal sequence is higher than 2 for values of k up to 10, indicating that the main opportunities of arbitrage using more than three currencies.
Interestingly, results in Table 1 also suggest both the GA relative arbitrage profit and the number of exchange rates used in the GA increase after the subprime crisis in August 2007. Moreover, there exists a positive and significant correlation among them (with an average correlation of 78.68% for k = {1, 5, 10, 15} and p-values of 0.000); it confirms our main result that the arbitrage profit is greater when applied to more than three currencies. This result could be an indication that foreign exchange markets were very tight at that time leading to upset exchange rates.
Table 2 shows the Pearson correlations between monthly GA arbitrage profits, as well as the monthly average number of exchange rates, and both the liquidity indicators proposed by reference [3] and the Chicago Board Options Exchange Market Volatility Index (VIX) and EUROVIX as measures of implicit volatility. As can be seen, in line with reference [4-6], we detect higher arbitrage profits
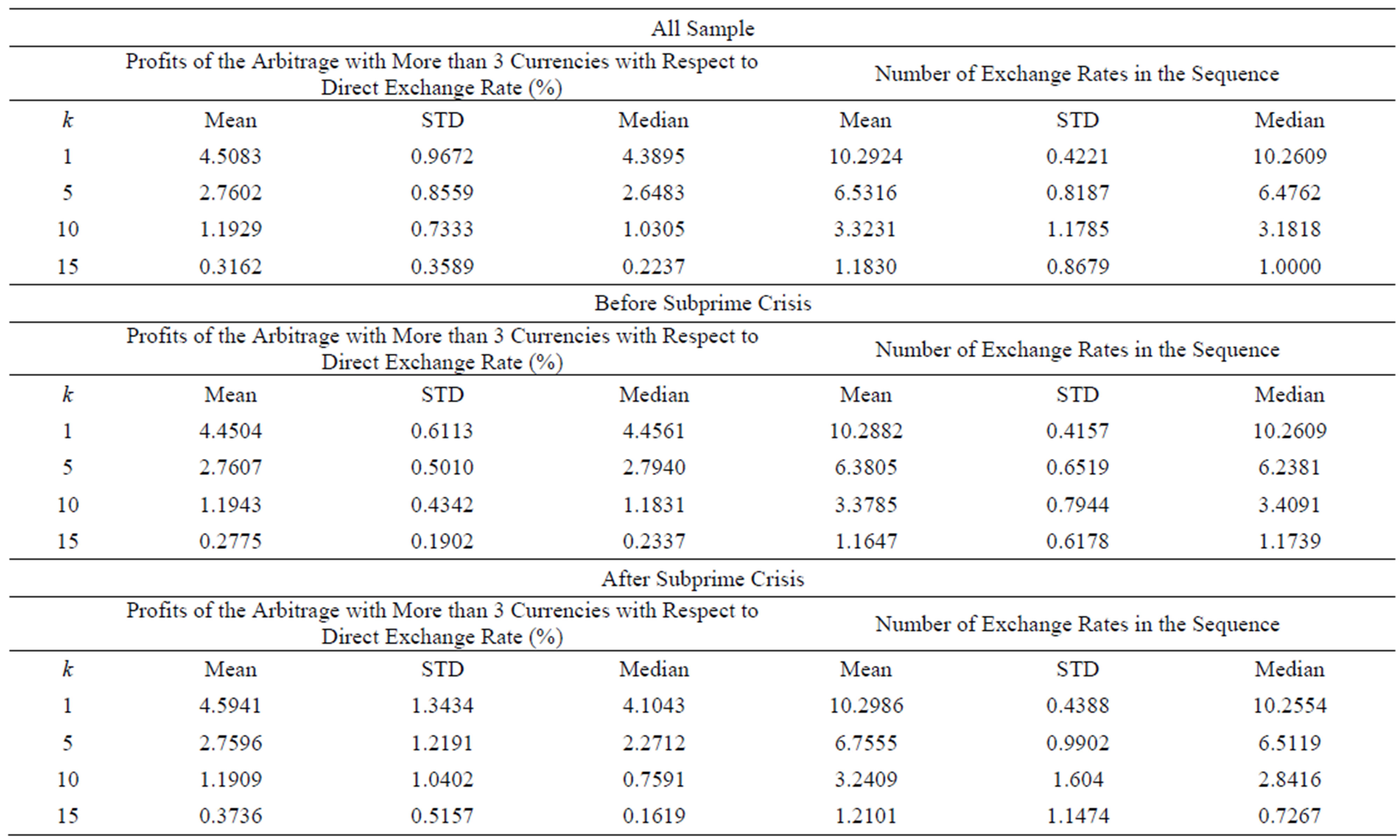
Table 1. GA arbitrage profits and number of exchange rates in each sequence.
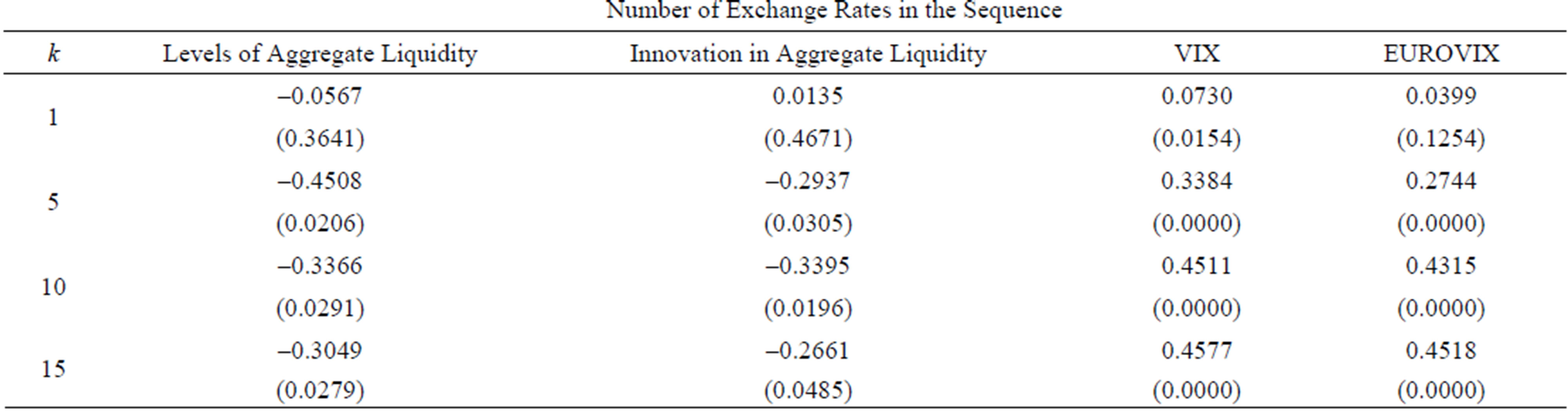
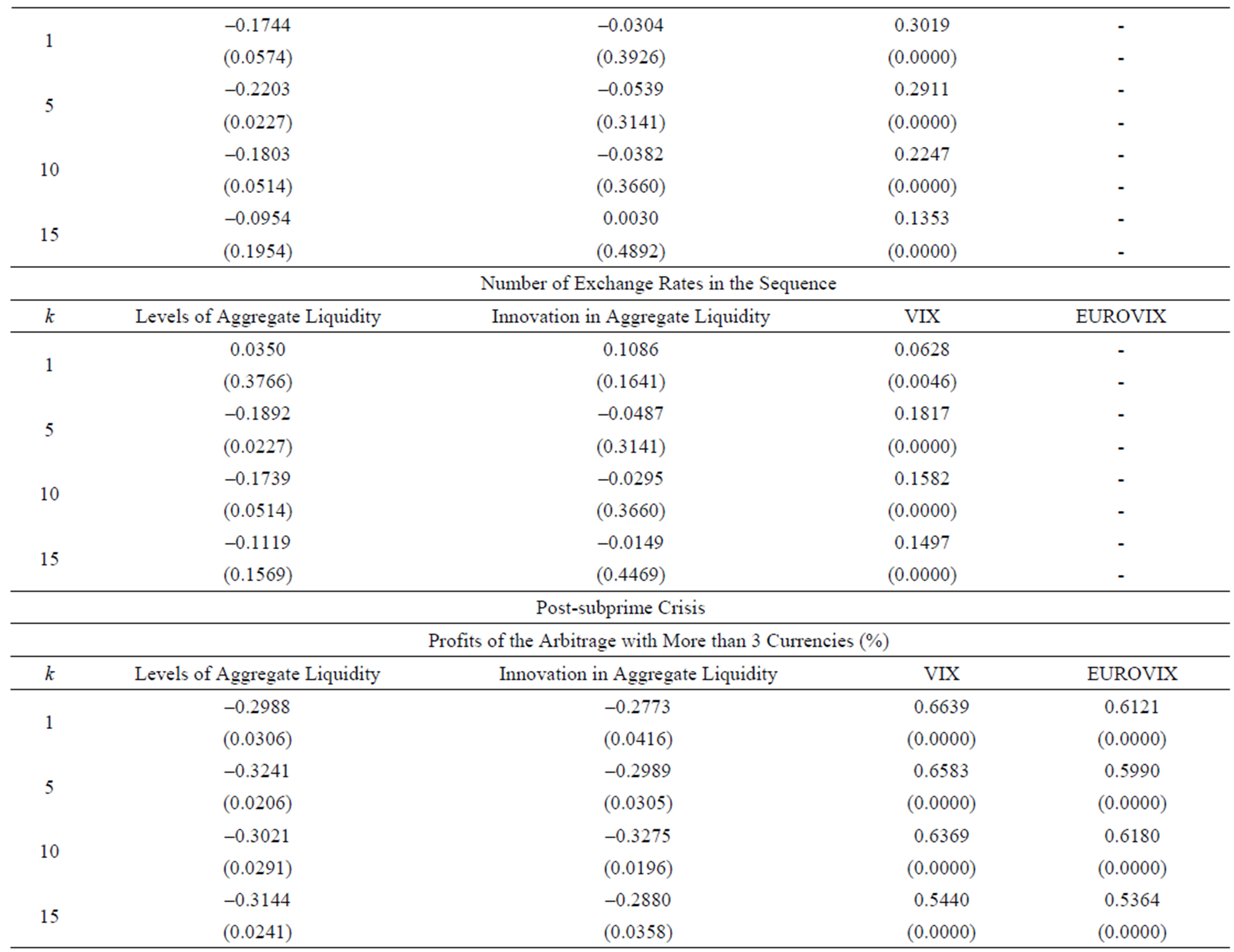
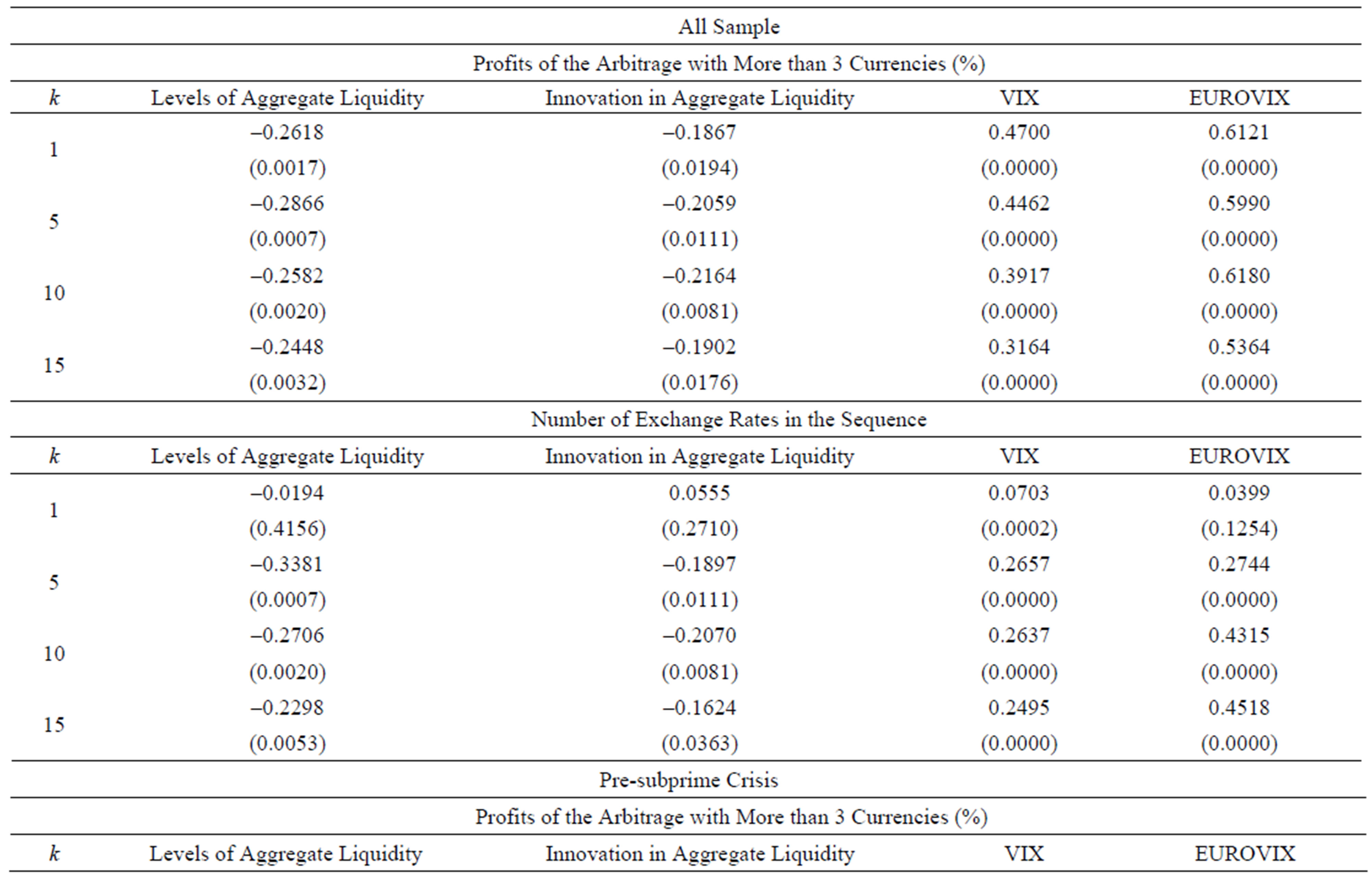
Table 2. Correlation between GA arbitrage profits and number of exchange rates in each sequence with liquidity and volatility indicators.
when markets are less liquid, and vice versa. We also detect a positive association between GA excess profit and market perceived volatility.
Finally, Figure 1 plots the monthly evolution of average GA arbitrage profits and mean number of exchange rates with more than three currencies for the entire sample and for k = 15.
Therefore, in view of the encouraging results of the present study, some optimism about the benefits from the use of a genetic algorithm to exhaustively examine all possible permutations to find the optimal sequence that achieves maximum arbitrage profit seems justified, specially given the fact determining the optimal exchange sequence takes minimal computation time (about 10 seconds on a laptop with Intel Core i3).
4. Concluding Remarks
We have presented empirical evidence on the existence of arbitrage opportunities in foreign exchange markets using more than three currencies using a genetic algorithm
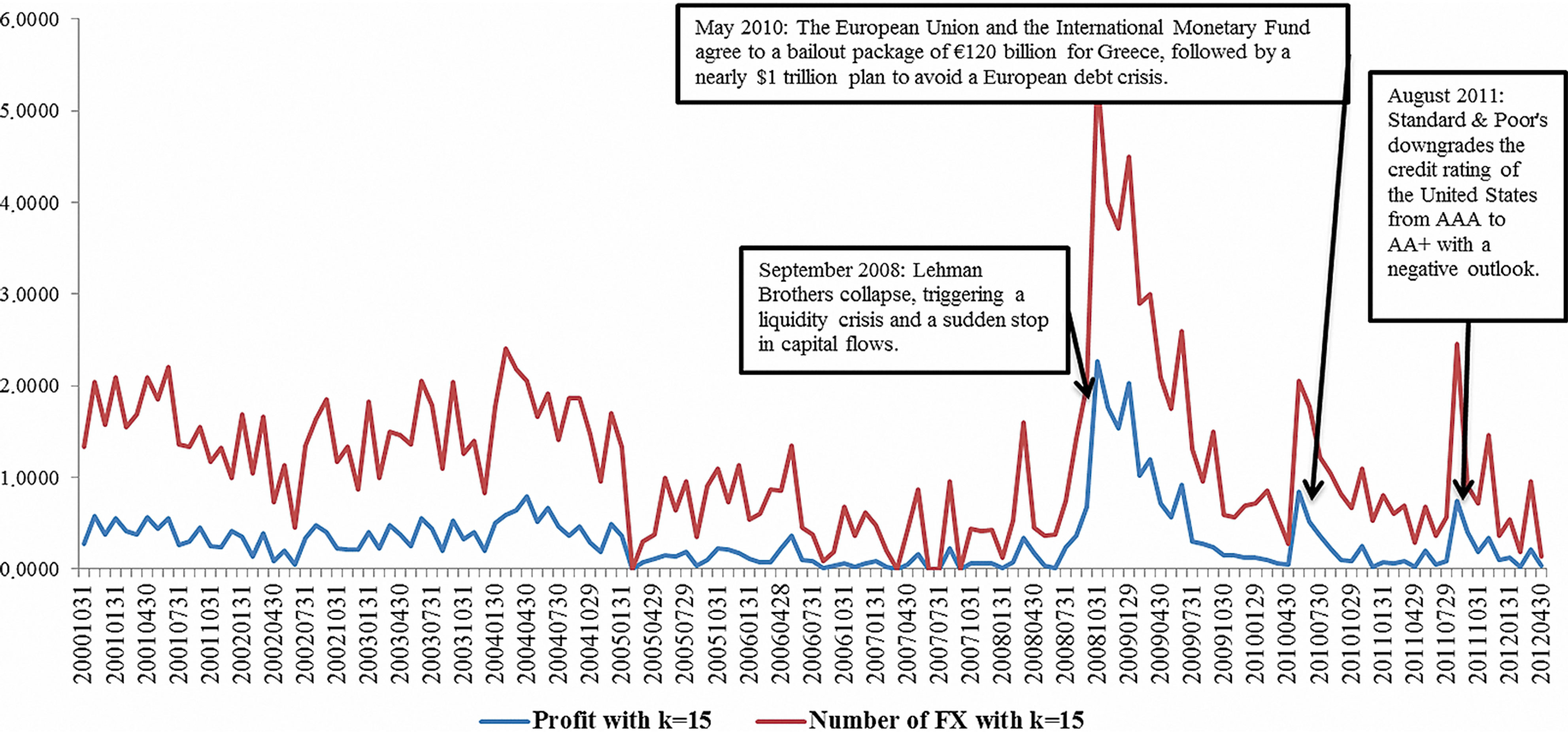
Figure 1. Monthly evolution of average GA arbitrage profits and mean number of exchange rates with more than three currencies (October 2000 to April 2012) for k = 15.
that is able to quickly find the optimal sequence of exchange rates that maximizes the arbitrage profit with respect to that from a simple direct exchange rate.
After correcting the database to avoid disturbances from errors in the data and taking into account several levels of transaction costs, we found arbitrage opportunities with more than three currencies during the 01 October 2000-30 April 2012 period for the EUR/USD case using AUD, CAD, HKD, INR, JPY, MXN, NZD, NOK, SGD, SEK, CHF and GBP as intermediate currencies and transaction costs of k·0.05%, k = {1, 5, 10, 15}. These results would be indicating the existence of market anomalies that, drawing on recent work on the theory of investment under uncertainty, could be interpreted as the tendency for traders to wait for sufficiently large arbitrage opportunities to open up before entering the market, Reference [7].
The authors are aware of the difficulty of finding information on all the exchange rates quoted in the real market in the same source, since exchange rates are traded on an OTC market and the available information is the daily average rate of market operations. Even though, we believe that the algorithm presented here is a useful tool for market operators seeking to maximize arbitrage profits in FX markets (where the number of global currencies is very high, and thus the proposed algorithm is more suitable and powerful) taking advantages of mismatches between quoted exchange rates at any given time, since our algorithm encompasses as particular cases both the triangular arbitrage and the direct exchange rate. Therefore, in the worst scenario where there are no arbitrage opportunities, our algorithm will render as optimal solution the direct exchange rate and, in the best scenario where there are arbitrage opportunities, our algorithm will select as the optimal solution a sequence of exchange rates that maximizes the arbitrage profits with three or more currencies.
5. Acknowledgements
The authors wish to thank two anonymous referee for helpful comments and Analistas Financieros Internacionales for kindly providing us with the data set. The authors gratefully acknowledge financial support from the Spanish Ministry of Science and Innovation (projects ECO2010- 21318 and ECO2011-23189).
REFERENCES
- J. Holland, “Adaptation in Natural and Artificial Systems,” MIT Press, Cambridge, 1975.
- E. Acosta-González and F. Fernández-Rodríguez, “Model Selection via Genetic Algorithms Illustrated with Crosscountry Growth Data,” Empirical Economics, Vol. 33, No. 2, 2007, pp. 313-337. doi:10.1007/s00181-006-0104-3
- L. Pástor and R. F. Stambaugh, “Liquidity Risk and Expected Stock Returns,” Journal of Political Economy, Vol. 111, No. 3, 2003, pp. 642-685. doi:10.1086/374184
- S. J. Grossman and J. E. Stiglitz, “Information and Competitive Price Systems,” The American Economic Review, Vol. 66, No. 2, 1976, pp. 246-253.
- S. J. Grossman and J. E. Stiglitz, “On the Impossibility of Informationally Efficient Markets,” The American Economic Review, Vol. 70, No. 3, 1980, pp. 393-408.
- B. R. Marshall, S. Treepongkaruna and M. Young, “Exploitable Arbitrage Opportunities Exist in the Foreign Exchange Market,” Discussion Paper, Massey University, Palmerston North, 2007.
- A. Carruth, A. Dickerson and A. Henley, “What Do We Know about Investment under Uncertainty?” Journal of Economic Surveys, Vol. 14, No. 2, 2000, pp. 119-154. doi:10.1111/1467-6419.00107
NOTES
1The 0.05% transaction costs include bid-ask spread, commissions and fixed costs of using the trading platform.
2The parameter k can also be conceived as a mean to account for the fact that the bid-ask spread could be different for any two currency pairs and that it could also change with the time under different market conditions.

