Technology and Investment
Vol.1 No.2(2010), Article ID:1765,6 pages DOI:10.4236/ti.2010.12017
Labor Investment in a New International Mixed Market
Institute for Basic Economic Science, Osaka, Japan
E-mail: ohnishi@e.people.or.jp
Received January 25, 2010; revised March 28, 2010; accepted March 30, 2010
Keywords: Lifetime Employment Contract, Continuous-Time Dynamic Model, Domestic Public Firm, Foreign Private Firm
Abstract
This paper considers a continuous-time dynamic mixed market model of labor investment decisions of a domestic public firm and a foreign private firm. The paper studies the optimal levels of preemptive investment for the long-run structure of the international mixed market. It is then demonstrated that there are no perfect equilibria in which neither firm invests to its steady-state reaction curve.
1. Introduction
Following the pioneering work of Merrill and Schneider [1], the analysis of mixed market models that incorporate welfare-maximizing public firms has received significant attention in recent years and has been widely studied by many economists, such as [2-19].1 However, these studies consider mixed markets with domestic private firms and do not include foreign private firms.
Some studies include foreign firms. For example, Fjell and Pal [20] extend the analysis to an international context by considering a model where a state-owned public firm competes with both domestic and foreign private firms and examine the effects of entry by an additional private firm. Pal and White [21] examine the effects of privatization on strategic trade policy by incorporating strategic trade policy instruments in an international mixed model where a state-owned public firm competes with both domestic and foreign private firms. Fjell and Heywood [22] consider a mixed oligopoly in which a public Stackelberg leader competes with both domestic and foreign private firms. Matsumura [23] examines a Stackelberg mixed duopoly where a public firm competes against a foreign private firm. Furthermore, Fernández-Ruiz [24] studies firm’ decisions to hire managers when a public firm with social welfare objectives competes against a foreign private firm with profit objectives.
As is well known, international mixed oligopolies are common in developed and developing countries as well as in former communist countries. Public firms compete against foreign private firms in many industries, such as banking, life insurance, automobiles, airlines, steel, shipbuilding, and tobacco.2
Therefore, we examine a continuous-time dynamic model of the strategic investment decisions of a domestic welfare-maximizing public firm and a foreign profit-maximizing private firm. The possibility of firms using excess capacity to strategic investment was studied by [25-27], and was also extended in two-stage models by [28-34]. Furthermore, Spence [35] examines the strategic investment decisions of profit-maximizing private firms in a new industry or market by using a continuous-time asymmetric dynamic model. In Spence’s model, there exist the leading and the following firms. He shows that the equilibrium is for the leading firm to invest as quickly as possible to some capital level and then stop. Fudenberg and Tirole [36] establish the existence of a set of perfect equilibria by using Spence’s dynamic model and suggest that the steady state of the game is usually on neither firm’s steady-state reaction curve; that is, there are early-stopping equilibria where neither firm invests to its steady-state reaction curve. Ohnishi [11] studies the perfect equilibria of a continuous-time mixed market model of the strategic investment decisions of welfare-maximizing public and profit-maximizing private firms and shows that the equilibrium outcomes of the mixed market model differ from those of Fudenberg and Tirole’s private market model; that is, there are no early-stopping equilibria where neither firm invests to its steady-state reaction curve.
All these studies focus on capital as strategic investment. On the other hand, we focus on labor; that is, we use lifetime employment contracts as strategic investment.3
The purpose of this study is to construct a set of perfect equilibria of a continuous-time dynamic model in which a domestic welfare-maximizing public firm and a foreign profit-maximizing private firm compete for labor investment.
The remainder of this paper is organized as follows. In Section 2, the elements of the continuous-time model are formulated. Section 3 characterizes the equilibrium outcomes of the continuous-time model. Section 5 concludes the paper.
2. The Model
Let us consider an international mixed market with one domestic welfare-maximizing public firm (firm D) and one foreign profit-maximizing firm (firm F). In the remainder of this paper, when 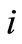 and
and 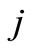 are used to refer to firms in an expression, they should be understand to refer to D and F with
are used to refer to firms in an expression, they should be understand to refer to D and F with . Time t is continuous, and the horizon is infinite. At each time, it is possible that each firm employs employees and legally enters into a lifetime employment contract with all of the employees.4
. Time t is continuous, and the horizon is infinite. At each time, it is possible that each firm employs employees and legally enters into a lifetime employment contract with all of the employees.4
Firm ’s net profit at time
’s net profit at time  is given by
is given by
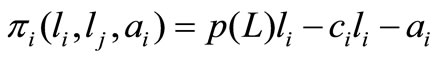 (1)
(1)
where  is firm
is firm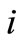 ’s current labor stock, namely the current number of employees in firm
’s current labor stock, namely the current number of employees in firm ,
,  is price as a function of labor stock
is price as a function of labor stock ,
, 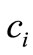 is firm
is firm ’s cost per employee, and
’s cost per employee, and  is firm
is firm ’s labor investment at time
’s labor investment at time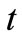 . We assume that
. We assume that .5 We also assume that
.5 We also assume that 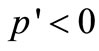 and
and . That is, this function is strictly concave. An increase in employment reduces the price through an increase in output.
. That is, this function is strictly concave. An increase in employment reduces the price through an increase in output.
Labor stocks cannot decrease, and each firm has a constant upper bound on the amount of its labor investment at every time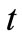 ; that is,
; that is,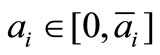 . At time zero, each firm enters the market with
. At time zero, each firm enters the market with  and can start investing. At each time, each firm employs employees, legally enters into lifetime employment contracts with them, and expands its scale. Therefore, there is an upper bound in the number of employees whom each firm can employ newly at each time.
and can start investing. At each time, each firm employs employees, legally enters into lifetime employment contracts with them, and expands its scale. Therefore, there is an upper bound in the number of employees whom each firm can employ newly at each time.
Domestic social welfare at time , which is the sum of domestic consumer surplus at time
, which is the sum of domestic consumer surplus at time 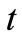 and firm D’s net profit at time
and firm D’s net profit at time , is given by
, is given by
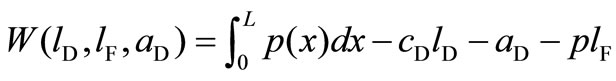 (2)
(2)
Each firm’s net present value of profits is
 (3)
(3)
where  is the common discount rate. This is firm F’s objective function.
is the common discount rate. This is firm F’s objective function.
Firm D maximizes the net present value of domestic social welfare, given by
 (4)
(4)
 is not included in
is not included in  because firm F is a foreign competitor. Therefore, it is thought that firm D behaves more aggressively toward firm F.
because firm F is a foreign competitor. Therefore, it is thought that firm D behaves more aggressively toward firm F.
If  is high, then future values have a lower weight compared to the situation with a lower
is high, then future values have a lower weight compared to the situation with a lower . If
. If  tends to zero, then firm D maximizes time-average social welfare, and firm F maximizes its time-average profit. Since the arguments in favor of the equilibrium outcomes of the discounting case are the same as in the no-discounting case, we shall devote our attention to the case in which firms do not discount their objectives.
tends to zero, then firm D maximizes time-average social welfare, and firm F maximizes its time-average profit. Since the arguments in favor of the equilibrium outcomes of the discounting case are the same as in the no-discounting case, we shall devote our attention to the case in which firms do not discount their objectives.
We examine the perfect equilibrium outcomes of a state-space game. The state-space game is a game in which both the payoffs and the strategies depend on the history only through the current state. The perfect equilibrium is a strategy combination that induces a Nash equilibrium for the subgame starting from every possible initial state in the state space.
Firm ’s steady-state reaction function
’s steady-state reaction function  is defined as the locus of points which give the final optimal level of
is defined as the locus of points which give the final optimal level of  for each final value of
for each final value of .
.
The equilibrium occurs where each firm maximizes its objective with respect to its own labor level, given the labor level of its rival. Firm D’s steady-state reaction function is derived as follows. Firm D aims to maximize social welfare with respect to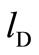 , given
, given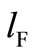 . The equilibrium must satisfy the following conditions. The firstorder condition for firm D is
. The equilibrium must satisfy the following conditions. The firstorder condition for firm D is
 , (5)
, (5)
and the second-order condition for firm D is
 . (6)
. (6)
Furthermore, we have
 . (7)
. (7)
Since ,
, 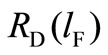 is upward sloping. This means that firm D responds to more aggressive play with more aggressive play.
is upward sloping. This means that firm D responds to more aggressive play with more aggressive play.
Next, we derive firm F’s steady-state reaction function. Firm F aims to maximize its profit with respect to , given
, given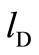 . The equilibrium must satisfy the following conditions. The first-order condition for firm F is
. The equilibrium must satisfy the following conditions. The first-order condition for firm F is
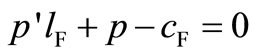 (8)
(8)
and the second-order condition for firm F is
 . (9)
. (9)
Furthermore, we have
 . (10)
. (10)
Since 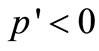 and
and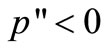 ,
,  is downward sloping. This means that firm F’s optimal response to more aggressive play by firm D is to be less aggressive. We assume that
is downward sloping. This means that firm F’s optimal response to more aggressive play by firm D is to be less aggressive. We assume that 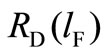 and
and 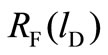 have a unique intersection which will be the Nash equilibrium of the state-space game.
have a unique intersection which will be the Nash equilibrium of the state-space game.
3. Equilibrium Outcomes
In this section, we analyze the perfect equilibrium outcomes of the continuous-time model. First, we consider the case shown in Figure 1, where  represents firm
represents firm ’s steady-state reaction curve. The figures in this paper
’s steady-state reaction curve. The figures in this paper
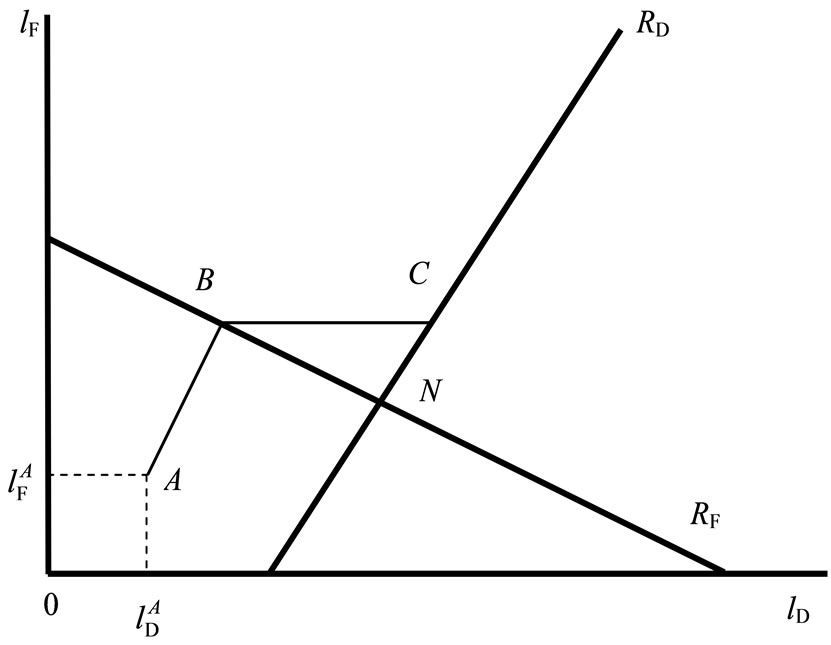
Figure 1. This investment path is ABC.
are drawn with straight lines for simplicity. Spence [35] and Fudenberg and Tirole [36] define the industrial growth path (IGP) as a locus on which each firm invests as quickly as possible. Firms are willing to invest as quickly as possible if there are only profit-maximizing firms in a market and the reaction curves are downward sloping. However, in this paper, we examine the case of a mixed market. As understood from this figure, social welfare increases as firm F increases its investment. Firm D hopes that firm F will invest more. Hence, firm D does not have the incentive to invest as early as firm F does. Therefore, we will not introduce the IGP.
We discuss each firm’s actual investment paths by using Figure 1. Let  be each firm’s initial labor stock. That is, each firm has an exogenously given labor stock,
be each firm’s initial labor stock. That is, each firm has an exogenously given labor stock,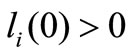 . Each firm can start investing at time zero. Each firm can employ new employees, given the constraints. Social welfare increases as firm F increases its investment, and therefore firm D hopes that firm F will invest more. Firm D will not have an incentive to invest as early as firm F does. Each firm continues to invest, given the constraints. If firm F continue to invest, then the industry continues to grow along
. Each firm can start investing at time zero. Each firm can employ new employees, given the constraints. Social welfare increases as firm F increases its investment, and therefore firm D hopes that firm F will invest more. Firm D will not have an incentive to invest as early as firm F does. Each firm continues to invest, given the constraints. If firm F continue to invest, then the industry continues to grow along , and each firm will stop investing at a point where it find optimal.
, and each firm will stop investing at a point where it find optimal.
The industry continues to grow along , and reaches
, and reaches  on
on . At
. At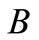 , if firm F continues to invest further, then its profit decreases. Hence, firm F invests up to
, if firm F continues to invest further, then its profit decreases. Hence, firm F invests up to 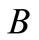 and then stops. However, social welfare increases if firm D invests whether firm F invests or not. Therefore, firm D continues to invest, given the constraints. If firm D continue to invest, then the industry continues to grow along
and then stops. However, social welfare increases if firm D invests whether firm F invests or not. Therefore, firm D continues to invest, given the constraints. If firm D continue to invest, then the industry continues to grow along , and firm D will stop investing at a point where it find optimal. The industry continues to grow along
, and firm D will stop investing at a point where it find optimal. The industry continues to grow along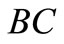 , and reaches
, and reaches 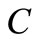 on
on . If firm D continues to invest further, then social welfare decreases. Hence, firm D invests up to
. If firm D continues to invest further, then social welfare decreases. Hence, firm D invests up to 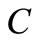 and then stops. Neither firm will have an incentive to invest at
and then stops. Neither firm will have an incentive to invest at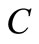 . This investment path becomes
. This investment path becomes 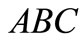 in the figure.
in the figure.
Firm F’s profit decreases as the industry grows along . Therefore, firm F may try to stop firm D’s investment before the investment path reaches
. Therefore, firm F may try to stop firm D’s investment before the investment path reaches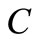 . Even though firm F invests further, the best firm D can do is to invest to
. Even though firm F invests further, the best firm D can do is to invest to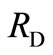 . Since this profit of firm F is lower than its profit at
. Since this profit of firm F is lower than its profit at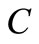 , this behavior of firm F is not a credible threat.
, this behavior of firm F is not a credible threat.
Second, we consider the case shown in Figure 2. Firm D has an exogenously given labor stock,  , while firm F has no labor,
, while firm F has no labor, . In this case, firm D’s initial labor stock level is equal to or larger than firm D’s labor stock level associated with the intersection
. In this case, firm D’s initial labor stock level is equal to or larger than firm D’s labor stock level associated with the intersection 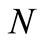 of both reaction curves. Since labor stocks cannot decrease, the equilibrium will never occur at any point to the left of
of both reaction curves. Since labor stocks cannot decrease, the equilibrium will never occur at any point to the left of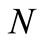 . Firm F can increase its own profit and social welfare by investing, and therefore it will invest. Firm D hopes that firm F will invest more. On the other hand, since firm D decreases social welfare by investing, the best it can do is not to invest. Therefore, firm F unilaterally continues to invest, given the constraints. The industry continues to grow along
. Firm F can increase its own profit and social welfare by investing, and therefore it will invest. Firm D hopes that firm F will invest more. On the other hand, since firm D decreases social welfare by investing, the best it can do is not to invest. Therefore, firm F unilaterally continues to invest, given the constraints. The industry continues to grow along 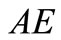 and reaches
and reaches 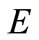 on
on . At
. At , if firm F continues to invest further, then its profit decreases. Hence, firm F invests up to
, if firm F continues to invest further, then its profit decreases. Hence, firm F invests up to  and then stops. Neither firm will have an incentive to invest at
and then stops. Neither firm will have an incentive to invest at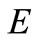 . This investment path is
. This investment path is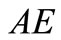 .
.
Social welfare increases as firm F increases its investment, and thus an incentive by which firm F’s investment is stopped before the investment path reaches 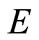 does not happen to firm D.
does not happen to firm D.
Third, we consider the case depicted in Figure 3. In this case, each firm has an exogenously given labor stock, . Each firm can start investing at time zero. Since firm D can increases social welfare by investing, the best it can do is to invest. On the other hand, firm D decrease its own profit by investing, and therefore it will not invest. Firm D unilaterally continues to invest, given the constraints. The industry continues to grow along
. Each firm can start investing at time zero. Since firm D can increases social welfare by investing, the best it can do is to invest. On the other hand, firm D decrease its own profit by investing, and therefore it will not invest. Firm D unilaterally continues to invest, given the constraints. The industry continues to grow along  and reaches
and reaches 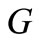 on
on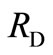 . At
. At , if firm D continues to invest further, then social welfare decreases. Hence, firm D invests up to
, if firm D continues to invest further, then social welfare decreases. Hence, firm D invests up to  and then stops. Since firm F decreases its own profit by investing, the best it can do is not to invest. Neither firm will have an incentive to invest at
and then stops. Since firm F decreases its own profit by investing, the best it can do is not to invest. Neither firm will have an incentive to invest at . This investment path is
. This investment path is .
.
From above discussions, we can see that there are no early-stopping equilibria in the international mixed market model. The main result of this study is described by the following proposition.
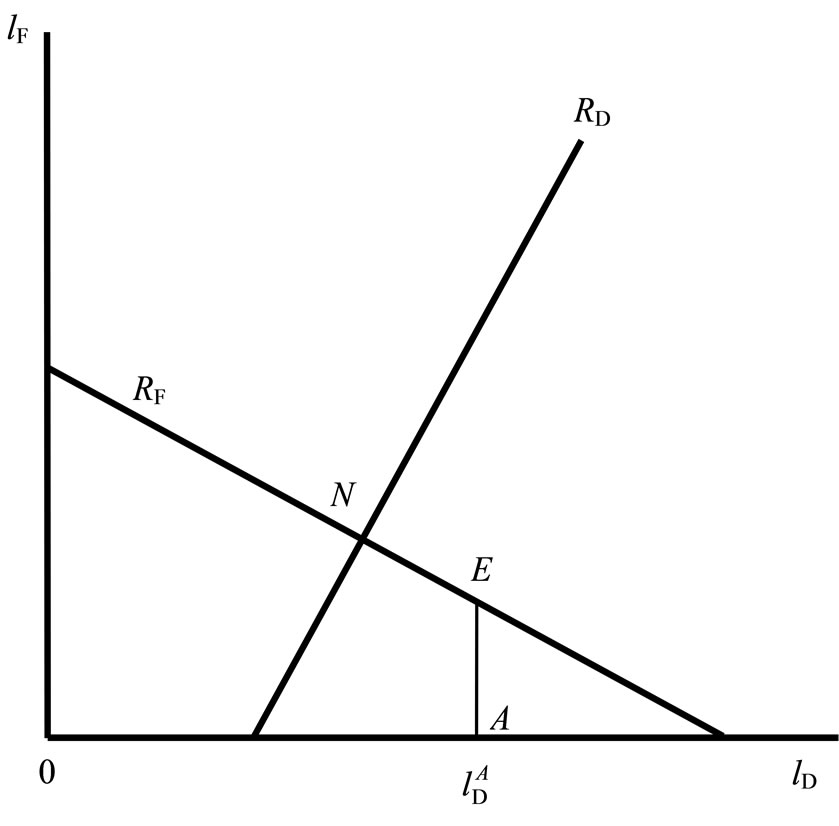
Figure 2. Firm D unilaterally continues investing from A to E.
Proposition 1. Call –for terminal surface–the line formed by the intersection of the reaction curves,
–for terminal surface–the line formed by the intersection of the reaction curves, 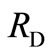 to the northeast of the intersection of the reaction curves, and
to the northeast of the intersection of the reaction curves, and  to the southeast of the intersection of the reaction curves.
to the southeast of the intersection of the reaction curves.  is depicted in Figure 4. One can construct perfect equilibrium strategies such that the equilibrium path stops on
is depicted in Figure 4. One can construct perfect equilibrium strategies such that the equilibrium path stops on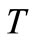 .
.
Proof. We divide the state space into three regions as depicted in Figure 4: Region I is the set below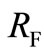 ; Region II is the set not below
; Region II is the set not below 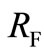 and above
and above ; and Region III is the set not below
; and Region III is the set not below  and not above
and not above .
.
First, we show each firm’s strategy in Region I. Since  is assumed to be concave in
is assumed to be concave in , firm F
, firm F
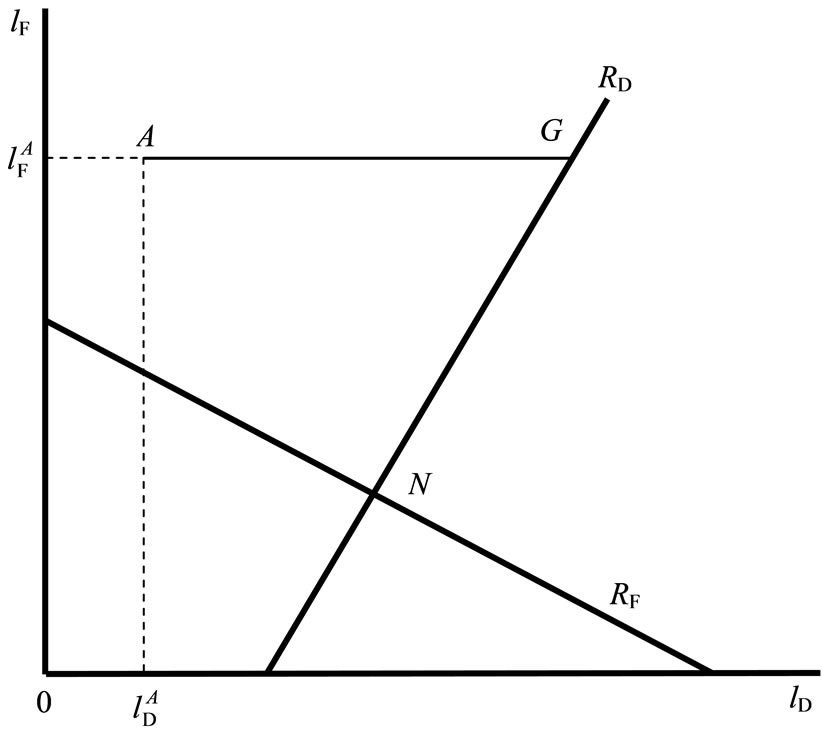
Figure 3. Firm F unilaterally continues investing from A to G.
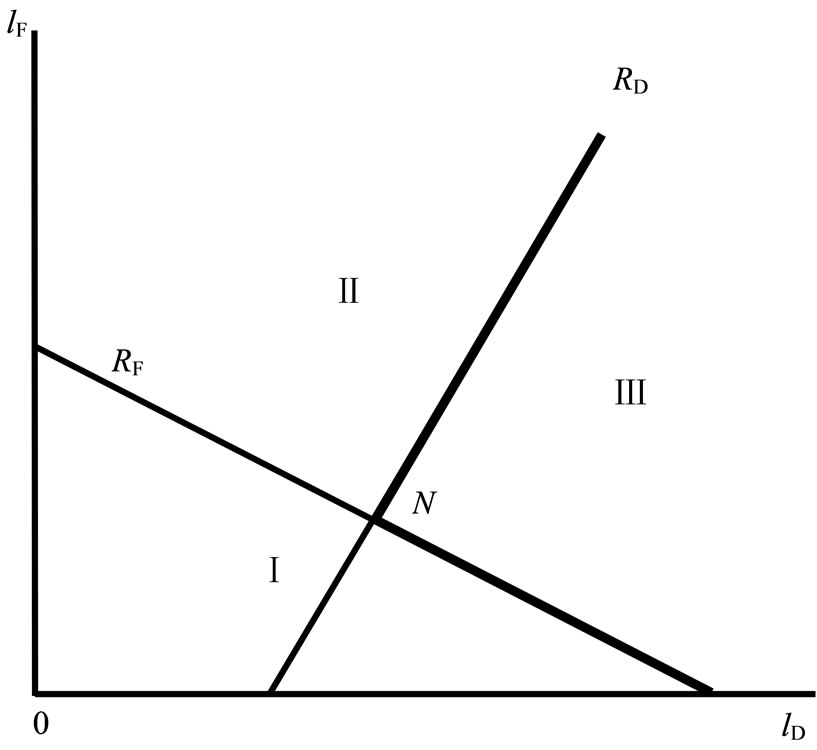
Figure 4. T is the bold line.
wishes to be as close to its reaction curve as possible. Therefore, the best firm F can do is to invest whether firm D invests or not. Both social welfare and firm F’s profit increase as firm F increases its investment. Therefore, firm F continues to invest, and firm D does not have an incentive to stop firm F from investing. In Region I, since at least firm F continues to invest, the state will reach from Region I to either Region II or Region III.
Second, we show each firm’s strategy in Region II. Since  is assumed to be concave in
is assumed to be concave in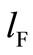 , firm F wishes to be as close to its reaction curve as possible. Firm F’s profit decreases if firm F invests whether firm D invests or not. Hence, firm F, which maximizes its own profit, never invests in this region. Firm D wishes to be as close to its reaction curve as possible. Therefore, the best firm D can do is to invest. Firm D will invest up to a point on its reaction curve. In Region II, since firm D unilaterally continues to invest, the state will reach from Region II to Region III.
, firm F wishes to be as close to its reaction curve as possible. Firm F’s profit decreases if firm F invests whether firm D invests or not. Hence, firm F, which maximizes its own profit, never invests in this region. Firm D wishes to be as close to its reaction curve as possible. Therefore, the best firm D can do is to invest. Firm D will invest up to a point on its reaction curve. In Region II, since firm D unilaterally continues to invest, the state will reach from Region II to Region III.
Third, we show each firm’s strategy in Region III. Each firm wishes to be as close to its own reaction curve as possible. If only firm F or both firms continue to invest, then firm F’s profit will decrease. Hence, firm F does not invest. If only firm D continues to invest, then social welfare will decrease, and therefore firm D does not invest either. Each firm’s best response to the other firm’s strategy at any point of this region is not to invest. Consequently, each firm’s optimization problem at any point in this region, given the other firm’s strategy, induces a Nash strategy at any point of this region. Thus, the strategies are in perfect equilibrium, and the result follows. Q.E.D.
4. Conclusions
We have examined continuous-time dynamic competition of labor investment decisions of a domestic welfare-maximizing public firm and a foreign profit-maximizing private firm. Fudenberg and Tirole [36] examine continuous-time dynamic competition of capital investment decisions of private firms and show that there are early-stopping equilibria in which neither firm invests up to its steady-state reaction curve. On the other hand, we have demonstrated that there are no equilibria in which neither firm invests up to its steady-state reaction curve. There are many studies dealing with mixed markets that incorporate welfare-maximizing public firms. We will pursue further research on these studies in the future.
5. References
[1] W. Merrill and N. Schneider, “Government Firms in Oligopoly Industries: A Short-Run Analysis,” Quarterly Journal of Economics, vol. 80, No. 3, 1966, pp. 400-412.
[2] L. Nett, “Why Private Firms are More Innovative Than Public Firms,” European Journal of Political Economy, vol. 10, no. 4, December 1994, pp. 639-653.
[3] J. Willner, “Welfare Maximization with Endogenous Average Costs,” International Journal of Industrial Organization, vol. 12, no. 3, September 1994, pp. 373-386.
[4] K. George and M. M. A. La Manna, “Mixed Duopoly, Inefficiency, and Public Ownership,” Review of Industrial Organization, vol. 11, no. 6, December 1996, pp. 853-860.
[5] M. D. White, “Mixed Oligopoly, Privatization and Subsidization,” Economics Letters, vol. 53, no. 2, November 1996, pp. 189-195.
[6] T. Matsumura, “Partial Privatization in Mixed Duopoly,” Journal of Public Economics, vol. 70, no. 3, December 1998, pp. 473-483.
[7] S. Mujumdar and D. Pal, “Effects of Indirect Taxation in a Mixed Oligopoly,” Economics Letters, vol. 58, no. 2, February 1998, pp. 199-204.
[8] D. Pal, “Endogenous Timing in a Mixed Oligopoly,” Economics Letters, vol. 61, no. 2, November 1998, pp. 181-185.
[9] J. Poyago-Theotoky, “R & D Competition in a Mixed Duopoly under Uncertainty and Easy Imitation,” Journal of Comparative Economics, vol. 26, no. 3, September 1998, pp. 415-428.
[10] A. Nishimori and H. Ogawa, “Public Monopoly, Mixed Oligopoly and Productive Efficiency,” Australian Economic Papers, vol. 41, no. 2, June 2002, pp. 185-190.
[11] K. Ohnishi, “Investment Decisions in a New Mixed Market,” Annals of Economics and Finance, vol. 7, no. 2, November 2006, pp. 271-281.
[12] K. Fujiwara, “Partial Privatization in a Differentiated Mixed Oligopoly,” Journal of Economics, vol. 92, no. 1, September 2007, pp. 51-65.
[13] Y. Lu and S. Poddar, “Firm Ownership, Product Differentiation and Welfare,” The Manchester School, vol. 75, no. 2, June 2007, pp. 210-217.
[14] P. R. Chowdhury, “Mixed Oligopoly with Distortions: First Best with Budget-Balance and the Irrelevance Principle,” Economics Bulletin, vol. 29, no. 3, August 2009, pp. 1885-1900.
[15] D. Bös, “Public Enterprise Economics,” North-Holland, 1986.
[16] D. Bös, “Privatization: A Theoretical Treatment,” Clarendon Press, 2001.
[17] J. Vickers and G. Yarrow, “Privatization: An Economic Analysis,” MIT Press, 1988.
[18] H. Cremer, M. Marchand and J.-F. Thisse, “The Public Firm as an Instrument for Regulating an Oligopolistic Market,” Oxford Economic Papers, vol. 41, no. 1, January 1989, pp. 283-301.
[19] L. Nett, “Mixed Oligopoly with Homogeneous Goods,” Annals of Public and Cooperative Economics, vol. 64, no. 3, July 1993, pp. 367-393.
[20] K. Fjell and D. Pal, “A Mixed Oligopoly in the Presence of Foreign Private Firms,” Canadian Journal of Economics, vol. 29, no. 3, August 1996, pp. 737-743.
[21] D. Pal and M. D. White, “Mixed Oligopoly, Privatization, and Strategic Trade Policy,” Southern Economic Journal, vol. 65, no. 2, April 1998, pp. 264-281.
[22] K. Fjell and J. S. Heywood, “Public Stackelberg Leadership in a Mixed Oligopoly with Foreign Firms,” Australian Economic Papers, vol. 41, no. 3, September 2002, pp. 267-281.
[23] T. Matsumura, “Stackelberg Mixed Duopoly with a Foreign Competitor,” Bulletin of Economic Research, vol. 55, no. 3, July 2003, pp. 275-287.
[24] J. Fernández-Ruiz, “Managerial Delegation in a Mixed Duopoly with a Foreign Competitor,” Economics Bulletin, vol. 29, no. 1, February 2009, pp. 90-99.
[25] J. T. Wenders, “Excess Capacity as a Barrier to Entry,” Journal of Industrial Economics, vol. 20, no. 1, November 1971, pp. 14-19.
[26] A. M. Spence, “Entry, Capacity, Investment and Oligopolistic Pricing,” Bell Journal of Economics, vol. 8, no. 2, Autumn 1977, pp. 534-544.
[27] K. Dixit, “A Model of Duopoly Suggesting a Theory of Enter Barrier,” Bell Journal of Economics, vol. 10, no. 1, Spring 1979, pp. 20-32.
[28] K. Dixit, “The Role of Investment in Entry-Deterrence,” Economic Journal, vol. 90, No. 357, March 1980, pp. 95-106.
[29] D. F. Spulber, “Capacity, Output, and Sequential Entry,” American Economic Review, vol. 71, no. 3, June 1981, pp. 503-514.
[30] C. Davidson and R. Deneckere, “Long-Run Competition in Capacity, Short-Run Competition in Price, and the Cournot Model,” Rand Journal of Economics, vol. 17, no. 3, Autumn 1986, pp. 404-415.
[31] O. Stehmann, “Entry Deterrence and Excess Capacity in a Stackelberg Game,” Economic Notes, vol. 21, no. 3, 1992, pp. 450-467.
[32] H. Kim, “Strategic Excess Capacity and First-Mover Advantage under Variable Demand,” Seoul Journal of Economics, vol. 9, no. 2, Summer 1996, pp. 105-122.
[33] J. J. Gabszewicz and S. Poddar, “Demand Fluctuations and Capacity Utilization under Duopoly,” Economic Theory, vol. 10, no. 1, June 1997, pp. 131-146.
[34] S. Poddar, “Excess Capacity: A Note,” Keio Economic Studies, vol. 40, no. 1, 2003, pp. 75-83.
[35] A. M. Spence, “Investment Strategy and Growth in a New Market,” Bell Journal of Economics, vol. 10, no. 1, Spring 1979, pp. 1-19.
[36] D. Fudenberg and J. Tirole, “Capital as a Commitment: Strategic Investment to Deter Mobility,” Journal of Economic Theory, vol. 31, no. 2, December 1983, pp. 227- 250.
[37] K. Ohnishi, “Lifetime Employment Contract and Strategic Entry Deterrence: Cournot and Bertrand,” Australian Economic Papers, vol. 40, no. 1, March 2001, pp. 30-43.
[38] K. Ohnishi, “On the Effectiveness of the Lifetime-Employment-Contract Policy,” The Manchester School, vol. 70, no. 6, December 2002, pp. 812-821.
NOTES
1Bös [15,16], Vickers and Yarrow [17], Cremer, Marchand, and Thisse [18], and Nett [19] provide excellent surveys.
2In the tobacco industries of France, Italy, Russia, Spain, Austria, Turkey, China, Japan, etc., we can find real-world examples in which state-owned public firms compete or competed against foreign private firms such as Philip Morris and R. J. Reynolds.
3For details see Ohnishi [37, 38].
4Spence [35] and Fudenberg and Tirole [36] focus on capital as strategic investment, while we focus on labor investment.
5The assumption concerning the inefficiency of public sectors is often used in literature studying mixed markets. See, for instance, George and La Manna [4], Mujumdar and Pal [7], Pal [8], Ohnishi [11], Cremer, Marchand, and Thisse [18], Nett [19], Matsumura [23], and Fernández-Ruiz [24]. If firm D is more efficient than firm F, then firm D will try to maximize social welfare by supplying monopolistically in the market. In this paper, this behavior of firm D brings the same result as the pure market model. This assumption is made to avoid such a trivial solution.

