Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 6 (2011) , Article ID: 5655 , 10 pages DOI:10.4236/jemaa.2011.36037
Design of Reflective, Photonic Shields for Atmospheric Reentry
![]()
1Swiss Federal Institute of Technology (ETH) Zurich, Zurich, Switzerland; 2Institute of Material Sciences, Technical University of Freiberg, Freiberg, Germany; 3NASA Ames Research Center, Moffett Field, USA.
Email: n.komarevskiy@ifh.ee.ethz.ch
Received April 3rd, 2011; revised May 5th, 2011; accepted May 13th, 2011.
Keywords: Multilayers, Reflective Coatings, Optimization
ABSTRACT
We present the design of one-dimensional photonic crystal structures, which can be used as omnidirectional reflecting shields against radiative heating of space vehicles entering the Earth’s atmosphere. This radiation is approximated by two broad bands centered at visible and nearinfrared energies. We applied two approaches to find structures with the best omnidirectional reflecting performance. The first approach is based on a band gap analysis and leads to structures composed of stacked Bragg mirrors. In the second approach, we optimize the structure using an evolutionary strategy. The suggested structures are compared with a simple design of two stacked Bragg mirrors. Choice of the constituent materials for the layers as well as the influence of interlayer diffusion at high temperatures are discussed.
1. Introduction
Reflecting photonic systems (RPS) are of high interest for many practical applications [1], including potentially as protective coatings for atmospheric reentry. During atmospheric reentry, space vehicles experience extreme environments which put high performance demands on their thermal protection systems. A major source of heating during reentry is radiation generated in the shock layer. Extreme temperatures ionize gaseous species, producing radiation which impinges on the surface of the vehicle. This radiative heating scales like 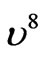 and can be a major factor especially in manned mission from the Moon or Mars. For Jupiter entries, 99% of the heating is radiative. Because planetary atmospheres have different chemical compositions, their radiation profiles will also be different. Therefore, an ideal RPS solution will reflect radiation in specified wavelength ranges for a given planet. The schematic illustration of the thermal protection system (TPS) of a vehicle is shown in Figure 1.
and can be a major factor especially in manned mission from the Moon or Mars. For Jupiter entries, 99% of the heating is radiative. Because planetary atmospheres have different chemical compositions, their radiation profiles will also be different. Therefore, an ideal RPS solution will reflect radiation in specified wavelength ranges for a given planet. The schematic illustration of the thermal protection system (TPS) of a vehicle is shown in Figure 1.
Shock layer radiation spectra at peak heating were modeled and analyzed [2-4]. Experimental data on radiation spectra of shock-heated air were obtained at flight-relevant conditions [5]. Radiation spectra were measured in the range of 190 - 1210 nm. These spectra contain two broad peaks which are mostly due to radiating species of 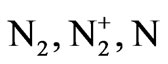 and O. The first peak is approximately in the range of 650 - 1200 nm
and O. The first peak is approximately in the range of 650 - 1200 nm 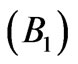 and the second is in the 300 - 500 nm range
and the second is in the 300 - 500 nm range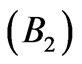 .
.
The goal of this paper is to propose an optimal design of a one-dimensional photonic structure with high omnidirectional reflection in these two wavelength intervals. The term “optimal” implies the best reflecting performance of the structure for a fixed number of layers. This design principle is quite general and can be used to

Figure 1. Schematic of a possible thermal protection system for a space vehicle. RPS protects against radiative heating. Thermal barrier coating retard conductive heat propagation.
make omnidirectional RPS for other wavelength ranges as well. The advantage of the proposed one-dimensional structures is that they are relatively simple to model and to fabricate.
The constituent materials silicon dioxide 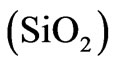 and zirconium dioxide
and zirconium dioxide  are chosen. These materials meet a number of the strict requirements of this application, such as high-temperature stability, low absorptivity, oxidation resistance and others. However, the
are chosen. These materials meet a number of the strict requirements of this application, such as high-temperature stability, low absorptivity, oxidation resistance and others. However, the 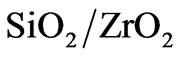 couple has small dielectric contrast, making the design of a omnidirectional RPS more difficult than for materials with a higher dielectric contrast.
couple has small dielectric contrast, making the design of a omnidirectional RPS more difficult than for materials with a higher dielectric contrast.
This paper is organized as follows. In Section 2, the optimization model of an omnidirectional RPS appropriate for two energy intervals is defined. Next, in Section 3, we apply a band gap analysis to 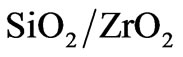 periodic multilayers and construct an omnidirectional RPS in the desired energy intervals. By combining (stacking) different periodic segments in one structure a high reflectivity can be achieved. In Section 4, we briefly discuss different optimizers, which are applicable for the optimization of layered structures. As an example, we optimize the omnidirectional reflectivity of a layered structure using ES and compare our results with the Bragg and optimized Bragg mirrors. Then, in Section 5 optimization of the RPS for either to
periodic multilayers and construct an omnidirectional RPS in the desired energy intervals. By combining (stacking) different periodic segments in one structure a high reflectivity can be achieved. In Section 4, we briefly discuss different optimizers, which are applicable for the optimization of layered structures. As an example, we optimize the omnidirectional reflectivity of a layered structure using ES and compare our results with the Bragg and optimized Bragg mirrors. Then, in Section 5 optimization of the RPS for either to 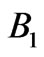 or to
or to 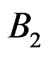 energy interval is performed. The optimization of the RPS for both energy intervals is performed in Section 6. Finally, in Section 7, changes of in the multilayer structure due to high temperature interdiffusion and the possible consequences on reflecting properties of RPS are discussed.
energy interval is performed. The optimization of the RPS for both energy intervals is performed in Section 6. Finally, in Section 7, changes of in the multilayer structure due to high temperature interdiffusion and the possible consequences on reflecting properties of RPS are discussed.
2. Definition of the Problem
The RPS for Earth reentry should be optimized for energy intervals 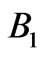 and
and 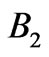 and should possess omnidirectional reflectivity. The energy ranges for
and should possess omnidirectional reflectivity. The energy ranges for 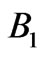 and
and 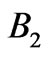 are 1 - 2 eV (
are 1 - 2 eV (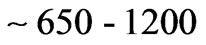 nm) and 2.4 - 4.2 eV (
nm) and 2.4 - 4.2 eV (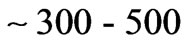 nm) respectively. We have chosen silicon dioxide
nm) respectively. We have chosen silicon dioxide 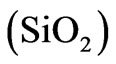 and zirconium dioxide
and zirconium dioxide 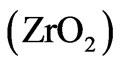 as the materials for the individual layers. Silicon dioxide and zirconium dioxide have high melting temperatures Tm = 1650˚C and Tm = 2715˚C respectively and are optically transparent in the ranges of interest.
as the materials for the individual layers. Silicon dioxide and zirconium dioxide have high melting temperatures Tm = 1650˚C and Tm = 2715˚C respectively and are optically transparent in the ranges of interest. 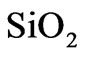 (quartz) and
(quartz) and  have similar coefficients of thermal expansions. The high-temperature interaction of
have similar coefficients of thermal expansions. The high-temperature interaction of 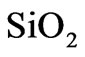 and
and 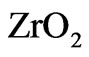 layers results in the formation of a high-temperature stable phase of
layers results in the formation of a high-temperature stable phase of 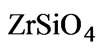 which may have possible diffusion barrier properties (see Section 7). This phase may prevent further Si and Zr interdiffusion, and therefore result in reduction of photonic properties. Permittivity data of the materials are shown in Figure 2. Both materials are dielectrics with a wide gap, so we assume that permittivity should not strongly change with temperature. However, all calculations are performed with permittivity values at room temperature, since data for permittivity at high temperature are not available. Basic properties for possible candidate materials for high-temperature photonic applications are given in Table 1.
which may have possible diffusion barrier properties (see Section 7). This phase may prevent further Si and Zr interdiffusion, and therefore result in reduction of photonic properties. Permittivity data of the materials are shown in Figure 2. Both materials are dielectrics with a wide gap, so we assume that permittivity should not strongly change with temperature. However, all calculations are performed with permittivity values at room temperature, since data for permittivity at high temperature are not available. Basic properties for possible candidate materials for high-temperature photonic applications are given in Table 1.
Our goal is to design a layered structure which maximizes the percentage of reflection  of unpolarized electromagnetic radiation within two energy intervals for a fixed number of layers N. Therefore, we define a fitness function as the average reflection in two energy intervals:
of unpolarized electromagnetic radiation within two energy intervals for a fixed number of layers N. Therefore, we define a fitness function as the average reflection in two energy intervals:
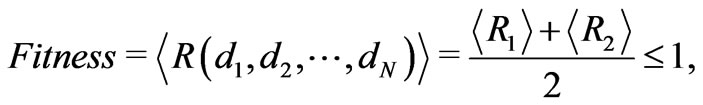 (1)
(1)
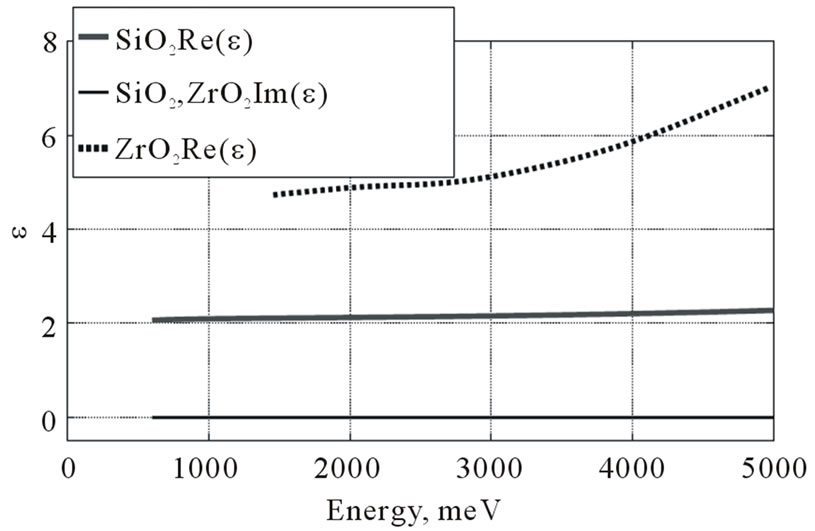
Figure 2. Permittivity of SiO2 and ZrO2 from [6].
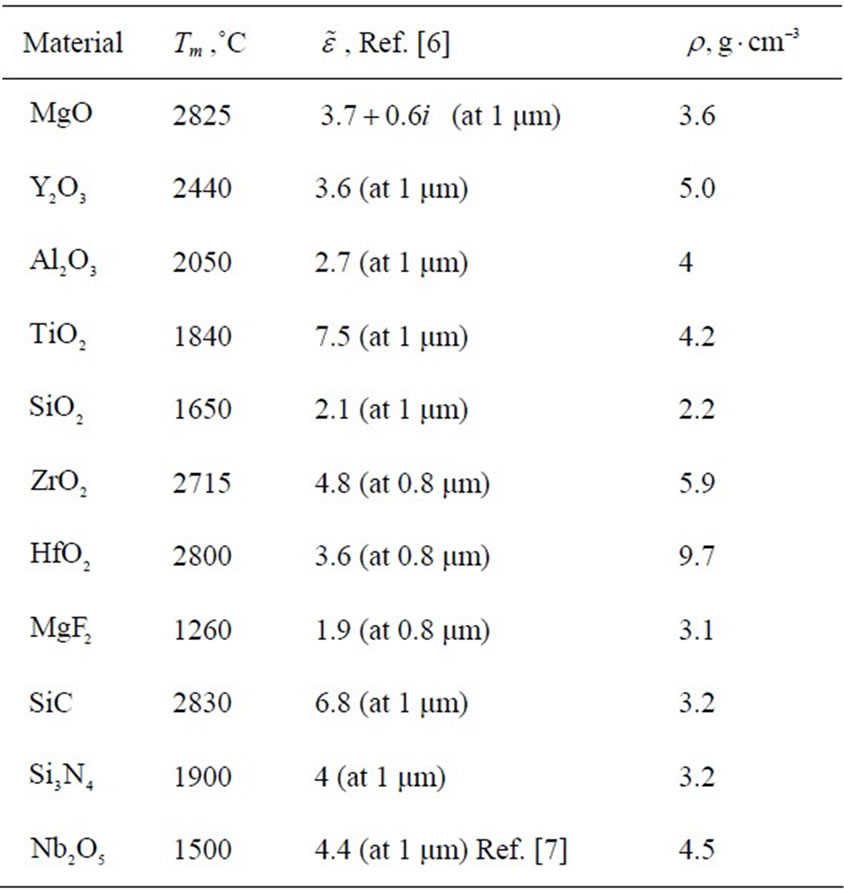
Table 1. Melting points (Tm), dielectric permittivity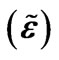 , and density
, and density 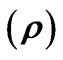 of some possible materials for the high temperature photonics.
of some possible materials for the high temperature photonics.
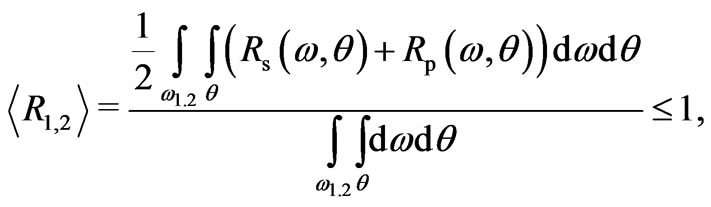 (2)
(2)
where 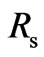 and
and  are the reflection coefficients for s- (electric field parallel to layers) and p-polarized (magnetic field parallel to layers) light respectively and are integrated over the angles of incidence
are the reflection coefficients for s- (electric field parallel to layers) and p-polarized (magnetic field parallel to layers) light respectively and are integrated over the angles of incidence  and energy intervals
and energy intervals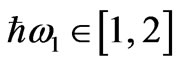 ,
, 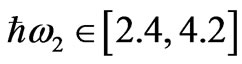 eV. The thickness of the i-th layer (
eV. The thickness of the i-th layer (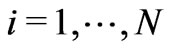 ) is
) is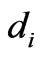 .
.
We need to maximize the function 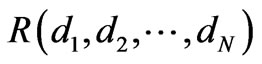 of N variables, which are layer thicknesses. Moreover, the obtained solution should also be robust. This implies that reflection
of N variables, which are layer thicknesses. Moreover, the obtained solution should also be robust. This implies that reflection 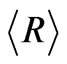 does not vary strongly with small deviation of layer thicknesses
does not vary strongly with small deviation of layer thicknesses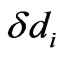 . In other words, unavoidable fabrication inaccuracies of layer thicknesses should not significantly change reflecting performance of the structure.
. In other words, unavoidable fabrication inaccuracies of layer thicknesses should not significantly change reflecting performance of the structure.
3. Design of the RPS Using Photonic Band Gap Approach
Construction of omnidirectional mirrors from layered media were analyzed and discussed in many works [8-10]. There are two necessary requirements to achieve omnidirectional reflection. The first is a sufficiently high dielectric contrast for the constituent materials. The second is that the dielectric constant of the lower index material is larger than the dielectric constant of the ambient medium by some critical amount. Reflection in a broader energy interval can be achieved by stacking several periodic layered media with different periods [11]. Another way to achieve reflection in a broad range is to use a chirped periodic layered medium [11,12]. Other optimization procedures, like the quasi-Newton algorithm [13] or genetic algorithms [14,15] have also been applied to improve the performance of finite multilayer mirrors.
Let us consider an infinitely-periodic structure consisting of 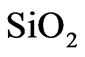 and
and 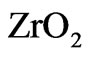 layers. The geometry is shown in Figure 3(a) For normal incidence light
layers. The geometry is shown in Figure 3(a) For normal incidence light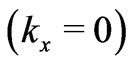 . the gap-midgap ratio is maximized when
. the gap-midgap ratio is maximized when  (quarter wave stack condition). For grazing incidence
(quarter wave stack condition). For grazing incidence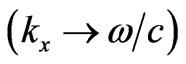 , the gap-midgap ratio is maximized when
, the gap-midgap ratio is maximized when
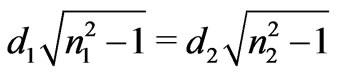 [16].
[16].
The main difficulty in designing a RPS with sufficiently broad band gaps for both 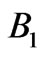 and
and 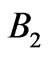 energy intervals is the low dielectric contrast of
energy intervals is the low dielectric contrast of 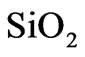 and
and 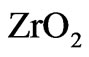 materials. A simple periodic Bragg mirror is not a suitable solution, because the band gaps are narrow and not omnidirectional. The band structure of a Bragg mirror with period
materials. A simple periodic Bragg mirror is not a suitable solution, because the band gaps are narrow and not omnidirectional. The band structure of a Bragg mirror with period 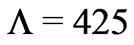 nm is shown in Figure 4. The band gap for p-polarized light becomes narrower for the inclined incidence light as can be seen in the plot. Since point B is slightly above point C, the structure has no omnidirectional reflection.
nm is shown in Figure 4. The band gap for p-polarized light becomes narrower for the inclined incidence light as can be seen in the plot. Since point B is slightly above point C, the structure has no omnidirectional reflection.
In order to circumvent the difficulty of narrow gaps,
 (a)
(a)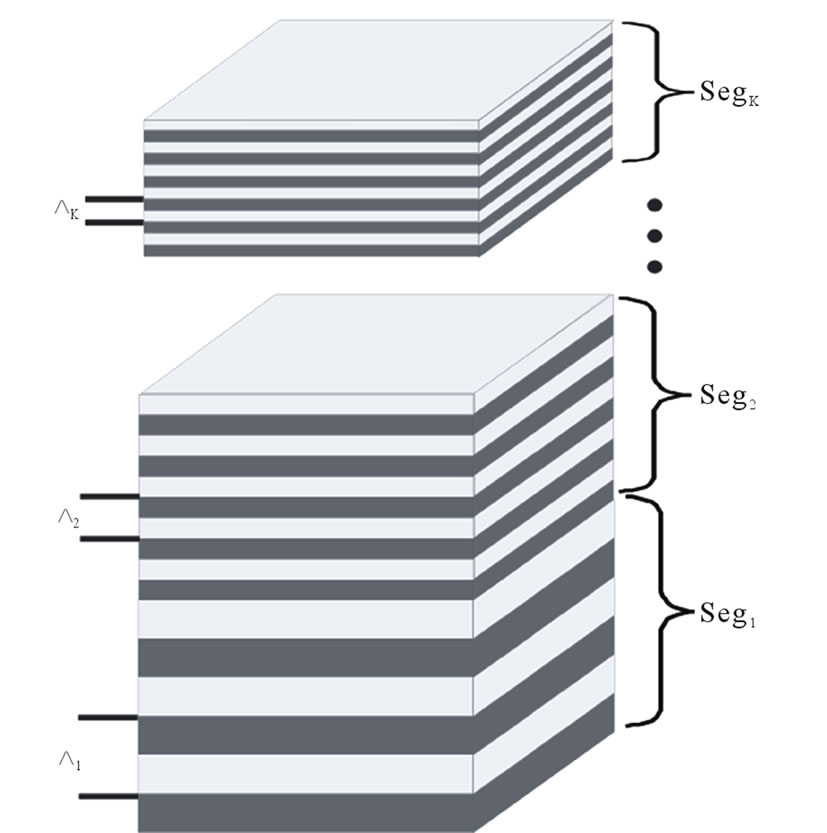 (b)
(b)
Figure 3. (a) Multilayer SiO2/ZrO2 with period 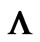 constant through the whole stack, d1,2 and n1,2 are thicknesses and refractive indexes of the layers respectively. (b) Multilayer stack consisting of segments with different periods. Angle of light incidence is
constant through the whole stack, d1,2 and n1,2 are thicknesses and refractive indexes of the layers respectively. (b) Multilayer stack consisting of segments with different periods. Angle of light incidence is ,
, 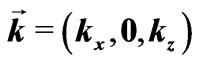 is the wave vector.
is the wave vector.
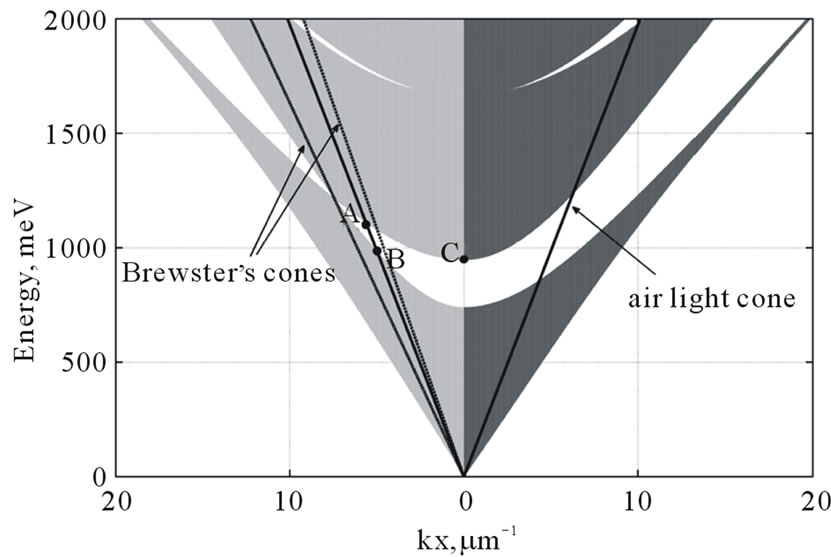
Figure 4. Band structure of SiO2/ZrO2 Bragg mirror with period 425 nm for sand p-polarized light. White region between shadowed regions corresponds to band gap. Solid black line denotes air light cone, dashed and dash-dotted lines denote Brewster’s cones of SiO2/ZrO2 and air/ZrO2 interfaces respectively (ZrO2 is on top of structure).
we can stack segments with different periods, as shown in Figure 3(b). If the periods of the segments are chosen appropriately, then the total omnidirectional band gap can include the entire desired energy range. As can be concluded from Figure 4, the condition for band gap overlapping in p-polarization is that point B of the next segment with a smaller period should be slightly below point A of the previous segment with a larger period. Band gap overlapping in s-polarization is automatically fulfilled using this criteria.
In order to generate an omnidirectional gap in the first range (1 - 2 eV) we need ten periodic segments with uniformly spaced periods from 200 to 425 nm. The band structure of ten segments is shown in one of the plots in Figure 5(a). Note that the 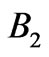 range 2.4 - 4.2 meV is already significantly covered with band gaps of higher orders. This means that reflection of finite structure for the
range 2.4 - 4.2 meV is already significantly covered with band gaps of higher orders. This means that reflection of finite structure for the 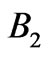 range will also be high. However, in order to completely cover the
range will also be high. However, in order to completely cover the 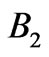 range with first order gaps, we need eight additional segments with uniformly spaced periods from 90 to 180 nm. The resulting band structure is shown in Figure 5(b). Thus, a total of 18 segments are required to cover both
range with first order gaps, we need eight additional segments with uniformly spaced periods from 90 to 180 nm. The resulting band structure is shown in Figure 5(b). Thus, a total of 18 segments are required to cover both 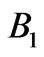 and
and 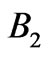 energy intervals with band gaps.
energy intervals with band gaps.
The magnitude of 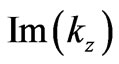 in Figure 5 determines the rate of exponential decay of the propagating wave and also affects the reflectivity of the structure. As seen in the plot, the magnitude of
in Figure 5 determines the rate of exponential decay of the propagating wave and also affects the reflectivity of the structure. As seen in the plot, the magnitude of 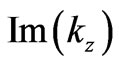 is larger for higher energies (or smaller periods of segments) in both
is larger for higher energies (or smaller periods of segments) in both 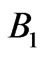 and
and 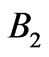 ranges. However, the product
ranges. However, the product 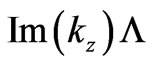 remains constant for all periods
remains constant for all periods  in the segments. Therefore, we take equal numbers of layers in each of the 18 segments. Calculations of the reflectivity of these stacked segments are discussed in Sections 5 and 6.
in the segments. Therefore, we take equal numbers of layers in each of the 18 segments. Calculations of the reflectivity of these stacked segments are discussed in Sections 5 and 6.
 (a)
(a)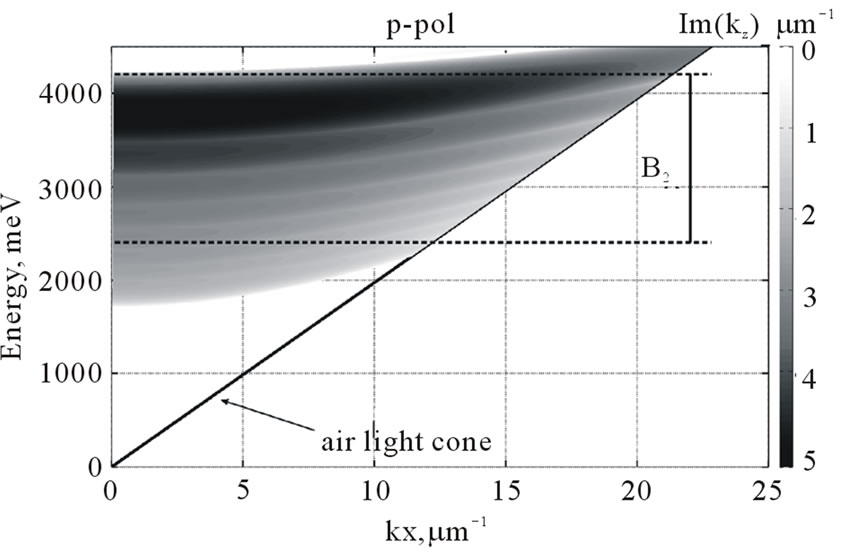 (b)
(b)
Figure 5. (a) Band structure of ten segments with uniformly spaced periods from 200 to 425 nm shown in one plot. The total omnidirectional band gap is in the B1 energy interval 1 - 2 eV. (b) Band structure of eight segments with uniformly spaced periods from 90 to 180 nm shown in one plot. The total omnidirectional band gap is in the B2 energy interval 2.4 - 4.2 eV. Colorbar corresponds to imaginary part of kz in  units.
units.
4. ES Optimizer for Layered Structures
Until now, our approach to designing structures with good reflection was based on band gap analysis. We stacked 18 segments of  with different periods in one structure to obtain reasonable performance. This is one possible way to design. However, it is not necesarily the best one and it is interesting to find out how close we are to the optimum. Different optimizers [17,18] can be helpful to find good solutions, that are often difficult to find analytically.
with different periods in one structure to obtain reasonable performance. This is one possible way to design. However, it is not necesarily the best one and it is interesting to find out how close we are to the optimum. Different optimizers [17,18] can be helpful to find good solutions, that are often difficult to find analytically.
If the structure consists of N layers, then there are N parameters (thickness of each layer) for the optimization. The search space should be defined for each parameter within a reasonable interval . For such optimizations different evolutionary algorithms, like genetic algorithm (GA), micro-genetic algorithms (MGA), or evolutionary strategy (ES) may be applied. The optimization task becomes difficult, if there are many parameters for optimization, and/or if the fitness function has a complicated behavior with many local optima. We used ES for the optimization of our RPS. In previous applications ES usually outperformed GA and MGA.
. For such optimizations different evolutionary algorithms, like genetic algorithm (GA), micro-genetic algorithms (MGA), or evolutionary strategy (ES) may be applied. The optimization task becomes difficult, if there are many parameters for optimization, and/or if the fitness function has a complicated behavior with many local optima. We used ES for the optimization of our RPS. In previous applications ES usually outperformed GA and MGA.
As an example of the ES approach, we maximized the average reflection  of the
of the  structure containing N = 8 layers, at wavelength
structure containing N = 8 layers, at wavelength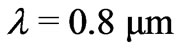 . Permittivities of
. Permittivities of 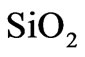 and
and  are taken to be
are taken to be 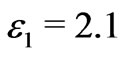 and
and 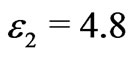 at
at 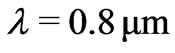 respectively. Layers are embedded between air interfaces.
respectively. Layers are embedded between air interfaces.
The average reflection to be optimized is defined as:
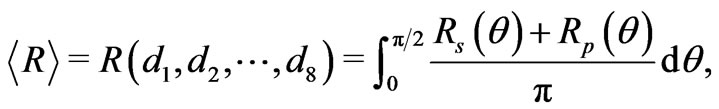 (3)
(3)
where 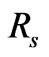 and
and 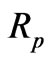 are reflectivities for sand p-polarized light respectively,
are reflectivities for sand p-polarized light respectively, 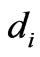 is the individual layer thickness, and
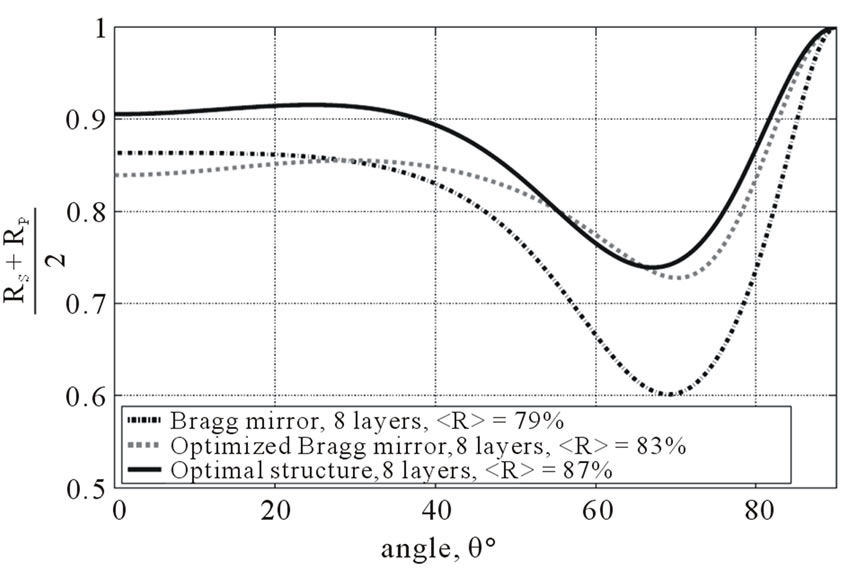
is the individual layer thickness, and 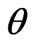 is the angle of light incidence. The results of ES optimization are shown in Figure 6(a). Dashdotted curve corresponds to a Bragg mirror with layer thicknesses:
is the angle of light incidence. The results of ES optimization are shown in Figure 6(a). Dashdotted curve corresponds to a Bragg mirror with layer thicknesses:
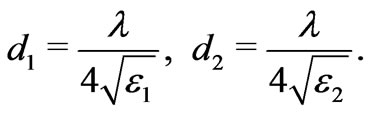 (4)
(4)
Dashed curve in the plot corresponds to an optimized Bragg mirror, with two optimized layer thicknesses. Solid line corresponds to a structure where all eight thicknesses are optimized. As seen from the plot, the optimization of all layer thicknesses (solid line) leads to the best performance. This reflects the fact that a Bragg mirror is not an optimal structure for omnidirectional reflection. A comparison of the layer thicknesses for three structures is shown in Figure 6(b).
5. Optimization of the RPS Adjusted to One Energy Interval
First we performed optimization of the RPS with respect to only one energy interval. Let us first consider RPS for the 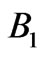 energy interval. The fitness function to be optimized is defined in the expression (2). Band gap analysis revealed that 10 stacked periodic segments may cover this range with band gaps. The dashed line in Figure 8(a) shows reflectivity
energy interval. The fitness function to be optimized is defined in the expression (2). Band gap analysis revealed that 10 stacked periodic segments may cover this range with band gaps. The dashed line in Figure 8(a) shows reflectivity 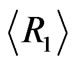 as a function of the number of layers in this structure. In order to improve the reflectivity, we performed an ES structure optimization in two ways.
as a function of the number of layers in this structure. In order to improve the reflectivity, we performed an ES structure optimization in two ways.
In the first way, optimization was done in the full search space. This means that the thickness of each layer could have any value below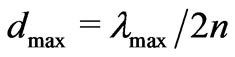 ,
,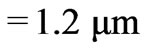
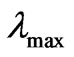 . This yields
. This yields 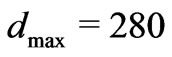 nm (
nm ( ) and
) and 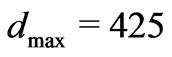 nm (
nm ( ). As mentioned earlier, optimi
). As mentioned earlier, optimi
 (a)
(a)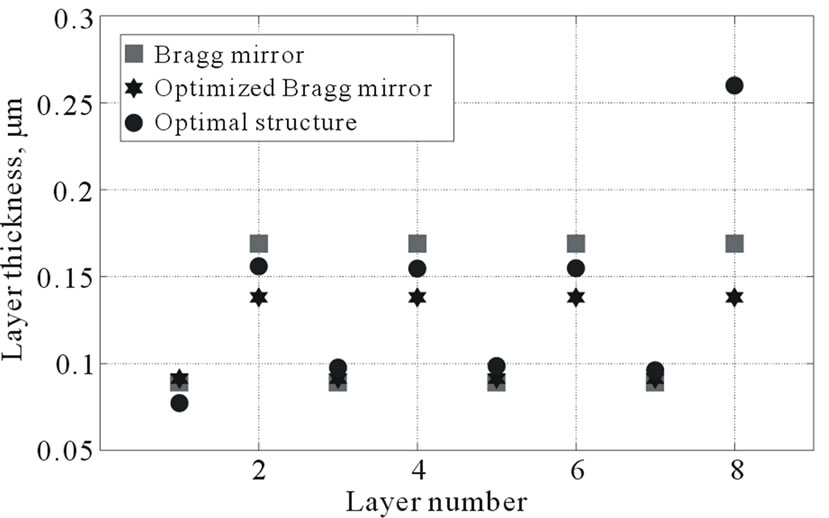 (b)
(b)
Figure 6. (a) Dash-dotted curve—reflectivity of the Bragg mirror, dashed curve—reflectivity of the optimized Bragg mirror, solid curve—reflectivity of the optimal structure. Wavelength λ = 0.8 μm (b) Thicknesses of individual layers for three structures, number of layers N = 8.
zation becomes demanding, if there are too many parameters for optimization and/or if the fitness function has a complicated behavior with many local optima. Therefore, it is helpful to visualize the dependence of the fitness function on the optimized parameters. Figure 7 shows the dependence of 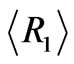 (fitness) on the thicknesses of two arbitrary layers in the structure (4-th and 10-th layers are taken) containing 20 layers. One can see that the fitness function has a rather smooth behavior, which is advantageous for optimization. Moreover, smoothness of the fitness function means that the obtained solutions are quiet robust and small deviations (fabrication inaccuracies) in layer thicknesses will have a small impact on the reflectivity. Results of the optimization in the full search space are shown in Figure 8(a) (dash-dotted line).
(fitness) on the thicknesses of two arbitrary layers in the structure (4-th and 10-th layers are taken) containing 20 layers. One can see that the fitness function has a rather smooth behavior, which is advantageous for optimization. Moreover, smoothness of the fitness function means that the obtained solutions are quiet robust and small deviations (fabrication inaccuracies) in layer thicknesses will have a small impact on the reflectivity. Results of the optimization in the full search space are shown in Figure 8(a) (dash-dotted line).
In our second optimization approach, we reduced the search space by using the thicknesses 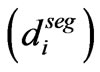 of 10 stacked periodic segments as a first order approximation for the ES optimizer. Then we varied the thickness of
of 10 stacked periodic segments as a first order approximation for the ES optimizer. Then we varied the thickness of
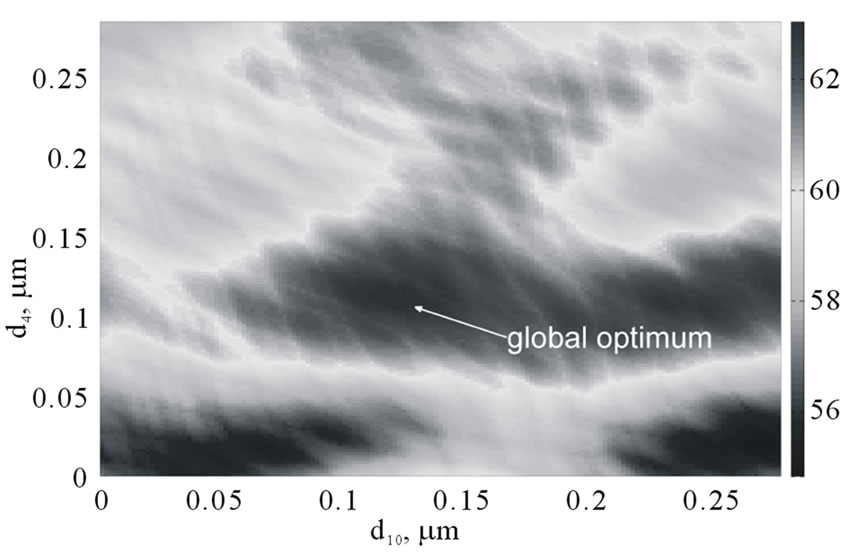
Figure 7.  (fitness) of the structure as function of the thicknesses of two layers (d4 and d10). Structure consists of 20 layers of
(fitness) of the structure as function of the thicknesses of two layers (d4 and d10). Structure consists of 20 layers of .
.
 (a)
(a) (b)
(b)
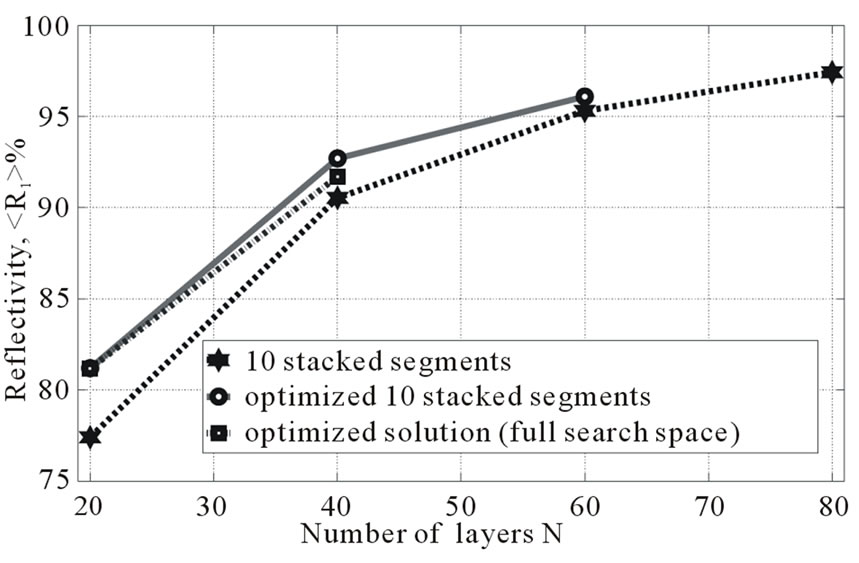
Figure 8. (a) Reflectivity 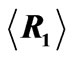 as function of the number of layers N in the structure. Dashed line—stacked periodic segments (periods from 200 to 425 nm), solid line—stacked segments optimized with ES, dash-dotted line—solution of the ES optimizer in the full search space. (b) Thicknesses of individual layers of the three structures, total number of layers is 20.
as function of the number of layers N in the structure. Dashed line—stacked periodic segments (periods from 200 to 425 nm), solid line—stacked segments optimized with ES, dash-dotted line—solution of the ES optimizer in the full search space. (b) Thicknesses of individual layers of the three structures, total number of layers is 20.
each layer in the range of 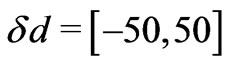 nm to obtain the optimum fitness. Thus, the obtained optimal thicknesses can be represented as:
nm to obtain the optimum fitness. Thus, the obtained optimal thicknesses can be represented as:
 (5)
(5)
Results for the optimization in the reduced search space are shown in Figure 8(a) (solid line). In both optimization procedures we restricted the number of fitness calls to 120,000 in order not to make the optimization very time-consuming. Of course, the reflectivity of the RPS can be further improved by means of simply increasing the time of optimization. Therefore, it should not be confusing that for N = 40 in Figure 8(a) dashdotted line is below the solid line.
As seen in Figure 8(a), the structure optimization in the full search space (dash-dotted curve) becomes less efficient (time-consuming) for a high number of parameters 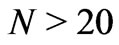 and the best performance comes from the optimized stacked segments. Thicknesses of individual layers for the three structures are compared in Figure 8(b). The improvement in reflectivity, however, is rather small and does not exceed
and the best performance comes from the optimized stacked segments. Thicknesses of individual layers for the three structures are compared in Figure 8(b). The improvement in reflectivity, however, is rather small and does not exceed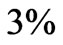 . We can therefore conclude that the stacked periodic segments is already a good solution for high reflection in
. We can therefore conclude that the stacked periodic segments is already a good solution for high reflection in 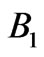 and only minor improvements can be achieved.
and only minor improvements can be achieved.
A similar procedure was also performed for the second energy range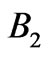 . Results are shown in Figure 9(b)
. Results are shown in Figure 9(b)
6. Optimization of the RPS Adjusted to Two Energy Intervals
In a similar way we can optimize the reflection of RPS with respect to two energy intervals simultaneously. Now the fitness function to be optimized is 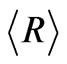 in the expression (1). Band gap analysis revealed that 18 stacked periodic segments may cover
in the expression (1). Band gap analysis revealed that 18 stacked periodic segments may cover 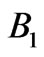 and
and 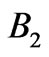 intervals with band gaps. Again we can apply two approaches to perform the structure optimization using ES. The first approach is an optimization in the full search space, where the thickness of each layer is any value below
intervals with band gaps. Again we can apply two approaches to perform the structure optimization using ES. The first approach is an optimization in the full search space, where the thickness of each layer is any value below ,
,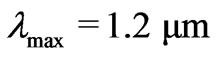 . However, as we saw in Section 5, this optimization procedure is not very efficient for many parameters
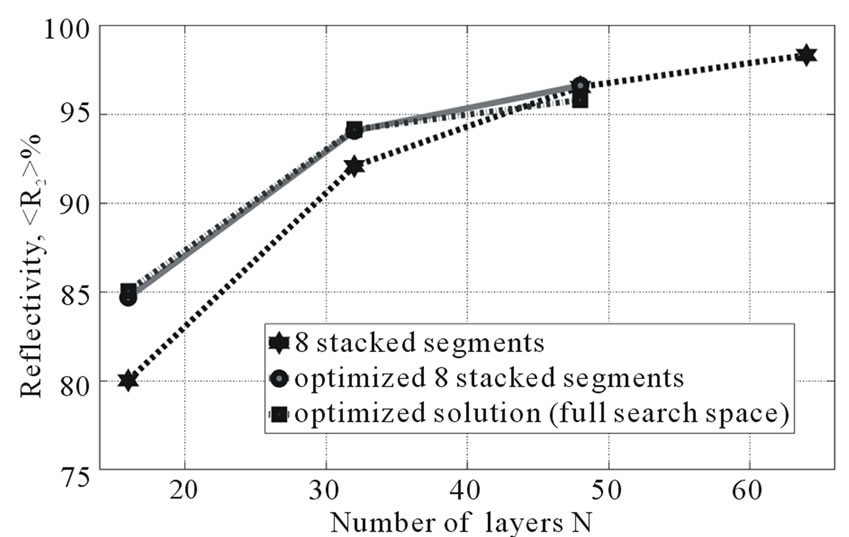
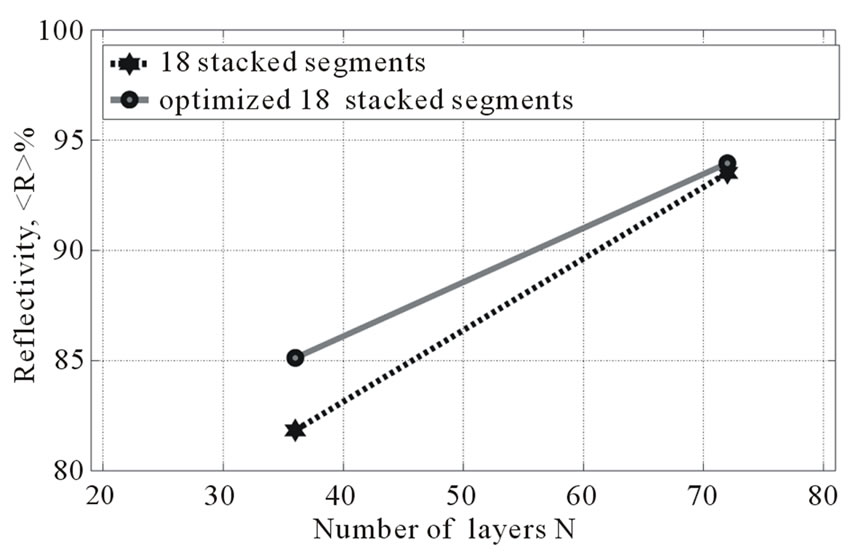
. However, as we saw in Section 5, this optimization procedure is not very efficient for many parameters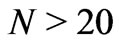 . So we used only the second approach, which optimizes 18 stacked segments in the reduced search space. We varied the thickness of each layer in the range [–30, 30] nm to find the optimum fitness. The obtained results are shown in Figure 10. As can be seen, optimization of 18 stacked segments (solid line) improves the reflecting performance. The improvement, however, is not large
. So we used only the second approach, which optimizes 18 stacked segments in the reduced search space. We varied the thickness of each layer in the range [–30, 30] nm to find the optimum fitness. The obtained results are shown in Figure 10. As can be seen, optimization of 18 stacked segments (solid line) improves the reflecting performance. The improvement, however, is not large 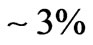 for 36 layers and
for 36 layers and 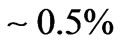 for 72 layers. So, if the structure contains more than 36 layers, stacked periodic segments are close to the optimal solution for high reflectivity in the
for 72 layers. So, if the structure contains more than 36 layers, stacked periodic segments are close to the optimal solution for high reflectivity in the 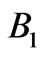 and
and 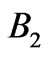 energy intervals.
energy intervals.
 (a)
(a) (b)
(b)
Figure 9. (a) Reflectivity 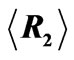 as function of the number of layers N in the structure. Dashed line—stacked periodic segments (periods from 90 to 180 nm), solid line—stacked segments optimized with ES, dash-dotted line—solution of the ES optimizer in the full search space. b) Thicknesses of individual layers of the three structures, total number of layers is 16.
as function of the number of layers N in the structure. Dashed line—stacked periodic segments (periods from 90 to 180 nm), solid line—stacked segments optimized with ES, dash-dotted line—solution of the ES optimizer in the full search space. b) Thicknesses of individual layers of the three structures, total number of layers is 16.
For the sake of completeness, it is also worth plotting reflectivity spectra of the obtained structures. Up to now we plotted only the average values of reflectivity. Reflectivity as a function of energy of the stacked segments (dashed line) and optimized stacked segments (solid line) is shown in Figure 11. At each energy point reflectivity is averaged over angle of incidence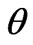 . Dash-dotted line in Figure 11 is shown for the sake of comparison with the simple design, where two Bragg mirrors are stacked in one structure. Band gaps of these Bragg mirrors are centered in the middle of
. Dash-dotted line in Figure 11 is shown for the sake of comparison with the simple design, where two Bragg mirrors are stacked in one structure. Band gaps of these Bragg mirrors are centered in the middle of 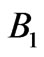 and
and  intervals, the corresponding periods are
intervals, the corresponding periods are 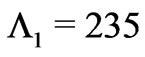 nm and
nm and 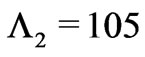 nm. A single Bragg mirror will partially cover only one interval (
nm. A single Bragg mirror will partially cover only one interval ( or
or ). When Bragg mirrors are stacked together, both intervals are partially covered. Therefore, two peaks are observed in Figure 11. It is obvious that optimized segments (solid line) show the best reflecting performance.
). When Bragg mirrors are stacked together, both intervals are partially covered. Therefore, two peaks are observed in Figure 11. It is obvious that optimized segments (solid line) show the best reflecting performance.
 (a)
(a)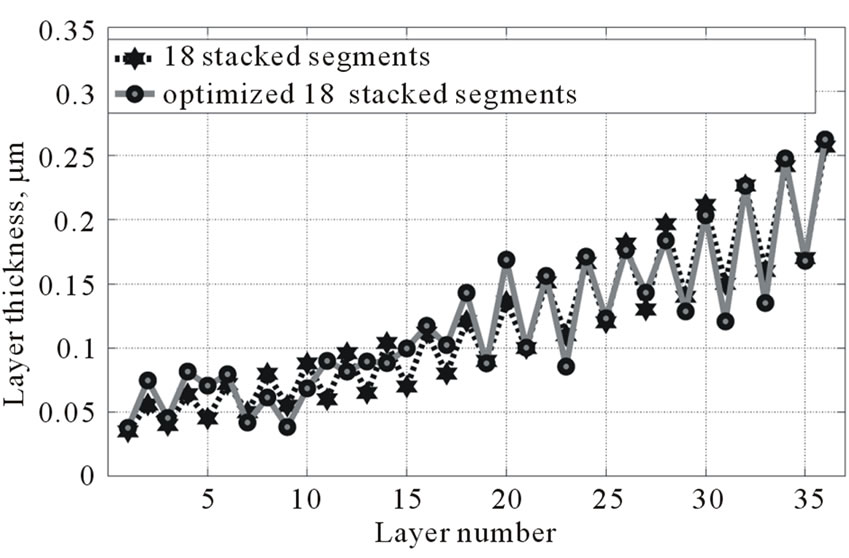 (b)
(b)
Figure 10. (a) Reflectivity  of the structure for
of the structure for  and B2 energy intervals as function of the number of layers. Dashed line—stacked periodic segments, solid line—stacked segments optimized with ES. (b) Thicknesses of individual layers of the two structures, total number of layers N = 36.
and B2 energy intervals as function of the number of layers. Dashed line—stacked periodic segments, solid line—stacked segments optimized with ES. (b) Thicknesses of individual layers of the two structures, total number of layers N = 36.
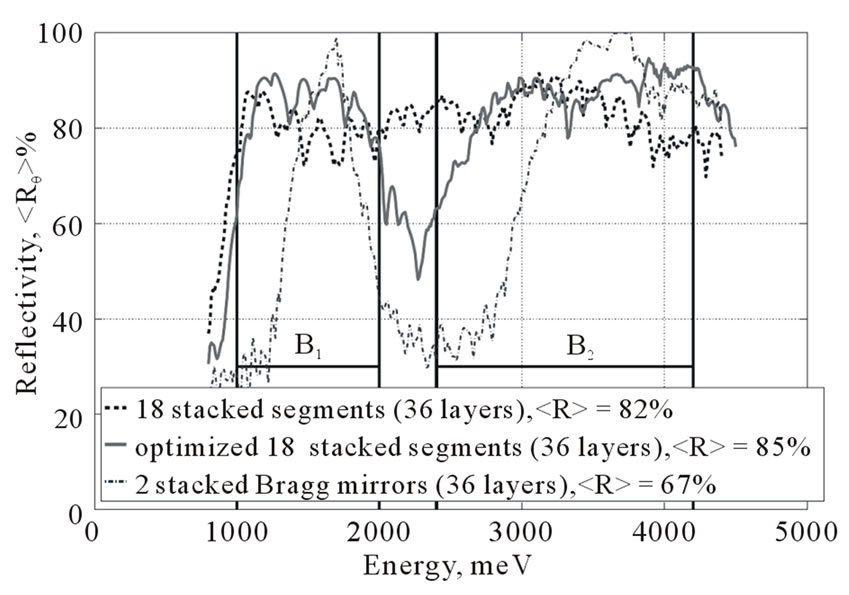
Figure 11. Reflectivity 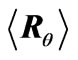 as function of energy. Dashed curve—18 stacked periodic segments, solid curve—18 stacked segments optimized with ES, dash-dotted curve— reflectivity of the stacked Bragg mirrors with periods
as function of energy. Dashed curve—18 stacked periodic segments, solid curve—18 stacked segments optimized with ES, dash-dotted curve— reflectivity of the stacked Bragg mirrors with periods 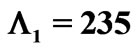 nm and
nm and 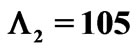 nm.
nm.
7. Possible Instabilities of the Designed Photonic Structure Due to High-Temperature Interaction of Individual Layers
At high-temperatures, the interaction of 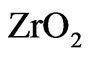 and
and 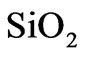 layers (Figure 12) may be a source of dynamic instability in the position and width of the photonic band gap in designed photonic heat-shields.
layers (Figure 12) may be a source of dynamic instability in the position and width of the photonic band gap in designed photonic heat-shields.
At temperature above 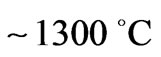 [19], irreversible reactions Equation (6) between of
[19], irreversible reactions Equation (6) between of 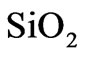 and
and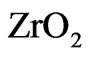 , will cause refractory zirconium orthosilicate
, will cause refractory zirconium orthosilicate 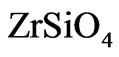 (zircon) interlayers to form at the interfaces
(zircon) interlayers to form at the interfaces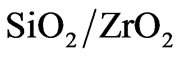 :
:
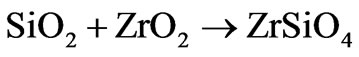 (6)
(6)
The upper limit of 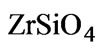 stability lies between 1669 and 1683˚C [20] which is close to the lowest eutectic temperature of 1687˚C. Reaction Equation (6) remains irreversible until 1550˚C at which point, a small fraction of
stability lies between 1669 and 1683˚C [20] which is close to the lowest eutectic temperature of 1687˚C. Reaction Equation (6) remains irreversible until 1550˚C at which point, a small fraction of 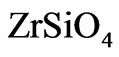 decays into constituent oxides. The rate of the
decays into constituent oxides. The rate of the 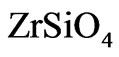 decomposition reaction increases at 1650˚C [19]. The decay of
decomposition reaction increases at 1650˚C [19]. The decay of  at 1673˚C was established based on an analysis of literature data, experimental results and thermodynamic assessments [19]. The lowest eutectic in the system was established at the slightly higher temperature of 1687˚C [19]. These results are in good agreement with DTA investigation of [21] where the zircon decomposition was determined to be at 1674˚C and the eutectic melting at 1680˚C. The preliminary literature analysis indicates that diffusivity of Si in
at 1673˚C was established based on an analysis of literature data, experimental results and thermodynamic assessments [19]. The lowest eutectic in the system was established at the slightly higher temperature of 1687˚C [19]. These results are in good agreement with DTA investigation of [21] where the zircon decomposition was determined to be at 1674˚C and the eutectic melting at 1680˚C. The preliminary literature analysis indicates that diffusivity of Si in 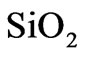 [22,23] is several orders of magnitude higher than diffusivity of Si in
[22,23] is several orders of magnitude higher than diffusivity of Si in 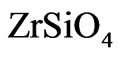 [24] and Zr in
[24] and Zr in  [25].
[25].
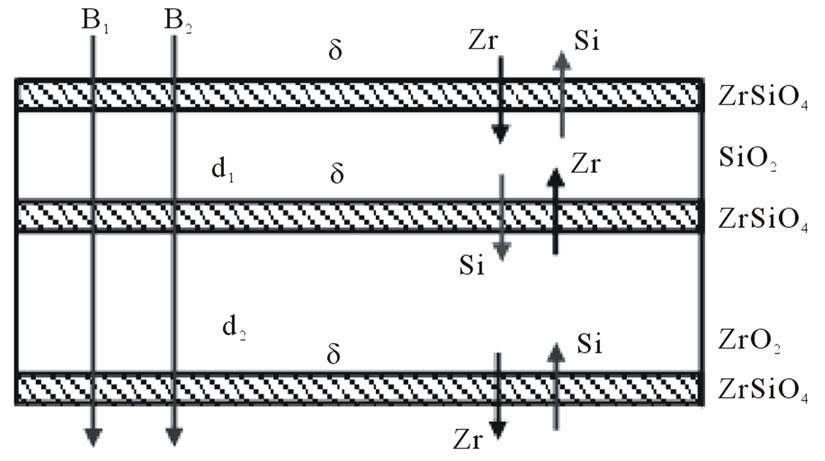
Figure 12. Scheme illustrating formation of ZrSiO4 interlayers as a result of high-temperature interaction 
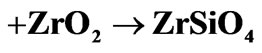 under external heat radiation in the wavelength ranges B1 and B2. Thickness of intermediate
under external heat radiation in the wavelength ranges B1 and B2. Thickness of intermediate  layers after exposure during operation time is much smaller than thickness of the
layers after exposure during operation time is much smaller than thickness of the 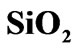 and
and 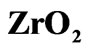 layers d1 and d2 (
layers d1 and d2 (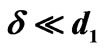 ,
,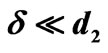 ) due to high activation energy of reaction of
) due to high activation energy of reaction of  formation. That is why erasing
formation. That is why erasing  interlayers do not change significantly position and width of the photonic band gaps of designed multilayers.
interlayers do not change significantly position and width of the photonic band gaps of designed multilayers.
Diffusivity of Zr in 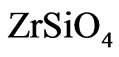 is assumed to be similar to diffusivity of Hf in
is assumed to be similar to diffusivity of Hf in , which is higher than diffusivity of Si [24]. Among tetravalent cations, the diffusivity of Si in
, which is higher than diffusivity of Si [24]. Among tetravalent cations, the diffusivity of Si in 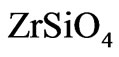 is approximately the same as that of Ti but about one order of magnitude faster than diffusivity of Hf and two orders of magnitude faster than diffusivity of U and Th [24]. A low speed of reaction Equation (6) and a small thickness of formed
is approximately the same as that of Ti but about one order of magnitude faster than diffusivity of Hf and two orders of magnitude faster than diffusivity of U and Th [24]. A low speed of reaction Equation (6) and a small thickness of formed 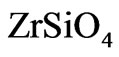 interlayer after exposure time of the photonic heat-shield of approximately 300 sec are expected (see Figure 5 in [24], measurement of temperature response for standard PICA sample at 570
interlayer after exposure time of the photonic heat-shield of approximately 300 sec are expected (see Figure 5 in [24], measurement of temperature response for standard PICA sample at 570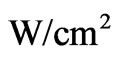 , 0.42 atm, total heat load of 14’250
, 0.42 atm, total heat load of 14’250 , surface temperature
, surface temperature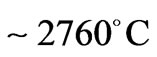 ). Based on diffusion measurements, the activation energy of diffusion of Si in zircon was calculated [22], which is higher in comparison with other silicates. These data also confirm slow rates of reaction 6 at 1200˚C indicated by [19].
). Based on diffusion measurements, the activation energy of diffusion of Si in zircon was calculated [22], which is higher in comparison with other silicates. These data also confirm slow rates of reaction 6 at 1200˚C indicated by [19].
The intermediate  layers consist of atoms of both contacted materials, and therefore, their dielectric permittivity has an intermediate value between the dielectric constants of
layers consist of atoms of both contacted materials, and therefore, their dielectric permittivity has an intermediate value between the dielectric constants of 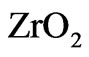 and
and 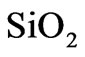 materials. This affects reflection of light at the boundary. The influence of the intermediate layer on the transparency of photonic crystals has been considered in [26]. It was found that the effect depends on the relation between the light wavelength and the interlayer thickness
materials. This affects reflection of light at the boundary. The influence of the intermediate layer on the transparency of photonic crystals has been considered in [26]. It was found that the effect depends on the relation between the light wavelength and the interlayer thickness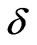 . Indeed, to estimate the effect, we can write the dielectric permittivity of the layer as a function of distance from the boundary
. Indeed, to estimate the effect, we can write the dielectric permittivity of the layer as a function of distance from the boundary 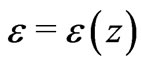 (here
(here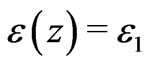 , if
, if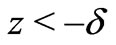 , but
, but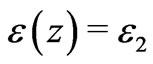 , if
, if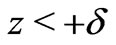 ). The effect depends on the relation between the thickness of the layer (
). The effect depends on the relation between the thickness of the layer (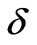 ) and the light wavelength
) and the light wavelength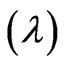 . Namely, the commonly used boundary conditions for the light wave fields hold at the abrupt boundary
. Namely, the commonly used boundary conditions for the light wave fields hold at the abrupt boundary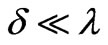 . This leads to the reflection and transmission coefficients used in this paper. On the contrary, at the smooth boundary
. This leads to the reflection and transmission coefficients used in this paper. On the contrary, at the smooth boundary 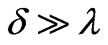 we can use the semiclassical approximation and the wave equation with the position depen-- dent wavelength
we can use the semiclassical approximation and the wave equation with the position depen-- dent wavelength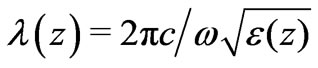 , which leads to the exponentially small reflectivity. Transition between these limiting cases for the similar quantum mechanical problem has been studied in [27,28]. Thus, the results presented here hold for
, which leads to the exponentially small reflectivity. Transition between these limiting cases for the similar quantum mechanical problem has been studied in [27,28]. Thus, the results presented here hold for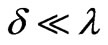 , i.e. if the diffusion length is much smaller than the thickness of the layers we have deposed. Apparently, evolution of the interlayer thickness makes the reflectivity of the multilayer coating time-dependent. Nevertheless, the expected thickness of formed
, i.e. if the diffusion length is much smaller than the thickness of the layers we have deposed. Apparently, evolution of the interlayer thickness makes the reflectivity of the multilayer coating time-dependent. Nevertheless, the expected thickness of formed  interlayer should not exceed several lattice constants (
interlayer should not exceed several lattice constants ( nm) after heat-shield operation time. This is significantly smaller than the wavelength of external heat radiation in both
nm) after heat-shield operation time. This is significantly smaller than the wavelength of external heat radiation in both 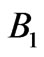 and
and 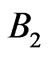 ranges and, therefore, does not change essentially the results of our modeling. It was found [26] that such small thickness of the
ranges and, therefore, does not change essentially the results of our modeling. It was found [26] that such small thickness of the 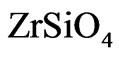 interlayer can change the depth, but not the position and width of the band gap of designed multilayer photonic structure.
interlayer can change the depth, but not the position and width of the band gap of designed multilayer photonic structure.
8. Conclusions
Modeling layered 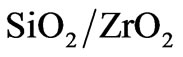 structure for potential use as photonic shield for Earth reentry was performed both analytically and numerically for shock layer radiation in near-IR and near-UV ranges. The analytical approach indicates that high omnidirectional reflectivity can be achieved by means of stacking 18 periodic segments in one structure. Optimization using evolutionary strategy resulted in structures with improved reflection performance. These structures demonstrate significantly enhanced reflectivity than a simple stack of two Bragg mirrors. The ES structure optimization method is quite general and can be used to design reflectors for other wavelength ranges without any restrictions on the constituent materials. High-temperature interactions at the
structure for potential use as photonic shield for Earth reentry was performed both analytically and numerically for shock layer radiation in near-IR and near-UV ranges. The analytical approach indicates that high omnidirectional reflectivity can be achieved by means of stacking 18 periodic segments in one structure. Optimization using evolutionary strategy resulted in structures with improved reflection performance. These structures demonstrate significantly enhanced reflectivity than a simple stack of two Bragg mirrors. The ES structure optimization method is quite general and can be used to design reflectors for other wavelength ranges without any restrictions on the constituent materials. High-temperature interactions at the 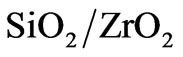 interface resulting in the formation of
interface resulting in the formation of 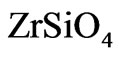 interlayers is expected to be slow. Therefore, the interlayer is not expected to have a significant impact on the reflecting performance of the suggested multilayer coatings.
interlayers is expected to be slow. Therefore, the interlayer is not expected to have a significant impact on the reflecting performance of the suggested multilayer coatings.
REFERENCES
- V. Shklover, L. Braginsky, G. Witz, M. Mishrikey and C. Hafner, “High-Temperature Photonic Structures. Thermal Barrier Coatings, Infrared Sources and Other Applications,” Journal of Computational and Theoretical Nanoscience, Vol. 5, 2008, pp. 862-893.
- C. Johnston, B. Hollis and K. Sutton, “Spectrum Modeling for Air Shock-Layer Radiation at Lunar-Return Conditions,” Journal of Spacecraft and Rockets, Vol. 45, No. 5, 2008, pp. 865-878. doi:10.2514/1.33004
- D. Bose, E. McCorkle, C. Thompson, D. Bogdanoff, D. Prabhu, G. Allen and J. Grinstead, “Analysis and Model Validation of Shock Layer Radiation in Air,” VKI LS Course on Hypersonic Entry and Cruise Vehicles, Palo Alto, 2008.
- C. Johnston, “A Comparison of EAST Shock-Tube Radiation Measurements with a New Air Radiation Model,” AIAA Paper 1245, 2008.
- J. Grinstead, M. Wilder, J. Olejniczak, D. Bogdanoff, G. Allen, K. Dang and M. Forrest, “Shock-Heated Air Radiation Measurements at Lunar Return Conditions,” AIAA Paper 1244, 2008.
- [Online]. Available: http://www.sopra-sa.com/.
- S. Venkataraj, R. Drese, C. Liesch, O. Kappertz, R. Jayavel and M. Wuttig, “Temperature Stability of Sputtered Niobium—Oxide Films,” Journal of Applied Physics, Vol. 91, No. 4863, 2002, pp. 61-68. doi:10.1063/1.1458052
- Y. Fink, J. Winn, S. Fan, C. Chen, J. Michel, J. Joannopoulos and E. Thomas, “A Dielectric Omnidirectional Reflector,” Science, Vol. 282, No. 5394, 1998, pp. 1679-1682. doi:10.1126/science.282.5394.1679
- E. Yablonovitch, “Engineered Omnidirectional External-Reflectivity Spectra from One-Dimensional Layered Interference Filters,” Optics Letters, Vol. 23, No. 21, 1998, pp. 1648-1649. doi:10.1364/OL.23.001648
- D. Chigrin, A. Lavrinenko, D. Yarotsky and S. Gaponenko, “Observation of Total Omnidirectional Reflection from a One-Dimensional Dielectric Lattice,” Applied Physics A: Materials Science & Processing, Vol. 68, No. 1, 1999, pp. 25-28. doi:10.1007/s003390050849
- P. Yeh, “Optical Waves in Layered Media,” John Wiley & Sons, New York, 1988.
- F. Kartner, N. Matuschek, T. Schibli, U. Keller, H. Haus, C. Heine, R. Morf, V. Scheuer, M. Tilsch and T. Tschudi, “Design and Fabrication of Double-Chirped Mirrors,” Optics Letters, Vol. 22, No. 11, 1997, pp. 831-833. doi:10.1364/OL.22.000831
- T. Yonte, J. Monz´on, A. Felipe and L. S´anchez-Soto, “Optimizing Omnidirectional Reflection by Multilayer Mirrors,” Journal of Optics A: Pure and Applied Optics, Vol. 6, No. 1, 2004, pp. 127-131. doi:10.1088/1464-4258/6/1/023
- M. del Rio and G. Pareschi, “Global Optimization and Reflectivity Data Fitting for X-Ray Multilayer Mirrors by Means of Genetic Algorithms,” Proceedings of SPIE, Vol. 4145, No. 88, 2001, p. 88. doi:10.1117/12.411624
- S. Martin, J. Rivory and M. Schoenauer, “Synthesis of Optical Multilayer Systems Using Genetic Algorithms,” Applied Optics, Vol. 34, No. 13, 1995, pp. 2247-2254. doi:10.1364/AO.34.002247
- J. Joannopoulos, S. Johnson, J. Winn and R. Meade, “Photonic Crystals: Molding the Flow of Light,” Princeton University, Princeton, 2008.
- A. Fallahi, M. Mishrikey, C. Hafner and R. Vahldieck, “Efficient Procedures for the Optimization of Frequency Selective Surfaces,” IEEE Transactions on Antennas and Propagation, Vol. 56, No. 5, 2008, p. 1340. doi:10.1109/TAP.2008.922678
- C. Hafner, C. Xudong, J. Smajic and R. Vahldieck, “Efficient Procedures for the Optimization of Defects in Photonic Crystal Structures,” Journal of the Optical Society of America A, Vol. 24, No. 4, 2007, pp. 1177-1188. doi:10.1364/JOSAA.24.001177
- A. Kaiser, M. Lobert and R. Telle, “Thermal Stability of Zircon (ZrSiO4),” Journal of the European Ceramic Society, Vol. 28, No. 11, 2008, pp. 2199-2211. doi:10.1016/j.jeurceramsoc.2007.12.040
- W. Butterman and W. Foster, “Zircon Stability and the ZrO2-SiO2 Phase Diagram,” American Mineralogist, Vol. 52, 1967, pp. 880-885.
- D. Kamaev, S. Archugov and G. Mikhailov, “Study and Thermodynamic Analysis of the ZrO2-SiO2 System,” Russian Journal of Applied Chemistry, Vol. 78, No. 2, 2005, pp. 200-203. doi:10.1007/s11167-005-0259-2
- F. B’ejina and O. Jaoul, “Silicon Diffusion in Silicate Minerals,” Earth and Planetary Science Letters, Vol. 153, No. 3-4, 1997, pp. 229-238. doi:10.1016/S0012-821X(97)00190-8
- D. Tsoukalas, C. Tsamis and P. Normand, “Diffusivity Measurements of Silicon in Silicon Dioxide Layers Using Isotopically Pure Material,” Journal of Applied Physics, Vol. 89, No. 12, 2001, pp. 7809-7813. doi:10.1063/1.1371003
- D. Cherniak, “Si Diffusion in Zircon,” Physics and Chemistry of Minerals, Vol. 35, No. 4, 2008, pp. 179-187. doi:10.1007/s00269-007-0210-6
- H. Drings, U. Brossmann, H. Carstanjen, A. Szokefalvi-Nagy, C. Noll and H. Schaefer, “Enhanced 95Zr Diffusion in Grain Boundaries of Nano-Crystalline ZrO2 9.5 mol% Y2O3,” Physica Status Solidi (A), Vol. 206, No. 1, 2008, pp. 54-58. doi:10.1002/pssa.200824077
- L. Braginsky and V. Shklover, “Light Propagation in an Imperfect Photonic Crystal,” Physical Review B, Vol. 73, No. 8, 2006. doi:10.1103/PhysRevB.73.085107
- E. Baskin and L. Braginsky, “Short-Wavelength Phonon Emission from a Metal-Semiconductor Interface,” Physical Review B, Vol. 50, No. 16, 1994, pp. 12191-12194. doi:10.1103/PhysRevB.50.12191
- L. Braginsky and V. Shklover, “Influence of Interface Structure on Transversal Electron Transport,” Solid State Communications, Vol. 105, No. 11, 1998, pp. 701-704. doi:10.1016/S0038-1098(97)10209-5

