Journal of Water Resource and Protection
Vol.5 No.6(2013), Article ID:33462,10 pages DOI:10.4236/jwarp.2013.56065
Two-Phase Multi Objective Fuzzy Linear Programming Approach for Sustainable Irrigation Planning
1Department of Civil Engineering, Government College of Engineering, Aurangabad, India
2Department of Civil Engineering, Amrutvahini College of Engineering, Sangamner, India
Email: regulwar@gmail.com, jyotiba.gurav@rediffmail.com
Copyright © 2013 D. G. Regulwar, Jyotiba B. Gurav. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 15, 2013; revised May 16, 2013; accepted June 11, 2013
Keywords: Sustainable Irrigation Planning; Multi Objective Fuzzy Linear Programming; Maxmin Approach; Two-Phase Approach
ABSTRACT
The objective of the present study is to develop the irrigation planning model and to apply the same in the form of TwoPhase Multi Objective Fuzzy Linear Programming (TPMOFLP) approach for crop planning in command area of Jayakwadi Project Stage I, Maharashtra State, India. The development of TPMOFLP model is on the basis of various Linear Programming (LP) models and Multi Objective Fuzzy Linear Programming (MOFLP) models, these models have been applied for maximization of the Net Benefits (NB), Crop production (CP), Employment Generation (EG) and Manure Utilization (MU) respectively. The significant increase in the value of level of satisfaction (λ) has been found from 0.58 to 0.65 by using the TPMOFLP approach as compare to that of MOFLP model based on maxmin approach. The two-phase approach solution provides NB = 1503.56 Million Rupees, CP = 335729.30 Tons, EG = 29.74 Million Man days and MU = 160233.70 Tons respectively. The proposed model will be helpful for the Decision Maker (DM) to take a decision under conflicting situation while planning for different conflicting objectives simultaneously and has potential to find out an integrated irrigation planning with prime consideration for economic, social and environmental issue.
1. Introduction
The management of agriculture irrigation water resource has always accompanied by uncertainties due to randomness and imprecision in irrigation. Therefore, the efficient management of limited water resources has always been a great concern for irrigation policy maker along with farmers. The fuzzy set theory is an alternative to deal with the uncertainty in irrigation planning. The term fuzzy was first introduced and inducted by Zadeh [1], which brought paradigm shift from classical set theory to fuzzy set theory. In fuzzy set theory, membership is in a set, which can range from incomplete (equals 0) to complete (equals 1). Vagueness in describing the planning goals/objectives and uncertainties involved in the decision parameter as well as decision variables can be done with the help of fuzzy set. Bellman and Zadeh [2] have focused on the concept of decision making in a fuzzy environment. Bellman and Zadeh [3] have provided a model for approximate rather than precise reasoning, to represent how the fuzzy logic differs from conventional logical systems. Zadeh has made novel contribution with his papers for the development, propagation and application of fuzzy logic to the real world problems ([4-15]). The successful attempts have been made to develop the Fuzzy Linear Programming (FLP) by Zimmermann ([16, 17]), Werners [18], Lee and Li [19] and, subsequently, Guu and Wu [20] and Wu and Guu [21] proposed a new method, in which the FLP has initially solved and later the efforts have been made to improve the optimal solution by enhancing the level of satisfaction (λ). Li and Li [22] have proposed the two-phase approach to compute the efficient solutions to fuzzy multiple objective linear programming problems.
Raju and Nagesh Kumar [23] have formulated the FLP model for three conflicting objectives and dealt with fuzzification of objective functions only. Raju and Duckstein [24] have developed the MOFLP model for sustainable irrigation planning considering the three objectives as fuzzy. Regulwar and Anand Raj ([25,26]) have developed a monthly Multi Objective Genetic Algorithm Fuzzy Optimization model. Regulwar and Gurav [27] have developed the MOFLP irrigation planning model, which considers the fuzziness in four objectives of the case study. Regulwar and Gurav [28] have presented the study on irrigation planning under uncertainty considering different cases using MOFLP approach. Gurav and Regulwar [29] have proposed the model for minimization of cost of cultivation along with interactive decision making under fuzzy environment. Regulwar and Gurav [30] presented the sustainable irrigation planning model to tackle imprecise parameters using fuzzy logic. Gurav and Regulwar [31] developed the MOFLP model, focused on multi objective sustainable irrigation planning with decision parameters and decision variables as fuzzy. Regulwar and Gurav [32] proposed the irrigation planning model with fuzzy parameters along with an interactive approach, which deals with the consideration of balance between the feasibility degree of constraints and satisfaction degree of objective. Mirajkar and Patel [33] developed the irrigation planning model with maxmin approach, two-phase approach and compromise approach to the case study of Ukai irrigation project in the State of Gujarat, India. Regulwar and Gurav [34,35] proposed the irrigation planning models using fuzzy logic for minimization of cost of cultivation along with the uncertainty/vagueness associated with the parameters of irrigation planning.
It has found from the literature review presented in the manuscript that no model has been found for sustainable irrigation planning using two-phase approach. In the present study, an attempt has been made to improve the solution obtained through MOFLP (max-min approach), by applying Two-Phase Multi Objective Fuzzy Linear Programming (TPMOFLP) model, for various objectives such as viz. maximization of Net Benefits (NB) , Crop Production (CP), Employment Generation (EG) and Manure Utilization (MU) simultaneously. The primary objective of the present study is to develop the TP-MOFLP model for sustainable irrigation planning, which improves the efficiency of the optimal solution obtained by maxmin operator approach suggested by Zimmermann ([16,17]). The developed methodology and model have been applied to the case study of Jayakwadi Project Stage-I in Godavari River sub basin in the State of Maharashtra, India. The LINGO 13 optimization package has been used to solve the FLP optimization models.
2. Model Development and Methodology
The objective of the present study is to find optimal cropping pattern for the 75% dependable inflow. The problem has been formulated as an optimization model based on deterministic inflows. In the formulation of the problem, various assumptions have been made: The irrigation intensity adopted is 22% (Kharif season), 45% (Rabi season) and 28% (Two Seasonal), Hot Weather crop 3%; Perennial 4.5% of the total command area and that becomes a total irrigation intensity of 102.5%. Only surface water has been considered for irrigation. Under certain overlapping situations, care is taken of by adding specific constraints. The input cost for each crop is considered as twenty percent of the total gross benefits to be gained.
2.1. Description of the Study Area
The lower Godavari River Basin, Maharashtra State, India is taken for present study. The Jayakwadi Project Stage-I is located across the eastward flowing river Godavari. The salient features of the Jayakwadi Project Stage-I are presented in Table 1. From the soil survey report, it is seen that near the canal alignment, the soils are shallow, consisting of a thin mantle of soil over the murum stratum. The area adjoining the Godavari River and its major tributaries are deep silt and black soils. Figure 1 shows index map of Jayakwadi Project, Maharashtra State, India.
2.2. Model Development
The following four objectives have been considered in the present study.
2.2.1. Maximization of Net Benefits (NB)
The decision maker tries to maximize the net benefits. The net benefits coefficients from the irrigated area under various crops are obtained by subtracting the input cost (20% of gross benefit) from gross benefit for different crops. The Gross benefits are calculated by multiplying the average yield of a crop per ha and current market price of that crop. The objective function for maximization of net benefits can be expressed as
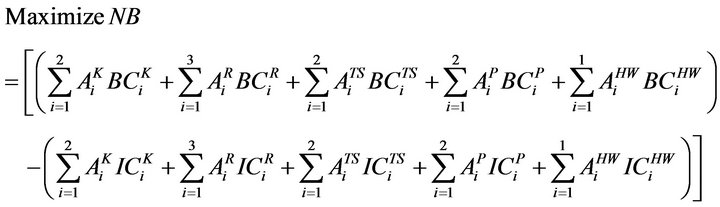 (1)
(1)

Table 1. Salient features of the Jayakwadi project stage-I.

Figure 1. Index map of Maharashtra state, India.
[In which i = crop index. 1 = Sugarcane (Perennial), 2 = Banana (Perennial), 3 = Chillies (Two Seasonal), 4 = L S Cotton (Two Seasonal), 5 = Sorghum (Kharif), 6 = Paddy (Kharif), 7 = Sorghum (Rabi), 8 = Wheat (Rabi), 9 = Gram (Rabi) and 10 = Groundnut (Hot Weather)]
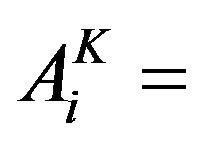 Area of ith
Area of ith crop in Kharif season (ha);
crop in Kharif season (ha);
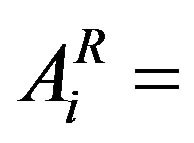 Area of ith
Area of ith crop in Rabi season (ha);
crop in Rabi season (ha);
 Area under Hot Weather crop (ha);
Area under Hot Weather crop (ha);
 Area under Perennial crop (ha);
Area under Perennial crop (ha);
 Area under Two Seasonal crop (ha);
Area under Two Seasonal crop (ha);
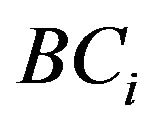 = Benefit coefficient for ith crop (Rs/ha);
= Benefit coefficient for ith crop (Rs/ha);
 Input cost for ith crop (Rs/ha);
Input cost for ith crop (Rs/ha);
 Kharif;
Kharif;
 Perennial;
Perennial;
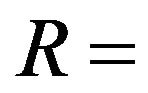 Rabi;
Rabi;
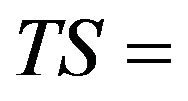 Two Seasonal;
Two Seasonal;
 Hot Weather.
Hot Weather.
2.2.2. Maximization of Crop Production (CP)
The decision maker tries to maximize the crop production. The crop production coefficients have been taken as the average yield of a crop per ha [36]. The objective function for maximization of crop production can be written as
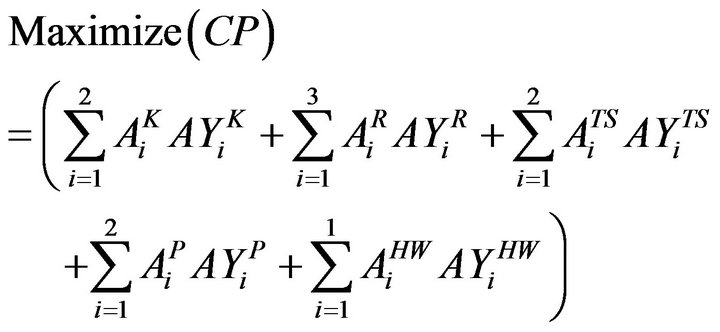 (2)
(2)
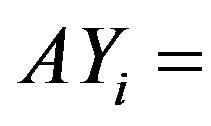 Average yield of ith crop (Tons/ha);
Average yield of ith crop (Tons/ha);
In case of second objective i.e. Maximization of CP has thought of from keeping the food sufficiency in the region. At least the survival of people of region can only be thought of if sufficient food is available. By considering this aspect, the sustainability has associated with second objective.
2.2.3. Maximization of Employment Generation (EG)
The decision maker (DM) has to concentrate on the maximization of employment generation with view of socioeconomic development.
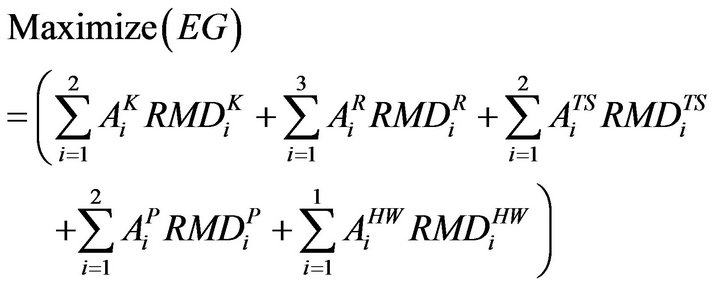 (3)
(3)
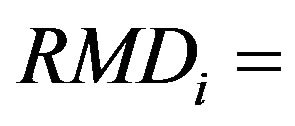 Requirement of Man Days for ith crop/ha;
Requirement of Man Days for ith crop/ha;
The labour requirement or number of Man Days (MD) for a particular crop/ha has arrived at by discussions with farmers and experts from agricultural field.
In case of third objective i.e. Maximization of EG has thought from the socio-economic point of view. In developing country like India, the distribution of agricultural land is uneven. Most of people they do not have their own land to cultivate and they can think of themselves in the form of labour to avail bread and butter for their survival. The irrigation policy maker has to think from employment generation point of view for sustainability in case social and economical aspects. Due to these reasons, the third objective has related to sustainability.
2.2.4. Maximization of Manure Utilization (MU)
In order to maintain the fertility and nutrient sufficiency of soil in proper manner, decision maker should concentrate on maximization of utilization of manures.
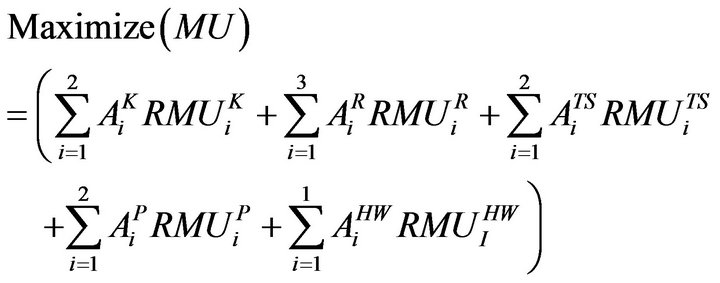 (4)
(4)
 Requirement of Manure Utilization in tons for ith crop/ha;
Requirement of Manure Utilization in tons for ith crop/ha;
The Requirement of Manure Utilization (RMU) for a crop/ha is arrived by discussion with farmers and experts from agricultural field.
In case of the fourth objective i.e. maximization of MU, the green manure has prepared by the farmer by decomposing the waste from the farming activity and waste from the live stock activities. This does not include any harmful chemicals, fertilizers and pesticides. This kind of manure helps to maintain nutrients sufficiency of soil for various crops. Nowadays, due to excessive use of fertilizers and chemicals, the soil is loosing its own ability to supply nutrients. Hence, it has tried to incorporate the MU as related to sustainability.
2.3. Constraints
2.3.1. Total Sowing Area Constraint
The total area constraint, for various crops, for the present study, has considered in order to take care of the total area available for cultivation in command area during different crop seasons. The total sowing area constraint has given by the following equation,
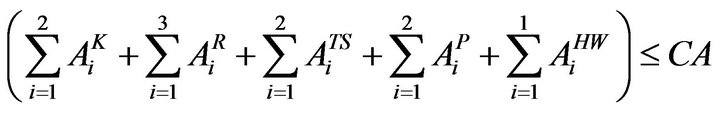 (5)
(5)
CA = Total command area.
Maximum Sowing Area Constraint (According to the existing cropping Pattern)
The maximum sowing area constraint for various crops has been defined, to account for maximum sowing area available for cultivation during various crop seasons according to existing cropping pattern of the project. The maximum sowing area constraint is given byKharif
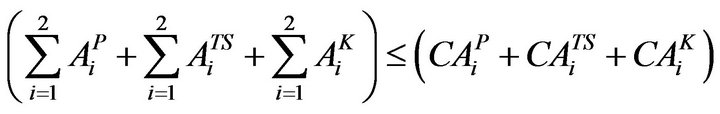 (6)
(6)
Rabi
 (7)
(7)
Hot Weather and Perennial
 (8)
(8)
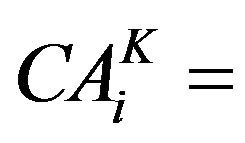 Command area for Kharif season for ith crop (ha);
Command area for Kharif season for ith crop (ha);
 Command area for Rabi season for ith crop (ha);
Command area for Rabi season for ith crop (ha);
 Command area under Hot Weather crop (ha);
Command area under Hot Weather crop (ha);
 Command area under perennial crop (ha).
Command area under perennial crop (ha).
2.3.2. Affinity Constraint
The farmers of the region have a tendency to grow cash crops and other crops according to their own interest and benefits. To safeguard the interest of the food requirement of the region according to the storage capacity of the reservoir, the following limitations (upper limit using the existing cropping pattern) for various crops have been incorporated as constraintsPerennial
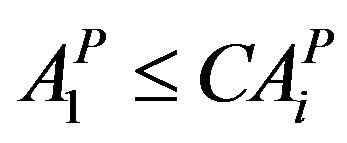 (9a)
(9a)
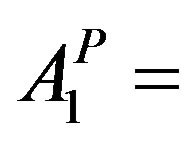 Area under Perennial crop (Sugarcane)
Area under Perennial crop (Sugarcane)
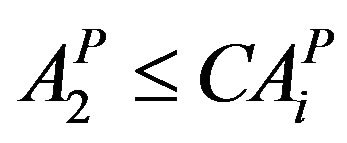 (9b)
(9b)
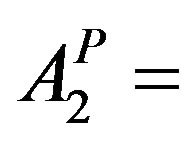 Area under Perennial crop (Banana)
Area under Perennial crop (Banana)
Two Seasonal
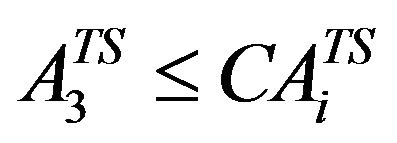 (9c)
(9c)
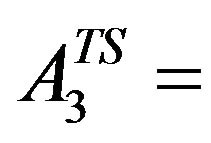 Area under Two Seasonal crop (Chilies)
Area under Two Seasonal crop (Chilies)
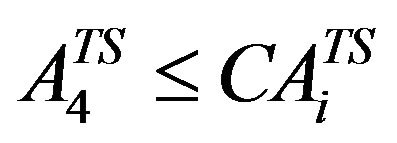 (9d)
(9d)
 Area under Two Seasonal crop (LS Cotton)
Area under Two Seasonal crop (LS Cotton)
Kharif
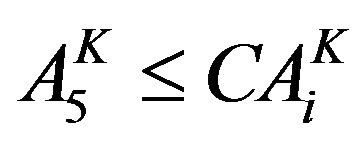 (9e)
(9e)
 Area under Kharif crop (Sorghum)
Area under Kharif crop (Sorghum)
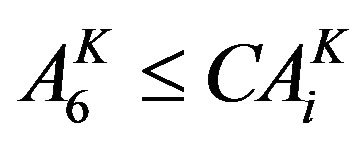 (9f)
(9f)
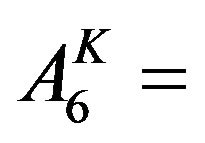 Area under Kharif crop (Paddy)
Area under Kharif crop (Paddy)
Rabi
 (9g)
(9g)
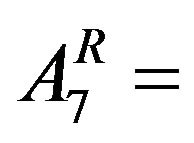 Area under Rabi crop (Sorghum)
Area under Rabi crop (Sorghum)
 (9h)
(9h)
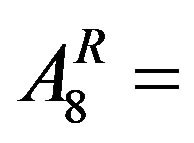 Area under Rabi crop (Wheat)
Area under Rabi crop (Wheat)
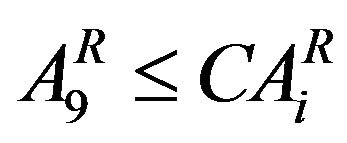 (9i)
(9i)
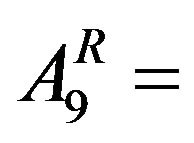 Area under Rabi crop (Gram)
Area under Rabi crop (Gram)
Hot Weather
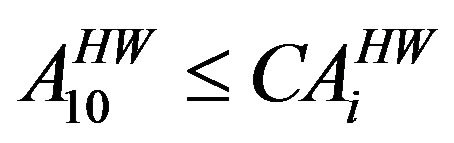 (9j)
(9j)
 Area under Hot Weather crop (Groundnut)
Area under Hot Weather crop (Groundnut)
2.3.3. Labour Availability Constraint
Refereeing to the problem of unavailability/shortage of labour during farming season it has suggested that to tackle the problem of uncertainty of availability of labour, the labour requirement should not exceed the total labour availability during that intervalKharif
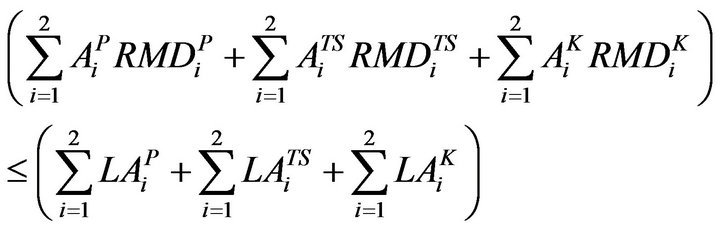 (10)
(10)
Rabi
 (11)
(11)
(Perennial and Hot Weather
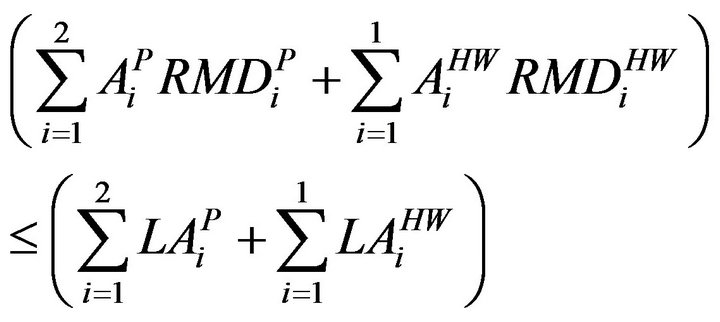 (12)
(12)
 Labour availability for ith crop;
Labour availability for ith crop;
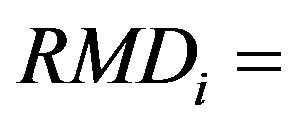 Requirement of Man Days for ith crop/ha.
Requirement of Man Days for ith crop/ha.
2.3.4. Manure Availability Constraint
Referring to the scarcity of manure, which is needed to ensure the fertility of soil, it is suggested that in order to maintain fertility of the soil, the total manure requirement should not exceed the total availability of the manure in that season.
Kharif
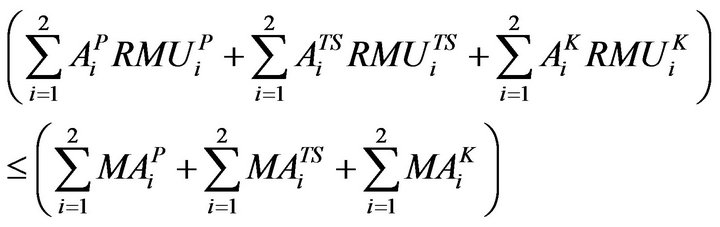 (13)
(13)
Rabi
 (14)
(14)
Perennial and Hot Weather
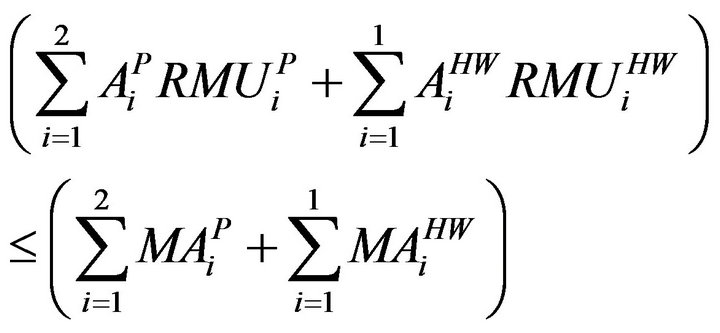 (15)
(15)
 Manure availability for ith crop;
Manure availability for ith crop;
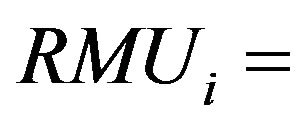 Requirement of Manure Utilization for ith crop/ha;
Requirement of Manure Utilization for ith crop/ha;
2.3.5. Water Availability Constraint
The total water requirement of different crops should not exceed the total water availability in the reservoir,
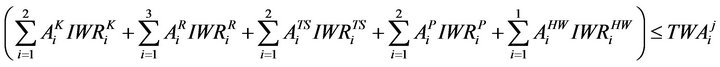 (16)
(16)
 (No of crop Seasons)
(No of crop Seasons)
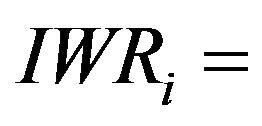 Irrigation water requirement (m) for ith crop;
Irrigation water requirement (m) for ith crop;
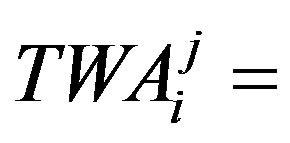 Total water availability for ith crop (all crops) for jth interval (all seasons);
Total water availability for ith crop (all crops) for jth interval (all seasons);
2.3.6. Non Negativity Constraint
 (17)
(17)
2.4. The Multiple Objective Linear Programming
The multiple objective linear programming problems can be formulated as:
 (18)
(18)
where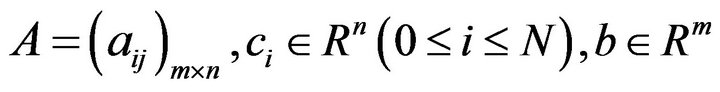 .
.
In problem (18) as stated above, all the objective functions can hardly reach their optima at the same time subject to the given constraints. Therefore in practice the decision-maker (DM) chooses some efficient solution as final decision according to the level of satisfaction 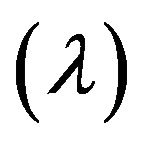 (or preference) of each objective value. The fuzzy approach for solving MOLP proposed by Zimmermann (1985) has given an effective way of measuring the level of satisfaction
(or preference) of each objective value. The fuzzy approach for solving MOLP proposed by Zimmermann (1985) has given an effective way of measuring the level of satisfaction  of MOLP.
of MOLP.
Let us consider the initial solution of objective vector given by the decision maker be represented as:
 (19)
(19)
To have the proper decision on the choice of initial solution, a decision maker (DM) can use the negative ideal solution as a reference point, namely, chooses the initial solution not less than negative ideal solution. In addition, the linear membership function of each objective function value’s satisfaction degrees can be defined as the following:
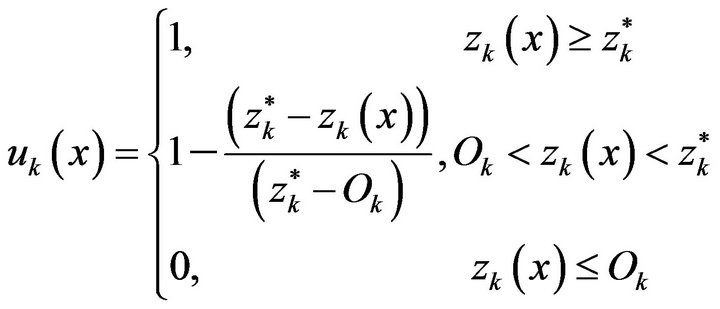 (20)
(20)
If the initial solution has chosen to be negative ideal solution, then linear membership function of each objective value’s satisfaction degrees has represented as below:
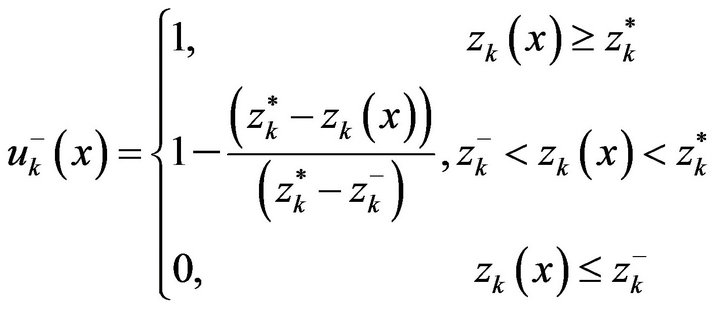 (21)
(21)
To solve the problem of irrigation planning, following the concept of membership function, Zimmermann’s proposed max-min operator approach may be represented as:
2.4.1. Zimmermann’s Max-Min Operator Approach
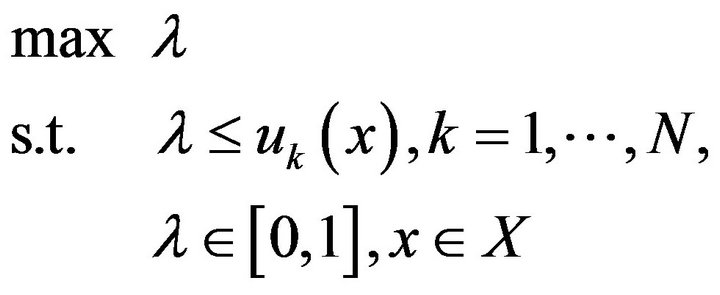 (22)
(22)
2.4.2. The Two-Phase Approach for MOLP
The optimal solution obtained by maxmin operator approach may not be efficient solution because the obtained level of satisfaction 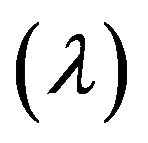 of compromised solution may not be same for all the objectives under consideration. This necessitate the solution obtained by maxmin approach needs to be improved. Moreover, the disadvantage of max-min operator (22) can be overcome for which the following modified form may be used.
of compromised solution may not be same for all the objectives under consideration. This necessitate the solution obtained by maxmin approach needs to be improved. Moreover, the disadvantage of max-min operator (22) can be overcome for which the following modified form may be used.
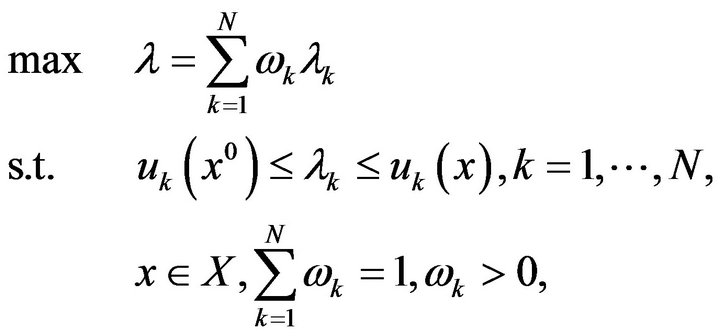 (23)
(23)
2.5. Two-Phase Multi Objective Fuzzy Linear Programming (TPMOFLP) Algorithm
In brief, the algorithm has represented in the following steps:
1) Solve the irrigation planning problem as a linear programming model, prioritizing only one objective at a time.
2) Find out the corresponding values of each objective from the solution obtained in step 1.
3) Find out maximum value of each objective as an ideal solution 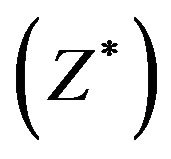 as well as minimum value of each objective function as a negative ideal solution
as well as minimum value of each objective function as a negative ideal solution 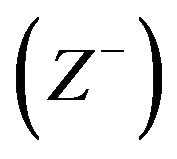 for each objective under consideration.
for each objective under consideration.
4) Construct the linear membership function with the values of  and
and 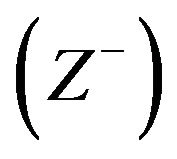 for each objective.
for each objective.
5) Introduce the dummy variable as level of satisfaction  and subsequently, maximize the level of satisfaction subjected to the additional constraints due to the fuzziness in the value of the objective functions and original constraints as a MOFLP model.
and subsequently, maximize the level of satisfaction subjected to the additional constraints due to the fuzziness in the value of the objective functions and original constraints as a MOFLP model.
6) Find out optimal solution with level of satisfaction  along with value of objectives
along with value of objectives 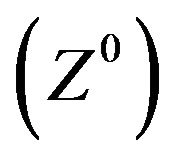 and decision variables as
and decision variables as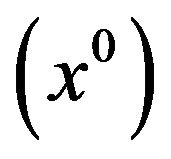 .
.
7) Find the membership function value of objective value’s level of satisfaction corresponding to (x0) as a 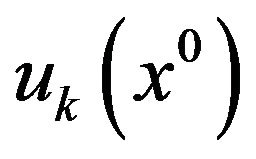 for each objective under consideration.
for each objective under consideration.
8) Compare the value of 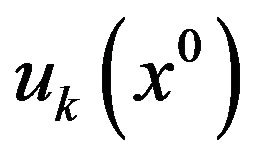 with
with 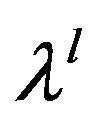 for each objective, if these values equal/are same then the feasible solution for the problem exits otherwise proceed to the next step.
for each objective, if these values equal/are same then the feasible solution for the problem exits otherwise proceed to the next step.
9) Set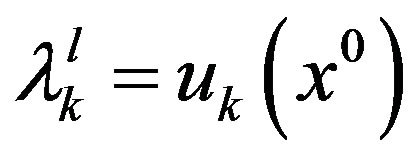 , and solve the TOMOFLP model Equation (23) to get an optimal solution
, and solve the TOMOFLP model Equation (23) to get an optimal solution 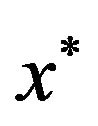 with level of satisfaction
with level of satisfaction .
.
3. Results and Discussion
The objective of the present study is to develop the sustainable irrigation planning model and analyze the same using two phase approach, considering the Equations (1) to (4) of the LP model, which are the maximization of the NB, CP, EG and MU for the command area of the Jayakwadi Project Stage-I. These objective functions are maximized separately subjected to constraints (Equations (5) to (17)) using the LINGO 13 (Language for INteractive General Optimization) software package. The results of this individual maximization of the four different objectives are used to construct the linear membership function for each objective with the help of the ideal solution and negative ideal solution. The corresponding linear membership functions are shown graphically in Figures 2-5. The same membership functions are written from the results shown in Table 2 in the form of mathematical Equation (24) to (27).

(24)
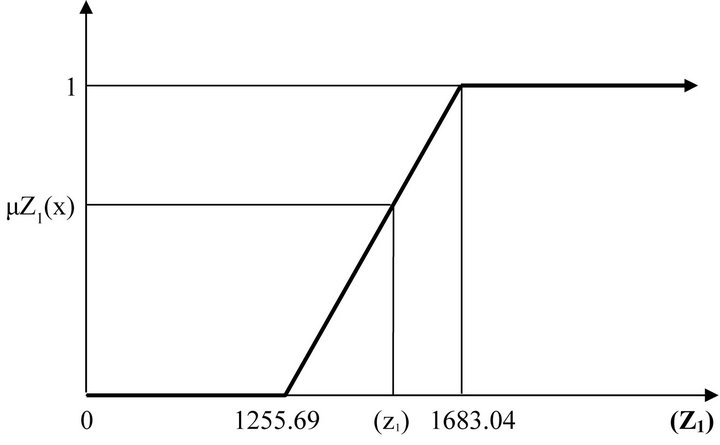
Figure 2. Membership function for Z1 (million rupees).

Figure 3. Membership function for Z2 (tons).
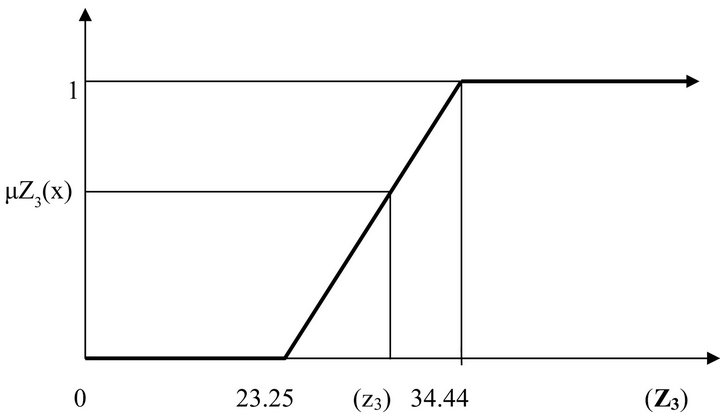
Figure 4. Membership function for Z3 (million man days).
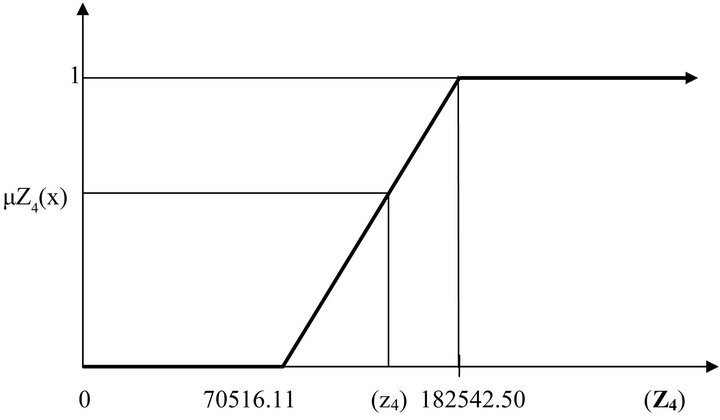
Figure 5. Membership function for Z4 (tons).

(25)
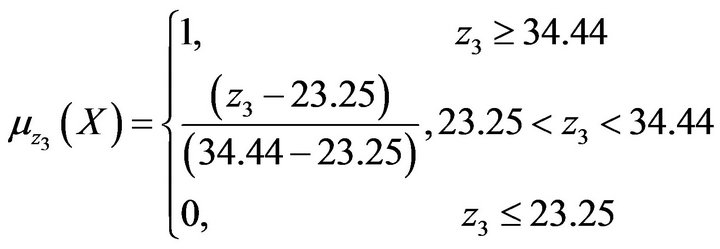
(26)

(27)
The membership functions  and
and  of the fuzzy sets characterizing the objective functions rise linearly from 0 to 1 at the highest achievable value of Z1 = 1683.04 Million Rs, Z2 = 473464.40 Tons, Z3 = 34.44 Million Man days and Z4 = 182542.50 Tons respectively. The level of satisfaction (λ) associated with NB rises from 0 if the NB is 1255.69 Million Rs or less to 1 if the total NB Z1 = 1683.04 Million Rs or more. The level of satisfaction with respect to CP rises from 0 if the CP is 106674.40 Tons or less to 1 if the CP Z2 = 473464.40 Tons or more and the level of satisfaction with EG rises from 0 for 23.25 Million Man days or less to 1 for EG Z3 = 34.44 Million Man days and more. Similarly The level of satisfaction associated with MU rises from 0 if the MU is 70516.11 Tons or less to 1 if the MU Z4 = 182542.50 Tons or more. The maximum level of satisfaction from the membership functions of four conflicting objectives has been designated as the “best” achieved/compromised solution and
of the fuzzy sets characterizing the objective functions rise linearly from 0 to 1 at the highest achievable value of Z1 = 1683.04 Million Rs, Z2 = 473464.40 Tons, Z3 = 34.44 Million Man days and Z4 = 182542.50 Tons respectively. The level of satisfaction (λ) associated with NB rises from 0 if the NB is 1255.69 Million Rs or less to 1 if the total NB Z1 = 1683.04 Million Rs or more. The level of satisfaction with respect to CP rises from 0 if the CP is 106674.40 Tons or less to 1 if the CP Z2 = 473464.40 Tons or more and the level of satisfaction with EG rises from 0 for 23.25 Million Man days or less to 1 for EG Z3 = 34.44 Million Man days and more. Similarly The level of satisfaction associated with MU rises from 0 if the MU is 70516.11 Tons or less to 1 if the MU Z4 = 182542.50 Tons or more. The maximum level of satisfaction from the membership functions of four conflicting objectives has been designated as the “best” achieved/compromised solution and ![]() the modified form of the optimization problem (MOFLP) by introducing the dummy variable i.e. level of satisfaction
the modified form of the optimization problem (MOFLP) by introducing the dummy variable i.e. level of satisfaction
 such that the objective is to:
such that the objective is to:
Maximize 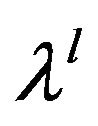
Subject to,

(28)
Table 2. Optimal solution for sustainable irrigation planning-LP/MOFLP model with max-min operator and two phase approach.
and all other original constraint given (Equation (5) to (17)) in the model; λ ≥ 0.
The compromised solution of MOFLP with level of satisfaction 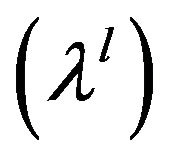 along with value of objectives (Z0) and decision variables as (x0) has represented in Table 2. After finding membership function value of objective value’s level of satisfaction corresponding to (x0) as
along with value of objectives (Z0) and decision variables as (x0) has represented in Table 2. After finding membership function value of objective value’s level of satisfaction corresponding to (x0) as  for each objective under consideration, it is seen that the value of uk(x0) i.e. (0.58, 0.58, 0.58 and 0.75) is equal to
for each objective under consideration, it is seen that the value of uk(x0) i.e. (0.58, 0.58, 0.58 and 0.75) is equal to  i.e. (0.58) for first three objective but for fourth objective uk(x0) i.e. 0.75 is not equal to
i.e. (0.58) for first three objective but for fourth objective uk(x0) i.e. 0.75 is not equal to 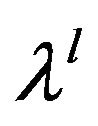 i.e. 0.58, which emphasizes that the obtained solution can be further improved. By following the concept of two phase approach, set
i.e. 0.58, which emphasizes that the obtained solution can be further improved. By following the concept of two phase approach, set  for each objective, and solve the modified form of model as TPMOFLP model Equation (23) to get an optimal solution
for each objective, and solve the modified form of model as TPMOFLP model Equation (23) to get an optimal solution 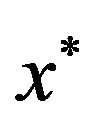 with level of satisfaction
with level of satisfaction  and substitute the value of
and substitute the value of 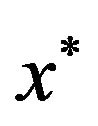 in the objective function in model. The optimal solution of TPMOFLP model with level of satisfaction
in the objective function in model. The optimal solution of TPMOFLP model with level of satisfaction 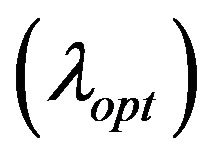 along with value of objectives (Z1) and decision variables as (x*) represented in Table 2. In addition, the results MOFLP model, and TPMOFLP model have been shown graphically in Figure 6.
along with value of objectives (Z1) and decision variables as (x*) represented in Table 2. In addition, the results MOFLP model, and TPMOFLP model have been shown graphically in Figure 6.
4. Conclusion
The objective of the study is to develop MOFLP model and apply the two-phase approach to find out optimal cropping pattern that maximizes NB, CP, EG and MU simultaneously. For this, maxmin approach based MOFLP model has been developed and applied to Jayakwadi Project Stage I, Maharashtra State, India. In addition, the twophase approach has been applied to the MOFLP model to improve the efficiency of the solution obtained. It has found that the level of satisfaction (λ) using two-phase approach for four conflicting objectives under fuzzy environment, which has improved from λ = 0.58 to 0.65. The TPMOFLP model solution provides NB = 1503.56 (-0.17) Million Rupees, CP = 335729.30 (+16165.80) Tons, EG = 29.74 Million Man days and MU = 160233.70
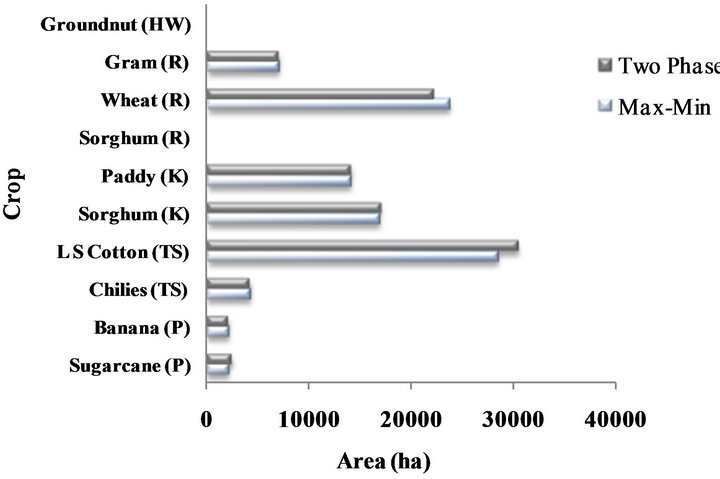
Figure 6. Optimal cropping pattern plan.
(+5727.20) Tons respectively to that of solution obtained by MOFLP model with maxmin approach. In addition, the irrigation intensity has also improved from 70.02% to 70.35%. The present model will be helpful for the decision maker (DM) to take decision under conflicting situation while planning for different conflicting objectives simultaneously. This model has potential to find out an integrated irrigation planning with prime consideration for economic, social and environmental issue. The study proposes a basis for sustainable irrigation planning associated with uncertainty/vagueness in irrigation parameters.
5. Acknowledgements
The authors would like to express their sincere thanks to Command Area Development Authority, Aurangabad, Maharashtra State, India and Mahatma Phule Krishi Vidyapeeth Rahuri, Ahmednagar, Maharashtra State, India for providing necessary data for analysis.
REFERENCES
- L. A. Zadeh, “Fuzzy Sets,” Information and Control, Vol. 8, No. 3, 1965, pp. 338-353. doi:10.1016/S0019-9958(65)90241-X
- R. E. Bellman and L. A. Zadeh, “Decision Making in a Fuzzy Environment,” Management Sciences, Vol. 17, No. 4, 1970, pp. 141-164. doi:10.1287/mnsc.17.4.B141
- R. E. Bellman and L. A. Zadeh, “Local and Fuzzy Logics,” Modern Uses of Multiple Valued Logic, 1977, pp. 283- 335.
- L. A. Zadeh, “The Concept of Linguistic Variable and Its Applications to Approximate Reasoning-I,” Information Sciences, Vol. 8, No. 3, 1975, pp. 199-249. doi:10.1016/0020-0255(75)90036-5
- L. A. Zadeh, “The Concept of Linguistic Variable and Its Applications to Approximate Reasoning-II,” Information Sciences, Vol. 8, No. 4, 1975, pp. 301-357. doi:10.1016/0020-0255(75)90046-8
- L. A. Zadeh, “The Concept of Linguistic Variable and Its Applications to Approximate Reasoning-III,” Information Sciences, Vol. 9, No. 1, 1975, pp. 43-80. doi:10.1016/0020-0255(75)90017-1
- L. A. Zadeh, “A Fuzzy-Algorithmic Approach to the Definition of Complex or Imprecise Concepts,” International Journal of Man-Machine Studies, Vol. 8, No. 3, 1976, pp. 249-291. doi:10.1016/S0020-7373(76)80001-6
- L. A. Zadeh, “Fuzzy Sets and Information Granularity,” North Holland Publishing Company, Amsterdam, 1979, pp. 3-18.
- L. A. Zadeh, “A Fuzzy-Set-Theoretic Approach to the Compositionality of Meaning: Propositions, Dispositions and Canonical Forms,” Journal of Semantics, Vol. II, No. 3/4, 1983, pp. 253-272. doi:10.1093/semant/2.3-4.253
- L. A. Zadeh, “Coping with the Imprecision of the Real World,” Communications of the ACM, Vol. 27, No. 4, 1984, pp. 304-311. doi:10.1145/358027.358032
- L. A. Zadeh, “Maximizing Sets and Fuzzy Markoff Algorithms,” IEEE Transactions on Systems, Man and Cybernetics-Part C: Applications and Reviews, Vol. 28, No. 1, 1998, pp. 9-15. doi:10.1109/5326.661086
- L. A. Zadeh, “From Computing with Numbers to Computing with Words-From Manipulation of Measurements to Manipulation of Perceptions,” IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, Vol. 45, No. 1, 1999, pp. 105-119. doi:10.1109/81.739259
- L. A. Zadeh, “From Imprecise to Granular Probabilities,” Fuzzy Sets and Systems, Vol. 154, No. 3, 2005, pp. 370- 374. doi:10.1016/j.fss.2005.02.007
- L. A. Zadeh, “Generalized Theory of Uncertainty (GTU) —Principal Concepts and Ideas,” Computational Statistics and Data Analysis, Vol. 51, No. 1, 2006, pp. 15-46. doi:10.1016/j.csda.2006.04.029
- L. A. Zadeh, “Is There a Need for Fuzzy Logic?” Information Sciences, Vol. 178, No. 13, 2008, pp. 2751-2779. doi:10.1016/j.ins.2008.02.012
- H. J. Zimmermann, “Fuzzy Programming and Linear Programming with Several Objective Functions,” Fuzzy Sets and Systems, Vol. 1, No. 1, 1978, pp. 45-55. doi:10.1016/0165-0114(78)90031-3
- H. J. Zimmermann, “Fuzzy Set Theory and Its Applications,” Kluwer Academic Publishers, Hingham, 1985. doi:10.1007/978-94-015-7153-1
- B. Werners, “An Interactive Fuzzy Linear Programming System,” Fuzzy Sets and Systems, Vol. 23, No. 1, 1987, pp. 131-147. doi:10.1016/0165-0114(87)90105-9
- E. S. Lee and R. J. Li, “Fuzzy Multiple Objective Programming and Compromise Programming with Pareto Optimum,” Fuzzy Sets and Systems, Vol. 53, No. 3, 1993, pp. 275-288. doi:10.1016/0165-0114(93)90399-3
- S. M. Guu and Y. K. Wu, “Weighted Coefficients in TwoPhase Approach for Solving the Multiple Objective Programming Problems,” Fuzzy Sets and Systems, Vol. 85, No. 1, 1997, pp. 45-48.
- Y. K. Wu and S. M. Guu, “A Compromise Model for Solving Fuzzy Multiple Objective Linear Programming Problems,” The Chinese Institute of Industrial Engineers, Vol. 18, No. 5, 2001, pp. 87-93. doi:10.1016/0165-0114(95)00360-6
- X. Q. Li, B. Zang and H. Li, “Computing Efficient Solutions to Fuzzy Multiple Objective Linear Programming Problems,” Fuzzy Sets and Systems, Vol. 157, No. 10, 2006, pp. 1328-1332. doi:10.1016/j.fss.2005.12.003
- K. S. Raju and D. Nagesh Kumar, “Irrigation Planning of Sri Ram Sagar Project using Multi Objective Fuzzy Linear Programming,” ISH Journal of Hydraulic Engineering, Vol. 6, No. 1, 2000, pp. 55-63. doi:10.1080/09715010.2000.10514665
- K. S. Raju and L. Duckstein, “Multiobjective Fuzzy Linear Programming for Sustainable Irrigation Planning: An Indian Case Study,” Soft Computing, Vol. 7, No. 6, 2003, pp. 412-418. doi:10.1007/s00500-002-0230-6
- D. G. Regulwar and P. Anand Raj, “Development of 3-D Optimal Surface for Operation Policies of a Multireservoir in Fuzzy Environment Using Genetic Algorithm for River Basin Development and Management,” Water Resour Management, Vol. 22, No. 5, 2008, pp. 595-610. doi:10.1007/s11269-007-9180-1
- D. G. Regulwar and P. Anand Raj, “Multi Objective Multireservoir Optimization in Fuzzy Environment for River Sub Basin Development and Management,” Journal of Water Resource Protection, Vol. 4, No. 4, 2009, pp. 271- 280. doi:10.4236/jwarp.2009.14033
- D. G. Regulwar and J. B. Gurav, “Fuzzy Approach Based Management Model for Irrigation Planning,” Journal of Water Resource and Protection, Vol. 2, No. 6, 2010, pp. 545-554. doi:10.4236/jwarp.2010.26062
- D. G. Regulwar and J. B. Gurav, “Irrigation Planning under Uncertainty—A Multi Objective Fuzzy Linear Programming Approach,” Water Resource and Protection, Vol. 25, No. 5, 2011, pp. 1387-1416. doi:10.1007/s11269-010-9750-5
- J. B. Gurav and D. G. Regulwar, “Minimization of Cost of Cultivation along with Interactive Decision Making under Fuzzy Environment,” ISH Journal of Hydraulic Engineering, Vol. 17, No. 2, 2011, pp. 30-42. doi:10.1080/09715010.2011.10515043
- D. G. Regulwar and J. B. Gurav, “Sustainable Irrigation Planning with Imprecise Parameters under Fuzzy Environment,” Water Resource Management, Vol. 26, No. 13, 2012, pp. 3871-3892. doi:10.1007/s11269-012-0109-y
- J. B. Gurav and D. G. Regulwar, “Multi Objective Sustainable Irrigation Planning with Decision Parameters and Decision Variables Fuzzy in Nature,” Water Resource Management, Vol. 26, No. 10, 2012, pp. 3005-3021. doi:10.1007/s11269-012-0062-9
- D. G. Regulwar and J. B. Gurav, “Irrigation Planning with Fuzzy Parameters-an Interactive Approach,” Journal of Agricultural Science Technology, Vol. 15, No. 5, 2013 (Accepted for publication).
- A. B. Mirajkar and P. L. Patel, “Optimal Irrigation Planning Using Multi-Objective Fuzzy Linear Programming Models,” ISH Journal of Hydraulic Engineering, Vol. 18, No. 3, 2012, pp. 232-240. doi:10.1080/09715010.2012.721661
- D. G. Regulwar and J. B. Gurav, “Fuzzy Optimization for Irrigation Planning with Minimization of Cost of Cultivation,” Proceedings of 8th International Conference of EWRA, Porto-Portugal, 26-29 June 2013 (Accepted for publication).
- D. G. Regulwar and J. B. Gurav, “Optimal Irrigation Planning with Minimization of Cost of Cultivation using Fuzzy Logic,” Proceedings of 35th IAHR World Congress, Chengdu, 8-13 September 2013 (Accepted for publication).
- The Report of Commissionerate of Agriculture Maharashtra State, “Agricultural Statistical Information Maharashtra State India, Part-II,” 2006.

