iBusiness
Vol.4 No.1(2012), Article ID:18372,6 pages DOI:10.4236/ib.2012.41009
Study on Stock Index Futures’ Mean Reversion Effect and Arbitrage in China Based on High-Frequency Data
![]()
1School of Management, Graduate University of Chinese Academy of Sciences, Beijing, China; 2School of Economics and Management, Beijing University of Posts and Telecmmunication, Beijing, China; 3Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, China.
Email: xjzhao@iss.ac.cn
Received January 5th, 2012; revised February 19th, 2012; accepted February 29th, 2012
Keywords: CSI 300 Index Future; High-Frequency Data; Futures-Spot Arbitrage; Mean Reversion Effect; Mispricing Ratio
ABSTRACT
Based on 1 minute high frequency data, this paper constructs no-arbitrage band for CSI300 index futures, and empirically studies the futures-spot arbitrage. Furthermore, the mean reversion and its time effect are analyzed by ADF model for the first time in Chinese index futures market and a logit model is used to investigate the related factors of arbitrage opportunities. We find that CSI300 index futures have cash-and-carry arbitrage opportunities; the existence of mean reversion effect of index futures when arbitrage is absent; cash-and-carry arbitrage has a significant impact for mean reversion of the mispricing, while the reverse has insignificant effect. As for the time effect of mean reversion, it indicates that the time which arbitrage effect reversion most is mispricing shows 14 minutes later. The probability of arbitrage opportunities is positive correlated to first-order lagged of volume, and negative correlated to the volume; the time to expiration, the highest price and lowest price differences are also positive related to arbitrage opportunities.
1. Introduction
Since Chinese first index futures launched on China Financial Futures Exchange (CFFE), the trading volume jumped to the biggest among all futures. Besides price discovery and hedging, the function of index futures includes arbitrage, which makes a stable relationship between spot and futures market. Generally, arbitrage on index futures can divide into three types: futures-spot arbitrage, inter-delivery arbitrage, and cross-market arbitrage. Future-spot arbitrage opportunity arises when index futures deviates its theoretical value which is calculated by cost of carry theory. Because of transaction cost, index futures normally would stay in a band which arbitrage trade cannot make profit and we called “no-arbitrage band”. When futures’ price stays out of the band, index futures are mispricing. Then, arbitrageur will obtain profit by cash-and-carry arbitrage, which means they short index futures and long spot when futures price is above the upper limit of noarbitrage band, and wind the position of both on expiration day. If index futures exceeds lower limit, they could do the opposite actions of above which named reverse cash-and-carry-arbitrage.
The research about index futures’ arbitrage has been popular. Cornell [1] proposed the cost of carry theoryand compared actual and model price of NYSE composite index futures and S & P500 index futures, which is the milestone for arbitrage research. Figlewski [2] analyzed several S & P500 index futures contracts statistically, and found there were many arbitrage opportunities indeed. Besides, Harris [3], Brennan [4], Chung [5], and Richie [6] made some similar conclusions. Fremault [7] discovered three effects of arbitrage trading for hedgers, speculators and arbitrageurs in futures and spot market. Sutcliffe [8] claimed that it is important to separate arbitrage opportunities from mispricing. McMillan [9] investigated mispricing of ISE30 index futures in Turkey, and found there was only cash-and-carry arbitrage opportunities when spot cannot be shorten.
Since profits cannot be obtained unless index futures return to no-arbitrage band, then the research has been involved into mean reversion effect of index futures. MacKinlay and Ramaswamy [10] discovered mean reversion effect existed in S & P500 index futures. Additionally, Lim [11] and Yadav [12] found Nikkei225 and FTSE-100 had this effect. Neal [13] employed logit regression model using one minute data to analyze arbitrage trades on the NYSE for first contract in 1989, who found that there mispricing reversal is significant positive related to absolute mispricing amount.
Then, some researches focused on explanation of mean reversion effect of index futures. Traditionally, reversion effect is viewed as a consequence of arbitrage in market. Garbade and Silber [14] used vector autoregression and found continuum of traders induces continuity in mean reversion. Chan [15], Kawaller [16], Stoll [17] have estimated similar model and obtain the same conclusion. Kawaller [18] and Tse [19] considered the effect was resulted from different arbitrageurs, and the reversion is a smooth auto-regression process. Yadav and Pope [20] suggested transaction was the trigger of reversion. Kempf [21] made the same conclusion by discussing the influence of short restriction and clear the position before expiration day. Fung [22] observed S & P500 index futures had price reversal phenomenon which due to the investors’ overreaction for information. Kumar [23], Holden [24-25] had some similar conclusion with arbitrage trade reason.
However, the liquidity theory challenges the traditional explanation, which argues the illiquidity in stock market cause the reversion of futures. One of the earliest illiquidity explanations was Kraus and Stoll [26], who found that large trade would bring about reversal price, which is consistent with Biais [27]. Alphonse [29] accounted the mean reversion of CAC40 index futures in France from spot’s illiquidity.
Therefore, some researches have been done around the mean reversion effect of index futures and its reasons. However, the timing effect of it was less involved. Dwyer [30] regressed S & P500 index futures by Threshold Error Correction Model (TECM) and did impulse response, who found the futures’ price need 5 - 7 minutes to go back to no-arbitrage band. The problem is the conclusion is sensitive to threshold’s value, and impulse response does not cover the test from tail to middle area.
Based on high frequency data, this paper empirically researches the mean reversion and its time effect by ADF model for the first time in Chinese index futures. Meanwhile, we explored some factors by a logit model which may influence arbitrage opportunities.
2. Methodology and Data
The arbitrage chances would appear if only the index futures exceeds no-arbitrage band. Taking transaction into account, we calculated no-arbitrage band of CSI300 index futures as following.
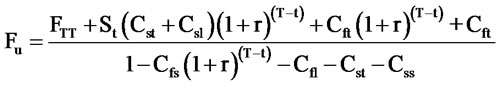
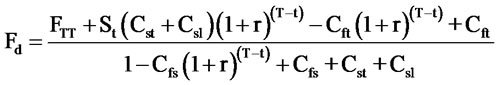
where Fu and Fd is upper and lower limit, respectively. FTT is theoretical price for index futures at T time. Ft and St is futures and spot price at t time. Cst and Cft is the spot commission and futures transactions. Csl and Css is impact price for longing and shorting spot, while Cfl and Cfs is impact price for long and shorting futures, respectively, and r is riskless interest rate.
Once the price exceeds no-arbitrage band, index futures is mispricing and we named mispricing ratio (MR) to value as following.
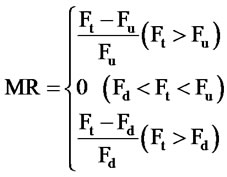
Referring Mackinlay’s [10] research which first and higher orders of autocorrelation coefficient show the persistence of mispricing, we estimated ADF functions as following.
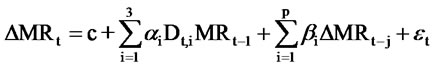 (1)
(1)
where,  is the first order difference of mispricing ratio. As for Dt,i, if there is no mispricing and arbitrage opportunity at t time, Dt,1 = 1. If there are positive mispricing ratio, we can short index futures, Dt,2 = 1; otherwise, negative mispricing ratio makes Dt,3 = 1. In addition, p lagged mispricing changes also included in the regression equation to correct for autocorrelation in mispricing changes.
is the first order difference of mispricing ratio. As for Dt,i, if there is no mispricing and arbitrage opportunity at t time, Dt,1 = 1. If there are positive mispricing ratio, we can short index futures, Dt,2 = 1; otherwise, negative mispricing ratio makes Dt,3 = 1. In addition, p lagged mispricing changes also included in the regression equation to correct for autocorrelation in mispricing changes.
In order to investigate the higher order difference, we also estimated functions as following.
 (2)
(2)
Finally, we estimated a logit model to test for some significance variables that may influence arbitrage opportunity including the expiration days, trading volumes, positions and spread between highest and lowest price in one minute of index futures.
Based on 1 minute high frequency data, this paper studies the arbitrage and mean reversion effect for CSI300 index futures. Since there are four contacts on the same time, we construct the continuous contract with the most active. The CSI300 index futures market open at 9:15, and close at 15:15, which is earlier and later 15 minutes than its underlying index, respectively. Therefore, the data we collected in 9:30 to 11:30 and 13:00 to 15:00 for the period from 23rd August 2010 to 18th February 2011.
As for transaction part, the commission for spot Cst is 0.3% from ETF. The trading fee for index futures is RMB30 for each deal, and price multiplier for each point of RMB 300, so the transaction cost for index futures Cft is 30/(30 × Ft). Since the trading volume is huge for spot and the continuous contract of index futures, we consider that the impact cost for them is zero, which means Css, Csl, Cfs, Cfl are all zero.
3. Empirical Analysis
3.1. No-Arbitrage Band and Mispricing Ratio
Based on these data, we calculated the no-arbitrage band and mispricing ratio of CSI300 index futures, which is drawn in Figure 1.
From Figure 1, we can see that most of time index futures stays out of upper limit of no-arbitrage band when mispricing exist. The detail of arbitrage opportunity and the time mispricing persist are shown in Table 1. There are 36.2% of the time that index futures exceeds upper limit, while only 0.2% for lower limit, which suggest there are much more cash-and-carry-arbitrage for CSI300 index futures than the reverse one. This is consistent with McMillan [7], who found there are only cash-and-carryarbitrage chances for ISE40 index futures, and the reason is margin trading and short selling just start in China, which cannot short spot. Thus, the deficiency for investment channel and limitation for trading mechanism lead to the asymmetrical arbitrage direction. Moreover, the persistent time for positive mispricing is 12.6 minutes on average, which illustrate that index futures need 12.6 minutes to return to no-arbitrage band.

Figure 1. No-arbitrage band and mispricing ratio of CSI300 index futures.

Table 1. Arbitrage opportunities and mispricing ratio.
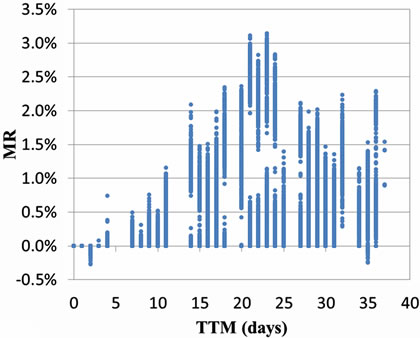
Figure 2 depicts the relationship between mispricing and the time to expiration. From Figure 2(a), the biggest mispricing is happened on 23 days before maturity, which suggest if investors start to arbitrage at this time, they will gain profit mostly. Besides, it shows that the closer to expiration day, the less the mispricing and it appears. Figure 2(b) shows the average mispricing ratio for different days to expiration. In general, the closer to expiration day, the less mispricing ratio, which state that CSI300 index futures convergent to its underlying as closing to maturity. While when days to expiration is more than 24 days, there are huge mispricing ratio occasionally, but it is not significant on statistical.
3.2. The Result of ADF Model
Figure 3 is the coefficient of first order difference of mispricing, which examines its persistence. As the Figure 3 shown, the coefficient reaches the biggest when its 4th lagged is used, and the value is decreasing, becoming insignificant when up to 14th lag. It explains that mispricing would disappear after shown in a while, and it has mean reversion effect, which is consistent with Alphonse [29]. Therefore, once mispricing is discovered, arbitrageurs could short futures and long spot, and wind position when
 (a)
(a) (b)
(b)
Figure 2. (a) Relationship between mispricing and TTE; (b) Average mispricing ratio and the number of TTE.

Figure 3. The coefficient of first order difference of mispricing.
the futures return to no-arbitrage band, instead clear positions on expiration day.
The result of model 1 is shown in Table 2. The coefficient of D2 is negative significantly while D3 is insignificant, which suggest two points. First, cash-and-carryarbitrage influences mean reversion effect strikingly. In a short time, if arbitrageurs found arbitrage opportunity, they would make the deal immediately, which drives futures going back to no-arbitrage band. Second, the coefficient of D1 is negative significantly indicates mean reversion exists even arbitrage is absent. Some hypotheses [31,32] demonstrate that the lead-lag relationship between futures and spot, which the response for information of spot is behind futures, can explain for non-arbitrage mean reversion effect. When some information shock financial market, index futures react fast, and mispricing would show up. Investors will take action to adjust their orders when they found the arbitrage, such as canceling the earlier order and submitting a new one, which will impel index futures get back to no-arbitrage band and mispricing disappear.
Higher orders autocorrelation coefficient of mispricing changes is estimated in model 2 to discuss the time that reversion of CSI300 index futures is biggest, including 2nd to 20th, 25th, 30th, 35th, 35th, 40th, 45th, 50th, 55th, and 60th order lag. The relationship between coefficient of D2 and the orders is shown on Figure 4" target="_self"> Figure 4. The coefficient of D2 in all orders are negative suggest cash-andcarry-arbitrage influences reversion effect invariably. The absolute value of 14th order difference is up to 0.0153, and of these orders more than 14th is maintaining around 0.015 to 0.016. It indicates arbitrage influence mean revision most is happening 14 minutes after mispricing emerge. The retardance may be caused by the whole process which need about 14 minutes from mispricing is found to finish the deal, such as orders distribution and approval.
3.3. Variables Effect Arbitrage
In order to analyze other factors that impact arbitrage opportunities, we regress arbitrage opportunities (AO) on a series of independent variables using logit model. Independent variables include time to expiration (TTE), trad
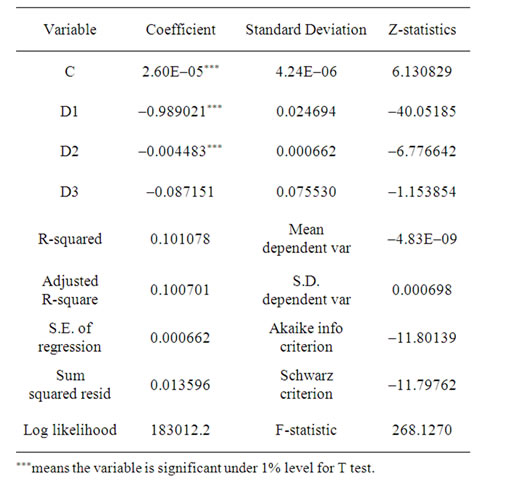
Table 2. The result of model 2.

Figure 4. Coefficient of D2 for different orders autocorrelation of mispricing changes.
ing volume of stock index futures(VOLUME) and its firstorder lag (VOLUME (–1)), position of stock index futures (because first-order difference of position is steady, we use D (POSITION) as independent variable); highest and lowest price spread within one minute (BASIS). First, we test the causal relationship between the above variables and the arbitrage opportunities through second-order lag Granger causality test, as shown in Table 3. Besides the first-order difference of position, the remaining variables are all the Granger causes of arbitrage opportunities.
The results of logit model are shown in Table 4. All independent variables are significant. The coefficient of VOLUME (–1) is positive, while the coefficient of VOLUME is negative, indicating that the larger volume in the previous period, the higher probability of arbitrage opportunities while the larger current volume, the less probability of arbitrage opportunities. When investors find a mispricing in the first period, they will complete the deals
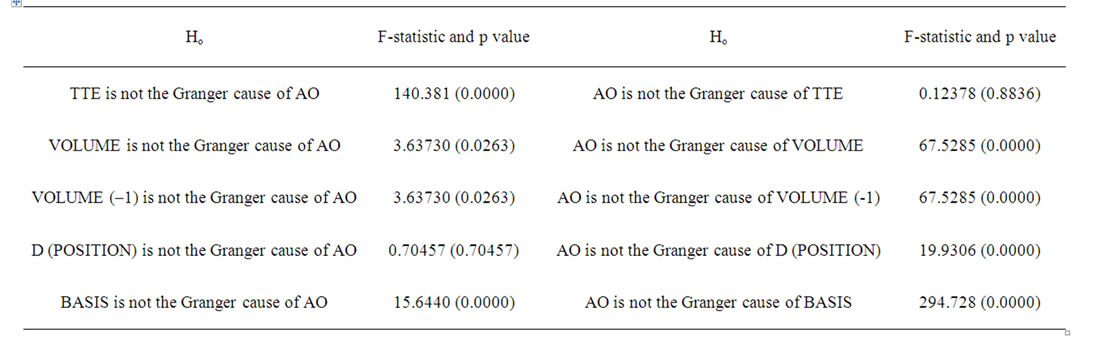
Table 3. The result of Grange causality test.

Table 4. Result of logit model.
rapidly, therefore the futures price return to the arbitragefree interval driven by the larger volume in the subsequent period, then the mispricing disappears, which is consistent with the findings of Merrick. The coefficient of TTE is positive, which means the closer to expiration, the more convergence to the theoretical value of stock index, lead to fewer arbitrage opportunities. The coefficient of BASIS, which to some extent reflects stock index futures volatility, is positive. The greater the spread, the more differences among investor’s limit orders, the higher the chance of mispricing occurred at this time, that is, the more arbitrage opportunities.
4. Conclusions
Based on high frequency data of CSI300 index futures, this paper construct no-arbitrage band of continuous contract by cost of carry theory, and empirically research future-spot arbitrage. Then, we investigate mean reversion effect of CSI300 index futures’ mispricing and the effect’s time for the first time by ADF model. Furthermore, a logit model is estimated to test for some variables that may influence arbitrage opportunity. The results are following.
First, CSI300 index futures had cash-and-carry arbitrage opportunities for the most part from 23rd August 2010 to 18th February 2011. Once it exceeds upper limit of noarbitrage band, it would cost 12.6 minutes to return to the band.
Second, cash-and-carry arbitrage influence mispricing’s mean reversion significantly, while the reverse arbitrage is insignificant. Due to deficiency of investment channels and limitation of trading mechanism, the arbitrage direction effects mean reversion of index futures asymmetrically.
Third, in absence of arbitrage, mean reversion exists still. This is because when financial market is shocked some information, index futures react fast, and mispricing would show up. Investors will adjust their orders for stock which drive index futures return to no-arbitrage band.
Fourth, arbitrage influence mean revision most is happening 14 minutes after mispricing appears. At this moment, if arbitrage orders deal and wind the position when index futures return to no-arbitrage, the profit will be obtained. This may result from the retardance from mispricing is found to finish the deal.
Finally, arbitrage opportunities are positive correlated to the first order lag of trading volume, while negative correlated to volume, which results from that large trading volume drives index futures return no-arbitrage band. Additionally, arbitrage opportunities are positive related to time to expiration, spread between highest and lowest price within one minute. This is because the closer to expiration, the more convergence to the theoretical value of stock index, lead to fewer arbitrage opportunities. The greater the spread, the more differences among investor’s limit orders, the higher the possibility of mispricing occurred at this time, which means the more arbitrage opportunities.
5. Acknowledgements
This research is supported by the National Natural Science Foundation of China (No. 70801006, No. 71173023) and the Fundamental Research Funds for the Central Universities.
REFERENCES
- B. Cornell and K. R. French, “The pricing of Stock Index Futures,” Journal of Futures Markets, Vol. 3, No. 1, 1983, pp. 1-14. doi:10.1002/fut.3990030102
- S. Figlewski, “Hedging performance and basis risk in Stock Index Futures,” Journal of Finance, Vol. 39, No. 3, 1984, pp. 657-669. doi:10.2307/2327924
- L. Harris, “The October 1987 S&P 500 stock-Futures Basis,” Journal of Finance, Vol. 44, No. 1, 1989, pp. 77-99. doi:10.2307/2328276
- M. J. Brennan and E. S. Schwartz, “Arbitrage in stock Index Futures,” Journal of Business, Vol. 63, No. 1, 1990, pp. 7-31. doi:10.1086/296491
- Y. P. Chung, “A Transactions Data Test of Stock Index Futures Market Efficiency and Index Arbitrage Profitability,” Journal of Finance, Vol. 46, No. 5, 1991, pp. 1791- 1809. doi:10.2307/2328573
- N. Richie, R. Daigler and K. C. Gleason, “The limit to Stock Index Arbitrage: Examing S&P 500 futures and SPDRS,” Journal of Futures Markets, Vol. 28, No. 12, 2008, pp. 1182-1205. doi:10.1002/fut.20365
- A. Fremault, “Stock Index Futures and Index Arbitrage in a Rational Expectations Model,” Journal of Business, Vol. 64, No. 4, 1991, pp. 523-525.
- C. Sutcliffe, “Stock Index Futures,” 3rd edition, Ashgate Publishing Company, Surrey, 2006.
- D. G. McMillan and N. Ülkü, “Persistent mispricing in a Recently Opened Emerging Index Futures Market: Arbitrageurs Invited,” Journal of Futures Markets, Vol. 29, No. 3, 2009, pp. 218-243. doi:10.1002/fut.20355
- A. C. MacKinlay and K. Ramaswamy, “Index-futures Arbitrage and the behavior of Stock Index Futures Prices,” Review of Financial Studies, Vol. 1, No. 2, 1988, pp. 137- 158. doi:10.1093/rfs/1.2.137
- K. G. Lim, “Arbitrage and Price Behavior of the Nikkei Stock Index Futures,” Journal of Futures Markets, Vol. 12, No. 2, 1992, pp. 151-161. doi:10.1002/fut.3990120204
- P. K. Yadav and P. F. Pope, “Stock Index Futures Mispricing: Profit Opportunities or Risk Premia,” Journal of Banking & Finance, Vol. 18, No. 5, 1994, pp. 921-953. doi:10.1016/0378-4266(94)00026-3
- R. Neal, “Direct tests of Index Arbitrage Models,” Journal of Financial and Quantitative Analysis, Vol. 31, No. 4, 1996, pp. 541-562.
- K. D. Garbade and W. L. Silber, “Price movements and Price Discovery in futures and Cash Markets,” Review of Economics and Statistics, Vol. 65, No. 21983, pp. 289-297.
- K. A. Chan, “further analysis of the Lead Lag Relationship between the Cash Market and Index Futures Market,” Review of Financial Studies, Vol. 5, No. 1, 1992, pp. 123-151. doi:10.1093/rfs/5.1.123
- I. G. Kawaller, P. D. Koch and T. W. Koch, “The temporal Price Relationship between the S&P 500 futures and the S&P 500 index,” Journal of Finance, Vol. 42, No. 5, 1987, pp. 1309-1329.
- H. R. Stoll and R. E. Whaley, “The dynamics of Stock Index and Stock Index Futures Returns,” Journal of Financial and Quantitative Analysis, Vol. 25, No. 4, 1990, pp. 441-468. doi:10.2307/2331010
- I. G. Kawaller, “Determining the Relevant Fair Value(S) of S&P 500 Futures: A Case Study Approach,” Journal of Futures Markets, Vol. 11, No. 4, 1991, pp. 453-460. doi:10.1002/fut.3990110405
- Y. Tse, “Index Arbitrage with Heterogeneous Investors: A Smooth Transition Error Correction Analysis,” Journal of Banking & Finance, Vol. 25, No. 10, 2001, pp. 1829- 1855. doi:10.1016/S0378-4266(00)00162-X
- P. K. Yadav and P F. Pope, “Stock Index Futures Arbitrage: International Evidence,” Journal of Futures Markets, Vol. 10, No. 6, 1990, pp. 573-603. doi:10.1002/fut.3990100603
- A. Kempf, “Short Selling, Unwinding, and Mispricing,” Journal of Futures Markets, Vol. 18, No. 8, 1998, pp. 903- 923. doi:10.1002/(SICI)1096-9934(199812)18:8<903::AID-FUT2>3.0.CO;2-V
- A. K. Fung, D. M. Mok and K. Lam, “Intraday Price Reversals for Index Futures in the US and Hong Kong,” Journal of Banking & Finance, Vol. 24, No. 7, 2000, pp. 1179-1201. doi:10.1016/S0378-4266(99)00072-2
- P. Kumar and D. Seppi, “Information and Index Arbitrage,” Journal of Business, Vol. 67, No. 4, 1994, pp. 481-509.
- C. W. Holden, “Index arbitrage as Cross-Sectional Market Making,” Journal of Futures Markets, Vol. 15, No. 4, 1995, pp. 423-455.
- C. W. Holden, “Intertemporal arbitrage Trading: Theory and Empirical Tests,” Working Paper, Indiana University, Bloomington, 1990.
- A. Kraus and H. R. Stoll, “Price impacts of Block Trading on the New York Stock Exchange,” Journal of Finance, Vol. 27, No. 3, 1972, pp. 569-588.
- B. Biais, P. Hillion and C. Spatt, “An empirical Analysis of the Limit Order Book in the Paris Bourse,” Journal of Finance, Vol. 50, No. 5, 1985, pp. 1655-1689.
- M. H. Miller, J. Muthuswamy and R. E. Whaley, “Mean reversion of Standard & Poor’s 500 Index Basis Changes: Arbitrage-Induced or Statistical Illusion?” Journal of Finance, Vol. 49, No. 2, 1994, pp. 479-513. doi:10.2307/2329160
- P. Alphonse, “Mispricing persistence and the effectiveness of Arbitrage Trading,” Multinational Finance Journal, Vol. 11, No. 1-2, 2007, pp. 123-56.
- G. P. Dwyer, P. Locke and W. Yu, “Index arbitrage and Nonlinear Dynamics between the S&P 500 futures and cash,” Review of Financial Studies, Vol. 9, No. 1, 1996, pp. 301-312. doi:10.1093/rfs/9.1.301
- Y. W. Cheung and H. G. Fung, “Information flows between Eurodollar spot and Futures Markets,” Multinational Finance Journal, Vol. 1, No. 4, 1997, pp. 255-271.
- J. Merrick Jr., “Volume determination in stock and stock Index Futures Markets: An Analysis of Arbitrage and Volatility Effects,” Journal of Futures Markets, Vol. 7, No. 5, 1987, pp. 483-496. doi:10.1002/fut.3990070503

