Journal of Geographic Information System
Vol.09 No.03(2017), Article ID:77159,18 pages
10.4236/jgis.2017.93023
GIS Integrated Spatio-Temporal Urban Growth Modelling: Colombo Urban Fringe, Sri Lanka
Padma Weerakoon
Department of Estate Management and Valuation, University of Sri Jayewardenepura, Nugegoda, Sri Lanka

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 23, 2017; Accepted: June 23, 2017; Published: June 26, 2017
ABSTRACT
Urban growth is a continuous spatial expansion, and happens as a spatial- temporal process. This physical process influenced by various driving factors on the sub-systems within the main urban system. Analysing this spatial- temporal process and the influencing factors behind it is a substantial and essential task as it facilitates the local planning process. Previous studies were concerned with the individual effect of each driver on the main urban system rather than with the interactions between the drivers in the different sub-sys- tems. This research aims to model urban growth and to consider the effect of the driving factors separately on the socio-economic, physical and environmental sub-systems. GIS based logistic regression modelling is used to model the fringe growth to find out the relationship between urban growth and its driving factors. These findings highlighted the positive and negative influencing factors in terms of, “where the growth should go?” and “how much of it should go?”. The factors in the socio-economic, physical, and environmental sub-systems can exert their influence in a positive or negative manner. The cumulative results of the various influences caused a unique pattern of growth in the Colombo urban fringe that is quite distinct from the pattern witnessed in other Asian countries.
Keywords:
Spatio-Temporal Urban Growth, Main Urban System, Sub Systems, Driving Factors, Urban Expansion

1. Introduction
Urban growth is generally uneven due to constant variations in the levels of the different driving factors. Urban growth takes place as a result of land use changes which occur due to physical, socio-economic and environmental forces acting on the land at different levels. Different driving factors operate to change land uses conferring different values to the land and so balancing land use change among those three different values is vital in land use planning and management [1] . A careful study of both land use changes in urban areas and the driving factors behind them is vital to understand the urban growth pattern. With regard to this, the urban area can be considered as the main urban system, which is comprised of certain organized and operated activity processes. These processes may be grouped into three major categories as physical, socio-economic, and environmental processes. Complex operation of these three processes has the effect of changing urban land uses and values in the main urban system. This research aims to analyse the activities and events involving these three processes in the physical, socio-economic and environmental sub-systems, which together make up the main urban system. Physical sub-system refers to physical settings of the land among natural and some of man-made factors (e.g. Land cover, land use) which can cause changes to the physical sub-system. Socio-economic sub-system is mainly controlled by socio-economic factors, such as proximity, density and socio-economic factors that drive the city’s economy and influence many aspects of the city’s social life. The environmental sub-system works as the lungs of the urban system and so considerable attention needs to be paid to that [2] (Ex. Wet land). By considering these three subsystems, the urban growth model is conceptualized. The first assumption is that, in the matter of land use changes, there is an interrelationship between the main urban system and the socio-economic, physical and environmental sub-systems. Urban growth (UG) is a result of changes (X) in the physical (PS), socio-economic (SS), and environment (ES) subsystems as indicated in Equation (1).
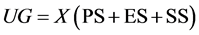 (1)
(1)
Different driving forces are involved in the land use changes caused in the different sub-systems and those factors are mentioned as 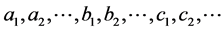 in Equation (2):
in Equation (2):
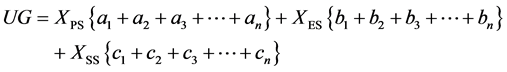 (2)
(2)
where a, b and c are different driving forces in each sub-system. Figure 1 depicts these three sub-systems and their interconnections.
Figure 1 indicates that UG is related to specific time periods such as t1 − t2, and it happens due to interactions among the three subsystems; the changes are measured in t2 periods (PSt2, SSt2, ESt2) because changes in each sub-system are based on several driving factors and those factors cannot be considered over a long period. Furthermore, driving forces interact among these three sub-sys- tems, and this is shown by the dotted arrows. All changes in the main sub-sys- tem are shown in thick arrows; they mean that the driving forces on each sub- system directly affect urban growth. The processes of these three sub-systems are involved in the changes of land use from non-urban to urban uses in the main urban system. Therefore, each sub-system has its own growth drivers that bring the changes to that sub-system. This study aims to develop the growth model to explore those driving factors that affected past urban growth within the three sub-systems. Table 1 indicates the different scholars who used growth drivers to identify urban growth classified by subsystem and driving factors.
Figure 1. Interrelation between urban growth and sub-systems.
Table 1. Scholarly used different driving factors.
2. Materials and Methods
2.1. Study Area
Sri Lanka is positioned in the Indian Ocean, located very close to the Southern strip of the Indian subcontinent, lying between Northern Latitudes 5˚55' and 9˚50' and Eastern Longitudes 79˚42' and 81˚52'. The land area of Sri Lanka is 65,610 sq. km., with an overall length of 432 km and, width of 224 km. Sri Lanka is divided into nine regions (or provinces) and the Western Region comprises 5.6% of the total land area of the country [23] . The Western Region consists of three districts: Kalutara, Gampaha and Colombo where is located the most urbanized region of the Country. The study area of this study is situated in the urban fringe of Colombo district namely Kaduwela MC and is sited about 20 km from the city of Colombo, which is the commercial capital in Sri Lanka (Figure 2).
The topography of the Colombo urban fringe has a gradual slope and in KMC the slope is at a high elevation in the South and a low elevation in the North. The Kelani River flows from East to West along the Northern boundary of the KMC. The lowest elevation is the bed level of Kelani River, which is about 6 m below Mean Sea Level (MSL). In the 1970s and earlier, when people selected this area
Figure 2. Location of the colombo district.
for housing, they were concerned about the shallow water table of the area. Therefore, most of the low-lying areas were used for mining earth for making bricks. Later however, with the commencement of new development projects, urban expansion began in earnest as accommodation and living facilities had to be provided for the influx of people into this area. After 1977, a new urban development projects boosted the massive development of this area.
2.2. Research Method
Main data sources are digital maps and images. Two types of maps are used for data analysis namely land use maps and criterion maps. Aerial photographs, digital maps, IKONOS images were used to update 4 land use maps for 1972, 1984, 2004, and 2014. The 1:2000 scale five base maps except the above mentioned land use maps namely main roads and local roads, main centres and local sub centers, flood contour, environmentally restricted area, and GND map preliminary maps, are used to derive criterion maps
2.2.1. Spatial Scale of Urban Growth Model
Spatial scale is a fundamental concept [1] and demarcation of the spatial extent is a fundamental requirement for urban growth modelling. The spatial and temporal scales chosen for modelling depend on the experience of the user, and the availability of data [24] . In order to visualise the urban growth pattern in the Colombo urban fringe, the spatial extent has to be defined as well. Urban studies usually demarcate the spatial extent using administrative boundaries at the national, regional, or municipal level. In reality, urban growth does not always physically occur within the administrative boundaries, as it expands and changes, especially over a long development period [25] . In Sri Lanka, the planning hierarchy operates at a national, regional, district and local level. In this context, the scope for decision-making is large, and the spatial process becomes a discrete process rather than a continuous process. Identification of relative spatial units is a required component for spatial analysis; the term “relative” means “subjective” instead of “objective” boundaries [26] . From the perspective of planning, decision making is at the tail end of planning, and this determines the required spatial and temporal scales. Spatial Modelling links with the decision making processes and the spatial extent needs to be considered in various decision making scales such as at a first broader level and a later detail level. In the urban growth modelling process, the initial research question of “Why model the spatial pattern of urban growth?” is a fundamental question, and can be split in two specific sub questions:
・ Which areas changed during the last four decades?
・ What is the extent of the change?
Hence, since the spatial extent is difficult to handle, the entire urban fringe cannot be considered for the modelling exercise. As such, a specific spatial unit (Kaduwela Municipal Council) based on administrative boundaries was selected. Within this administrative boundary, the above mentioned two scales, were considered. To answer the first question (what areas were changed), the entire municipal council area was selected as the spatial entity. For the second question (to what extent did they change), only the urban change areas were considered. The two spatial scales concerned were the macro and micro scales.
2.2.2. Data Preparation
Data preparation is mainly focused on urban change maps, change density map and criterion maps. By comparing changes of urban to non-urban land uses, the change urban map was created. Through comparing urban change category with population and building density, change density map was created. There are different factors influence the changes in urban growth, based on literature review, personal knowledge, and experience of the researcher, 20 driving factors are derived and used (Table 2) to prepare the criterion maps.
ArcGIS 10analysis tools (proximity, density, spatial interpolation) were used in this preparation process of the 20 criterion maps.
2.2.3. Logistic Regression Modelling
Statistical modelling is extensively used in developing urban models. Linear and logistic regression models have been widely used in urban growth modelling and they can accommodate socio-economic and environmental variables as independent variables. Urban change tends to fall into binary categories and does not usually follow normal assumptions because its influential factors are a mixture of continuous and categorical variables. Therefore, this study used logistic regression modelling to develop the urban growth model. The statement of the logistic regression model can be expressed to find the relationship between urban growth and its driving factors. The data analysis was carried out in the raster GIS
Table 2. Selected driving factors.
environment. In this case urban change cells were dichotomous, displaying either the presence or absence of urban growth. Binary values 1 and 0 were used to represent whether the urban change had occurred or not. It is assumed that the probability of a cell changing to urban use follows the logistic curve as described by the logistic function [27] (Equation (3)).
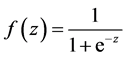 (3)
(3)
Then the probability of a cell being converted to urban use is estimated by the following logistic regression (Equation (4)):
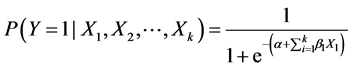 (4)
(4)
where 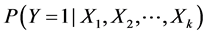 is the probability of dependent variable Y being 1, given,
is the probability of dependent variable Y being 1, given,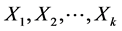 . X1 to Xk is an independent variable representing the driving forces of urban growth. Those are interval, ordinal or categorical, and
. X1 to Xk is an independent variable representing the driving forces of urban growth. Those are interval, ordinal or categorical, and  is the coefficient for variable X1. To interpret the meaning of the above coefficients, the logistic model can be rewritten in terms of the ratio of the probability that causes the urban change. The log of the ratio is called logit [27] .
is the coefficient for variable X1. To interpret the meaning of the above coefficients, the logistic model can be rewritten in terms of the ratio of the probability that causes the urban change. The log of the ratio is called logit [27] .
The logistic regression model considered in this study mentioned two spatial scales, namely macro (change urban) and micro (change density) scales. Based on the pattern of urban built-up area, the macro scale depicted the pattern of urban growth in terms of where the change took place. The micro scale showed how much of a change occurred using the density indicators. In the macro scale, the area in which the growth took place and its pattern was considered. Subsequently, micro scale models were used to derive the relationship between high and low density changes.
2.2.4. Dependent and Independent Variables
This study focused on identifying the urban growth on the basis of two scales and therefore two dependent variables were used. Thus, the binary variation considered in the two dependent variables was described in Table 3.
Figure 3 represent two binary maps used to define the dependent variables.
The identified driving factors based on criterion maps were considered as independent variables. Accordingly, 20 independent variables were initially derived for the model. The criterion maps (Figure 4) were created using the spatial analyst tools for proximity, density and reclassification, found in ArcGIS 10.2. All criterion maps were prepared using 10 × 10 meters pixel size in order to
Table 3. Dependent variables.


Figure 3. Two binary maps used to define dependent variables. (a) Change urban map; (b) Change density map.




















Figure 4. Criterion maps.
maintain high accuracy. The resulting 1551 × 964 grid was used for data analysis.
Based on the criterion maps used in this study the independent variables were developed. Table 4 shows the dependent and independent variables used for analysis at the macro scale and micro scale.
2.2.5. Spatial Sampling
Spatial sampling is the process of collecting observations from a two dimensional framework. “As a rule of thumb it is generally desirable to have a higher concentration of samples where exhaustive and accurate information is needed and the number of samples should always be as representative as possible of the entire population” [28] .
The most commonly applied sampling procedure is that based on point sampling within a regular grid framework. In this case, a set of regularly spaced
Table 4. Dependent and independent variables.
sample points in the sample square region have to be set out first. Systematic sampling is effective in reducing spatial dependence, but sometimes with this process, some significant information is lost. Random sampling is also effective in representing a population, but its spatial dependence reduction is less. Therefore, a combination of these two sampling techniques creates a good sampling method related spatial sampling and most scholars used these two methods for define spatial sample [3] [9] [26] . Therefore, this research used both systematic and random sampling methods for balancing the sample size and the spatial interdependence.
3. Results and Discussion
3.1. Model Results
Minimum sample size requirement of the logistic regression is 15 - 20 cases per independent variable and the most preferred minimum ratio of valid cases to independent variables is 20:1 [27] . The Model 1 dataset had taken 2140 cases to 20 independent variables and the ratio was 202:1. It is more than the required number of cases for the independent variable. The Model 2 dataset consisted of 1706 cases and 20 independent variables for a ratio of 33:1 and it was again more than the required number of cases for the model. Therefore, the requirement of accepted sample size is good in both models. It is similar to the urban growth analysis done by [3] [4] [26] etc. Results for the two models are indicated in Table 5.
Omnibus test of model coefficient says that both models appear good but it is necessary to evaluate the goodness of fit in the model and the significance as well. A maximum likelihood estimator was used to fit the model [29] . The Model 1 Chi-Square value of 381.8 has a significance of less than 0.01 and the Model 2 Chi-Square value is 151.1 with a significance of less than 0.01. So it can be concluded that there is a significant relationship between the dependent variable
Table 5. Model results.
and the set of independent variables, which includes a single variable at this step. The verification strength of the relationship between the dependent variables and the independent variables is measured using R² like in multiple regression. The Cox and Snell R² measure operates like R², with higher values indicating greater model fit. However, this measure is limited in that it cannot reach the maximum value of 1, so Nagelkerke proposed a modification that does range from 0 to 1. Nagelkerke’s measure indicates the strength of the relationship. The Nagelkerke modification that does range from 0 to 1 is a more reliable measure of the relationship. Nagelkerke’s R2 of Model 1 is 0.412 indicating strong relationship of 41.2% between the predictors and prediction of the model and Cox and Snell R2 is 0.309 and it is less than Nagelkerke’s R2. Model 2 results are similar and it shows good fit of the data. Somehow, good fit of data is indicated in both models.
Rather than using a goodness-of-fit statistic, it is better to look at the proportion of cases that managed to classify correctly. The classification table tells how many of the cases, where the observed values of the dependent variable were 1 or 0 respectively, have been correctly predicted. In the Classification table, the columns are the two predicted values of the dependent, while the rows are the two observed (actual) values of the dependent. In a perfect model, all cases will be on the diagonal and the overall percentage correct will be 100%. The estimated logistic regression models of both models are significant at 1% level of significance. Model 1, 74% was correctly classified for the urban change and 76.4% for no change. Overall, 75.2% was correctly classified. This is a considerable improvement on the 50% correct classification with the constant model with predictors and it is a significantly better mode. Therefore, the rate of urban change is good and it means that the urban conversion rate is high and urban-built up is growing at a fast rate. Model 2 of the study classified 71.4% as high density change and 63% indicated low density change. Overall correctness of the density of change in Model 2 is 67.2%. It means the high density category of the land is growing fast and the urban built-up conversion rate of the high density category is high.
Hosmer and Lemeshow Statistic test (H-L Test) is an alternative to the Chi square test which divides subjects into 10 ordered groups and then compares the number actually in each group (observed) to the number predicted by the logistic regression model (predicted). The H-L statistic assumes sampling adequacy, with a rule of thumb being that there should be enough cases so that 95% of cells (typically, 10 decile groups times 2 outcome categories = 20 cells) have an expected frequency > 0.05. The H-L statistics of both the models have significance at conventional levels. The result of the fitted logistic regression model with the 10 variables is indicated in Table 6 (all acronyms described in the Table 4).
From the 18 variables Model 1 selected only 10 significant variables and Model 2 selected only 8 significant variables. In the Model 1 PROX_GREEN was positively significant in predicting innovative performance by recording β = 0.471, p < 0.05 while LAND_VALUE positively contributed to CHANGE_URBAN at
Table 6. Results model 1.
conventional levels reporting the beta weight as 0.382, p < 0.05. Further, POP_DEN significantly influenced the outcome, recording a coefficient value of β = 0.049, p < 0.05. As shown by the odds ratios PROX_GREEN has the strongest influence on the probability of being innovative while LAND_VALUE has a lesser effect. POP_DEN has the least effect compared with the other two positive variables. Unit increase in PROX_GREEN has more than 1.6 times increase in the urban change while unit increase in LAND_VALUE would increase the odds of being CHANGE_URBAN by only 1.4 times. Unit increase in POP_DEN shows the odds of CHANGE_URBAN by 1 time.
Other seven variables are significant and associate negatively in predicting CHANGE_URBAN. PROX_IND performance recorded β = −0.141, p < 0.05 while QNA(1) negatively contributed to CHANGE_URBAN at conventional levels reporting a coefficient of −0.292. The association of PROX_PBR and WTD is negative and significant to predict CHANGE_URBAN with beta value −0.276 and −0.288, p < 0.05 respectively, while coefficient of PROX_EMP contributed β = −0.375, p < 0.05. The coefficients of WBZ(1) and PHY_CONS(1) recorded as -1.633 and 4.336 respectively, which are negatively significant at conventional levels. Once PROX_IND is considered, increase in this variable significantly reduces urban change 0.86 times while increase in QNA would decrease the odds of being CHANGE_URBAN by only 0.74 times. Unit increase in PROX_PBR and WTD decrease the odds of CHANGE_URBAN by 0.759 and 0.75 times while PROX_EMP shows a 0.687 contribution. The unit increase of WBZ and PHY_CONS have negligible, albeit significant impact recording the odds ratios as 195 and 0.013 respectively.
In Model 2, eight variables were selected from 17 variables (Table 7). Four variables are positively significant and the other four show negative significance.
In Model 2, the ROAD_DEN, and PROX_PBR variables are positively significant in prediction, recording β = 0.986 and β = 0.224; p < 0.05, while PROX_
Table 7. Results-model 2.
GREEN and WTD positively contribute to CHANGE_DENSITY at conventional levels reporting comparatively weak effect (0.165, p < 0.05 and 0.178). With regard to the unit performance, unit increase in ROAD_DEN has more than 2 fold increase in the CHANGE_DENSITY while unit increase in PROX_PBR expresses the odds of CHANGE_DENSITY by 1 time. A unit change in PROX_ GREEN and WTD increase CHANGE_ DENSITY by 1.1 times.
Five variables in Model 2 are negatively significant in predicting innovative performance. PROX_LSC is significant with performance, recording β= −0.237, p < 0.05. The beta values of PROX_MC and PROX_IND are β = −0.395 and β = −0.433, p < 0.05, whereas the coefficient of QNA shows β = −1.071, with level of p < 0.05. In addition, unit decrease in PROX_LSC has strong influence on (by 0.789 times) the decrease of CHANGE_DENSITY. However, odds ratio of PROX_MC, PROX_IND, and QNA are 0.674, 0.649, and 0.343, respectively. Therefore, PROX_LSC has a stronger influence on decreasing the probability of density of change than the other three.
3.2. Discussion
Many driving factors influence the Colombo fringe growth and identifying the most influential factors is vital for decision making in urban development and planning. Hence, next important point is to view the driving factors which influence the growth of Colombo urban fringe, in terms of two questions that we need to answer: “where should the change take place?” and “how much should the change be?”. From the perspective of modelling, those questions are conceptually transformed to CHANGE URBAN and CHANGE DENSITY, as defined below.
・ CHANGE URBAN is defined as the possibility of land cover transition from non-urban to urban in any place.
・ CHANGE DENSITY is defined as the possibility of land cover change agglomeration in any place.
The above two aspects were modelled using logistic regression modelling and the results led to the following conclusions. When developing a logistic model, understanding the main urban system that interacts with the dynamic subsystems (socio-economic, physical, and environmental) is important (Section 2). Spatial logistic regression proved successful in quantifying the land conversion pattern. Dependent variables described the two stages of this phenomenon, and the independent variables were used to determine the spatial patterns. The two dependent variables were discussed in two scales labeled CHANGE URBAN (macro level) and CHANGE DENSITY (micro level). Initially, 20 factors were recognized as influencing factors that affect urban change based on extensive literature review, expert opinions, and researcher’s own experience related to socio-economic, physical and environmental sub-systems. The 20 driving factors consist of 10 driving factors from the socio-economic sub-system, 5 from the physical sub-system, and the other 5 factors from the environmental sub-system. Logistic regression results indicate that 10 driving factors influenced the land use change from non-urban to urban over the past four decades. Three factors namely, land value, proximity to green areas, and population density were the ones that positively influenced land use change from non-urban to urban uses. Of these three factors, proximity to green areas was the most influential in stimulating urban growth while the other two factors had a minor influence. Fringe growth consists of 80% residential developments and these are mostly situated near green areas because people wish to avoid congested main centers and sub-centers due to air and noise pollution [21] . That is the reason why proximity to green areas is highly valued by home owners.
Two socio-economic variables that positively influence changes in urban growth are land value and population density. Population density and land value are closely related factors; land value in areas with low population density is relatively low but these areas have high growth potential. Just two decades ago, fringe areas had low population due to absence of physical infrastructure. In line with urban development strategies, most of the manufacturing industries moved to the fringe and new expressway projects passed through the fringe. Physical infrastructure also developed simultaneously and more of the available areas were opened up to provide room for new residential developments. The other seven factors proximity to industries, quality neighborhood area, proximity to public bus routes, water table depth, proximity to employment centers, water buffer zone, and physical constraints negatively affected the change in land uses from non-urban to urban.
Urban density is not equal throughout the fringe area generally and the researcher explored to identify the drivers that influenced the increase in density. Hence, urban change area was again analysed based on high and low density patches. The density of change model highlighted “how much urban growth has changed” to high density and low density zones. In this regard, road density, proximity to public bus routes, proximity to green areas and water table depth positively influenced the change in high density areas. The criteria of proximity to local subcenters, proximity to main center, proximity to industries and quality neighborhood area negatively affected the high density of change. Hence, factors in the socio-economic subsystem and physical subsystem affected the change urban uses, and factors in the socio-economic subsystem, physical subsystem and environmental subsystem positively affected the high density change.
These experimental results were compared with opinions obtained from experts and residents. When this drivers was discussed with experts, they were of the opinion that proximity to the main city centre, proximity to main roads, proximity to public bus routes, proximity to schools, proximity to local sub- centres, land values, road density, housing density are influencing factors, but they unable to clarified those as positive or negative. In addition, they mentioned population density is the main factor that is influencing Colombo urban growth during the last 40 years. All these factors mentioned by the experts and residents fall under the socio-economic subsystem. However, a scientific analysis concluded that the factors come under all three of the subsystems. The scientific results and the results of the residents and experts’ views had similarities as well as dissimilarities. The scientific results had the power to separate negative and positive influences. However, experts mentioned the improvement of physical infrastructure, especially development of new urban transportation network and accessibility to cheap private vehicles mitigated the barriers to the spread of urban development in the Colombo district.
4. Conclusion
This study analyzed the Colombo urban fringe over the past forty years, with extensive studies on the dynamics of the driving factors affecting urban growth. This study found that a decreasing role was played by physical factors (water table depth and water buffer zone) in restricting urban expansion in the fringe, suggesting an increase of development pressure in the low lying areas and green areas. As these areas are the lungs of the urban ecosystem, it is important to preserve them to maintain drainage, biodiversity and a healthy ecosystem. Presently, most agricultural lands are being converted to urban uses, and the extent of paddy fields being converted or abandoned is significant. Some of those lands were developed and put to urban uses without following any policies or guidelines, and therefore strong regulations and measures should be enforced to mitigate future environmental threats. In addition, as mentioned earlier, there has been heavy development in the urban fringe, indicating a highly dispersed spatial pattern [30] . Dispersed spatial pattern of development causes greater ecological and environmental damage than a more compact development pattern [30] . Hence, strict planning regulations are needed to control this dispersed pattern of urban growth in the Colombo fringe.
Acknowledgements
This paper was done based on my PhD research and I express my gratitude to my supervisor Professor Dr. Lee LikMeng, University Sains, Malaysia, for his valuable contribution through-out my research and for accepting to publish this research with only my authorship. In addition, I thank urban development authority of Sri Lanka for providing data for my study.
Cite this paper
Weerakoon, P. (2017) GIS Integrated Spatio-Temporal Ur- ban Growth Modelling: Colombo Urban Fringe, Sri Lanka. Journal of Geographic Information System, 9, 372-389. https://doi.org/10.4236/jgis.2017.93023
References
- 1. Kaiser, E.J., Godschalk, D.R. and Chapin Jr., F.S. (1995) Urban Land Use Planning. 4th Edition, University of Illinois Press, Champaign.
- 2. McHarg, I.L. (1995) Design with Nature. 25th Anniversary Edition, USA.
- 3. Luo, J. and Wei, Y.H.D. (2009) Modeling Spatial Variations of Urban Growth Patterns in Chinese Cities: The Case of Nanjing. Landscape and Urban Planning, 91, 51-64.
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1559272 - 4. Allen, J. and Lu, K. (2003) Modeling and Prediction of Future Urban Growth in the Charleston Region of South Carolina: A GIS-Based Integrated Approach. Conservation Ecology, 8, 2.
http://www.consecol.org/vol8/iss2/art2/ - 5. Weber, C. and Puissant, A. (2003) Urbanization Pressure and Modeling of Urban Growth: Example of the Tunis Metropolitan Area. Remote Sensing of Environment, 86, 341-352.
- 6. Dubovyk, O., Sliuzas, R. and Flacke, J. (2011) Spatio Temporal Modelling of Informal Settlement Development in Sancaktepe District, Istanbul, Turkey. ISPRS Journal of Photogammetry and Remote Sensing, 66, 235-246.
- 7. He, C., Okada, N., Zhang, Q., She, P. and Zang, J. (2006) Modelling Urban Expansion Scenarios by Coupling Cellular Automata Model and Systematic Dynamic Model in Bejing China. Applied Geography, 26, 323-345.
- 8. Hu, Z. and Lo, C.P. (2007) Modeling Urban Growth in Atlanta Using Logistic Regression. Computers, Environment and Urban Systems, 31, 667-688.
- 9. Huang, B., Zhang, L. and Wu, B. (2009) Spatio-Temporal Analysis of Rural-Urban Land Conversion. International Journal of Geographical Information Science, 23, 379-398.
https://doi.org/10.1080/13658810802119685 - 10. Reilly, M.K., O’Mara, M.P. and Seto, K.C. (2009) From Banglore to the Bay area’ Comparing Transportation and Activity Accessibility as Drivers of Urban Growth. Landscape & Urban Planning, 92, 24-33.
- 11. Wu, B. and Fung, T. (2009) Projection of Land Use Change Patterns Using Kernel Logistic Trgression. Photogrammetric Engineering & Remote Sensing, 75, 971-979.
https://doi.org/10.14358/PERS.75.8.971 - 12. Ye, Y., Zhang, H., Liu, K. and Wu, Q. (2011) Research on the Influence of Site Factors on the Expansion of Construction Land in the Perl River Delta, China: By Using GIS and Remote Sensing. International Journal of Applied Earth Observation and Geoformation, 21, 366-373.
- 13. Dewan, A.M. and Yamaguchi, Y. (2009) Land Use and Land Cover Change in Greater Dakha Bangladesh: Using Remote Sensing to Promote Sustainable Urbanisation. Applied Geography, 29, 390-401.
- 14. Yang, X. and Lo, C.P. (2003) Modelling Urban Growth and Landscape Changes in the Atlanta Metropolitan Area. International Journal of Geographical Information Science, 17, 463-488.
https://doi.org/10.1080/1365881031000086965 - 15. Roy, M. (2009) Planning for Sustainable Urbanisation in Fast Growing Cities: Mitigation and Adaptation Issues Addressed in Dhaka, Bangladesh. Habitat International, 33, 276-286.
- 16. Fan, F. and Fan, W. (2014) Understanding Spatial-Temporal Urban Expansion Pattern (1990-2009) Using Impervious Surface Data and Landscape Indexes: A Case Study in Guangzhou (China). Journal of Applied Remote Sensing, 8, Article ID: 083609.
- 17. Seto, K.C., Fragkias, M., Guneralp, B. and Reilly, M.K. (2011) A Meta-Analysis of Global Urban Land Expansion. PLoS ONE, 6, e23777.
https://doi.org/10.1371/journal.pone.0023777 - 18. Long, H., Tang, G., Li, X. and Heilin, G.K. (2007) Socio Economic Driving Forces of Land Use Change in Kunshan, the Yangtze River Delta Economic Area of China. Journal of Environmental Management, 83, 351-364.
- 19. Cheng, J. and Masser, I. (2003) Modelling Urban Growth Patterns: A Multiscale Perspective. Environment and Planning A, 35, 679-704.
https://doi.org/10.1068/a35118 - 20. Dadras M., Shafri, H.Z.M., Ahmad, N, Pradhan, B. and Safarpour, S. (2015) Spatio-Temporal Analysis of Urban Growth for Remote Sensing Data in Bandar Abbas city, Iran. The Egyptian Journal of Remote Sensing and Space Sciences, 18, 35-52.
- 21. Dadhich, P.N. and Hanaoka, S. (2011) Spatio-Temporal Urban Growth Modeling of Jaipur, India. Journal of Urban Technology, 18, 45-65.
https://doi.org/10.1080/10630732.2011.615567 - 22. Poelmans, L. and Van Rompaey, A. (2009) Detecting and Modelling Spatial Patterns of Urban Sprawl in Highly Fragmented Areas: A Case Study in the Flanders-Brussels Region. Landscape and Urban Planning, 93, 10-19.
- 23. UN Habitat (2012) Turning Sri Lanka’s Urban Vision into Policy and Action. Policy Paper, The World Bank Colombo Office.
- 24. Michael, J.H. and Richard, J.A. (2000) Spatial Information for Land Use Management. Gordon & Breach Science Publishers.
http://www.thefreedictionary.com/exurban - 25. Weerakoon, P. (2017) Analysis of Spatio-Temporal Urban Growth Using GIS Integrated Urban Gradient Analysis; Colombo District, Sri Lanka. American Journal of Geographic Information Systems, 6, 83-89.
- 26. Cheng, J.Q. (2003) Modelling Spatial & Temporal Urban Growth. PhD Thesis, Utrecht University, Utrecht.
https://www.itc.nl/library/Papers_2003/phd_theses/cheng_jianquan.pdf - 27. Hosmer Jr., D.W., Lemeshow, S. and Sturdivant, R.X. (2013) Applied Logistic Regression. 3rd Edition, John Wiley & Sons, Hoboken, NJ.
https://doi.org/10.1002/9781118548387 - 28. Delmelle, E. (2008) Chap. 10. Spatial Sampling. In: Fotheringham, A.S. and Rogerson, P.A., Eds., Sage Handbook of Spatial Analysis, Sage Publication, The Cromwell press Ltd, UK.
- 29. Field, A. (2009) Discovering Statistics Using SPSS for Windows. 2nd Edition, Sage Publications, London.
- 30. Li., X., Zhou, W. and Ouyang, Z. (2013) Forty Years of Urban Expansion in Beijing: What Is the Relative Importance of Physical, Socioeconomic, and Neighborhood Factors? Applied Geography, 38, 1-10.




