Journal of Geographic Information System
Vol. 4 No. 6 (2012) , Article ID: 26324 , 9 pages DOI:10.4236/jgis.2012.46061
Integrated Approach of Universal Soil Loss Equation (USLE) and Geographical Information System (GIS) for Soil Loss Risk Assessment in Upper South Koel Basin, Jharkhand
University Department of Geology, Ranchi University, Ranchi, India
Email: *res1077@gmail.com, kumaruday10@gmail.com
Received October 3, 2012; revised November 3, 2012; accepted December 5, 2012
Keywords: Universal Soil Loss Equation (USLE); Remote Sensing & GIS; Soil Loss
ABSTRACT
Soil erosion is a growing problem especially in areas of agricultural activity where soil erosion not only leads to decreased agricultural productivity but also reduces water availability. Universal Soil Loss Equation (USLE) is the most popular empirically based model used globally for erosion prediction and control. Remote sensing and GIS techniques have become valuable tools specially when assessing erosion at larger scales due to the amount of data needed and the greater area coverage. The present study area is a part of Chotanagpur plateau with undulating topography, with a very high risk of soil erosion. In the present study an attempt has been made to assess the annual soil loss in Upper South Koel basin using Universal Soil Loss Equation (USLE) in GIS framework. Such information can be of immense help in identifying priority areas for implementation of erosion control measures. The soil erosion rate was determined as a function of land topography, soil texture, land use/land cover, rainfall erosivity, and crop management and practice in the watershed using the Universal Soil Loss Equation (for Indian conditions), remote sensing imagery, and GIS techniques. The rainfall erosivity R-factor of USLE was found as 546 MJ mm/ha/hr/yr and the soil erodibility K-factor varied from 0.23 - 0.37. Slopes in the catchment varied between 0% and 42% having LS factor values ranging from 0 - 21. The C factor was computed from NDVI (Normalized Difference Vegetative Index) values derived from Landsat-TM data. The P value was computed from existing cropping patterns in the catchment. The annual soil loss estimated in the watershed using USLE is 12.2 ton/ha/yr.
1. Introduction
Erosion is a natural geological phenomenon resulting from removal of topsoil by natural agencies like wind, water transporting them elsewhere while some human intervention can significantly increase erosion rates. It is a major agricultural problem and also one of the major global environmental issues. Erosion is triggered by a combination of factors such as slope steepness, climate (e.g. long dry periods followed by heavy rainfall), inappropriate land use, land cover patterns (e.g. sparse vegetation) and ecological disasters (e.g. forest fires) [1]. Moreover, some intrinsic features of a soil can make it more prone to erosion (e.g. a thin layer of topsoil, silty texture or low organic matter content [2]. Thus, some scholars even categorized soil erosion into two major types: geological erosion and man-induced erosion [3]. It has been estimated that about 113.3 m ha of land is subjected to soil erosion due to water and about 5334 million tonnes of soil is being detached annually due to various reasons in India [4]. The process of soil erosion involves detachment, transport and subsequent deposition [5]. Urbanization, deforestation leading to change in land use patterns is the major cause of soil erosion in recent times. Erosion process result in soil loss from a watershed and it is difficult to estimate soil loss as it arises from a complex interaction of various hydro-geological processes [6].
Estimating the soil loss risk and its spatial distribution are the one of the key factors for successful erosion assessment. Spatial and quantitative information on soil erosion on a regional scale contributes to conservation planning, erosion control and management of the environment. Identification of erosion prone areas and quantitative estimation of soil loss rates with sufficient accuracy are of extreme importance for designing and implementing appropriate erosion control or soil and water conservation practices [7]. Researchers have developed many predictive models that estimate soil loss and identify areas where conservation measures will have the greatest impact on reducing soil loss for soil erosion assessments [8]. These models can be classified into three main categories as empirical, conceptual and physical based models [9]. Despite development of a range of physical, conceptual based models, Universal Soil Loss Equation (USLE) and modified Universal soil loss equation (MUSLE) or revised Universal soil loss equation (RUSLE) are the most popular empirically based models used globally for erosion prediction and control and has been tested in many agricultural watersheds in the world. The main reason why empirical regression equations are still widely used for soil erosion and sediment yield predictions is their simplicity, which makes them applicable even if only a limited amount of input data is available.
Remote sensing and GIS techniques have become valuable tools specially when assessing erosion at larger scales due to the amount of data needed and the greater area coverage. For this reason use of these techniques have been widely adopted and currently there are several studies that show the potential of remote sensing techniques integrated with GIS in soil erosion mapping [10,11]. The main objective of the study involved estimation of soil loss using USLE model with the input parameters generated using remote sensing and GIS.
2. Geographical Setting of the Study Area
The present study area (Figure 1) is a part of South Koel basin with an area of 942.4 sq. km. , bounded by latitude 23˚17'16"N & 23˚32'16"N and longitude 84˚14'15"E & 85˚46'51"E, falling in Lohardaga and Ranchi districts of Jharkhand. South Koel is the main river flowing in the study area with Kandani and Saphi River as its major tributaries.
The climate of the area is subtropical. The watershed experiences precipitation with an annual average of 1380 mm. The mean maximum and mean minimum temperature in the watershed are 36˚C and 7˚C respectively. The study area is a part of Chotanagpur plateau with undulating topography. The elevation ranges from 640 m to 925 m above the mean sea level. The watershed is an agricultural watershed with 84% of the geographical area under agriculture.
3. Materials and Methodology
The soil loss of the watershed was calculated using
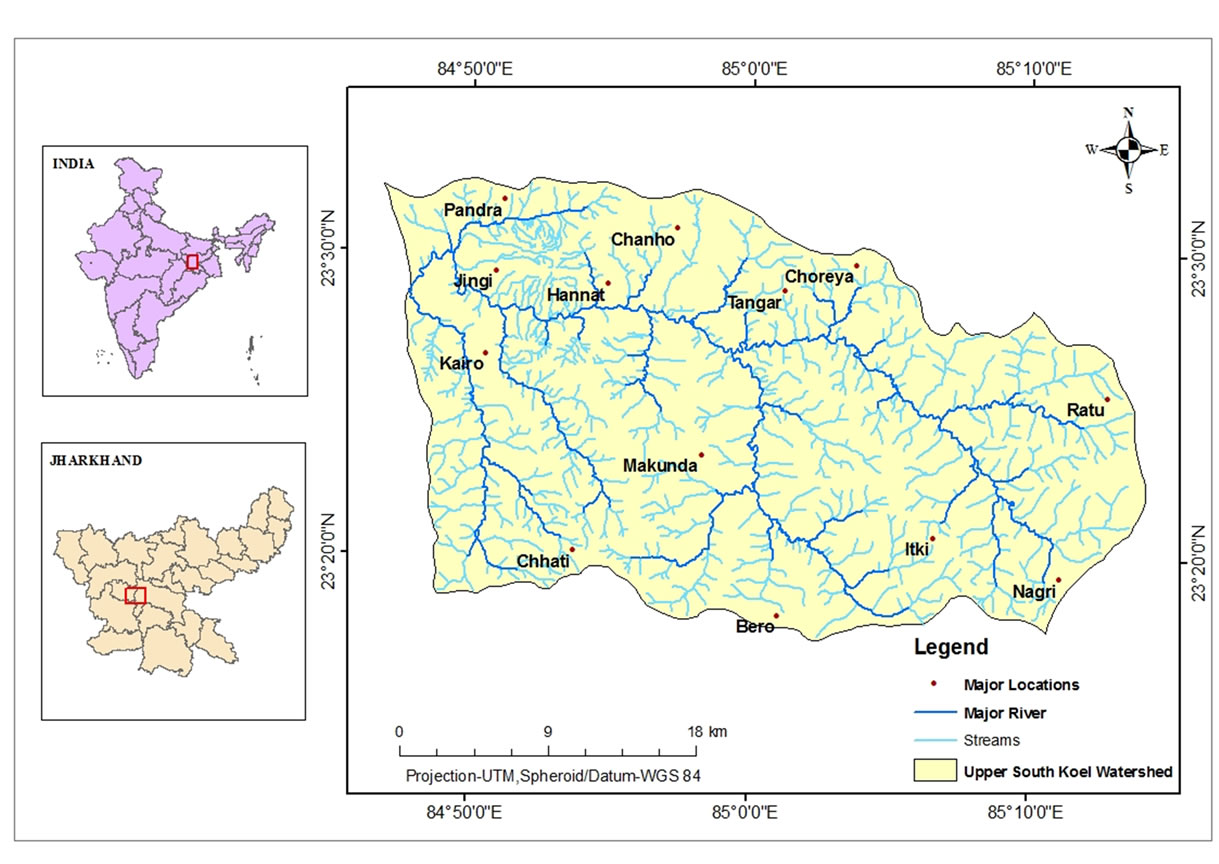
Figure 1. Location map of study area.
USLE [12] with some modification in its parameter estimation to suit Indian conditions. The general universal soil loss equation is as follows:
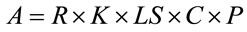 (1)
(1)
where, A is average annual soil loss (ton∙ha−1∙yr−1); R is the Rainfall and Runoff erosivity index (in MJ mm/ha/ hr/yr); K is the soil Erodibility factor (in ton/MJ/mm); LS is the Slope and Length of Slope Factor; C is the Cropping Management Factor; P is the is the supporting conservation practice factor.
3.1. Rainfall and Runoff Erosivity Factor (R)
R is the long term annual average of the product of event rainfall kinetic energy and the maximum rainfall intensity in 30 minutes in mm per hour [13]. Rainfall erosivity estimation using rainfall data with long-time intervals have been attempted by several workers for different regions of the world [14,15]. Using the data for storms from several rain gauge stations located in different zones, linear relationships were established between average annual rainfall and computed EI30 values for different zones of India and iso-erodent maps were drawn for annual and seasonal EI30 values [16]. The derived relationship is given below
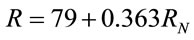 (2)
(2)
where RN is the average annual rainfall in mm.
A 5-year average annual data has been used to calculate the average annual R-factor values. Since the rainfall data available for the study area is not homogenous, an interpolation of average annual rainfall data is applied to have a representative rainfall distribution map. This rainfall distribution map is used as input for calculation of R-factor.
3.2. Soil Erodibility Factor (K)
The soil erosivity factor, K, relates to the rate at which different soils erode. However, it is different than the actual soil loss because it depends upon other factors, such as rainfall, slope, crop cover, etc. K values reflect the rate of soil loss per rainfall-runoff erosivity (R) index.
Soil map of the study area was prepared from soil survey report prepared by the National Bureau of Soil and Landuse Planning. Details such as fraction of sand, silt, clay, organic matter and other related parameters information for different mapping units were taken from the same report.
In this study, Soil erodibility (K) of the study area can be defined using the relationship between soil texture class and organic matter content proposed by [17]. Table 1 presents the soil erodibility factor (K) based on the soil texture class.
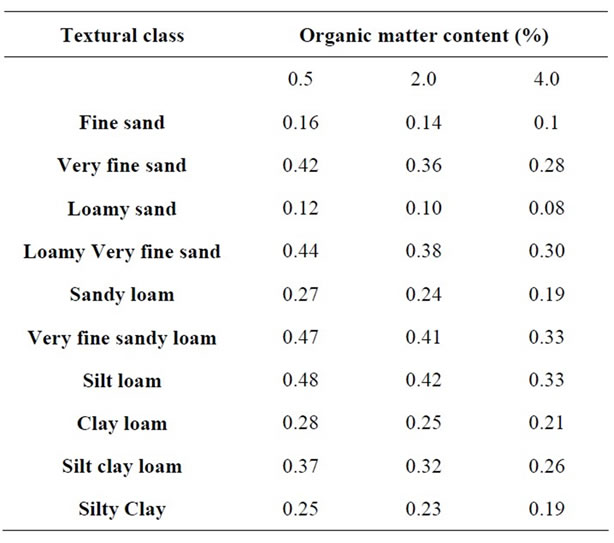
Table 1. Soil erodibility factor K (by Schwab et al., 1981 [17]).
3.3. Topographic Factor (LS)
Topographic factor (LS) in USLE accounts for the effect of topography on sheet and rill erosion. The two parameters that constitute the topographic factor are slope gradient and slope length factor and can be estimated through field measurement or from a digital elevation model (DEM).
There are many relationships available for estimation of LS factor. Among these the best suited relation for integration with GIS is the theoretical relationship proposed by [18-20] based on unit stream power theory given below.
 (3)
(3)
where A is the upslope contributing factor, B is the slope angle.
Slope shape, the interaction of angle and length of slope, has an effect on the magnitude of erosion. As a result of this interaction, the effect of slope length and degree of slope should always be considered together [21].
With the incorporation of Digital Elevation Models (DEM) into GIS, the slope gradient (S) and slope length (L) may be determined accurately The precision with which it can be estimated depends on the resolution of the digital elevation Model (DEM).Here in this study 30 m ASTER DEM has been used.
Raster calculator was used to derive LS map based on flow accumulation and slope steepness [22].The expression used is as follows
 (3a)
(3a)
3.4. Cropping Management Factor (C)
The C factors are related to the land-use and are the reduction factor to soil erosion vulnerability. It is an important factor in USLE, since they represent the conditions that can be easily changed to reduce erosion. C factor is basically the vegetation cover percentage and is defined as the ratio of soil loss from specific crops to the equivalent loss from tilled, bare test-plots. The value of C depends on vegetation type, stage of growth and cover percentage. Therefore, it is very important to have good knowledge concerning land-use pattern in the basin to generate reliable C factor values. The most widely used remote-sensing derived indicator of vegetation growth is the Normalized Difference Vegetation Index, which for Landsat-TM is given by the following equation:
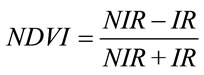 (4)
(4)
where NIR: the reflection of the near infrared portion of the electromagnetic spectrum and IR: the reflection in the visible spectrum. NDVI values range between −1.0 and +1.0 where higher values are for green vegetation and low values for other common surface materials. Bare soil is represented with NDVI values which are closest to 0 and water bodies are represented with negative NDVI values [23-25].
Landsat TM data of the study area with spatial resolution of 30 m was used for generation of NDVI image. After the production of the NDVI image, the following formula was used to generate a C factor map from NDVI values [26-28]:
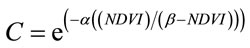 (5)
(5)
where α and β are unit less parameters that determine the shape of the curve relating to NDVI and the C factor. [26,27] found that this scaling approach gave better results than assuming a linear relationship. Finally, the values of 2 and 1 were selected for the parameters α and β, respectively which seems to give good results as mentioned in related literatures. As the C factor ranges between 0 and 1, a value of 0 was assigned to a few pixels with negative values and a value of 1 to pixels with value greater than 1.
3.5. Supporting Conservation Practice Factor (P)
The support practice factor P represents the effects of those practices such as contouring, strip cropping, terracing, etc. that help prevent soil from eroding by reducing the rate of water runoff. Table 2 shows the value of support practice factor according to the cultivating methods and slope [29]. The P value range 0 to 1 where 0 represents very good manmade erosion resistance facility and 1 represents no manmade erosion resistance facility.
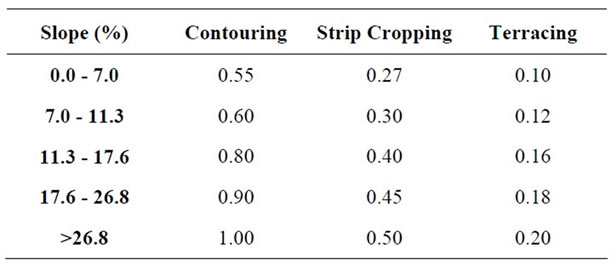
Table 2. Support practice factor according to the types of cultivation and slope.
4. Result and Discussion
4.1. Rainfall and Runoff Erosivity Factor (R)
The average annual rainfall data of nine surrounding rain gauge stations was used to get the rainfall distribution map of the entire watershed. The average annual rainfall in the study area varied between 880 mm to 1480 mm.
The rainfall & runoff erosivity factor map (Figure 2) was generated in Arc-GIS from average annual rainfall map. The erosivity factor varied from 508 - 584 MJ ha/mm/hr/yr.
4.2. Soil Erodibility Factor (K)
Soil erodibility is a quantitative estimation of erodibility of particular soil type and the main factor affecting the capability of the soil to erode is its soil texture. However the other factors affecting K factor are soil structure, permeability and the organic matter content.
Soil erodibility factor map (Figure 3) was prepared from soil map of the study area based on different soil textures. The soil distribution in the study area and derived erodibility factor is given in Table 3.
4.3. Topographic factor (LS)
The topographic factors slope gradient and slope length significantly influence soil erosion. Slope and flow accumulation grid was prepared from ASTER DEM.
Since USLE is only applicable to rill and inter-rill erosion, there should be upper bound to slope length. To enforce such an upper bound the flow accumulation grid was modified to make sure the flow length did not exceed 180 m, which seems a reasonable flow length according to [30]. Since DEM has a resolution of 30 × 30 m; the flow accumulation cannot exceed 6 grid cells. Therefore using raster calculator all cells with flow accumulation greater than and equal to 6 were assigned the value 6. Slope was calculated using the available slope function in ARCGIS. Using ASTER DEM derived flow accumulation and slope grid, a LS-factor map was created, which is shown in Figure 4. LS factor values range from 0 - 20 but most of the area are in 0 - 2 range with some high values occurring in the hilly areas.

Figure 2. Rainfall & runoff erosivity factor map of study area.

Figure 3. Soil erodibility factor map of the study area.

Table 3. Soil types statistics and soil erodibility factor values of the study area.
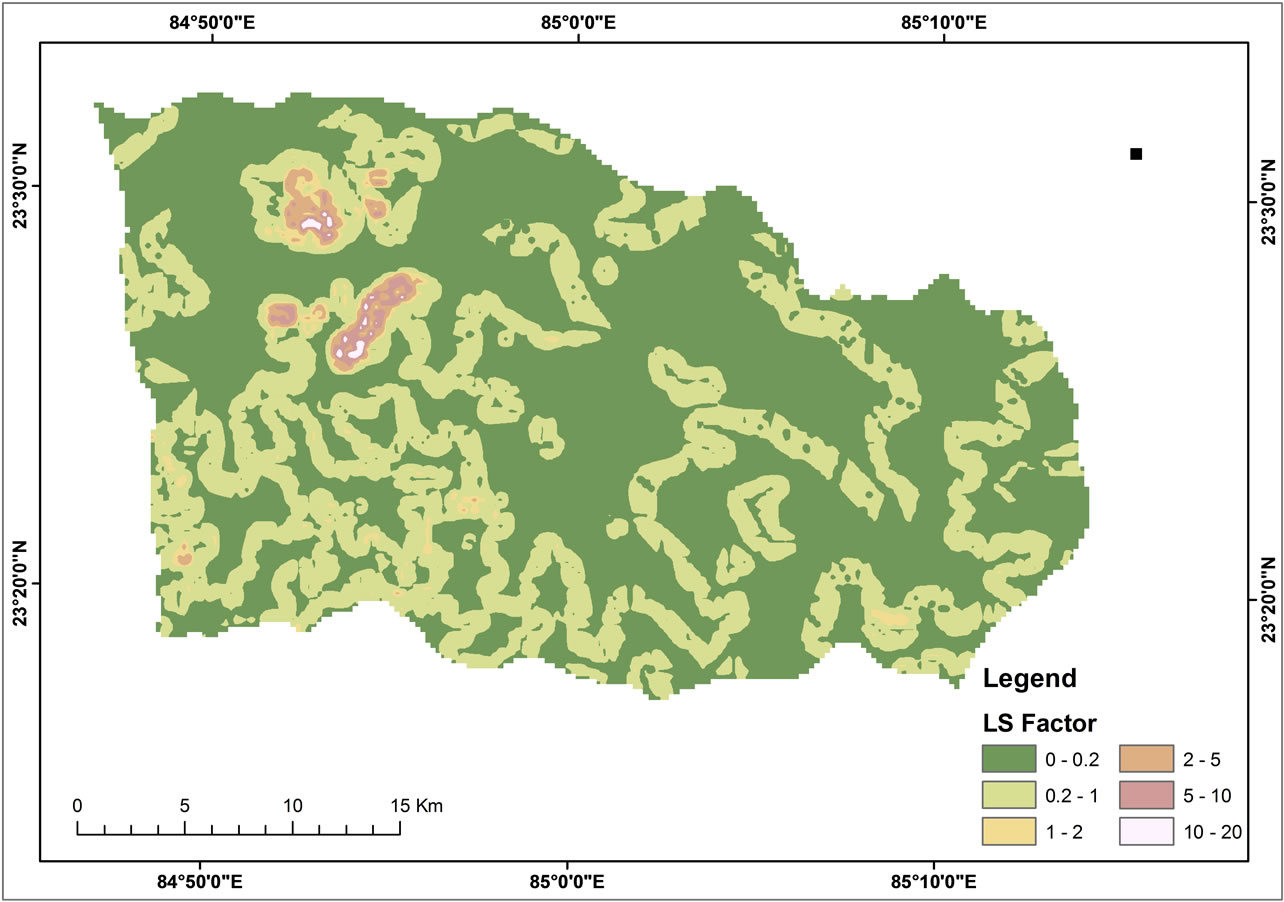
Figure 4. Topographic factor (LS) map of study area.
4.4. Cropping Management Factor (C) & Conservation Practice Factor (P)
Using the NDVI image derived from Landsat TM satellite data of the study area C factor map was generated as shown in Figure 5. The C factor values in the study area varied between 0.058 to 1.The forest areas shows C values between 0.05 to 0.2 with waterbodies showing values approaching 1. Agricultural areas in the study area show c factor values varying between 0.3 to 0.6.
In the study area no major conservation practices are followed except that the agricultural plots under cultivation are bunded. On the basis of value suggested by [31], agricultural land were assigned P factor of 0.28 and other land uses were assigned P factor of 1.
4.5. Soil Loss Mapping
The main goal of this study was to test the USLE model in the study area. The main result of USLE is prediction of erosion risk. All the USLE parameters determined for the study area were either in spatial format and/or in numerical format. The spatial maps and other factors were integrated using USLE empirical formula Equation (1)

Figure 5. C-factor map of study area.

Figure 6. Average annual soil loss map of study area.

Table 4. Area under various soil loss zones of the study area.
and analyzed in Arc GIS module. The annual soil loss map obtained were grouped in the following scales of priority: Slight (0 to 5 ton/ha/yr), Moderate (5 to 10 ton/ha/yr), High (10 to 20 ton/ha/yr), Very High (20 to 40 ton/ha/yr), Severe (40 to 80 ton/ha/hr), Very Severe (>80 ton/ha/yr) annual erosion classes as per guidelines suggested by [32] for Indian conditions. Figure 6 shows annual erosion map of study area, helpful in identification of areas vulnerable to soil erosion. Table 4 shows the spatial distribution of different erosion classes in the study area. The mean annual soil loss estimated for the entire watershed is 12.20 ton /ha/yr. As expected hilltops and bare land witness the highest annual soil loss (>80 ton/ha/yr). There is an increase in soil loss with increased slope gradient. Major part of the watershed is under slight to moderate soil loss zone. Only 18.2% of the study area is under high or very high soil loss. We find that the agricultural lands with increase in slope gradient experience more soil loss. Therefore more emphasis should be provided to high slope gradient areas for soil conservation planning.
5. Conclusion
Creation of database through conventional methods is time consuming, tedious and is difficult to handle. Therefore various thematic layers representing different factors of USLE were generated and overlaid in GIS framework to compute the spatially distributed average annual soil erosion map for the Upper South Koel basin. A quantitative assessment of average annual soil loss was done for the study area. The study revealed that area covered under slight, moderate, high, very high, severe, very severe soil loss potential zones are 64.70%, 17.10%, 10.05%, 4.65%, 1.60%, 1.90% respectively. The average annual soil loss map will definitely be helpful in identification of priority areas for implementation of soil conservation measures and effective checking of soil loss.
REFERENCES
- C. S. Renschler, C. Mannaerts and B. Diekkrüger, 1999. Evaluating Spatial and Temporal Variability in Soil Erosion Risk—Rainfall Erosivity and Soil Loss Ratios in Andalusia, Spain,” Catena, Vol. 34, No. 3-4, 1999, pp. 209-225. doi:10.1016/S0341-8162(98)00117-9
- C. Kosmas, N. Danalatos, H. N. Cammeraat, M. Chabart, J. Diamantopoulos, R. Faand, L. Gutierrez, A. Jacob, H. Marques, J. Martinez-Fernandez, A. Mizara, N. Moustakas, J. M. Niclau, C. Oliveros, G. Pinna, R. Puddu, J. Puigdefabrgas, M. Roxo, A. Simao, G. Stamou, et al., “The Effect of Land Use on Runoff and Soil Erosion Rates under Mediterranean Conditions,” Catena, Vol. 29, No. 1, 1997, pp. 45-59. doi:10.1016/S0341-8162(96)00062-8
- G. O. Schwab, D. D. Fangmeier, W. J. Elliot, et al., “Soil and Water Conservation Engineering,” 4th Edition, John Wiley & Sons, Inc., New York, 1993, pp. 131-138.
- D. V. V. Narayan and R. Babu, “Estimation of Soil Erosion in India,” Journal of Irrigation and Drainage Engineering, Vol. 109, No. 4, 1983, pp. 419-431. doi:10.1061/(ASCE)0733-9437(1983)109:4(419)
- L. D. Meyer and W. H. Wischmeier, “Mathematical Simulation of the Processes of Soil Erosion by Water,” Transactions on American Society of Agricultural and Biological Engineers, Vol. 12, No. 6, 1969, pp. 754-758.
- P. K. Singh, P. K. Bhunya, S. K. Mishra and U. C. Chaube, “A Sediment Graph Model Based on SCS-CN Method,” Journal of Hydrology, Vol. 349, No. 1-2, 2008, pp. 244- 255. doi:10.1016/j.jhydrol.2007.11.004
- Z. H. Shi, S. F. Cai, S. W. Ding, T. W. Wang and T. L. Chow, “Soil Conservation Planning at the Small Watershed Level Using RUSLE with GIS: A Case Study in the Three Gorge Area of China,” Catena, Vol. 55, No. 1, 2004, pp. 33-48. doi:10.1016/S0341-8162(03)00088-2
- S. D. Angima, D. E. Stott, M. K. O’Neill, C. K. Ong and G. A. Weesies, “Soil Erosion Prediction Using RUSLE for Central Kenyan Highland Conditions,” Agriculture, Ecosystems and Environment, Vol. 97, No. 1-3, 2003, pp. 295-308. doi:10.1016/S0167-8809(03)00011-2
- W. S. Merritt, R. A. Letcher and A. J. Jakeman, “A Review of Erosion and Sediment Transport Models,” Environmental Modelling & Software, Vol. 18, No. 8-9, 2003, pp. 761-799. doi:10.1016/S1364-8152(03)00078-1
- P. Pilesjo, “GIS and Remote Sensing for Soil Erosion Studies in Semi-Arid Environments,” Ph.D. Thesis, University of Lund, Lund, 1992.
- G. I. Metternicht and A. Fermont, “Estimating Erosion Surface Features by Linear Mixture Modeling,” Remote Sensing of Environment, Vol. 64, No. 3, 1998, pp. 254- 265. doi:10.1016/S0034-4257(97)00172-7
- W. H. Wischmeier and D. D. Smith, “Predicting Rainfall Erosion Losses from Crop Land East of Rocky Mountains—Guide for Selection of Practices for Soil and Water Conservation, US Department of Agriculture Hand Book No. 282,” Agricultural Research Service—US Department of Agriculture, Washington DC, 1965.
- W. H. Wischmeier and D. D. Smith, “Predicting Rainfall-Erosion Losses: A Guide to Conservation Planning, Agricultural Handbook No. 537,” Agricultural Research Service—US Department of Agriculture, Washington DC, 1978.
- M. Grimm, R. J. A. Jones, E. Rusco and L. Montanarella, “Soil Erosion Risk in Italy: A Revised USLE Approach, European Soil Bureau Research Report No. 11,” Office for Official Publications of the European Communities, Luxembourg, 2003.
- A. Shamshad, M. N. Azhari, M. H., Isa, W. M. A. Wan Hussin and B. P. Parida, “Development of an Appropriate Procedure for Estimation of RUSLE EI30 Index and Preparation of Erosivity Maps for Pulau Penang in Peninsular Malaysia,” Catena, Vol. 72, No. 3, 2008, pp. 423-432. doi:10.1016/j.catena.2007.08.002
- G. Singh, S. Chandra and R. Babu, “Soil Loss and Prediction Research in India,” Bulletin No. T-12/D9, Central Soil and Water Conservation Research Training Institute, Dehra Dun, 1981.
- G. O. Schwab, R. K. Frevert, T. W. Edminster and K. K. Barnes, “Soil Water Conservation Engineering,” 3rd Edition, Wiley, New York, 1981.
- I. Moore and J. P. Wilson, “Length Slope Factor for the Revised Universal Soil Loss Equation: Simplified Method of Solution,” Journal of Soil and Water Conservation, Vol. 47, No. 4, 1992, pp. 423-428.
- I. Moore and G. Burch, “Physical Basis of the LengthSlope Factor in the Universal Soil Loss Equation,” Soil Science Society of America Journal, Vol. 50, No. 5, 1986, pp. 1294-1298. doi:10.2136/sssaj1986.03615995005000050042x
- I. Moore and G. Burch, “Modeling Erosion and Deposition: Topographic Effects,” Transactions of the American Society of Agricultural and Biological Engineers, Vol. 29, No. 6, 1986, pp. 1624-1630, 1640.
- K. Edwards, “Runoff and Soil Loss Studies in New South Wales, Technical Handbook No. 10,” Soil Conservation Service of NSW, Sydney, 1987.
- H. Mitasova and L. Mitas, “Modeling Soil Detachment with RUSLE 3d Using GIS,” University of Illinois at Urbana-Champaign, 1999. http://www.gis.uiuc.edu:2280/modviz/erosion/usle.html
- T. M. Lillesand, R. W. Kiefer and J. W. Chipman, “Remote Sensing and Image Interpretation,” 5th Edition, John Wiley & Sons, Inc., New York, 2004.
- M. F. Jasinski, “Sensitivity of the Normalized Difference Vegetation Index to Subpixel Canopy Cover, Soil Albedo, and Pixel Scale,” Remote Sensing of Environment, Vol. 32, No. 2-3, 1990, pp. 169-187. doi:10.1016/0034-4257(90)90016-F
- S. A. Sader and J. C. Winne, “RGB-NDVI Colour Composites for Visualizing Forest Change Dynamics,” International Journal of Remote Sensing, Vol. 13, No. 16, 1992, pp. 3055-3067. doi:10.1080/01431169208904102
- J. M. Van der Knijff, R. J. A. Jones and L. Montanarella, “Soil Erosion Risk Assessment in Europe,” Office for Official Publications of the European Communities, Luxembourg, 2000, 34 pp.
- M. Van der Knijff, R. J. A. Jones and L. Montanarella, Soil Erosion Risk in Italy,” Office for Official Publications of the European Communities, Luxembourg, 1999, 54 pp.
- W. J. D. Van Leeuwen and G. Sammons, “Vegetation Dynamics and Soil Erosion Modeling Using Remotely Sensed Data (MODIS) and GIS,” 10th Biennial USDA Forest Service Remote Sensing Applications Conference, US Department of Agriculture Forest Service Remote Sensing Applications Center, Salt Lake City, 5-9 April 2004.
- G. J. Shin, “The Analysis of Soil Erosion Analysis in Watershed Using GIS,” Ph.D. Dissertation, Department of Civil Engineering, Gang-Won National University, Chuncheon, 1999.
- M. T. Jabbar, “Application of GIS to Estimate Soil Erosion Using USLE,” Geo-Spatial Information Science, Vol. 6, No. 1, 2003, pp. 34-37. doi:10.1007/BF02826699
- Y. P. Rao, “Evaluation of Cropping Management Factor in Universal Soil Loss Equation under Natural Rainfall Condition of Kharagpur, India,” Proceedings of the Southeast Asian Regional Symposium on Problems of Soil Erosion and Sedimentation, Bangkok, 27-29 January 1981, pp. 241-254.
- G. Singh, R. Babu, P. Narain, L. S. Bhusan and I. P. Abrol, “Soil Erosion Rates in India,” Journal of Soil and Water Conservation, Vol. 47, No. 1, 1992, pp. 97-99.
NOTES
*Corresponding author.

