Natural Science
Vol.08 No.03(2016), Article ID:64668,8 pages
10.4236/ns.2016.83018
Quantum Dark Energy from the Hyperbolic Transfinite Cantorian Geometry of the Cosmos
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 February 2016; accepted 14 March 2016; published 17 March 2016
ABSTRACT
The quintessence of hyperbolic geometry is transferred to a transfinite Cantorian-fractal setting in the present work. Starting from the building block of E-infinity Cantorian spacetime theory, namely a quantum pre-particle zero set as a core and a quantum pre-wave empty set as cobordism or surface of the core, we connect the interaction of two such self similar units to a compact four dimensional manifold and a corresponding holographic boundary akin to the compactified Klein modular curve with SL(2,7) symmetry. Based on this model in conjunction with a 4D compact hy- perbolic manifold M(4) and the associated general theory, the so obtained ordinary and dark en- ergy density of the cosmos is found to be in complete agreement with previous analysis as well as cosmic measurements and observations such as WMAP and Type 1a supernova.
Keywords:
Dark Energy, Accelerated Cosmic Expansion, Hyperbolic Geometry, Fractal Geometry, Transfinite set Theory, ‘tHooft Dimensional Regularization, Hardy’s Quantum Entanglement, Davis Hyperbolic Manifold, Compactified Klein Modular Curve, Fractal Counting, Lie Symmetry Groups, Stein Spaces

1. Introduction and Preliminary Information
The present work gives explicit analysis for determining the ordinary and the dark energy density of the universe [1] [2] based on an unorthodox combination of modern extension of hyperbolic geometry [3] [4] and recent advances in nonlinear dynamics, deterministic chaos and random fractals [5] . We start from two parallel lines of thinking, namely first from our topological conception of a pre-quantum particle described by a bi dimension
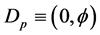 zero set [6] [7] and a pre-quantum wave modelled by
zero set [6] [7] and a pre-quantum wave modelled by 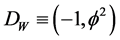 empty set [6] [7] where
empty set [6] [7] where 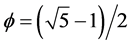 as found from the generic von Neumann-Connes dimensional function of an x manifold corresponding to Penrose fractal tiling universe [6]
as found from the generic von Neumann-Connes dimensional function of an x manifold corresponding to Penrose fractal tiling universe [6]
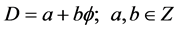 (1)
(1)
The second line of thinking within the present scheme is the compact 4D hyperbolic manifold M(4) of M.W.
Davis [4] which has 1400 cells and a hyperbolic volume equal 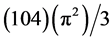 [4] . Incidentally the Euler characteristic of this manifold is
[4] . Incidentally the Euler characteristic of this manifold is 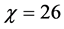 which differs from that of E-infinity Cantorian spacetime [6] - [14] by only
which differs from that of E-infinity Cantorian spacetime [6] - [14] by only 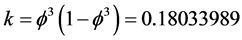 being
being 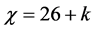 where k is the ‘tHooft renormalon [11] [15] . The possibility of a Hardy entangleon elementary particle
where k is the ‘tHooft renormalon [11] [15] . The possibility of a Hardy entangleon elementary particle  as well as an entangleon particle
as well as an entangleon particle 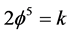 was proposed by the
was proposed by the
present Author as well as others a relatively short time ago [11] [15] - [17] . From here onwards and as we will see momentarily, the two lines of though mentioned will converge towards a common conclusion, namely that the holographic boundary of our universe can be modelled exactly by 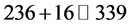 degrees of freedom of a compactified Klein modular curve plus gravity and spacetime [6] - [11] and that the exact ordinary energy density of the cosmos is given by [8]
degrees of freedom of a compactified Klein modular curve plus gravity and spacetime [6] - [11] and that the exact ordinary energy density of the cosmos is given by [8]
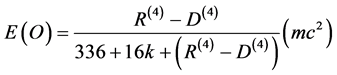 (2)
(2)
where R(4) = 20 is the number of independent components of the Riemann-Einstein tensor in D(4) = 4 dimensional Einstein spacetime. Inserting in E(O) of equation (2) one finds the obvious result [8]
 (3)
(3)
That means E(O) is about 4.5% of the maximal energy density of the cosmos, i.e. Einstein’s density while the dark energy density is clearly the self explanatory formula  which is nearly 95.5% of Einstein’s maximal energy density E = mc2 as found in earlier publications and in full agreement with the actual cosmic measurements [1] [2] [7] . Our next task is to give the details of the analysis leading to the preceding result using the suggested methodology of E-infinity theory [6] - [9] [11] - [15] [18] [19] .
which is nearly 95.5% of Einstein’s maximal energy density E = mc2 as found in earlier publications and in full agreement with the actual cosmic measurements [1] [2] [7] . Our next task is to give the details of the analysis leading to the preceding result using the suggested methodology of E-infinity theory [6] - [9] [11] - [15] [18] [19] .
2. The Making of Davis M(4) Hyperbolic 4D Manifold with c = 26 to a Transfinite Hyperbolic Manifold with c = 26 + k
M.W. Davis found in [4] a compact hyperbolic 4-manifold built upon 120-cell PCH(4) where P can be cut into 14,400 congruent orthoschemes, each with a volume equal to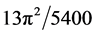 . Consequently we have the total hyperbolic volume [3] [4]
. Consequently we have the total hyperbolic volume [3] [4]

Now the transfinite harmonization methods of E-infinity theory [6] - [9] suggest immediately upon inspecting
the above expression that 104 should be replaced by 104.7213596, 


[12] - [14] [20] . Now for the reader not familiar with E-infinity transfinite correction, the simplest thing to make the above plausible is to compute the expression of equation 4 first explicitly [3] [4]

Subsequently alone from the magnitude of the integer value 342 we notice that (342)(2) = 684 which is almost the value of the sum of all the dimensions of the two and three Stein spaces, namely [9] [18]

This result in turn is shown in E-infinity theory to be related to the theoretical exact value of the inverse electromagnetic fine structure constant 

where 


as we concluded earlier on. Confining ourselves to the integer theory only, it is easily reasoned that the 342.7 is approximately equal to 343 the hyperbolic volume of our manifold could be seen as the dimensions of a Klein modular space with its well known 336 degrees of freedom when we add to it the 7 embedding dimension of 


which is simply equal to the compactified fractal degrees of freedom of 

where 336 may be seen as say the dim SL(2,7) or R(8) of Riemannian tensor in super space D = 8 or alternatively the number of kissing spheres 
compactified holographic boundary of our actual spacetime which in an integer approximation of the standard model amounts to 336 plus |SU(2)| = 3 giving us the well known 339. Recalling that the first massless level in Heterotic string theory [16] is given by 8064 and that this may be found either from the bulk or alternatively from the holographic boundary by a multiplication of the degree of freedom of 
Consequently by squaring 

From the above we see that we are back to the same holographic boundary of our theory and that 

the Immirzi parameter of our analysis which may be interpreted as the entanglement probability of two self entangled points in our space, each with self entanglement probability

This way we see that our analysis is circulatory consistent.
3. The Energy Density of Our Cosmos
Now we are in a position to tackle the task of determining the energy density of ordinary energy and consequently that of dark energy of the cosmos. Using the so far obtained insight into the “fuzzy” or transfinite M4 it is not difficult to reason that the maximal E of Einstein density was based on 4D space. That would mean that

of the holographic boundary of our theory. Since E = mc2 is the maximal one hundred percent energy density, then writing 




Consequently we have to expect the measured ordinary energy density to be [11] - [15]

This then implies a “missing” dark energy density of

Setting k @ 0, this simplifies to our previously obtained results [11] - [15]

Note here, as elsewhere, how k plays a crucial role in smoothing the analyses and easing the reaching of general conclusions and deeper insight. In a manner of speech we could say that we put the entire problem under a transfinite microscope enabling us to see how ‘tHooft’s renormalon hypothetical elementary particle works [11] [15] . This normalon is actually made of two other hypothetical particles, namely Hardy’s entangleon 

Pondering this situation we see that the real power of transfinite correction is the following: while overwhelmingly integer based theories are to a far extent consistent, we notice that we have many different theories leading to similar results although they differ substantially from each other at various stages. Transfinite correction fuses different theories and shows that they are exactly the same and that everything fits with everything else at all stages of the analysis. We will address the same subject at various occasions in the rest of the present paper.
4. Transfiniteness―A View from the Standard Model
Seen in the conventional way the standard model contains twelve messenger particles given by the symmetry breaking ofSU(3) SU(2) U(1) dimensions. The experimental discovery of the Higgs is not included in the above, nor is the not discovered yet graviton let alone all super symmetric partners. However seen under the transfinite microscope, E-infinity theory tells us something quite if not radically different. The reason for this deviation is that E-infinity extends fuzziness, i.e. transfiniteness to the counting of particles. It is ordinary counting but with a fractal-Cantorian weight linked to it. This so called fractal logic of counting particles mutates the standard model to a truly magical structure by the following transformation from integer to transfinite counting were we will write on the left hand side the classical counting vis-à-vis the transfinite weight counting on the right hand side of the following Table 1 [17] .
Of course the standard model is not meant to include the Higgs nor graviton in its original form so that when we count following the left hand side of the above Table 1, we find 1 + 3 + 8 = 12. However adding the Higgs and the graviton we find 12 + 1 + 1 = 14. In this way one could come to the conclusion that the standard model plus gravity and massive particles is best served by a Lie symmetry group such as G2 of the exceptional family with 14 isometries corresponding to dim G2 = 14 [12] [13] [16] . The story on the left hand side of the above table tells us however a far more interesting as well as intricate tale. When adding all the fractal numbers of the particles together we find that [21]

This happens to be the square root of the E-infinity exact transfinite value of the inverse electromagnetic fine structure constant 

However adding a quantum pre-wave 






be much harder which was indeed the case while the graviton with 0.032522 would be double as hard. In addi-
tion our 

plication, does indeed simplify the calculations considerably all apart from bringing all valid theories harmoniously together. In all events one or two things should not be lost sight of, namely that Hardy’s entanglement 
[1] [2] [6] [13] . It amounts to 


which is another way to say a fractal eleven dimensional theory. Postulating 



exactly as we derived it earlier on. In fact what could be more convincing than finding E(D) by simply noting that E = mc2 must be multiplied with the ratio of the ‘tHooft dimensionally regularized spacetime 


In this way our Turing transfinite computer using the golden mean based “binary” system [21] may help us dispense with month long super computer calculations and endless Feynman graphs evaluation [10] [16] . At a minimum the present method deserves a careful study.
5. Conclusions
Hyperbolic geometry tamed the problem of geometrical infinity so that we can virtually hold it “in the palm” of our hand as implied in the famous poem of J. Black. Transfiniteness does the rest as far as high energy physics theories are concerned. Applying both theories together, determining the ordinary and the dark energy density of the cosmos becomes a simple back of an envelope calculation for which nothing more is needed other than an ordinary scientific pocket calculator. One should not loose sight of the fact that the ordinary energy density

the dark energy density

as well as Hardy’s quantum entanglement of two quantum particles [17] [20]
are all highly accurate experimentally verified quantities [1] [20] and therefore our conjectured ‘tHooft renormalon particle with the topological index 
mathematical artefact and should in principle be found in the laboratory [7] [13] [15] [20] . The index k could of course be many things as the label index implies. It is the Hausdorff dimension of the renormalon. It could also
be taken to be its topological mass charge or its quantum probability in the same vein as 
[11] - [14] [17] [20] . We stress again that this extra flexibility is not a weakness but rather a strength of the present theory.
Some may ask why we do not start from a differential equation or as it is believed to be the best, if not the only way in high energy particle physics, a Lagrangian? The question is justified logically [16] but not evolutionary [18] [21] . Real life evolves Darwinistically with occasional Lamarckian mutational jumps. The same applies here. Without the scouts and explorers of largely integer theories, we could not recognize where the perfect transfinite theory is located in the vast rugged mountain landscape of the scientific truth. We could discover the power of the golden mean scaling only because pioneers like Gerardus ‘tHooft, Steven Weinberg, Kenneth Wilson and David Gross discovered logarithmic scaling, renormalization and the basic structure of the standard model [10] [16] . With that we rest our case, at least for the moment.
Acknowledgements
The Author is seriously indebted to the work of G. ‘tHoot, L. Hardy and M.W. Davis which forms the basis of the present work. Thanks is also due to his colleagues J.H. He, L. Marek-Crnjac, M.A. Helal as well as all the authors of the papers listed in the references.
Cite this paper
Mohamed S. El Naschie, (2016) Quantum Dark Energy from the Hyperbolic Transfinite Cantorian Geometry of the Cosmos. Natural Science,08,152-159. doi: 10.4236/ns.2016.83018
References
- 1. Ruiz-Lapuente, P. (2010) Dark Energy, Observational and Theoretical Approaches. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139193627
- 2. El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
- 3. Ratcliffe, J.G. (1994) Foundations of Hyperbolic Manifolds. Springer, New York. http://dx.doi.org/10.1007/978-1-4757-4013-4
- 4. Davis, M.W. (1985) A Hyperbolic 4-Manifold. Proceedings of American Mathematical Society, 93, 325-328.
- 5. Gilmore, R. and Lefranc, M. (2002) The Topology of Chaos. John Wiley, New York.
- 6. Marek-Crnjac, L., et al. (2013) Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology. International Journal of Modern Nonlinear Theory and Application, 2, 78-88. http://dx.doi.org/10.4236/ijmnta.2013.21A010
- 7. Marek-Crnjac, L. (2013) Cantorian Space-Time Theory: The Physics of Empty Sets in Connection with Quantum Entanglement and Dark Energy. Lambert Academic Publishing, Saarbrucken.
- 8. El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory & Application, 2, 43-54. http://dx.doi.org/10.4236/ijmnta.2013.21005
- 9. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- 10. ‘tHooft, G. (1994) Under the Spell of Gauge Principle. World Scientific, Singapore.
- 11. El Naschie, M.S. (2015) Dark Energy and Its Cosmic Density from Einstein’s Relativity and Gauge Fields Renormalization Leading to the Possibility of a New ‘tHooft Quasi Particle. The Open Journal of Astronomy, 8, 1-17. http://dx.doi.org/10.2174/1874381101508010001
- 12. Helal, M., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M.S. El Naschie’s Research in E-Infinity Quantum Physics. Open Journal of Microphysics, 3, 141-145. http://dx.doi.org/10.4236/ojm.2013.34020
- 13. Marek-Crnjac, L. and He, J.-H. (2013) An Invitation to El Naschie’s Theory of Cantorian Spacetime and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471.
- 14. El Naschie, M.S. (2015) Mathematical Models and Methods in Dark Energy Theory: Dvoretzky’s Theorem, Casimir Effect, Mobius Geometry. Problems of Nonlinear Analysis in Engineering Systems, 2, 1-16. (University of Kazan Press, Russia, Published in Russian and English language versions)
- 15. El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and ‘tHooft’s 4-ε Fractal Spacetime. American Journal of Astronomy and Astrophysics, 2, 34-37. http://dx.doi.org/10.11648/j.ajaa.20140203.12
- 16. Kaku, M. (1999) Introduction to Superstrings and M-Theory. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0543-2
- 17. Hardy, L. (1993) Nonlocality of Two Particles without Inequalities for Almost All Entangled States. Physical Review Letters, 71, 1665-1668.
- 18. Marek-Crnjac, L. (2008) Stein Spaces in Connection with El Naschie’s Exceptional Lie Groups Hierarchies in High Energy Physics. Chaos, Solitons & Fractals, 38, 309-315. http://dx.doi.org/10.1016/j.chaos.2008.01.022
- 19. El Naschie, M.S. (2013) The Hyperbolic Extension of Sigalotti-Hendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy. Journal of Modern Physics, 4, 354-356. http://dx.doi.org/10.4236/jmp.2013.43049
- 20. Guo, W., Fan, D. and Wei, L. (2015) Experimentally Testing Bell’s Theorem Based on Hardy’s Nonlocal Ladder Proofs. Science China Physics, Mechanics & Astronomy, 58, 1-5. http://dx.doi.org/10.1007/s11433-014-5495-0
- 21. El Naschie, M.S., Olsen, S., He, J.H., Nada, S., Marek-Crnjac, L. and Helal, A. (2012) On the Need for Fractal Logic in High Energy Quantum Physics. International Journal of Modern Nonlinear Theory and Application, 1, 84-92. http://dx.doi.org/10.4236/ijmnta.2012.13012




