Natural Science
Vol.06 No.11(2014), Article ID:48375,64 pages
10.4236/ns.2014.611087
On the Physics inside a Closed, Static, Rotating Einsteinian Hypersphere in Due Consideration of the Galaxy
Ernst Karl Kunst
Im Spicher Garten 5, Königswinter, Germany
Email: ernstkunst@aol.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 May 2014; revised 20 June 2014; accepted 2 July 2014
ABSTRACT
Einstein’s weak equivalence principle suggests that gravity and acceleration (centrifugal force) are indistinguishable from each other and, therefore, equivalent. We maintain that they are not only equivalent, but even identical, or to rephrase the main statement of this work: A gravitational force does not exist. Rather, gravity is a fictitious force, or, more pointedly: Gravity is the centrifugal force which acts upon material bodies within the rotating S -hypersphere of the Universe. These in turn warp the adjacent space-fabric, shaping it to the well-known field geometry of general relativity.
Keywords:
Cosmology, Hypersphere, Cosmological Redshift, Redshift by Deflection, Redshift “Anomalies” of the Supernova Data, “Dark Energy”, CMB ≡ Enthropic Planck Radiation, Gravity ≡ Diverted Centrifugal Force; Time, Mass and “Dark Matter”, Foucault’s Law Raises Kicks of Gyros, The Galaxy’s Former Position and Present Drift

1. Introduction
As widely known proposed Georges Lemaître in 1927 and Edwin Hubble in 1929 a redshift of far-away galaxies, which is proportional to their distance (to a high degree in the “nearer” neighborhood of the Milky Way Galaxy) [1] [2] . Since that time “Hubble’s law” is considered as due to the isotropic expansion of the Universe and, thus, apart from the nearly uniform cosmic microwace background (CMB) radiation of 2.725 K, as the main observational pillar for the standard cosmological model. Within the framework of the latter the Universe is described by a spacetime manifold endowed with the homogeneous and isotropic Friedmann-Robertson-Walker metric. In summary the picture that emerges from imposition of the Einstein equations on this metric is of the Universe expanding away from an initial singularity of infinite density (big bang). However, between the predictions of the expansion hypothesis and the observations made by astronomers especially in the last decades are fatal contradictions. These only partially could be evaded through the recourse to new hypothetical things, e.g. the so called dark energy, an enigmatic negative pressure in the expanding Universe which presumingly dominates and accelerates the latter at late times. This hypothetical energy component has been invented solely to adjust theory to observational results, i.e. direct luminosity measurements of very distant type Ia supernovae in comparison to distance calculations of the latter from their redshift on the grounds of big bang theory (e.g. Riess et al., 2001 [3] ). Other recent observations strongly hind at further incostencies in current big bang paradigm, e.g.:
1) Red galaxies are clustered more strongly than blue galaxies, with both the brightest and faintest red galaxies showing the strongest clustering. Furthermore, red and blue galaxies tend to occupy different regions of space (Swanson, 2008 [4] ). 2) The evidence is overwhelming that the vicinity of the Galaxy is the domain of relative small star-forming galaxies, while farther away (in earlier epochs according to big bang theory) giant galaxies exist(ed) and preveil(ed). This phenomenon, which is dubbed down-sizing, is obviously at odds with the basic premise of hierarchical structure formation paradigm of big bang theory (see e.g. Renzini and Daddi, 2008 [5] ). 3) High-z UV surface brightness data for galaxies from the Hubble Ultra Deep Field (HUDF) and low-z data from the Galaxy Evolution Explorer (GALEX) have been used to test predictions of a Friedmann- Robertson-Walker expanding Universe and a non-expanding Universe up to z = 6. The data from HUDF as well as from GALEX are clearly compatible with a non-expanding Universe and incompatible with the expansion hypothesis (Lerner, 2005 [6] ). 4) Full-sky temperature maps of the CMB at very low temperature from the “Wilkinson Microwave Anisotropy Probe” (WMPA) exhibit some statistically significant anomalies compared to standard inflationary cosmology (e.g. Craig, 2005 [7] ).
It is well known that from a purely mathematical point of view it is indemonstrable whether the spatial section M of the spacetime manifold M4 = R × M of the Universe we happen to live in is Euclidian (E3), spherical (S3) or hyperbolic (H3). Or, to rephrase this within in the framework of standard cosmology, whether the Gaussian curvature of M is k = 0, 1, or, −1, respectively. Here we demand k = 1 and maintain and will show in the following that:
1) The Universe is a closed, static, self-containing three-sphere S3 rotating steadily in four-dimensional space spatially with Euclidian E4 metric geometrically (locally) and neither expanding nor retracting;
2) The Hubble (Cosmological) redshift is due to the four-dimensional orthogonal displacement spatially of the emitter from the receiver’s tangential Minkowski space in the three-sphere S3, being equivalent to the bending of the light’s trajectory in the curved space of the latter and not to its expansion;
3) The deviations of distance calculations on the grounds of supernova data from the standard expansion model, which currently are ascribed to the mentioned putative dark energy, correctly reflect the light’s redshift due to curvature of the hypersphere and, thus, are no deviations at all;
4) Gravity is a fictitious force caused by the S3-latitude dependent centrifugal force within the rotating hypersphere in association with the warping of the local space fabric around material bodies and not a special attracting force of nature;
5) The cosmic microwave background radiation (CMB) is the enthropic (Planckian) radiation in the closed, static three-sphere S3 and not relic radiation of the big bang;
6) The large-angle “anomalies” in the CMB are imprints of the Universe’s four-dimensional shape and of the floating Milky-Way Galaxy’s location in the latter in ever more distant past and no anomalies at all. The same applies to the recently detected very regular tiny temperature fluctuations of the CMB, which falsely have been interpreted as gravitational waves in the very beginning of the putative expanding Universe;
7) Rest mass and energy of the protron are equivalent to quantum of rest time, being the physical projection of minor four-dimensional warpings spatially of three-dimensional flat space locally of the three-sphere S3 into local four-dimensional space and are not associated with a special field of nature;
8) Mass of celestial bodies results from their four-dimensional height cubed spatially and is calculable from the latter;
9) The so-called Dark matter is the calculable gravitational mass of the S3-latitude dependent energy content of a cosmic body’s exterior and interior Schwarzschild field―Schwarzschild mass―and not a form of whatever matter;
10) Owing to Foucault’s law, according to which rotation axis and direction of rotation of a spinning heavy gyro in a rotating system tend to come in coincidence with the respective parameters of the latter by the shortest way, a fast rotator will warp its local S3-space and divert the universal centrifugal force within the rotating S3- hypersphere with the physical consequence that its state of motion in and outside of gravitational fields can be calculably altered.
The proposed physical notion of the Universe explains all contradictions and constraints of current cosmological theory, as will be shown below, especially delivers the redshift by bending of lightpath the correct data of the supernova observations (e.g. of SN 1997ff) and, thus, reveals the “deviations” from standard big bang theory being an illusionary effect. A hypothetical dark energy to explain the deviations of distance calculations on the grounds of supernova data from the standard model is not needed in the correct cosmological theory. Fur- thermore, among others delivers the novel cosmologigal notion a convincing explanation of the origin of mass and time, and, in connection with this, of “dark matter”.
However, the greatest preference of the emerging novel picture of the Universe’s true geometry and the associated physics doubtlessly is the possibility of testing it in accordance with the above No. 10) in the Earthly laboratory by relative unsophisticated experiments―aside from the mentioned observational support―, as will be shown in chapters 10 and 11 (see also Appendix 4 and Appendix 5).
The implications are also of major technological importance in the widest sense.
In a first step we explicitly take recourse to Einstein’s static cosmological model of 1917, but without the famous constant Λ [8] . Thus, relying on and in accord with the latter, we assume the metric of the Universe to be one of a perfect static, but time-independent and spinning three-sphere S3 with a fixed volume 2π2Ρ3 (as a first step for convenience and reasons of simplicity; later on it will be shown that the observed “anomalies” in the CMB suggest an ellipsodial Universe as a more realistic approach), where Ρ (capital RHO) denotes constant radius of the Universe, i.e. the metric induced on the set of fixed points at unit distance from the origin in a geometrically four-dimensional space with (locally) Euclidian E4 metric with the coordinate differences squared:
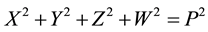 .
.
2. Heuristic Arguments in Favor of Reddening of Deflected Light
In order to underlay the latter assumption and the above thesis 2), respectively, obviously first and foremost convincingly has to be shown that redshift of light also necessarily follows from the light’s curved trajectory owing to the curvature of the S3-sphere embedded in flat four-dimensional Euclidian space besides the known relativistic causes: Translational motion, acceleration and gravity in four-dimensional spacetime. This for, in the following the heuristic-physical arguments in favour of redshift by bending of light-path will be discussed before we turn to the relativistic derivation further below. In general relativity the ratio of the frequencies at the receiver S2 to the emitter S1 in a weak uniform gravitational field is of value
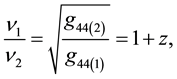 (1)
(1)
where 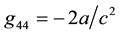 of the approximate Minkowskian metric
of the approximate Minkowskian metric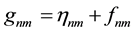 , z denotes the red shift at point
, z denotes the red shift at point
S2 and the acceleration of the observer in accord with Newtonian gravity. Therefore, the red shift of light due to the gravitational field is not regarded as a unique characteristic and, therewith, not as a direct test of general relativity.
The geodesic equations in the Schwarzschild solution deliver for the deflection of light the well known value
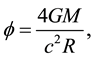 (2)
(2)
which is considered to be one of the classical tests of general relativity. If the radius of the Sun is taken as R, this gives, expressed in units of arc, the experimentally confirmed deflection ϕ = 1.75'. Note that a Newtonian derivation delivers halve this [9] . From the properties of the Schwarzschild solution
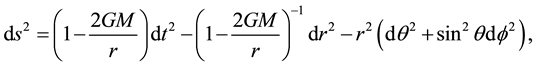 (3)
(3)
which otherwise lead to all known general relativistic effects in the slow motion approximation, the redshift due to bending of light cannot be derived right forwardly. But the following equivalence considerations show that analogously to redshift by gravity from bending of lightpath a redshift has to be expected, too, whereby in both cases (‒g44)1/2 being the very cause. The―not quite correct―physical notion underlying the gravitational effect, that light loses energy in climbing out of a gravitational potential well, is quite the same in the case of light deflection, although with the alteration that the light ray moves tangentially with respect to the potential well. The basic premise in the latter case is that (in the slow motion approximation) by deviation  from the time-like geodesic of the Minkowski metric ηnm (the non deflected path) light loses energy as well (see below).
from the time-like geodesic of the Minkowski metric ηnm (the non deflected path) light loses energy as well (see below).
On condition that 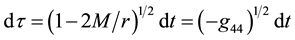 and the coordinate time interval
and the coordinate time interval 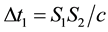 (of the
(of the
undeflected path; see Figure 1), on the grounds of general relativity one can write the following approximate Pythagorean expression for the deflection as well as for the associated reddening of light:
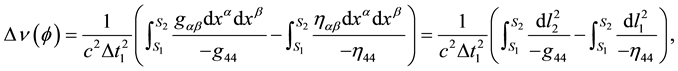 (4)
(4)
where  (see Figure 1). From the preceding Schwarzschild formula we take
(see Figure 1). From the preceding Schwarzschild formula we take
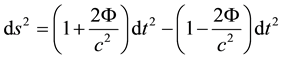
and, thus, if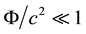 , Equation (4) becomes to
, Equation (4) becomes to
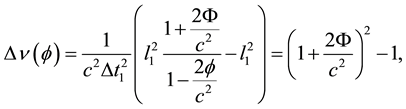 (5)
(5)
where from eventually is deduced:
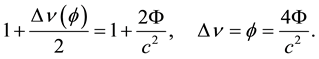 (6)
(6)
From Equations (4) to (6) it is obvious that the receiver S2 “observes” the emitter S1 lifted up to a less negative gravitational potential, the difference being exactly proportinal to the deflection 4Φ/c2 and, therewith, to a corresponding loss of energy and redshift of the same order of magnitude (see Figure 1).
However, it is clear that this is the classical approach to our result, whereas the real meaning of (6) must be that the redshift of the light is solely due to the curvature of its path, or, deflection Δν = 4Φ/c2 from pseudo- Euclidian (Minkowskian) geodesics (see below).
The previous considerations have been leading to the result that reddening of light by deflection and by gravity are both of origin (‒g44)1/2, i.e. they are equivalent. This implies redshift due to the gravitational field being a special case of Equation (6), thus, taking the form
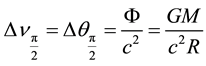 (6a)
(6a)
if the total redshift is restricted to θ = 1/2π, the highest possible deflection which light, travelling from out a gravitational potential well, can experience―as observed from flat Minkowski metric ηnm “outside” the gravitational field. This point of view necessarily follows because, as widely known, the simplest metric of the Schwar- zschild field requires t = const and θ = 1/2π and thus, if the coordinate r → ∞, Δθ becomes small in accord with Equation (6a).
Therefore, redshift according to Equation (6) as well as (6a) in neither case is caused by gravity alone, but also by the curvature of light path due to the metric of the gravitational field.
In the following it will be shown this heuristically derivated assumption to be the correct physical notion, being of relativistic origin.
Figure 1. Redshift of light by deflection: the undeflected paths are shown dashed.
3. Relativistic Derivation of the Redshift of Deflected Light and of the Equivalence of Kinematics, Metric, or, Acceleration as Its Cause; Conservation of Photon Energy in the Closed Universe
3.1. Kinematical Deflection of Light and Associated Redshift
Suppose, the light emitted from a far distant inertially and reversely to the line of sight moving emitter with regard to the resting receiver be aberrationally deflected according to the special relativistic formula
We require φ = 1/2π such that the above equation becomes to

where

Thus, it follows that

where vapp denotes apparent velocity.
Evidently fulfills relation (7b) the equation of the circle:
from the emitter moving with any velocity reversely to the line of sight for the receiver seems to be emitted from
a point of a circle defined by the above relations. i.e. all points

angular dimension 1/2π to zero, apparently must lay on a quarter circle 1/2πr such that the velocity of the emitter be 

where φ = 0 → 1/4π and 
point


(-) sign of velocity vapp is neglectable because it denotes the above pointed out withdrawel of the emitter from the receiver (see Figure 2).
Note that the receiver’s line of sight extends tangentially into the direction of the tangent vector to the apparently curved light path rΑ with the consequence that the former generally will observe all emitters deflected by some angle
Figure 2. Appearent circular deflection of moving emitter.
It follows in the case 
sight and if 
angle φ (see Figure 2). i.e. the Minkowski projection of the ingoing light under those conditions is the very cause of the above apparent circular order of velocity in dependence on its magnitude. This implies that all light ingoing from emitters moving in accord with the above discussed requirements relative to the receiver’s Minkowski projection at reception to be red shifted relativistically in the order of

where λobs and λ0 denote observed wavelength of the emitter and the standard wavelength as measured in the receiver’s rest frame, respectively. It should be underlined that no direct measurements of velocity are possible but only derivation of the latter due to changes of wavelength through Equation (8) squared with the result:

The red shift of light expressed in the apparent circular units of Equation (7b) takes the simple form

and the sum of two redshifts z and, therewith according to Equation (8a) of two velocities, the value:

where
It follows, the emitter’s time in comparison to the receiver’s rest time to be dilated by the factor

Also should be noticed that dimensionless velocity v/c according to Equation (8a) be about that point in space
geometrically where the tangent referring to angle
of the quarter circle, intersects the vector of the emitter’s motion with dimensionless velocity → 1 orthogonal to the receiver’s tangential Minkowski space at z = 1 (see Figure 2).
In conclusion it is indistinguishable for the receiver, whether the redshift of the light ingoing from the emitter in accord with the preceding or, equivalently, time dilation of the latter is dependent on the former’s dimensionless velocity v/c or his orthogonal displacement from the receiver’s tangential Minkowski space.
3.2. Equivalence of Kinematical and Spatial Deflection of Light and the Associated Redshift
It arises the question, whether the red shift of the released light associated with the apparent curvature of its path due to the emitter’s movement relative to the resting receiver directly off the latter might also occur if the apparent curvature of the light path from the emitter is a real one, enforced through the metric of the three-sphere S3.With other words: Arekinematics and metric equivalently associated with red shift of bended light paths?
From the above Euclidian E4-metric the three-sphere is given by
with curvature Ρ‒2. It is clear that photons released from a resting emitter and travelling in such an Universe will indeed follow curved paths, i.e. geodesics, and that the full circle in the three-sphere S3 of volume 2π2Ρ3 can be described as
Y and Z neglected. For the time being we restrict to geodesics 
to the receiver, both resting.
From the preceding it is clear that the emitter’s position must be deflected by value

space, which is orthogonal to Ρ (see Figure 3), i.e., equivalently to the kinematically induced light deflection also the bending of light path through the warped space of the S3-hypersphere causes the receiver to observe pseudo four-dimensional Euclidian projections (Minkowski space) of all ingoing geodesics Δσ in the direction of the tangent vector to the latter (see Figure 3).
Now, our hypothesis is that the dimensionless space-like difference 

where the four-dimensional coordinate difference W necessarily is replaced by X4 of tangential spacetime. This implies that any receiver at any point of the three-sphere will perceive the emitter’s time be apparently dilated
by factor 

Hence, the main difference to the above discussed kinematical case which needs to be emphasized is that not the emitter’s motion off the receiver causes red shift but the former’s four-dimensional distance spatially, not perceivable in the receiver’s pseudo four-dimensional Euclidic (non-curved) space with three spatial and one time dimension. This implies that the velocity derivated from the latter red shift also be only an apparent one. Analogously to the above three-dimensional kinematic case, redshift z is directly associated with some angle Α,
Figure 3. Deflection of emitter inside the three-sphere into local tangential Minkowski space.
such that in association with the above equations applies:


In this way fixed four-dimensional distance w of the emitter’s position within the three-sphere from pseudo four-dimensional Minkowski projection of the ingoing light at the receiver in the latter is transformed into the simulacrum of the emitter’s apparent recession velocity.
Consequently every receiver within the sphere can the spatial four-dimensional coordinate difference w in accord with Equation (8d) also perceive as pseudo four-dimensional (Minkowskian) in the form of dilation of the emitter’s time through the Lorentz factor:

It is obvious that all other previously derivated equations for the kinematical case are also directly applicable to light propagating inside the curved hypersphere with the only modifications to be considered: Angles 


of the quarter circle 1/2Ρπ pretty though not quite exactly intersects radius Ρ orthogonally to the receiver’s tangential Minkowski space at z = 1, where r4D denotes “real” four-dimensional distance between emitter and receiver, both resting in the curved hyperspace (see Figure 3).
From Equation (9a) can be derived

It is clear that the right-hand expression w/c vanishes if vapp/c = 1. But if not, such that applies

this results in 


implying that W > Ρ by the very tiny four-dimensional coordinate difference dw ≡ cdtw which according to the preceding in three-dimensional space be perceivable as rest time only (see below).
In conclusion, apparent bending of light path by inertial motion and real bending of the latter path by four- dimensional metric, respectively, are associated with the redshift of the ingoing light. In either case this is due to projection into quasi Euclidic Minkowski space, every receiver naturally will observe as the tangential projection of all ingoing geodesics. The difference is that real inertial motion in spacetime with three spatial dimensions generates redshift associated with apparent bending of light path, whereas distance w of four-dimensional Euclidian space, embedding the three-dimensional warped space of the three-sphere, in the receiver’s tangential Minkowski pseudo E4-space is transformed into apparent time dilation and redshift of the ingoing light associated with apparent recession velocity. It is obvious that in the receiver’s tangential Minkowski projection of all ingoing geodesics both cases are indistinguishable from each other, i.e. they are equivalent. It needs not to bestressed, this result also to be valid in the case of acceleration, as has been extensively shown above. And it is clear, now, that the heuristically derivated redshift according to Equations (4), (6) and (6a), respectively, also must be due to this basic physical projection effect of geodesics.
3.3. Conservation of Photon Energy in the Closed Universe
Equation (9) predicts light which has been released within the three-sphere S3 at distance 1/4σ = 1/2πΡ from the receiver to be redshifted up to the highest possible value (1 + z) → ∞, independently of direction which, by the way, implies that in the static Universe a light horizon at distance 1/2πΡ from any observer rather than a time horizon exists. Furthermore, this novel physical notion of the Universe’s true topography implies that cosmic reionization and the associated early phase of galaxy formation in the sense of the big bang hypothesis never existed and, thus, also predicts that even at the highest red shifts accessible to astronomical observation still galaxies will be found. At present this observational border lies already at z ≈ 8.6 (Lehnert et al., 2010 [10] ) and, therewith, very near to the very limit where big bang paradigm will break down observationally.
On the other hand does the energy conservation law not allow vanishing of the photon energy. After circling the sphere on the great circle σ = 2πΡ without any interaction, it should arrive at the emitter’s position exhibiting the same energy it previously had been emitted with. Does this requirement contradict the preceding?
There we restricted our analysis to geodesics Δσ ≤ 1/2πΡ or angle Α ≤ 1/2π, respectively, such that eventually z → ∞ if Δσ → 1/2πΡ. We extend our considerations to geodesics with angle Α>1/2π, i.e. beyond the light horizon (1 + z) → ∞, and require Δσ > 1/2πΡ whereras the receiver does not change position. For the time being the geodesics Δσ ≤ 1/2πΡ outgoing from the emitter in the three-sphere S3 have tacitly been signed (+). Therefore, beyond Δσ = 1/2πΡ implying angle 
This is valid for all points of the three-sphere with respect to all radially ingoing geodesics. It implies that the photons of all ingoing great circle geodesics σ repeatedly loose and fully regain their energy after a respective quarter circle 1/4σ, in order to arrive at the receiver (emitter) with the original energy. For this during the course of σ occuring cyclic red, blue, red and again blueshift and the associated apparent recession velocity according to the preceding can be defined
so that the cyclic red and blueshift of the light following the great circle geodesics σ of the three-sphere successively from Α1 to Α4 in extension of (9) takes the form:

Figure 4. Cyclic red and blueshift of light during one great cir- cle geodesics.
It is clear that according to the preceding any dimensionless velocity referring to one of the angles Α1 to Α4 of the succeeding fractions of Equation (11) also can be expressed through the tangent of the respective angle by:

4. Reddening of Light Owing to the Universe’s Four-Dimensional Curvature Explains the Observed Redshift Anomalies of the Supernova Data, Hitherto Interpreted as Due to “Dark Energy”
The immediate consequence of the preceding evidently is that to gain information about the emitter’s correct distance up to light horizon (1 + z) → ∞ one just needs to consider the geodesic path Δσ = r Α ≤ 1/2πΡ of the light travelling in S3 between the emitter and the receiver, without taking any recurrence to the metric of the three-sphere itself. From Equation (9b) in connection with (7) follows vice versa

where rΑ denotes apparent distance in tangential Minkowski projection of r4D according to Equation (10) on the grounds of the dimensionless apparent velocity vapp/c.
One should note that Equation (12) delivers the constant value vapp/rΑ = 2c/(πΡ) = const. The latter enables one to equate radius Ρ and, therewith, the circumference of the three-sphere S3 by considering that, to mention it again, vapp denotes apparent recession velocity per distance r of 1/4σ = 1/2πΡ, which is identified as the Hubble constant
Thus, we can write

With 
of S3 to amount to 16.34 × 103 Mpc, whereas the light horizon being 4.08 × 103 Mpc away from any observer within the three-sphere. But it is obvious that rΑ = ΡΑ, implying that curvature radius Ρ in relation (12) can take any given value. In the case of the Universe it is gauched through the empirical value H0 with the above result (see also below).
Clearly in the closed, static three-sphere S3 the meaning of the Hubble constant is restricted to its definition as empirical value of vapp/r Α = const for any distance r and the associated apparent recession velocity. A Hubble law in the sense of expansion theory does not exist. From equation (12) in connection with the above Hubble relation we receive the distance formula in dependence on observed (comological) redshift of very distant astronomical objects of value

Comparision with the distance formula (14a) of the Einstein-de Sitter standard model (empty space)

at once reveals that with growing cosmological distance rΑ , i.e. redshift, calculated distances r0 on the grounds of the latter Equation must considerably deviate from cosmological reality expressed by the former distance formula (14).
Indeed is rΑ > r0 up to about z ≈ 1.3 and vice versa after this, thus, faking an extra acceleration within distance r ≲ 1.3z and a deceleration at r ≳ 1.3z in the picture of the expansion hypothesis. The crossing point rΑ = r0, i.e. the only point where the distances computed from the redshift z according to Equation (14) as well as (14a) coincide, is, of course, given by

Where from is calculated:
celerating to apparent accelerating expansion, is computed to beat z = 0.50, in good accord with astronomical findings (see e.g. Cunha and Lima, 2008 [11] ).
The following table I compares distance calculations of rΑ and r0 in light years, respectively, on the grounds of the same redshift from z = 0.05 to z = 4 and a Hubble constant H0 = 75 km×s‒1×Mpc‒1. The calculated distances as well as the apparent crossing point rΑ = r0 and the apparent transition point at z = 0.50 depend on the chosen value of H0, i.e. distances become smaller if H0 > 75 km×s‒1×Mpc‒1 and vice versa if H0 takes a smaller value and, furthermore, the Universe to be a perfect three-sphere S3. Clearly with growing redshift after the apparent transition point at distance rΑ = r0 with z = 1.314585 the divergance between rΑ and r0 increases. The last column lists results of magnitude calculations according to Equations (14d) and (14e) from rΑ /r0 = up to 0 ≤ z ≤ 2, which are also visualized in Figure 5.
As already mentioned, introduces current expansion (big bang) hypothesis an acceleration phase of the Universe, propelled by a putative “dark energy”, as the cause of the observed faintness of supernovae of the type Ia between ≈0.5 > z ≳ 1.0, whereas the rather unexpected brightness of the supernova SN 1997ff at z ≈ 1.7 has been explained as the decelerating phase of the early and smaller cosmos due to gravity of the then denser dark matter and baryonic matter, but predominately of the former (Riess et al., 2001 [3] ; on the physical cause of “dark matter” see below).
It is obvious that the ratio of flux fΑ /f0 from the “standard candles” Sne Ia in dependence on apparent distance rΑ and faked distance r0 according to (14a), respectively, can be expressed in the form

(Einstein-de Sitter) takes the form

One should note that this ratio delivers at crossing point z =1.314585, of course, the result ‒2.5 × log(vapp/v0)4
= 0. Thus, at crossing the coasting line at z =1.314585 the scalar 
comes the ratio wherefrom the relative magnitude below the former of the then apparently nearer Sne Ia has to be computed in the form

In Figure 5 the full points are magnitude deviations from 0 < z < 2 according to Equations (14c) and (14d) from what is expected on the grounds of an Einstein-de Sitter (empty) Universe of the expansion theory (coasting = 0) as also listed in table 1.
The magnitude points Δmag of table I and Figure 5 also have been transfered into Figure 11 of reference [3] from Riess et al. (here not shown) and they show that the astronomer’s direct magnitude measurements of very distant supernovae nearly exactly comply with results of magnitude calculations on the grounds of Equations (14d) and (14e) and, thus, fully explain those deviations from standard big bang theory as apparent ones. The. apparent transition point at z = 0.50 and Δmag = ‒0.541 of SN 1997ff at z ≈ 1.7 according to (14e) neatly comply with modeling of the authors.
Thus, without any further assumptions the reddening of light due to curvature of the three-sphere S3 delivers the correct values of apparent magnitude variations with distance. But, of course, in fact deviations of distance calculations on the grounds of the expansion hypothesis according to Equation (14a) from a more realistic phys-
Figure 5. Measured redshift coincides with theory (dotted line) deviating from prediction of big bang (zero line).
Table 1. evolution of 2v /c in big bang theory (Einstein-de Sitter) vs. v /c of pseudo four-dimensional tangential Minkows- ki-space (static universe) in dependence on redshift z from z = 0 to z = 4 in light years × 10 . Apparent transition (i.e. v /(2v ) = max), crossing (i.e. v = 2v ) and redshift z = 1.70 of sn 1997ff are indicated by fat type.
ical notion, obviously correctly expressed through distance Equation (14), are reflected.
5. CMB Is Enthropic (Planckian) Radiation within the Closed, Static Three-Sphere
The physical picture developed above requires that the cosmic microwave background radiation cannot be relic radiation of the big bang but, instead, rather should be enthropic (Planckian) radiation. The latter naturally must occur within the closed, static three-sphere S3. Thereby it is obvious that the expansion concept to explain the nearly uniform cosmic microwace background (CMB) radiation of 2.725 Kelvin (K) can analogously be adapted for the enthropic radiation within the closed, static three-sphere with fixed radius Ρ ≈ 2.6 × 103 Mpc, although more in the sense of a thought experiment and not as physical reality as in the frame work of big bang theory.
As widely known traces the latter the Planckian distribution of CMB radiation back to interactions of photons with stable particles in the earliest epoch of the presumed cosmic expansion, whereby a (otherwise unmotivated and unexplained) short extra acceleration or boost is introduced to explain isotropy and homogeneity of the CMB (horizon problem). With the decoupling of photons and remnant matter at T ≈ 3000 K the radiation is thought to have reached its final Planckian distribution, but to be cooled down to current CMB temperature 2.725 K in the course of further cosmic expansion.
However, according to the above the three-sphere with constant volume 2π2Ρ3 a hot epochin the sense of big bang theory never underwent. Therefore, the CMB, especially its spectral distribution in thermal equilibrium, must be of other origin. As already previously remarked, offers the closed, static Universe such one as the sum of all ever emitted and not absorbed light. According to equation (11) will these photons on their repeated tra- vels on great circle geodesics σ around the entire Universe undergo cyclic red, blue, red and again blueshift after every respective quarter circle 1/4σ. This results in the observed equilibrium of radiation energy, i.e. perfect thermal emission (black-body) spectrum for every observer in the three-sphere. From its energy density be-
ing equivalent to mass density, which in the literature is given with 
ing to this theory the temperature of the universal black-body radiation (CMB) right forwardly can be computed. The relations
(Stefan-Boltzmann law) and

expressing the density of the “rest mass” of a photon gas, are also valid in the case of the electromagnetic radiation filling the three-sphere S3 in accord with the preceding and, thus, also the relation
without restrictions. From the latter equation is given

which also reflects the definition of T as the basic temperature of the “empty” static three-sphere S3. Therefrom is taken

whereby T = 1 in the Kelvin scala. If now TS > 1 and
relation between temperature of the enthropy radiation TS of all ever emitted and not absorbed electromagnetic radiation of the three-sphere and T simply is applied

where Ρ ≈ 2.6 × 103 Mpc and Ephot/c2 = 4.4 × 10‒34 gr×cm‒3, gr denotes gram, AMU Atomic Mass Unit = 1.6605 × 10‒27 kgr = 6.68‒1 × 1024 K, respectively. The remarkable result (15) in units T = K is fairly exactly the measured temperature of the CMB.
One should note that expansion hypothesis does not allow a derivation of this result so right forwardly, because the above pointed out correlations, but especially the constant radius Ρ of the three-sphere S , are completely unknown to the former. The interpretation of the CMB as enthropic (Planckian) radiation in the closed, static Universe easily explains the observed isotropy and homogeneity of the latter. A “horizon problem” as in big bang theory does not exist.
Nevertheless, it is clear that fluctuations on small and large scale as well in the CMB must occur owing to the previously discussed redshift associated with the deflection of CMB photons passing either nearby or more distantly large scale structures in the closed, static three-sphere S (see above and also Appendix 1). For the latter neither the integrated nor the non-integrated Sachse-Wolf effect of Big Bang hypothesis can be accepted as appropriate physical explanations of fluctuations of the enthropic (Planckian) radiation on any scale, because in a steady state Universe such an effect does not exist physically.
Furthermore, this novel physical notion―CMB being the Planckian radiation in the closed, static but spinning Universe―delivers a convincing physical explanation of the recently observed and most recently confirmed statistically significant anomalies in the CMB, including those which have been ascribed to gravitational waves in the putative early phase of the Universe (see paragraph 11.2).
6. The Physical Cause of the Gravitational Field, of Gravity and of the Definite, Limited Velocity of Light
In the preceding we considered physical implications solely following from the curvature of the static, self- contained three-sphere S3, whereas its rotation could be fully neglected. Mathematically the three-sphere including its four-dimensional rotation has been thoroughly investigated so that its geometric, topological and group structure properties are well known (see the numerous literature to these points). Thus, we can concentrate on the physical effects which are to expect owing to the rotation of the hypersphere on local as well as on global scale.
Considering our home galaxy’s age and advanced evolution it seems highly reasonable to assume its present lateral position in the three-sphere being somewhere between one of the rotation poles (which we denote arbitrarily the “northern” one) and the equatorial plane, and, likewise arbitrarily, the three-sphere to spin clockwise about the former.
The Galaxy’s distance from the cosmic equator region would then, as a first guess, be ≈1/4πΡ, or, latitude ΑG ≈ 45˚ (analogously to the Galaxy’s coordinate system). The more exact value of ΑG is derivated below.
It is clear that the rotation of the self-contained three-sphere, i.e. of its curved three-dimensional space-fabric (not space-time; see below), gives rise to internal centrifugal forces, which act upon all matter in the equatorial zone and beyond, causing it to oscillate between the cosmic hemispheres and thereby regularly to cross the cosmic equatorial zone (in due course of billions of years). Also should moving bodies in the rotating three-sphere experience a fictitious Coriolis force. This global inertial force, which also will give rise to gravity, is the centripedal acceleration

arising from the rotation of the three-sphere S3, considered to be perfectly elastical, about its axis in flat E4-space locally, where aΑ denotes centripedal acceleration and ΡΑ rotation radius at latitude Α, respectively, ωS angular velocity of the sphere and c rotation velocity. As a certain geometric consequence this rotation in four-dimen- sional space is about a two-dimensional plane, which we nevertheless will further on refer to as the axis.
The absolute value of the rotation velocity c = ωSΡ can be derived by considering an emitter resting relative to the space fabric of the three-sphere, i.e. a fixed metric connected with the latter, at the sphere’s equator, where c = max. From the emitter shall be released simultaneous signals parallel and antiparallel to the vector of c, which for we demand 1) that the velocity of the antiparallel signal’s carrier shall suffice to cancel the angular velocity ωS so that the velocity of the carrier relative to E4 equals to zero, 2) that the signals arrive simultaneously at the emitter after time 2πΡ/c, i.e. after completion of a great circle σ, as “observed” from the emitter. Evidently are these requirements only fulfilled by the carriers of light signals, i.e. photons, whereby it is clear that relative to the photon with ωS = 0 the emitter (point of emittance in coordinates of the three-sphere) arrives at the point of emittance in coordinates of the embedding Euclidian E4 after time 2πΡ/c and the counter directed photon also after time 4πΡ/2c = 2πΡ/c (on the probable physical cause of the coincidence of light speed and rotation velocity c = ωSΡ, see below).
Now, suppose the above light signals be emitted perpendicularly to the vector of c in direction of the sphere’s poles. In Euclidian space they would withdraw from the emitter with velocity c. But the metric of the three-sphere S3 constrains the geodesic trajectory Δσ or the great circle σ, respectively. Therefore, if 
light reaching latitude ΡcosdΑ must have slower velocity
the infinitely small angle between Ρ and ΡcosdΑ. But anyhow, because rotation radius varies in dependence on latitude it is clear that according to the preceding the velocity of light must be dependable on latitude as well. Furthermore, it is clear that, other than the light travelling parallelly to the cosmic equator, both counter parallel pole-crossing light signals must arrive at the point of emittance after completion of a great circle σ. This requires the above two demands to be extended, namely: Every point of emittance at any latitude in coordinates of the three-sphere shall depart with latitude dependent velocity c from the respective point of emittance at rest relative to the embedding E4such that the transversality of the light’s polarization vector always points towards the Universe’s rotation axis. From this follows that the light propagating off the point of emittance into the general direction of the sphere’s rotation till meeting the counter directed signal at the former point of emittance
will cover distance 

versality of the light’s polarization vector the latter inside the three-sphere seems to be swirled in the order of 2π during one complete revolution. Thereby those vector turbulences should be centered at the rotation poles and somewhat broader distributed at the cosmic equator. This phenomenon has very recently been observed but wrongly interpreted as a proof for gravitational waves in the early phase of the expanding Universe (see below chapter 10). Furthermore, if the velocity of light at the three-sphere’s equator is denoted cE, and, cA at a certain latitude 0 ≤ Α ≤ 1/2π, where angle Α will be given in degrees counting from the equator to the rotation pole (see below), than

Taken together follows for all observers in the Universe that all released light will need same time σ/c (as measured locally) for a full great circle geodesics of the three-sphere, independently of the latitudenal position of the emitter. Thus, the very origin of the limited velocity of light in vacuum as we know it, is its above correlation with the rotation velocity c = ωSΡ of the three-sphere S3, also implying its variation with the sphere’s latitude.
As a further consequence must the photon energy Ephot vary with latitude as well, because cA = λAνA = λνEcosΑ.
Because, furtheron, frequency is inversely proportional to time, especially
be valid λA = λE = const such that the photon energy takes the form

where here Planck’s constant h is assumed to be constant at all latitudes (for a proof see below). This implies that for a vantage point somewhere between the equator and one of the rotation poles of the hypersphere (as e.g. to assume for the Milky Way) the light ingoing from emitters located considerably nearer to the pole or the equator must be differently energetic, i.e. less energetic from emitters located towards the pole and vice versa from emitters positioned more equator-wards, respectively. Assumably are the classes of luminious red galaxies and of ultraluminious IR galaxies detected by the Infrared Astronomical Satellite (IRAS) in 1983 due to the latter effect (see e.g. Younger, 2007 [13] ). If these galaxies are positioned at considerably higher latitude than the Milky Way they should emit the bulk of their energy at red and infrared wave lengths. Their extreme massiveness―they are the most massive galaxies in the Universe―is also explained through their proximity to the rotation pole, because with the galaxies’ drift towards the polar region there is associated a mutual approach or increase of density of galaxies, i.e. also increase of probability of merger (see below). This predicted increase of IR galaxy concentration has also recently been observed [14] .
An observer resting at the equator of the rotating sphere will on himself and all material objects ascertain the centrifugal force

as the respective counter force, which leads to a bending of the elastic S3space-fabric and its metric, respectively, directed radially “outwards” off the rotational axis in E4. This warping of S3space through the action of the centrifugal force FΡ upon mass is described by the well known field equations of general relativity as deviation from the locally flat metric ηnm, where the energy-momentum tensor Tmn represents distribution of matter and the Ricci tensor Rmn curvature of spacetime (see below). Note that from the cosmic equator up to the polar regions, FΡ must decrease in the order ‒mc2cos2Α/(ΡcosΑ) such that applies

where F Ρ(Α) denotes FΡ at latitude Α.
Every observer within the three-sphere S3 on principle cannot measure the kinematical status of an isolated single material object, but only in relation to another object, e.g. the collision of two bodies with different mass but equal oppositely directed velocity, i.e.

Hence, the existence of the universal centrifugal force FΡ remains hidden to him and he must arrive at the interpretion of mass as always being associated with inertia. In addition to this generates the rotation of the S3-sphere (assumed to be at rest in E4) the centrifugal energy

being proportional to the quadradic product of the angular velocity ω and the sphere’s radius ΡcosΑ at latitude Α, where ωΡ × ΡcosΑ = cΑ , according to the previous derivation of velocity of light within the sphere.
Obviously is the centrifugal energy E , every material body owing to the rotation of the hypersphere will obtain, the very origin of the Poisson potential U of the gravitational field

Since also in this case the direct effect of the centrifugal energy is not perceptible within the sphere and again only comparison of different potentials is possible, an observer must this only in steadily rotating systems occuring additional potential energy interpret as a rest energy

falling to every material body’s share in the sphere. The S3-observer thus comes to the conclusion that every material body must have “rest mass” m = E/c2.
On the other hand, due to the local warping of the fabric of space in the vicinity of material objects and in direct dependence on the latter’s mass will the universal centrifugal acceleration aΑ partly be diverted towards the well of the field such that its vector constantly, points into the latter’s direction, furthermore, to increase steadily with decreasing distance owing to the constant increase of the angle enclosing pseudo Euclidic distance and four-dimensional distance from the latter (see below). Thus, bodies with smaller mass (the warped space ≡ gravitational field around them negated) are accelerationally propelled towards bigger ones. The observer within the rotating S3-sphere can this physical behaviour of masses in a first step interpret as gravitational force acting between material objects (Newton). With further insight it becomes clear that this “force” is associated with the warping of space and dilation of time in dependence on rest energy of the gravitating body. This dependence is described by the Einsteinian field equation
in the well known manner: The energy-momentum tensor Tmn, whose dependence on latitude Α for now we neglect, represents the distribution of matter (energy), and the Ricci tensor Rmn the respective symmetric warping of space [15] .
We replace constant ϰ of the left-hand side of the Einsteinian field equation through the respective Newtonian value ϰ = 8πG/c2, whereas Tmn = T44 = ϱc2, i.e. the density of energy, is the essential well of the gravitational field, and all other components of the energy-momentum tensor are considered to be neglectably small. Now, we introduce the Poisson potential U = 4πGϱ of the Newtonian theory so that with Tmn = T44 = ϱc2 eventually ϰTmn = 2U. If we replace the Poisson potential U by the centrifugal energy E according to the above equation, then the left-hand side of the Einsteinian field equation takes the form

Therewith, it is shown that the centrifugal energy E be the decisive factor which governs the geometry 
7. Origin and Equivalence of Rest Mass (m0) and Energy (E0) of the Protron, Quantum of Rest Time (τ0) and Four-Dimensional Elementary Length (λw); Derivation of the Milky Way’s Latitude within the Rotating Three-Sphere S3
Above an association between four-dimensional spatial extent dw orthogonally to Minkowski space and time t in the latter in the order

has been assumed., or, with other words, that a quantum of rest time τw and minimum length dw ≡ λw = cτw possibly exists. To prove this, consider the de Broglie wave of a fast moving stable baryon with smallest known mass, say, protron, of wavelength λ which for we require λ = λw ≡ cτw:
where m0 denotes rest mass and h Planck’s constant. Obviously must be valid
= 1/2m0c2, where m denotes dynamical mass and γ Lorentz factor. Obviously this is the case if 
that the previous de Broglie formula takes the form

whereof is derivated:

The same result follows from 
We write 1/2m0 = μ and in the above formulae clearly the similarity of the term μ = h/(τwc2) to τw = h/(μc2) is recognizable and exposed as identity if their relativistic conservation in the usual three-dimensional notation, i.e. relativistic association, is considered (see also Figure 2 and Figure 3):

The result 

at all latitudes of the three-sphere and, furthermore, that at all latitudes the measurement of the velocity of light in any unit of time results in the same indissoluble constant product ct, taken for c. Thus, any observer at any latitude of the three-sphere has to correct the measured inseparable quantity ct ≡ c in comparison to real constants, as e.g. Ρ or h, respectively, by the factor cosΑ, i.e. cA = (ct)cosΑ.
Furthermore, the similiarity of the above derivation λw = 2h/(m0c) to the golden ratio (sectio aurea) is not accidental, but owing to the fact that the ratio of four-dimensional λw and m0c be really =1:2 (as to the association with energy see below). Thus, it follows from the previous definition E0 /c = λw = 1/2m0c:

Equally follows that the four-dimensional spatial extent w orthogonal to Minkowski space and in the latter being equivalent to the product of three-dimensional time tv and velocity vapp to be identical with mass by order of magnitude
Previously has been derived the product 

is to expect, i.e. that 2τw will become rest mass m0 entirely. At all other latitudes obviously

pseudo Euclidian Minkowski space tangential to the local metric of the hypersphere intersects FΡ (Α) at angle Α so that the through centrifugal acceleration aΡ (Α) generated momentum or velocity of mass m = 2W/c (m0 = 2τw) is diverted by value sin Α (see Figure 7):

Because, thus, the local plane of S3-space is aligned parallelly to sinΑ × FΡ (Α) it must possess gravitational mass of the same order of magnitude as well. But this gravitational mass, or, energy of space, respectively, will only become manifest where differences of potential exist, i.e. in the interior and exterior Schwarzschild field of matter (see below). Therefore, only part W(1 ‒ sinΑ)/c of W/c warps through the impact of FΡ (Α) local space of the three-sphere S3 to become rest mass:

Thus, variable κ = 1 ‒ sinΑ, which implies that minimum rest mass m0 (protron) be directly dependable on latitude according to

whereby m0(Α) denotes m0 at any latitude Α and h = invariant according to Equation (30). From the known values of h = 6.626176 × 10‒27 erg × s, cΑ = 2.99792458 × 1010 cm × s‒1 and m0(Α) (protron) = 1.672623 × 10‒24 gr, the exact latitudenal position of our vantage point in the Universe, the Galaxy, straightforwardly is derivated:

being very close to the previous first guess of ΑG ≈ 45˚.
One should note that part λw∙sinΑ of λw in local Minkowski tangent space also appears as

server at any latitude of the static, self-contained three-sphere S3 his local spatial environment perceive as pseudo Euclidian Minkowski space, which for the Pythagorean rules are valid such that the physical laws take the same form everywhere. Especially is the spatial symmetry of the above Einsteinian field equation maintained, independently of latitudenal position. This effect―as we know―also is valid for all gravitational fields at our vantage point in the Universe.
According to the above result the numerical value of the minimum (four-dimensional) length must be (state of rest in the rest frame)

and the quantum of time

It is clear that the apparent rest time continuum of any observation every observer in the three-sphere will experience in reality is the finite sum

of the finite time quanta 
second with reference to the respective rest-frame in the sphere. This implies that a constant cosmic time in the sense of general relativity, i.e. independently of a real existing λw/c and, furthermore, past and future do not exist physically.
The previous results are in accord with the CGS-system, where h is defined by erg × s = 1gr × cm2×s‒2 × s, because according to these findings be valid m (gr) = λw (cm)/c= τw (s), so that 
Thus, according to the previous and the following are e.g. Planck time tp = ( ħG/c5)1/2 = 5.39 × 10‒44 s, or, Planck length lp = ( ħG/c3)1/2 ≈10‒33 cm, respectively, no really existing physical parameters of nature (see also below and Appendix 3).
Knowing the exact value of angle ΑG, the possibility arises to calculate radius Ρ of the three-sphere S3 from m0 = 2τw(1 ‒ sinΑ), or, vice versa, m0 or τw, respectively, from radius Ρ in association with centripedal acceleration a = ‒ c2/Ρ and energy ϰTmn = 2U = ‒m0c2. We take from the left-hand side of the above Einsteinian field equation at the equatorial plane of the three-sphere the relation

Figure 6. Illustrating (exaggerated) m0(A)=2τW(1 − sinA).
where the gravitational energy of 2λw/c is set unity =1. Then, at any latitude of the three-sphere this must take the form

since tE is the unit measure of time in the sphere, i.e. according to the previous tE/tΑ = c Α/cE = cosΑ, and the
product 

With the canonical values of m0 (mass of protron) and c , furthermore, the derivated angle ΑG, given above, is calculated Ρ = 8.3999 × 109 ly. One should note that the latter result matches practically exactly the one previously calculated from cosmological data according to ratio (13). Of course does the reverse procedure with the respective values of Ρ, cΑ and angle ΑG exactly lead to the tabular mass of the protron given above. This result is not particularly strange, as from the first sight, but expresses just the latitude-dependent ratio between the largest and smallest four-dimensional dimensions of our Universe:

Note that already more than 70 years ago Dirac assumed the ratio: Size of the Universe vs. size of the protron ≈ 1040.
Thus, it has been shown that rest mass of the protron and rest time-quantum in the rest frame be generated in three-dimensional space by the hidden vector-like four-dimensional spatial dimension λw of all stable baryonic matter. This implies, contrary to common view, all material bodies spatially to be built up four-dimensionally, though with the extreme tiny fourth dimension 2λw. Obviously is the instability of all baryon masses (resonances) >m0(Α) (protron) =2τw(Α) and of the meson masses
8. Excursus on Quantum Geometry: Association of Rest Energy, m0, λw, and τ0 (See Also Appendix 3)
Given the quantum of length or fundamental length in one-dimensional manifold R1 be λ1, in two-dimensional R2 be λ2 and so on, then the hypotenuse of the smallest possible Pythagorean triangle (simplex) in the respective manifold must be the fundamental length of the next higher manifold, namely:

This follows since in Euclidian Micro-space 1) a smallest Pythagorean 2-simplex formed by the fundamental lengths 2λ1 + 1λ2 is only possible on the condition that 2-cube (λ2)2 exists, whereas a Pythagorean 2-simplex smaller than the former is not possible; 2) a smallest Pythagorean 3-simplex formed by the fundamental lengths 3λ1 + 2λ2 + 1λ3 is only possible on the condition that 3-cube (λ3)3 exists, whereas a Pythagorean 3-simplex smaller than the former is not possible; 3) a smallest Pythagorean 4-simplex formed by the fundamental lengths 4λ1 + 3λ2 + 2λ3 + 1λ4 is only possible on the condition that 4-cube (λ4)4 exists, whereas a Pythagorean 4-simplex smaller than the former is not possible. Hence, it must be valid

where λw ≡ λ4. It is clear that this reasoning runs reversely as well, i.e. back from λ4 to λ1.
Considering that the n-dimensional volume of a n-dimensional simplex be λn/n, furthermore, assuming the protron to be build up with absolute minimum four-dimensional volume, say, Pythagorean double 4-simplex, the mass of the latter must be of value

whereas the product of 3-simplex as base and λw as four-dimensional height takes the form

Neglecting variable κ = (1 ‒ sinΑ), from the foregoing one straightfordwardly can derive the rest energy of the protron to be E0 = m0c2 = 2τwc2, or, E0/c = m0c = 2λw, respectively and, thus, showing that E0 is rooted in λw/c or τw, respectively. The previous two equations set equal results in

as well. If one demands that in the relativistic conservation law λw always be conserved and the former is written in the form

then, it is obvious that momentum squared 

i.e. the fundamental conservation of λw obviously is the very origin of the association of rest energy and rest mass
9. Origin of Mass of Spherical Material Bodies ≫ m0; The Energy Content of the Exterior Schwarzschild Field as the Origin of “Dark Matter” and, in Connection with This, as the Very Cause of the “Pioneer Anomaly”; Derivation of the Newtonian Constant
9.1. Mass of Material Bodies ≫ m0 and the Origin of Its Density
It has been proven long since that the time-independent Schwarzschild field outside an isolated spherically symmetric body takes the form of a parabolic three-dimensional manifold embedded in a four-dimensional Euclidian space (locally), whereas the metric of the interior Schwarzschild field be the one of a three-dimen- sional hypersphere with oppositely directed constant curvature (with respect to the former) under the condition that pressure ρ = const, also embedded in the latter (see e.g. [18] [19] ). The spherical symmetry of either metric automatically follows from the above finding that every observer at any latitude of the three-sphere S3 will perceive his local spatial environment as pseudo Euclidian Minkowski tangent space.
Analogously to the previous derivation of the protron’s rest mass also the mass of Earth and all other celestial bodies principally must be due to the four-dimensional height of the Schwarzschild field, which we denote Η (upper-case eta) to differentiate from cosmic coordinate difference w. But other than in the case of the protron one has to consider yet that Η refers to the four-dimensional distance from two-dimensional “rim” (Euclidian sphere with radius R) of a spherical solid cosmic body (gravitational well) to undisturbed local Minkowski-space, intersecting the latter perpendicularly. Analogously to (10)-(10c) will four-dimensional Η or the associated curvature of the Schwarzschild field in one dimension, respectively, be projected into three-dimensional Minkowsky space spatially, whilst v2 = (2GM/R)1/2 takes the place of cosmic apparent velocity vapp, where v2 denotes second Newtonian cosmic velocity. Thus, with respect to all three dimensions of the gravitational field and considering that analogously to the mass of the protron only part (1 ‒ sinΑ) of Η3 through the impact of FΡ (Α)warps local space of the three-sphere S3 to become rest mass, for Earth the simple relation must hold

which with respect to Me(w) takes the form

where, as already mentioned, v2(e) denotes second cosmic velocity (2GMe/Re)1/2 with respect to Earth, Me(w) mass of Earth induced through the latter’s four-dimensional height Ηe and Re radius of Earth. For all celestial bodies other than Earth this becomes to

where v2 denotes second cosmic velocity of the respective cosmic mass and ϱ mean density of the latter.
Note that this approach to mass calculation on the grounds of the physical picture developed above on principle delivers masses of solar system bodies which are not inconsiderably smaller than the standard tabular ones, e.g. for Earth 5.8166 × 1027 gr and for the Sun 1.934 × 1033 gr, respectively, in comparison to the tabular values 5.9737 × 1027 gr and 1.989 × 1033 gr. The reason is that the above ansatz takes account of fourth-dimensional height Η only, i.e. it delivers the value of mere inertial mass. Also taking into consideration the energy content or gravitational mass of the interior Schwarzschild field of Earth (see below) delivers the ansatz

or, generally

where M(w+V) denotes the cube of the sum of four-dimensional height Η plus four-dimensional height η (lower-case eta) of the interior Schwarzschild field of the body. Obviously expresses M(w+V) = (Η + η)3 gravitational mass (see below).
Contrary to the first mass equations deliver the latter principally higher mass values than the tabular ones, e.g. for Earth Me(w+V) = 6.123 × 1027 gr and for the Sun M ☼(w+V) = 2.044 × 1033 gr. In the case of Earth the difference of mass calculation in accord with the above mass equations is of the order of

and for the Sun

These differences express the respective interior Schwarzschild mass and are also calculable from first principles (see below).
The above formulae enable one to calculate the four-dimensional height of Earth and all other symmetric cosmic bodies simply with

The four-dimensional height of Earth is calculated with ηe ≈ 330 km and and the one of the Sun with η☼ ≈ 23,187 km, respectively. If the angle enclosing Euclidian three-dimensonal radius R and the approximation (η2 + R2)1/2 of the curved four-dimensional “radius” of a spherical cosmic body is denoted ϖ, then it applies

and

Both equations deliver the correct values of the Sun’s and the planet’s respective values of velocity v2 and gravitational acceleration g, respectively.
From the preceding one calculates the four-dimensional height 


Therefrom in association with the preceding for any gravitating body with defined radius generally is given

9.2. The Mass-Energy Content of the Interior Gravitational Field
Above has been shown the interior gravitational field of material bodies to contribute to the total gravitational rest mass of the latter, owing to the inclination of local pseudo Euclidian Minkowski space tangentially to the metric of the hypersphere by angle Α relative to centrifugal acceleration a (Α). Thus it is evident that the gravitationally observable effect of “dark matter” has to be attributed to the interaction of matter with the mass-energy of the Einsteinian field as well with the previously in Equation (33a) derived general value on cosmic scale.
As already mentioned, is cosmic vapp in gravitational fields replaced by second cosmic velocity v2 at radial point R of M. Although product 
aΡ = c2/Ρ. If one demands aΡ = c/tv = 1/2c in unit time, then this leads to 
integrated interior field mass of Earth one can write

With respect to 

and in the general case

These formulae deliver for the mass of the Sun’s interior Schwarzschild field 
for the inner field of Earth
with the values (Equations (50a) and (50b)) which have been derived as difference M(w+V) ? M(w) of the mass formulae (48)-(50b) in association with astronomical data.
The same is found for the other planets and the moon.
Thus, the conclusion is unavoidable the tabular mass values of all gravitating bodies in the solar system to be the median of the mass solely induced through the respective four-dimensional height Η cubed such that M(w) = Η3 (inertial mass) and the sum Η + η cubed, M(w+V) = (Η + η)3 (gravitational mass) so that difference (Η + η)3 ? Η3 be the mass content of the interior gravitational field. This phenomenon is due to the fact that only the gravitational constant G and the gravitational acceleration ge of Earth, induced through its integrated mass Me(w+V) = 6.123 × 1027 gr, be directly measurable, whilst all other masses in the solar system are derived from orbital velocities in accord with the Newtonian formulae (inertial mass; see also below “Derivation of the gravitational constant G”).
The previously derived physical relations referring to the mass of material bodies and their respective interior gravitational field are also applicable to the mass of the protron, which now can be calculated independently of the latter’s above mass derivation. According to the previous results is the protron’s gravitational mass (2λw/c + mass of interior field) also given by

whereas the mass of its interior field alone takes the form

Calculation results in m0(w+V) = 1.679358 × 10‒24 gr and m0(V) = 6.660289 × 10‒27 gr, respectively, with differ-
ence
Note that difference
mass value. This is owing to the fact that the laboratory value of m0 is not derived as gravitational, but rather as inertial mass m0(w).
9.3. The Gravitational Mass of the Exterior Schwarzschild Field as the Origin of “Dark Matter”
As widely known, has Dark Matter or missing mass, respectively, been postulated long since to explain the discrepancies between the observed kinematics of some components of astrophysical systems like e.g. clusters of galaxies [20] and spiral galaxies [21] - [24] , furthermore, predictions on the grounds of Newtonian dynamics from the directly observable masses (stars and gas clouds). Whereas Zwicky in 1937 an explanation still sought in the existence of undetected, baryonic matter [20] , it is widely assumed currently that the non-detected carrier of this gravitational mass is constituted by non-baryonic, weakly interacting particles of yet unknown origin which shall account for about 23% of the mass-energy content of the Universe (e.g. [25] ).
Especially show all galaxies up to multiples of the optical radius nearly constant or even rising orbital velocities instead of expected Keplerian behaviour. The rotational data of low surface brightness dwarf galaxies require an even much higher amount of the unseen mass component. The same is true for pairs of galaxies, galaxy clusters and superclusters. e.g. do the Milky Way Galaxy and Andromeda approach each other much faster than one would expect from the gravitational attraction of the visible masses alone (e.g. [26] ).
The previous derivation of the inner field mass can right forwardly be adopted for the exterior Schwarzschild field of mass assemblies with massive material core and definable radius, as e.g. stars and the innermost bulge of galaxies, by considering that the energy content of the latter be not a constant as the integrated interior field mass of the former, but rather variable depending on distance R from the boundary between the inner and outer field, i.e. one has to calculate the mass of the field in dependence on R, which leads in the case of the Sun to

whereby R runs radially from the boundary of the Schwarzschild field. With regard to mass 

being also valid for all other solid cosmic bodies with defined radius as well. One should notice that the dependence of the exterior Schwarzschild mass on latitude runs contrary to the of the protron’s mass by factor (1 ‒ sinΑ)‒1 such that in the cosmic polar regions the former gradually outnumbers the latter and at the very cosmic poles only Schwarzschild mass can exist.
For galaxies and still larger cosmic systems with no surface and, thus, defined boundary of interior and exte-
rior Schwarzschild field one obtains from Newtonian 
hand side of the latter Equation (60) 

where vorb denotes orbital velocity at Rorb ≤ R (see also below). This implies to simply derive the field mass of the latter in dependence on the respective radius if orbital velocity vorb and radius Rorb, respectively, of an orbiting object, say star, are known, from the relation

whereby R2 ≥ R1. For galaxies other than the Milky Way this takes the form

where v2(2) denotes second cosmic velocity of the galaxy and v2(1) the respective value of the Milky Way derived below (Equation (65)). Accordingly for the velocity of a cosmic body orbiting a galaxy, e.g. the Milky Way Galaxy at radius R beyond radius Rorb ≤ R, one obtains

This delivers e.g. for the Milky Way at its assumed boundary R = 5 × 104 Lj orbital velocity
Vorb(→ R) = 233 km×s‒1 and at R = 1.8 × 105 Lj, the distance of the Large Magellanic cloud (LMC), Vorb(→ R) = 322 km×s‒1, where vorb = 220 km×s‒1denotes the Sun’s orbital velocity. This implies the Milky Way’s rotation curve to steadily rise with increasing radius out to the utmost range of its exterior Schwarzschild field (see below).
From the above mass formula of the exterior Schwarzschild field in connection with the Sun’s vorb one derives the Milky Way’s second cosmic velocity in cm×s‒1 cubed with value

numerically. Assumably refers Equation (65) to the second cosmic velocity cubic of the innermost central core of the Milky Way, spinning like a rigid rotator with about constant angular velocity. Thus, disregarding the radius of the innermost galactic rotator, the total mass MG of the Milky Way in dependence on radius takes the simple form

The latter and the above mass equations deliver e.g. for the Galaxy’s total mass MG(w) + MG(V) inside Rorb = 5 × 104 Lj a value of ≈ 3.86 × 1044 gr = 1.93 × 1011M☼ and for MG(w) + MG(V)inside Rorb = 1.8 × 105 Lj (distance of the LMC) 2.64 × 1045 gr = 1.32 × 1012M☼ , both results being in excellent agreement with recent astronomical estimations (see below).
Because, as previously derived, the local S3-space plane is aligned parallelly to sinΑ × F Ρ(Α), which implies that merely one radial direction of the Schwarzschild field runs parallelly to the latter, it principally turns possi-
ble to also calculate the infinitesimal Schwarzschild mass 

Integration results in

where C = M(w+V), i.e. sum of baryonic mass plus mass of the interior Schwarzschild fields, which can be neglegted in the case of huge mass assemblies as e.g. galaxies, clusters and clouds. From Morb inside the Sun’s orbit one calculates

numerically. Insertion of √2GM into the right-hand side of the lower Equation (68) results as well as the former formulae in the same amount of total gravitational mass MG(w) + MG(V) inside Rorb = 5 × 104 ly of the Milky Way as the previous calculations, i.e. 3.86 × 1044 gr = 1.93 × 1011M☼ .
From the foregoing follows the non-existence of “Dark Matter” in which form ever as the cause of the observed dynamical behaviour of galaxies, clouds and clusters. Rather the gravitational mass of the exterior Schwarzschild field, i.e. mass of the gravitational field―Schwarzschild mass―, truly traces the transformation of four-dimensional geometry spatially of the latter into four-dimensional spacetime being three dimensional spatially so that for all gravitational systems always the simple relation holds:

whereby, as previously shown, the left-hand side is dependable on the ratio (v2(1)/v2(2))3 for every galaxy individually. This explains easily the astronomical observation that the “Dark Matter” content of each successive concentric shell of the gravitational field remains constant for all R.
9.4. Derivation of the Newtonian Constant G and Some Implications of the Southward Drift of the Milky Way Galaxy
In gravitational theory the ratio of gravitational and inertial material mass Mg/Mi is set equal to one, whereas the inertial mass Mi customarily is measured in arbitrary units of e.g. gram:
In a first step it will be shown that the above findings enables one to derivate G in natural units at the equator of the three-sphere. According to Equation (19) will upon a body of unity mass = 1, located at the equator of the S3-sphere, act the centrifugal force

where GE(M=1) denotes gravitational constant derived from a material body with arbitrary mass = 1 at zero cosmic latitude. Changing sign (+), then analogously to the derivation of the protron mass, this must vary with latitude A as

and, because cE = cΑ/cosΑ, the latter at any latitude takes the form

As one observes, be only the product

always constant. Calculation of Equation (76b) with the known values of cA, Ρ and Α results in

This slight deviational surplus relative to the above tabular value owes its existence to the uncertainties in calculating the correct values of radius Ρ and cosmic angle Α of the Galaxy’s lateral position within the northern cosmic hemisphere, because according to the preceding Ρ = 2c/πH0. i.e. slight differences in determining the
Hubble constant H0 directly affect the theoretical derivation of the “constant” 
low).
The second cosmic velocity v2 = (2GM/R)1/2 in mass Equation (48) and the following ones has to be considered constant independently of latitude with the result that the latitude-dependent value of the mass scalars results only in association with variable (former constant) Equation (76b). Thus, if one puts the ratio of 

where Rorb(Α ) and Rorb(E) denote orbital radius at latitude Α and the equatorial plane, respectively. i.e. orbital radius Rorb(Α ) will expand by value

whilst the gravitational bound orbiting system is gradually floating from latitude Α towards the equatorial plane of the hypersphere. The latter effect explains the recently observed secular increase of the Astronomical Unit and some other related phenomena (see below and Appendix 4). The previous results are also simply derived by considering that be valid

implying an associated increase of the Einsteinian curvature radius and, therewith, of any orbital radius at the same order of magnitude, i.e. (1 ‒ sinΑ)‒1 if the gravitational system is drifting towards the Universe’s equator.
The same relation is derived for the gravitational acceleration of Earth

The ratio of ge at the equatorial plane and any latitude of the three-sphere thus becomes to

implying that ge will increase by value

in the course of the Milky Way’s drift from its present position at latitude Α = 43.788˚ towards the equator of the Universe, i.e. that in this case ge must have been weaker in former times.
9.5. Schwarzschild Mass of the Exterior Gravitational Field of Stars (Sun) and of Huge Mass Assemblies Explains the “Pioneer Anomaly” and the Latter’s Dynamics
As widely known, consists the so called Pioneer anomaly of an unmodelled acceleration ap directed towards the Sun, which has been observed acting on both Pioneer spacecraft, launched in 1972 (Pioneer 10) and 1973 (Pioneer 11), respectively, which since are travelling on about opposite tracks outbound ranging the solar system. The former has been detected by the Pioneer team in 1980 at ≈20 AU after Pioneer 10 had passed Saturn and the direct solar radiation pressure acceleration off the Sun had decreased such that ap became manifest in the data (Anderson et al., [27] [28] ). Meanwhile acceleration data of both spacecraft have been gathered and evaluated in the range from 20 AU to 70.5 AU. After corrections considering systematics generated external to the spacecraft and on-board, furthermore, computational systematics, the authors give a final value ap = 8.74 ± 1.33 × 10‒8 cm×s‒2, whereby over a range of 40 to 60 AU no magnitude variation within a sensitivity of 2 × 10‒8 cm×s‒2 has been found [27] .
From the above formula of the Sun’s exterior Schwarzschild field mass we receive directly the value of the acceleration induced through the Schwarzschild mass at any range R on an inertially outbound travelling spacecraft of the order

The latter Equation delivers at distance 10 AU ap = 20.02 × 10‒8 cm×s‒2. Anderson et al. adopted for modeling of the strength of solar pressure at 10 AU acceleration ap☼ = 18.9 × 10‒8 cm×s‒2 off the Sun, so that at 70 AU of the former be only 0.39 × 10‒8 cm×s‒2 left. But one should observe that the value of solar pressure at this distance is not known for sure and, thus, can vary over a wide range. Nevertheless, for the following calculations of ap at distances from 20 - 70 AU the Anderson value of ap(☼) = 18.9 × 10‒8 cm×s‒2 at 10 AU has been adopted. Considering this, from Equation (87a) is calculated:

As one observes, decreases ap(☼) steadily, but nevertheless does the mean from 20 to 70 AU be of value 8.46 × 10‒8 cm×s‒2 (the mean up to 60 AU be = 8.7 × 10‒8) and, therewith, very near to the observational data of Anderson et al.
Furtheron, it will be demonstrated that the infall velocity in the Bullet cluster system of value vi > 3000 km/s, which recently has been derived from the observed X-ray brightness and considerably deviates from calculations on the grounds of Newtonian Gravitation with vi ≈ 980 km×s‒1, directly follows from the above mass formulae of the Schwarzschild field [29] [30] . For reasons of simplicity both systems are considered to have same baryonic mass Mma = 3.55 × 1013 M☼ so that the baryonic center is located midway at R = 2.3 Mpc with both systems
falling onto this point in space with combined kinetic energy:
total energy 

With respect to one of the clusters the total gravitational mass according to Equation (68) is calculated with

whereby for reasons of simplicity the latitudenal position of the cluster is also taken as Α = 43.788˚. Inserting

The above formulae for calculating the Schwarzschild mass also easily explain the measured increase of spiral rotation curves [31] and of the Galaxy’s Halo stars and the Magellanic clouds’ (LMC and SMC) proper motion [32] [33] .
10. Owing to Foucault’s Law Warp Rapidly Spinning Rotators within the Rotating S3-Sphere the Local Space-Fabric and Cause the Universal Centrifugal Force to Divert; Implications for Rotators in Space and on Earth
To begin with, the simple cross-section in Figure 7 illustrating a photon’s great circle geodesics σ = 2Ρπ about the S3-hypersphere’s rotation poles with crossing its equatorial sphere perpendicularly, may also visualize directions and distances in the three-sphere. As previously shown, does the rotation of the three-sphere give rise to internal centrifugal force FΡ .
The Galaxy’s present lateral position in the three-sphere in accord with Equation (35) is calculated with ΑG = 43.788˚ and it has been shown this derivation to be fairly exact, whereas the previously introduced direction of rotation of the hypersphere to be clockwise about its rotation pole, here arbitrarily designated as the northern one, is a reasonable assumption, which will be proven in detail further below. Thus, the Galaxy’s distance r4D from the equator E then would be ≈(43.788/90) × Ρπ/2 = 6.42 × 109 ly in comparison to distance ≈ 6.78 × 109 ly from the nearest, say northern, rotation pole of the closed, static, self-containing, steadily rotating three-sphere S3.
Furthermore, it is obvious that the rotating three-sphere in four-dimensional space with Euclidian E4 metric can be considered as a hyper-gyro, which for the basic Newtonian laws, especially for the rotation of rigid bodies, must be fully valid. This must also apply to fast spinning gyros inside the rotating three-sphere with respect
Figure 7. Cross-section of a photon’s great circle geodesics about the Universe’s rotation poles.
to the latter’s rotation, because FΡ acts upon every moving mass point of the rotator individually. In the latter case a body with mass m moving with velocity v in the rotating three-sphere will experience the fictitious Coriolis force

being dependent on velocity and acting perpendicularly to vector ω . Analogously to high- and low-pressure systems on spinning Earth must in the spinning three-sphere also arise Coriolis forces, which enforce all material to stream towards or off big cosmic systems, as e.g. galaxies and clusters of galaxies, into the well-known helical form. This manifestation of the Coriolis force within the spinning hypersphere has aside from spiral galaxies recently also been found in spiral-like structures at the center of galaxy clusters on the grounds of X-ray data analysis of Chandra observations of 15 nearby clusters of galaxies (see e.g. Laganá, 2009 [34] ).
But the most important physical phenomena in the spinning Universe are to expect as a result of the well- known law of Foucault, according to which a fast-spinning axially symmetric gyro will set its rotation axis so that the angle with the axis of the enforced rotation tends to a minimum and the direction of both rotations coincides. As well known, enforces Foucault’s law on rotating Earth a gyro’s axis of rotation (e.g. of a gyro compass) to adjust in the horizontal plane to the north-south direction so that the angle with the axis of rotation of Earth becomes as small as possible. The torque, or, self-aligning torque at angle β in reference to the north-south direction (Earth) amounts to

whereby J denotes angular momentum of the gyro, ωe angular velocity of Earth and α latitude on Earth. As widely known results Equation (83) from the integration of the gyro’s mass elements torques, caused by the Coriolis force.
In principle it is to expect that a fast-spinning gyro behaves analogously in the steadily rotating S3-hypers- phere by turning its axis of rotation so as to shape the smallest possible angle with the sphere’s rotation axis and, simultaneously, to bring its direction of rotation in coincidence with that of the former. Depending on the gyro’s direction of rotation within the sphere, results a tilt of the same rotation pole either to the northern or to the southern rotation pole of the three-sphere. As a consequence will the gyro the locally flat Minkowsi metric ηnm of its volume (and probably the adjacent space) deform or warp with regard to the hypersphere’s axis of rotation and, thus, by diverting the centrifugal force FΡ , increase or decrease the latter so that the gyro under consideration is set in northward or southward motion (in dependence on its direction of rotation). The principle is visualized in Figure 8.
Because of the absolute elasticity of the sphere’s spatial fabric it is to expect that angular velocity ωK of the gyro and the sine of the angle α enclosed by the sphere’s and the gyro’s axes of rotation and the resulting transversal velocity vtrans due to reversion of FΡ be linearly connected. Thereby, according to special relativity the gyro has to be considered resting in its coordinate system at rest. Because of the linearity of the physical situation in the sense of Newtonian physics takes the above momentum equation the transitional form

which then can be directly applied to gyros in the steadily rotating three-sphere, where α now denotes the angle of the self-aligning torque in reference to the north-south direction of the spinning Universe, μK self-aligning
Figure 8. Divertion of the centrifugal force FP by fast-rotating gyros in the rotating Universe. Fat line denotes gyro.
torque and JK angular momentum of the gyro, ωΡ angular velocity of the sphere at radius Ρ, Α the gyro’s latitude in the sphere, respectively.
Consider the most simple hypothetical case of a gyro in a gravitational field at the equator of S3 so that cosΑ = 1 and the above formula takes the simpler form

Torque M shall suffice to divert the centrifugal force FΡ in the sphere such that the part of the latter which locally acts as gravity, vanishes. This for, angle α obviously must be given a value, which just causes the according to general relativity warped spacetime of the field around the points (0, r) = r of the gyro’s axis with approximated Minkowski metric gnm = ηnm + fnm to switch into the flat state ηnm and fnm, describing the gravitational potential and, thus, to vanish. i.e., the fundamental tensor of the field shall take the form g44 = η44 = ‒1. Because only very small angles are concerned and the Newtonian gravitational potential U being associated with the metric of general relativity by the relations

one receives:
M mass and R radius of the body constituting the well of the gravitational field. Thus, the previous formula of the self-aligning torque for angle α takes the form

Furthermore, according to the previous is ωΡ = c/(Ρ × cosΑ) and, thus, defining velocity of light as the three- sphere’s circumferential speed ω Ρ × Ρ × cosΑ at latitude Α. Because JKωΡ × cosΑ = Mcor denotes the torque the Coriolis force will exert within the S3-hypersphere, may the left-hand side of the above formula now also be written as

(with cosΑ = 1),where arot = (vrot)2/r denotes circular acceleration, vrot circumferential (rotation) speed and r radius of gyro. Cancelling factor JKωΡ from both sides of the right hand side of the second line, the simple relation between the rotation speed vrot of a gyro and the decrease of gravity of value

is obtained. Thus, the circumferential velocity 

Outside of gravitational fields with metric gnm = ηnm this simply becomes to

But these relations are by no means complete yet. As already mentioned, has to be considered yet that referring to the gyro’s direction of rotation in the S3-space this leads either to a northern or southern alignment of the gyro’s axle such that the vector of the resulting velocity vtrans always points into the opposite direction. Furthermore, does the latitude of angle Α play an important role, because e.g. in the “northern hemisphere” the centrifugal force Fc = FΡ × cos2Α will increase with latitude proportional to sinΑ and, thus, counterclockwise rotating gyros must be set back and clockwise rotating ones ahead by factor sinΑ (see Figure 9).
Thus, for gyros spinning counterclockwise in space with flat metric ηnm must be valid

For the Galaxy’s previously calculated position at cosmic northern latitude ΑG ≈ 43.788 the latter equation takes the form

Likewise, gyros spinning clockwise in the northern cosmic hemisphere must be ahead by the factor

such that at the lateral position of the Galaxy applies:

It is predicted that the translational velocity which according to the latter equations results from rapid spinning, independently of mass, dimension and other physical properties of the rotator, be the very cause of velocity kicks of fast spinning neutron stars, black holes and white dwarfs at their birth. Furthermore, should in accord with the previous all rapid rotators in the Universe, including spiral galaxies, show a distinct parallelism of their rotation axes (see extensive discussion in Appendix 4).
Applied to gravitational fields at the lateral postion of the Galaxy one receives the formulae

and

Figure 9. Gyros with oppositely directed rotation in dependen- ce on cosmicl atitude A. Fat line denotes gyro, CC counter- clockwise and C clockwise rotation, respectively.
These Equations enable one to calculate the circumferential rotation speed vrot which just suffices to cancel the inertia of a rotator in the gravitational field of Earth, i.e. neutralize its weight on the surface of Earth. Ob-
viously, this for the gravitational potential 
(96) is put

and for clockwise rotation (c), parallel to the S3-sphere’s direction of rotation

whereby, to mention it again, the three-sphere’s sense of rotation still is mere assumption (but see below). Thus, a gyro on the surface of Earth spinning freely (unconfined) counterclockwise with respect to the northern rotation pole of the three-sphere S3 loses its inertia, i.e. becomes “weightless”, at a circumferential speed of 4.39 km×s‒1 absolute independently of the rotator’s material condition, spatial dimensions and moment of inertia or angular momentum, respectively. The same is valid for the rotator now spinning clockwise with respect to the northern rotation pole at a circumferential speed of 10.29 km×s‒1. In both cases only rotation speeds on the surface of Earth > 4.39 km×s‒1, or, 10.29 km×s‒1, respectively, are transformed into translational motion. These results are, of course, first theoretical derivations, which need confirmation or correction, respectively, through experiment (see Appendix 4 and Appendix 5).
From the previous follows, furthermore, in the case
bound local cancellation of the gravitational potential 
gravity locally, on the surface of a gravitating cosmic body to be valid

and

This implies on the surface of all solid cosmic bodies, i.e. stars, planets and moons, to be directly valid

i.e. the induction of vtrans/c through the spinning gyro is reflected by a corresponding alteration of the gravitational field’s 
Because 

velocity gain vtrans and simultaneous twist of the rotator’s axle relative to the rotation axis of the S3-sphere, this implies also simultaneous warping of local Minkowski-space into E4 by angle δ (see below). These warps necessarily must be small four-dimensional divertions spatially from local flat Minkowski-space, directed oppositely to another referred to the rotational axis of the hyperspere. It is obvious that a fast-spinning gyro first of all causes the warping of space it occupies with its body, i.e. volume. Note that this implies a symmetric but counter directed diversion leap of the gyro’s metric from its spatial surrounding by angle δ on either side of the rotation axle. This in turn causes vtrans to be diverted to velocity v(trans(ax) = vtrans parallelly to the gyro’s axle by angle δ toward the northern rotation pole in the case of counterclockwise rotation in respect to the latter and vice versa in the case of clockwise rotation, respectively, if δ = const. But because of velocity vtrans already being imparted to the rotator, must velocity v(trans(ax) be nullified by the counter directed velocity ‒v(trans(ax) above the latter’s other rotational plane with the result that v(trans(ax) + (‒v(trans(ax)) = 0. Thus, it applies

and for angle δ

whereas δ of the gravitational field, counter-balanced by (103) takes the form

where ωrad denotes rad = 180˚/π.
Thus, one arrives at the physical picture of a columnar expansion of space warping or diversion field over both sides of a fast-spinning gyro in S3 in the direction of its rotational axis. i.e. in these opposite directions axially symmetric fields (dipol field) of a repulsive quasi force are induced in accord with the above equations. The lateral expansion coincides with the gyro’s lateral dimensions, i.e. the plane of the cycle perpendicular to the spin axis. Assumably does this local disturbance of the metric at both sides of the gyro’s plane decrease analogously to the decrease of gravitation reversely with distance squared from the source of the gravitational well.
Therefore, the diversion field can be described as a potential Urot aligned parallelly to the rotation axis above both sides of a rotor

where Rrot denotes radius of the rotator and R = Rrot perpendicular distance from one of the former’s rotational planes. According to this, e.g. should spinning Earth generate a weak diversion field above both hemispheres in extension of its equatorial plane, directed parallelly to its rotation axis of value

whereby R ≥ Re. This diversion field above both hemispheres of Earth explains the so called flyby anomalies (see discussion Appendix 4). Furthermore, have the weak repulsion fields associated with slowly spinning gyros already been measured in the laboratory and are controversially discussed in the literature since (see Appendix 5).
It is proposed that counter directed jets proceding from the center of cosmic systems (e.g. AGN) and above the rotation poles of fast-spinning Milky Way stars are also due to this effect, which implies that the very inner core of the latter rotates like a rigid body. Since the Milky Way’s very core seems to exhibit the same spinning properties, one has to expect weak repulsion fields above the former’s rotation poles too, which should be perceptible through oppositely directed particle streams and associated secondary high-energy photons.
11. The Direction of Rotation of the Three-Sphere S3 with Respect to the Surface of Earth and the Main Directions of the Former’s Rotation Poles on the Plane of the Sky with Regard to the Galaxy
11.1. The Direction of Rotation of the Closed Three-Sphere S3 with Respect to Its “Northern Rotation Pole”
A first unmistakable hint at the global location of the three-sphere’s rotation poles on the plane of the sky contains the study of Lorimer and Ramachandran (1999) [35] , which also will be discussed in Appendix 4. According to this analysis show twenty out of twenty-seven pulsars with respect to their parent remnant shells negative offsets in Galactic longitude, whereby the northward pointing galactic longitude is defined as negative. Because the galactic plane is inclined by 57˚ against the Sun’s ecliptic, it is evident that the negative offset of the 20 pulsars implies their northward motion from the geometric center of the respective supernova remnant with respect to the ecliptic plane.
The explanation in the framework of the foregoing obviously is that, globally seen, fast-spinning pulsars translationally move in the three-sphere either northward or southward in dependence on the pulsar’s direction of rotation. The ratio 20:7 in favor of northward moving pulars merely reflects the approximate higher quantity of counterclockwise rotating relative to clockwise spinning ones in the Milky Way, i.e. the direction of spin of the pulsars’ majority coincides with the spin direction of the majority of the other stars, which is counterclockwise. Thus, the globally northward directed translational movement of the counterclockwise rotating pulsars implies:
1) The previously defined northern rotation pole of the closed three-sphere S3, our Universe, is located on the plane of the northern hemisphere’s sky, somewhere in the vicinity of the pole of the ecliptic;
2) The closed three-sphere S3 rotates with respect to its northern rotation pole in clockwise direction.
11.2. CMB Alignments Due to Ellipticity of the Rotating Three-Sphere S3 and the Galaxy’s Former Position and Present Drift
This derivation of the approximate location of the Universe’s northern rotation pole on the plane of the sky is also supported by the results from measurements of the CMB radiation (see e.g. Craig et al., 2005 [7] ).
Full-sky temperature maps of the CMB at very low temperature (milli Kelvin) from the “Wilkinson Microwave Anisotropy Probe” (WMPA) exhibit some statistically significant anomalies compared to the standard inflationary cosmology (big bang). In particular the correlations at large angular seperarations exhibit several peculiarities. It has been shown that there exist hot and cold spots in the so called quadrupole and octopole anisotropies, which lie nearly in a plane. Moreover, the combined quadrupole and octopole is unexpectedly aligned with the geometry (and direction of motion) of the solar system in so far as the plane they define is perpendicular to the ecliptic plane and the ecliptic plane exactly seperates stronger from weaker extrema, the stronger ones being located in the north and, thus, revealing an obvious north-south ecliptic asymmetry.
The standard inflationary picture of the cosmos predicts a CMB temperature anisotropy pattern that is statistically isotropic and delivers no explanation of the observed correlations on so large scales.
To the quadrupole map of Craig et al. (first Figure 1 in reference [7] , here not shown) is to remark that the white stars indicate the minimum and maximum temperature locations (coldest and warmest spots in the CMB sky), thus, revealing that the extrema on the north side are stronger than those in the south. The solid line is the ecliptic plane and the dashed one, crossing the ecliptic amidst nearly perpendicularly, the line connecting the extrema. Exactly on this line lies the northpole of the ecliptic, denoted NEP.
We give a qualitative description on the grounds of the previously discussed physical picture of the Universe. According to the latter is the CMB enthropic (Planckian) radiation within the closed, static three-sphere S3 and it is clear that no deviations from a perfect Planckian distribution of the CMB even at lowest temperatures, as has been measured by the WMPA, should occur if the Universe really exhibits the assumed geometrical properties of a perfect hypershere. This assumption has been introduced for reasons of simplicity. But because of the assumed perfect elasticity of the space fabric it is to expect that the Universe due to its rotation slightly deviates from the shape of a perfect hypersphere rather to take the form of a rotation hyperellipsoid.
On the other hand should these geometrical deviations be of minor value because of the smallness of the Universe’s angular velocity ωΡ = c/(Ρ × cosΑ), where Ρ (radius of the three-sphere S3) ≈ 2.6 × 103 Mpc. And from Equation (11) it is clear that the variable value of a hyperellipsoid’s radius must directly lead to slight temperature differences of the enthropic (Planckian) radiation. In Figure 10 the cross-section of a photon’s great
elliptic geodesics (lightpath ellipse) 
tion poles with perpendicularly crossing its equator is (exageratedly) visualized, where Ρ here denotes the major half-axis, ρmin the smallest of the minor half-axes ρ and Εel the definite elliptic integral.
It is clear that the elliptic lightpath σel follows the global metric of the three-ellipsoid and, thus, the lightpath of CMB photons ingoing from the polar regions of the Universe is less and from the equatorial zone stronger curved than the median according to the relations

Figure 10. Cross-section (exaggerated) of a photon’s great elliptic geodesics about the Universe’s rotation poles.
where ρPol and ρE denote radius of curvature at the poles and at the equator, respectively. This implies according to Equation (12) the photons from the poles to be less and the ones from the equator more reddened than the median CMB photons, i.e. the poles appear slightly warmer and the equator region cooler, respectively.
Now, we can interpret the said quadrupole map as the CMB photons ingoing from about halfway the Universe, the extrema in the north picturing the warmer appearing northern pole and behind it the cooler appearing antipodal equatorial zone, furthermore, the extrema in the south the cooler appearing near equatorial belt and behind it the warmer southern rotation pole.
Obviously is the impression that our vantage point exactly seperates stronger from weaker extrema due to the Galaxy’s position about halfway between the northern pole and the cosmic equator (Α = 43.788˚). The alignment of the extrema with the geometry of the solar system, especially that the plane they define be perpendicular to the ecliptic plane, must be caused by a real alignment of the Sun’s rotation axis with the cosmic north-south direction and, therewith, of the eclipsis directed perpendicularly to the latter. A relative fast rotation velocity of the proto Sun, which according to the previous would lead to a general orientation of the e rotation axis parallelly to the rotation axis of the Universe and, thus, the plane of the later forming planetary system perpendicularly to the latter, offers a convincing explanation of this particular alignment of the eclipsis. After fusion started and the proto Sun inflated due to radiation pressure, the angular velocity rapidly decreased and simultaneously the angular momentum has been transmitted to the evolving planetary system. As a consequence, the diversion effect vanished, but the cosmic north-south alignment of the Sun’s rotation axis and―perpendicularly to the latter―of the equatorial plane of the ancient Sun, the nowadays eclipitic plane, remained (see also Appendix 4).
Since due to its rotation the Universe happens to be more elliptically than spherically shaped must the light path from the equator to the assumed lateral position of the Galaxy be stronger curved than the one from the northern pole. This fact is convincingly reflected by the above mentioned map, where the distance from the Galaxy’s position (crossing point of eclipsis and σel to the equator (center of the cold spot in the south) is markedly shorter than the one to the northern pole (center of the warm spot in the north, shown by a white star).
The octople mapin reference [7] (second Figure 1, also not shown) exhibits an additional extremum on both sides of the map: a cold spot in the outermost south and a warm spot in the extreme north. The latter again ap- pears somewhat warmer than the one in the south. The physical interpretation of the octopole is that we now see
the CMB at distance
great circle (ellipse) geodesics on either side. i.e. the additional warm spot in the utmost north designates the Universe’s southern pole, now also seen from north and the additional cool spot in the extreme south is the CMB ingoing from the antipodal equator region, which we also have in the north as the second (cold) extremum.
An open question is why in the combined map Figure 3 of [7] (quadrupole plus octopole, here also not shown) this energy (temperature) relation reverses and the three extrema in the north now appear considerably, even visibly weaker than those in the south. This pronounced north-south ecliptic asymmetry in the combined map is found in neither single multipole map alone.
Comparison of those maps shows that in the quadrupole the ecliptic, i.e. the Galaxy’s position, is also visibly nearer to the equatorial plane in the south than in the octopole map. According to the previous is this phenomenon not accidental, but reflects a by ≈13.4 × 109 years earlier state of the Universe (because this is the time which light from the most distant new extrema in the octopole roughly needed longer) and, therewith, a real movement of the Galaxy (or its progenitor) towards the equator. The proceeding is illustrated in Figure 11.
Compared to the Galaxy’s nowadays position amidst the north pole and the equator (quadrupole), does in the northern hemisphere CMB radiation ingoing from the south pole need time l/c longer for the assumed southward motion of the Galaxy, where l means distance the Galaxy travelled in ≈13.4 × 109 years; i.e. the light must have started time l/c earlier in the north and later in the south, respectively. Therefore, the positions of the extrema in both hemispheres are shifted southward by distance l relative to the ecliptic and the utmost northern and southern edge of the respective CMB map. This southward drift of the eclipsis due to the respective equatorial directed motion of the Galaxy is the indirect cause of the aforementioned increase of power in the south ecliptic hemisphere of the combined quadrupole-octopole maps, or, an obvious north-south ecliptic asymmetry, respectively.
From the above Equation (108) in association with equation (15) follows the relation

i.e. the energy density Ephot(E) of the CMB photons ingoing from the equatorial belt is somewhat higher than the energy density Ephot(Pol) of the polar CMB photons. Thus, in the course of the gradual drift of the Galaxy from the more flatly curved pole near regions towards the stronger curved equator zone necessarily the intensity of CMB photons ingoing from south of the ecliptic must increase. And it is clear that only a combined map showing this shift can reveal this (very) small imbalance of power: a difference of power in time of ≈13.4 × 109 years (see below).
One should notice that the latter view into the farer past of the Universe has been made possible through an extreme decrease of the CMB-temperature maps to some milli-Kelvin. According to the preceding this is to expect since the lowest CMB temperatures should reflect the most ancient revolutions of the hyperellepsoid. i.e. the lower the temperature the more revolutions should be imprinted in the CMB and perceivable as “cold” and “hot” spots in the latter. Indeed this also has been observed by Telemark et al. (2003 [36] ), who additionally to the above discussed quadrupole and octopole maps, published a hexadecopole map with a resolution of −34 to 0.34 μK which show already 10 “cold” and “hot” spots and, therewith, at least two complete revolutions of the Universe. Most recently the BICEP2 Collaboration even published results in the temperature regions −0.3 to 0.3 and 1.7 to 1.7 μK, respectively, with lots of “cold” and “hot” spots, multipoles, not in the whole sky but in a region of some degrees squared only. But the published maps also clearly indicate the −0.3 μK-map to contain more spots than the1.7 μK-map. i.e. the former map represents more revolutions of the Universe or its older status. The authors attributed their results to gravitational waves in the very early phase of the Universe in the sense of the big bang hypothesis. To this assumption they have been led through a definite polarization pattern of the received light. But as already pointed out above is the latter finding inside the sphere to expect owing to the revolution of the Universe relative to the transversality of the electromagnetic waves associated with the
Figure 11. The Galaxy’s southward drift in ~1/4 time of the Universe’s revolution.
latter’s rest relative to E4 or partly two-fold rotational velocity. Additionally, the perturbated polarization pattern clearly is concentrated around the “hot” spots of the rotation poles and more broadly distributed at the cooler equatorial regions, exactly as expected. Thus, the mentioned astrophysical results clearly show that the Universe has absolved immense numbers of revolutions and, thus, must be very, very old at least, perhaps even exists eternally. Possibly could this question be answered through a still higher resolution of the CMB as the above experiment of the BICEP2 Collaboration.
We compute the distance which the Galaxy travelled from its position ≈13.4 × 109 years ago to its nowadays vantage point according to a recent extension of special relativity [37] with:

where vG ≈ 216.57 km×s‒1 denotes mean velocity of the Galaxy relative to the CMB as the absolute rest frame on its southbound way from the birth place at high northern latitude assumably with about zero velocity to its present position with nowadays velocity vG ≈ 600 km×s‒1, furthermore, the mean results from vG × 1/2cosAG and γG ≈ 1, denoting the Lorentz factor. From the combined map one infers that 13.4 × 109 years ago the latter birth place was located about 1/3r ≈ 4.467 × 109 ly south of the cosmic northern pole or ≈30˚ northern latitude. Addition of the result from Equation (110) and the latter distance results in 6.562 × 109 ly as the nowadays distance of the Galaxy from the northern pole or 44.07˚ northern latitude. Considering the uncertainties, is this result in exellent accordance with the above calculated value ΑG = 43.788˚.
Because the whole equatorial belt of the elliptically shaped Universe should for reasons of symmetry exhibit the same curvature, one intuitively would expect that the cooler equatorial regions of the CMB in the maps would show up as somewhat more extended features.
From the preceding it is clear that the Minkowski projection of the CMB from those regions delivers not an imprint of the local equatorial metric but rather of the light path’s curvature. For the observer within the rotation hyperellipsoid at the lateral position ΑG = 43.788˚ of the Milky Way Galaxy is this the elliptic equivalent to the great circle σ = 2πΡ of the three-sphere S3 going over the rotation poles, i.e. the great elliptic geodesics

elliptic geodesics σel at any point between equator and pole must be an ellipse with mayor half-axis Ρ and a minor half-axis ρ with value Ρ > ρ > ρmin. Especially at the lateral position of the Galaxy (and the antipode) must be
valid
going through this point exactly one ellipse σel(max) exists with the half-axes Ρ and ρmax exhibiting the greatest circumference of the whole set of ellipses. This must be the light path of all photons ingoing from the two points at the equator which are shifted relative to the nearest equator point by a quarter great circle 1/4σ = 1/2πΡ. The former are the crossing points of the curves σ and σel(max), which intersect at an angle of 1/4π, whilst at the observer’s vantage point (Galaxy) the light path σel(max) intersects perpendicularly with the shortest closed elliptic light path σel(min) going over the poles and the equator, crossing the latter perpendicularly. Thus, the path of all light ingoing from equatorial regions other than the nearest and its antipode, respectively (crossing point of curves σ and σel(min)), is less curved and, therewith, reddened, i.e. it appears warmer than light ingoing from the nearest equatorial point and its antipode. Therefore, and due to the particular alignment of the eclipsis appears the CMB of the quadrupole ingoing from the equatorial belt as two distinct cold spots, with the nearest exactly in the south and its antipode in the north behind the northern rotation pole. It is evident that this reasoning, although with reverse reddening process, also is true for the pole regions.
Finally, it should be remarked that depending on the observational direction on the sky and owing to slightly varying radius Ρ of the ingoing light’s geodesics σel the Hubble-“constant” H0 must vary, too.
11.3. The “Spheres of Action” of the Universal Centrifugal Force FΡ on the Surface of Earth
It is clear that according to Foucault the rotation axis of a fast rotator in free space tends to directly align parallelly with the rotation axis of the clockwise spinning three-sphere S3 by turning its clockwise side towards the northern pole. But other than in free space result in this part of the Universe two fixed hemisheres on large bodies owing to the absolute north-south alignment of the universal centrifugal force FΡ with reference to the latter and, thus, some complications for the application of the above gyro equations to rotators in the gravitational field of rotating Earth.
Consider a shortest, closed (or, nearly closed) great elliptic geodesics

of the hypersphere. It is clear that the tangent vector or tiny section Δσel and local pseudo-euclidic Minkowski projection are aligned parallelly to ‒Δσel at the antipodal point in the sphere and to the rotation axis of the latter in geometrically four-dimensional E4-space.
Analogously to a well-known axiom of three-dimensional geometry will all straight lines, which intersect at a given point at a plane in three-dimensional manifold, stand perpendicularly on a line which in turn intersects the latter also perpendicularly in E4. This implies that all straight lines intersecting the geometric center of a spherical body at the equatorial region of the Universe, including also all possible rotation axes of a rotating body, must intersect vector of FΡ perpendicularly too. Because the latter in turn intersects the rotation axis of the S3- hypersphere also perpendicularly, will the rotation axis of the body which is directed parallelly to Δσel also be directed parallelly to the Universe’s rotation axis. As a consequence must the whole Northen hemisphere of this rotating body permanently be orientated towards cosmic north and the southern hemisphere to cosmic south, respectively.
According to Equation (35) are Galaxy and Earth within the three-sphere S3 laterally positioned at 43.788˚. This implies that vector of FΡ orthogonal to the rotation axis of the Universe intersects Δσel of the great elliptic geodesics at the Earth’s lateral position also at latitude 43.788˚. Since according to the previous the northern ecliptic pole and, thus, approximately, the north pole of Earth also point towards the northern rotation pole of the three-sphere S3, also the rotation axis of Earth must be aligned roughly in the same direction spatially. This implies that vector of FΡ meets Earth’s rotation axis roughly at angle 45˚ too, so that any point on the surface of Earth at latitude roughly ≥± 45˚ must be permanently orientated toward one of the cosmic main directions, whereas any point between will during one rotation period in dependence on its latitude prevail somewhat less then 24 h directly below latitude ≈± 45˚ and exactly 12 h at the equator in the sphere of action of one cosmic hemisphere and the rest of the rotation period in the other one. Generally a point on Earth below latitude ≈± 45˚ will during the day prevail for time in hours (h)

within the sphere of action of the opposite hemisphere and for

within its own hemisphere. These values are to understand as a first approach, which expect correction by experiment (see Appendix 5).
12. Concluding Remarks
It has been proposed and at least also partly shown the Universe to be a near spherical rotation hyperellipsoid spinning in a geometrically four-dimensional space with Euclidian E4 metric.
As a main result gravitational force has been demonstrated to be identical with centrifugal acceleration within the hypersphere and, thus, to be a fictious force. The very nature of mass could be revealed. Also has been de- monstrated that, other than according to current gravitational theory, inertial and gravitational mass to be different, although indistinguishable from each other, and all tabular mass values being the median of the former.
Furthermore, the deviations from Newtonian dynamics in the gravitational field of large cosmic systems, as e.g. galaxies and cluster of galaxies could be explained through the gravitational action of the mass of the exterior Schwarzschild field―Schwarzschild mass.
Last but not least it has been shown the validity of Foucault’s law within the spinning near hypersphere or hyperellipsoid to imply that fast rotators will warp their local space and divert the universal centrifugal force inside the rotating hypersphere with the physical consequence that their state of motion in and outside of gravitational fields can be calculably altered. This cosmic law enables experimental proof of the above introduced novel cosmological concept on laboratory scale (see also Appendix 5) and is of major technological importance too, because it opens up the possibility to propel e.g. spacecraft and aircraft without burning fuel and with much higher efficiency and velocity as common propulsion systems.
Acknowlegements
Dedicated to my beloved Ingrid.
References
- Lemaître, G. (1927) Un Univers Homogène de Masse constant et de rayon croissant rendant compte de la vitesse radiale des nebuleuses extra-galactiques (A homogene Universe of Constant Mass and Increasing Lightpath Calculated from the Radial Velocity of Extra-Galactic Nebulae). Annales de la Sciétéscientifique de Bruxelles, Sèrie A, 47, 49.
- Hubble, E.P. (1929) A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae. Proceedings of the National Academy of Sciences, 15, 168.
- Riess, A., Nugent, P.E., Schmidt, B.P., Tonry, J., Dickinson, M., Gilliland, R.L., Thompson, R.I., Budavari, T., Casertano, S., Evans, A.S., Filippenko, A.V., Livio, M., Sanders, D.B., Shapley, A.E., Spinrad, H., Steidel, C.C., Stern, D., Surace, J. and Veilleux, S. (2001) The Farthest Known Suoernovae: Support for an Accelerating Universe and a Glimpse of the Epoch of Deceleration. arXiv: 0104455 [astro-ph]
- Swanson, M.E.C. (2008) Particle Physics in the Sky and Astrophysics Underground: Connecting the Universe’s Largest and Smallest Scales. arXiv: 0804.0002 [astro-ph]
- Renzini, A. and Daddi, E. (2005) Witnessing Galaxy―SMBH Co-Evolution at Redshift ~ 2. arXiv: 0800.0094 [astro-ph]
- Lerner, E.J. (2008) Evidence for a Non-Expanding Universe: Surface Brightness Data from HUDF. arXiv: 0509611 [astro-ph]
- Craig, J., Huterer, D., Schwarz, D.J. and Starkman, G.D. (2006) The Uncorrelated Universe: Statistical Anisotropy and the Vanishing Angular Correlation Function in WMAP Years 1 - 3. arXiv: 0605135 [astro-ph]
- Einstein, A. (1917) Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie (Cosmological Considerations to the General Theory of Relativity). Sitzungsberichte der königlich Preussischen Akademie der Wissenschaften,, 142-152.
- Einstein, A. (1911) Über den Einfluss der Schwerkraft auf die Ausbreitung des Lichts (On the influence of gravity on the Propagation of Light). Annals of Physics, 35, 898-908. http://dx.doi.org/10.1002/andp.19113401005
- Lehnert, M.D., Nesvadba, N.P.H., Cuby, J.-G., Swinbank, A.M., Morris, S., Clement, B., Evans, C.J., Bremer, M.N. and Basa, S. (2010) Spectroscopic Confirmation of a Galaxy at Redshift z = 8.6. arXiv: 1010.4312 [astro-ph]
- Cunha, J.V. and Lima, J.A.S. (2008) Transition Redshift: New Kinematic Constraints from Supernovae. arXiv: 0805.1261v2 [astro-ph]
- Stephani, H. (1980) Allgemeine Relativitätstheorie (General Theory of Relativity). Deutscher Verlag der Wissenscha- ften, Berlin, 253.
- Younger, J.D., Fazio, G.G., Huang, J.-S., Yun, M.S., Wilson, G.W., Ashby, M.L.N., Gurwell, M.A., Lai, K., et al. (2007) Evidence for a Population of High-Redshift Submillimeter Galaxies from Interferometric Imaging. arXiv: 07081020 [astro-ph]
- Melbourne, J., Bussman, S., Brand, K., Desai, V., Armus, L., Dey, A., Jannuzi, B.T., Houck, J.R., Matthews, K. and Soifer, B.T. (2009) High Redshift Dust Obscured Galaxies, a Morphology-SED Connection. arXiv: 0904.1231v1 [astro-ph.Co]
- Einstein, A. (1916) Die Grundlage der allgemeinen Relativitätstheorie (The Basis of the General Theory of Relativity). Annalen der Physik, 49, 769-822.
- Heisenberg, W. (1938) Über die in der Theorie der Elementarteilchen auftretende universelle Länge (On the Universal Length Occuring in the Theory of Elementary Particles). Annalen der Physik, 32, 20-32. http://dx.doi.org/10.1002/andp.19384240105
- Pohl, R., Antognini, A., Nez, F., Amaro, F.D., Biraben, F., Cardoso, J.M.R., et al. (2010) The Size of the Protron. Nature, 466, 213-216.
- Stephani, H. (1980) Allgemeine Relativitätstheorie. Deutscher Verlag der Wissenschaften, Berlin, 98-121.
- Burghardt, R. (2005) Erweiterte Methoden zum Verständnis von Gravitationsmodellen (Extended Methods for Understanding of Gravitational Models). Lectures in Geophysics and Physics, 6, 103-106.
- Zwicky, F. (1933) Die Rotverschiebung von extragalaktischen Nebeln (The Redshift of Extra-Galactic Nebulae). Helvetica Phisica Acta, 6, 110-127.
- Bosma, A. (1981) 21-cm Line Studies of Spiral Galaxies. The Astronomical Journal, 86, 1791-1846. http://dx.doi.org/10.1086/113062
- Rubin, V.C., Ford Jr., W.K., Thonnard, N. and Burstein, D. (1982) Balance of Dark and Luminious Mass in Rotating Galaxies. The Astronomical Journal, 261, 439-456. http://dx.doi.org/10.1086/160355
- Rubin, V.C. (1983) The Rotation of Spiral Galaxies. Science, 220, 1339-1344. http://dx.doi.org/10.1126/science.220.4604.1339
- Zwicky, F. (1937) On the Mass of Nebulae and Clusters of Nebulae. The Astronomical Journal, 86, 217-246. http://dx.doi.org/10.1086/143864
- Hinshaw, G., Weiland, J.L., Hill, R.S., Odegard, N., Larson, D., Bennett, C.L., Dunkley, J., Gold, B., Greason, M.R., Jarosik, N., Komatsu, E., Nolta, M.R., Page, L., Sperge, D.N., Wollack, E., Halpern, M., Kogut, A., Limon, M., Meyer, S.S., Tucker, G.S. and Wright, E.L. (2009) Five-Year Wilkinson Microwave Anisotropy-Probe (WMAP) Observations: Data processing, Sky Maps, and Basic Results. The Astronomical Journal, 180, 225-245. http://dx.doi.org/10.1088/0067-0049/180/2/225
- Schneider, P. (2006) Extragalactic Astronomy and Cosmology. Springer Verlag, Berlin Heidelberg.
- Anderson, J.D., Laing, P.A., Lau, E.L., Liu, A.S., Nieto, M.M. and Turyshev, S.G. (1998) Indication from Pioneer 10/11, Galileo and Ulysses Data of an Apparent Anomalous, Weak Long-Range Acceleration. arXiv: 9808081 [gr-qc]
- Anderson, J.D., Laing, P.A., Lau, E.L., Liu, A.S., Nieto, M.M. and Turyshev, S.G. (2001) Study of the Anomalous Acceleration of Pioneer 10 and 11. arXiv: 0104064v5 [gr-qc]
- Mastropietro, C. and Burkert, A. (2008) Hydrodynamical Simulations of the Bullet Cluster. Reviews in Modern Astronomy, 20, 228.
- Walker, M.G., McGaugh, S.S., Mateo, M., Olszewski, E. and de Naray, R.K. (2010) Comparing the Dark Matter Halos of Spiral Low Surface Brightness and Dwarf Spheroidal Galaxies. arXiv: 1004.5228v2 [astro-ph]
- Przybilla, N., Tillich, A. and Heber, U. (2010) Extended HI Rotation Curve and Mass Distribution of M31. arXiv: 1005.5026v1 [astro-ph]
- Przybilla, N., et al. (2007) Weighing the Galactic Dark Matter Halo: A Lower Mass Hint from the Farthest Halo Star Known. arxiv: 1005.5026
- Besla, G., Kallivayalil, N., Hernquist, L., Robertson, B., Cox, T.J., van der Marel, R.P. and Alcock, C. (2007) Are the Magellanic Clouds on their First Passage about the Milky Way? arxiv: 0703196 [astro-ph]
- Kunst, E.K. (2014) Is the Kinematics of Special Relativity Incomplete? Natural Science, 6, 226-247. http://dx.doi.org/10.4236/ns.2014.64027
- Lorimer, D.R. and Ramachandran, R. (2009) Puzzling Pulsar and Supernovae Remnants. arXiv: 0703196 [astro-ph.Co]
- Ade, P.A.R., Aikin, R.W., Barkats, D., Benton, S.J., Bischoff, C.A., Bock, J.J., Brevik, J.A., et al. (2014) BICEP2 I: Detection of B-Mode Polarization at Degree Angular Scale. arXiv: 1403.3985 [astro-ph].
- Tegmark, M., de Oliveira-Costa, A. and Hamilton, A. (2003) A High Resolution on Foreground Cleaned CMB Maps from WMAP. arXiv: 0302496v4 [astro-ph]
Appendix 1: Discussion of Astronomical Observations Referring to the Redshift of Light by Bending of Its Path Outside the Sun’s Gravitational Field and Its Imprint on the CMB
Astronomers have known of systematic red shifts across the disks of galaxies, which are inclined to the line of sight, for more than 70 years. It has been found that generally radial velocities increase towards the far side. A thorough survey of this has been given by Jaakhola et al. (1974) [1] . Because the light from the far side of the inclined galaxy grazes at some distance the galaxy’s bulge it must be deflected and, thus, redshifted according to (4) and (6). We apply the formulae to observations of Münch (1962) in the bright nuclear region of M31, near the minor axis, 200 pc from the center to the far and to the near side, who found at these locations outflow motions with velocities + 100 and − 40 km×s‒1, respectively [2] . For reasons of symmetry it is clear that the motions at the far side should also be of the order ≈+ 40 km×s‒1, leaving an excessive redshift v ≈ 60 km×s‒1 unexplained by current theory (following common usage, redshift is preferentially expressed in terms of velocity).
If the inclination angle between the equatorial plane of the Galaxy and the line of sight is denoted i, then the point of closest approach of the deflected light to the center of mass of M31 must be R200pc × sini and the redshift of the light from this location at the far side of M31 can right forwardly be written as v = c × 4GMM31/(5c2R200pcsini), where MM31 = 2 × 1011M☼, M☼ = 2 × 1033 gr, pc = 3.1 × 1018 cm and i = 12˚ (W. Baade). Astronomers estimate the Milky Way Galaxy’s bulge to contain ≈1/5 of its total mass; assumably this is about valid for the core of M31, too so that only MM31/5 (within R = 200 pc) has to be considered in our formula. Computation yields 56.8 km×s‒1, which is in rather good accord with the ≈60 km×s‒1 of observational result. Similiarly to this, Equations (4) and (6) also predict a redshift v = c × 4GM/(c2R) in peculiar binary star systems, if the line of sight to the farer star grazes tangentially the nearer companion star. The existence of such “anomalous” redshifts in binary stars has been known already for a long time [3] [4] . A reviewal of this has been given by Kuhi et al. (1974) [5] . We restrict to the binary HD 217312, which has been well studied by Heard and Fernie (1968) [6] . According to these authors at the time of eclipse one star is definitely redshifted v with respect to the other with the following characteristics of the system’s components:
If A is the foreground star deflecting the light from star B, the total general relativistic redshift must be
Galaxies which happen to be located behind a companion galaxy with respect to an observer at Earth must analogously to binary star systems exhibit a higher redshift, too. Astronomical studies of companion galaxies revealed a redshift excess in most cases [7] .
The previous formulae also predict an excessive redshift of the light emitted from galaxies situated behind or inside rich cluster if it is deflected by the cluster’s mass (see e.g. [8] ).
According to Equations (6) and (11) we also have to expect a slight redshift of CMB photons as the photons’ pathway is bent by far away, but also by relative nearby mass assemblies, i.e. galaxies, clusters and superclusters. This relative weak but nevertheless certain correlation of cosmic large scale structures with CMB fluctuations has recently been found by two all sky probes, the hard X-ray background observed by the HEAO-1 satellite and the NVSS survey of radio galaxies [9] . We predict that also the smaller fluctuations in the latter will be brought in correlation with very far away cosmic masses soon.
References
- Jaakhola, T., Teerikorpi, P. and Donner, K.J. (1975) On Possible Systematic Redshifts across the Discs of Galaxies. Astronomy and Astrophysics, 40, 257-266.
- Münch, G. (1962) Motions of the Interstellar Gas in the Central Regions of Galaxies in Problems of the Extragalactic Research.
- Trumpler, R. J. (1935) Observational Evidence of a Relativity Redshift in Class O Stars. Publications of the Astronomical Society of the Pacific, 47, 249. http://dx.doi.org/10.1086/124604
- Struve, O. and Sherman, F. (1941) The Spectroscopic Binary 29 Canis Majoris. Astrophysical Journal, 93, 84. http://dx.doi.org/10.1086/144247
- Kuhi, L.V., Pecker, J.-C. and Vigier, J.P. (1974) Anomalous Redshifts in Binary Stars. Astronomy and Astrophysics, 32, 111-114.
- Heard, J.F. and Fernie, J.D. (1968) A Massive Spectroscopic Binary System in the III Cephei Association. Proceedings from IAU Symposium No. 30, Toronto, 20-24 June 1966, 219.
- Bottinelli, L. and Gouguenheim, L. (1973) Redshifts in Companion Galaxies. Astronomy Astrophysics, 26, 85.
- Karoji, H. (1978) A Numerical Simulation Test of “Cluster Effect” in Hubble Modulus. Astronomy Astrophysics, 69, 375.
- Boughn, S. and Crittenden, R. (2003) A Correlation of the Cosmic Microwave Sky with Large Scale Structure. arXiv: 0305001v1 [astro-ph]
Appendix 2: Discussion of Astronomical Observations Referring to the Redshift of Light by Bending of Its Path in the Sun’s Gravitational Field
Some Remarks on Freely Falling Observers and Emitters
In the case of freely falling receivers we take from (6) as the relativistic slow motion approximation of the previous Newtonian derivation of the reddening of gravitationally deflected light:
The underlying physical notion is that the red shift by deflection, which is due to the Newtonian part of gravitation alone, i.e. (‒g44/2)1/2, is exactly cancelled by the free fall of the receiver within the potential well so that the red shift of the bent light decreases to a fourth of that predicted by Equation (6). It is clear that this physical picture leads to a further decrease of the red shift, if additionally the emitter and the photons themselves are considered freely falling within the same gravitational potential well. As widely known, is the geometrical picture of the gravitational redshift considered as an analogy of the special relativistic transversal Doppler-shift


Schwarzschild solution. For the freely falling receiver with velocity 
cord with Equation (7) to a remaining redshift of
constant). Analogously to this would emittance from a “falling” emitter and reception at an also “falling” frame
of reference lead to velocity 


ber of reflections a light ray will experience by freely falling frames, including emittance, the free fall of the photons themselves and reception. Thus, although the deflection of the signal by the Sun always remains constant, will it experience a decrease of reddening in dependence on the number n of reflections within the Sun’s gravitational field in the order
implying a total red shift
whereas the deflection φ = 4GM/(c2R) = constant, as already mentioned.
Bending of Light in the Sun’s Gravitational Field
“Anomalous” redshifts in the vicinity of the Sun are well-known for a long time. E.g. an apparent decrease in the frequency of the 21 -cm absorption spectrum in Taurus A has been observed by Sadeh et al. (1968), when the Sun passed near the line of sight [1] . The experiment showed a still unexplained redshift of ≈ 150 Hz out of 1420 Mhz, when the rays passed at five solar radii. Considering that the received photons and the (receiver) Earth, both were falling freely within the Sun’s potential well and, thus, n = 2, the above equation delivers: Δν2 = GM☼/(4c2) × (5R☼)‒1 × 1.420 × 109 = 150 Hz, the exact experimental value.
This excellent agreement between theory and experiment is also found in the well-known results of Goldstein (1968) with Pioneer 6 [2] .
Spectograms of the radio signals at 2300 Mhz from Pioneer 6 were taken as the spacecraft was occulted by the Sun. When Pioneer 6 passed behind the Sun an “anomalous” redshift has been found, being symmetrical with respect to the center of the Sun. In this case, with emitter (Pioneer 6), photons and receiver (Earth) all falling freely within the Sun’s gravitational field, we have n = 3 and, thus, accordingly Δν3 = GM☼/(16c2) × (R☼(1.5 - 10))‒1× 2.292 × 109.
Theoretical calculations from 1.5R☼ out to 10R☼ neatly comply with solid curves given by the author in a figure of reference [2] . A slight increase of the redshift above the theoretical values probably corresponds to activities in the solar photosphere [3] .
An experiment of Shapiro (1966) in which the frequency of radar pulses reflected from Venus and Mercury could not detect the effect [4] . Because the radar pulses passed 80 solar radii away from the Sun and in all these cases (reflection of the signal by a planet) n = 6, the formula above becomes to Δν6 = GM☼/(1024c2) × (80R☼)‒1 and, therefore, the redshift much too small for detection.
It has been known for some time that light from the limb of the solar disk generally exhibits an anomalous excessive redshift (more than the gravitational redshift). On the other hand, it is an established astronomical fact that there also exists an anomaly in the gravitational redshift of the spectral lines of the Sun in such a way that the redshift increases from a minimum of ≈1/3 of the correct general relativistic value at the center up to the mentioned over-relativistic maximum at the limb, overshooting the theoretical value of the gravitational redshift by ≈1/3. The former effect is generally ascribed ascending flows in the Sun’s photosphere. However, this reasoning is not very convincing, because then this effect should also be observable at other stars, which is not the case.
With n = 1 due to orbiting Earth (receiver) Equation (6) predicts at the center of the Sun a fourth and at the limb Δν1 = GM☼[(c2R☼)‒1 + (4c2R☼)‒1] = 5/4 of the gravitational redshift. The first term in the right-hand member of the latter formula is a half of the tangentially emitted light and, therefore, only to a half of the value according to Equations (4) and (6) deflected and redshifted , whereas the second term is a fourth of the gravitational part of the total redshift from the Sun at its limb. This physical notion also explains the observed steep slope of the rise of the redshift at the very limb in a full way. The generally slightly higher redshift across the whole solar disk than predicted by the previous formula probably is due to descending flows in the photosphere of the Sun.
References
- Sadeh, D., Knowles, S.H. and Yaplee, B.S. (1968) Search for a Frequency Shift of the 21-cm Line from Taurus A near Occultation by Sun. Science, 159, 307-308. http://dx.doi.org/10.1126/science.159.3812.307
- Goldstein, R.M. (1969) Superior Conjunction of Pioneer 6. Science, 144, 598-601. http://dx.doi.org/10.1126/science.166.3905.598
- Chastel, A.A. and Heyvaerts, J.F. (1974) Perturbations of of Pioneer 6 Telemetry Signal during Solar Occultation. Nature, 249, 21-22. http://dx.doi.org/10.1038/249021a0
- Shapiro, I.I., Pettengill, G.H., Ash, M.E., Stone, M.L., Smith, W.B., Ingalls, R.P. and Brockelman, R.A. (1968) Fourth Test of General Relativity: Preliminary Results. Physical Review Letters, 20, 1265 http://dx.doi.org/10.1103/PhysRevLett.20.1265
Appendix 3: Discussion of Experimental Results Referring to the Existence of Quanta of Length and Time
Quanta of Time Hidden in Mean Life-Times of Short-Lived Elementary Particle Resonances
If the mean life-times of short-lived elementary particle resonances are divided by τw
where T means life time and Γ full width, in by far the most cases nearly integers result, e.g. 0.98 for the top quark (computed Γ ≈ 1.55 GeV) implying its life-time be exactly one quantum of time (1τw) , and 3.95 = 4τw for the 1370 MeV “exotic” meson (Γ ≈ 385 MeV), which has been found at Brookhaven’s AGS [1] .
These results predict that no particle resonances with life-times <τw in Euclidian micro-space exist.
Quantum Geometry Explains the Anomalous Conductance―Plateaus in Quantum Point Contacts and Related Quantum Physical Phenomena
Above has been shown that in the space of the three-sphere S3 locally each dimension or manifold is associated
with a fundamental length, namely 



That with these fundamental lengths really the very limit spatially of nature on microscopic scale has been exposed is also strongly supported by the so-called anomalous conductance features in quantum point contact experiments.
Quantum point contacts represent the simplest system in microscopic physics. If at zero magnetic field a closed constriction (quantum point contact) between two reservoirs of electrons in a two-dimensional electron gas is opened up, the conductance increases through the narrow quantum point contact in quantized units of 2e2/h [2] [3] .
There are normal integer conductance plateaus, G = n2e2/h, seen and the well-known half-plateaus, G = (n + 1/2)2e2/h, where 
Especially of the 0.7 structure, discovered in 1996 [4] , have extensive studies been made, looking at the effects of temperature, magnetic field, electron density, point contact geometry and other factors. Nevertheless, has its nature prove delusive. But one should note that the actual position of the 0.7 feature can vary between 0.6 and 0.8.
To begin with, we identify the unit quantum of conductance e2/h according to the above at once as the unit quantum of Coulomb force
λ denoting a not yet designated quantum of length according to the previous. At zero magnetic field should the Coulomb formula for the smallest possible constriction between two reservoirs of a two-dimensional electron
gas be dependable on the fundamental length in R2, i.e.
Obviously is this relation the micro-physical basis of the previously mentioned normal integer conductance plateaus G = n2e2/h, where all further steps are simply integer multiples of the right-hand member of the above ratio. The “anomalous” conductance plateaus should then result from variations of the quanta of dimension-de- pendent length in dependence on the experimental conditions. These possible variations are:










Clearly in the right-hand members all “anomalous” conductance features show up, even the variation of the actual position of the 0.7 feature between 0.6 and 0.8 is neatly explained by the narrow neighborhood of the 0.58 and 0.67 structures, respectively, to the former.
Furthermore, from this novel microphysical notion results the “additional” factor of two to e2/h quite uncon- strained as a consequence of quantum-geometry without any recourse to a special physical model. This leaves but one question to answer: How do the half-plateaus, G = (n + 1/2) × 2e2/h, come into existence? According to Equation (14) is 
= 1; in this case would be valid 
step has to be written as
If all further conductance steps switch to the above normal mode, then we receive from the latter equation (n + 1/2) × 2e2/h and, therewith, the conductance half-plateaus. Again we see also the half-plateaus (including the factor of two) to follow without any physical assumption alone from quantum-geometry, developed above.
The similiarity of the above conductance formula to the expression for calculating the magnetic flux quantum, i.e. the quantum of magnetic flux passing through a superconductor, which is given by
where 

form
The integer “n” simply results from the fact that the number of magnetic flux quanta must be proportional to
the reciprocal of the unit quanta of Coulomb force e2/(2h), i.e. 
must be valid:
The quantum-geometrical picture also offers a convincing explanation of the puzzling properties of the quantum Hall effect (von Klitzing, 1980 [5] ) which occurs as so called integer or, at extremely low temperatures, fractional quantum Hall effect (Strömer, Hill, 1984 [6] ), depending on whether n is an integer or fraction, respectively. In the case of the integer effect n takes the values 1, 2, 3, ××× , and in the fractional form the principal series 1/3, 2/5, 3/7, ××× , and 2/3, 3/5, 4/7, ××× , which can be expressed as n = m/(2m + 1) and n = 1 ‒ m/(2m + 1), respectively.
In the case of n = 1 follows according to the previous RH = h/e2 = (λ4)2/e2. According to the above is valid:
where 
The underlying physical notion is the successive opening of quantized gates of the order of magnitude (λ4)2 with the physical consequence that reciprocally the Hall resistance dwindles at the same order of magnitude.
In the case of the fractional quantum Hall-effect n = m/(2m + 1) and n = 1 ? m/(2m + 1) = (m + 1)/(2m + 1) owing to the particular physical situation we obviously observe a fractionalization of (λ4)2 such that only the sum of the fractions` reciprocals results again in (λ4)2, namely:
where 
i.e. the sum of these fractionally quantized Hall resistances remains constant.
In 2004 the fractional quantum Hall-effect has been observed in the new material graphen in steps of n = 4(m + 1/2), with the lowest plateau h/(2e2), even at room temperature, i.e. ≈20˚C (Novoselov, 2004 [7] ). In the quantum-geometrical picture this effect is just a special case of the integer quantum Hall effect, which owes its existence to the fact that at the mentioned particular experimental conditions the first step of the Hall resistance is not (λ4)2 but rather(λ2)2 = 1/2h, where
References
- Thompson, D. R. et al. (1997) Evidence for Exotic Meson Production in the Reaction pi ? p→ eta pi at 18 GeV/c. Physical Review Letters, 79, 1630-1633. http://dx.doi.org/10.1103/PhysRevLett.79.1630
- Van Wees, B.J., van Houten, H., Beenakker, C.W.J., Williamson, J.G., Kouwenhoven, L.P., van der Marel, D. and Foxon, C.T. (1988) Quantized Conductance of Point Contacts in a Two-Dimensional Electron Gas. Physical Review Letters B, 60, 848. http://dx.doi.org/10.1103/PhysRevLett.60.848
- Wharam, D.A., Thornton, T.J., Newbury, R., Pepper, M., Ahmed, H., Frost, J.E.F., Hasko, D.G., Peacock, D.C., Ritchie, D.A. and Jones, G.A.C. (1988) One-Dimensional Transport and the Quantization of the Ballistic Resistance. Journal of Physics C, 21, L209.
- Thomas, K.J., Nicholls, J.T., Appleyard, N.J., Pepper, M., Simmons, M.Y., Mace, D.R., Tribe, W.R. and Ritchie, D.A. (1996) Interaction Effects in a One-Dimensional Constriction. Physical Review Letters, 77, 135. http://dx.doi.org/10.1103/PhysRevLett.77.135
- von Klitzing, K., Dorda, G. and Pepper, M. (1980) New Method for High Accuracy Determination of the Fine Structure Constant Based on Quantized Hall Resistance. Physical Review Letters, 45, 494-497. http://dx.doi.org/10.1103/PhysRevLett.45.494
- Störmer, H.L. and Hill, M. (1984) Der fraktionale QHE (The Fractional QHE). Phys. Blätter, 9.
- Novoselov, H.L. Geim, A.K., Morozov, S.V., Jiang, D., Katsnelson, M.I., Grigorieva, I.V., Dubonos, S.V. and Firsov, A.A. (2005) Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature, 438, 197-200. http://dx.doi.org/10.1038/nature04233
Appendix 4: Discussion of Astronomical Observations Referring to the Kicks of Fast Spinning Neutron Stars (Also Black Holes and White Dwarfs), Flyby Anomalies of Spacecraft in the Gravitational Field of Earth, Preferred Spin Orientation of Spiral Galaxies, the Secular Increase of the Astronomical Unit and the Related Phenomena of Lopsidedness of Spiral Galaxies and the Anomalous Retrograde Perihelion Recession of Saturn and, Furthermore, of the Milky Way’s and Other Spirals’ Warp
Kicks of Fast Rotating Celestial Objects in the Milky Way (e.g. Neutron stars)
In the Milky Way show many neutron stars (pulsars) an extremely fast rotation speed, as can be determined from their regularly pulsed radiation and the theoretically known radius of 5 ≲ Rrot ≲ 15 km, whereby in the sense of the previous Rrot denotes rotational radius. Thus, depending on the direction of the spin, we have to expect that according to formulae (92) to (95) they should be conspicious for their especially fast translational motion. Indeed have rotational periods up to ≈0.002 s been measured, wherefrom rotational speeds vrot > 20,000 km×s‒1 can be deduced (see below).
Many pulsars have much larger peculiar space velocities than their progenitors so that they frequently appear significantly offset from the geometric center of the expanding progenitor remnant. Also the orbital characteristics of many binaries, with one or both members being pulsars, can only be explained through velocity increase at the pulsar’s birth (see e.g. Lai, D., 2002 [1] ). These space velocity gains up to ≲1600 km×s‒1 of natal origin are known as kicks, which for, but also for some of their statistically revealed properties, no physically convincing explanation has been proposed yet. Aside from the physical cause of the kicks itself, the most puzzling astronomical observations associated with them are:
1) The distribution-function of the pulsars’ velocity is bimodal, i.e. it is described by two Gaussian components with mean velocities of 127 km×s‒1 and 707 km×s‒1, respectively [2] , or, 90 km×s‒1 and 500 km×s‒1, respectively [3] . This dichotomy seems to imply that in the Milky Way Galaxy two distinct pulsar populations exist, with the mean velocity maxima at the ratio of 707:127 ≈ 5.57, or, 500:90 ≈ 5.55, respectively, i.e. the median ratio being ≈5.6.
2) Pulsars appear frequently significantly offset from the geometric center of the supernova remnant, indicating their removal from birthplace with considerable space velocity. An examination of the distribution of twenty seven pulsars in respect of their parent remnant shells has shown that twenty out of the twenty-seven pairs have negative offsets in Galactic longitude [4] .
3) Recent X-ray observations of the compact X-ray nebulae of several young pulsars revealed an approximate alignment of the rotation and velocity vectors [5] .
4) The strong observational evidence that pulsar proper motion and spin axis are aligned has also been found for the Crab pulsar with a proper motion of 140 ± 8 km×s‒1 and a rotation period of ≈30 Hz [6] .
The neutron star’s birth is marked by the explosion of the proto-neutron-star. It is well known that the former’s fast rotation speed results from the rapid collapse of the progenitor’s interior to the neutron star with mass 1.2M☼ ≲ MNS ≲ 3.0M☼ and radius 5 km ≲ RNS ≲ 15 km, wheras its main mass expands in a shell-like structure around the neutron star’s birthplace. Thus, the fast rotation speed is initiated by the conservation of the supernova’s angular momentum and the simultaneous decrease of angular mass (due to the neutron star’s smaller mass in comparison to the supernova’s mass of 8 - 10M ☼≲ MNS ≳ 30M☼ ). This leads to an over-proportional increase of angular velocity and rotation speed. Thus, neutron stars with their enormous rotation speed are natural rotators and from the above formulae results readily that they, inspite of their tremendous masses, must move translationally in relation to the rotation speed squared with the very onset of the accelerated spin, being the long sought physical cause of the “kick”. Furthermore, also the above listed puzzling astronomical observations 1) - 4) comply with the previously developed physical picture of the rotating S3-hypersphere, e.g., consider the Crab pulsar with a period ≈ 30 Hz, as already mentioned, and unknown radius. According to current theory must the latter be 5 km ≲ RNS ≲15 km.
Present rotation period and assumably largest radius delivers in the case of counterclockwise rotation just 93.3 km×s‒1, consideraby less than the observed proper motion of 140 ± 8 km×s‒1. But according to Guns and Ostriker (G + O; 1969) decreases the pulsar period regularly since birth, and, since the Crab progenitor’s explosion has been observed by Chinese astronomers in 1054, a natal rotation period of 52.6 Hz has been equated for the Crab pulsar. According to the preceding it is clear that the pulsar’s natal rotation speed in association with the spin direction exclusively determines its translational velocity and that the following spin down, as e.g. in the case of the Crab pulsar, has no impact upon the latter. Assuming anticlockwise rotation we receive from Equation (2) and the above data for the Crab pulsar’s rotation radius
in good accord with the above mentioned theoretically derived mean range of pulsar radii (clockwise rotation would result in Rrot = 25.4 km). Vice versa one concludes from the measured highest translational pulsar velocities ≈ 1500 km×s‒1 and most rapid rotations of ≈500 Hz to the underlying rotation speeds. In the case of counterclockwise rotation yield Equations (92) and (95) for these values a rotation speed of 27,716 km×s‒1 and, therewith, a rotation radius of Rrot = 8.5 km, likewise in accordance with theory and observation.
Thus, we have a novel reliable and independent method to verify the proposal of Migliazzo et al. (2002) [7] ) that the initial spin period of the pulsar B1951+32 was 27 ± 6 ms, to explain the discrepancy between the evident pulsar age ≈ 64 kyr on the grounds of the measured transverse velocity of 240 ± 40 km×s‒1 and distance of 2 kpc to the pulsar birth-place and its characteristic age of 107 kyr according to Guns and Ostriker. If we take the measured proper motion at face value, the initial spin period Prot of the pulsar with assumed counterclockwise rotation must according toequations (101a) and (101b) have been (in ms)
at least, where the pulsar rotation radius is assumed with Rrot = 5 km. Clockwise rotation results in a still faster spin period of Prot = 2.8 ms. A larger Rrot will, of course, result in a slower spin period, e.g. if Rrot = 10 km than Prot = 13.36 ms at counterclockwise rotation and 5.7 ms at clockwise rotation, respectively. It is clear that Migliazzo’s proposal is invalid and, thus, the above mentioned age-discrepancy remains.
Also the above elusive relation of ≈5.6 (5.5) between velocity maxima of seemingly existing, differently rapid pulsar populations in the Milky Way Galaxy finds a simple explanation, because according to equations (101a) to (102b) for pulsars with in the mean like rotation velocity but oppositely directed rotational motion the simple ratio must hold
where angle 43,788˚ designates the previously derivated Galaxy’s latitudenal position in the “northern hemispere” of the S3-hypersphere.Now, the accordance of our theoretically derived result with the empirical ratio≈ 5.6 (5.5) looks very impressive and does reversely support the previous deduction of angle ΑG. That the rotation and velocity vectors of all pulsars, as e.g. the Crab pulsar, must more or less be aligned, showing into the global direction of the S3-sphere’s rotation poles, is according to the underlying physical notion (Foucault’s law) quite obvious and needs not be stressed particularly. Furthermore, it is clear that other celestial bodies in the Milky Way Galaxy with comparable rotation velocities, as e.g. massive black holes and white dwarfs, must start to move translationally, too, with the onset of considerably faster spin at birth. Indeed have studies of the behaviour of massive black holes in the galaxy revealed that they must have received a considerable natal velocity kick (see e.g. Mirabel et al., 2002 [8] , or, Kornreich, D. A. et Lovelace, R. V. E., 2008 [9] ).
By comparison of the radial distribution of white dwarfs with the one of main sequence stars in globular clusters it has been found that the former are less centrally concentrated than the latter. The observational data thus clearly indicate that white dwarfs in clusters get a velocity kick, which enables them to travel through the cluster to its limb (see e.g. Calamid, A. et al., 2007 [10] , or, Heyl, J.S., 2008 [11] ).
Preferred Spin Orientation of Spiral Galaxies
Recent studies of the distribution of 22,704 spiral galaxies in the Sloan Digital Sky Survey (∼40,000 galaxies) over the whole sky with redshift up to z = 0.04 revealed the rotation axes of the majority to be more or less parallelly aligned (Longo, M.J., 2007 [12] ). It has been found the mean of the rotation axes to show independently of the respective redshift into a direction perpendicular to the ecliptic. Because the innermost core with radius of R ≈ 3 pc of the Milky Way Galaxy and most probably of the other spirals as well practically rotate like a rigid fast rotator with considerable circumferencial velocity, this is according to the preceding a likely alignment.
In a study of a sample of 200,000 elliptical galaxies with redshifts <0.20 also from the Sloan Digital Sky Survey the same author (Longo, M. J., 2007 [13] ) found those galaxies to tend to have their ellipticities aligned along a particular axis with overwhelming statistical significance. This axis is also close to that of the spiral galaxy spins and the CMB alignments. It is clear that the alignment of the axis of the innermost nearly rigid fast rotator in elliptical galaxies with the rotation axis of the S3-hypersphere is not dependent on its presently observable rotation (or, non-rotation), but of the most rapid rotation velocity it once could have obtained in its past (see above).
Flyby Anomalies of Spacecraft in the Gravitational Field of Earth
During six Earth flybys of the Galileo, Near, Cassini, Rosetta and MESSENGER spacecraft significant anomalous velocity increases (and some decreases) of a few m×ms‒1 were observed using radio Doppler data as well as ranging methods [14] [15] . These deviations from theoretically expected data are known as the flyby anomalies because no explanations on the grounds of known physical and technological parameters have been found yet. Its source is unknown (see e.g. Lammerzähl et al., 2006 [16] ). But Anderson et al. (2008) could from a study involving the data analysis and interpretation of six flybys show that the velocity anomalies (Δv ) generally observe the empirical formula
where 
where v is the inertial spacecraft velocity at closest approach, G the gravitational constant, Me the mass of Earth and r the sum of the Earth’s mean radius Re and the altitude h of the spacecraft at closest approach. The proportionality coefficient K in the above formula is according to Anderson et al. expressed in terms of the Earth’s angular rotational velocity ωe, its mean radius Re and the speed of light c in the order of
The following table A1 gives an overview of the observed flybys and predictions according to the above empirical formula (in extracts adopted from Anderson et al.).
All parameters have the meaning as defined above, the last column of the table gives the estimated realistic error in Δ according to Anderson et al.
From the previous it is clear that analogously to other spinning celestial objects (as e.g. neutron stars) rotating Earth has to be considered as a natural gyro, too. Equations (107a) to (108b) predict in this case for inward or outward moving small bodies in the gravitational field of Earth above both hemisperes a velocity kick parallel to
Table A1. Earth flyby parameters at closest approach for the spacecraft.
the rotational axis and antiparallel to the vector of gravitational acceleration at the poles. Strength and lateral extension of these repulsion fields above both hemispheres depend on rotational speed vrot(e) of Earth at the equator, direction of spin and Earth’s equatorial cross-section. The latter is determined by the equatorial radius Req = 6378 km plus the height of the atmosphere as far as it can be considered as a component of the rotator Earth (see also below: Warp of the Milky Way). In the following the utmost range of the homosphere, the Kármán-line, about 100 - 130 km high, is considered to be part of Earth’s rotation radius so that the latter be of value ≈6530 km. Thus, and because Earth is spinning anticlockwise, the velocity jump a spacecraft moving on an outbound trajectory parallelly to the former’s rotation axis will experience, is according to (108b) of value
in either hemisphere Note that this result corresponds only roughly numerically with the rather artificial, not physically founded constant K = 3.099 × 10‒6 of Anderson et al in the above equation. It is clear that the velocity jump refers to the gain or loss of kinetic energy which the flyby spacecraft according to equation (108a) against or aligned with Urot will experience. Furthermore, there exists no plausible physical argument to restrict the im- pact of the latter onto the craft’s kinetic energy to the hyperbolic excess velocity 
meter so that the kinetic energy of the craft at closest approach be
latter. Therefore, the energy gain or loss ±Δvi through the diversion field over both hemispheres of spinning
Earth must be 
implies
so that 

thus, cancelling each other in the oppositely directed repulsion zones. The oppositely directed vectors of vtrans(ax) span 180˚ counting (arbitrarily) from 0 at the southern rotation pole of Earth (+vtrans(ax)) to ‒180˚ at the northern rotation pole (‒vtrans(ax)). Thus, all ingoing and outgoing trajectories signed (‒) of the above table I referenced to the equatorial plane sum up to (‒180˚+ φ) and the former signed (+) to (‒180˚ ‒ φ), respectively, so that if the inbound or outbound trajectory intersects the northern repulsion zone under some angle φ ≤ ‒1/2π it is obvious that
and, if φ1 ≤ 1/2π, i.e. the inbound or outbound trajectory intersects the southern repulsion zone:
too. Thus, the theory explains the empirically found dependence of velocity loss or gain on inbound and outbound angle, respectively, of fly by spacecraft in a fully way.
From the above considerations we receive the general formulation
But it should be remarked that angles φ1 and φ2 are not coincident with geocentric latitude and, furthermore, that the craft’s incident and outgoing straight trajectories are approximations of the in reality hyperbolic trajectories around Earth. Considering this and that angles φ1 and φ2 are referenced to the equatorial plane, whereas the incident and outbound angle of the real missions in the above table are referenced to their height above point of closest approach, we have to introduce a correction factor k in order to approximately compensate for these differences. Depending on the altitude h at closest approach the latter factor has to be calculated for every craft individually according to:
where φL denotes the larger and φS the smaller of the two angles φ1 and φ2, respectively. Thus, one calculates Δvi by replacing the latter in the above formula with 




With these corrections deliver the above formulae the following results (vi, h, φ1 and φ2 adopted from Anderson et al.):
The Secular Increase of the Astronomical Unit
From the analysis of the huge wealth of radiometric measurements of distances between Earth and the major planets including observations from Mars probes from 1966 to 2003 an unexpected secular increase of Astronomical Unit (AU), the length scale of the Solar System, has been reported by Krasinsky and Brumberg [17] , who quote
The existence of this centennial AU increase has been confirmed by Standish [18] and Ptjeva [19] . At present, there are no explanations able to accommodate such an observed phenomenon in current theory (see e.g. Iorio, L., 2005 [20] , or, Arakida, H., 2008 [21] ).
According to our previous results must the Galaxy’s latitudenal position in the “northern hemispere” of the S3 -hypersphere be Α = 43.788˚. In equations (77b) and (c) it has been shown that the radius of the Schwarzschild field outside an isolated spherically symmetric static body from the equator to the cosmic poles must vary in dependence on latitude in the S3-three-sphere at ratio 1:(1 − sin Α), and, therewith, the radii of orbits in those gravitational fields in the same relation, whereas all other parameters remain constant. Accordingly with the south-ward drift of the Sun’s system generally should be associated a gradual increase of the planets’ distances from the Sun, too. It is clear that this effect considerably must vary during the Sun’s revolution about the galactic center. Presently the Sun is travelling toward galactic coordinates 


and the distance d travelled in a century according to Equation (110) then would be
where γ ≈ 1. Hence, the above predicted increase of orbital radius in dependence on latitude for Earth can be calculated with:
AU denotes the well known derived constant, which is approximately the mean distance between Earth and the Sun, equal to ≈1.5 × 1011 m and for the very small angle dΑ is calculated:
where 1/2Ρπ = 13.4 × 109 ly. Note that a difference of 88˚ (see above) would require cos5˚ in the above velocity formula to be replaced by cos4˚, which would yield 9.00 m×cy‒1.
It is predicted that this physical effect is also responsible for the recent findings of the Chandra team that more distant galaxy clusters (z ≈ 0.55) are much more massive than those at lesser distances (z ≈ 0.05)―which has been wrongly interpreted as due to “dark energy” [22] ―implying that the former are located more polewards spatially. Furthermore, the following two astronomical findings seem to owe their existence to the former effect as well.
The Lopsidedness of Spiral Galaxies
The so called lopsidedness is a common feature of spiral galaxies, i.e. the mass distribution in disks of spiral galaxies is not strictly axisymmetric. It has been found the isophotes to be elongated in one half of the galaxy up to ≈ 10% of the radial range, with the highest amplitiude at larger radii (see e.g. Jog, Chanda, J., 2008 [22] ). This seems to be true for the distribution of all orbiting stars and gas as well and for all kinds of spiral galaxies. A convincing physical explanation of this phenomenon has not been found yet, especially for the fact that lopdsidedness is observed in most galaxies including the Milky Way.
According to the preceding an increase of the Milky Way’s disk ordiameter, respectively, on its way toward the equator of the S3-hypersphere with velocity vG ≈ 550 km×s‒1 of the galactic center relative to the CMB is to expect, too. In principle the above considerations referring to the increase of the AU are also applicable to the increase of the Galaxy’s disk and the associated lopdsidedness. Considering that the median diameter of our home galaxy’s disk be δ ≈ 105 ly and the elapse of time for a complete orbit at this distance be torb ≈ π × δ × c/vorb≈ 4.098 × 108 y, where in accord with Equation (64) vorb ≈ 230 km×s‒1 orbital velocity of the most peripheral stars, furthermore, the orbital velocity after halve an orbit or time 2.049 × 108 y in southward direction in the median must increase from 550 km×s‒1 to ≈ 550 + 1/2π × 230 = 696.4 km×s‒1,the diameter parallel to the vector of vG in accord with the above must increase in the order of magnitude
As in the preceding paragraph in accord with Equation (110) is calculated:
such that for calculation of angle dΑ applies
It is clear that the increase of diameter of the Galaxy due to the increase of the universal centrifugal force FΡ towards the three-sphere’s equator cannot be symmetric with respect to the Galaxy’s center. As the above formula shows will the increase of orbit diameter or the elongation effect, respectively, steadily become stronger
with growing time 
the angle of an orbital section. Thus, we observe in the Galaxy (and all other spirals) an axisymmetric distribution of all orbiting matter into the global direction of cosmic south.
The Anomalous Retrograde Perihelion Precession of Saturn
A thorough analysis of a large number of planetary observations including three-dimensional normal point observations of the Cassini spacecraft (2004-2006) has recently led to the detection of an anomalous retrograde deviation from the general relativistic and Newtonian secular precession ϖ of the longitude of the perihelion of Saturn (Pitjeva, E.V., 2008: see Iorio, L. [23] ) which amounts to
This anomalous retrograde apsidial precession of Saturn cannot be explained by current theory (see extensive discussion in [24] ). But it is clear that the previously discussed expansion effect of radii of orbits in dependence on latitude in the S3 three-sphere with ratio (1 ‒ sinΑ)‒1 will also affect the perihelion advance predicted by general relativity for all planets of the solar system, including Saturn, in the order of
where a denotes major half-axis of the orbit-ellipse and e eccentricity of the latter. The reason is that the Saturnian major half-axis in a century or about four orbits’ time will according to the above result for the AU of Earth, which we directly can apply, grow by 14.25 m × a /AU = 140.06 m. Thus, the planet’s orbit will steadily lenghten, i.e. the perihelion advance seemingly retard, so that after a century we have
where da = 140.06 m. This tiny apparent retrograde perihelion precession can be calculated according to the simple relation
delivering
It is clear that a much smaller value of dϖ results if dAU/dt = 9.00 m×cy‒1 is applied as alternatively calculated above. Of course, is this result not restricted to Saturn, in the contrary: It is equally large (or tiny) for all planets, even for circular orbits, since it just reflects the universal steady expansion of all gravitational fields connected with the Galaxy and her stars on their present way toward the Cosmic equatorial region.
Warp of the Milky Way and other Spiral Galaxies
The majority of the spiral galaxies, including our home galaxy, are warped, i.e. the galaxy’s outer plane deviates by some angle from the disk defined by the inner regions. E.g. according to this definition the disk of the Milky Way in its outer parts warped to distances ≤2 kpc from the plane above and below the Galaxy’s disk at radius of ≈12.5 kpc on either side of the latter’s center (see e.g. [25] ). No current theory can account for the orign and maintenance of warps, neither in general nor in some peculiar cases as e.g. of the radio galaxy 3C 449 with near parallelism of the bipolar jet emanating from the core of the galaxy and the warped disk of the latter [26] . Above has been found that the innermost central core of the Milky Way Galaxy can be considered as a rigid rotator spinning with about constant angular velocity. The same must be true for most spiral galaxies. And because of the previously stated linear connection between the sine of the tilt by angle α of a fast rotator’s axel toward the rotation axis of the S3-three-sphere and the former’s rotation velocity so that outside of gravitational fields with metric gnm = ηnm be valid
it is to expect that this relation for a fast rotating galactic core be valid too. Thus, besides other factors as e.g. the latitudenal position, largeness and shape of a galaxy’s warp generally should be dependent on the rotation speed of the innermost core as well as on the one of the gravitationally bound disk. Especially a galaxy’s core and disk in association with the Schwarzschild mass of its gravitational field, though differentially rotating, must be considered as bound system which for Foucault’s law and the previously derived relations for rotators in the rotating Universe are applicable, likewise as for rigidly spinning ones. The only differences are that the above relation for warps becomes to
since all spinning material in and with the gravitationally bound disk must after one revolution about the core take on vtrans = vrot and, that other than in the case of solid gyros, the edge of the disk will be thinned out with the result that these outer parts cannot act as rotator anymore. Considering this, from the previously calculated cube of the second cosmic velocity of the Milky Way (Equation (65)) with value
in connection with Newtonian 
and eventually: α = 0.0427˚. Note that the equated sinα according to the above corresponds very well with
from the Sun’s orbital velocity in the Milky Way’s disk, i.e. the inner disk itself in general has the same inclination as the core or, to say it another way, is orientated perpendicularly to the latter. Thus, it is clear that all orbital velocities of the disk beyond the Sun’s orbit which according to the above derivated formula (64)
Exceed ≈ 220 km×s‒1 will lead to a larger inclinitation of the disk, i.e. core centered warping of the orbiting material off the inner disk plane with value
where R > Rorb. The latter Equation delivers for R = 13 kpc sinα = 8.43 × 10‒4, or, α = 0.0483˚, respectively, which corresponds very well with the value of angle α which in accord with the previous can be caculated from the observational data given above by [26] straightforwardly in the form
where R = 13 kpc has been assumed. Thus, e.g. from the observational data of the radio galaxy 3C 449 [26] can be inferred that the latter be positioned at considerably higher cosmic latitude than the Milky Way with the consequence of much more Schwarzschild mass in its exterior field and respective higher rotation velocities of the disk.
References
- Lai, D. (2002) Core-Collapse Supernovae and Neutron Star Kicks. arXiv: 0212140 v1 [astro-ph]
- Bombaci, I. and Popov, S.B. (2004) On the Nature of Bimodal Inertial Velocity Distribution of Neutron Stars. arXiv: 0405250 v1 [astro-ph]
- Arzoumanian, Z., Chernoff, D.F. and Cordes, J.M. (2002) The Velocity Distribution of Isolated Radio Pulsars. The Astrophysical Journal, 568, 289. http://dx.doi.org/10.1086/338805
- Lorimer, D.R. and Ramachandran, R. (1999) Puzzling Pulsars and Supernovae Remnants. arXiv: 9911010 v1 [astro-ph]
- Johnston, S., Hobbs, G., Vigeland, S., Kramer, M., Weisberg, J.M. and Lyne, A.G. (2005) Evidence for Alignment of the Rotation and velocity Vectors in Pulsars. Mathematics & Physical Sciences, 36, 1697-1412.
- Ng, C.-Y. and Romani, W. (2006) Proper Motion of the Crab Pulsar Revisited. arXiv: 0602255 v1 [astro-ph]
- Migliazzo, J.M., Gaensler, B.M., Backer, D.C., Stappers, B.W., van der Swaluw, E. and Strom, R.G. (2002) Proper Motion Measurements of Pulsar B1951 + 32 in the Supernovae Remnant CTB 80. arXiv: 0202063 [astro-ph]
- Mirabel, I.F., Mignani, R., Rodrigues, I., Combi, J.A., Rodriguez, L.F. and Guglielmetti, F.. (2002) The Runaway Blackhole GRO J 1655-40. Astronomy and Astrophysics, 395, 595-599.
- Kornreich, D.A. and Lovelace, R.V.E. (2008) Dynamics of Kicked and Accelerated Massive Black Holes in Galaxies. arXiv: 08002.2058 v1 [astro-ph]
- Calamid, A., Corsi, C.E., Bono, G., Stetson, P.B., Prada Moroni, P.G., Degl’Innocenti, S., Ferraro, I., Iannicola, G., Koester, D., Pulone, L., Monelli, M., Amico, P., Buonanno, R., Freyhammer, L.M., Marchetti, E., Nonino, M. And Romaniello, M. (2007) On the Radial Distribution of of White Dwarfs in the Galactic Globular Cluster Omega Cen. arXiv: 0712.0602 [astro-ph]
- Heyl, J.S. (2008) Constraining White-Dwarf Kicks in Globular Clusters: III. Cluster Heating. arXiv: 0803.2704 [astro- ph]
- Longo, M.J. (2007) Evidence for a Preferred Handedness of Spiral Galaxies. arXiv: 0707.3793 [astro-ph]
- Longo, M.J. (2007) The Axis of Opportunity: The Large-Scale Correlation of Elliptical Galaxies. arXiv: 0707.4013 [astro-ph]
- Anderson, J.D., Campbell, J.K., Ekelund, J.E., Ellis, J. and Jordan, J.F. (2008) Anomalous Orbital-Energy Changes Observed during Spacecraft Flybys of Earth. Physical Review Letters, 100, 091102. http://dx.doi.org/10.1103/PhysRevLett.100.091102
- Antreasian, P.G. and Guinn, J.R. (1998) Investigation into the Unexpected Delta-v Increase during the Earth Gravity Assist of Galileo and Near. Paper No. 984287, AIAA/AAS Astrodynamics Specialist Conference and Exhibition, Boston.
- Lammerzähl, C., Preuss, O. and Dittus, H. (2006) Is the Physics in the Solar System Really Understood? arXiv: 0604052 [gr-qc]
- Krasinsky, G.A. and Brumberg, V.A. (2004) Secular Increase of Astronomical Unit from Analysis of the Major Planets Motions and its Interpretation. Celestial Mechanics and Dynamical Astronomy, 90, 267-288. http://dx.doi.org/10.1007/s10569-004-0633-z
- Standish, E.M. (2005) The Astronomical Unit Now. Proceedings IAU Colloq., 196, 263-179.
- Pitjeva, G.W. (2005) High-Precision Ephemerides of Planets-EPM and Determinations of Some Astronomical Constants. Solar System Research, 39, 176-186. http://dx.doi.org/10.1007/s11208-005-0033-2
- Iorio. L. (2008) Secular Increase of the Astronomical Unit and Perihelion Precessions as Tests of the Dvali-Gabadadze- Porrati multi-dimensional braneworld scenario. arXiv: 0508047 [gr-qc]
- Arakida, H. (2006) Time-Delay in Robertson-McVittie Spacetime and its Application to Increase of Astronomical Unit. arXiv: 0808.3828 [gr-qc]
- Vikhlinin, A., Kravtsov, A.V., Burenin, R.A., Ebeling, H., Forman, W.R., Hornstrup, A., Jones, C., Murray, S.S., Nagai, D., Quintana, H. and Voevodkin, A. (2008) Chandra Cluster Cosmology Project III: Cosmical Parameter Cons- traints. arXiv: 0812.2720 v1 [astro-ph]
- Jog, Ch.J. (2008) Pattern Speed of Lobsidedness in Galactic Disks. arXiv: 0812.0670 v1 [astro-ph]
- Iorio. L. (2008) On the Recently Determined Perihelion Precession of Saturn. arXiv: 0811.0756 [gr-qc]
- Levine, E.S., Blitz, L. and Heiles, C. (2006) The Vertical Structure of the Outer Milky Way HI Disk. arXiv: 0601697 [astro-ph]
- Tremblay, G.R., Quillen, A.C., Floyd, D.J.E., Noel-Storr, J., Baum, S.A., Axon, D., O’Dea, C.P., Chiaberge, M., Macchetto, F.D., Sparks, W.B., Miley, G.K., Capetti, A., Madrid, J.P. and Perlman, E. (2005) The Warped Nuclear Disk of Radio Galaxy 3C 449. arXiv: 0510650 [astro-ph]
Appendix 5: Discussion of Experiments Referring to the Influence of Spinning Gyros or Superconductors on Gravitation
In the last decades repeatedly attempts have been made to show that gravity can be influenced (screened) by spinning gyros including superconductors, though current theory (GR) does not support such an expectation. Especially experiments at the end of the last century conducted by Hayasaka and Takeuchi (1989, [1] ) and Hayasaka et al. (1997, [2] ) found broader attention. In all cases the discovery of a gravity screening effect has been claimed, but which could not be confirmed by other experiments without doubt and has been heavily attacked from the theoretical side particularly with regard to the impossibility of the claimed screening effect within the framework of GR. More recently Tajmar et al. (e.g. 2007 [3] , 2008 [4] ) reported to have been measuring an unexplained tiny acceleration, equivalent to an increase of gravity, induced by clockwise rotating supercooled rings. The experiments have been conducted to find an enhanced frame dragging effect―with respect to predictions of GR―, which has been proposed by the authors. In later experiments with anticlockwise spinning rings a similiar small effect has been found as well [5] [6] . Graham et al. (2008 [7] ) conducted a similiar experiment with a rotating superconducting lead ring and did not find this effect. It should be noticed that the experiments of Tajmar et al. and Graham et al. have been conducted with confined rotors, i.e. in either case was the axle rigidly connected with the immovable stator. Through laser beams overhead or nearby of the spinning rotors, thus, possibly alterations of the dipol field Urot according to (107a)-(e) and (108a) could have been measured. Hayasaka and Takeuchi directly measured changes of inertia of rigidly connected though movable stator-rotor systems in dependence on rotor speed according to Equations (103) to (106c). Eventually, Hayasaka et al. measured the falling time of freely falling movable stator-rotor systems in dependence on rotor speed also according to (103) to (106c).
We discuss those experiments in the framework of the physical notion developed above.
The Hayasaka Experiments
In 1989 measured Hayasaka and Tekeuchi at Tohoku university, located in the city of Sendai, Japan, with a chemical balance the weight of three clockwise rotating gyros made of different metals, with slightly different weight and outer diameters between 5.2 and 5.8 cm. They found in all cases the weight clearly reduced, as compared to the gyros at rest. These weight reductions are according to Hayasaka und Tekeuchi also clearly associated to the gyros’ revolutions in the order of 10‒5 as compared with the gyro’s weight at rest. According to Equation (100) should the city daily stay for roughly 6.9 hours within the influence sphere of the cosmic southern rotation pole. This delivers a good explanation why in the northern hemisphere of Earth also clockwise spinning gyros exhibit weight reduction, i.e. that their translational movement is directed towards the cosmic southern pole. Thus, we come to the conclusion that just at the time of the experiments the city of Sendai was directed towards the cosmic south pole roughly so that clockwise rotation could result in the southerly directed diversion effect (in contrast to this, Hayasaka found in 1997 weight reduction in the case of anticockwise rotation; see below). Therefore, a straightforward Computation on the grounds of the given data is not possible.
In 1997 Hayasaka et al. in 10 runs have been measuring the time a gyro with diameter 5.8 cm and rotating anticlockwise with 18,000 rpm needs to fall freely distance 1.7 m, as compared to falling times of the non-rotating and clockwise rotating gyro. The authors claim to have found Earth’s gravitational acceleration g = 980.0658 gal at Sendai in the mean (10 runs) be altered so that in the case of counterclockwise rotation the former decreased to gcc = 979.9266 ± 0.0716 gal and at clockwise rotation increased to gc = 980.0678 ± 0.0663 gal. The mean values of their differences with respect to g at Sendai are:
Thus, the authors conclude that gc be almost identical with g (zero spinning) and gcc significantly smaller than g, being equivalent to a gravity screening effect of ≈ 1/7000.
According to this theory the authors by chance must have caught a time period open for the cosmic northern hemisphere, which at Sendai prevails for about 17 hours daily (see above). In this case―rotation speed 18000 rpm, gyro’s diameter 5.8 cm, g = 980.0678 gal―the above equations predict for counterclockwise rotation
and for clockwise spinning
Whereas in the first case theory and experiment well comply, is in the latter case the predicted difference gc ‒ g about 10 times larger than the experimental value. But one should notice that the authors possibly, though unintentionally, have been prejudiced against a gravitational effect of clockwise rotating gyros because they had developed a theory which predicts generation of “anti-gravity” preferentially at counterclockwise spinning [3] . This also would explain that the uncertainty of the difference gc ‒ g ≈ 23 times larger than the latter’s value 0.0029 gal. Note that the mean of experimental value and its uncertainty, i.e. 1/2(0.0029 + 0.0663) = 0.0346 gal, pretty fairly matches the theoretical prediction.
The Tajmar Experiments
The experimental program started in 2003 and is still going on. The supercooled rotating rings were made of superconducting as well as of non-superconducting material, i.e. aluminium (Al), Niob (Nb), YBCO, stainless steel and TEFLON with the geometrical proportions (in mm):
with a fastest rotation of 6500 rpm (∼108.33 rps) [4] . With respect to the repulsion effect it is important to know that the rings were fixed to aluminium sample holders with outer diameter 160 mm in the case of the Al (Nb, steel)-rings and 165 mm for the YBCO (TEFLON)-ring, which implies a highest rotation speed of 54.45 m×s‒1 for the former and 56.16 m×s‒1 for the latter, respectively. The bottom was made of stainless steel. Thus, the rings did not rotate freely, but were due to their fast connection with the aluminium sample holder, which itself was fixed to the motor’s axle, exchangeable parts of the rigid spinning sample holder, being the gyro. Neither mention the authors other geometrical proportions nor the mass of the sample holder. Judging from illustrations in [4] and [5] one infers the Al-sample holder’s height be about twice the height of the rings, i.e. ≈30 mm, and the width in the case of the Al-ring be 10 mm in the upper part with height 15 mm, whereas the lower part was 16 mm wide and also 15 mm high. The respective measures of the sample holder for the YBCO-ring must also have been about 30 mm, 5 mm and 15 mm, respectively, furthermore, for the lower part 20 mm vs. 15 mm. Thus, for the 150 mm-rings we have the relation: volumina of sample-holder/ring ≈ 369/83 and for the 160 mm-rings ≈ 369/216, respectively. These approximate ratios are needed to derive the mean density ϱm of the respective rotor sytem (sample-holder + ring; see below) according to the relation
ϱm Al = 2.7, ϱm Nb = 3.78, ϱm Steel = 3.52, ϱm YBCO = 4.3, ϱm TEFLON = 2.48, whereby the bottom of the respective system (stainless steel) is negated.
The rotor systems were spinning alternately clockwise and counterclockwise in vacuum with temperature of some Kelvin and probably has this special physical situation―near absolute zero―it rendered measuring the diversion effect at such slow rotational speeds.
The authors found in [4] the rings to exhibit a coupling factor of ≈3 to 5 × 10‒8, when rotating clockwise at highest rotational velocity of 6500 rpm, where coupling factor denotes reaction of the fixed measurement devices (laser gyros) versus angular velocity of the rings (in rads−1). i.e. the coupling effect could be seen on the sensors (laser gyros), mounted above the rotor, though they are mechanically de-coupled from the spinning systems. This implies according to the previous that the counter-directed repulsion fields Urot above (below) both rotational planes of the respective spinning rotor system have been perceived. The highest coupling factor of ≈5 × 10‒8 showed the YBCO-ring and the smallest of ≈2.2 × 10‒8 the Al-ring, whereas the Nb-ring with ≈3.5 ? 3.75 × 10‒8 lay in between (see [4] , Figure 8). In a later paper the authors corrected the coupling factor for the Nb-ring system to ≈3.2 ± 0.5 × 10‒8 [6] .
From a comparison of all experimental results at the gyro location in Seibersdorf [6] a shortened overview is given, which strongly points to a variability of gravity in dependence on rotational speed, which the authors think to be of unknown origin. The data will be analysed below.
The sample holders of the Teflon-ring and the steel-ring consisted of the respective same material and of Al in the case of all other rings. Notice that all sensors were mounted at radial distance 53.75 mm and, thus, positioned well within the repulsion zones of the respective rotors. The experiments have been conducted in Seibersdorf (Austria), located at latitude 47˚57'N and, thus, according to Equation (111a) assumably within the permanent northern sphere of action of the universal centrifugal force FΡ on the surface of rotating Earth. Therefore, with clockwise rotating gyros a seeming increase of weight or gravity basically is to expect. It is clear, that not the respective ring but rather the whole system, sample holder + ring, is to interpret as gyro in the sense of the preceding, with outer diameter of 160 mm and 165 mm, respectively. Moreover, not a seeming increase of
gravity has been measured, but of sudden momentum 
vtrans ax, according to (108a) induced through the gyro’s clockwise or anticlockwise rotation and associated repulsion zone Urot above and below the rotor, which for clockwise or counterclockwise spinning, respectively, takes the general form:
From the experiment’s setup it is obvious that the fixed rotor system has been confined with respect to local three-dimensional space, but especially to the gravitational gradient, implying that the rotation speed could not induce the rotor’s movement with transverse velocity vtrans according to Equation (100). Instead, owing to the latter’s three-dimensional confinement has according to Equation (106) with the onset of its rotation been associated an immediate twisting of the rotation axis by angle α towards E4. Therefore, the likewise confined laser gyros (fixed to the building) could not sense vtrans but the repulsion field Urot of the gyros momenta.
From the above it is clear that clockwise rotation induces vtrans with momentum ptrans of the gyro to be parallelly aligned with the gravitational gradient. Because the gyro remains confined to local three-dimensional space is the variable factor of momentum ptrans the product ptrans × ϱ alone, whereas volume V of the confined gyro remains constant with the result
i.e. also the gyro’s dipolar repulsion fields Urot will show the respective counterdirected velocities vtrans × ϱ = vtrans(ax). The opposite is to expect if the vector vtrans(ax) or momentum ptrans(ax) of the gyro pointsanti-parallelly to the gravitational gradient, i.e. if the confined rotor system happens to spin counterclockwise. In this case acts the confinement as a counter-force with the result
Thus, we receive from the latter Equation coupling factor C of Tajmar et al. in the case of clockwise spinning from the ratios
and
for counterclockwise rotation, respectively, where ϱm denotes mean density of the respective gyro in gcm-3 as calculated above and ωrad angular velocity in rad×s‒1.
These formulae deliver with the previously derived rotation speeds of the gyros the rotation speeds according to Equations (105a) and (105b) and with the above calculated mean densities of the respective gyros with the ring made of:
Note that the above mentioned former experimental result for Nb (clockwise) of value ≈3.2 × 10‒8 be in better accord with theory than the value in the previous overview. Clearly shows up that in this very special physical situation clockwise rotation leads to somewhat higher results, as has already been noticed by the authors.
More recently Tajmar and Plesescu (2009 [6] ) have been reporting experimental results from a rotating pot made of stainless steel and filled with 30 l liquid helium. The measures of the pot were: outer radius 211 mm, inner radius 93.5 mm, outer height 271 mm, inner height 177 mm. The rotational top speed of the pot was 60 rad×s‒1, equivalent to ≈10.26 m×s‒1. Inside the pot were 4 fins made of Al and Nb-cylinder with outer radius 93.5 mm and thickness 5 mm was glued to the lower innermost part of the pot. The three laser sensors were positioned at the pot’s center and directly beneath the middle of the pot and its utmost circumference (boundary of the rotor system). From the latter, which alone is of interest with respect to the full diversion effect, a coupling factor of 1.0 ± 0.3 × 10‒ for clockwise and of ‒0.5 ± 0.3 ×10‒ in the case of anticlockwise rotation has been reported. From the above measures a volume of the pot’s metallic construction of ≈5273 cm and, thus, considering the densities of the employed metals a mean density of ϱm ≈ 1.223 (ϱ of liquid helium = 0.125 kg×l‒1) for the complete rotor system is calculated in accord with the above relation. Calculation according to the above equations delivers for clockwise spinning a coupling factor of 0.37 × 10‒9 and for counterclockwise rotation 1.36 × 10‒9. Note that the difference of both rotation directions of ≈1 × 10‒9 of the theoretical prediction neatly complies with experimental finding (1.0 ± 0.3 ×10‒9) ‒ (‒0.5 ± 0.3 × 10‒9). Taken together, the experimental results of Tajmar et al. and predictions of theory are in good accord.
The Graham Experiment
The experiment aimed at the detection of the gravitational effect reported by Tajmar et al., which falsely has been interpreted as to be of gravitomagnetic origin. The rotating and superconducting ring of Graham et al. was made of high-purity lead with the geometrical proportions (mm):
Thus, the rotor was a compact lead cylinder with density 11.635 [7] . From the measures of the cylinder a mean density of ϱm ≈ 2.53 of the whole rotor system is computed in accord with the above relations. The authors report that the rotor speed was 15 rps in the clockwise direction and 12 rps in the counterclockwise direction, which is equivalent to 4.3 m×s‒1 and 3.4 m×s‒1, respectively, i.e. less than 10‒1 of the rotation speed in the expe- riments of Tajmar et al. The result―non-detection of the Tajmar effect―came from an analysis of a run of 5 minutes clockwise followed by 5 minutes stationary followed by 5 minutes counterclockwise. Due to the very slow rotational velocity of the rotor the negative outcome of this experiment is to expect―in accordance with the previous. The difference in rotation speed in comparison to the Tjamar experiments implies that the diversion effect in the Graham experiment be about 102 times smaller than in the former. And other than in the former, clockwise spinning in the southern hemisphere generally does induce decrease of gravity of value
expressed as coupling factor and counterclockwise rotation seeming increase of gravity to the amount of
Possibly the latter effect could have been detected, but one should notice that in this experiment the sensors (laser gyros) were placed in the equatorial plane of the spinning lead cylinder with the result that the rotation axis was 195 mm outside the beam path of the laser, whereas the rotor’s radius = 45.5 mm. According to the previous should the diversion field induced through the spinning rotor be perceptible above and below the lateral dimensions of the latter only. Furthermore, was the experiment carried out at Christchurch, Newzealand, which is located at 43˚31'48'' in the southern hemispere of Earth. Thus, according to our findings should this location in the course of the day stay for approximately 18 hours within the influence sphere of the cosmic southern rotation pole and 6 hours in the influence sphere of the northern one, respectively. In these circumstances are considerable additional experimental complications to expect, as has been discussed at some length above.
Taken together this experiment could by no means meet the requirements for the detection of the cosmic repulsion effect.
References
- Hayasaka, H. and Tekeuchi, S. (1989) Anomalous Weight Reduction on a Gyroscope’s Right Rotations around the Vertical Axis on Earth. Physical Review Letters, 25, 63.
- Hayasaka, H., et al. (1997) Possibility for the Existence of Anti-Gravity: Evidence from a Free-Fall Experiment Using a Spinning Gyro. Speculations in Science and Technology, 20, 173-181.
- Tajmar, M. et al. (2007) Search for Frame-Dragging-Like Signals Close to Spinning Superconductors. arXiv: 0707.3806 [gr-qc]
- Tajmar, M., Plesescu, F., Seifert, B., Schnitzer, R. and Vasiljevich, I. (2008) Anomalous Fiber Optics Gyroscope Signals Observed above Spinning Rings at Low Temperature. arXiv: 0806.2271v2 [gr-qc]
- Tajmar, M., Plesescu, F., Seifert, B., Schnitzer, R. and Vasiljevich, I. (2008) Anomalous Fiber Optics Gyroscope Signals Observed above Spinning Rings at Low Temperature. AIP Conference Proceedings, 969, 1080. http://dx.doi.org/10.1063/1.2844946
- Tajmar, M. and Plesescu, F. (2009) Optic Gyroscope Measurements Close to the Rotating Liquid Helium. arXiv: 0911.1033 v1 [gr-qc]
- Graham, R.D., Hurst, R.B., Thirkettle, R.J., Rowe, C.H. and Butler, P.H. (2008) Experiment to Detect Frame Dragging in a Lead Superconductor. Physica C: Superconductivity, 468, 383-387. http://dx.doi.org/10.1016/j.physc.2007.11.011


























































































