Natural Science
Vol.6 No.4(2014), Article ID:43350,6 pages DOI:10.4236/ns.2014.64028
The 5-dimensional model for electromagnetism and gravity
![]()
1Lebedev Physics Institute of Russian Academy of Sciences, Moscow, Russia; andrvlad@yandex.ru
2Prochorov General Physics Institute of Russian Academy of Sciences, Moscow, Russia; tsip@kapella.gpi.ru
Copyright © 2014 V. A. Andreev, D. Yu. Tsipenyuk. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property V. A. Andreev, D. Yu. Tsipenyuk. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received 9 December 2013; revised 9 January 2014; accepted 18 Janaury 2014
Keywords: Gravity; Electromagnetism; (1+4)-Dimensional Space; Mass of Photon; Negative Mass
ABSTRACT
The generalization of Einstein’s special theory of relativity (SRT) is proposed. In this model, the possibility of unification of scalar gravity and electromagnetism into a single unified field is considered. Formally, the generalization of the SRT is that instead of (1+3)-dimensional Minkowski space the (1+4)-dimensional extension  is considered. As the fifth additional coordinate the interval
is considered. As the fifth additional coordinate the interval  is used. This value is saved under the usual Lorentz transformations in Minkowski space
is used. This value is saved under the usual Lorentz transformations in Minkowski space , but it changes when the transformations in the extended space
, but it changes when the transformations in the extended space  are used. We call this model the extended space model (ESM). From a physical point of view, our expansion means that processes in which the rest mass of the particles changes are acceptable now. If the rest mass of a particle does not change and the physical quantities do not depend on an additional variable
are used. We call this model the extended space model (ESM). From a physical point of view, our expansion means that processes in which the rest mass of the particles changes are acceptable now. If the rest mass of a particle does not change and the physical quantities do not depend on an additional variable , then the electromagnetic and gravitational fields exist independently of each other. But if the rest mass is variable and there is a dependence on
, then the electromagnetic and gravitational fields exist independently of each other. But if the rest mass is variable and there is a dependence on , then these two fields are combined into a single unified field. In the extended space model a photon can have a nonzero mass and this mass can be either positive or negative. In this model the 5- vectors which components correspond to energy, pulse and mass of a particle are isotropic both for massive and massless particles. The rotations in the (1+4) dimensional extended space
, then these two fields are combined into a single unified field. In the extended space model a photon can have a nonzero mass and this mass can be either positive or negative. In this model the 5- vectors which components correspond to energy, pulse and mass of a particle are isotropic both for massive and massless particles. The rotations in the (1+4) dimensional extended space  can transform massive particles into massless and vice versa.
can transform massive particles into massless and vice versa.
1. INTRODUCTION
We consider a generalization of Einstein’s special theory of relativity (STR) on a 5-dimensional space, or more specifically on a (1+4)-dimensional space with a metric . However, it is well known that the photon can be considered as a massless particle, and described by the plane wave only in an infinite empty space [1,2]. But if a photon falls into the environment or in confined space, such as a resonator or waveguide, it acquires a nonzero mass [3,4].
. However, it is well known that the photon can be considered as a massless particle, and described by the plane wave only in an infinite empty space [1,2]. But if a photon falls into the environment or in confined space, such as a resonator or waveguide, it acquires a nonzero mass [3,4].
Under the particle mass m, we will understand its rest mass, which is a Lorentz scalar. No other masses will not appear in this work. Here we follow the recommendations of [5]. Similarly, we can consider the process of changing the mass of other particles, such as electrons, assuming that it depends on external conditions and influences.
Thus, it seems natural to expand the space of parameters characterizing particle, taking into account the fact that under an interaction of its mass it can vary. We call it the extended space.
In the STR the rest mass m of a particle is constant. It is a Lorentz scalar. We assume that in the extended space model (ESM) a rest mass m may vary in some processes. Such a change of a rest mass is the result of external influences.
This possibility indicates by the phenomenon of “mass defect” in nuclear reactions. The same situation is with the change of photon mass. We believe that in the empty Minkowski space photon moves with velocity c, and its mass is zero. But when photon falls into a medium, or in an external field, its velocity ν becomes smaller than c, and the mass becomes nonzero. In this case, we assume that the non-zero mass can be both positive and negative.
The ESM is formulated in extended (1 + 4)-dimensional space. As a 5th coordinate we use a parameter, which describes the environment in which the particle is located. It can be conventionally considered as a “refractive index” of the environment. The process of movement along the 5th coordinate corresponds physically to transition from a medium with one “refractive index” into a medium with another “refractive index”. The group 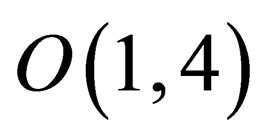 is the grope of transformations of the extended space. The group
is the grope of transformations of the extended space. The group  of Lorentz transformations is the subgroup of group
of Lorentz transformations is the subgroup of group .
.
The transformations from Lorentz group change position and time, but do not change the value of the “index of refraction”. This value can be changed only by that transformations from the group , which do not belong to the Lorentz group.
, which do not belong to the Lorentz group.
Accordingly, in the dual space with coordinates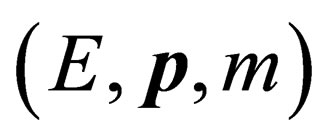 , the Lorentz transformations act in the subspace
, the Lorentz transformations act in the subspace . These transformations don’t change a value of mass m. The value of mass m can be changed only by that transformations from the group
. These transformations don’t change a value of mass m. The value of mass m can be changed only by that transformations from the group , which do not belong to the Lorentz group.
, which do not belong to the Lorentz group.
The change of mass of the particles leads to appearing of gravitational field. The unified field, which combines gravitation and electromagnetism is generated by 5-vector potential. Electric charge of the photon with zero mass is equal to zero. By continuity, we assume that the charge of the photon with nonzero mass is equal to zero. In the ESM electric charge is a constant and does not change under transformations of the group .
.
2. THE STRUCTURE OF THE EXTENDED SPACE
Each particle having a mass m, corresponds to a hyperboloid in Minkowski space, in the limiting case this hyperboloid degenerates into a cone.
 (1)
(1)
Since the change of the mass of a particle corresponds its transition from one hyperboloid to the other, i.e. change of the corresponding interval, it seems natural to choose interval s as an additional fifth coordinate. Thus, we will work in a space with coordinates 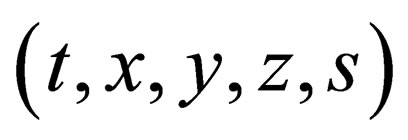 and metric
and metric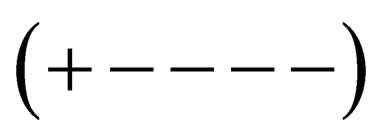 . The objects under consideration are located on a cone
. The objects under consideration are located on a cone
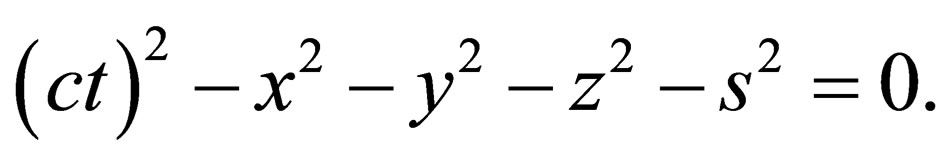 (2)
(2)
We will denote it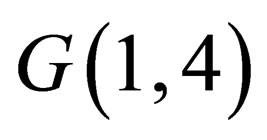 . The usual (1+2)-dimensional cones and hyperboloids occur as sections of the surface (2) by hyperplanes
. The usual (1+2)-dimensional cones and hyperboloids occur as sections of the surface (2) by hyperplanes . In the space of
. In the space of 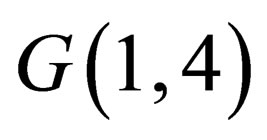 one can constructed in usual way the objects that have different tensor nature and transform appropriately under linear transformations of the space
one can constructed in usual way the objects that have different tensor nature and transform appropriately under linear transformations of the space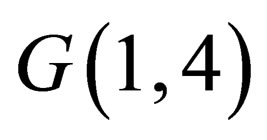 .
.
In Minkowski space 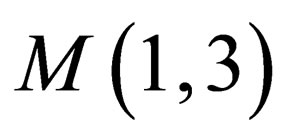 a 4-vector of energy and momentum
a 4-vector of energy and momentum
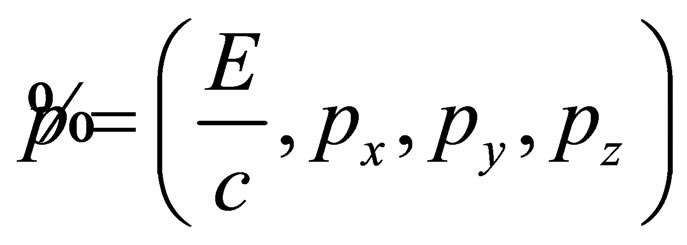 (3)
(3)
is associated to each particle [1]. In the extended space of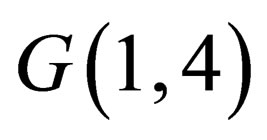 , we completes its to 5-vector
, we completes its to 5-vector
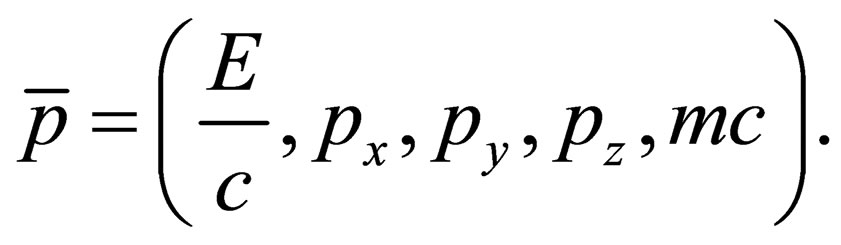 (4)
(4)
For free particles, the components of the vector (4) satisfy the equation
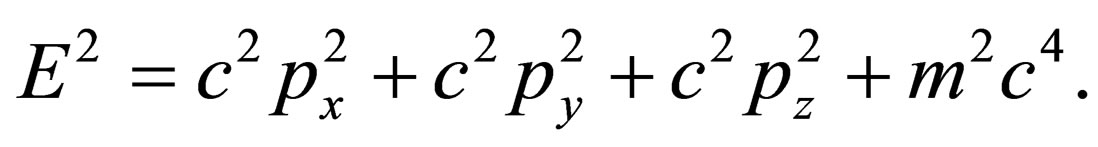 (5)
(5)
It is well-known relation of relativistic mechanics, which relates the energy, momentum and mass of a particle. Its geometric meaning is that the vector (4) is isotropic, i.e. its length in the space of 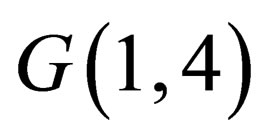 is equal to zero. However, in contrary to the usual relativistic mechanics, we now suppose that the mass m is also a variable, and it can vary at motion of a particle on the cones (2) and (5). It should be understood so that the mass of the particle changes when it enters the region of the space that has a nonzero density of matter. Since in such areas the speed of light is reduced, they can be characterized by value n-optical density. The parameter n relates the rate of light in vacuum c with the speed of light in a medium ν.
is equal to zero. However, in contrary to the usual relativistic mechanics, we now suppose that the mass m is also a variable, and it can vary at motion of a particle on the cones (2) and (5). It should be understood so that the mass of the particle changes when it enters the region of the space that has a nonzero density of matter. Since in such areas the speed of light is reduced, they can be characterized by value n-optical density. The parameter n relates the rate of light in vacuum c with the speed of light in a medium ν.
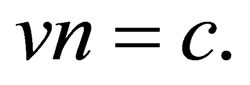
A set of variables (4) forms a 5-pulse, its components are conserved, if the space 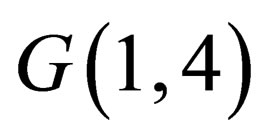 is invariant under the corresponding direction. In particular, its fifth component
is invariant under the corresponding direction. In particular, its fifth component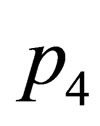 , having sense of mass, does not change if the particle moves in the area with constant value n.
, having sense of mass, does not change if the particle moves in the area with constant value n.
3. THE VECTORS OF THE FREE PARTICLES
In the usual relativistic mechanics and field theory the mass of a particle is constant, and for particles with zero masses and nonzero rest masses different methods of description are used. The particles with nonzero rest masses are characterized by their mass m and speed . The particles with zero mass (photons) are characterized by frequency
. The particles with zero mass (photons) are characterized by frequency  and wavelength
and wavelength . These
. These 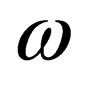 and
and 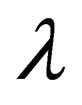 are connected with energy
are connected with energy 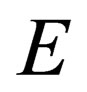 and pulse
and pulse 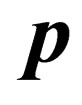 as follows
as follows
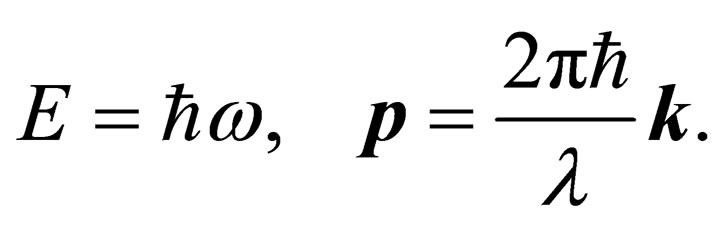 (6)
(6)
The 4-vector
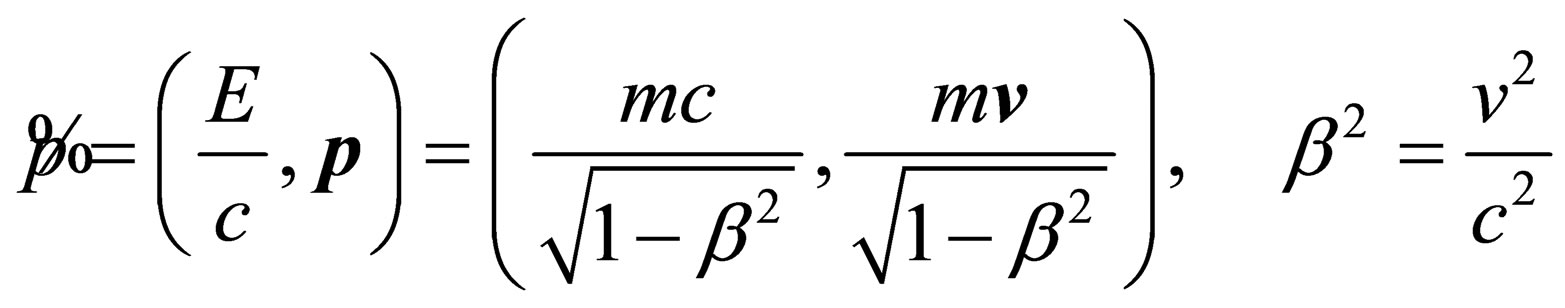 (7)
(7)
corresponds to a particles with nonzero rest mass.
The 4-vector
 (8)
(8)
corresponds to a particles with zero mass.
In the frames of our approach, there is no difference between massive and massless particles, and therefore should establish a connection between these two methods of description [6,7]. This can be done using the relation (6) and the hypothesis of de Broglie, according to which these relations hold for the massive particles [8]. Now, substituting (6) in (4), we obtain the relation between the mass m, frequency 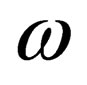 and wavelength
and wavelength 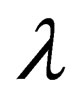
 (9)
(9)
 (10)
(10)
It follows that if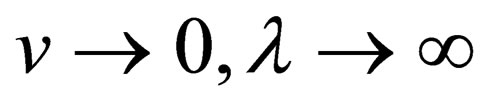 , but
, but . Here
. Here 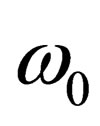 determines the energy of a particle at rest.
determines the energy of a particle at rest.
Now we construct 5-vectors from 4-vectors (7), (8). We suppose that to a stationary particle of mass m corresponds a 5-vector
 (11)
(11)
The 5-vector of a particle, which moves with velocity , can be obtained by transformation to the moving coordinate system. Then the vector (11) takes the form
, can be obtained by transformation to the moving coordinate system. Then the vector (11) takes the form
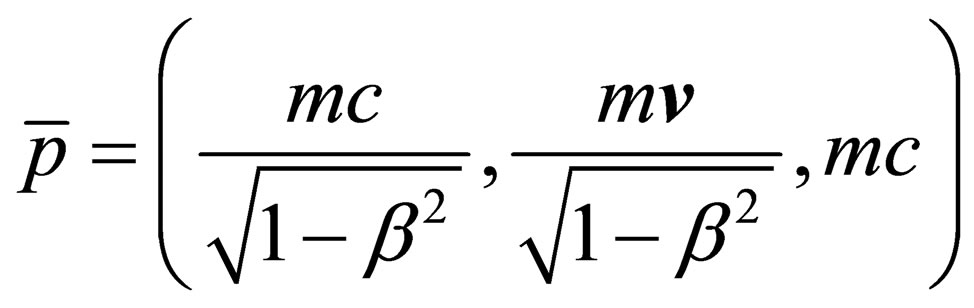 (12)
(12)
Similarly the 4-vector (8) transforms into 5-vector
 (13)
(13)
At the transition to a moving coordinate system the vector (13) does not change its form, only the frequency 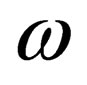 changes its value.
changes its value.
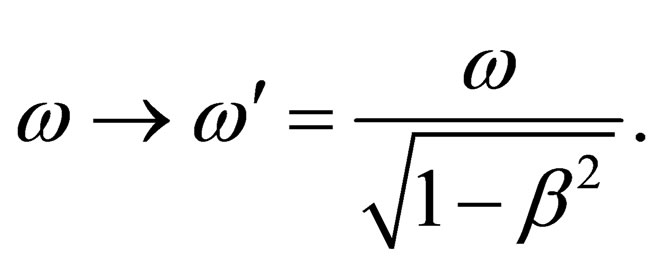 (14)
(14)
Thus, in an empty space in a stationary reference frame there are two fundamentally different objects with zero and nonzero masses, which in the space of 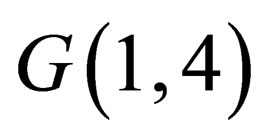 correspond to the 5-vectors
correspond to the 5-vectors
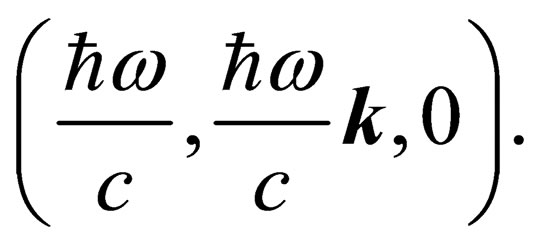 (15)
(15)
 (16)
(16)
For simplicity, we write the vectors (15), (16) in (1+2)-dimensional space. The vector (15) describes a photon with zero mass, the energy , and the velocity c. The vector (16) describes a stationary particle of mass m. The photon has a momentum
, and the velocity c. The vector (16) describes a stationary particle of mass m. The photon has a momentum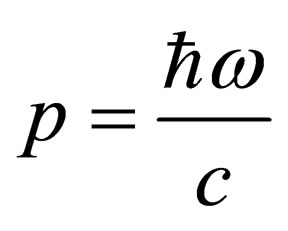 , a massive particle has a momentum equal to zero. In the 5-dimensional space, these two vectors are isotropic, in Minkowski space only the vector (15) is isotropic.
, a massive particle has a momentum equal to zero. In the 5-dimensional space, these two vectors are isotropic, in Minkowski space only the vector (15) is isotropic.
The length of the vector 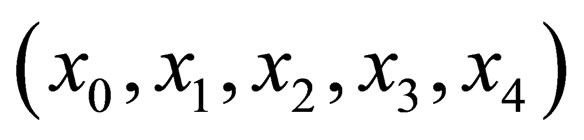 is equal to
is equal to
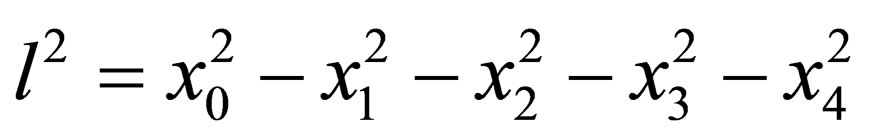
If we restrict ourselves to Lorentz transformations in Minkowski space it is impossible to transform an isotropic vector into anisotropic one and vice versa. In other words in frames of the SRT photon cannot acquire mass, and a massive particle cannot be a photon. But in the extended space 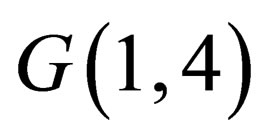 a photon and a massive particle can be related to each other by a simple rotation.
a photon and a massive particle can be related to each other by a simple rotation.
4. ELECTRODYNAMICS AND GRAVITATION IN THE EXTENDED SPACE
The source of the electromagnetic field is a current. In the traditional formulation of the electromagnetic the current is described by a 4-vector in Minkowski space .
.
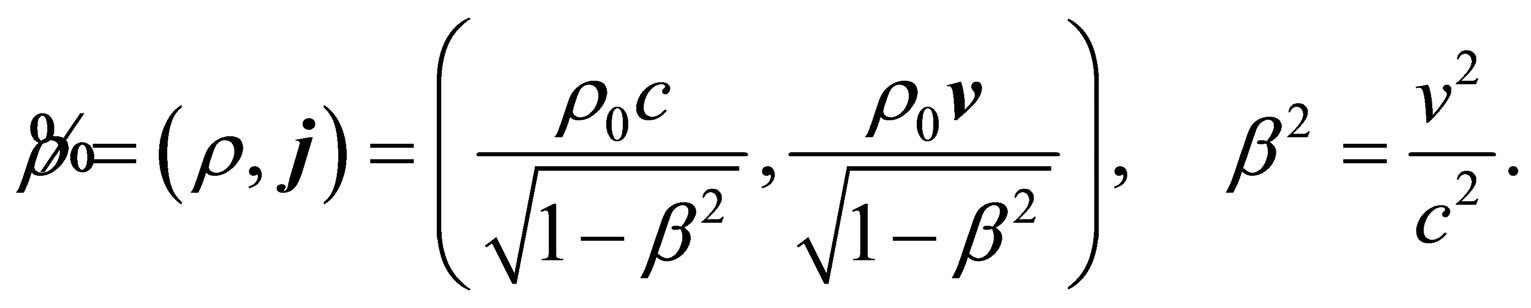 (17)
(17)

Here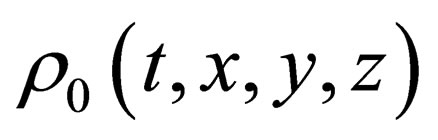 —an electric charge density in the point
—an electric charge density in the point  Of the space
Of the space , and
, and  —is a local velocity of a charge density.
—is a local velocity of a charge density.
At the transition to the extended space  it is necessary to change a (1 + 3)-current vector
it is necessary to change a (1 + 3)-current vector  by a (1 + 4)-vector
by a (1 + 4)-vector . In accordance with the principles of the developed model, an additional coordinate of the vector
. In accordance with the principles of the developed model, an additional coordinate of the vector 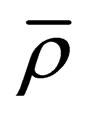 must be an isotropic (1 + 4)-vector. In addition, we want our model describes both the electromagnetic and gravitational field, so the fifth component of the current should be defined so that it be the source of the gravitational field. In our model there are no charged particles with zero mass. The problem of existence of such particles will be discussed in a separate article.
must be an isotropic (1 + 4)-vector. In addition, we want our model describes both the electromagnetic and gravitational field, so the fifth component of the current should be defined so that it be the source of the gravitational field. In our model there are no charged particles with zero mass. The problem of existence of such particles will be discussed in a separate article.
Here we suppose that the source of a unit electromagnetic and gravitational field, is a particle which has both a mass and a charge. In this case, we assume that the mass may not have any charge, but the charge should always have a mass.
In our model we assume that the charge is constant and does not change under transformations of the rotation group  of the extended space
of the extended space . And the rest mass, which is a scalar with respect to the Lorentz group, is a fifth component of the vector with respect to the group of
. And the rest mass, which is a scalar with respect to the Lorentz group, is a fifth component of the vector with respect to the group of .
.
We want to construct a 5-dimensional current vector of 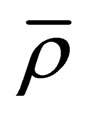 as a generalization of 4-dimensional current vector
as a generalization of 4-dimensional current vector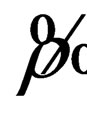 . To do this one must add one component to it.
. To do this one must add one component to it.
In the ordinary electrodynamics 4-dimensional current vector 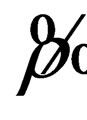 has the form
has the form
 (18)
(18)

Its structure it similar to structure of the energy-momentum vector (7) of the particle, having a rest mass. The difference between them is that in the vector (17) instead of the rest mass 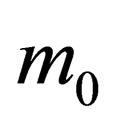 there is a local density of a charge of
there is a local density of a charge of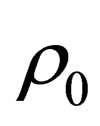 . In the expanded space
. In the expanded space  we consider the energy-momentum-mass vector (18) instead of the energy-momentum vector (7).
we consider the energy-momentum-mass vector (18) instead of the energy-momentum vector (7).
Thus, the 5-dimensional vector of current, generating a unit electro-gravitational field, has the form
 (19)
(19)
It is an isotropic vector
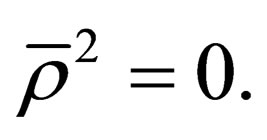
The continuity equation, as in the usual case, is expressed by the vanishing of the 5-divergence of the 5- current (18)
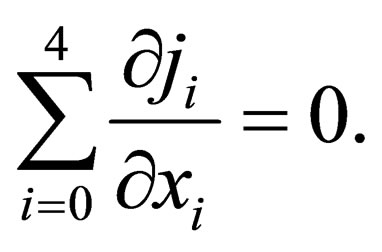 (20)
(20)
If the charge is at rest, the continuity equation takes the form
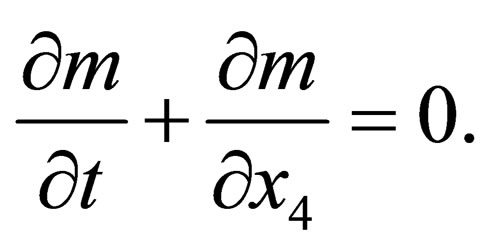 (21)
(21)
Eq.21 can be interpreted as the variation of the rest mass of the particle by changing the properties of the environment.
In ordinary electrodynamics from the continuity equation should be the law of conservation of charge
 (22)
(22)
There is an integral over the volume in the left side of this equation, and the right side—is the integral over the surface bounding this volume.
In electro-gravidynamics there is a law of conservation of the value, which is the product of the charge at the mass of a particle, which holds this charge. This law reads
 (23)
(23)
In this case, the change in the product of  of a charge at the mass inside a volume is defined as a stream of charged particles across the surface of the volume and change of masses of particles within the volume due to their dependence on the coordinate
of a charge at the mass inside a volume is defined as a stream of charged particles across the surface of the volume and change of masses of particles within the volume due to their dependence on the coordinate .
.
The current (18) generates the electro-gravitational field in the extended space of . The potentials of this field are determined by the equations
. The potentials of this field are determined by the equations
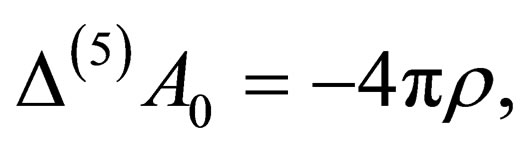 (24)
(24)
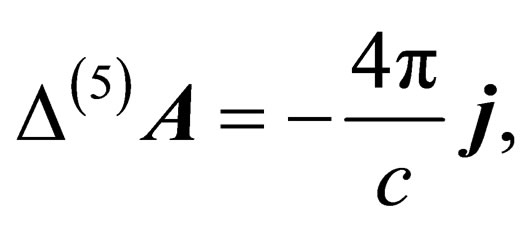 (25)
(25)
 (26)
(26)
Here
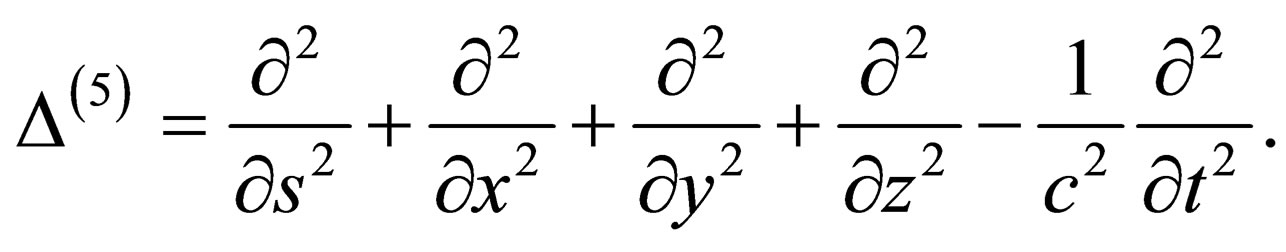 (27)
(27)
5. TENSION FIELDS
With the help of the potentials 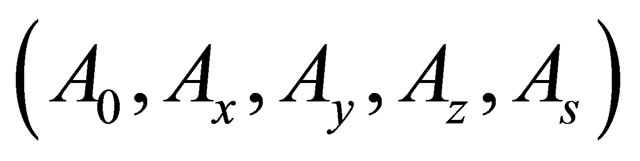 one can construct a tension tensor
one can construct a tension tensor
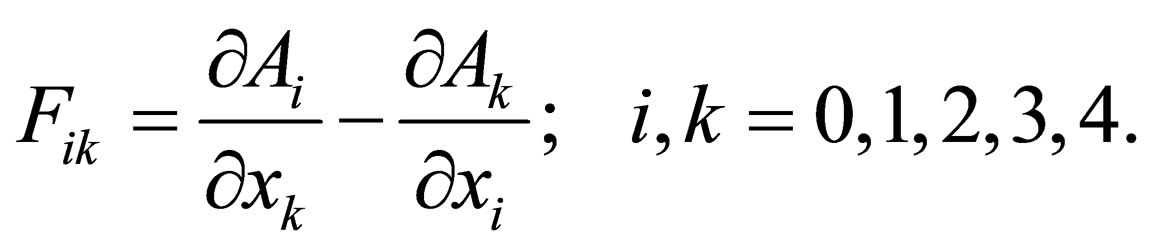 (28)
(28)
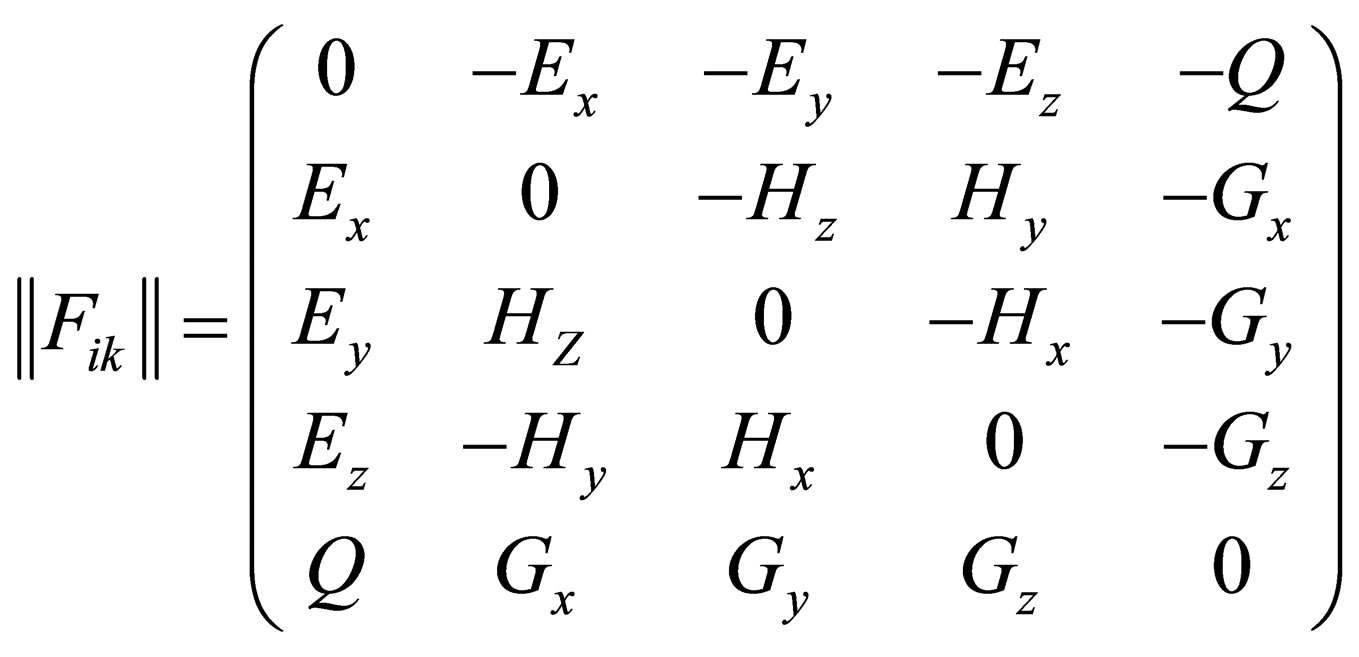 (29)
(29)
Here
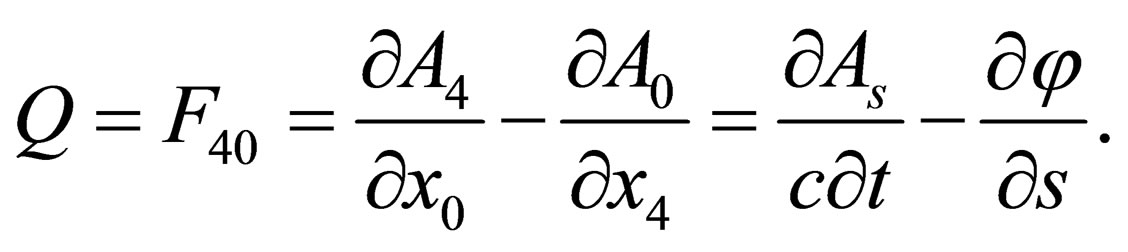 (30)
(30)
 (31)
(31)


With the help of the stress tensor (29) one can construct the energy-momentum-mass tensor
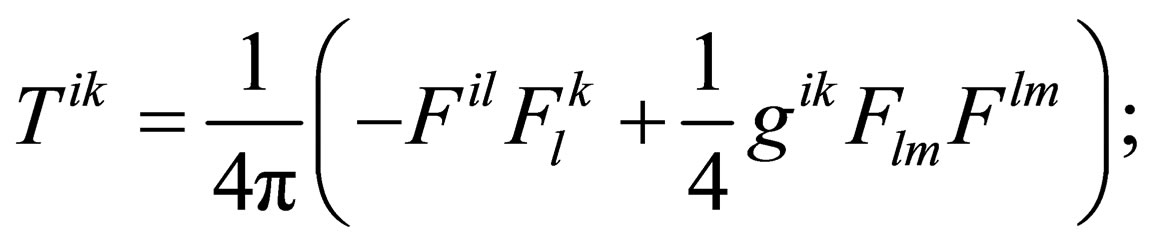
Here is the equation satisfied by the intensity of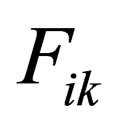 . We’ll call them the extended Maxwell system. The usual system of Maxwell equations consists of two pairs of equations, which have fundamentally different structures. They are usually well known, the first and second pair of Maxwell’s equations. Extended system of Maxwell’s equations also consists of two types of equations fundamentally different structure. We shall call them the equations of the first and second types.
. We’ll call them the extended Maxwell system. The usual system of Maxwell equations consists of two pairs of equations, which have fundamentally different structures. They are usually well known, the first and second pair of Maxwell’s equations. Extended system of Maxwell’s equations also consists of two types of equations fundamentally different structure. We shall call them the equations of the first and second types.
The equations of the first type are formal consequence of the formula (31), which expresses the tension via potentials. It follows immediately from their form that for any three indexes  the relation
the relation
 (32)
(32)
is satisfied. The validity of (32) can be verified by direct substitution of the expression (28) in the Eq.32.

There exist 10 such equations. Let us consider now the specific form of these equations, using the tension tensor (29).
If we restrict ourselves to the sets of indexes taking values (0,1,2,3), then corresponding 4 equations are simply the first pair of Maxwell’s equations
 (33)
(33)
This is one equation. The three other equations which correspond to sets of indices ,
, 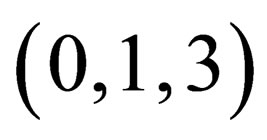 ,
, 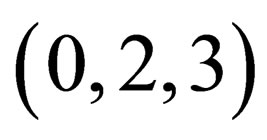 form a unit vector equation
form a unit vector equation
 (34)
(34)
Thus, the first pair of Maxwell’s equations retains its form. In the extended space 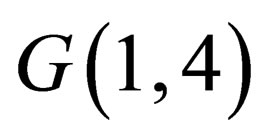 another 6 equations are added to them. Three of them, which are corresponding to the sets
another 6 equations are added to them. Three of them, which are corresponding to the sets 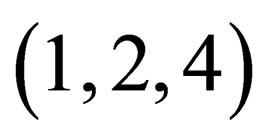
 ,
,  , can be combined into one vector equation
, can be combined into one vector equation
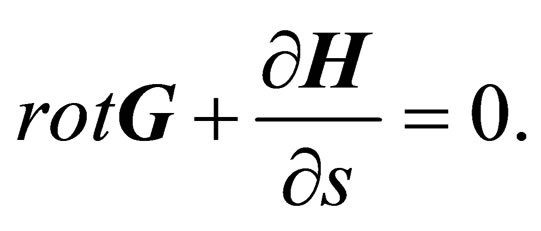 (35)
(35)
The other three triples 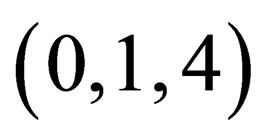
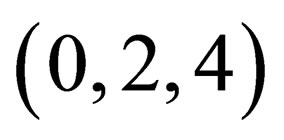
 give us the three remaining equations of the first type. They also can be merged into a single vector equation
give us the three remaining equations of the first type. They also can be merged into a single vector equation
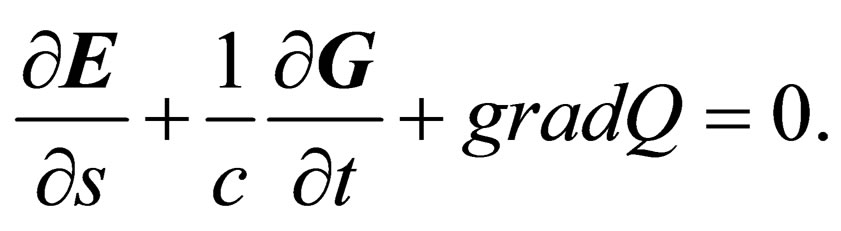 (36)
(36)
Thus, the equation of the first type from the expanded system of Maxwell’s equations in the space of 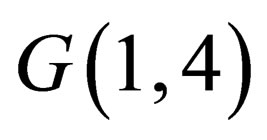 has the forms (33) - (36). These 10 equations are combined into three vector equations and one scalar equation. Note that the vector operators
has the forms (33) - (36). These 10 equations are combined into three vector equations and one scalar equation. Note that the vector operators 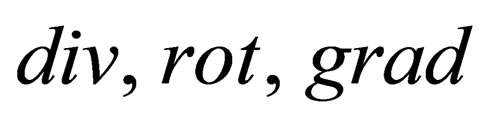 that appear in these equations have the usual three-dimensional form.
that appear in these equations have the usual three-dimensional form.
Let’s turn now to construction of the Maxwell equations of the second type. These equations are followed from the equations for the potentials (24) - (26). However, it is necessary first to impose the Lorentz gauge condition, which must satisfy potential (23). In the space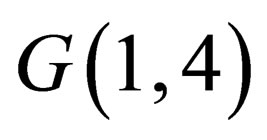 , it has the form
, it has the form
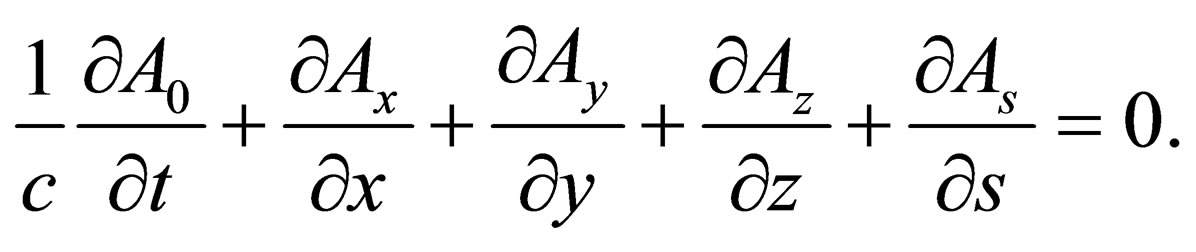 (37)
(37)
The second type of Maxwell’s equations from the extended system has the form
 (38)
(38)
Substituting into Eq.38 the elements of the tension tensor (29) and taking into account the Lorentz gauge condition (37), one can obtain five vector equations.
 (39)
(39)
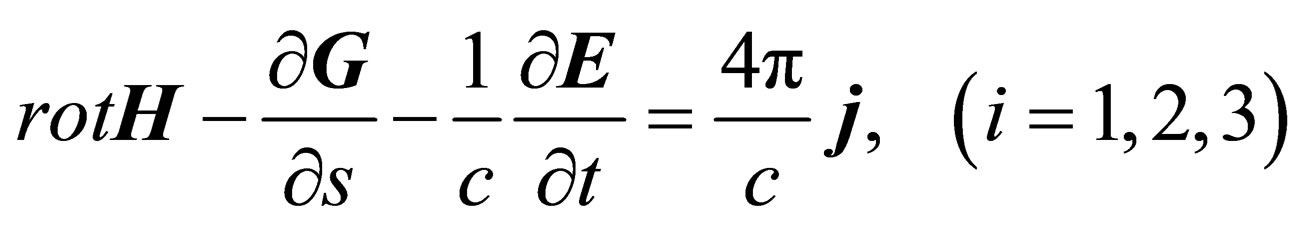 (40)
(40)
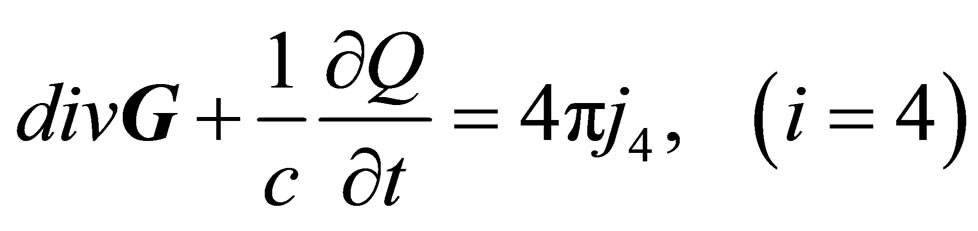 (41)
(41)
The tension tensor (29) contains, in addition to the components that are analogous to the usual electric and magnetic fields, some additional components that describe the gravitational field. More precisely, in the case where the components of the 5-current (18) depend on the coordinate , all the components of (29) describe a single electro-gravitational field, if the current does not depend on the coordinate
, all the components of (29) describe a single electro-gravitational field, if the current does not depend on the coordinate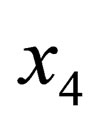 , the system of Eqs.34, 36, 38, 41 splits into two systems. One of them is the system of Maxwell’s equations and the other is a Laplace equation for the scalar gravitational field.
, the system of Eqs.34, 36, 38, 41 splits into two systems. One of them is the system of Maxwell’s equations and the other is a Laplace equation for the scalar gravitational field.
Thus, according to our model, in an empty space of the gravitational and electromagnetic fields, there exist two different fields, but in the region where there are particles and fields, they form a unit electromagnetic-gravitational field.
Within the framework of Extended Space Model (ESM) [6,7], the processes connected to birth of photons in a gravitational field are studied. These photons have a nonzero mass, which can be both positive and negative, and photon’s energy and strength of the gravitational field absolutely determine this photon mass value. It is shown that in ESM, model formation of bubble gravitational structures is possible. In the frame of ESM one can obtain the following physical picture. Bubble gravitational objects have a halo formed by dark matter generated by photons with a positive mass. The comparison ESM bubble structures with similar objects of a type “gravastar” [9], existing in a General Theory of Relativity (GR) was made [7,10,11]. Now it becomes possible to predict some future results of visible size of supermassive objects in our Universe due to new stage of experimental astronomy development in the RadioAstron Project [12-14]. In RadioAstron Project which has to reach an unprecedented angular resolution equal to 0.00001, it becomes possible to distinguish real size of such objects active galactic nuclei to investigate the size of supermassive objects applying for black hole role and to obtain direct results of comparison of event horizon with its radius. In the case when the visible radius of supermassive object will not exceed the gravitational radius we will agree that this object is real black hole. In the case when visible radius will be in 2 to 3 times larger than gravitational radius appropriated to the mass of supermassive object, we will discuss the nature of such objects with taking into account that one of the possible answers is the gravastar [9].
REFERENCES
- Landau, L.D. and Lifshitz, E.M. (1980) The classical theory of fields. 4th Edition, Volume 2, Butterworth-Heinemann, Amsterdam-Boston-Oxford.
- Schweber, S.S. (1961) An introduction to relativistic quantum field theory. Row, Peterson and Company, IllinoisNew York.
- Ginzburg, V.L. (1981) Theoretical physics and astrophysics, monographs in natural philosophy (Book 99), Pergamon Press, Oxford.
- Rivlin, L.A. (1997) Photons in a waveguide (some thought experiments). Soviet Physics Uspekhi, 40, 291-303. http://dx.doi.org/10.1070/PU1997v040n03ABEH000215
- Okun, L.B. (1989) The concept of mass (mass, energy, relativity). Soviet Physics Uspekhi, 32, 629-638. http://dx.doi.org/10.1070/PU1989v032n07ABEH002739
- Tsipenyuk, D.Yu. and Andreev, V.A. (2000) Structure of extended space. Bulletin the Lebedev Physics Institute (Russian Academy of Sciences), 6, 23-34.
- Tsipenyuk, D.Yu. and Andreev, V.A. (2004) Gravitational effects in extended space. Bulletin of the Lebedev Physics Institute (Russian Academy of Sciences), 10, 13-25.
- Bohm, D. (1952) Quantum theory? New York PrenticeHoll, Inc., New York.
- Mazur, P.O. and Mottola, E. (2001) Gravitational condensate stars: An alternative to black holes, arXiv:gr-qc/ 0109035.
- Tsipenyuk, D.Yu. and Andreev, V.A. (2006) Dark matter and condensed bubble object formation. Gravitation and Cosmology, 12 (46-47), 235-238.
- Tsipenyuk, D.Yu. and Andreev, V.A. (2006) Results of experimental testing of extended space model predictions. Gravitation and Cosmology, 12, 239-242.
- RadioAstron Project. http://www.asc.rssi.ru/radioastron/index.html
- Radioastron: The ground-space interferometer: Radio telescope much larger than the Earth. http://www.asc.rssi.ru/radioastron/_files/booklet_en.pdf
- Radioastron handbook. http://www.asc.rssi.ru/radioastron/documents/rauh/en/rauh.pdf

