Natural Science
Vol.6 No.7(2014), Article ID:45361,8 pages DOI:10.4236/ns.2014.67052
Linear Entropy of a Driven Central Spin Interacting with an Antiferromagnetic Environment
Mahmoud Abdel-Aty1,2
1Scientific Publishing Center, University of Bahrain, Sakhair, Bahrain
2Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt
Email: amisaty@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 26 December 2013; revised 26 January 2014; accepted 3 February 2014
ABSTRACT
We exploit a scheme to obtain a long-lived entanglement using a driven central spin interacting with an antiferromagnetic spin bath. Our numerical results show the effects of different parameters on the population inversion and the entanglement dynamics in terms of the linear entropy. It is shown that the long-lived entanglement is an intriguing result corresponding to the collapse region of the atomic inversion. As illustration, we examine the long-time interaction of the entanglement under the resonance and off-resonance regimes.
Keywords:Linear Entropy, Antiferromagnetic Spin Bath, Entanglement

1. Introduction
One of the outstanding challenges for multi-particle quantum information processing is to accurately find the states of many particles in a scalable fashion [1] . Quantum decoherence, relaxation and thermalization of a central system coupled to a closed and finite-size spin bath environment are fundamental concepts of physics [2] . Also, antiferromagnets subjected to an external magnetic field have received considerable attention [3] . One of the interesting phenomena in antiferromagnetic materials when one applies magnetic field is the magneticfield-induced spin-flop transition. As the magnetic field is increased to the critical field point, the antiferromagnetic polarization flips into the direction perpendicular to the field. These phenomena is called the spin-flop transition and has been observed experimentally [4] . They have reported the direct observation of the formation of ferromagnetic domains which appears at the first-order spin-flop transition. In this regard a direct link between the magnetic structure on the atomic scale and the macroscopic transport and magnetic properties of the sample has been obtained.
Recently experimental interest has been increased in electronic spin systems, where the most prominent source of decoherence is thought to be electronic. Examples of these systems are superconducting quantum dots [5] [6] and large-spin magnetic molecules [7] [8] and nitrogen-vacancy centers in diamond [9] [10] . In addition, fluctuating two level defects are thought to be the major source of decoherence in solid state Josephson junction qubits [11] . Also, different aspects of the decoherence and spin bath environment interaction have been considered [12] -[17] , e.g. the importance of level statistics for the decoherence of a central spin due to a spin environment [12] , geometric phase of a central spin interacting with an antiferromagnetic environment [13] , influence of an external magnetic field on the decoherence of a central spin coupled to an antiferromagnetic environment [17] etc. It is thus particularly interesting to investigate how the dynamics of the entanglement of a driven central spin interacting with an antiferromagnetic spin bath is affected.
There is an elegant way of studying fundamental information inequality in term of the quantum relative entropy [18] [19] and an increasing appreciation in recent times of the connections between entropy and entanglement is shown [20] -[30] . In the atom-field interaction without considering the decoherence effect, it is possible to use entropy as an entanglement measure. But for the interaction of central spin with an antiferromagnetic spin bath (environment) range, the situation is at best problematic. We are not in a position to judge whether this can be viewed as a mathematical difficulty which can be overcome soon. Thus it may well be meaningful to keep in mind the possibility of using some new indicators, where the linear entropy discussed in this paper would be of immediate relevance.
It is the purpose of this paper to give an analysis of the entanglement dynamics of a central spin interacting with an antiferromagnetic spin environment. The article is organized as follows: we display the Hamiltonian in Section 2. Then some dynamical aspects related to the population inversion and linear entropy are discussed in Section 3. Finally concluding remarks are drawn in Section 4.
2. The Model
The system, which is considered here, represents a central spin interacting with an antiferromagnetic spin environment [13] [14] . The central spin and the antiferromagnetic spin environment are made of spin-1/2 atoms and the frequency 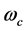 of the magnetic field is tuned to be resonant with the central spin to detect the central spin and control its states. Here we follow the previous treatment and consider the following approximations, low excitation limit, low temperatures, the environment is in the low-temperature and low-excitation limit, the number of excitations is small and the coupling constant between the central spin and the antiferromagnetic spin environment is scaled such that a nontrivial finite limit of
of the magnetic field is tuned to be resonant with the central spin to detect the central spin and control its states. Here we follow the previous treatment and consider the following approximations, low excitation limit, low temperatures, the environment is in the low-temperature and low-excitation limit, the number of excitations is small and the coupling constant between the central spin and the antiferromagnetic spin environment is scaled such that a nontrivial finite limit of ![]() can exist. Using the above approximations, one can write the total Hamiltonian of the system in the following form [12] -[14]
can exist. Using the above approximations, one can write the total Hamiltonian of the system in the following form [12] -[14]
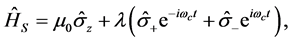 (1)
(1)
 (2)
(2)
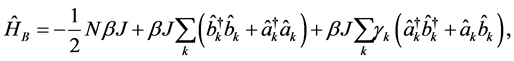 (3)
(3)
where 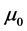 is the Larmor frequency which describes the coupling constant with a local magnetic field in the
is the Larmor frequency which describes the coupling constant with a local magnetic field in the 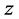 direction. We denote by
direction. We denote by![]() the coupling strength which is proportional to the amplitude of the driving field,
the coupling strength which is proportional to the amplitude of the driving field, ![]() is the number of atoms in each sublattice,
is the number of atoms in each sublattice, 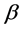 is the number of the nearest neighbors of an atom,
is the number of the nearest neighbors of an atom, ![]() is the exchange interaction,
is the exchange interaction, 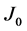 is the scaled interaction between the central spin and the antiferromagnetic environment and
is the scaled interaction between the central spin and the antiferromagnetic environment and 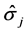 are the spin operators. The operators
are the spin operators. The operators ![]() and
and 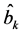 connected with the atomic operators through the Holstein-Primakoff transformation as
connected with the atomic operators through the Holstein-Primakoff transformation as
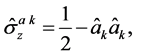
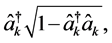
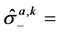
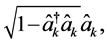
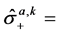
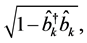
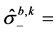
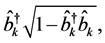
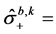 and
and 
where 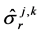 is the spin operator of
is the spin operator of 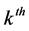 atom. We set
atom. We set
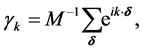
where the connection between any atom and its nearest neighbors is described by the vector![]() .
.
The dynamical model used here is similar to the well-known spin-boson model discussed earlier [15] [16] . For all previous variants of such type of driven systems, quantum entanglement is known to range from pure state to maximal entangled state as well as standard increasing followed by sudden change [23] . Our finding of long-living entanglement is thus an intriguing result corresponding to the collapse regions of the atomic inversion. In a broader context, the linear entropy used here is different from other entanglement measures of fast calculations when high demission problem is involved.
Consider then the following initial state of the system
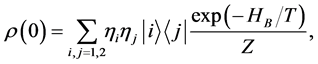 (4)
(4)
where 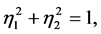 and
and  is the partition function which can be calculated as
is the partition function which can be calculated as
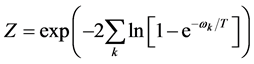
with a unity of the Boltzmann constant. We denote by 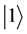 and
and  the system states.
the system states.
Following the standard procedure and assume that the density matrix of the antiferromagnetic bath is assumed to satisfy the Boltzmann distribution [26] , we obtain the general solution of the following master equation
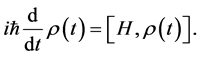 (5)
(5)
From Equation (5), we obtain a set of algebraic equations for the complex probability amplitudes of the quantum states which can be solved in the usual way [15] [16] . Consequently, the general solution to Equation (5) is given by
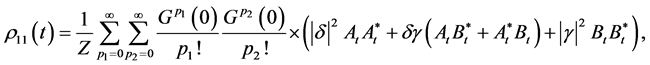 (6)
(6)
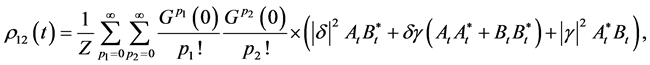 (7)
(7)
where
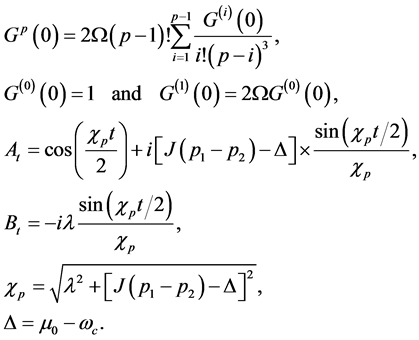 (8)
(8)
It is also possible to compute the general solution of the system by considering more general initial states. Here, we have considered a system with a separable initial density matrix of the composed system, so that it makes sense how entanglement dynamics propagates. In the following section, we are interested in examining the relation between the long-lived entanglement and atomic inversion collapse.
3. Entanglement
In an effort to present a numerical characterization, we have performed some calculations of the linear entropy and atomic inversion quantities for a particular set of parameters, some of which can be considered as realistic, while some other parameters look perhaps too optimistic. However, dimensionless parameters are used and our results can be useful under different scenarios.
As an entanglement measure von Neumann entropy has been used when the system starts from a pure state and many generalizations have been proposed. Among them the Tsallis entropy [38] generalizes the concept of the von Neumann Entropy, encompassing, among the others linear entropy and is given by
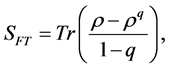 (9)
(9)
where ![]() is a real number. For
is a real number. For 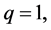 Equation (9) reduces to the well-known von Neumann entropy
Equation (9) reduces to the well-known von Neumann entropy 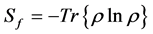 which satisfies some standard properties as concavity, additivity and sub-additivity [29] . When
which satisfies some standard properties as concavity, additivity and sub-additivity [29] . When 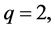 Equation (9) reduces to what is called, linear entropy
Equation (9) reduces to what is called, linear entropy
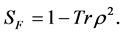 (10)
(10)
It is pointed out in a straightforward way that such a quantity, the linear entropy of the reduced density matrix, can be used as a measure of the entanglement. Even if linear entropy is not additive in the usual sense [31] -[33] , it has some interesting properties so far not fully exploited.
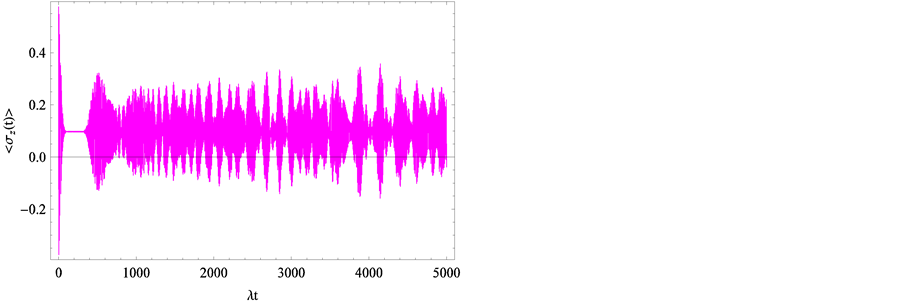
Since the resulting series, Equations (6)-(8), cannot be analytically summed in a closed form, we evaluate them numerically. In Figure 1, we plot the linear entropy and atomic inversion against the scaled time ![]() The other parameters are chosen according to the typical experiments at NIST [39] , where we set
The other parameters are chosen according to the typical experiments at NIST [39] , where we set 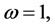

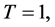


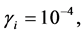
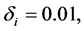 and
and ![]() The initial state of the atoms is assumed to be a superposition state. From Figure 1(a), one can infer that before the interaction, i.e. frequency correlations are not present, the linear entropy is equal to zero and information about energy levels is not available. This implies that entanglement cannot be performed before the interaction is switched on. As time goes on, one see that the linear entropy is growing and reaches a local maximum value but after a longer time interaction the difference between local maximum and local minimum becomes bigger. It is interesting to treat the frequency,
The initial state of the atoms is assumed to be a superposition state. From Figure 1(a), one can infer that before the interaction, i.e. frequency correlations are not present, the linear entropy is equal to zero and information about energy levels is not available. This implies that entanglement cannot be performed before the interaction is switched on. As time goes on, one see that the linear entropy is growing and reaches a local maximum value but after a longer time interaction the difference between local maximum and local minimum becomes bigger. It is interesting to treat the frequency, ![]() as a continuous function and expand the dispersion curve of
as a continuous function and expand the dispersion curve of 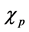 around a point
around a point ![]() Let us write
Let us write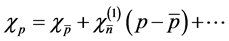 . The first term of the
. The first term of the 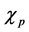 expansion is responsible for observed rapid oscillations (see Figure 1(a)) of the linear entropy while the remaining terms are responsible for their envelope. With the aim of
expansion is responsible for observed rapid oscillations (see Figure 1(a)) of the linear entropy while the remaining terms are responsible for their envelope. With the aim of
 (a)
(a)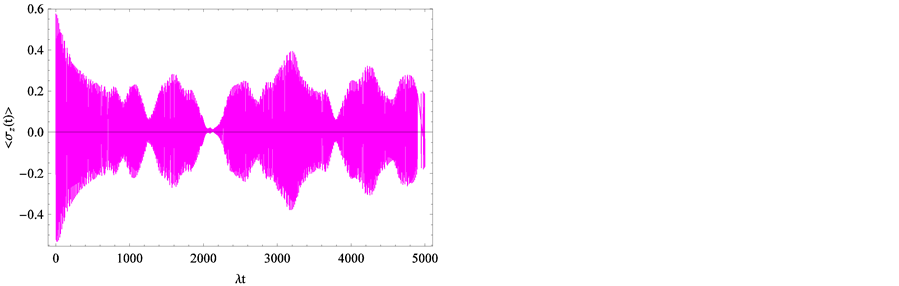 (b)
(b)
Figure 1. The evolution of the linear entropy as an entanglement measure and atomic inversion as functions of the scaled time![]() . Calculations assume that detuning parameter
. Calculations assume that detuning parameter 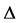 has zero value, and
has zero value, and 
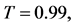
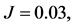

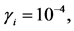
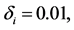 and
and ![]()
recognizing in which situations entanglement can be performed, we compute the atomic inversion in Figure 1(b), using the same parameters. In view of the atomic inversion general behavior, and the results presented in [13] , it naturally arises the following question: is there any long-lived entanglement or completely disentanglement that allows to access information about the energy level structure of the system, for long time limit? In Figure 1(b), we show that the use of long time interaction does not guarantee the successful retrieval of completely collapse of the atomic inversion and the revival reappears with different amplitude. Rather, the use of the current parameters makes the realization of the collapse-revival phenomena is more pronounced, even for a short interaction time. Surprisingly, in the off-resonance case, 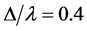 , the linear entropy shows constant value followed by the usual oscillations, which means that information about the energy level structure of the system can be retrieved during this period (see Figure2(a)). Also, it is noticed that this period is exactly corresponding to collapse period of the atomic inversion (see Figure2(b)). This result is of great interest since it tells us that the collapse periods of the atomic inversion can be used as an indicator for purity but, in general does not guarantee the successful retrieval of the system information or entanglement creation, since the entanglement calculations contain the off-diagonal elements of the density matrix while the atomic inversion is the difference between the diagonal elements only. We need to consider another measure that is needed in order to state clearly when the entanglement or purity occur. It is noted, previously, that a purely sinusoidal dynamical behavior of the atomic inversion is shown for the general two-level system with the cavity field initially prepared in the photon number state [28] [29] . From Figure 2, it is shown that the detuning effect leads to early appearance of the collapse and also the atomic inversion oscillates around positive value instead of zero. One observes that the inversion shows rapid oscillations around a non-zero value,
, the linear entropy shows constant value followed by the usual oscillations, which means that information about the energy level structure of the system can be retrieved during this period (see Figure2(a)). Also, it is noticed that this period is exactly corresponding to collapse period of the atomic inversion (see Figure2(b)). This result is of great interest since it tells us that the collapse periods of the atomic inversion can be used as an indicator for purity but, in general does not guarantee the successful retrieval of the system information or entanglement creation, since the entanglement calculations contain the off-diagonal elements of the density matrix while the atomic inversion is the difference between the diagonal elements only. We need to consider another measure that is needed in order to state clearly when the entanglement or purity occur. It is noted, previously, that a purely sinusoidal dynamical behavior of the atomic inversion is shown for the general two-level system with the cavity field initially prepared in the photon number state [28] [29] . From Figure 2, it is shown that the detuning effect leads to early appearance of the collapse and also the atomic inversion oscillates around positive value instead of zero. One observes that the inversion shows rapid oscillations around a non-zero value,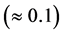 . After the first collapse period, we see that the inversion oscillates regularly around the same value with very short collapse’s periods. This effect comes from the nonlinear nature of the coupling in this model which results in the Rabi frequency being proportional to the detuning. It is clear that a long-lived entanglement depends on different parameters contributions such as the detuning, environment and coupling strength which is proportional to the amplitude of the driving field intermediate-state transitions [34] -[44] . The physical reason why the linear entropy and atomic inversion are very sensitive to any change of the detuning, comes from the fact that the detuning is the main factor in the Rabi oscillation,
. After the first collapse period, we see that the inversion oscillates regularly around the same value with very short collapse’s periods. This effect comes from the nonlinear nature of the coupling in this model which results in the Rabi frequency being proportional to the detuning. It is clear that a long-lived entanglement depends on different parameters contributions such as the detuning, environment and coupling strength which is proportional to the amplitude of the driving field intermediate-state transitions [34] -[44] . The physical reason why the linear entropy and atomic inversion are very sensitive to any change of the detuning, comes from the fact that the detuning is the main factor in the Rabi oscillation,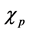 . Finally, iin contrast to the long-distance of the steady-state entanglement predicted in this model and its generalizations, the conformal calculations show that the coupling strength parameter,
. Finally, iin contrast to the long-distance of the steady-state entanglement predicted in this model and its generalizations, the conformal calculations show that the coupling strength parameter, ![]() plays an important role in controlling the length of this period, where the scaled time has been considered as units of
plays an important role in controlling the length of this period, where the scaled time has been considered as units of 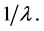
At the end of this Section, we point out that the different values of the system parameters lead to the same one-to-one correspondence between the atomic inversion and the entanglement. One interesting problem in quantum information processing that exhibits connections between the collapse-revival phenomenon and long-lived entanglement, where the long collapse period of the atomic inversion has been shown at the same time of the steady-state entanglement known as the long-lived entanglement. In this equivalence the divergence of the collapse’s length depends on the system parameters. It is interesting to note that the basic features of entanglement in this model at different values of the detuning parameter turn up in the context of localization phenomena.
4. Conclusion
We have shown that long-distance steady state entanglement in a driven central spin interacting with antiferromagnetic spin bath systems can be coherently controlled through the tuning difference between the Larmor frequency and the magnetic field frequency. This entanglement is measured by analyzing the dynamical behavior of the linear entropy. We also found that there exist one-to-one correspondence between the long-lived entanglement and collapse regime of the atomic inversion. Surprisingly enough, using different values of the system parameters the steady state entanglement can be achieved whenever the off-resonant case is considered. The results presented here help to identify clearly which types of parameters can be used to obtain a long-lived entanglement. The entanglement dynamics become quite irregular as the coupling strength of the spin bath increases. This happens because of the competing interaction of the field between the atom and the spin bath. Since the interest in spin bath is quite relevant in relation to the so-called quantum non-demolition measurements hence, our results may be useful in that context.
Acknowledgements
I would like to acknowledge the support from Deanship for Scientific Research, University of Bahrain, project No. 19/2014.
References
- Clark, C.R., Chou, C., Ellis, A.R., Hunker, J., Kemme, S.A., Maunz, P., Tabakov, B., Tigges, C. and Stick, D.L. (2013) Characterization of Fluorescence Collection Optics Integrated with a Micro-Fabricated Surface Electrode Ion Trap. arXiv:1305.4706
- Buchleitner, A., Viviescas, C. and Tiersch, M. (2009) Entanglement and Decoherence. Foundations and Modern Trends, Lecture Notes in Physics. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-88169-8
- Tanaka, A., Totsuka, K. and Hu, X. (2009) Geometric Phases and the Magnetization Process in Quantum Antiferromagnets. Physical Review B, 79, Article ID: 064412. http://dx.doi.org/10.1103/PhysRevB.79.064412
- Welp, U., Berger, A., Miller, D.J., Vlasko-Vlasov, V.K., Gray, K.E. and Mitchell, J.F. (1999) Direct Imaging of the First-Order Spin-Flop Transition in the Layered Manganite La1.4Sr1.6Mn2O7. Physical Review Letters, 83, 4180. http://dx.doi.org/10.1103/PhysRevLett.83.4180
- Ladd, T.D., Press, D., De Greve, K., McMahon, P.L., Friess, B., Schneider, C., Kamp, M., Hofling, S., Forchel, A. and Yamamoto, Y. (2010) Pulsed Nuclear Pumping and Spin Diffusion in a Single Charged Quantum Dot. Physical Review Letters, 105, Article ID: 107401. http://dx.doi.org/10.1103/PhysRevLett.105.107401
- Tsyplyatyev, O. and Loss, D. (2011) Spectrum of an Electron Spin Coupled to an Unpolarized Bath of Nuclear Spins. Physical Review Letters, 106, Article ID: 106803. http://dx.doi.org/10.1103/PhysRevLett.106.106803
- Takahashi, S., Hanson, R., van Tol, J., Sherwin, M.S. and Awschalom, D.D. (2008) Quenching Spin Decoherence in Diamond through Spin Bath Polarization. Physical Review Letters, 101, Article ID: 047601. http://dx.doi.org/10.1103/PhysRevLett.101.047601
- Takahashi, S., Tupitsyn, I.S., van Tol, J., Beedle, C.C., Hendrickson, D.N. and Stamp, P.C.E. (2011) Decoherence in Crystals of Quantum Molecular Magnets. Nature, 476, 76-79. http://dx.doi.org/10.1038/nature10314
- Hanson, R., Dobrovitski, V.V., Feiguin, A.E., Gywat, O. and Awschalom, D.D. (2008) Quantum Control over Single Spins in Diamond. Science, 320, 352-355. http://dx.doi.org/10.1126/science.1155400
- Zhang, J.-S. and Chen, A.-X. (2012) Review on Quantum Discord of Bipartite and Multipartite Systems. Quantum Physics Letters, 1, 69-77.
- Bergli, J., Galperin, Y.M. and Altshuler, B.L. (2009) Decoherence in Qubits Due to Low-Frequency Noise. New Journal of Physics, 11, Article ID: 025002. http://dx.doi.org/10.1088/1367-2630/11/2/025002
- Brox, H., Bergli, J. and Galperin, Y.M. (2012) The Importance of Level Statistics for the Decoherence of a Central Spin Due to a Spin Environment. Physical Review A, 85, Article ID: 052117. http://dx.doi.org/10.1103/PhysRevA.85.052117
- Yuan, X.-Z., Goan, H.-S. and Zhu, K.-D. (2010) Geometric Phase of a Central Spin Coupled to an Antiferromagnetic Environment. Physical Review A, 81, Article ID: 034102. http://dx.doi.org/10.1103/PhysRevA.81.034102
- Yuan, X.-Z., Goan, H.-S. and Zhu, K.-D. (2011) Dynamics of a Driven Spin Coupled to an Antiferromagnetic Spin Bath. New Journal of Physics, 13, Article ID: 023018. http://dx.doi.org/10.1088/1367-2630/13/2/023018
- Leggett, A.J., Chakravarty, S., Dorsey, A.T., Fisher, M.P.A., Garg, A. and Zwerger, W. (1987) Dynamics of the Dissipative Two-Level System. Reviews of Modern Physics, 59, 1. http://dx.doi.org/10.1103/RevModPhys.59.1
- Irish, E.K., Gea-Banacloche, J., Martin, I. and Schwab, K.C. (2005) Dynamics of a Two-Level System Strongly Coupled to a High-Frequency Quantum Oscillator. Physical Review B, 72, Article ID: 195410. http://dx.doi.org/10.1103/PhysRevB.72.195410
- Yuan, X.-Z., Goan, H.-S. and Zhu, K.-D. (2007) Influence of an External Magnetic Field on the Decoherence of a Central Spin Coupled to an Antiferromagnetic Environment. New Journal of Physics, 9, 219. http://dx.doi.org/10.1088/1367-2630/9/7/219
- Pramanik, T., Chowdhury, P. and Majumdar, A.S. (2013) Fine-Grained Lower Limit of Entropic Uncertainty in the Presence of Quantum Memory. Physical Review Letters, 110, Article ID: 020402. http://dx.doi.org/10.1103/PhysRevLett.110.020402
- Wilde, M.M., Hayden, P., Buscemi, F. and Hsieh, M.-H. (2012) The Information-Theoretic Costs of Simulating Quantum Measurements. Journal of Physics A: Mathematical and Theoretical, 45, Article ID: 453001. http://dx.doi.org/10.1088/1751-8113/45/45/453001
- Zhang, J.S., Chen, A.X. and Abdel-Aty, M. (2010) Two Atoms in Dissipative Cavities in Dispersive Limit: Entanglement Sudden Death and Long-Lived Entanglement. Journal of Physics B: Atomic, Molecular and Optical Physics, 43, Article ID: 025501. http://dx.doi.org/10.1088/0953-4075/43/2/025501
- Obada, A.S.F., Hessian, H.A. and Mohamed, A.B.A. (2008) Entropy and Entanglement in the Jaynes-Cummings Model with Effects of Cavity Damping. Journal of Physics B: Atomic, Molecular and Optical Physics, 41, Article ID: 135503. http://dx.doi.org/10.1088/0953-4075/41/13/135503
- Abdel-Aty, M., Abdalla, M.S. and Obada, A.S.F. (2001) Quantum Information and Entropy Squeezing of a Two-Level Atom with a Non-Linear Medium. Journal of Physics A: Mathematical and General, 34, 9129. http://dx.doi.org/10.1088/0305-4470/34/43/303
- Mohamed, A.B.A. (2013) Pairwise Quantum Correlations of a Three-Qubit XY Chain with Phase Decoherence. Quantum Information Processing, 12, 1141-1153. http://dx.doi.org/10.1007/s11128-012-0460-1
- Eisert, J., Cramer, M. and Plenio, M.B. (2010) Colloquium: Area Laws for the Entanglement Entropy—A Review. Reviews of Modern Physics, 82, 277. http://dx.doi.org/10.1103/RevModPhys.82.277
- Abdel-Aty, M. and Yu, T. (2008) Entanglement Sudden Birth of Two Trapped Ions Interacting with a Time-Dependent Laser Field. Journal of Physics B: Atomic, Molecular and Optical Physics, 41, Article ID: 235503. http://dx.doi.org/10.1088/0953-4075/41/23/235503
- Mohamed, A.B.A. (2013) Quantum Discord and Its Geometric Measure with Death Entanglement in Correlated Dephasing Two Qubits System. Quantum Information Review, 1, 1-7. http://dx.doi.org/10.12785/qir/010101
- Abdel-Aty, M. (2003) Quantum Field Entropy and Entanglement of a Three-Level Atom Two-Mode System with an Arbitrary Nonlinear Medium. Journal of Modern Optics, 50, 161. http://dx.doi.org/10.1080/09500340308235167
- Ficek, Z. (2009) Quantum Entanglement Processing with Atoms. Applied Mathematics & Information Sciences, 3, 375.
- Sun, L.H., Li, G.X. and Ficek, Z. (2010) Continuous Variables Approach to Entanglement Creation and Processing. Applied Mathematics & Information Sciences, 4, 315.
- Al-Showaikh, F.N.M. (2008) Entropy of a Two-Level Atom Driven by a Detuned Monochromatic Laser Field and Damped by a Squeezed Vacuum. Applied Mathematics & Information Sciences, 2, 21.
- Abdel-Aty, M. (2007) Quantum Information Entropy and Multi-Qubit Entanglement. Progress in Quantum Electronics, 31, 1. http://dx.doi.org/10.1016/j.pquantelec.2007.03.002
- Yuan, X.Z., Goan, H.S. and Zhu, K.D. (2007) Non-Markovian Reduced Dynamics and Entanglement Evolution of Two Coupled Spins in a Quantum Spin Environment. Physical Review B, 75, Article ID: 045331. http://dx.doi.org/10.1103/PhysRevB.75.045331
- Eleuch, H. and Rachid, N. (2010) Autocorrelation Function of Microcavity-Emitting Field in the Non-Linear Regime. European Physical Journal D, 57, 259. http://dx.doi.org/10.1140/epjd/e2010-00031-x
- Eleuch, H. (2010) Entanglement and Autocorrelation Function in Semiconductor Microcavities. International Journal of Modern Physics B, 24, 5653. http://dx.doi.org/10.1142/S0217979210057511
- Buzek, V. and Jex, I. (1991) Emission Spectra of a Two-Level Atom in a Kerr-Like Medium. Journal of Modern Optics, 38, 987-996. http://dx.doi.org/10.1080/09500349114550961
- Jabri, H., Eleuch, H. and Djerad, T. (2005) Lifetimes of Atomic Rydberg States by Autocorrelation Function. Laser Physics Letters, 2, 253. http://dx.doi.org/10.1002/lapl.200410184
- Eleuch, H., Ben Nessib, N. and Bennaceur, R. (2004) Quantum Model of Emission in Weakly Non Ideal Plasma. European Physical Journal D, 29, 391-395. http://dx.doi.org/10.1140/epjd/e2004-00061-y
- Tsallis, C. (1988) Possible Generalization of Boltzmann-Gibbs Statistics. Journal of Statistical Physics, 52, 479-487. http://dx.doi.org/10.1007/BF01016429
- Rajagopal, A.K. and Rendell, R.W. (2005) Nonextensive Statistical Mechanics: Implications to Quantum Information. Europhysics News, 36, 221-224. http://dx.doi.org/10.1051/epn:2005613
- Buscemi, F., Bordone, P. and Bertoni, A. (2007) Linear Entropy as an Entanglement Measure in Two-Fermion Systems. Physical Review A, 75, Article ID: 032301. http://dx.doi.org/10.1103/PhysRevA.75.032301
- Manfredi, G. and Feix, M.R. (2000) Entropy and Wigner Functions. Physical Review E, 62, 4665. http://dx.doi.org/10.1103/PhysRevE.62.4665
- Leibfried, D., Meekhof, D.M., King, B.E., Monroe, C., Itano, W.M. and Wineland, D.J. (1996) Experimental Determination of the Motional Quantum State of a Trapped Atom. Physical Review Letters, 77, 4281-8285. http://dx.doi.org/10.1103/PhysRevLett.77.4281
- Abdel-Aty, M., Abdel-Khalek, S. and Obada, A.S.F. (2001) Entropy Evolution of the Bimodal Field Interacting with an Effective Two-Level Atom via the Raman Transition in Kerr Medium. Chaos, Solitons & Fractals, 12, 2015-2022. http://dx.doi.org/10.1016/S0960-0779(00)00116-8
- Obada, A.S.F., Abdel-Khalek, S. and Plastino, A. (2011) Information Quantifiers’s Description of Weak Field vs. Strong Field Dynamics for a Trapped Ion in a Laser Field. Physica A, 390, 525-533. http://dx.doi.org/10.1016/j.physa.2010.09.003



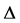 has a nonzero value,
has a nonzero value,