Natural Science
Vol.5 No.4(2013), Article ID:30256,6 pages DOI:10.4236/ns.2013.54064
Short-range action and long-range action of the electrostatic forces within atomic nuclei
![]()
Plovdiv University “Paisii Hilendarski”, Plovdiv, Bulgaria; *Corresponding Author: kolikov@uni-plovdiv.bg
Copyright © 2013 Dragia Ivanov, Kiril Kolikov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 30 January 2013; revised 28 February 2013; accepted 15 March 2013
Keywords: Nucleon; Electrostatic Force of Interaction; Strong Interaction; Long-Range-Acting Forces; Short-Range-Acting Forces
ABSTRACT
We study the interaction forces in atomic nuclei based on our expressions for the electrostatic interaction between spheres of arbitrary radii and charges. We prove that at small distances the proton-neutron electrostatic attraction forces are short-range-acting and the proton-proton electrostatic repulsion forces are long-rangeacting. We obtain that these forces are commensurate with the nuclear forces. The protonneutron electrostatic attraction forces and the proton-proton electrostatic repulsion forces at the same distance between nucleons differ in absolute value by about an order of magnitude. It follows that based on electromagnetic interactions the neutrons are the binding building blocks in nuclear structures.
1. INTRODUCTION
Let 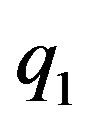 and
and 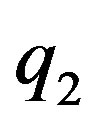 be two point electric charges and R be the distance between them. Then, according to Coulomb’s law the magnitude of the interaction force between them in vacuum is
be two point electric charges and R be the distance between them. Then, according to Coulomb’s law the magnitude of the interaction force between them in vacuum is 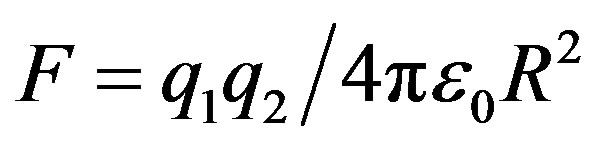 (
(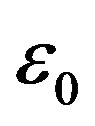 is the dielectric constant of vacuum). Thus the Coulomb forces are inversely proportional to
is the dielectric constant of vacuum). Thus the Coulomb forces are inversely proportional to 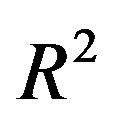
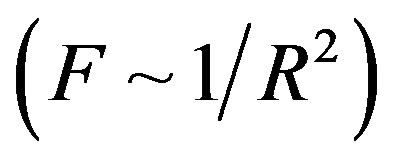 and decrease slowly with the increase of the distance R. Therefore they are so-called long-range-acting forces.
and decrease slowly with the increase of the distance R. Therefore they are so-called long-range-acting forces.
For dimensional objects however, it is possible that electrostatic forces be short-range-acting. A typical example in this regard is the attraction and repulsion force between molecules. These forces are electrostatic in nature and change very fast with distance. At small distances between molecules the attraction forces (van der Waals forces) are inversely proportional to the seventh power of distance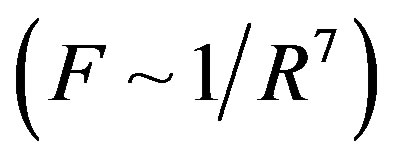 , and the repulsion forces are inversely proportional to the thirteenth power
, and the repulsion forces are inversely proportional to the thirteenth power 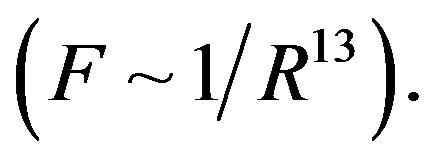 So the intermolecular forces are shortrange-acting.
So the intermolecular forces are shortrange-acting.
As is well known from numerous experiments, one of the main features of the forces acting inside the nucleus between protons and neutrons (so-called nuclear forces) is their short-range action. From various scattering experiments it has been determined that the radius of interaction between nucleons is of the order of 10−15 m. It is claimed that at such distances the nuclear forces are substantially bigger than electromagnetic forces. Moreover, inside the nucleus these forces are huge, but to its outside even in close proximity they are insignificant. With the increase of the distance between nucleons the nuclear forces decrease significantly faster than electromagnetic forces.
Back in 1956 Hofstadter [1] conducted experiments showing that protons and neutrons have a complex internal electric structure. Studies with fast electrons allowed uncovering distribution of the charges along the radius of nucleons [2]. The proton possesses an elementary positive charge  [3]. The neutron has both a positive and a negative charge, which cancel out so that the neutron can be considered as electrically neutral, i.e. has a charge of
[3]. The neutron has both a positive and a negative charge, which cancel out so that the neutron can be considered as electrically neutral, i.e. has a charge of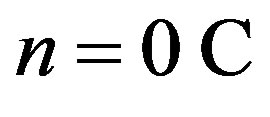 .
.
The structure of nucleons and the fact that they are located at very small distances between each other inside the nucleus presents a strong argument to model them as dimensional objects, whose charges can redistribute within their volumes when they interact with external charges. This assumption is completely natural if we assume that the charges of the proton and the neutron are made up of quarks.
In [4] using the method of image-charges we solve analytically the problem of electrostatic interaction between two charged conducting spheres with arbitrary charges ,
, 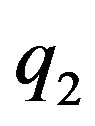 and radii
and radii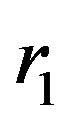 ,
,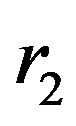 . As a result, we derive in the most general way exact analytical expressions for the magnitude of the force and the binding energy of their interaction. We also determine the potential in an arbitrary point of the electromagnetic field created by the two spheres. These results can be applied with some approximation to non-spherical bodies with a single center of symmetry by modeling them with spheres of equivalent surface area [4].
. As a result, we derive in the most general way exact analytical expressions for the magnitude of the force and the binding energy of their interaction. We also determine the potential in an arbitrary point of the electromagnetic field created by the two spheres. These results can be applied with some approximation to non-spherical bodies with a single center of symmetry by modeling them with spheres of equivalent surface area [4].
Through the general formulas we have obtained, it is possible to determine for the first time the force and energy of interaction between two charged spheres located at a distance significantly smaller than their radii. In [5,6] we have used these results to determine the electrostatic interaction between nucleons in atomic nuclei.
At the root of intermolecular forces lies the electrostatic interaction, while the magnetic forces play an insignificant role. In our considerations, we can assume with some approximation that the magnetic force between the nucleons will not play a significant role, so that the electrostatic forces are dominant in the interaction. This assumption is justified by the results we have obtained in [5,6].
The experimentally measured radii of the proton and neutron are rp = 0.84184 × 10−15 m [7] and rn = 1.1 × 10−15 m [2], respectively. Therefore, we consider the nucleon couples at a distance of 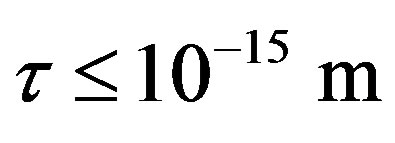 between their surfaces.
between their surfaces.
We prove that in atomic nuclei authoritative are the short-range-acting proton-neutron electrostatic attraction forces as well as the long-range-acting proton-proton electrostatic repulsion forces. We also obtain that these forces are commensurate with the nuclear forces.
2. QUANTIFICATION OF THE ELECTROSTATIC INTERACTION FORCES BETWEEN NUCLEONS MODELED AS SPHERES
We consider the nucleons as spheres similar to their representation in the standard model [8-10]. Let us denote with 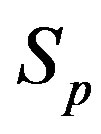 the sphere that models the proton and with
the sphere that models the proton and with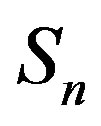 —the sphere modeling the neutron. Based on the assumption that the charges of the proton and the neutron can be redistributed within their volumes, we shall assume with some approximation that
—the sphere modeling the neutron. Based on the assumption that the charges of the proton and the neutron can be redistributed within their volumes, we shall assume with some approximation that 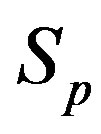 and
and 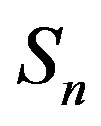 are conducting spheres. Following the procedure outlined in [4], we find the interaction force
are conducting spheres. Following the procedure outlined in [4], we find the interaction force  between the spheres
between the spheres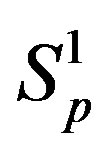 ,
, 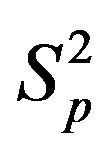 (modeling two protons), and the force
(modeling two protons), and the force 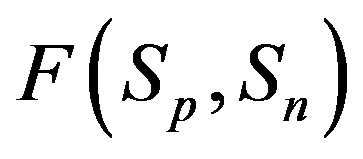 between the spheres
between the spheres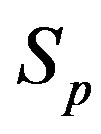 ,
, 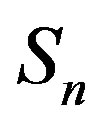 (modeling a proton and a neutron) as a function of the distance between their centers R.
(modeling a proton and a neutron) as a function of the distance between their centers R.
The results are presented on Figure 1. For the sake of demonstrability and clear comparison, we have also plotted the force  between two protons assumed as point charges according to Coulomb’s law.
between two protons assumed as point charges according to Coulomb’s law.
The curve representing interaction force for the proton-neutron system is displaced to the right along the R axis, because the radius rn = 1.1 × 10−15 m and the radius rp = 0.84184 × 10−15 m so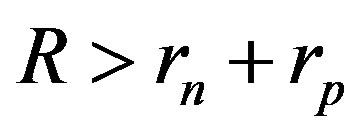 .
.
For better clarity in the comparison between the interaction forces we present on Figure 2 the dependence of the forces 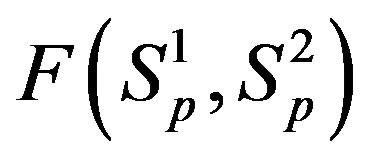 and
and 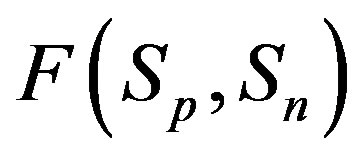 on the distance
on the distance 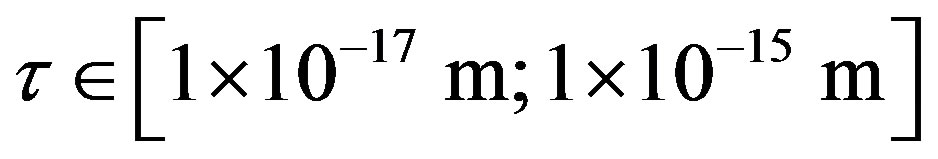 between the surfaces of the nucleon modeling spheres.
between the surfaces of the nucleon modeling spheres.
Close examination of the curves depicted in Figures 1

Figure 1. Example plot of the interaction forces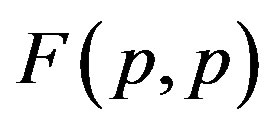 ,
, 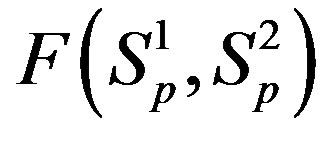 and
and 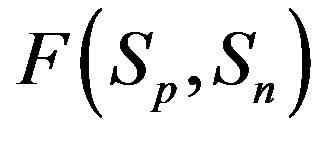 depending on the distance R between: point charges p, p; the centers of spheres
depending on the distance R between: point charges p, p; the centers of spheres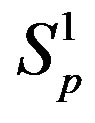 ,
,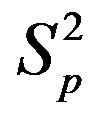 ; the centers of spheres Sp, Sn.
; the centers of spheres Sp, Sn.

Figure 2. Plot of the forces between the spheres ,
, 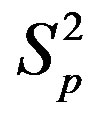 and Sp, Sn depending on the distance τ between their surfaces.
and Sp, Sn depending on the distance τ between their surfaces.
and 2 leads to some very interesting and quite unexpected conclusions about the electrostatic forces between nucleons (modeled as conducting spheres) within the nuclei:
1) The proton-proton repulsion force  is long-range-acting, with its plot lying even lower than the force
is long-range-acting, with its plot lying even lower than the force 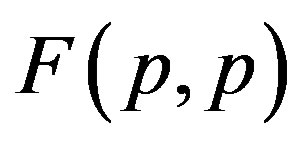 between protons assumed to be point charges (Figure 1);
between protons assumed to be point charges (Figure 1);
2) The proton-neutron attraction force 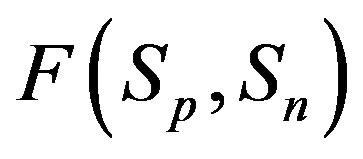 is short-range-acting with characteristic radius of the order of 10−15 m between the centers of the spheres, and is practically zero at distances greater than this radius (Figure 1).
is short-range-acting with characteristic radius of the order of 10−15 m between the centers of the spheres, and is practically zero at distances greater than this radius (Figure 1).
3) At small distances between the proton and the neutron the attraction force  rapidly increases in absolute value (Figures 1 and 2).
rapidly increases in absolute value (Figures 1 and 2).
4) At the same small distances 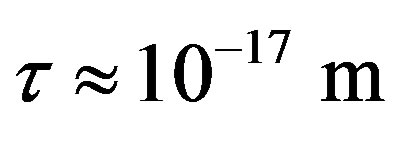 between the surfaces of the interacting nucleons the proton-neutron attraction force
between the surfaces of the interacting nucleons the proton-neutron attraction force  is one order of magnitude larger in absolute value than the proton-proton repulsion force
is one order of magnitude larger in absolute value than the proton-proton repulsion force 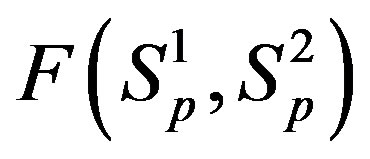 (Figure 2).
(Figure 2).
It is worthwhile to note that according to Figure 1 one can assume (with some approximation) that the forces 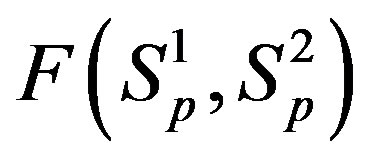 and
and 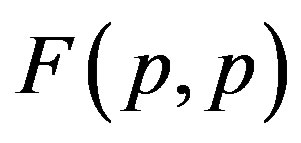 are equal, i.e. for protonproton interactions we can assume the proton charge to be point-like. However, when we calculate the interaction between a proton and a neutron, as we proved in [5], the proton should not be considered as a point charge.
are equal, i.e. for protonproton interactions we can assume the proton charge to be point-like. However, when we calculate the interaction between a proton and a neutron, as we proved in [5], the proton should not be considered as a point charge.
For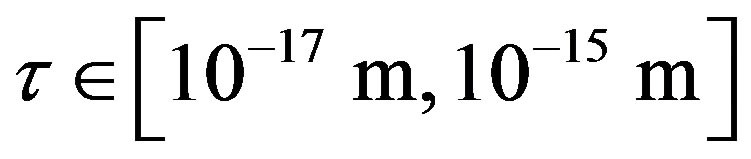 , based on [4] as well as in [5], we can determine the potential energy of interaction
, based on [4] as well as in [5], we can determine the potential energy of interaction  and
and 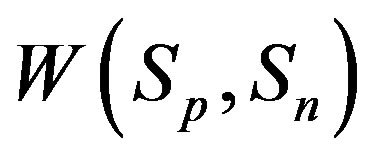 correspondingly between the spheres
correspondingly between the spheres ,
, 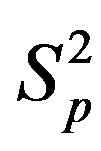 and the spheres
and the spheres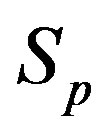 ,
,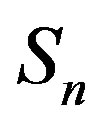 . The numeric values for the force and potential energy for different distances
. The numeric values for the force and potential energy for different distances 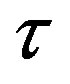 between the nucleon surfaces are presented in Table 1.
between the nucleon surfaces are presented in Table 1.
For 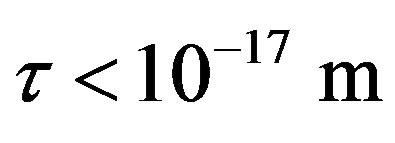 the force and interaction energy increase in absolute value.
the force and interaction energy increase in absolute value.
Taking into account the shape of the curve for the proton-neutron attraction force 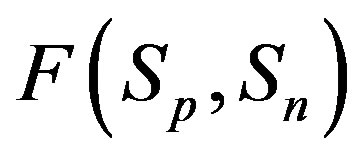 from Figure 1, we shall assume that
from Figure 1, we shall assume that
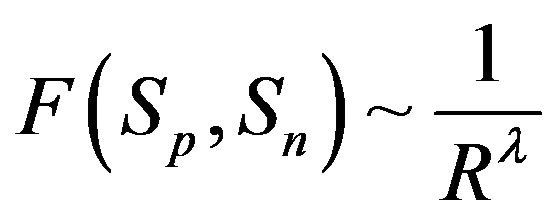 , i.e.
, i.e.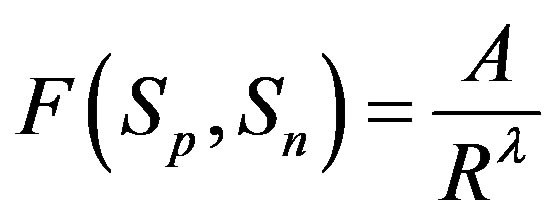 where
where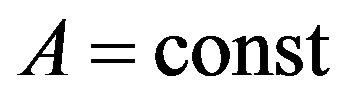 . Then, if
. Then, if 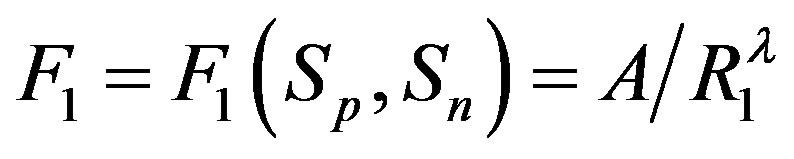 and
and
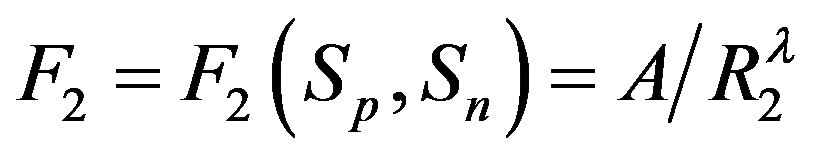 , it follows that
, it follows that , or equivalently
, or equivalently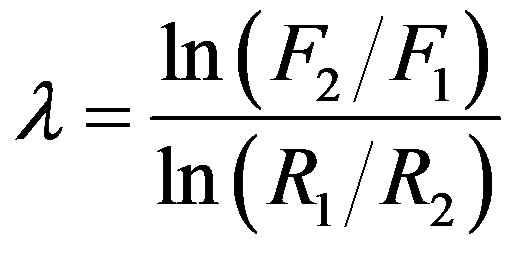 .
.
Since 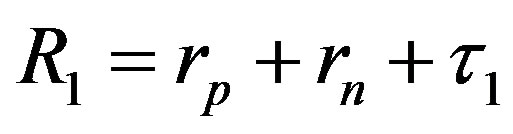 and
and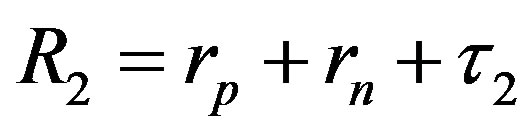 , then according to Table 1 for
, then according to Table 1 for 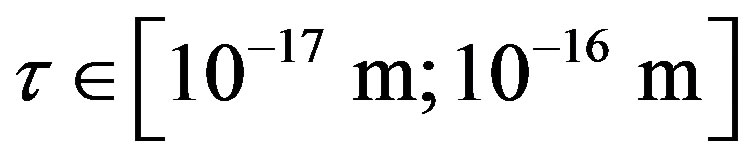 we obtain that
we obtain that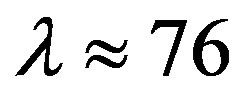 , i.e.
, i.e.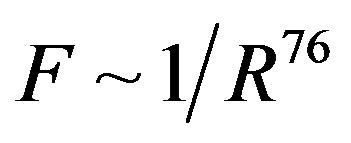 . This perfectly proves that at small enough distances the proton-neutron electrostatic attraction force is strongly short-range-acting.
. This perfectly proves that at small enough distances the proton-neutron electrostatic attraction force is strongly short-range-acting.
In [5] we have shown that the interaction energy
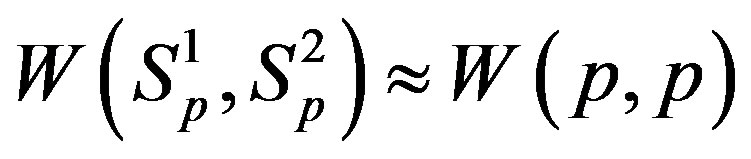 . We have also found that the binding energy
. We have also found that the binding energy 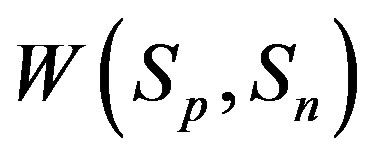 between the spheres
between the spheres 
and 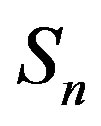 can take values within the range of the known binding energy of the deuteron
can take values within the range of the known binding energy of the deuteron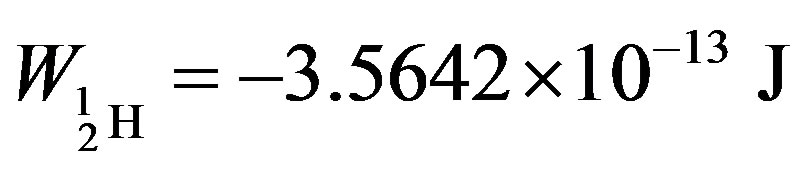 . However, based on the standard model it is not possible to obtain the larger binding energies of the triton, hellion,
. However, based on the standard model it is not possible to obtain the larger binding energies of the triton, hellion,  -particle, etc. It is hard to explain by means of interaction between spheres other known results for nuclei such as stability, radii, magnetic moments, etc. That is why in [5,6] we introduce the toroidal model of nucleons which
-particle, etc. It is hard to explain by means of interaction between spheres other known results for nuclei such as stability, radii, magnetic moments, etc. That is why in [5,6] we introduce the toroidal model of nucleons which
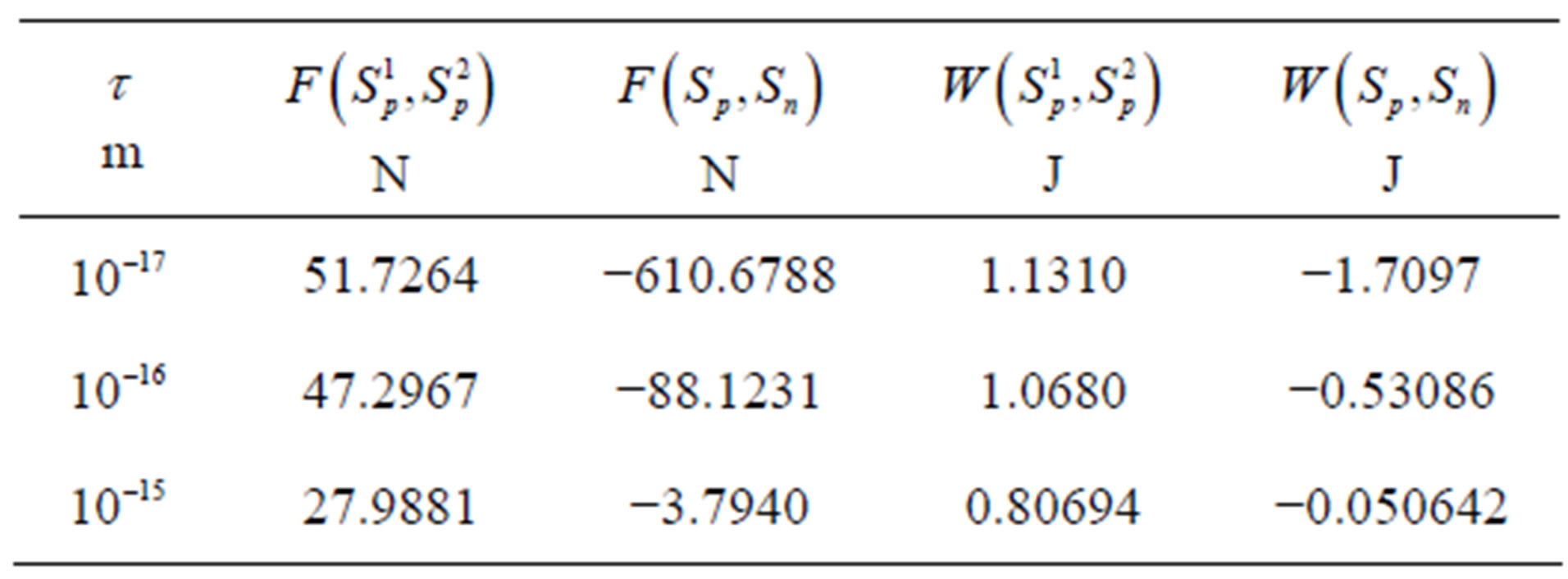
Table 1. Force and interaction energy between the spheres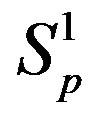 ,
, 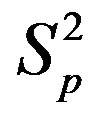 and Sp, Sn.
and Sp, Sn.
explains all the basic experimental results.
3. DETERMINING THE ELECTROSTATIC INTERACTION FORCES BETWEEN NUCLEONS MODELED AS TORI
We consider the nucleons as tori spinning with constant angular velocity around an axis z, passing through their center of masses (geometrical center) O and perpendicular to their plane of rotation (Figure 3).
Denote by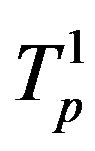 ,
, 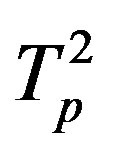 the tori of the two protons and assume that the force
the tori of the two protons and assume that the force  and the energy
and the energy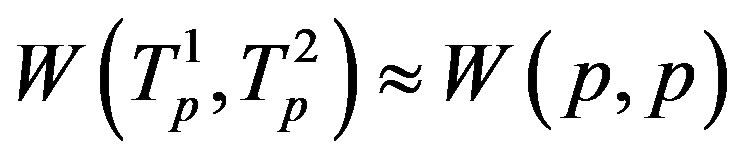 , that is in the case of proton-proton interactions we assume their charges as pointlike situated in the centers of the tori.
, that is in the case of proton-proton interactions we assume their charges as pointlike situated in the centers of the tori.
Let the proton and neutron be two tori 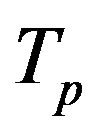 and
and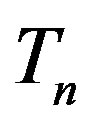 , respectively, where the charge of
, respectively, where the charge of 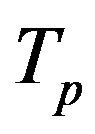 is p and the charge of
is p and the charge of 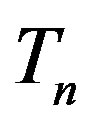 is 0. The centers of the tori we denote as
is 0. The centers of the tori we denote as 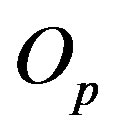 and
and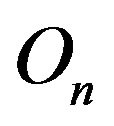 . Moreover, we assume that the central circles of
. Moreover, we assume that the central circles of 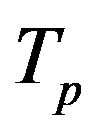 and
and 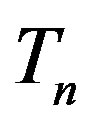 with corresponding radii
with corresponding radii  and
and 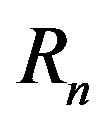 lie in parallel or coinciding planes and spin in the same or opposite direction with constant angular velocities
lie in parallel or coinciding planes and spin in the same or opposite direction with constant angular velocities  around an axis z, passing through
around an axis z, passing through  and
and  and perpendicular to their plane of rotation. If
and perpendicular to their plane of rotation. If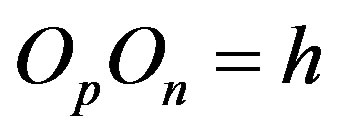 , then
, then 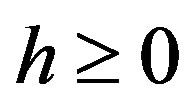 (Figure 4).
(Figure 4).
The radii of the proton 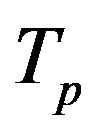 and the neutron
and the neutron 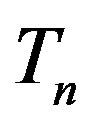 are correspondingly rp = 0.84184 × 10−15 m and rn = 1.1 × 10−15 m. Let us denote with
are correspondingly rp = 0.84184 × 10−15 m and rn = 1.1 × 10−15 m. Let us denote with 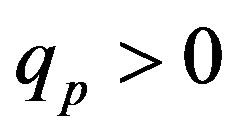 the radius of the circle of the empty part of the torus
the radius of the circle of the empty part of the torus 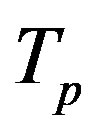 of the proton, i.e.
of the proton, i.e.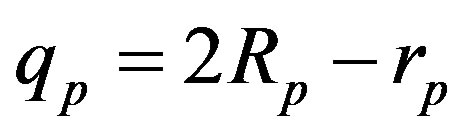 .
.
We remodel the proton 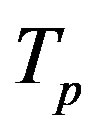 with a sphere
with a sphere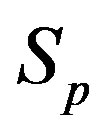 , and the neutron
, and the neutron 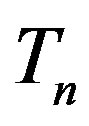 with a torus
with a torus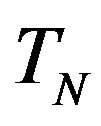 , equivalent in area. In addition,
, equivalent in area. In addition, 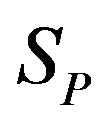 and
and 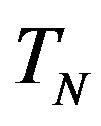 have the same centers and stand at the same distance
have the same centers and stand at the same distance 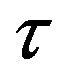 as in the case of
as in the case of 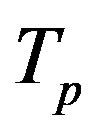 and
and 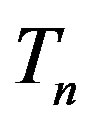 (Figure 5).
(Figure 5).
We apply a similar reasoning [5] for the interaction between conducting spheres. Therefore, for different values of the radius 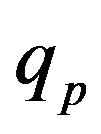 of the empty part of
of the empty part of  and the distance
and the distance 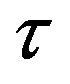 between the surfaces of the nucleons, we obtain the following results for the forces and interaction energies between nucleons, which are presented in Table 2.
between the surfaces of the nucleons, we obtain the following results for the forces and interaction energies between nucleons, which are presented in Table 2.
For , or
, or 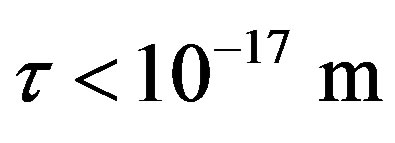 the force and binding
the force and binding

Figure 3. Toroidal model of a nucleon.
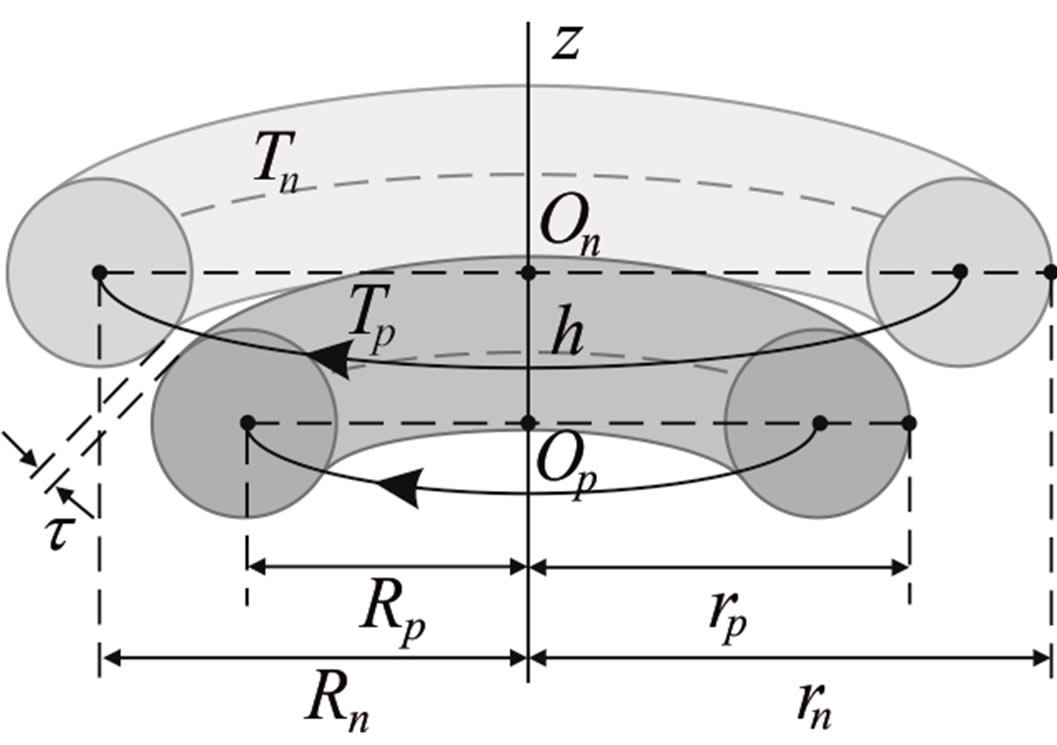
Figure 4. Cross-section of a proton-neutron system.
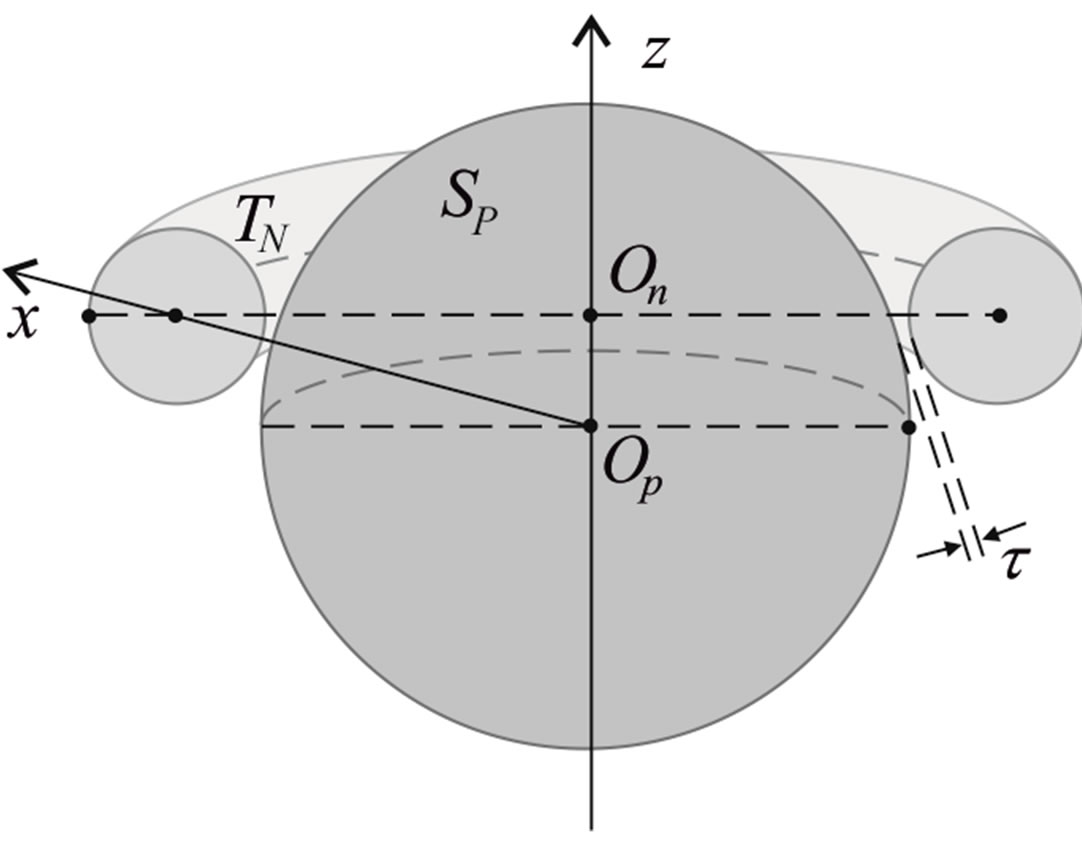
Figure 5. Cross-section of the reduced model of a proton-neutron system.
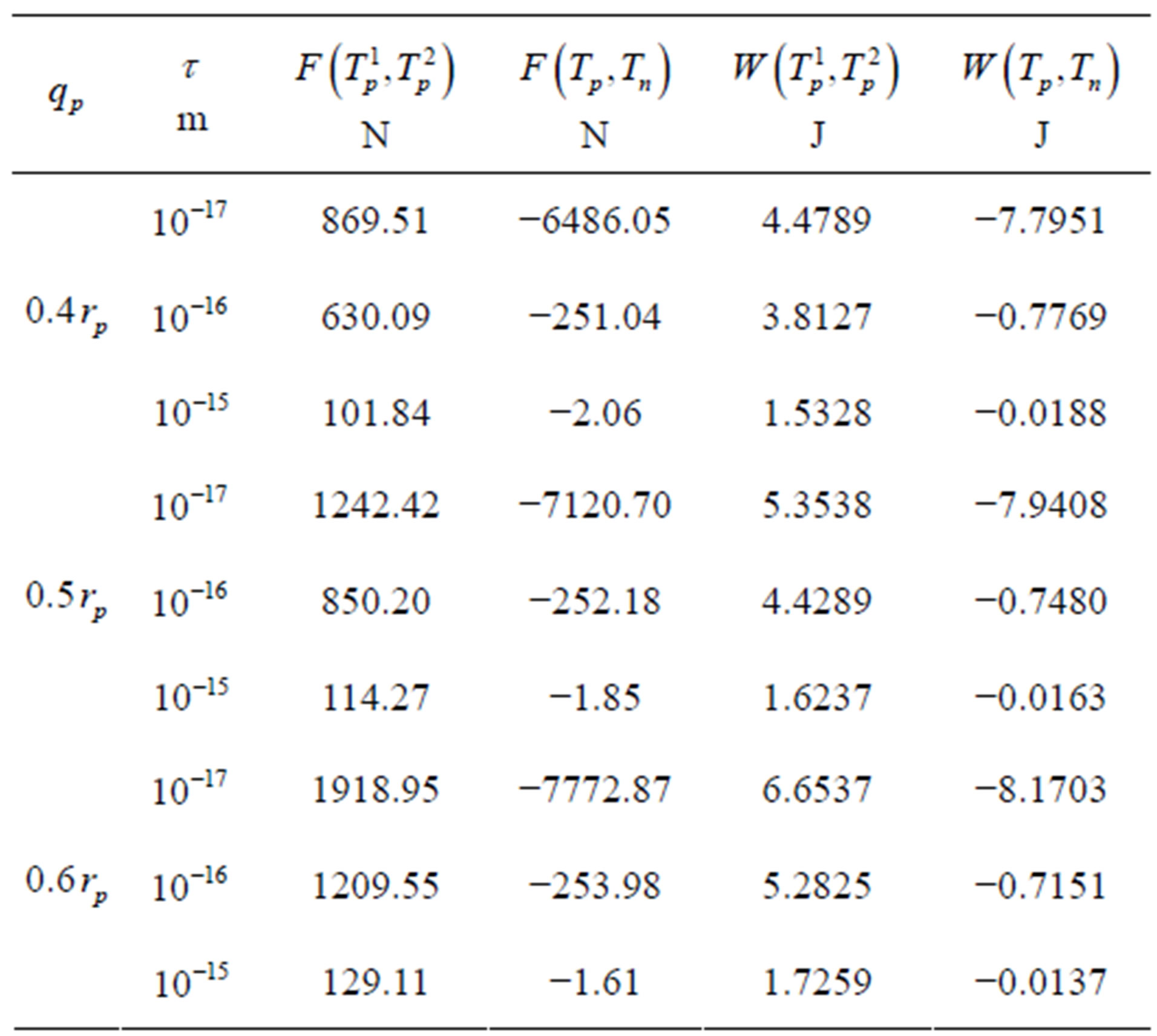
Table 2. Force and interaction energy between the tori ,
,  and Tp, Tn, remodeled respectively as point charges p, p and surface-equivalent sphere SP, torus TN.
and Tp, Tn, remodeled respectively as point charges p, p and surface-equivalent sphere SP, torus TN.
Figure 6. Plot of the interaction forces between the tori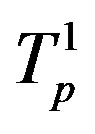 ,
,  and Tp, Tn, remodeled correspondingly as point charges p, p and surface equivalent sphere SP, torus TN depending on the distance τ between the tori for qp = 0.5rp.
and Tp, Tn, remodeled correspondingly as point charges p, p and surface equivalent sphere SP, torus TN depending on the distance τ between the tori for qp = 0.5rp.
energy increase in absolute value.
For 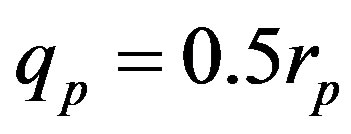 and
and 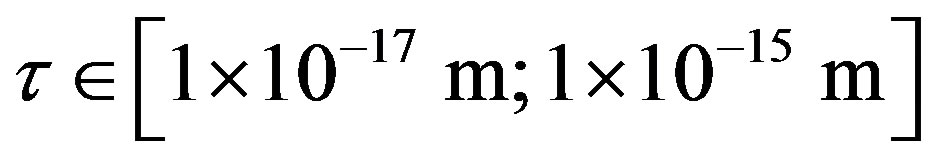 on Figure 6 are presented the curves of
on Figure 6 are presented the curves of 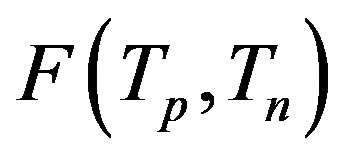 and
and  as a function of the distance between the objects.
as a function of the distance between the objects.
From the curves plotted on Figure 6 can be drawn conclusions for the short-range scope of the electrostatic force of interaction  between a proton and a neutron modeled as tori, which are similar to those when modeled as spheres (see Figure 2). For
between a proton and a neutron modeled as tori, which are similar to those when modeled as spheres (see Figure 2). For  in the order of 10−17 m, according to Tables 1 and 2, the absolute value of F in the toroidal model is an order of magnitude larger than that in the standard model.
in the order of 10−17 m, according to Tables 1 and 2, the absolute value of F in the toroidal model is an order of magnitude larger than that in the standard model.
From the values of the binding energy and the interaction force between the proton and neutron modeled as tori it follows that the nuclear interactions may have an electromagnetic nature.
4. DISCUSSION
Atomic nuclei are characterized by short-range-acting proton-neutron electrostatic attraction forces as well as long-range-acting proton-proton electrostatic repulsion forces.
The presence of a proton in immediate proximity to a neutron disrupts its neutral electrical structure. Due to its charge redistribution, it also interacts with other neutrons. Thus, the entire nucleus acts as a unified complexly interacting electrostatic system. But the short-range-acting nature and the large values of the attraction forces show that the neutrons are the binding particles in nuclear structures!
As is well known, with the exception of protium, all nuclei are made up of protons and neutrons. According to the Segre diagram [11], if A is the mass number of the nucleus, then the stability of the nucleus depends on the parameter , that is the ratio between the number of neutrons
, that is the ratio between the number of neutrons 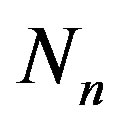 and the number of protons
and the number of protons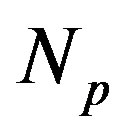 . The light nuclei for which
. The light nuclei for which 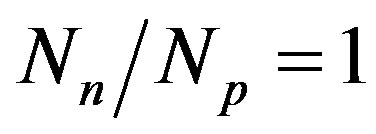 are the most stable. With the increase of the mass number A the multiplication of the electrostatic repulsion between the protons is ever more manifested and the area of stability is shifted to values
are the most stable. With the increase of the mass number A the multiplication of the electrostatic repulsion between the protons is ever more manifested and the area of stability is shifted to values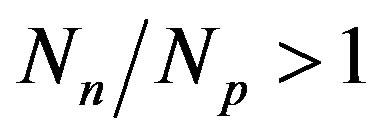 . For the heaviest nuclei, the parameter
. For the heaviest nuclei, the parameter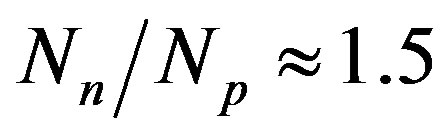 . The latter once again underlines the huge role of the neutrons for the stability of atomic nuclei.
. The latter once again underlines the huge role of the neutrons for the stability of atomic nuclei.
As can be seen from the plots on Figures 1 and 3 the proton-neutron forces of attraction are short-range-acting on distances of the order of 10−15 m. This interval covers the experimentally observed interval for short-range action of nuclear forces which is commonly accepted.
When kernels of proton and neutron penetrate each other, a huge force of repulsion occurs between them. This force can also be explained on the basis of our theory, taking into account the complex distribution of the internal charge in the nucleons. This will be done by us in the next article.
It is also interesting to note that in the standard model of the nucleus the role of the Coulomb repulsion between protons is considered as destabilizing factor for the nucleus and the “nuclear attraction forces” between protons are not taken into account. According to contemporary nuclear physics the nuclear forces are huge and significantly surpass the Coulomb repulsion forces, from which it follows that there should be no problem with nucleus stability. Since the electrostatic repulsion forces are longrange-acting they permeate the entire volume of the nucleus. Thus every proton in the nucleus interacts with all other protons and the repulsion force is multiplied as opposed to the attraction force. It turns out that the longrange action between protons is very effective. Because of that in heavy nuclei the number of neutrons is larger than the number of protons.
In more complicated nuclei very indicatively is being observed the action of the universal law of unity and struggle of opposites. Balance between the opposing forces—of attraction (short-range-acting) and repulsion (long-range-acting) leads to the unity—the presence of nuclei of chemical elements.
It is hardly the case that in the nucleus the short-rangeacting electrostatic forces of attraction are combined with short-range-acting forces of a completely different nature —the so-called nuclear forces.
5. CONCLUSIONS
Based on our results for the short-range-acting character of the proton-neutron electrostatic forces the basic properties of nuclear forces can be explained. Eloquent example is the property of “saturation of nuclear forces”. It is important to mention that the electromagnetic forces between two nucleons depend on whether they spin in the same or opposite directions, that is on the orientation of their spins.
The binding energies for the nuclei of deuterium—
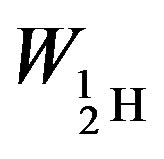 = −3.5642 × 10−13, tritium—
= −3.5642 × 10−13, tritium—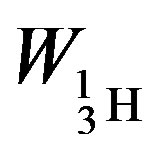 = −13.5895 ×
= −13.5895 ×
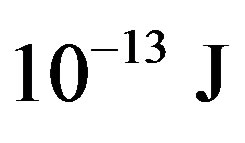 , helium-3—
, helium-3—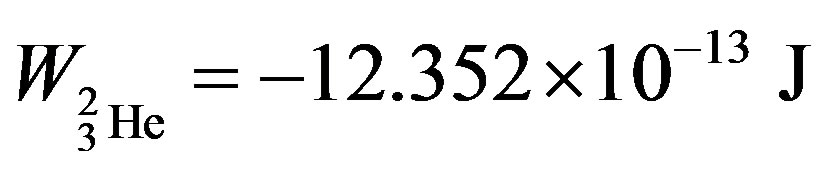 and helium-4—
and helium-4—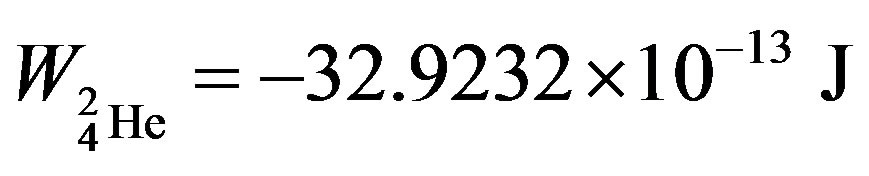 , obtained in [6] are known and commonly accepted values. The binding energy—one of the most important nuclear characteristics has been obtained from solely electrostatic considerations. We believe this fact cannot be due to an insignificant coincidence.
, obtained in [6] are known and commonly accepted values. The binding energy—one of the most important nuclear characteristics has been obtained from solely electrostatic considerations. We believe this fact cannot be due to an insignificant coincidence.
In conclusion, we can assume that the nuclear forces have an electromagnetic nature.
6. ACKNOWLEDGEMENTS
The authors express their gratitude to the computer specialist Stefan Bozhkov, who with the help of Wolfram Mathematica 7.0 performs the calculations in this article. The results of the present studies are published with the financial support of the Fund for Scientific Research with the Ministry of Education and Science under contract DTC No. 02/35.
REFERENCES
- Hofstadter, R. (1956) Electron scattering and nuclear structure. Reviews of Modern Physics, 28, 213. doi:10.1103/RevModPhys.28.214
- Sardin, G. (1999) Fundamentals of the orbital conception of elementary particles and of their application to the neutron and nuclear structure. Physics Essays, 12, 204. doi:10.4006/1.3025378
- Mohr, P., Taylor, B. and Newell, D. (2008) CODATA recommended values of the fundamental physical constants: 2006. http://arxiv.org/abs/0801.0028
- Kolikov, K., Ivanov, D., Krustev, G., Epitropov, Y. and Bozhkov, S. (2012) Electrostatic interaction between two conducting spheres. Journal of Electrostatics, 70, 91-96. doi:10.1016/j.elstat.2011.10.008
- Kolikov, K., Ivanov, D. and Krustev, G. (2012) Electromagnetic nature of the nuclear forces and a toroid model of nucleons in atomic nuclei. Natural Sciense, 4, 47-56. doi:10.4236/ns.2012.41008
- Kolikov, K., Ivanov, D. and Krustev, G. (2012) Electromagnetic nature of the nuclear forces and toroid structure of the deuteron and triton. Natural Sciense, 4, 123-130. doi:10.4236/ns.2012.42018
- Sick, I. (2003) On the rms-radius of the proton. Physics Letters B, 576, 62-67.
- Standard model. http://en.wikipedia.org/wiki/Standard_Model.
- Standard model. University of Tennessee. http://electron6.phys.utk.edu/phys250/modules/module%206/standard_model.htm
- Fehling, D. The standard model of particle physics: A Lunchbox’s guide. http://www.pha.jhu.edu/~dfehling/
- http://www.meta-synthesis.com/webbook/33_segre/segre.html

