ABSTRACT

In this paper, we apply the differential transformation method to high-order nonlinear VolterraFredholm integro-differential equations with separable kernels. Some different examples are considered the results of these examples indicated that the procedure of the differential transformation method is simple and effective, and could provide an accurate approximate solution or exact solution.

1. INTRODUCTION

Integral and integro-differential equations play an important role in characterizing many social, biological, physical and engineering problems; for more details see [1-3] and references cited therein. Nonlinear integral and integro-differential equations are usually hard to solve analytically and exact solutions are rather difficult to be obtained. Many numerical methods have been studied such as the Legendre wavelets method [4], the Haar functions method [5,6], the linearization method [7], the finite difference method [8], the Tau method [9,10], the hybrid Legendre polynomials and block-pulse functions [11], the Adomian decomposition method [12,13], the Taylor polynomial method [14-16] and the collocation approach (for linear case) [17].

In this paper, we will use the differential transform method (DTM) to solve a high-order nonlinear VolterraFredholm integro-differential equation given by

,(1.1)

with the initial conditions

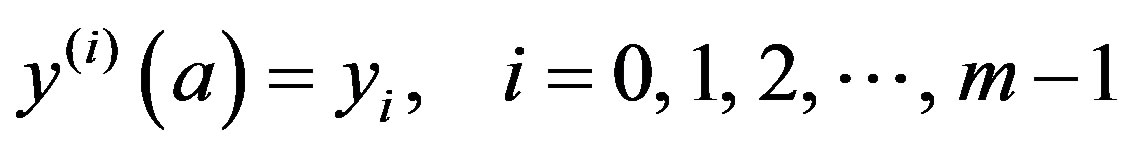,(1.2)

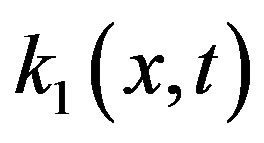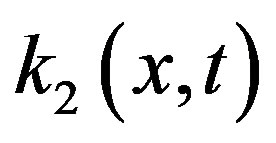where are constant values, , , and with are known functions that have suitable derivatives on an interval, 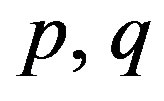are integers and 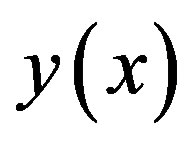is the unknown function. The concept of the DTM was first proposed by Zhou [18] and has been used to solve both linear and nonlinear initial value problems, in electric circuit analysis. The DTM is a distinguished form of the Taylor series method, which requires symbolic computation of the necessary derivatives of the data functions. Taylor polynomials method is computationally tedious for high orders. DTM leads to an iterative procedure for obtaining an analytic series solution of functional equations. It is possible to solve differential equations, difference equations, differential difference equations, fractional differential equations, pantograph equations, integral equations and integro-differential equations by using this method.

In this work, we apply the DTM to solve high-order nonlinear Volterra-Fredholm integro-differential equations with separable (degenerate) kernels; i.e. 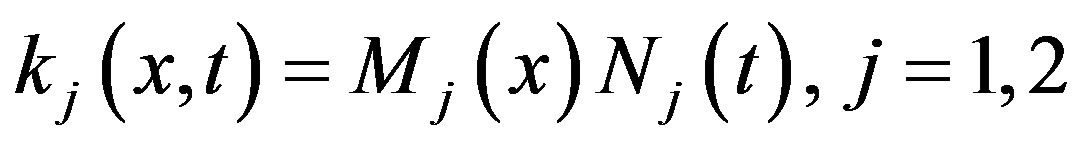. Five different problems are solved to make clear the application of the DTM on such class of integro-differential equations. We introduce theorems in general forms to be able to apply any kind of integro-differential in any order.

2. DIFFERENTIAL TRANSFORM METHOD

The basic definition and the fundamental theorems of the differential transformation and its applicability for various kinds of differential and integral equations are given in [19-22]. For convenience of the reader, a review of differential transformation will be presented here. The transformation of the kth derivative of a function in one variable is as follows.

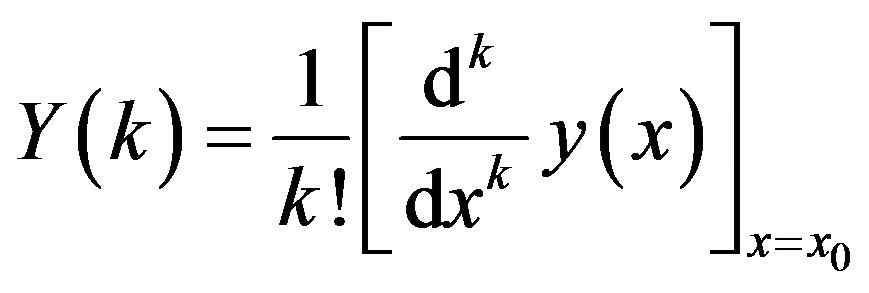, (2.1)

and the inverse transformation is defined by

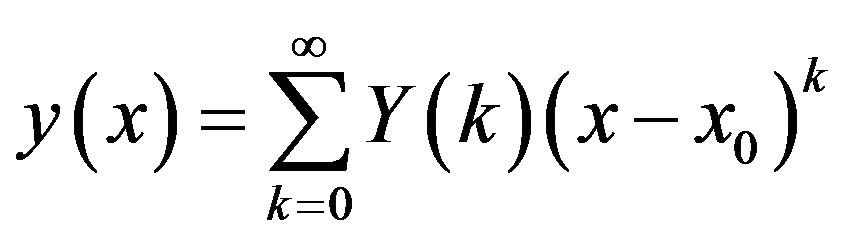. (2.2)

The following theorems can be deduced from eqs.2.1 and 2.2.

Theorem 1. If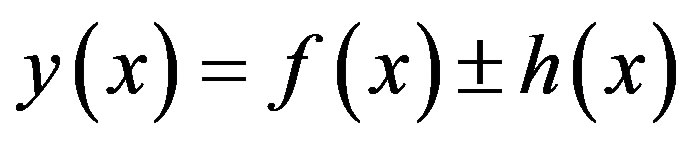, then.

Theorem 2. If, then, where is a constant.

Theorem 3. If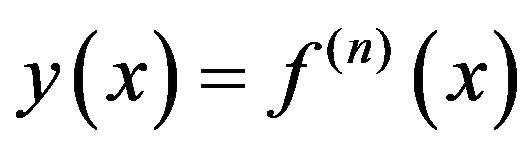, then.

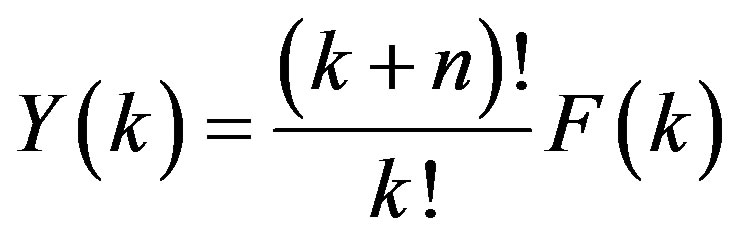Theorem 4. If, then.

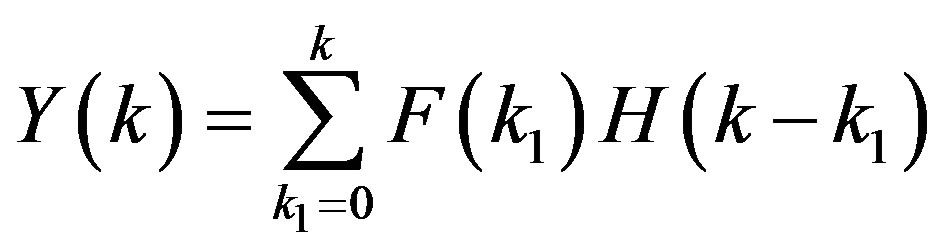Theorem 5. If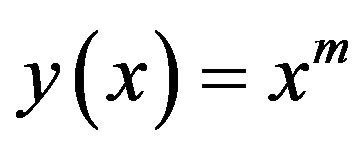, then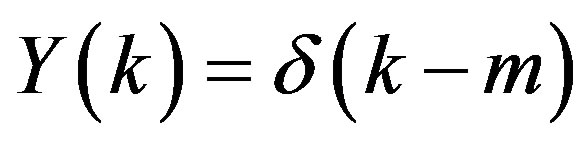, where.

Theorem 6. If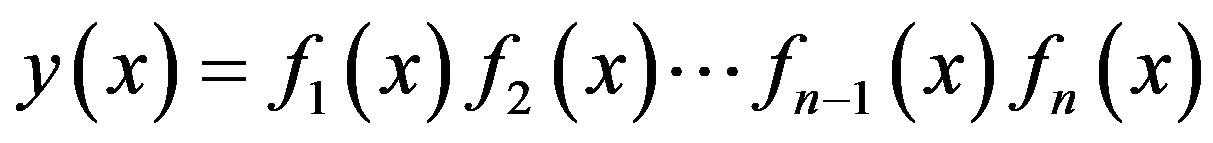, then

.

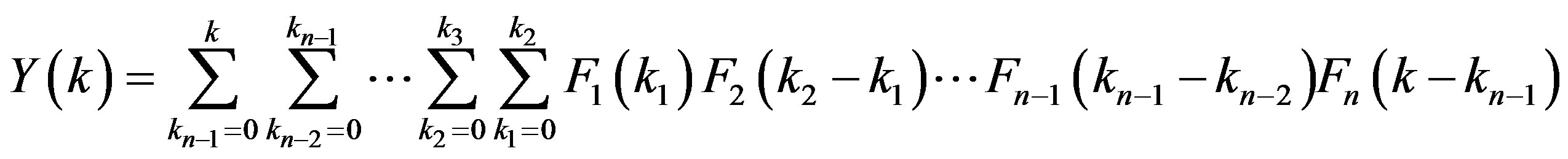Theorem 7. If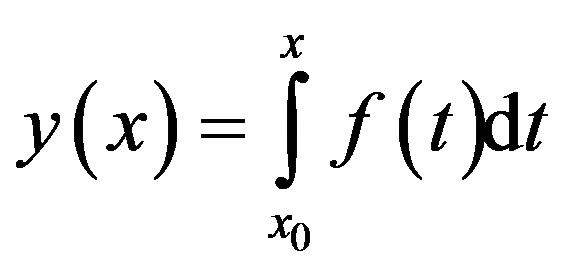, then.

Theorem 8. If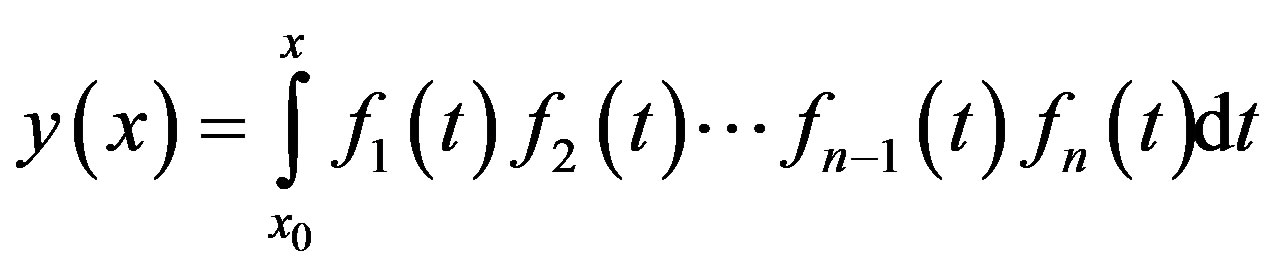, then

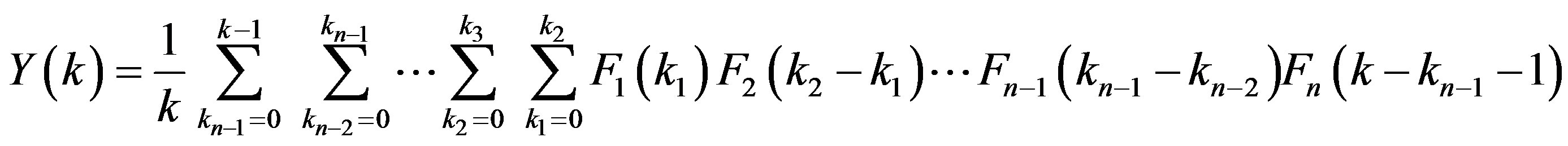
Theorem 9. If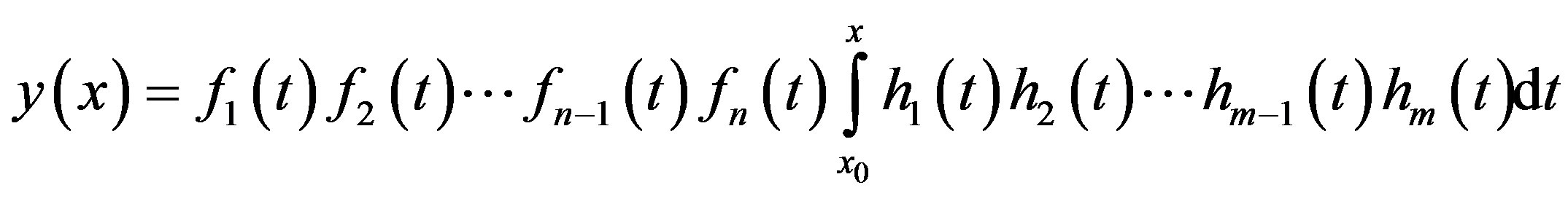, then

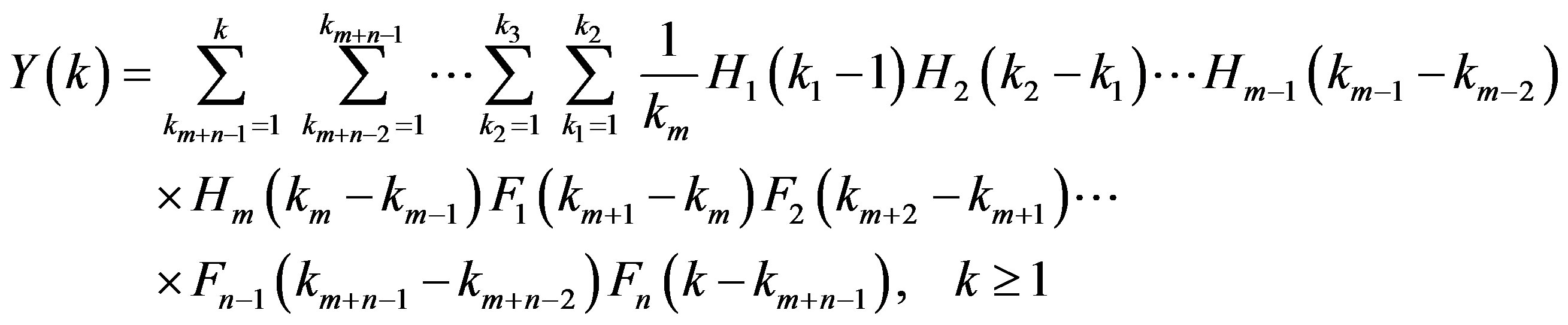
The following relation is quite useful in the solution of Fredholm integrals; it can be obtained from theorem 8 and eq.2.2

(2.3)

Also, we introduce the differential transformations for some basic functions, which are encountered in the following examples. The proof of these differential transforms follows directly from the definition (2.1) and (2.2) and the operations of the differential transformation given in the above theorems.

• If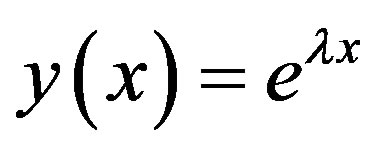, then.

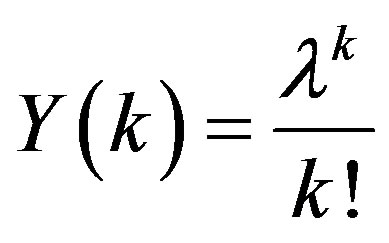• If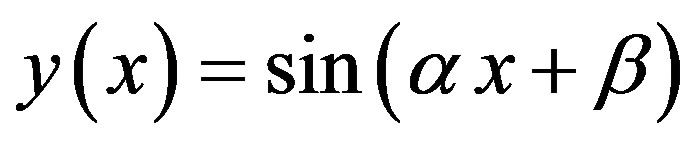, then

.

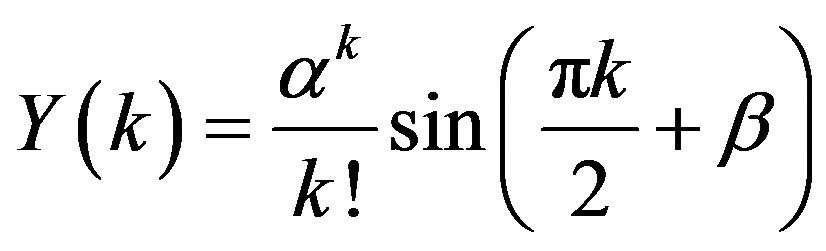• If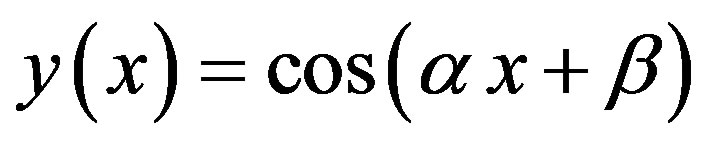, then

.

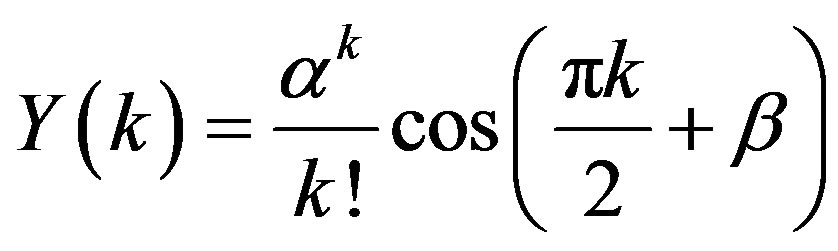3. APPLICATIONS AND NUMERICAL RESULTS

In this section, we implement the DTM on some different examples.

Example 3.1. Consider the nonlinear Volterra-Fredholm integro-differential equation

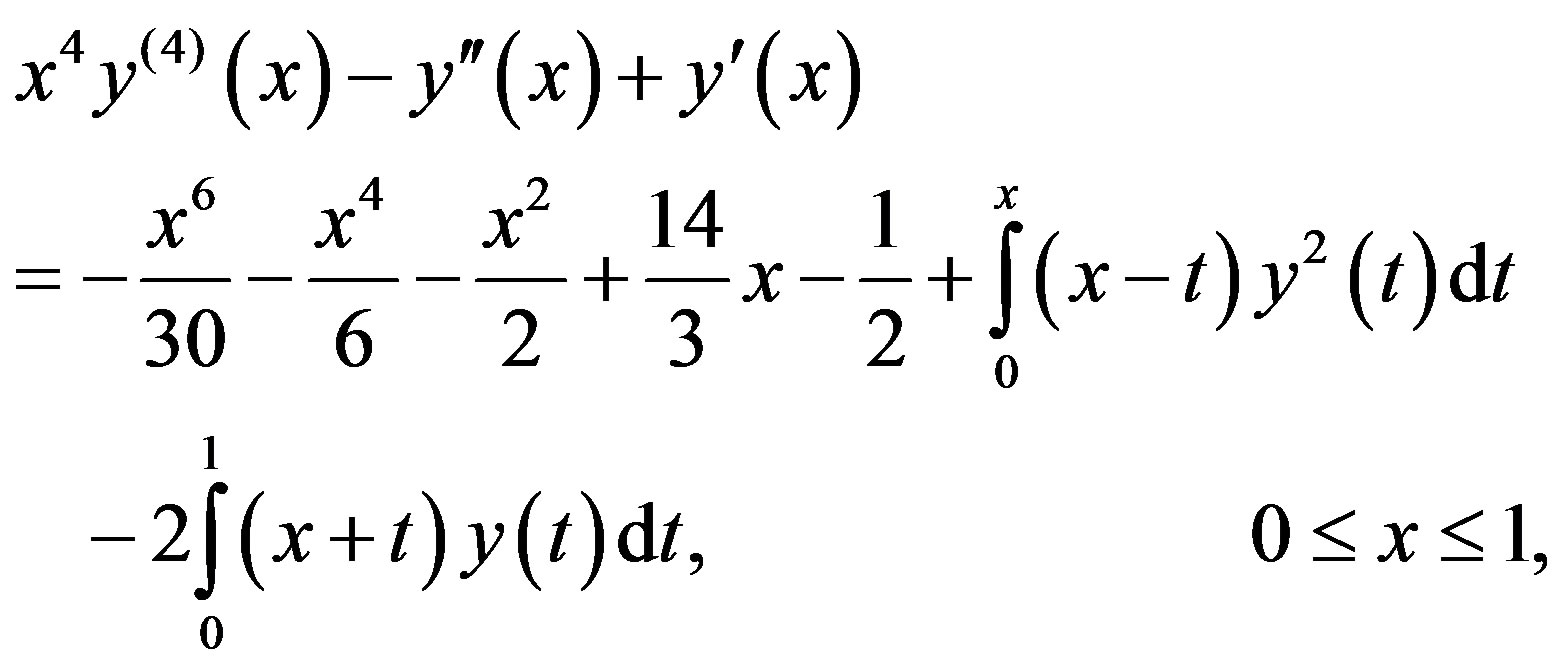(3.1)

with the initial conditions

(3.2)

Application of the differential transform to eq.3.1 gives

(3.3)

where.

Substitute 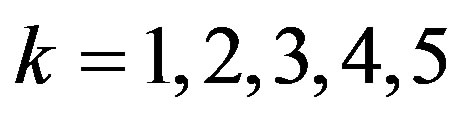and 6 into eq.3.3, one can get the following relations

,

,

,

,

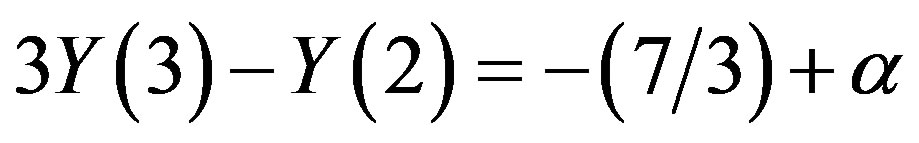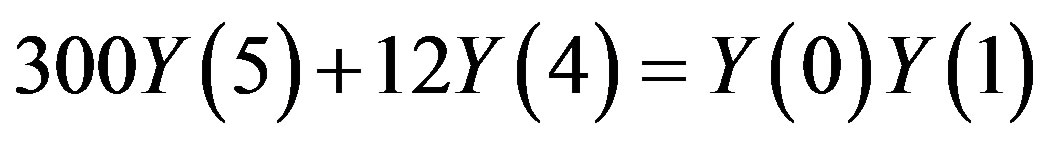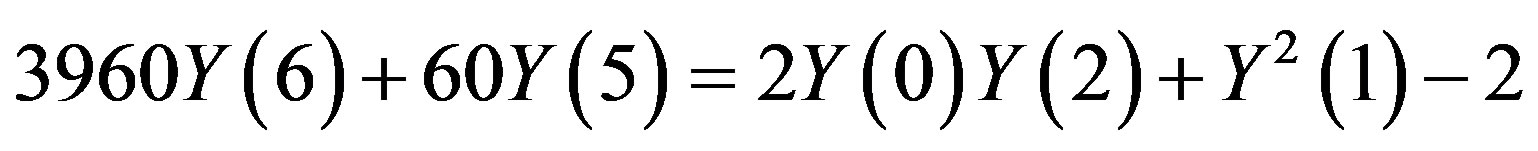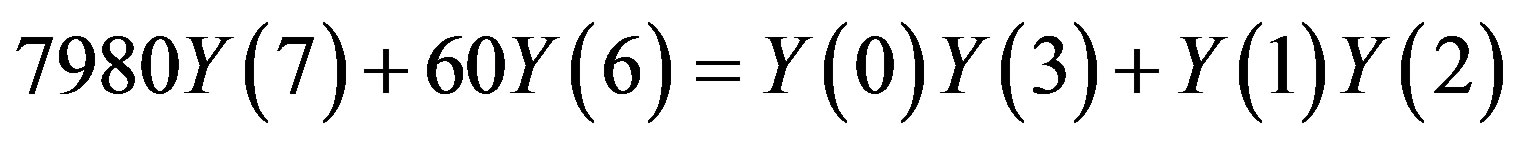and

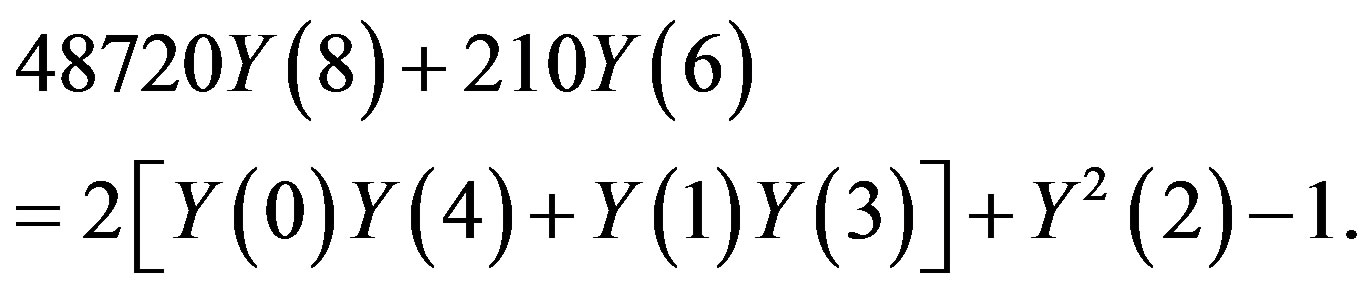
Also, for 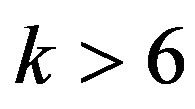in eq.3.3, the following recurrence relation can be obtained

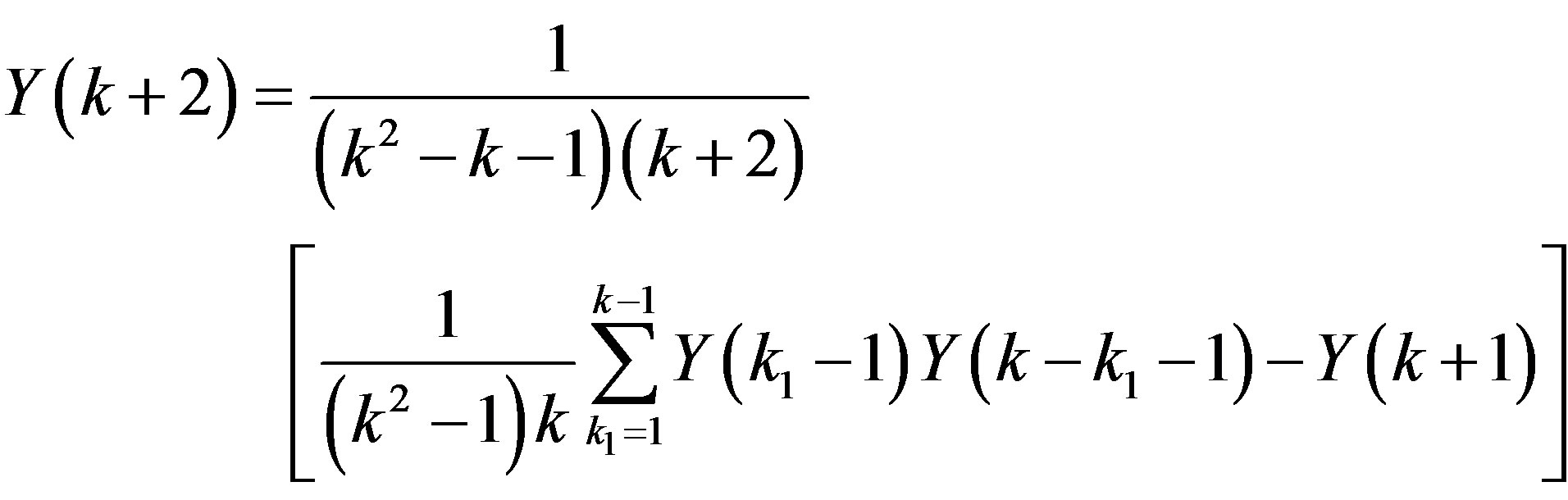
The initial conditions in eq.3.2 is transformed by using (2.1) to

Consequently, from the above recurrence relations we can easily find that.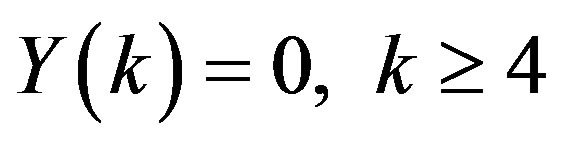

Hence by using eq.2.2, the solution of the integrodifferential eq.3.1 with its initial conditions (3.2) is obtained to be

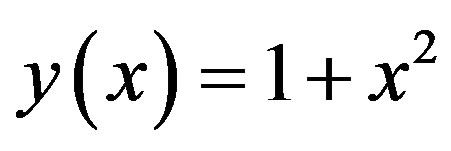which is the exact solution.

Example 3.2. Consider the integro-differential equation

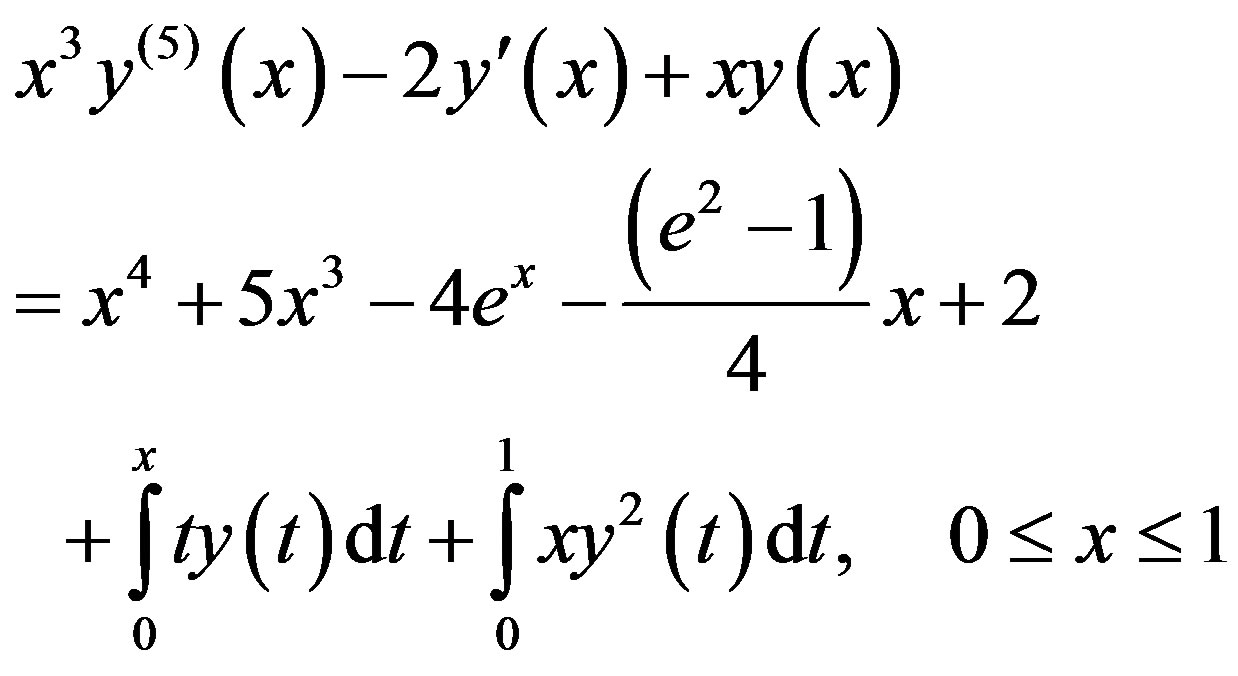(3.4)

with the initial conditions

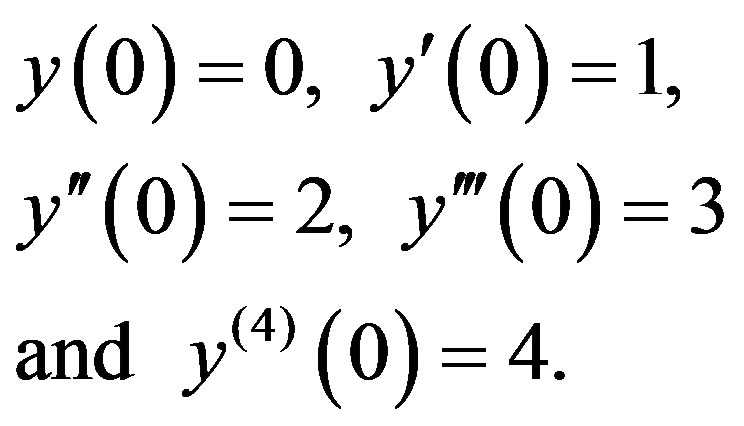(3.5)

The differential transformation of eq.3.4 and the initial conditions (3.5) are

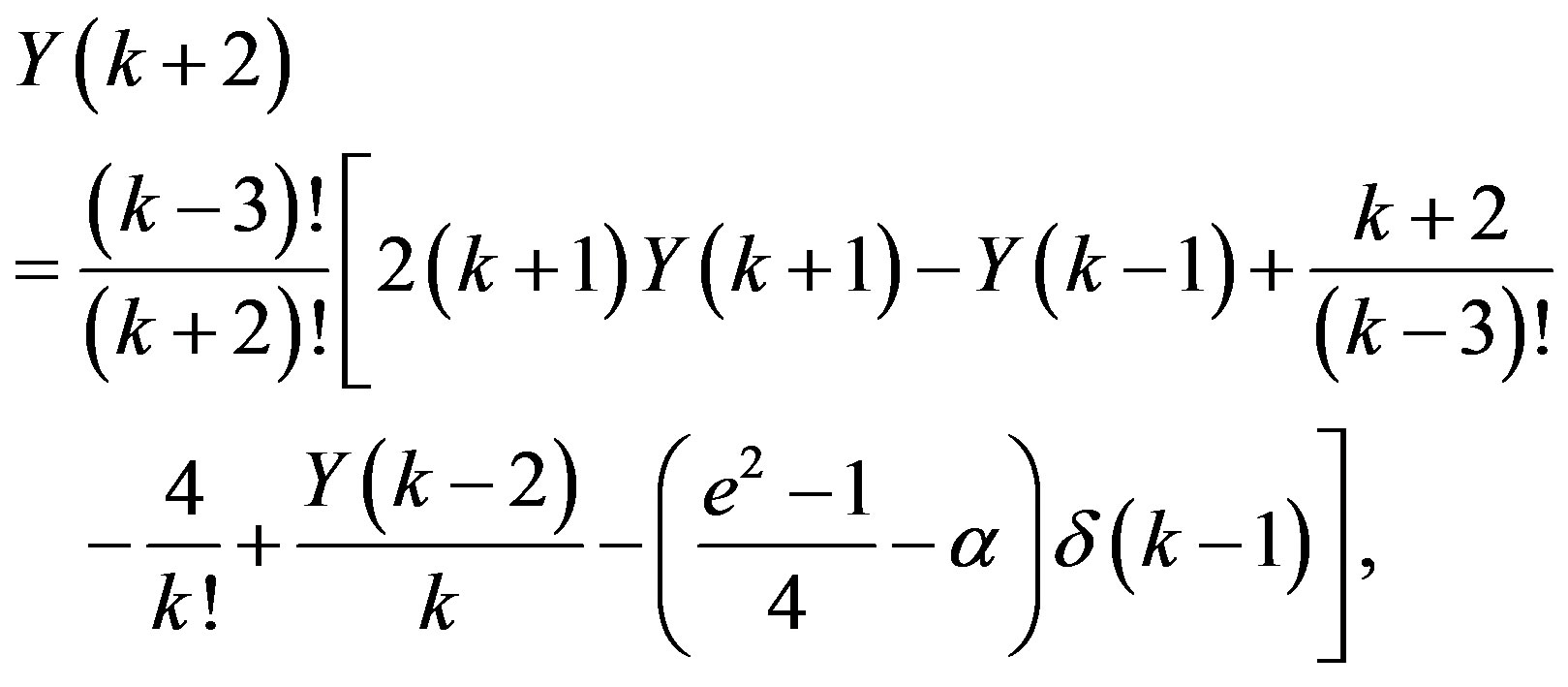(3.6)

where, and

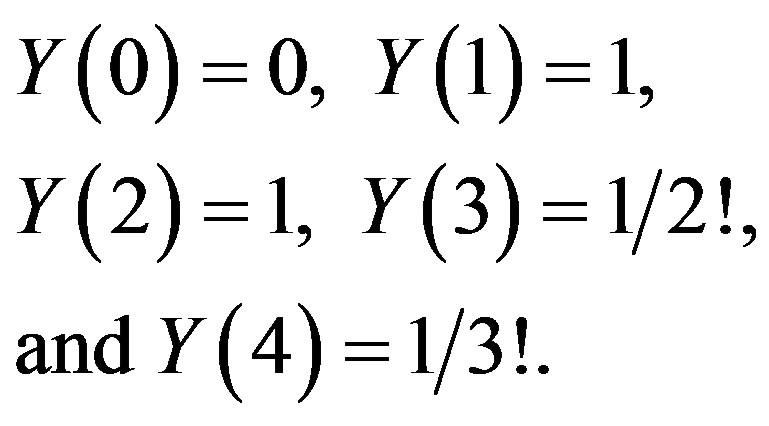(3.7)

Utilizing the recurrence relation (3.6) and the transformed initial conditions (3.7), we can obtain

Substitute 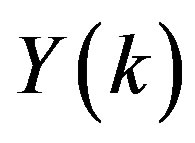into eq.2.2 to obtain the solution of the nonlinear Volterra-Fredholm integro-differential equation in this example

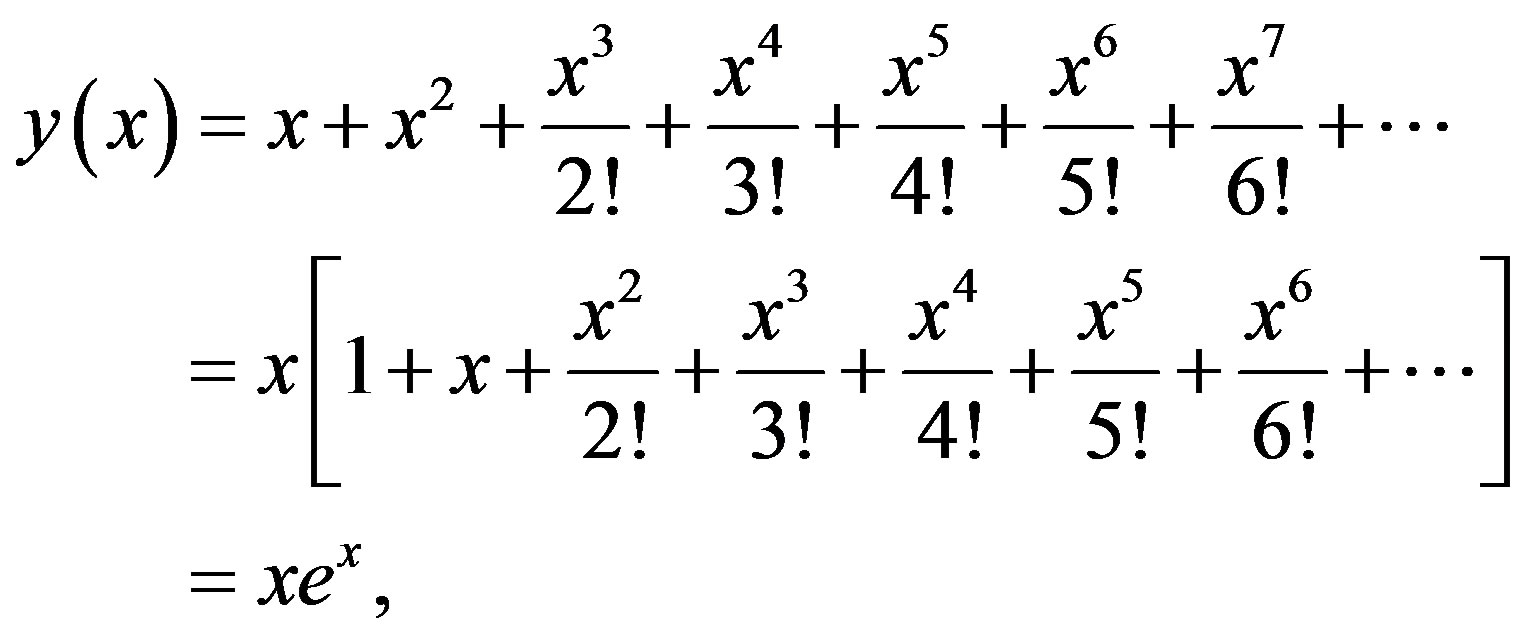
which is its exact solution.

Example 3.3. Consider the following sixth order Volterra-Fredholm integro-differential equation

(3.8)

with the initial conditions

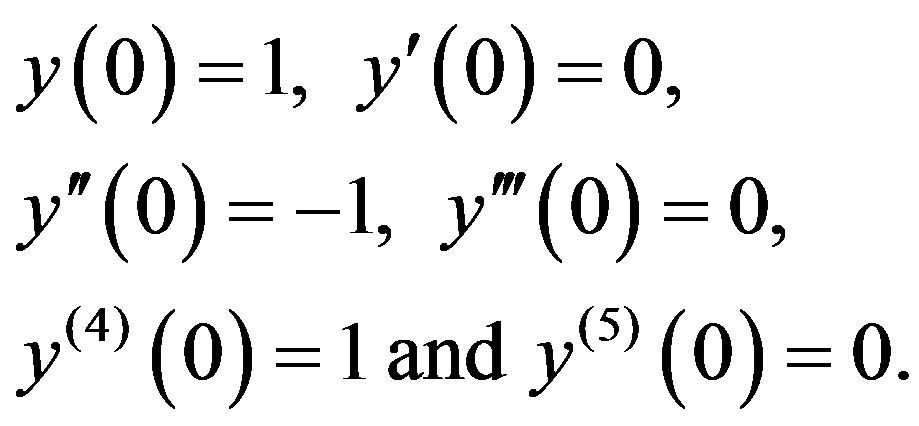(3.9)

The differential transformation of eq.3.8 and the initial conditions (3.9) are

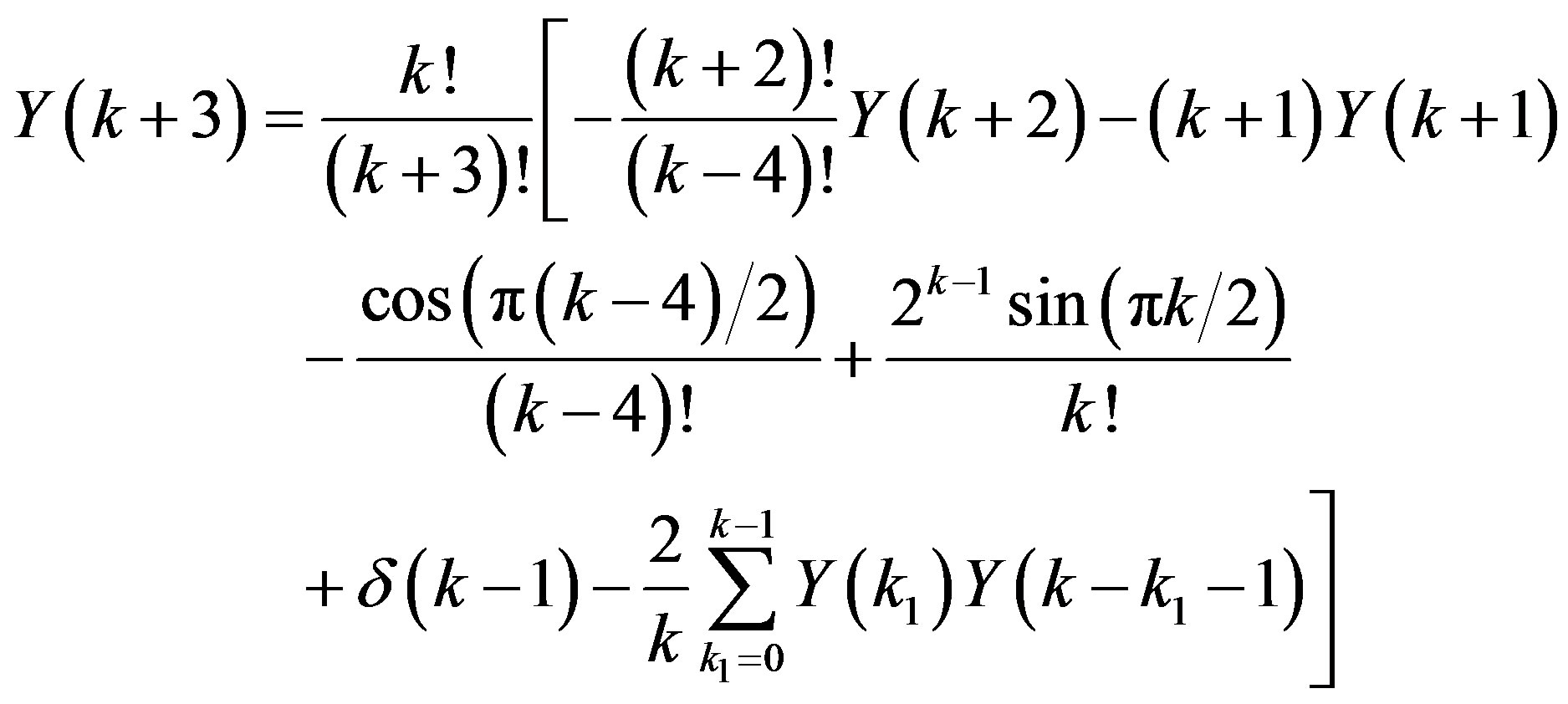(3.10)

and

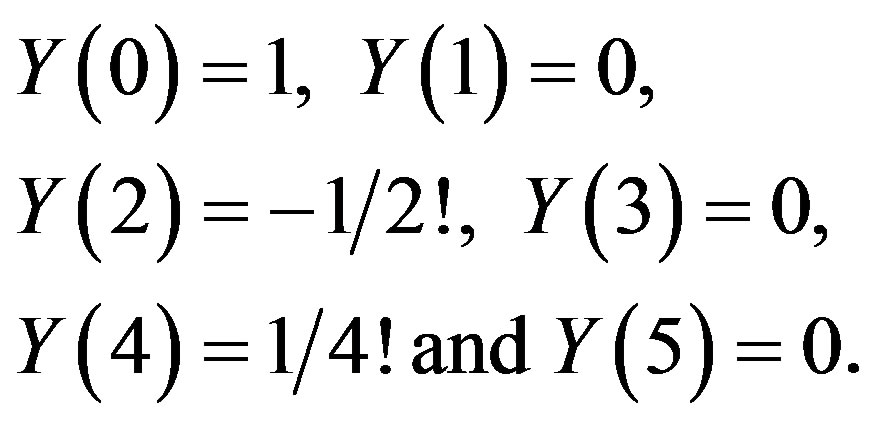(3.11)

Note that, in eq.3.10 the first and third terms in left hand side vanish as.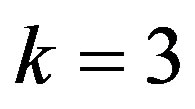

Utilizing the recurrence relation (3.10) and the transformed initial conditions (3.11), we can get

Therefore, the solution of eq.3.8 is given by

which is the exact solution.

Example 3.4. Let us consider the nonlinear VolterraFredholm integro-differential equation [23]

(3.12)

with the initial conditions

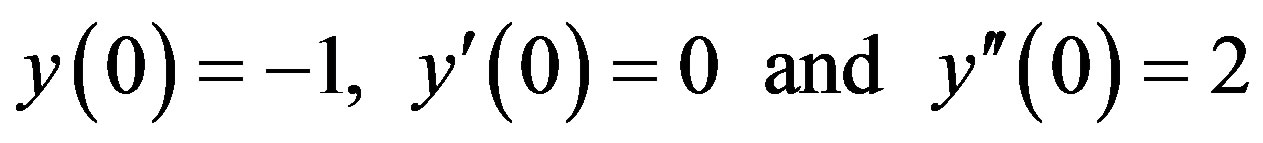(3.13)

The differential transformation of this equation and its initial conditions are

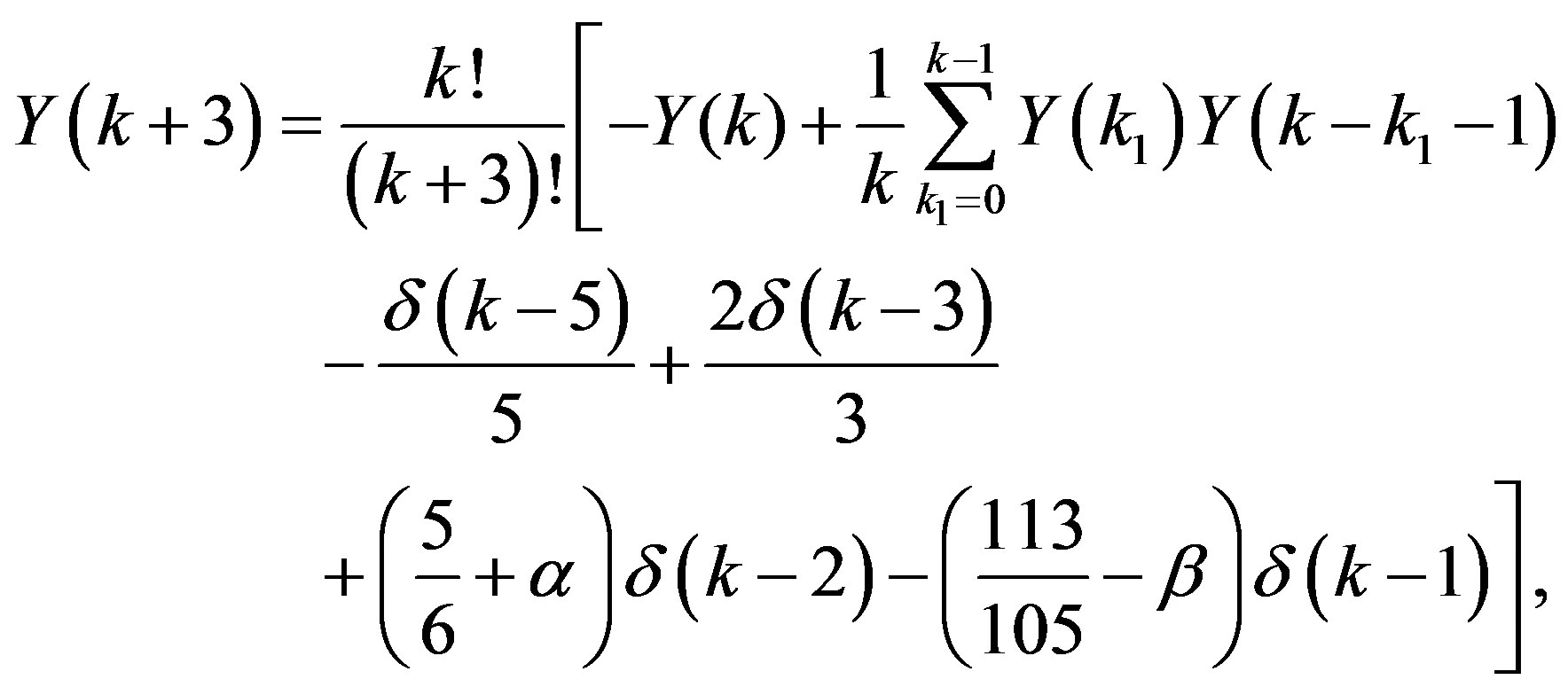(3.14)

where

, (3.15)

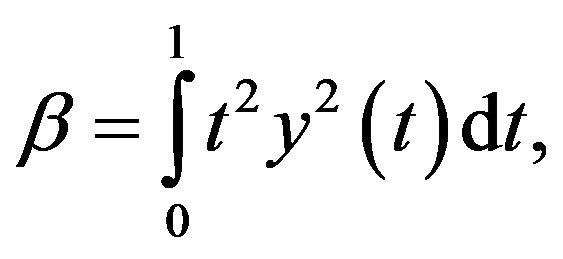(3.16)

and

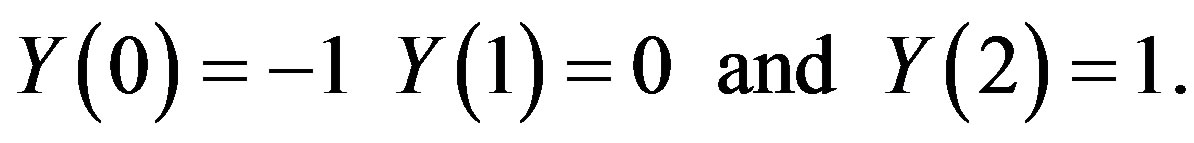(3.17)

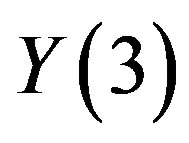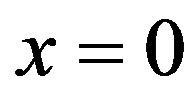To obtain, put into eq.3.12 and utilizing the transformation (2.1), hence. 

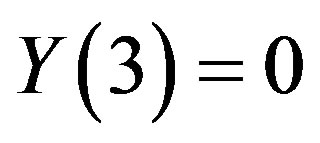Substitute and 5 into eq.3.14, one can get the following relations

, (3.18)

, (3.19)

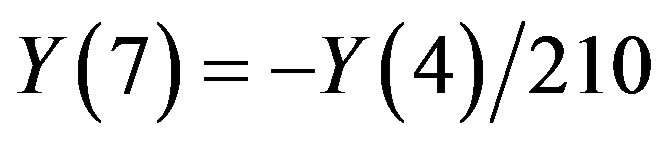, , and .

Also, for in eq.3.14, the following recurrence relation can be obtained

.

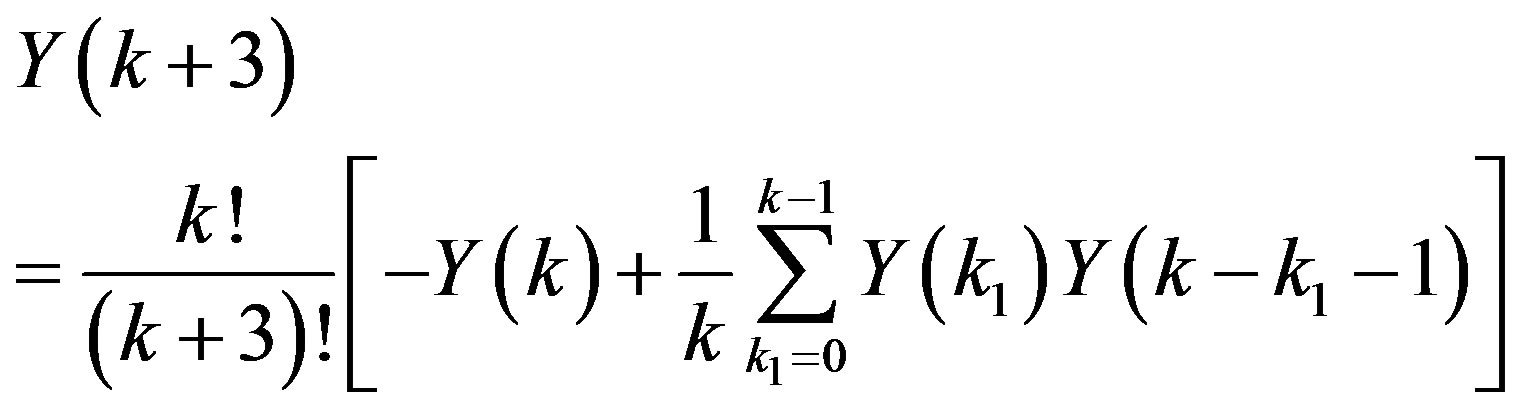Utilizing eqs.2.3, 3.15 and 3.16, it can be shown that the following equalities hold for 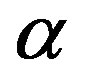and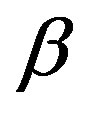

, (3.20)

, (3.21)

where 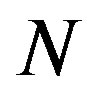is a suitably large integer that represents the number of terms to be chosen. Solving eqs.3.20 and 3.21 with eqs.3.18 and 3.19 by taking 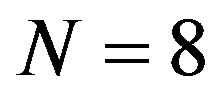terms, one can obtain the following results

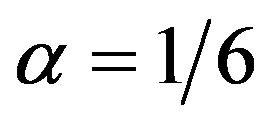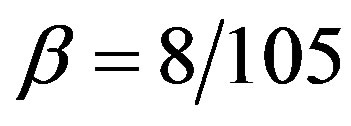, , and.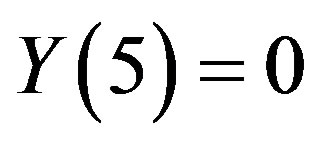

Hence one can get all the missing coefficients of 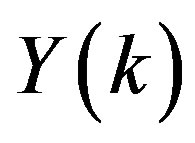of the expansion for the unknown function, that is

which is the exact solution.

Example 3.5. Consider the nonlinear Volterra-Fredholm integro-differential equation

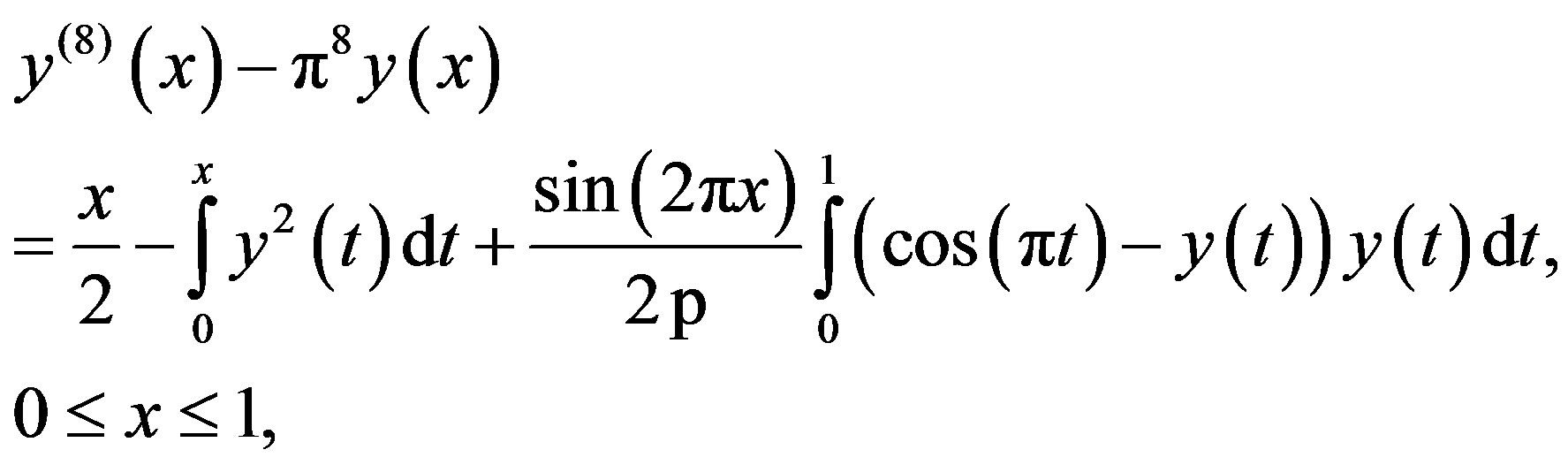(3.22)

with the initial conditions

(3.23)

Eq.3.22 can be written in the following form

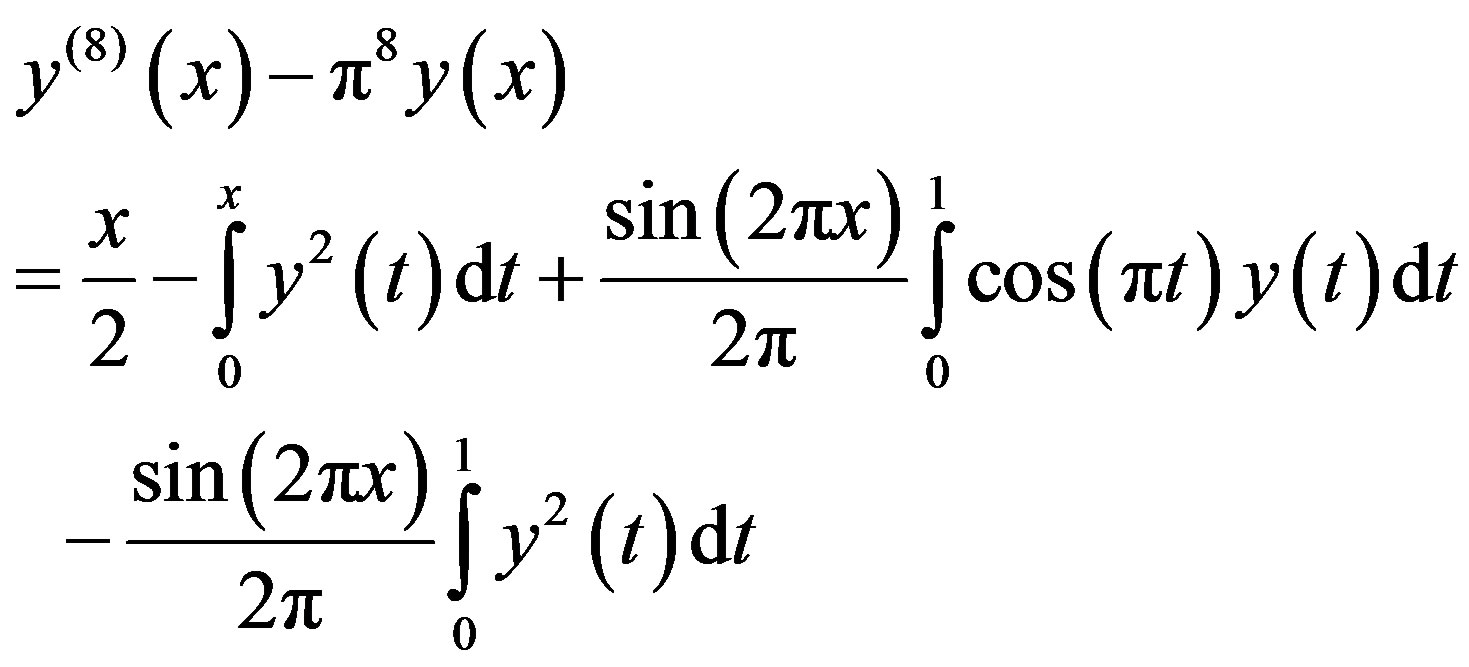(3.24)

The differential transformation of the eq.3.24 gives the following recurrence relation

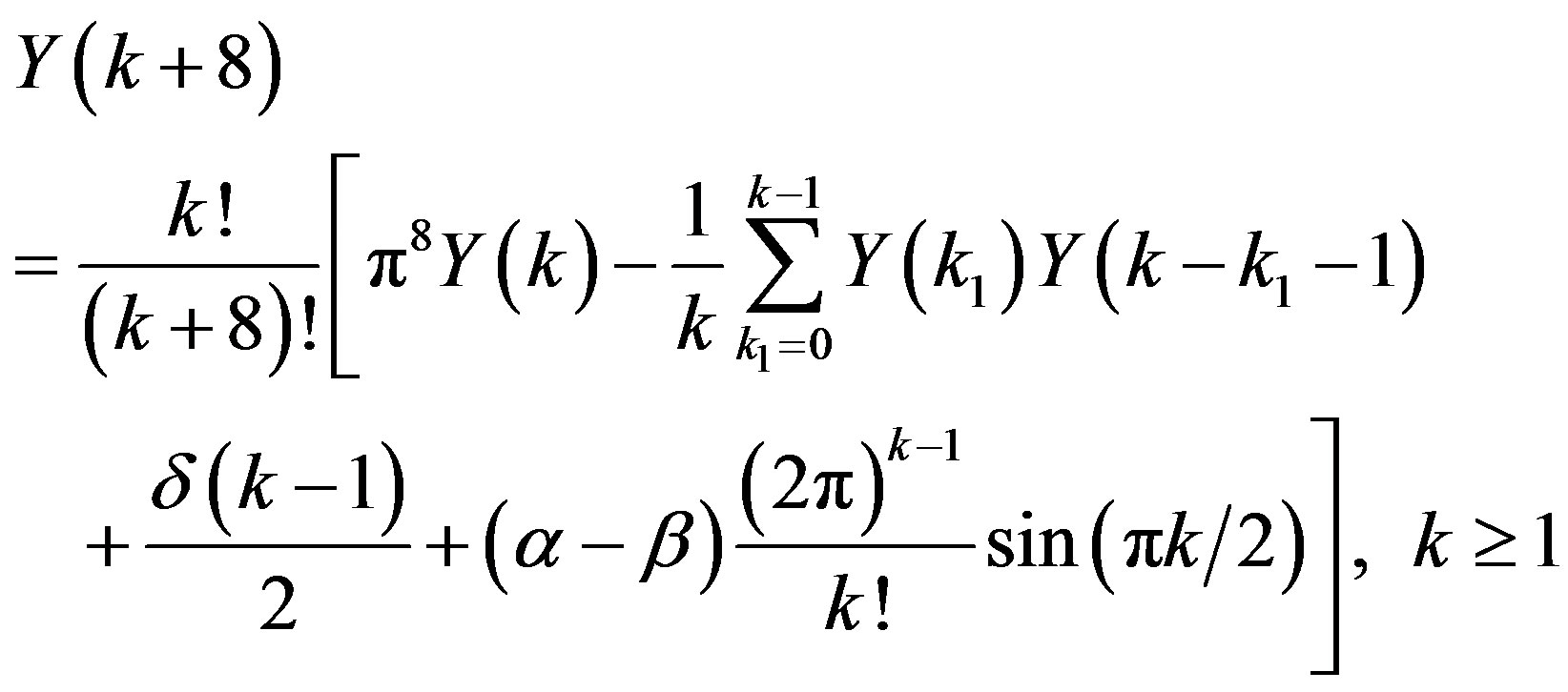(3.25)

where

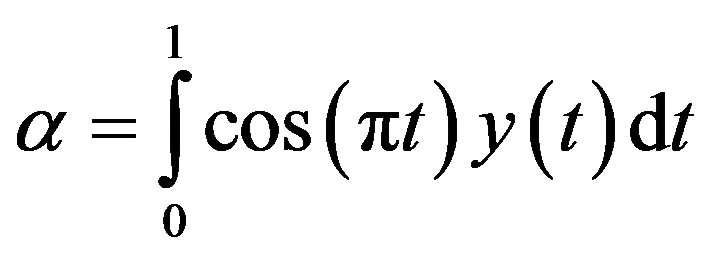, and 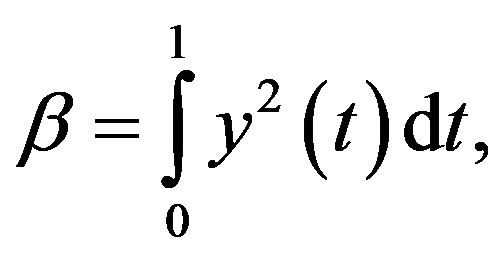(3.26)

The initial conditions in eq.3.23 are transformed by using eq.2.1 as follows

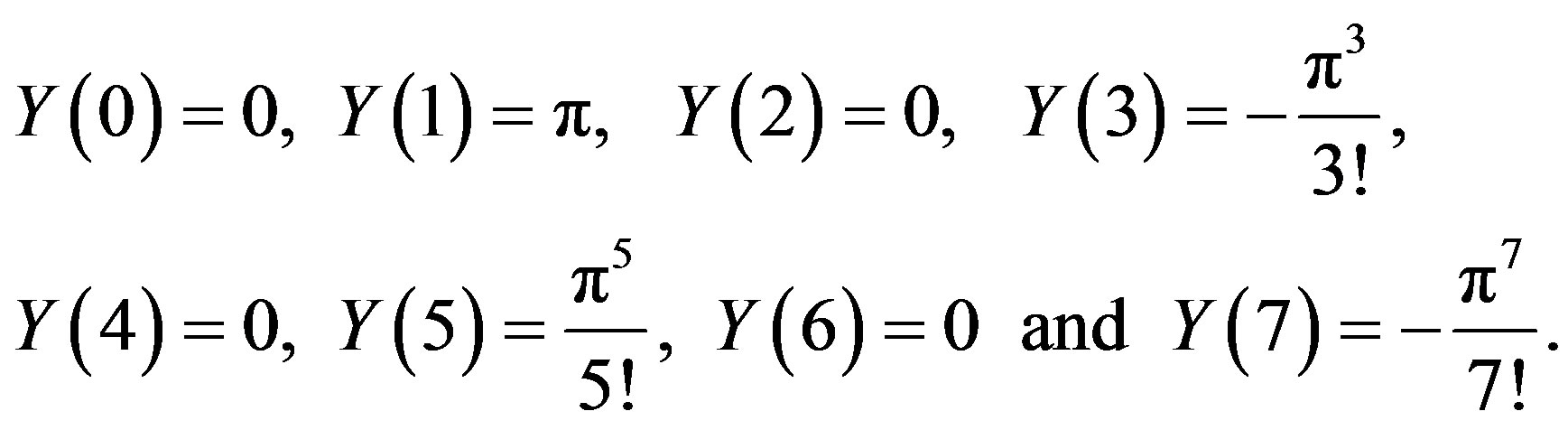(3.27)

Also, for obtaining, put into eq.3.22 and utilize (2.1), one can get

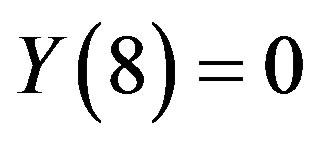. (3.28)

By using the transformed initial conditions in (3.27) and (3.28) and the recurrence relation in eq.3.25, the series solution is then evaluated for up to

(3.29)

Utilizing eqs.2.3 and 3.26, one can show

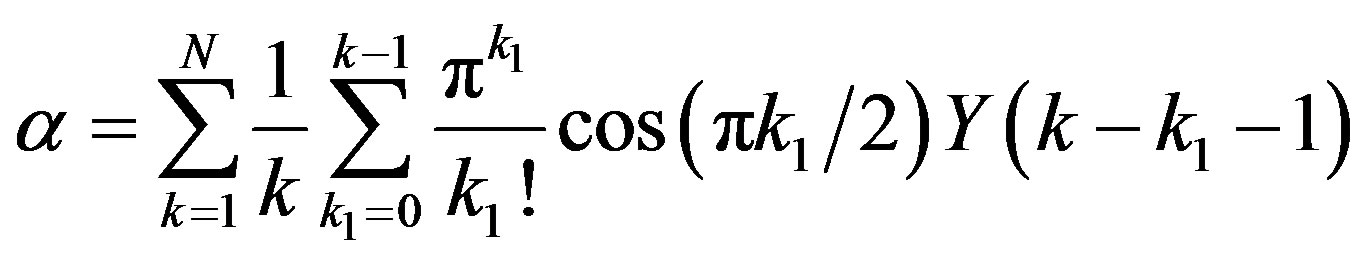, (3.30)

, (3.31)

where 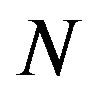is a sufficiently large integer. Solving eqs. 3.30 and 3.31 by taking 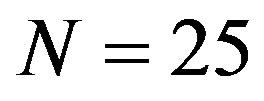terms, we can get, and.

The unknown function is evaluated by using eq.3.29 for these values of 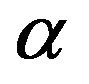and. The numerical results are shown in Table 1 with comparison to the exact solution.

4. CONCLUSION

In this work, the differential transform method for the solution of high-order nonlinear Volterra-Fredholm integro-differential equations is successfully implemented. The present method reduces the computational difficulties of other traditional methods and all the calculation can be made simple manipulations. The accuracy of the obtained solution can be improved by taking more terms in the solution. In many cases, the series solution obtained with differential transform method can be written in exact closed form.

REFERENCES