Natural Science
Vol.4 No.2(2012), Article ID:17332,4 pages DOI:10.4236/ns.2012.42021
Research and application of sidewall stability prediction method based on analytic hierarchy process and fuzzy integrative evaluation method
![]()
Hailaer Exploration and Development Headquarters of Daqing Oilfield Co., Ltd, Daqing, China; *Corresponding Author: xcxcxc1432@163.com
Received 20 December 2011; revised 22 January 2012; accepted 31 January 2012
Keywords: Instability of Sidewall; Forecast; Fuzzy Integrative Evaluation Method; Analytic Hierarchy Process; Maximum Subjection Principle
ABSTRACT
As a difficult problem, sidewall instability has been beset drilling workers all the time. Not only does it cause huge economic losses, but also it determines the success or failure of drilling engineering. Due to complex relationship between various factors which influence sidewall stability, it hasn’t been found a widely applied method to predicate sidewall stability so far. Therefore, in order to formulate corresponding measures to ensure successful drilling, searching for a kind of better method to forecast sidewall stability before drilling becomes an imperative and significant topic for drilling engineering. On the basis of traditional sidewall stability analytical method, we have put forward the Fuzzy Comprehensive Evaluation Method to forecast sidewall stability regulation using physico-chemical performance parameters of the clay mineral. This method has been improved by introducing the Analytic Hierarchy Process (AHP) and the Maximum Subjection Principle in the application process. After introducing Analytic Hierarchy Process to identify weight, and Maximum Subjection Principle to obtain evaluation results, it has reduced the influence of human factors and enhanced the accuracy of the fuzzy evaluation results. The application in Hailaer Area indicates that this method can predict sidewall stability of gas-oil well with high credibility and strong practicability.
1. INTRODUCTION
Sidewall stabilization is a key technology as well as a big problem in the drilling process. Sidewall instability will cause great difficulties to the drilling engineering, such as shrinking diameter, sticking of drilling rod, borehole enlargement and lowering cementing job quality. These accidents not only extend the drilling cycle, but also raise the drilling cost [1-3]. From the angle of reducing the drilling cost and speeding up exploration and development of oil and gas, further researching sidewall stability of clay shale has an extremely vital significance. For a long time, many domestic and foreign scholars devote to the research of sidewall stabilization, but so far there is no way to evaluate accurately the stability condition of the sidewall. This article elaborates the comprehensive use of analytic hierarchy process and fuzzy comprehensive evaluation method for forecasting sidewall stability which is scientific and reasonable from two aspects of theory and practice.
2. ANALYTIC HIERARCHY PROCESS
Analytic Hierarchy Process (AHP) is a qualitative and quantitative decision analysis method. It is a kind of process that the decision-maker makes decision thinking process of complex system modeling and quantification. When we use this method, the complex problem will be decomposed into some levels or several factors. The comparison and simple calculation between different levels or various factors can show the weight of different factors for providing the basis of decision-making, controlling or predicting.
3. ANALYTIC HIERARCHY PROCESS DETERMINES WEIGHT STEPS
Weight plays a critical role in the fuzzy comprehensive evaluation. The conventional method that determines the weights by experience can not assign accurately the weight size for each factor sometimes, especially when there are many factors and the relationship between the factors is not clear. So using the analytic hierarchy process to determine weights of factors can reduce the interference of personal factor and make weight distribution more reasonable [4].
3.1. Structuring Judgment Matrix
Showing the corresponding importance degree level of paired solutions by the form of the ratios of paired importance degree is an important characteristic of AHP. For a certain standard, making its n schemes to paired comparison, and grading them according to the degree of importance. Remembering it as ratio of importance of the first factor i and factor j. Table 1 displays nine importance grades and corresponding assignments that Saaty offers. Structuring a matrix according to the paired comparison results is called judgment matrix.
In order to distil useful information from judgment matrix, to understand of the regularity of things and provide a scientific basis for decision-making, the weight vector of judgment matrix needs to be calculated. For the judgment matrix which meets the consistency condition, we can work out the corresponding feature vector of the maximum eigenvalue as the weight value after normalizing [5]. So the judgment matrix of structure needs to meet the following consistency conditions:
Judgment matrix P, for example, as to the pij > 0; Pii = 1; Pij = 1/Pji; Pij = Pik/Pjk (i, j, k = 1, 2,∙∙∙, n) is founded, we say that P meets complete consistent and P is called consistency matrix. But in fact it is impossible to request to meet the above numerous equations when comparative matrixes in pairs are structured. So we request comparative matrix in pairs to have a certain degree of consistency, which is to say, the matrix have an acceptable consistency.
3.2. Consistency Check
Calculate the biggest characteristic root and the corresponding characteristic vector for each judgment matrix. Use the consistency index, random consistency index and the consistency ratio to do the consistency check. If the check is right, the characteristic vectors (normalized) are weight vectors; if not, we need to reconstruct pairs of judgment matrix. The procedure to inspect the consistency of pairs of judgment matrices P is as follows:
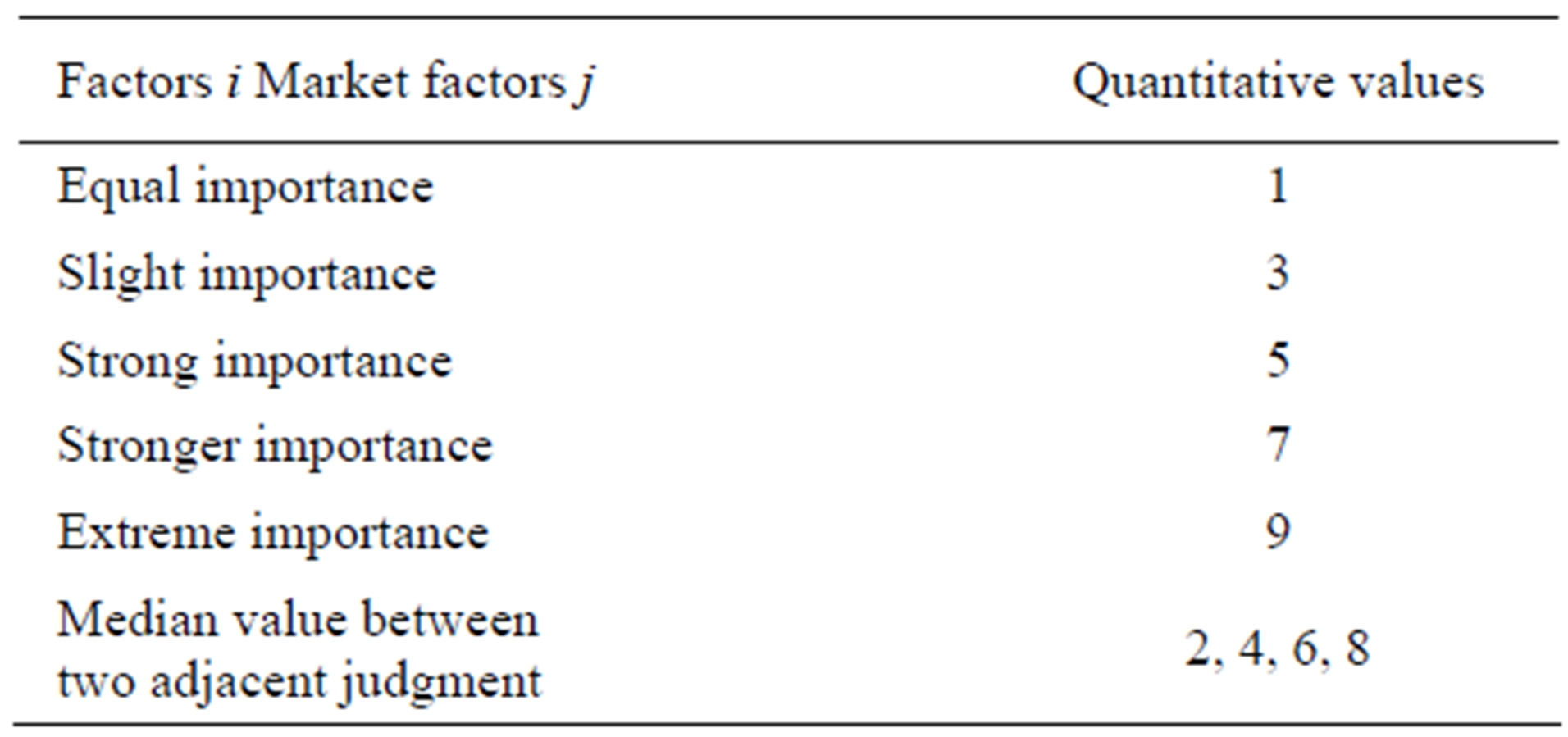
Table 1. Proportion scale.
Calculate index CI that measures the inconsistent level of a judgment matrix P by Eq.1 (the order of square n is above and beyond 1):
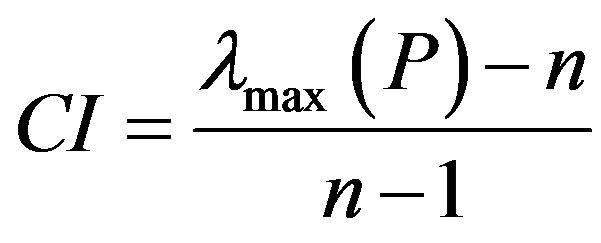 (1)
(1)
Among them, λmax is the maximum eigenvalue of the matrix P. The bigger the value of the consistency index CI is, the more far judgment matrix deflects from complete consistency is. The smaller the value of CI is, the more closely judgment matrix approach to complete consistency. Generally the greater the order n of judgment matrix is, the greater the value of CI as an index shows man-made deviation from complete consistency is, and the smaller the value of n, the smaller the value of CI.
• For judgment matrix P of more order, considering its deviation from the consistency could be caused by random reasons, when inspecting whether judgment matrix has the satisfactory consistency, we bring in average random consistency standard RI (Random Index) which is only relevant to the order n of the matrix. Generally speaking, the greater the order of the matrix is, the more probably consistent random deviation appears. It is given the average consistency index calculated 1000 times by the positive reciprocal matrix of 1 - 15 order in Table 2.
• Random consistency ratio CR. When n < 3, judgment matrix is complete consistent forever. The consistency index CI of judgment matrix divided by the average random consistency index RI with the same order is called random consistency ratio CR, which is showed in Eq.2.
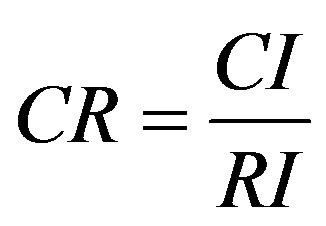 (2)
(2)
when CR < 0.10, we think that judgment matrix is of satisfactory consistency, or its inconsistent degree is acceptable. When CR > 0.10, we need to adjust and rectify judgment matrix to make it satisfy the condition of CR < 0.10, which has the satisfactory consistency.
3.3. Calculate Weight Vectors with Sum Product Method
For the matrix that meets the consistency, we can use sum product method to obtain feature vectors as weights after normalized. The specific procedure is as follows:

Table 2. Standard values of average random consistency index RI.
• Each column of judgment matrix is normalized and its general elements are Eq.3.
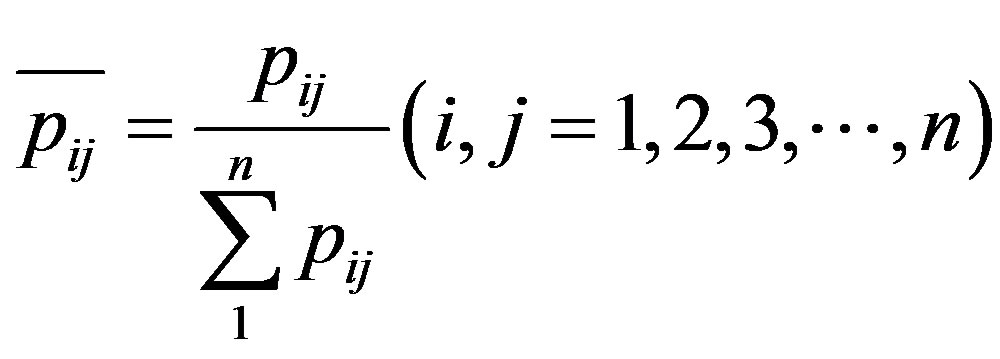 (3)
(3)
• Add each element in line of the judgment matrix whose each column has been normalized and the following type is shown in Eq.4.
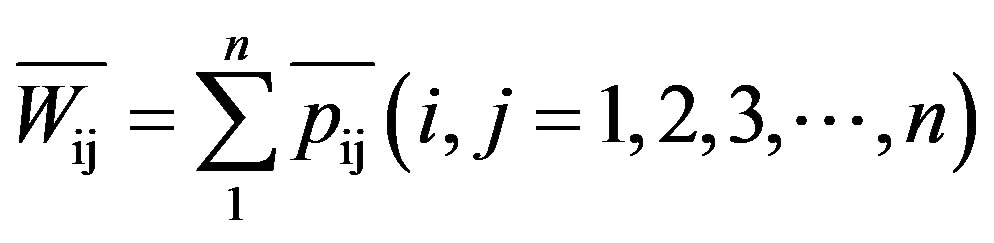 (4)
(4)
• The normalization is carried out to the vector by Eq.5.
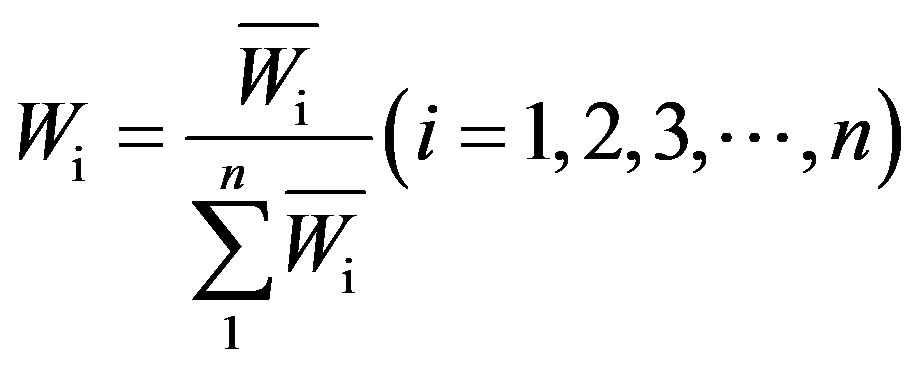 (5)
(5)
Get Eq.6.
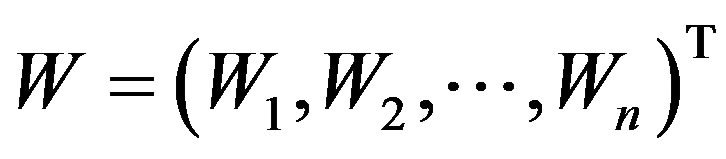 (6)
(6)
4. THE METHOD OF FUZZY COMPREHENSIVE EVALUATION
Comprehensive evaluation is a kind of overall evaluation of things with many attributes or things whose overall quality can be affected by many factors, which can comprehend these attributes and factors reasonably. The fuzzy comprehensive evaluation method, based on the fuzzy mathematics thought and method, is a kind of mathematical method which can work out the things accurately that can’t be clearly defined, and evaluate inaccurate imprecise and incomplete information. The most obvious feature of the comprehensive fuzzy evaluation method is dealing with the initiative and fuzziness of human thinking easily. Consequently, only by taking all these factors into consideration can we make a reasonable evaluation. In most cases, as evaluation involves fuzzy factors, it is a feasible and good way to use the fuzzy mathematics evaluation method [6-10].
5. STEPS OF FUZZY COMPREHENSIVE EVALUATION METHOD
5.1. Found Factors Group
Let’s suppose that the problem which is under research has n kinds of influencing factors.
A common set is made up by some elements consisted of the factors which have some influence on evaluation objects, called Factors Group.
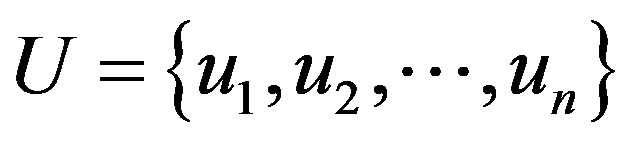
5.2. Found Evaluation Group
Evaluation group is a set consist of m kinds of evaluation with many factors. The number and the name of its elements can be determined by practical problems.
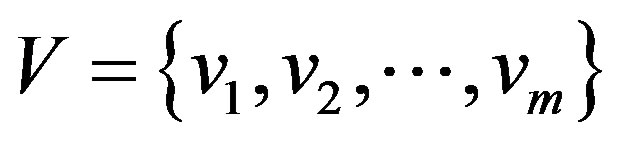
5.3. Determine Membership Functions
The thought of membership degree is the basic idea of fuzzy mathematics. In general, we can determine membership by using fuzzy statistics method or expert experience method. After establishing the membership functions, we should count up the number of the factors whose value corresponds to a certain delimited level and calculate the proportion in these factors. And the proportion is rij in the fuzzy evaluation matrix R.
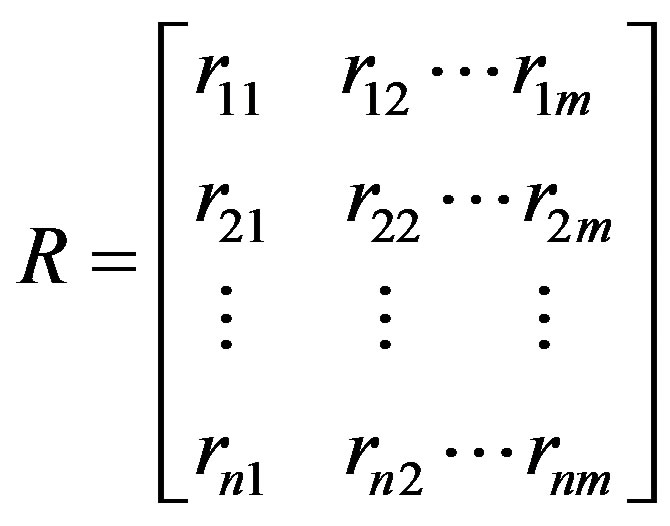
5.4. Establish Vector Set
Weight set means the impact degree of a single factor among all the evaluation factors. A large number of drillling engineering practice shows that, for different oil and gas well, all these above factors’ impact degree is not the same in general. The evaluation factors for the selected clay stability have different effects on the final evaluation purpose and the results. For this reason, in order to reflect the importance degree of these factors, we should give these factors corresponding weight number. The set which is consists of all these weight numbers is called factors weights set.
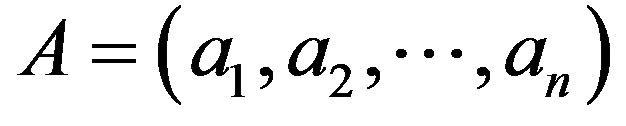
At the same time, all these weight numbers should meet the normalization condition, namely:

5.5. Establish Fuzzy Comprehensive Evaluation Model
The purpose of using the fuzzy comprehensive evaluation method is obtaining the evaluation result on the basis of the comprehensive consideration of influential factors, so as to make valuable reference of the stability evaluation of mud shale. According to the knowledge of fuzzy mathematics, the formula of fuzzy comprehensive evaluation is Eq.7.
B = AR(7)
In the formula:
A: weight set,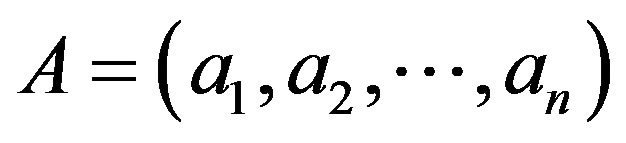 ;
;
R: fuzzy comprehensive judgment matrix, ;
;
B: evaluation results,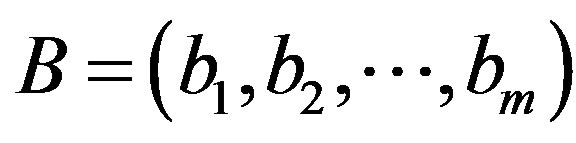 ,
, .
.
6. APPLICATIONS
The physico-chemical performance of clay mineral is the basic to study mechanism of sidewall instability and technical measures. For this, we conducted some indoor experiments such as cation exchange capacity CEC determination, ζ potential measurement, swelling test, rolling recovery experiments, formation water activity measurement, with the use of experimental data to evaluate swelling and dispersion of the clay mineral [11]. The 15 groups of experimental data of shale samples in Yimin from the upper layer in Hailaer Area Wuerxun Depression shows in Table 3.
6.1. Determine the Factors Set
We can see from the table, there are six factors evaluating the shale wellbore stability. The collection composed is

Of which: u1 for the density; u2 for the expansion; u3 for the recovery rate; u4 for the cation exchange capacity; u5 for the ζ potential; u6 for water activity.
6.2. Determine the Evaluation Set
Here identified five types of evaluation results of the shale sidewall stability. The class of shale sidewall stability (stability in decreasing order) is expressed as 1, 2, 3, 4, 5. That

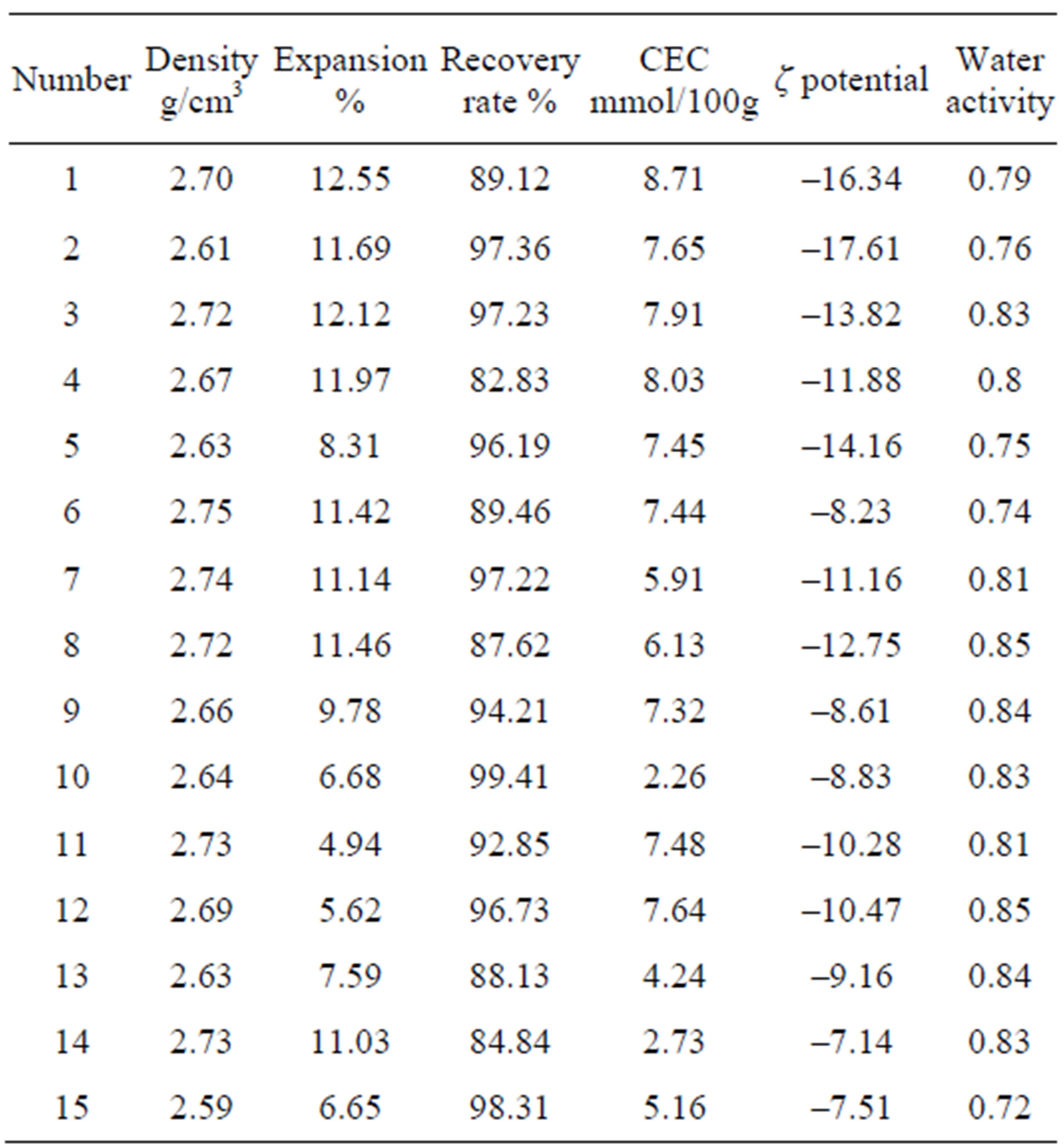
Table 3. The sidewall stability analytic data of shale samples in Hailaer Area.
Of which: v1 is very stable; v2 is relatively stable; v3 is stable; v4 is unstable; v5 is very unstable.
6.3. Determine the Weight Set
According to this example, the judgment matrix determined by the relationship between the factors is showed in Table 4.
In the Table 4: P1 for the density; P2 for expansion; P3 for the recovery rate; P4 for the cation exchange capacity; P5 for the ζ potential; P6 for the water activity.
According to the proposed test method that determines the matrix consistency, the calculated consistency index and random consistency index were: CI = 0.0268, RI = 1.25, resulting in the value of consistency ratio: CR = 0.03392.
In this case the judge of the matrix P does not have complete consistency, but because of random consistency ratio CR = 0.03392 < 0.10, we determine that the matrix P can be satisfied with the consistency. Therefore, the obtained eigenvectors of P can be calculated as the weight vector A. The weight vector calculated by sum product method is Eq.8.
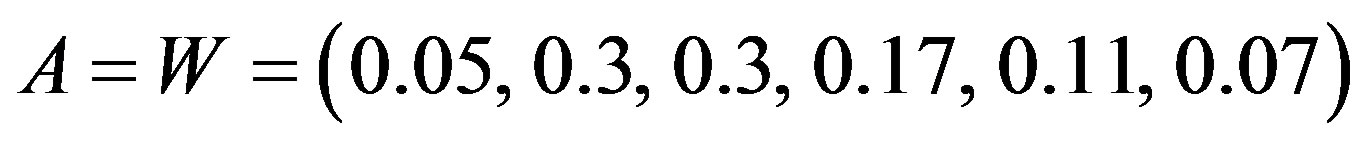 (8)
(8)
6.4. Determine the Fuzzy Evaluation Matrix
Establish the membership function of each factor. Due to different dimensions of factors, we can not directly calculate the matrix. We should first establish the membership function of each factor and normalize various factors. The membership function established in this example is a gradient distribution function.
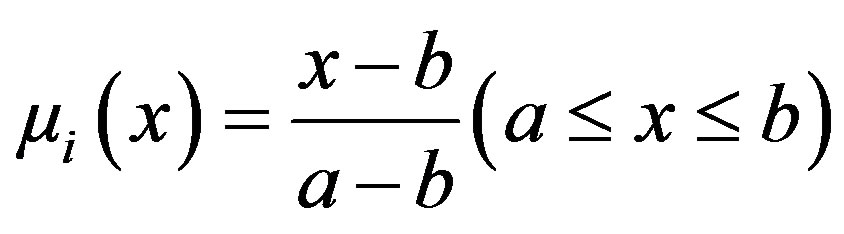 (9)
(9)
Of which: a is a minimum of evaluation factors; b is a maximum of evaluation factors. Greatest benefit of this model is to normalize data while determining the membership function.
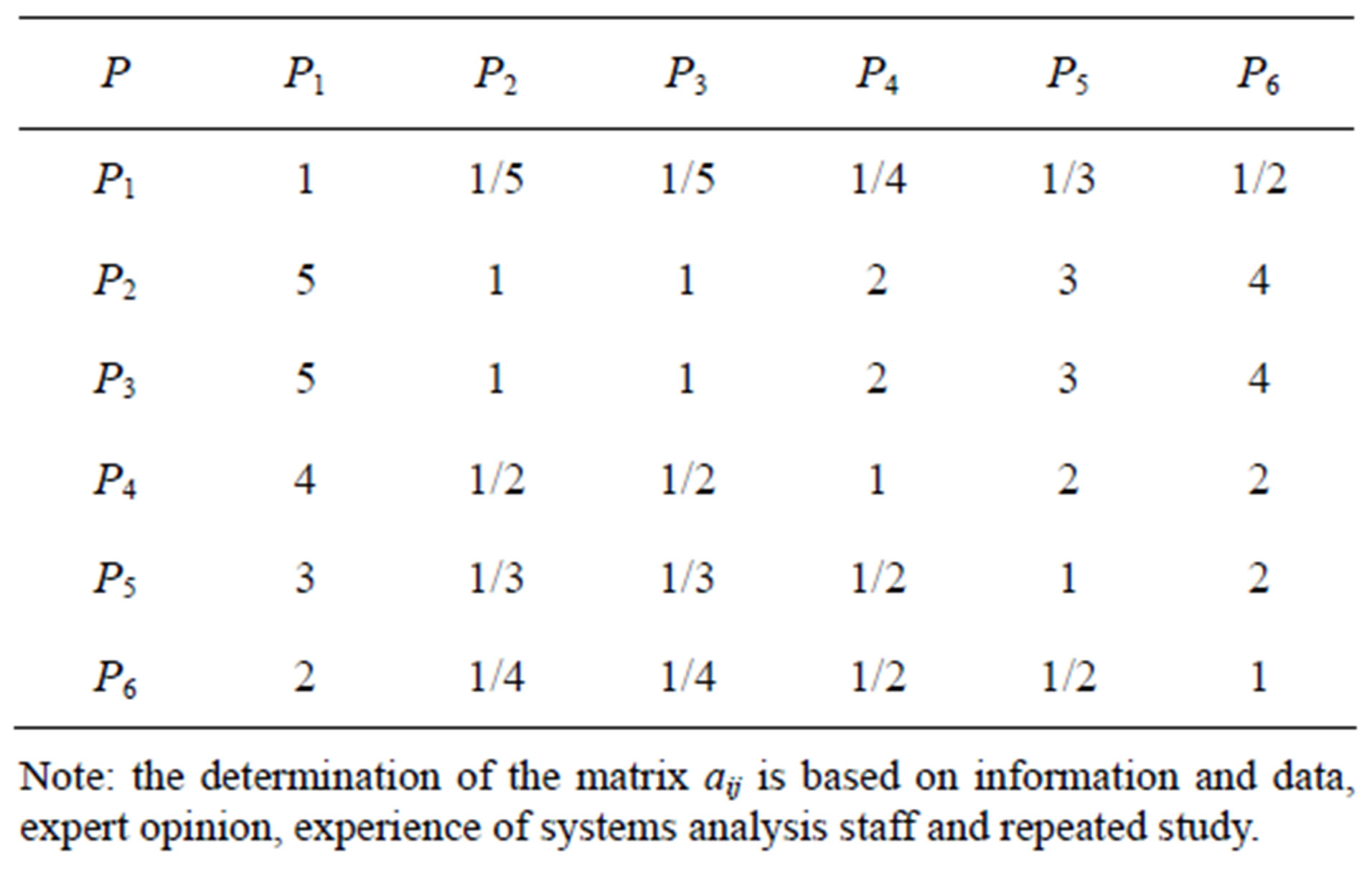
Table 4. Judgment matrix.
• Determine the evaluation matrix. The function is used to calculate the membership value of μ. When 0 ≤ μ < 0.2, the evaluation is focused on the v1 level in the evaluation set; 0.2 ≤ μ < 0.4, the evaluation is focused on the v2 level; 0.4 ≤ μ < 0.6, the evaluation is focused on the v3 level; 0.6 ≤ μ < 0.8, the evaluation is focused on the v4 level; 0.8 ≤ μ < 1.0, evaluation is focused on the v5 level. According to the distribution function based on the gradient to determine the subjection of each single factor, the following matrix can be obtained by calculation:

6.5. Calculate the Evaluation Results
After determining the evaluation matrix and the weight set, you can use them to judge, according to the formula Eq.10.
 (10)
(10)
So the results obtained are:

6.6. Results Analysis
Before applying the principle of maximum subjection to deal with the evaluation results, you need to discuss the results, to test the validity of the principle of maximum subjection. Using “The validity deciding method of the principle of maximum subjection” [12] to calculate evaluation indicators:
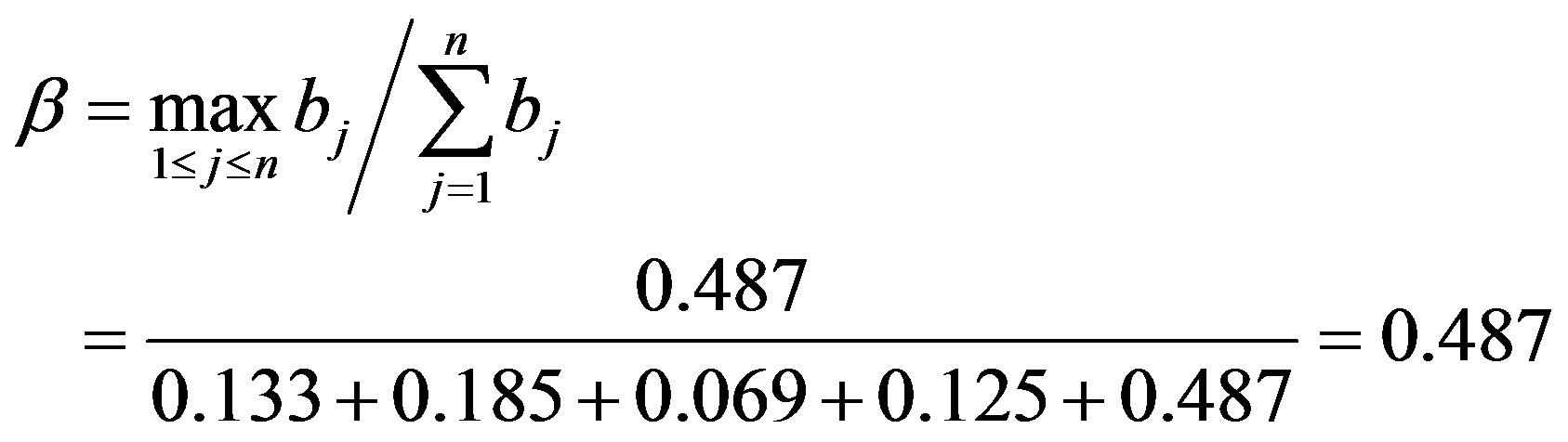
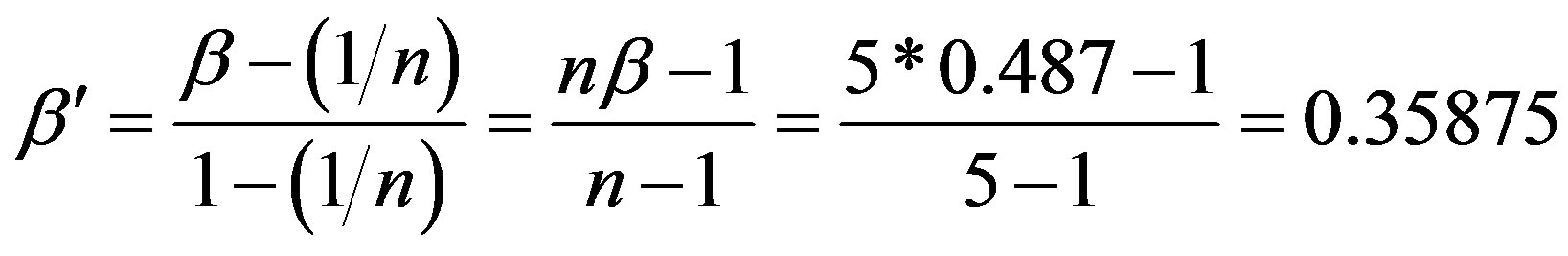
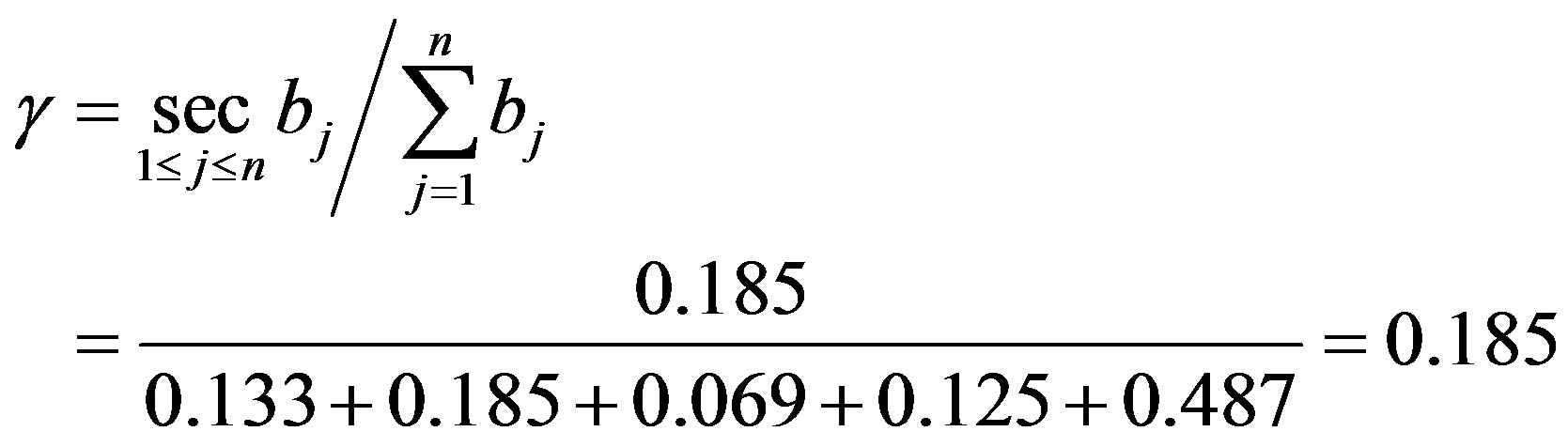
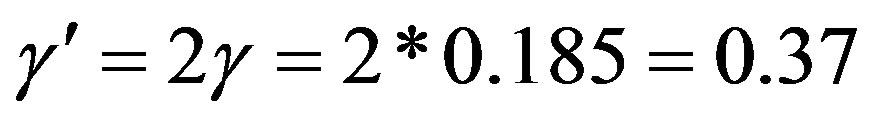
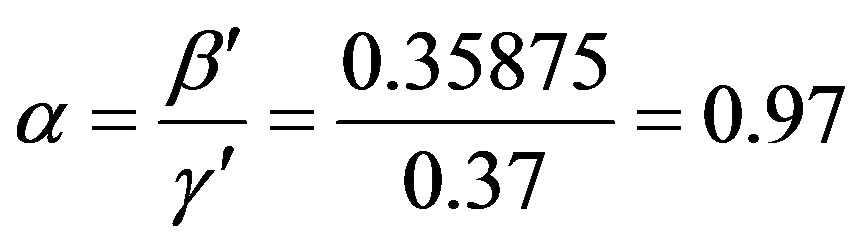
Evaluation index α = 0.97, very close to 1, indicating that for this result the implementation of the principle of maximum subjection is very effective and the relative degree of confidence is high. So using the maximum subjection principle to deal with the evaluation results bj (j = 1, 2, 3, 4, 5), which means taking the maximum of the evaluation results as the final evaluation results. We can see from the calculation that the fifth-grade is the maximum, therefore, its evaluation result is that the sidewall is very unstable. This result is very consistent with the real situation in well drilling, indicating that evaluation result is correct. The method can accurately evaluate the stability of shale sidewall, providing a scientific theoretical basis for on-site drilling decision makers.
• 7. CONCLUSIONS
• We determine the cation exchange capacity CEC, ζ potential, swelling, rolling recoveries, formation water activity and other physico-chemical properties of clay mineral through indoor experiments, and evaluate the mineral swelling and dispersion properties to lay the foundation for sidewall instability mechanism and the development of anti-collapse response.
• On the basis of comprehensive analysis of various factors affecting the borehole stability, combined with specific oil and gas well engineering practice, as well as information related to the experimental data and field conditions, using improved Fuzzy Integrative Evaluation Method to evaluate the stability of shale sidewall in Yimin Fm from the upper layer in Hailaer Area Wuerxun Depression, and found that the region is in very unstable shale level. This result is very consistent with the real situation in this section while well drilling.
• By introducing the AHP and the maximum subjection principle, using Fuzzy Integrative Evaluation Method to predict sidewall stability is of theoretical enrichment, simple to operate, of accurate result, and also provides a new scientific method of sidewall stability evaluation for decision-makers on the drilling site.
REFERENCES
- Hoang, S. and Abousleiman, Y. (2004) The analytical solution for wellbore stability in multilateral junctions in nonhydrostatic in-situ stress field. SPE No. 90245.
- Feng, Z.Q., Ren, Y.G., Zhang, X.D., et al. (2004) Law of oil and gas distribution in Hailaer Basin and orientation of exploration at next stage. Chinese Journal of China Petroleum Exploration, 9, 19-22.
- Guz', A.N. and Kuliev, G. (1983) Stability of drill wells. International Applied Mechanics, 19, 97-105.
- Tan, X.C., Ding, X., Chen, J.S., et al. (2008) Application of hierarchic analysis to quantitative evaluation of carbonate reservoir. Chinese Journal of Southwest Petroleum University (Science & Technology Edition), 30, 38-40.
- Lei, Z.X., Chen, Y.M. and Xu, Y.D. (2007) Integrated evaluation on reservoir profile modification suitability degree using fuzzy hierarchy determination. Petroleum Geology & Oilfield Development in Daqing, 26, 82-86.
- Liang, B.S. and Cao, D.L. Eds. (2007) Fuzzy mathematics and its application. Science Publishing Company Press, Beijing, 56-60.
- Zeng, Z.J., Guo, J.C., Zhao, J.Z., et al. (2006) Refracturing candidate well multilevel fuzzy decision method. Petroleum Geology & Oilfield Development in Daqing, 25, 73-76.
- Peng, S.P., Pu, X.L., Lei, G., et al. (2004) Use fuzzy comprehensive evaluation method to judge well sidewall stability. Chinese Journal of Fault-block Oll & Gas Field, 11, 58-62.
- Jiang, Y.F., Liu, H., Liu, Z.H., et al. (2009) Study and application of formation water production and borehole wall stability prediction technologies in Daqing Gas/ Foam Drilling. SPE No. 13499.
- Cuddy, S. (1997) The application of the mathematics of fuzzy logic to petrophysics. SPWLA No. 1997-S.
- Li, Z.D., Zhou, J.L., Wen, H., et al. (2008) Characteristics of reservoirs in northern Beixixiepo area of Hailar Basin and their influencing factors. Chinese Journal of Acta Petrologica et Mineralogica, 27, 45-51.
- Chen, Y.H. and Sun, C.Y. (2001) Effective degree of maximum subjection principle in fuzzy comprehensive evaluation method. Chinese Journal of Chongqing Normal University (Natural Science Edition), 11, 45-47.

