Natural Science
Vol.4 No.5(2012), Article ID:19120,4 pages DOI:10.4236/ns.2012.45046
Generalized general and special relativity in the presence of the gravitation, related to the space-time curvature
![]()
1Department of Physics, Faculty of Education, Al-Zaiem Al-Azhari University, Omdurman, Sudan; *Corresponding Author: mahmoudhilo@gmail.com
2Department of Physics, Faculty of Science and Arts at Al-Rass, Qassim University, Al-Rass, Saudi Arabia
3Department of Physics, Faculty of Science, Sudan University of Science and Technology, Khartoum, Sudan
4Department of Physics, Unizah Community College, Qassim University, Unizah, Saudi Arabia
5Department of Physics, Faculty of Science and Arts at Al-Muznib, Qassim University, Al-Muznib, Saudi Arabia
Received 28 October 2011; revised 20 November 2011; accepted 15 December 2011
Keywords: Space-Time; Curvature; Generalized; Gravitation; Red-Shift
ABSTRACT
Using the equation of motion expression in a curved space proper time is a useful method to explain the relation between the curvature of space-time and the potential of any field obtained. Taking into account the expression for the Hamiltonian density, the effect of fields, as well as the effect of motion, on the mass, and, their effect on energy is found. The new expression of energy reduced to the ordinary Newton’s energy expression. It also explains the gravitational red shift.
1. INTRODUCTION
Einstein’s theory of special relativity (SR) is one of the great achievements in physics. It makes radical modification in the concept of space, time, and energy. It explains a wide variety of physical phenomena, like pair production, photoelectric effect, and meson decay. Despite these successes (SR) suffers from noticeable setbacks. For instance, in the classical limit the energy expression for (SR) does not coincide with the Newtonian energy expression, since it does not include a term representing the potential energy. Moreover, the gravitational red shift of light indicates that the photon mass is affected by the gravitational field, which is in direct conflict with the fact that the mass in (SR) is not a function of the field potential. The same holds for the expression of time and length, in (SR), which does not recognize the effect of gravitational field in the weak limit, which is not in conformity with that of general relativity (GR), where time and length are affected by gravitational field [1].
Many attempts were made to modify Special Relativity (SR) to include the effect of gravity and other fields [2-4]. These attempts concentrated on the motion of mass and energy without considering the influence of both fields and motion on time and length.
Some attempts were also made to include the effect of curvature of space-time, on energy and momentum [5], but their expression of energy is incomplete, since they stem from the equation of motion instead of using the Hamiltonian. Generalized Special Relativity (GSR) is used by others [6] to find the effect of gravity on space and energy.
In this work the equation of motion in curved spacetime is used to relate the potential of any field to the space-time curvature. A useful expression for the mass and energy in the presence of any field beside the effect of motion is derived in Section 2.
Section 4 is devoted for comparing the classical energy expression with the expression of energy in the classical limit for the model.
2. SPECIAL RRELATIVITY IN THE PRESENSCE OF THE GRAVITATION
The Generalized Special Relativity theory is a new form of the special relativity theory that adopts the gravitational potential, and it gives the formula of relative mass to be as follows [7]:
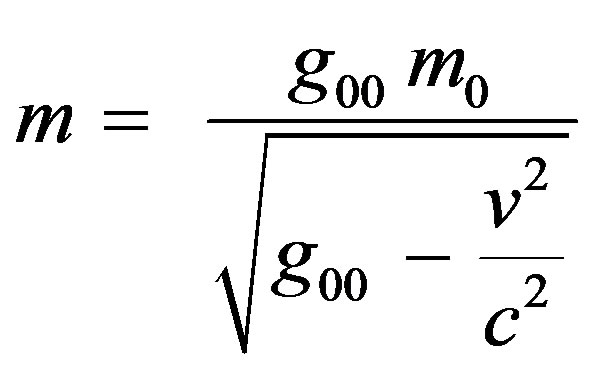 (1)
(1)
where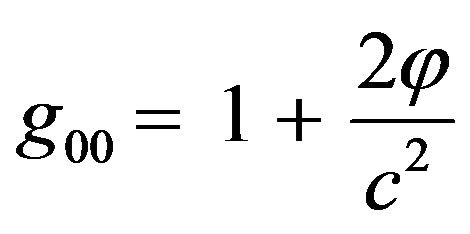 , and
, and 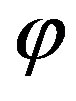 denotes the gravitational potential, or the field in which the mass is measured.
denotes the gravitational potential, or the field in which the mass is measured.
The derivation of the mass Eq.1 using the generalized special relativity (GSR) can be find as follows:
In the special relativity (SR), the time, length, and mass can be obtained in any moving frame by either multiplying or dividing their values in the rest frame by a factor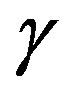 .
.
 (2)
(2)
where v is the velocity of the particle, and c is the speed of light.
It is convenient to re-express  in terms of the proper time, associated with the impact of gravity on the previous physical quantities, (time, length, and mass) [8].
in terms of the proper time, associated with the impact of gravity on the previous physical quantities, (time, length, and mass) [8].
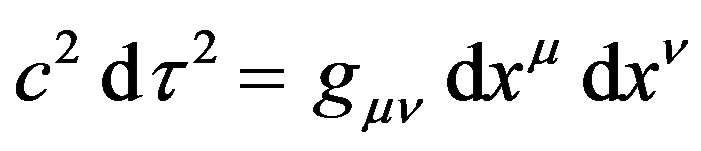 (3)
(3)
where 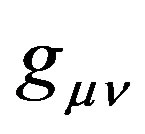 is the metric tensor, and,
is the metric tensor, and, 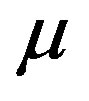 and
and 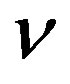 denotes the contra variant (covariant) vectors.
denotes the contra variant (covariant) vectors.
Which is a common language to both special relativity (SR), and general relativity (GR). We know that in special relativity (SR) Eq.3 reduces to: [9].
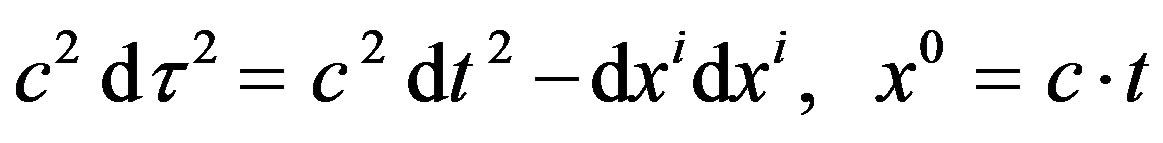 (4)
(4)
where i denotes the particle position (covariant) vector according to Lorentz covariance.
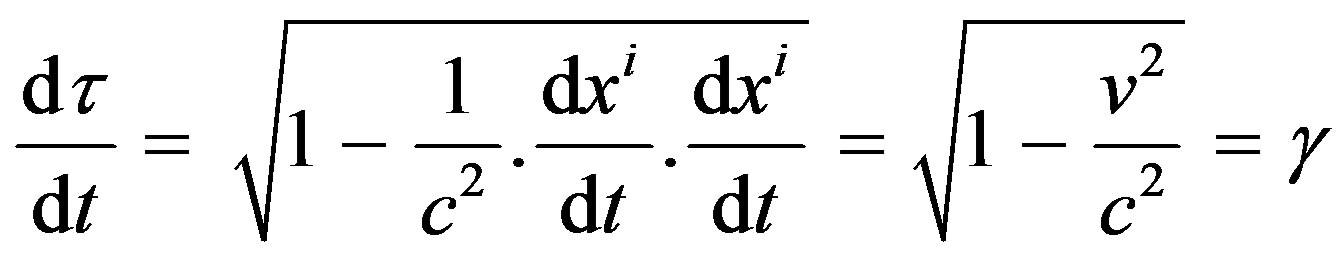 (5)
(5)
Thus we can easily generalize  to include the effect of gravitation by using Eq.3 and by adopting the weak field approximation where [7].
to include the effect of gravitation by using Eq.3 and by adopting the weak field approximation where [7].
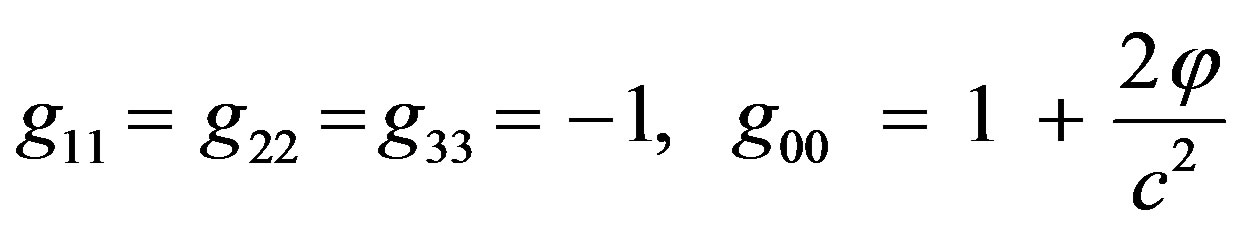 (6)
(6)
and 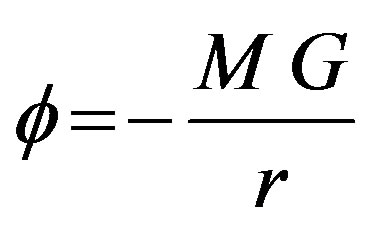
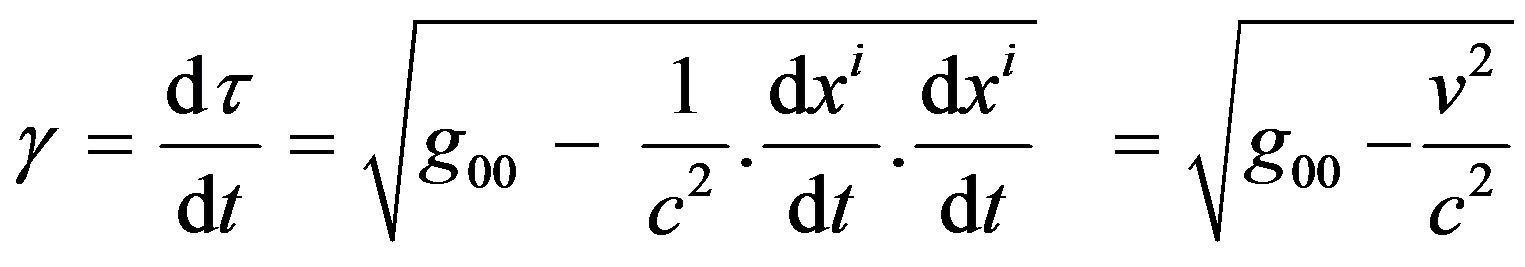 (7)
(7)
When the effect of motion only is considered, the expression of time in the special relativity (SR) is found to be [8].
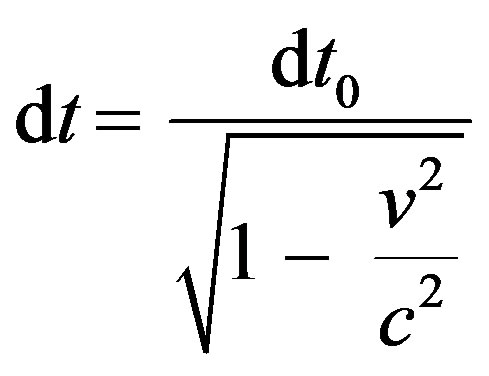 (8)
(8)
where the subscript 0 stands for the quantity measured in the rest frame. While if gravity only affect time, its expression is given by [9].
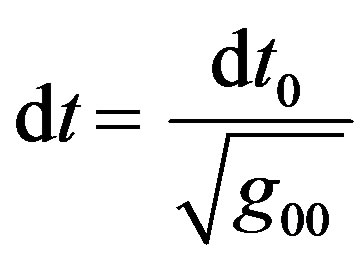 (9)
(9)
In view of Eqs.7-9 the expression
 (10)
(10)
can be generalized to recognize the effect of motion as well as gravity on time, to get
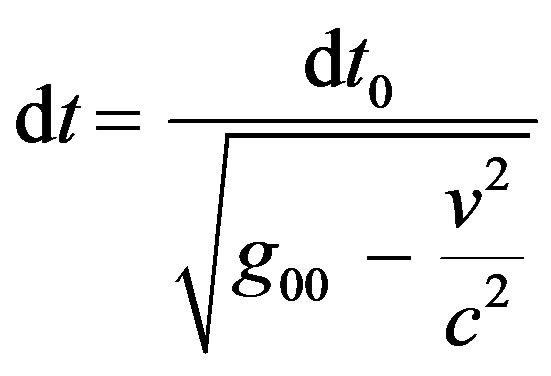 (11)
(11)
The same result can be obtained for the volume where the effect of motion and gravity respectively gives [7].
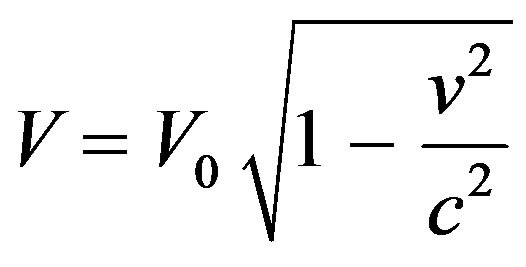 (12)
(12)
 (13)
(13)
The generalization can be done by utilizing Eq.7 to find that
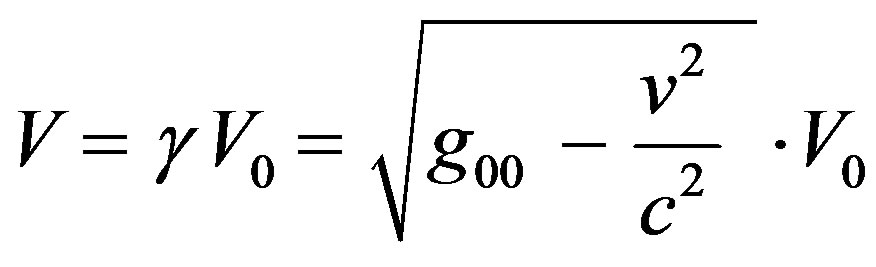 (14)
(14)
To generalize the concept of mass to include the effect of gravitation we use the expression for the Hamiltonian in general relativity, i.e. [8].
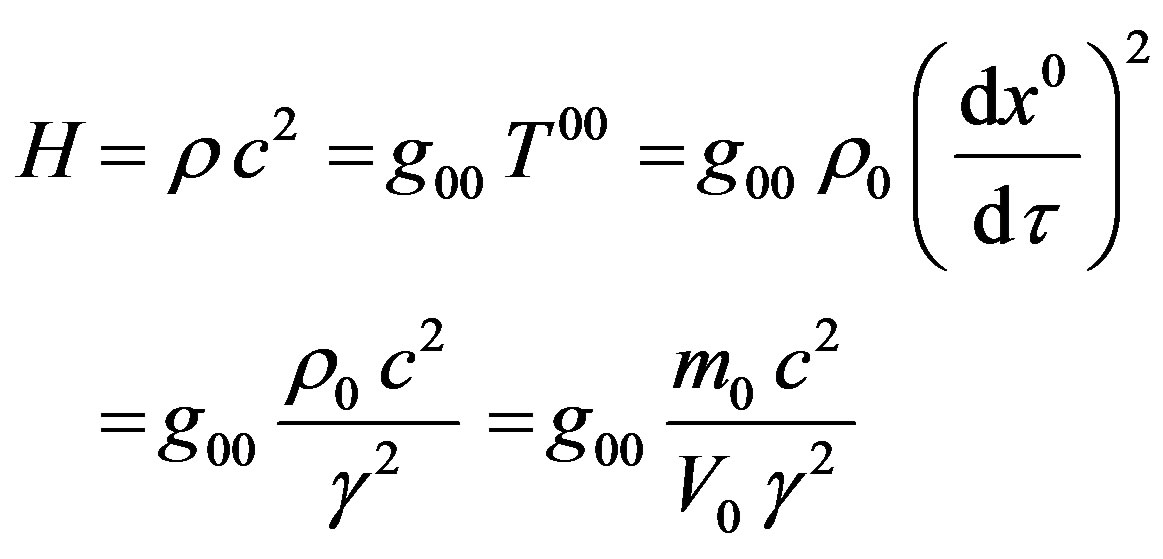 (15)
(15)
where H is Hamiltonian, 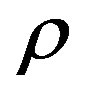 is the density, and
is the density, and 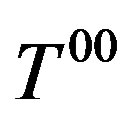 is energy tensor.
is energy tensor.
Using Eqs.14 and 15, yields:
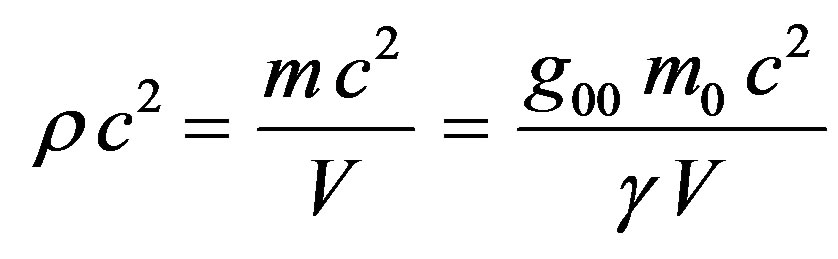 (16)
(16)
Therefore
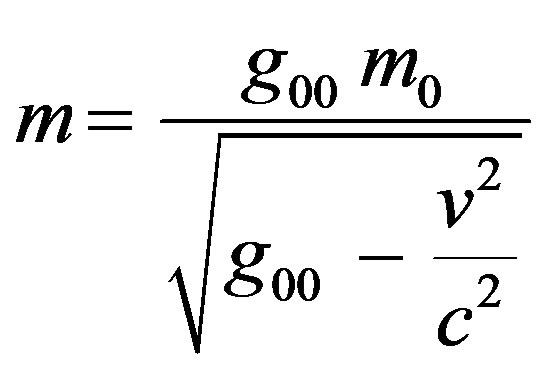 (17)
(17)
Which is the expression of mass in the presence of gravitational potential and it named the generalized special relativity (GSR) theory.
Thus, the energy is given by
 (18)
(18)
3. GENERALIZATION OF THE GENERAL RELATIVITY TO INCLUDE THE OTHER FIELDS
The expression of time length and mass in General Relativity (GR) can be generalized to include all other fields by proving that the space can be curved by all fields, the first approach is based on general relativity (GR) while the second is based on the standard model.
In General Relativity (GR) the equation of motion in a curved space-time is given by
 (19a)
(19a)
In the weak field this is reduced to
 (19b)
(19b)
where
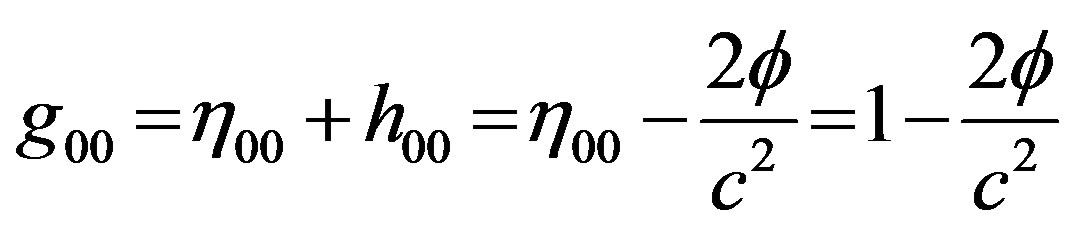 (20)
(20)
It is important to note that Eq.18 and Eq.19a indicate that the curvature of space-time 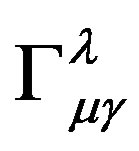 is affected by acceleration and speed only, and have nothing to do with the mass.
is affected by acceleration and speed only, and have nothing to do with the mass.
On the other hand the lagrangian L of matter in the presence of a field of Ф is a function of x and Ф, i.e.
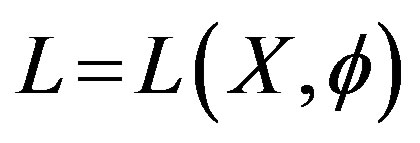 (21)
(21)
The mass m is part of this lagrangian through the reined term. Therefore m is a function of x and Ф, too, i.e.
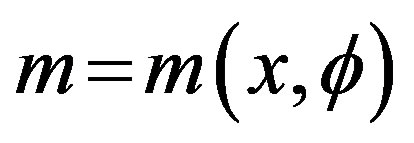 (22)
(22)
Usually m does not depend on x explicitly but depends on it implicitly via and through the potential Ф. Hence
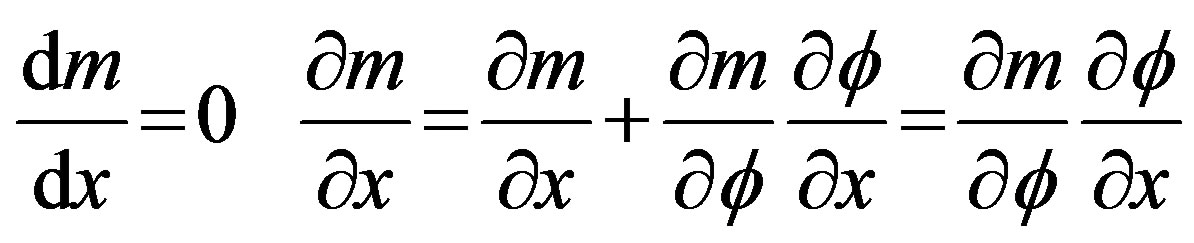 (23)
(23)
That means the partial differentiation of m with respect to x vanishes, while the total does not vanish. Therefore
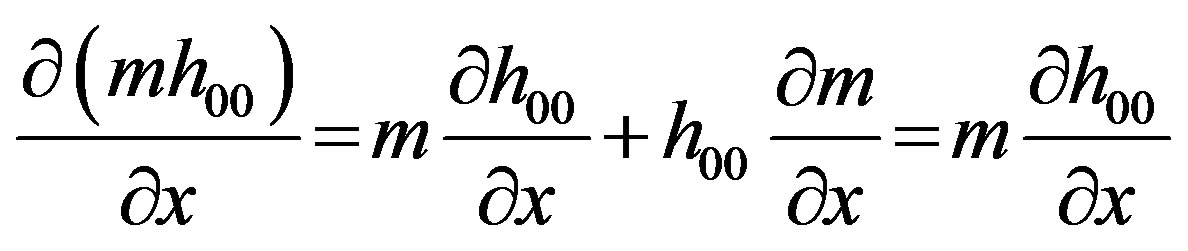 (24)
(24)
With the aid of (24) Eq.19b becomes:
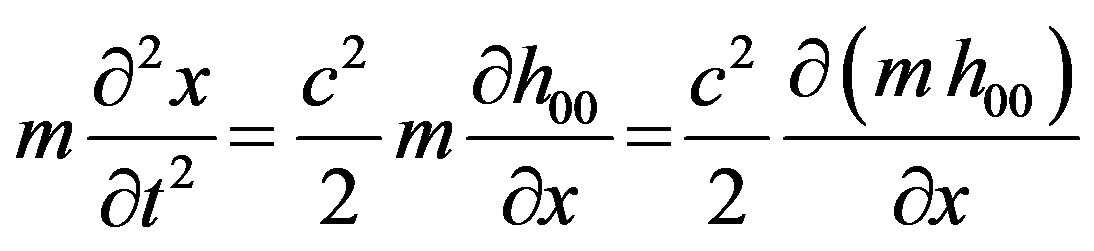 (25)
(25)
The potential V of any field satisfies the Newtonian equations of motion the potential
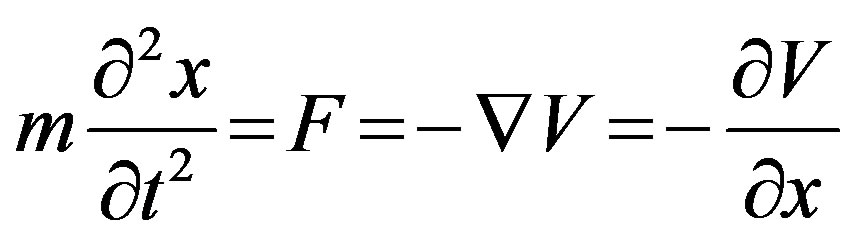 (26)
(26)
Comparing Eq.24 with Eq.25 yields
 (27)
(27)
Substituting Eq.27 in Eq.20 we get
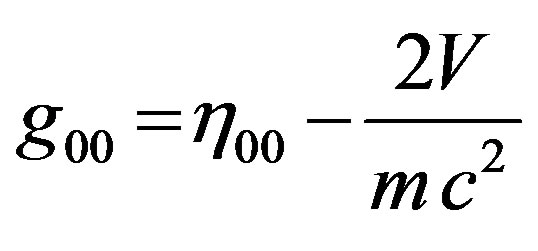 (28)
(28)
The potential V can be expressed in terms of the potential per unit mass Ф in the form
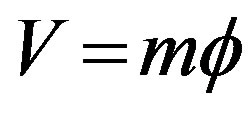 (29)
(29)
As a result Eq.28 becomes
 (30)
(30)
It is important to note that Ф here is the potential per unit mass for any field.
The relation between fields and space deformation can also be determined from the standard model of electro weak interaction (SM).
According to SM the gauge fields wµ and Bµ deform the space by changing the ordinary derivative  to the covariant one Dµ
to the covariant one Dµ
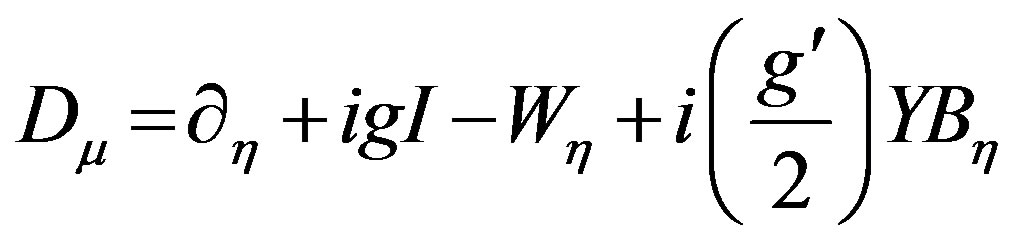 (31)
(31)
where the parameters g, g', I and Y are parameters determining the interaction type. on the other hand the covariant derivative in (GR) IS given by
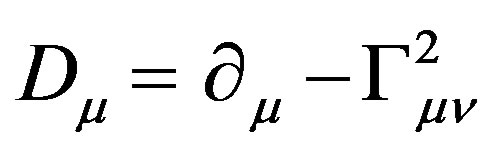 (32)
(32)
Comparing Eq.31 with Eq.32 yields
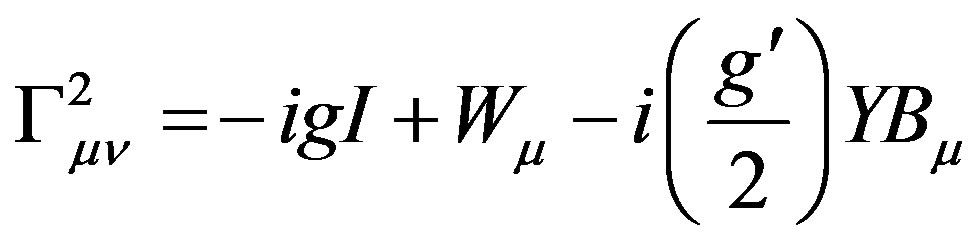 (33)
(33)
Again Eq.33 indicates that gauge fields deform the space as well as the gravitational field. Thus the expressions for time, mass and energy are given by
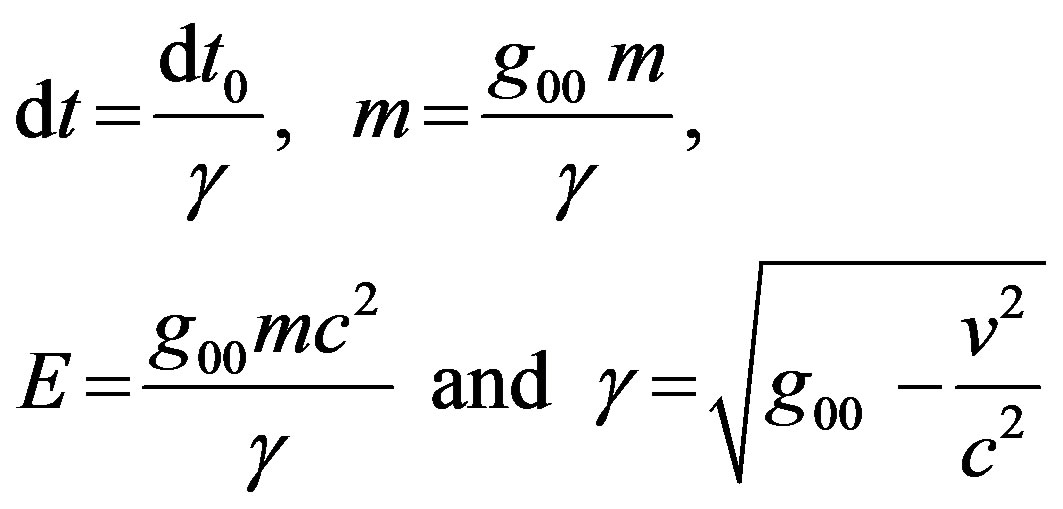 (34)
(34)
Indicates that time, mass and energy are affected by all fields.
4. CLASSICAL LIMIT OF THE GENERALIZED SPECIAL RELATIVITY
When the field is weak g00 is given by Eq.5. In this case the energy in Eq.17 is given by

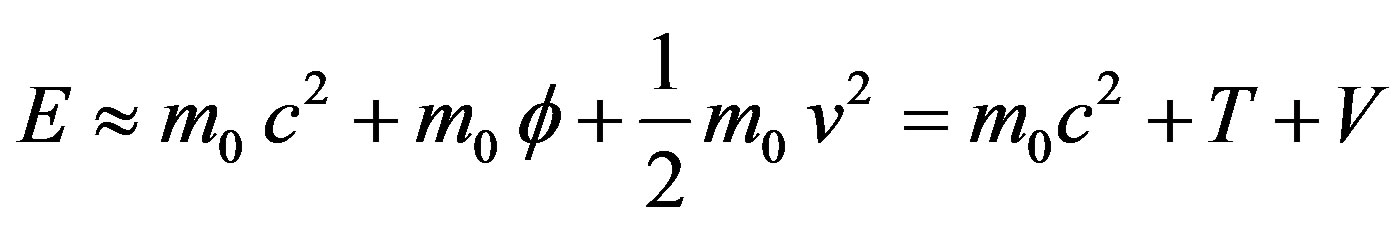 (35)
(35)
where one was the identity 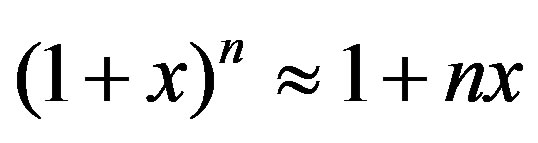 for
for 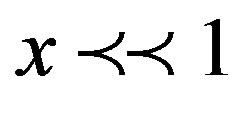 here all terms quadratic in
here all terms quadratic in 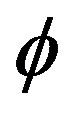 and
and 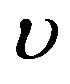 are neglected. Unlike SR which does not include potential energy, Eq.35 shows that the energy is reduced to the classical expression which include potential energy
are neglected. Unlike SR which does not include potential energy, Eq.35 shows that the energy is reduced to the classical expression which include potential energy
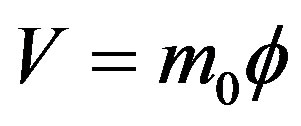 (36)
(36)
the gravitational red shift can be obtained by setting 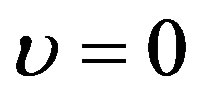 and bearing in mind that
and bearing in mind that 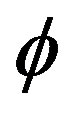 is small to get
is small to get
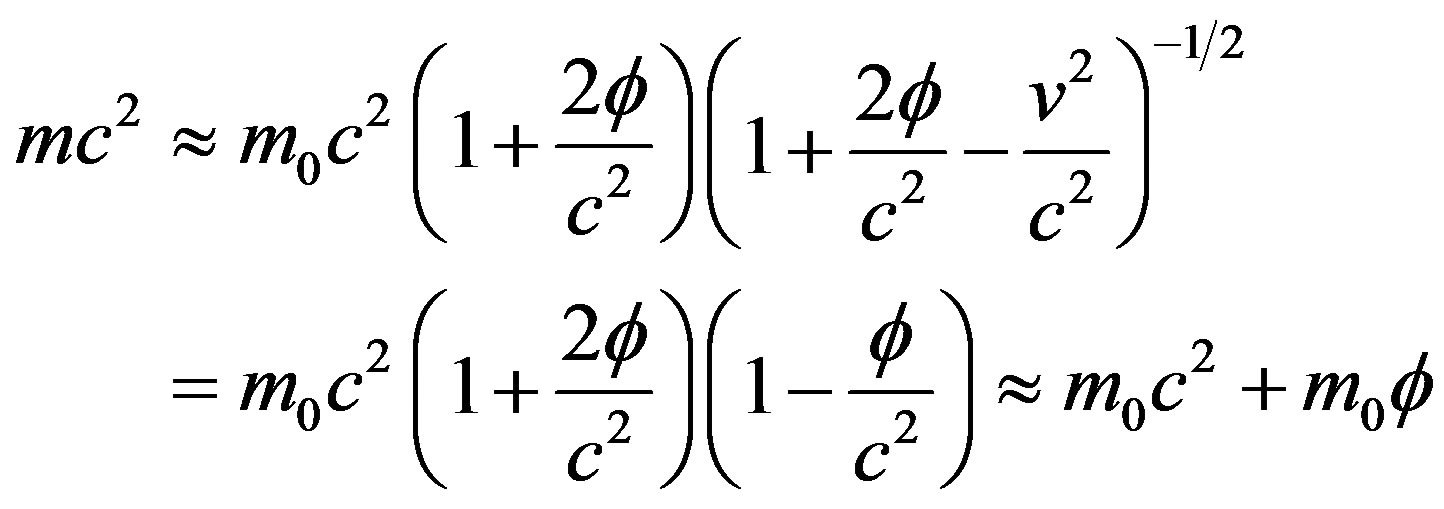
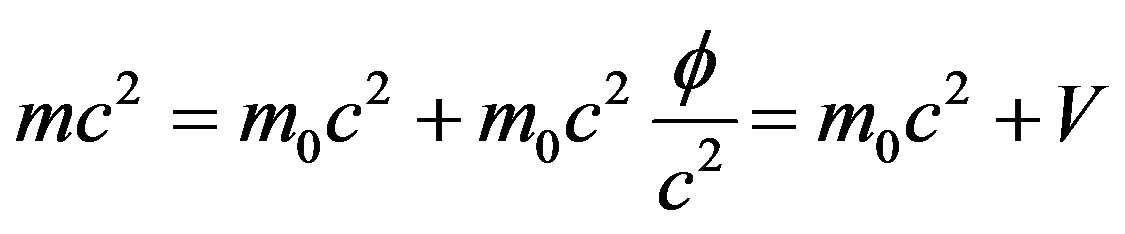 (37)
(37)
For the photon :
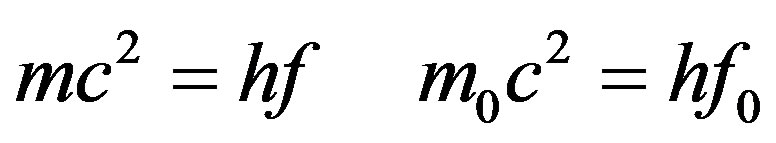 (38)
(38)
Hence
 (39)
(39)
Then
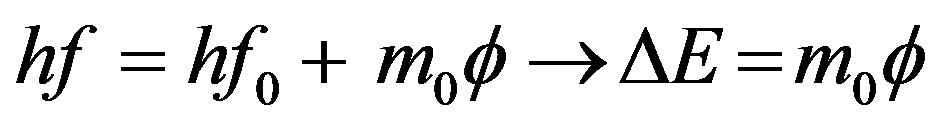 (40)
(40)
Therefore
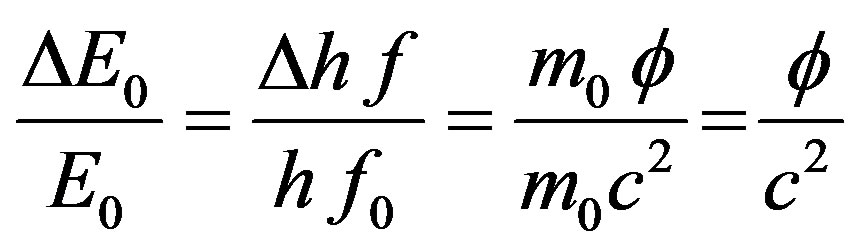 (41)
(41)
While 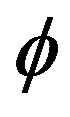 denotes the potential field and given by:
denotes the potential field and given by:
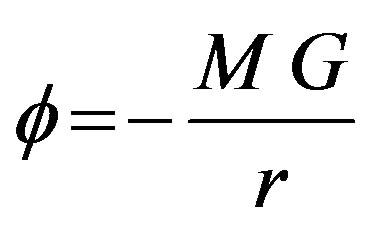
as mentioned before, then Eq.41 becomes:
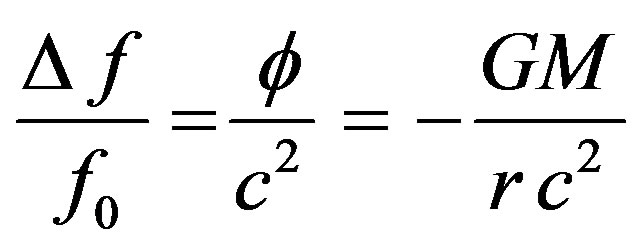 (42)
(42)
This means that the gravitational red shift can be explained with the framework of our model [9].
5. CONCLUSION
The effect of gravity as well as motion on time, volume and mass shows the dependence of them on the potential on the same footing as velocity. Unlike SR the expression of energy include the potential energy when the classical limit is considered. It is very interesting to note that when the effect of gravity alone is considered on mass as shown in Eq.16 the mass increases which indicate that the field increase the mass. The generalized expression of time, volume, mass, and energy in which the effect of fields on them is present through the metric is also exhibited. The expression for minimum energy and minimum potential indicate that the ground state energy contains both the mass of both particle and antiparticle agree with the Dirac relativistic quantum theory.
REFERENCES
- Silvast, W.T. (1999) Laser fundamentals. 2nd Edition, Cambridge University Press, Cambridge.
- Yariv, A. (1987) Quantum electronics. 3rd Edition, John Wiley & Sons, New York.
- Ghoshal, S.N. (2004) Atomic physics. 5th Edition, S. Chand & Co, New Delhi.
- Savickas, D. (2003) Relations between Newtonian Mechanics, general relativity, and quantum mechanics. American Journal of Physics, 70, 798-806.
- Jaroszynski, D.A., et al. (1995) Free-electron laser efficiency enhancement, gain enhancement, and spectral control using a step-tapered undulator. Physical Review Letters, 74, 2224-2227.
- Schiff, C.I. (1984) Quantum mechanics. McHill Company, Tokyo.
- Hilo, M.H.M., et al. (2011) Using of the generalized special relativity in estimating the proton (nucleon) mass to explain the mass defect. Natural Science, 3, 141-144. doi:10.4236/ns.2011.32020
- Hilo, M.H.M. (2011) Using of the generalized special relativity in estimating the neutrino masses to explain the conversion of electron neutrinos. Natural Science, 3, 334-338. doi:10.4236/ns.2011.34044
- Hilo, M.H.M. (2011) Using of the generalized special relativity in deriving the equation of the gravitational red shift. Journal of Modern Physics, 2, 370-373. doi:10.4236/jmp.2011.25045

