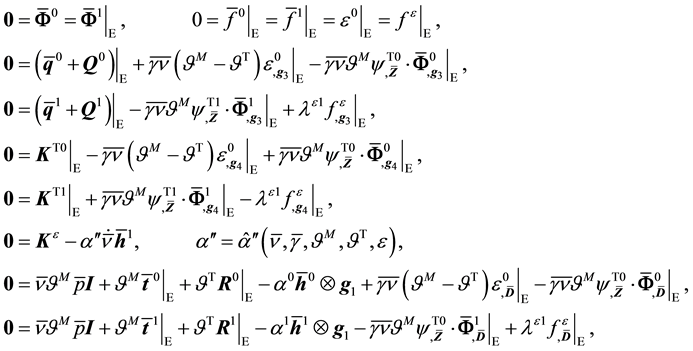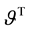Engineering
Vol.06 No.13(2014), Article ID:52463,12 pages
10.4236/eng.2014.613087
Solid Boundary as Energy Source and Sink in a Dry Granular Dense Flow: A Comparison between Two Turbulent Closure Models
Chung Fang
Department of Civil Engineering, National Cheng Kung University, Tainan City, Taiwan
Email: cfang@mail.ncku.edu.tw
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 October 2014; revised 23 November 2014; accepted 7 December 2014
ABSTRACT
Solid boundary as energy source and sink of the turbulent kinetic energy of the grains, and its in- fluence on the mean and turbulent features of a dry granular dense flow, are investigated by using the proposed zero- and first-order turbulent closure models. The first and second laws of ther- modynamics are used to derive the equilibrium closure relations, with the dynamic responses postulated by a quasi-static theory for weak turbulent intensity. Two closure models are applied to analyses of a gravity-driven flow down an inclined moving plane. While the calculated mean porosity and velocity correspond to the experimental outcomes, the influence of the turbulent eddy evolution can be taken into account in the first-order model. Increasing velocity slip on the inclined plane tends to enhance the turbulent dissipation nearby, and the turbulent kinetic energy near the free surface. The turbulent dissipation demonstrates a similarity with that of Newtonian fluids in turbulent boundary layer flows. While two-fold roles of the solid boundary are apparent in the first-order model, its role as an energy sink is more obvious in the zero-order model.
Keywords:
Dry Granular Dense Flow, Gravity Flow, Turbulent Closure Model, Velocity Slip

1. Introduction
Dry granular dense flows are continuous motions of a large amount of discrete solid particles with interstitial space filled by a gas, moving with slow to moderate speed. The grain-grain interaction, in contrast to creeping or rapid flows, results from ong-term enduring frictional contact and sliding, and short-term instantaneous inelastic collision [1] - [4] . Two-fold grain-grain interactions induce fluctuations on the field quantities at the macroscopic level, a phenomenon similar to turbulent motion of Newtonian fluids with two distinctions: 1) it emerges from grain-grain interactions, in contrast to those resulted from incoming flow instability, instability in transition region, or flow geometry in Newtonian fluids; and 2) it emerges at slow speed, in contrast to those in Newtonian fluids which are strongly velocity-dependent, characterized by the critical Reynolds’ number [5] [6] .
Solid boundary has been demonstrated to be an energy source and sink of the turbulent kinetic energy of the grains, and conventional no-slip condition of velocity is not valid [7] [8] . Whereas these influences were hardly accounted for in laminar flow formulations, e.g. [9] - [17] , they were not appropriately taken into account in the limiting turbulent flow formulations, e.g. [18] - [21] . Thus, the goal of the present study is to propose a ther- modynamically consistent turbulent closure model to account for these effects, with their influence on the mean and turbulent flow features. Specifically, a zero- and a first-order closure models are proposed, with the focus on the intercomparison of the roles played by the solid boundary, and the influence of velocity slip.
In the following sections, the mean balance equations, state space and entropy inequality are presented for two models. The closure relations are summarized as results from thermodynamic considerations of the first and second laws. Two closure models are applied to analyses of stationary gravitational flows down an inclined moving plane. While solutions of two models demonstrate a qualitative agreement with experimental outcomes in the mean porosity and velocity profiles, the distributions of the turbulent dissipation are similar to those of Newtonian fluids in turbulent boundary layer flows, with their vanishing and finite values obtained on the free surface by the zero- and first-order models, respectively. Increasing velocity slip near the inclined plane tends to enhance the turbulent dissipation nearby, resulting in larger mean porosity and turbulent kinetic energy near the free surface. While boundary as energy source and sink is apparent in the first-order model, its latter role is more obvious in the zero-order model.
2. Mean Balance Equations and Equilibrium Closure Relations
To account for the distribution of solid volume and its microstructural effect, the (solid) volume fraction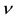 , defined as the total solid volume divided by the volume of a granular representative volume element (RVE), is introduced, with its time evolution described by the Wilmánski model for dense flows [12] [22] . A dense flow is considered a rheological fluid, which must satisfy the basic laws of motion for continuum mechanics. Since in turbulent motion the field quantities experience fluctuations, with solutions random and unpredictable, their sta- tistically averaged values (e.g. Reynolds-averaging) should be defined and investigated. With these, the fol- lowing mean balance equations must be satisfied [5] [12] [23] [24]
, defined as the total solid volume divided by the volume of a granular representative volume element (RVE), is introduced, with its time evolution described by the Wilmánski model for dense flows [12] [22] . A dense flow is considered a rheological fluid, which must satisfy the basic laws of motion for continuum mechanics. Since in turbulent motion the field quantities experience fluctuations, with solutions random and unpredictable, their sta- tistically averaged values (e.g. Reynolds-averaging) should be defined and investigated. With these, the fol- lowing mean balance equations must be satisfied [5] [12] [23] [24]
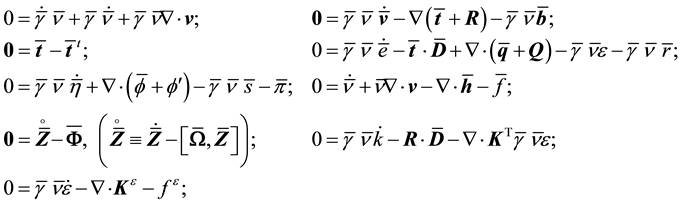
with the ergodic terms,
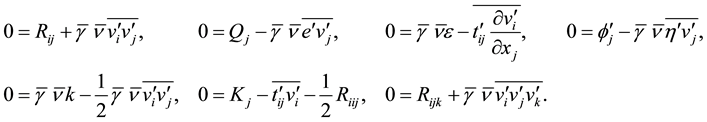 (6)
(6)
The variables and parameters in (1)-(6) are defined in Table 1.
Equations (1)1.2, (2)1.2 and (3)1 are respectively the conventional mean balances of mass, linear momentum, angular momentum, internal energy and entropy for a continuum, with the mean density 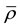 decomposed into
decomposed into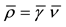 , and the symmetry of the mean Cauchy stress is required. Equation (3)2 is the Wilmánski model for
, and the symmetry of the mean Cauchy stress is required. Equation (3)2 is the Wilmánski model for
Table 1. Variables and parameters in the mean balance equations.
the time evolution of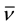 , Equation (4)1 is the phenomenological generalization of the Mohr-Coulomb model for the mean internal friction in a granular material at low energy and high-grain volume fraction [12] [25] [26] , while Equations (4)2 and (5) are the balances of turbulent kinetic energy and dissipation, respectively. They are included to denote the influence of the energy cascade from the mean flow scale toward the smallest (dissipation) scale in turbulent flows. In doing so, two turbulent closure models are constructed: Equations (1)-(4) apply for the zero-order model with the turbulent dissipation considered a closure relation, and Equations (1)-(5) apply for the first-order
, Equation (4)1 is the phenomenological generalization of the Mohr-Coulomb model for the mean internal friction in a granular material at low energy and high-grain volume fraction [12] [25] [26] , while Equations (4)2 and (5) are the balances of turbulent kinetic energy and dissipation, respectively. They are included to denote the influence of the energy cascade from the mean flow scale toward the smallest (dissipation) scale in turbulent flows. In doing so, two turbulent closure models are constructed: Equations (1)-(4) apply for the zero-order model with the turbulent dissipation considered a closure relation, and Equations (1)-(5) apply for the first-order 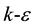 model, in which the time evolutions of the turbulent kinetic energy and dissipation are des- cribed independently and separately.
model, in which the time evolutions of the turbulent kinetic energy and dissipation are des- cribed independently and separately.
For the application of two models, the quantities
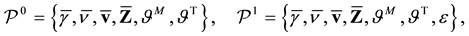 (7)
(7)
are introduced as the primitive mean fields, with the superscripts 0 and 1 denoting the model specification, while the closure relations
 (8)
(8)
are constructed based on the state spaces given by
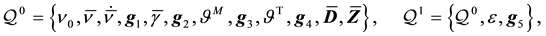 (9)
(9)
with , and
, and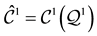 , where
, where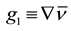 ,
, 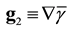 ,
, 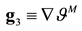 ,
, 
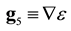
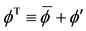
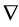

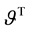

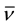


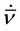



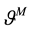

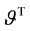
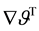

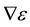
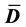
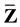
The forms of the closure relations are reduced by the second law of thermodynamics, which is formulated here as the Müller-Liu entropy principle. In its local form, it represents the restriction that the mean entropy production must be non-negative, i.e.,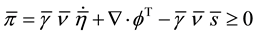
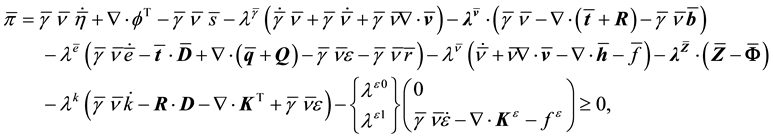
with the mean balance equations appearing as constraints of the entropy inequality, and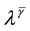

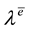
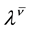

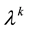
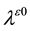
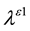
Substituting (8) and (9) into (10) with the assumption of material isotropy and chain rule of differentiation, the corresponding restrictions on forms such as (8) have been defined elsewhere [23] [24] . They are expressions for 
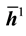

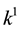


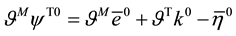
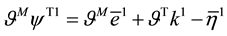
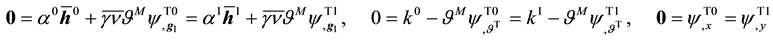
with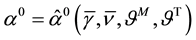
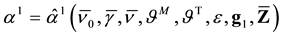
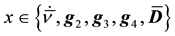
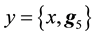
expressions of 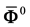
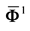
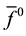

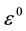
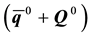

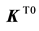
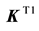


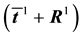

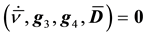
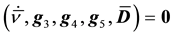
where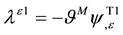
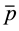
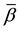
pressures, respectively, viz.,
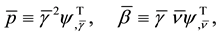
for both models. Otherwise, for incompressible grains, 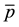
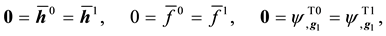

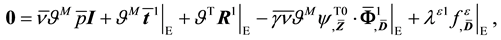
while (11)2-3 and (12)-(16) remain unchanged, with (17) reducing to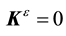
3. Closure Models
For isothermal flows with incompressible grains, we assume that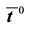

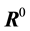
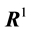
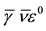
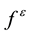

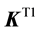

with
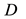
with 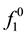
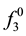
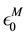


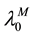
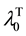

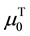
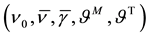
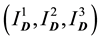
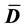

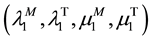
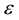
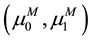
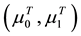

with 

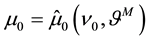
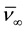
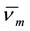
For explicit expressions of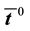
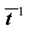
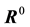
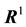

with the plastic contribution confined within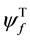
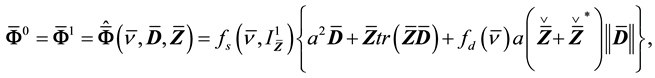
to account for rate-independent characteristics, in which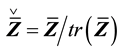
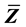
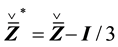

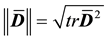

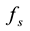

The specific forms (28)-(30) are assigned for both models, for they are proposed based on experiments. With these, the closure relations of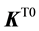

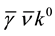

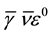
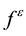
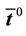
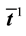
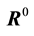


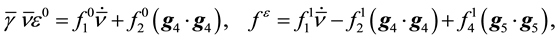


with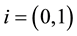

are used. Substituting (20), (21), (30)-(34) into (1)-(5) yields the field equations for both models.
4. Inclined Gravity-Flow Problem
4.1. Field Equations and Boundary Conditions
Consider a fully-developed, isothermal, two-dimensional stationary turbulent shear flow down an inclined mov- ing plane, as shown in Figure 1. With this,
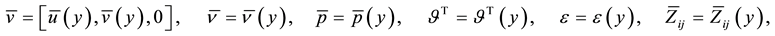
and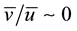

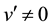

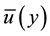
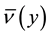


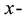

The flow corresponds to the critical state, defined as the state in which 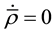
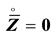


in which
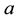
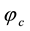
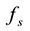
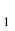

with


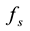
Figure 1. Gravity-driven stationary flow down an inclined moving plane and the coordinate.
Table 2. Dimensionless parameters in the dimensionless field equations.
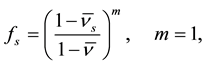
with 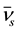

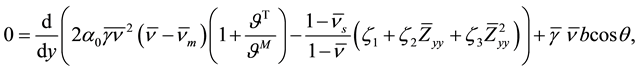


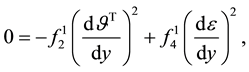
for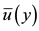
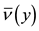
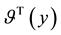

Due to velocity slip, the grains on the solid plane may not assume the plane velocity. Velocity slip provides extra energy flux toward to, or away from the granular body, which is proportional to the square of the slip velocity and with the same direction of the momentum flux on the boundary [7] [8] . On the contrary, due to the experimental setup [37] , 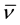

with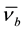
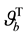
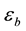
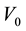
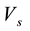
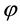
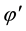
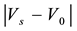
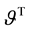
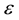

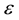
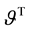


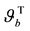
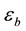
4.2. Nondimensionalization and Numerical Method
With the dimensionless parameters defined in Table 2, Equations (40)-(44) are recast respectively by

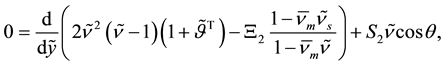
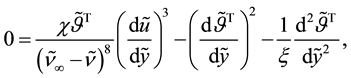
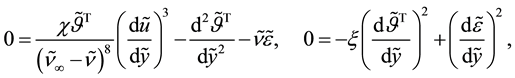
with the dimensionless boundary conditions,
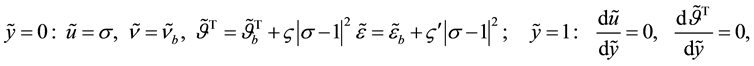
where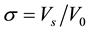
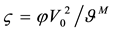

The two-point nonlinear BVPs (46)-(50) are solved numerically by means of the method of successive ap- proximation with under-relaxation scheme. For the implementation of numerical simulation, the values of
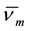
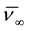

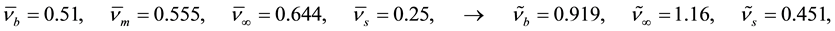
with fixed values of 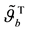
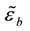
4.3. Numerical Results
As a parametric study, numerical simulations are carried out for variations in
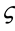
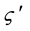


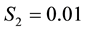
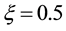

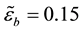
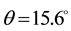
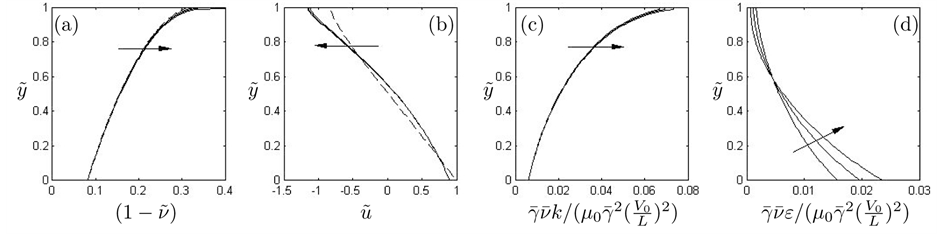
Figure 2 illustrates the profiles of 
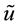

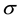
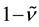
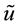
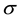
The dimensionless turbulent dissipations, shown in Figure 2(f) and Figure 2(j), decrease from their ma- ximum values on the solid plane toward the minimum values on the free surface with an “exponential-like” tendency in variations in 
Figure 2. Profiles of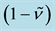
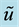
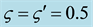
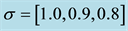
and
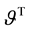
Difference between two models can further be recognized by the profiles of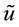
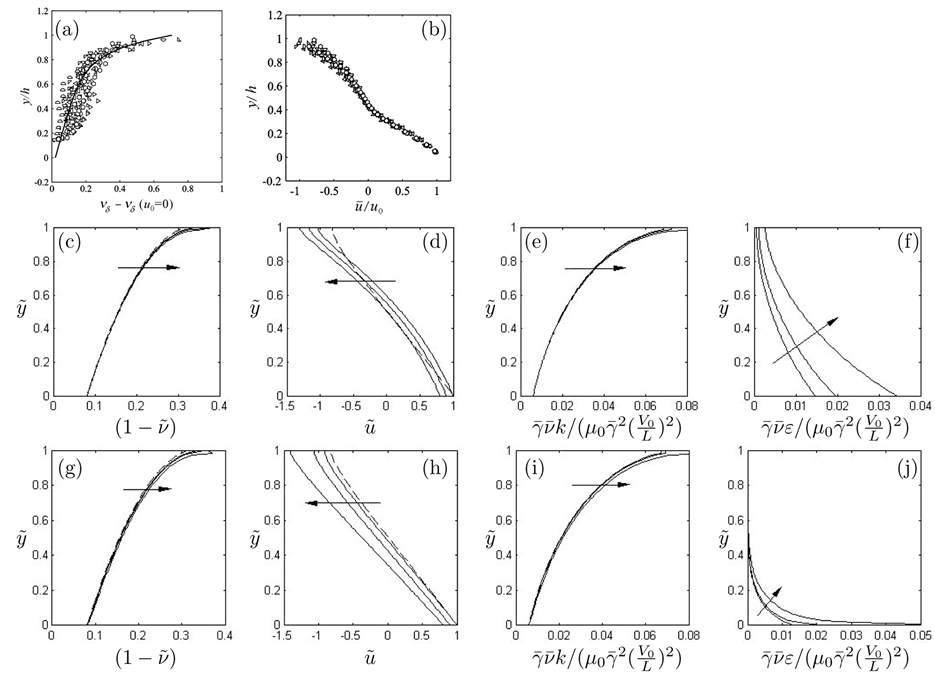
Numerical simulations have been carried out for variations in 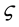
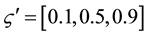

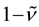
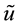
Figure 3. Profiles of
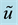


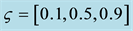
those described in Figure 2. Boundary as energy source and sink is apparent in the first-order model, while its latter role is more obvious in the zero-order model.
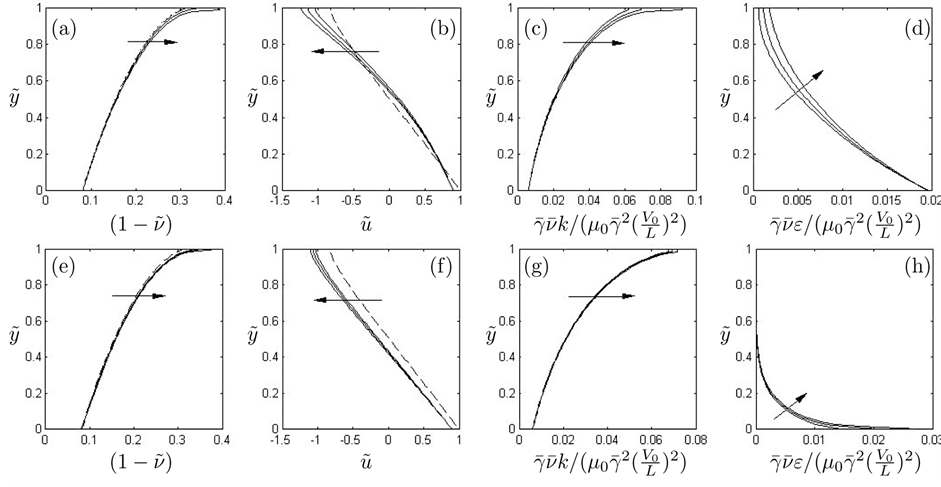
Figure 4 illustrates the profiles of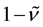


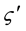
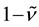
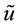
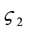
5. Conclusions and Discussions
Boundary as energy source and sink, and the influence of velocity slip near solid boundary on the mean and turbulent features of a dry granular dense flow, were investigated by the proposed zero- and first-order closure models, in which the granular coldness was introduced to index both variations in the turbulent kinetic energy and dissipation in the former model, while they were indexed separately by two independent fields in the latter model. Both models were applied to analyses of isothermal, stationary turbulent shear flows with incompressible grains down an inclined moving plane.
Velocity slip near solid boundary tends to enhance turbulent dissipation in both models. The turbulent dis- sipation profile is similar to that of Newtonian fluids in turbulent boundary layer flows. The first-order model is however more justified, for it asserts that intensive turbulent kinetic energy induces intensive turbulent dis- sipation, with non-vanishing turbulent dissipation obtained on the free surface, in contrast to vanishing turbulent dissipation identified by the zero-order model. In both models, the mean shearing of the solid plane is less
Figure 4. Profiles of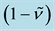
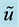
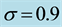
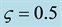

efficiently transferred toward the granular body, and the turbulent dissipation is confined within a thin layer above the solid plane. Outside this thin layer, the grains are dominated by gravity, and collide with one another in a free manner, resulting in significant short-term grain interaction, as reflected by larger mean porosity, vel- ocity and turbulent kinetic energy near the free surface.
Two-fold roles played by the solid boundary are more apparent in the first-order model, while boundary as energy source is less apparent in the zero-order model. Comparison with experiments shows qualitative agree- ment in the 

Acknowledgements
The author is indebted to the Ministry of Science and Technology, Taiwan, for the financial support through the project MOST 103-2221-E-006-116.
References
- Aranson, I.S. and Tsimring, L.S. (2009) Granular Patterns. Oxford University Press, Oxford.
- Ausloos, M., Lambiotte, R., Trojan, K., Koza, Z. and Pekala, M. (2005) Granular Matter: A Wonderful World of Clusters in Far-from-Equilibrium Systems. Physica A, 357, 337-349. http://dx.doi.org/10.1016/j.physa.2005.06.034
- Pöschel, T. and Brilliantov, N.V. (2013) Granular Gas Dynamics. In: Lecture Notes in Physics (Book 624), Springer- Verlag, New York.
- Rao, K.K. and Nott, P.R. (2008) Introduction to Granular Flows. Cambridge University Press, London. http://dx.doi.org/10.1017/CBO9780511611513
- Batchelor, G.K. (1993) The Theory of Homogeneous Turbulence. Cambridge University Press, Cambridge.
- Tsinober, A. (2009) An Informal Conceptual Introduction to Turbulence. Springer, Heidelberg. http://dx.doi.org/10.1007/978-90-481-3174-7
- Richman, M.W. (1988) Boundary Conditions Based upon a Modified Maxwellian Velocity Distribution for Flows if Identical, Smooth, nearly Elastic Spheres. Acta Mechanica, 75, 227-240. http://dx.doi.org/10.1007/BF01174637
- Richman, M.W. and Marciniec, R.P. (1990) Gravity-Driven Granular Flows of Smooth, Inelastic Spheres down Bumpy Inclines. Journal of Applied Mechanics, 57, 1036-1043. http://dx.doi.org/10.1115/1.2897623
- Campbell, C.S. (2005) Stress-Controlled Elastic Granular Shear Flows. Journal of Fluid Mechanics, 539, 273-297. http://dx.doi.org/10.1017/S0022112005005616
- Daniel, R.C., Poloski, A.P. and Sáez, A.E. (2007) A Continuum Constitutive Model for Cohesionless Granular Flows. Chemical Engineering Science, 62, 1343-1350. http://dx.doi.org/10.1016/j.ces.2006.11.035
- Faccanoni, G. and Mangeney, A. (2013) Exact Solution for Granular Flows. International Journal for Numerical and Analytical Methods in Geomechanics, 37, 1408-1433. http://dx.doi.org/10.1002/nag.2124
- Fang, C. (2009) Gravity-Driven Dry Granular Slow Flows down an Inclined Moving Plane: A Comparative Study between Two Concepts of the Evolution of Porosity. Rheologica Acta, 48, 971-992. http://dx.doi.org/10.1007/s00397-009-0378-4
- Fang, C. (2010) Rheological Characteristics of Solid-Fluid Transition in Dry Granular Dense Flows: A Thermodynamically Consistent Constitutive Model with a Pressure-Ratio Order Parameter. International Journal for Numerical and Analytical Methods in Geomechanics, 34, 881-905.
- Jop, P. (2008) Hydrodynamic Modeling of Granular Flows in a Modified Couette Cell. Physical Review E, 77, Article ID: 032301. http://dx.doi.org/10.1103/PhysRevE.77.032301
- Jop, P., Forterre, Y. and Pouliquen, O. (2006) A Constitutive Law for Dense Granular Flows. Nature, 441, 727-730. http://dx.doi.org/10.1038/nature04801
- Savage, S.B. (1993) Mechanics of Granular Flows. In: Hutter, K., Ed., Continuum Mechanics in Environmental Sci- ences and Geophysics, Springer, Heidelberg, 467-522. http://dx.doi.org/10.1007/978-3-7091-2600-4_6
- Wang, Y. and Hutter, K. (1999) A Constitutive Theory of Fluid-Saturated Granular Materials and Its Application in Gra- vitational Flows. Rheologica Acta, 38, 214-223. http://dx.doi.org/10.1007/s003970050171
- Ahmadi, G. (1985) A Turbulence Model for Rapid Flows of Granular Materials. Part I. Basic Theory. Powder Technology, 44, 261-268. http://dx.doi.org/10.1016/0032-5910(85)85008-7
- Ahmadi, G. and Shahinpoor, M. (1983) Towards a Turbulent Modeling of Rapid Flow of Granular Materials. Powder Technology, 35, 241-248. http://dx.doi.org/10.1016/0032-5910(83)87014-4
- Luca, I., Fang, C. and Hutter, K. (2004) A Thermodynamic Model of Turbulent Motions in a Granular Material. Continuum Mechanics and Thermodynamics, 16, 363-390. http://dx.doi.org/10.1007/s00161-003-0163-z
- Ma, D. and Ahmadi, G. (1985) A Turbulence Model for Rapid Flows of Granular Materials. Part II. Simple Shear Flows. Powder Technology, 44, 269-279. http://dx.doi.org/10.1016/0032-5910(85)85009-9
- Wilmánski, K. (1996) Porous Media at Finite Strains. The New Model with the Balance Equation of Porosity. Archives of Mechanics, 48, 591-628.
- Fang, C. and Wu, W. (2014) On the Weak Turbulent Motions of an Isothermal Dry Granular Dense Flow with Incompressible Grains, Part I. Equilibrium Turbulent Closure Models. Acta Geotechnica, 9, 725-737. http://dx.doi.org/10.1007/s11440-014-0313-4
- Fang, C. (2014) A k-ε Turbulent Closure Model of an Isothermal Dry Granular Dense Matter, Part I: Equilibrium Closure Relations. Acta Mech. (In Review)
- Hutter, K. and Wang, Y. (2003) Phenomenological Thermodynamics and Entropy Principle. In: Greven, A., Keller, G. and Warnecke, G., Eds., Entropy, Princeton University Press, Princeton, 57-77.
- Kirchner, N. (2002) Thermodynamically Consistent Modeling of Abrasive Granular Materials. I: Non-Equilibrium Theory. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 458, 2153-2176. http://dx.doi.org/10.1098/rspa.2002.0963
- Goldhirsch, I. (2008) Introduction to Granular Temperature. Powder Technology, 182, 130-136. http://dx.doi.org/10.1016/j.powtec.2007.12.002
- Vescovi, D., di Prisco, C. and Berzi, D. (2013) From Solid to Granular Gases: The Steady State for Granular Materials. International Journal for Numerical and Analytical Methods in Geomechanics, 37, 2937-2951. http://dx.doi.org/10.1002/nag.2169
- Fang, C. and Wu, W. (2014) On the Weak Turbulent Motions of an Isothermal Dry Granular Dense Flow with Incompressible Grains: Part II. Complete Closure Models and Numerical Simulations. Acta Geotechnica, 9, 739-752. http://dx.doi.org/10.1007/s11440-014-0314-3
- Fang, C. (2014) A k-ε Turbulent Closure Model of an Isothermal Dry Granular Dense Matter, Part II: Closure Model and Numerical Simulations. Acta Mech. (In Review)
- Fellin, W. (2013) Extension to Barodesy to Model Void Ratio and Stress Dependency of the Ko Value. Acta Geotechnica, 8, 561-565. http://dx.doi.org/10.1007/s11440-013-0238-3
- Fuentes, W., Triantaftllidis, T. and Lizcano, A. (2012) Hypoplastic Model for Sands with Loading Surface. Acta Geotechnica, 7, 177-192. http://dx.doi.org/10.1007/s11440-012-0161-z
- Ai, J., Langston, P.A. and Yu, H.S. (2014) Discrete Element Modeling of Material Non-Coaxiality in Simple Shear Flows. International Journal for Numerical and Analytical Methods in Geomechanics, 38, 615-635. http://dx.doi.org/10.1002/nag.2230
- Kirchner, N. and Teufel, A. (2002) Thermodynamically Consistent Modeling of Abrasive Granular Materials. II: Ther- modynamic Equilibrium and Applications to Steady Shear Flows. Proceedings of the Royal Society A, 458, 3053-3077. http://dx.doi.org/10.1098/rspa.2002.1020
- Bauer, E. and Herle, I. (2000) Stationary States in Hypoplasticity. In: Kolymbas, D., Ed., Constitutive Modeling of Granular Materials, Springer Verlag, Berlin, Heidelberg, New York, 167-192. http://dx.doi.org/10.1007/978-3-642-57018-6_7
- Herle, I. and Gudehus, G. (1999) Determination of Parameters of a Hypoplastic Constitutive Model from Properties of Grain Assemblies. Mechanics of Cohesive-Frictional Materials, 4, 461-486. http://dx.doi.org/10.1002/(SICI)1099-1484(199909)4:5<461::AID-CFM71>3.0.CO;2-P
- Perng, A.T.H., Capart, H. and Chou, H.T. (2006) Granular Configurations, Motions, and Correlations in Slow Uniform Flows Driven by an Inclined Conveyor Belt. Granular Matter, 8, 5-17. http://dx.doi.org/10.1007/s10035-005-0213-2