Engineering
Vol. 4 No. 10 (2012) , Article ID: 23363 , 4 pages DOI:10.4236/eng.2012.410084
Multi-Objective Optimization of Pilots’ FFS Recurrent Training Problem
Institute of Policy and Management, Chinese Academy of Sciences, Beijing, China
Email: mggao@casipm.ac.cn
Received July 21, 2012; revised August 24, 2012; accepted September 3, 2012
Keywords: PFRT Problem; Multi-Objective Programming; Bipartite Graph; Longest-Route Problem; Graphic Method
ABSTRACT
Two multi-objective programming models are built to describe Pilots’ full flight simulator (FFS) recurrent training (PFRT) problem. There are two objectives for them. One is the best matching of captains and copilots in the same aircraft type. The other is that pilots could attend his training courses at proper month. Usually the two objectives are conflicting because there are copilots who will promote to captains or transfer to other aircraft type and new trainees will enter the company every year. The main theme in the research is to find the final non-inferior solutions of PFRT problem. Graph models are built to help to analyze the problem and we convert the original problem into a longest-route problem with weighted paths. An algorithm is designed with which we can obtain all the non-inferior solutions by a graphic method. A case study is present to demonstrate the effectiveness of the algorithm as well.
1. Introduction
With the rapid development of the air transportation, aviation safety has become an important issue in Chinese airline companies. FFS (full flight simulator) recurrent training is an important method to ensure airmen’s flight safety. Pilots need to take FFS (full flight simulator) recurrent training every half a year in order to keep the pilot qualification in Chinese airways [1]. It allows two airmen to be trained in an FFS at the same time and the two men had better be a captain and a copilot for the best training effect. Moreover, an airman’s fitting month for the training is from the fifth month to the seventh month after his last training. And the sixth month after his last training is his optimal training month because it is a resource waste for him to be trained in the fifth month and he will not get the best training effect when the training is implemented in the seventh month. To make the plan, we should take these two objectives into account. So PFRT problem is a multi-objective problem.
Pan et al. studied the problem and present a decomposition algorithm [1]. However, the algorithm is not a polynomial time algorithm. Liu [2] described the problem with multiple resource constraints and a Genetic Algorithm was designed to solve it. The algorithm is an approximation algorithm which cannot get the optimal results in general. PFRT problem with resource constraints is an NP-hard problem in theory [3].
Multi-objective programming involves recognition that the decision maker is responding to multiple objectives. Generally, the objectives are conflicting, so that not all objectives can simultaneously arrive at their optimal levels. An assumed utility function is used to choose appropriate solutions. Several fundamentally different utility function form s have been used in multi-objective models. These forms may be divided into three classes: lexicographic, multi-attribute utility and unknown utility. The lexicographic utility function specification assumes that the decision maker has a strictly ordered preemptive preference system among objectives with fixed target levels. Multi-attribute utility approaches allow tradeoffs between objectives in the attainment of maximum utility. The third utility approach involves an unknown utility function assumption. Here the entire Pareto efficient (nondominated) solution set is generated so that every solution is reported wherein one of the multiple objectives is as satisfied as it possibly can be without making any other objective worse off [4]. Many techniques have been developed to solve the multi-objective programming, such as tabu search [5,6], simulated annealing [7], and foremost evolutionary algorithms [8,9]. And other important publications on metaheuristics for multi-objective optimization include the work of Gandibleux et al. [10,11].
PFRT problem is analyzed in this study. In part 2, we describe the problem with mathematical programming models. We generate graphs with which we transform the problem into a longest-route problem on weighted paths. A polynomial time algorithm is developed to solve PFRT problem. In part 3, a case study is given. In last part, we summarize the work.
2. Models and Methodology
2.1. Mathematical Programming Models
The two objectives of PFRT problem are conflicting and the problem can be described as programming (a) and (b).
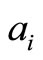 : the number of the captains whose optimal training month is
: the number of the captains whose optimal training month is .
.
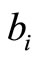 : the number of the copilots whose optimal training month is
: the number of the copilots whose optimal training month is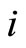 .
.
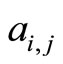 : the number of the captains whose optimal training month is i and who will attend the training in month
: the number of the captains whose optimal training month is i and who will attend the training in month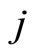 .
.
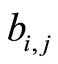 : the number of the captains whose optimal training month is i and who will attend the training in month
: the number of the captains whose optimal training month is i and who will attend the training in month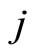 .
.
We describe the PFRT problem as the following multi-objective mathematical programming model:
Programming (a):
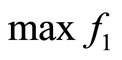 (1)
(1)
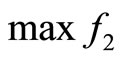 (2)
(2)
where
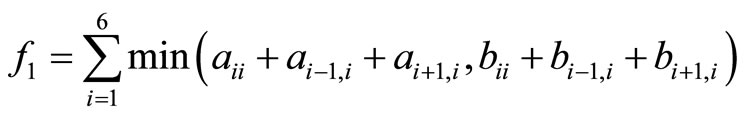
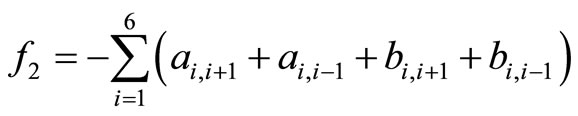
Subject to
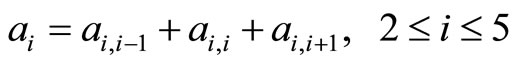 ; (3)
; (3)
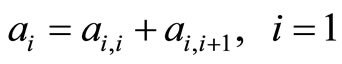 ; (4)
; (4)
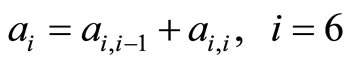 ; (5)
; (5)
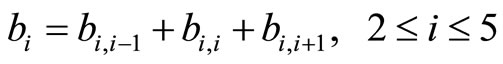 ; (6)
; (6)
 ; (7)
; (7)
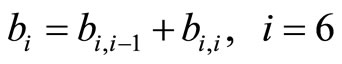 ; (8)
; (8)
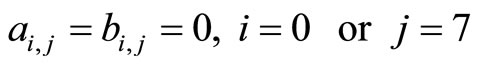 ; (9)
; (9)
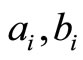 are positive integers and
are positive integers and 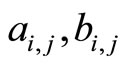 are all nonnegative integers.
are all nonnegative integers.
The first objective of the programming is to maximize the number of captains who are matched with copilots. The other objective is to minimize the number of the pilots who will not be trained in their optimal training months. The Formulas (3)-(9) assure all pilots will be trained.
The general model for the problem can be described as:
Programming (b):
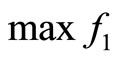 (10)
(10)
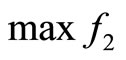 (11)
(11)
Subject to
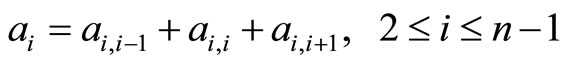 ; (12)
; (12)
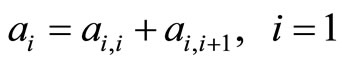 ; (13)
; (13)
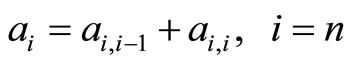 ; (14)
; (14)
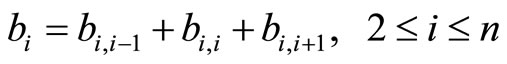 ; (15)
; (15)
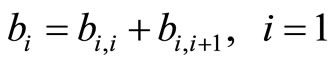 ; (16)
; (16)
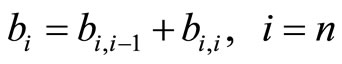 ; (17)
; (17)
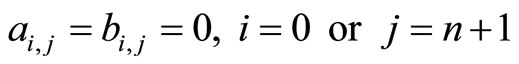 (18)
(18)
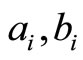 are all positive integer and
are all positive integer and 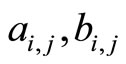 are all nonnegative integer.
are all nonnegative integer.
The key work of this research is to find the non-inferior solutions. We will find an initial non-inferior solution by two steps. Firstly, we consider the programming with a single objective as follows. Secondly we will convert get other non-inferior solution by a graphic method in part 2.2.
Programming (c):
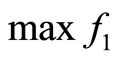 (19)
(19)
Subject to the constraints (12)-(18).
Here let 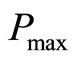 denote the optimal value for this programming. Then we solve the following programming.
denote the optimal value for this programming. Then we solve the following programming.
Programming (d):
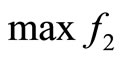 (20)
(20)
Subject to the constraints (12)-(18) and
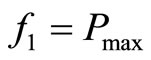 (21)
(21)
Let 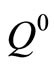 denote the optimal value for this programming and the optimal solutions is the initialization for the following graph models. We will give a graphic method to find all the other non-inferior solutions sequentially.
denote the optimal value for this programming and the optimal solutions is the initialization for the following graph models. We will give a graphic method to find all the other non-inferior solutions sequentially.
2.2. Graph Models
We draw a bipartite graph 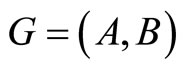 in Figure 1. The vertex
in Figure 1. The vertex 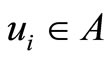 denotes the captains whose optimal training month is i. And the vertex
denotes the captains whose optimal training month is i. And the vertex 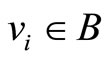 denotes the copilots whose optimal training month is i. Here
denotes the copilots whose optimal training month is i. Here 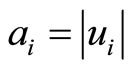 denotes the module of
denotes the module of , i.e. the number of the captains in
, i.e. the number of the captains in 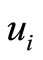 and
and 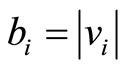 denotes the module of
denotes the module of 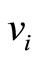 and
and 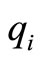 denotes the number of the pilots trained in their optimal training month i. There is an edge
denotes the number of the pilots trained in their optimal training month i. There is an edge 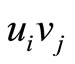 weighted by
weighted by 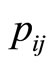 ended by
ended by 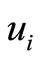 and
and 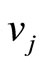 when there exist
when there exist 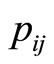 pairs of captains and copilots we match between
pairs of captains and copilots we match between
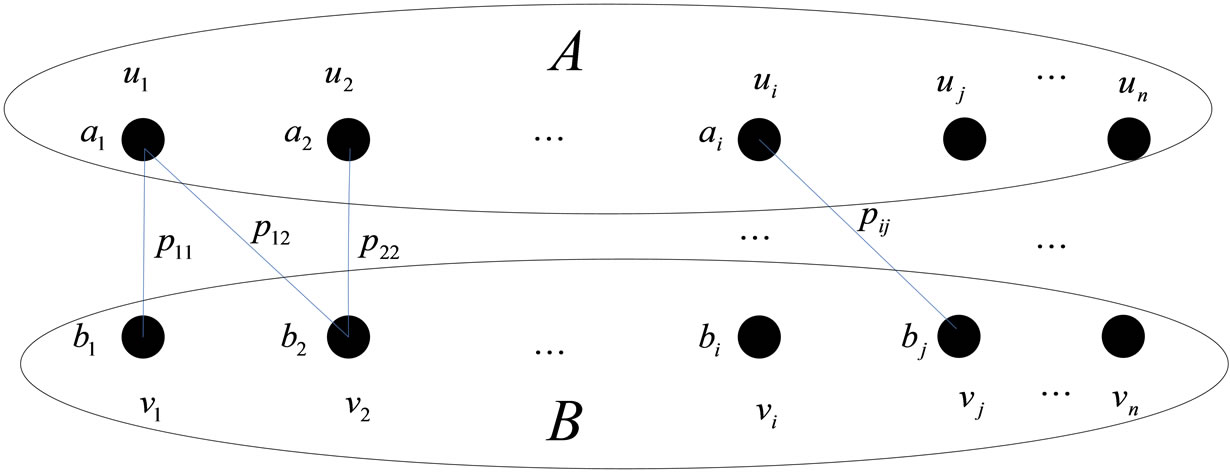
Figure 1. Bipartite graph G.
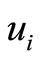 and
and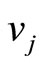 .
.
In graph 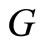 there may be an edge
there may be an edge  ended by
ended by 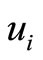 and
and 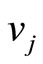 where
where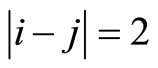 . In other words, there are a captain
. In other words, there are a captain 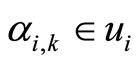 and a copilot
and a copilot 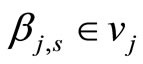 matched where
matched where 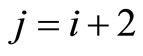 (or
(or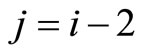 ). Suppose
). Suppose 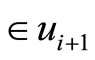
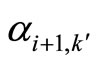 (or
(or ) and
) and 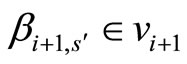 (
(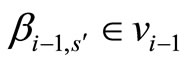 ) are matched in graph
) are matched in graph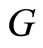 , we can change the training plan by matching
, we can change the training plan by matching 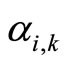 to
to 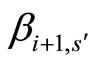 and
and 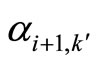 to
to 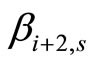 (or
(or 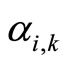 to
to 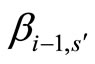 and
and 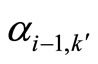 to
to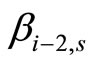 ). Then we suppose there are no
). Then we suppose there are no 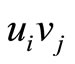 ended by
ended by 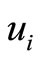 and
and 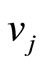 where
where 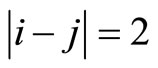 in the following part of the study.
in the following part of the study.
Let 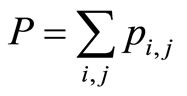 and
and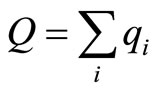 . What we will do in next parts of this study is to find the largest Q when
. What we will do in next parts of this study is to find the largest Q when 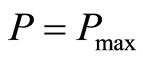 is decreased by k where k = 1, 2, ....
is decreased by k where k = 1, 2, ....
We assume there are three possible nexus among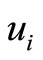 ,
, 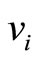 ,
, 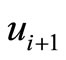 and
and 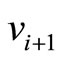 in graph G shown in Figure 2.
in graph G shown in Figure 2.
We consider two types to change the nexus among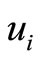 ,
, 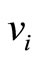 ,
,  and
and 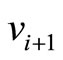 in
in 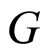 as follows. One is to break a pair on edge
as follows. One is to break a pair on edge 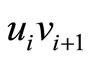 in case 1 in Fiugre 3 or to break a pair on edge
in case 1 in Fiugre 3 or to break a pair on edge 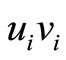 and a pair on edge
and a pair on edge 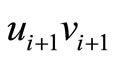 and rebuilt a new pair between
and rebuilt a new pair between  and
and 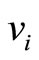 in case 2 and case 3. It is denoted by
in case 2 and case 3. It is denoted by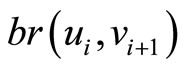 . The other is to break a pair on edge
. The other is to break a pair on edge 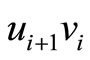 in case 2 in Figure 3 or to break a pair on edge
in case 2 in Figure 3 or to break a pair on edge 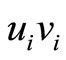 and a pair on edge
and a pair on edge 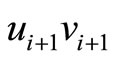 and rebuilt a new pair between
and rebuilt a new pair between 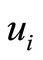 and
and 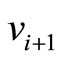 in case 1 and 3. It is denoted by
in case 1 and 3. It is denoted by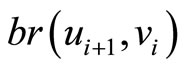 .
.
Then we can conclude that we can find the solution of the problem with 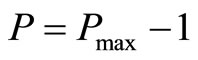 by
by 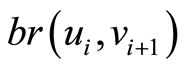 or
or 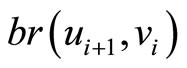 for all
for all 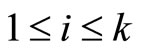 where
where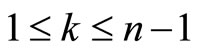 .
.
We generate another two weighted graphs 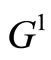 and
and 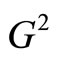 in Figure 3 from the recurrent training graph
in Figure 3 from the recurrent training graph 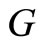 in Figure 1.
in Figure 1.
Here 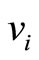 denotes month
denotes month 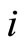 in Figure 3 and
in Figure 3 and 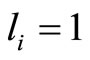 when there exist edge
when there exist edge 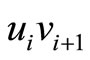 in graph
in graph , or else,
, or else, . And
. And 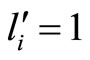 when there exists edge
when there exists edge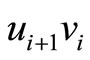 , or else,
, or else,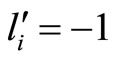 . Let
. Let 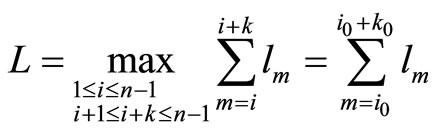 and
and 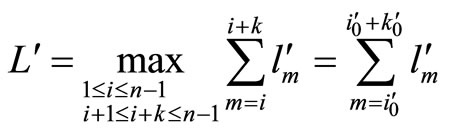 .
.
Then we have the follow theorem.
Theorem 1:
Let 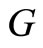 be the graph with
be the graph with 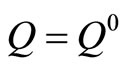 and
and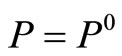 , we got a non-inferior solution
, we got a non-inferior solution 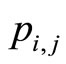 in graph
in graph 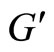 with the largest
with the largest 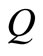 where
where 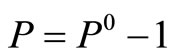 when we change the nexus among vertices in graph G by:
when we change the nexus among vertices in graph G by:
(a) 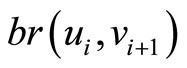 for all
for all 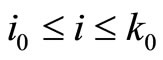 when
when 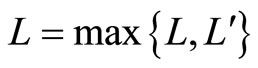 and
and
(b) 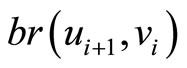 for all
for all 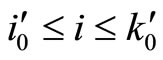 when
when 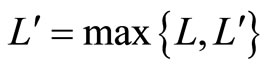 .
.
Proof:
In case (a) we find that the nexus among the vertices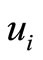 ,
, 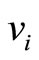 ,
, 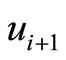 and
and 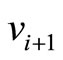 is case 1 in Figure 3 when
is case 1 in Figure 3 when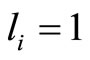 . When we change the nexus among
. When we change the nexus among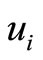 ,
, 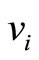 ,
, 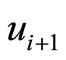 and
and 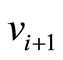 by
by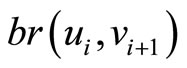 ,
, 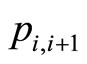 reduces one and the sum of
reduces one and the sum of 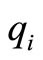 and
and 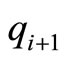 increases 1, which equals to
increases 1, which equals to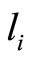 , as an result. The nexus among
, as an result. The nexus among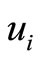 ,
, 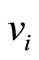 ,
, 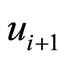 and
and 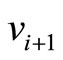 is case 2 or case 3 when
is case 2 or case 3 when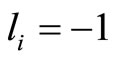 , and when we change the nexus by
, and when we change the nexus by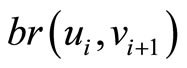 , we will get a new pair between
, we will get a new pair between 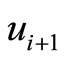 and
and 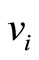 where
where 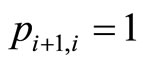 and the sum of
and the sum of 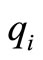 and
and 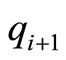 is decreased by one and the sum of
is decreased by one and the sum of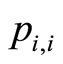 ,
, 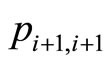 and
and 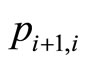 is reduced by one as well, corresponding to
is reduced by one as well, corresponding to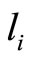 . In conclusion, when we change the nexus among
. In conclusion, when we change the nexus among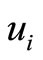 ,
, 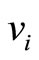 ,
, 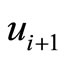 and
and 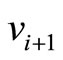 by
by 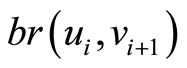 we increase the sum of
we increase the sum of 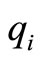 and
and 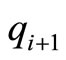 by
by 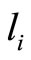 and increase
and increase 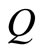 by
by 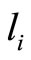 in other words. Then to find the largest
in other words. Then to find the largest 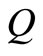 where
where 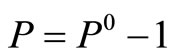 in graph
in graph 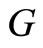 is to find the longest path in graph
is to find the longest path in graph 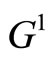 when
when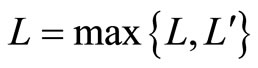 . Case (b) can be proved similarly.
. Case (b) can be proved similarly.
2.3. Algorithm
In this part an algorithm as follows is designed to solve PFRT problem.
Step 1: Initialize: t = 0; for all 1≤ i ≤ n, ai = the number of the captains whose optimal training month is i and bi = the number of the copilots whose optimal training month is i.
Step 2: Find the optimal solutions of programming (c) and (d). 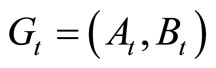 denotes the graph with
denotes the graph with 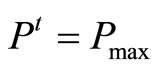 and
and 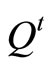 = the maximum quantity of pilots who will be trained in their optimal training month.
= the maximum quantity of pilots who will be trained in their optimal training month.
Step 3: Generate the weighted graphs 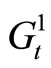 and
and 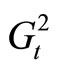
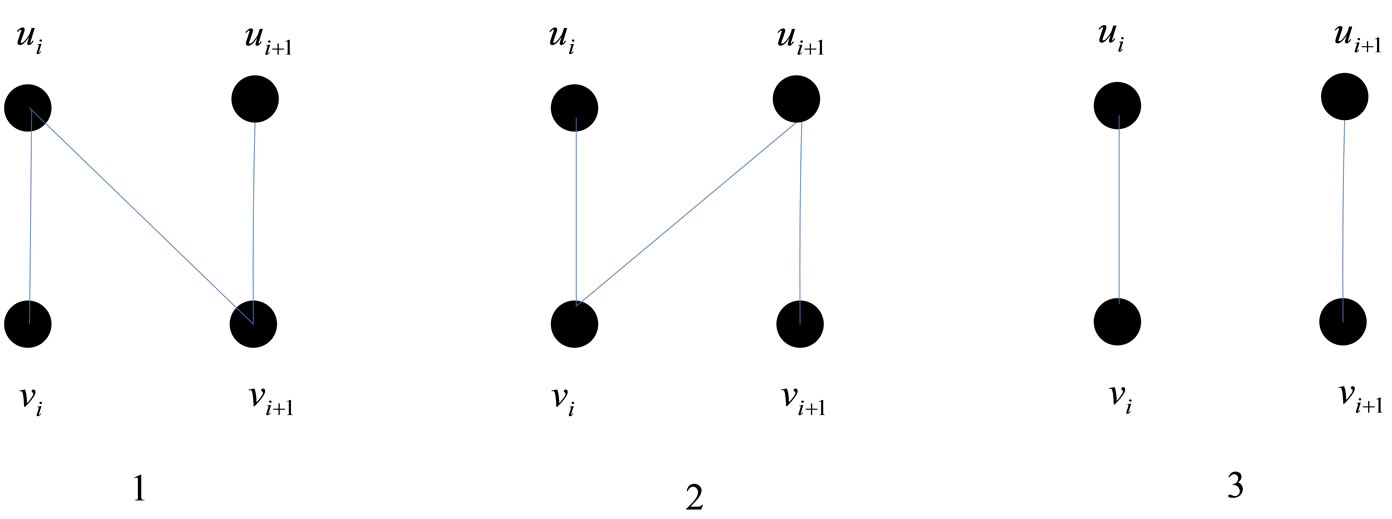
Figure 2. Nexus among ui, vi, ui+1 and vi+1 in graph G.
from the graph . Find the longest path in the graphs
. Find the longest path in the graphs
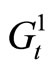 and
and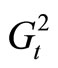 .
. 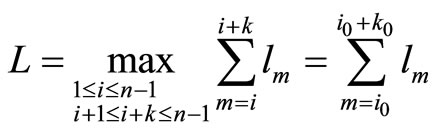 and
and
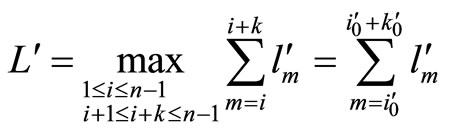 . If
. If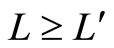 , go to step 4.
, go to step 4.
Else go to step 5.
Step 4: Change the nexus among the vertice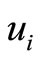 ,
, 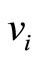 ,
, 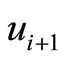 and
and 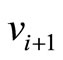 by
by 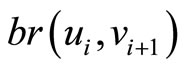 for
for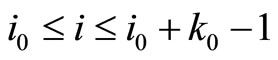 . Go to step 6.
. Go to step 6.
Step 5: Change the nexus among the vertices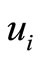 ,
, 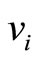 ,
, 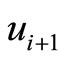 and
and 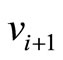 by
by 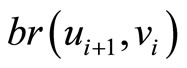 for
for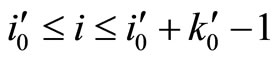 . Go to step 6.
. Go to step 6.
Step 6: If the non-inferior solution we got in the previous step is not the final solution, let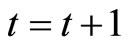 ,
, 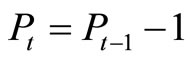 , go to step 3, else go to step 7.
, go to step 3, else go to step 7.
Step 7: Output the final solution, stop.
3. A Case Study
There are 314 captains and 313 copilots in an airline company. Their FFS training demand is shown in Table 1 and 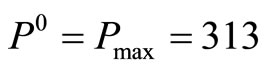 is achieved in Table 2 and Figure 4 where
is achieved in Table 2 and Figure 4 where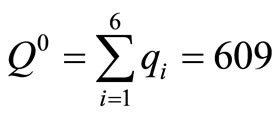 . We paired up 313 pairs of captains and copilots. 609 pilots will attend FFS training in their optimal training months. There are 18 pilots who have to attend the training in the previous month or the succeeding month of their optimal training months.
. We paired up 313 pairs of captains and copilots. 609 pilots will attend FFS training in their optimal training months. There are 18 pilots who have to attend the training in the previous month or the succeeding month of their optimal training months.

Table 1. FFS training demand for all pilots

Table 2.  and
and .
.

Figure 4. The initial non-inferior solution with P0 = 313 in graph G0.
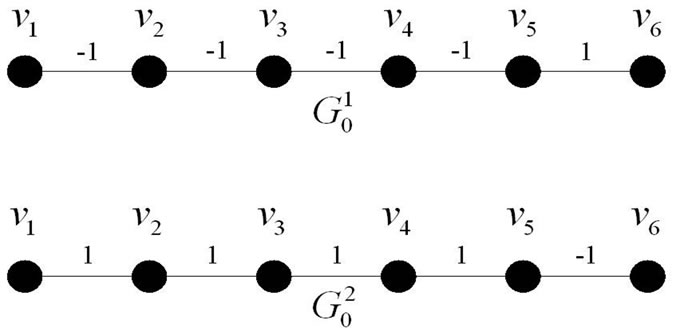
Figure 5. Generated graphs of G0.
And there is one captain in month 5 who cannot be trained with copilots because the sum of captains is more than that of copilots.
We draw a couple of new graphs 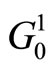 and
and 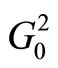 as follows.
as follows.
We can find that the longest route in graph 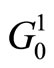 is
is 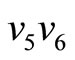 where L = 1 and the longest route in graph
where L = 1 and the longest route in graph 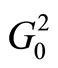 is
is 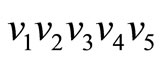 where L = 4. We change the nexus among
where L = 4. We change the nexus among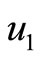 ,
, 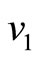 ,
, 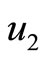 and
and 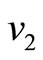 by
by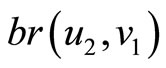 . Then
. Then 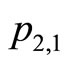 will reduce one and
will reduce one and 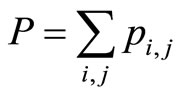 will reduce one as well. In the same time
will reduce one as well. In the same time 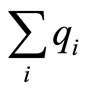 will increase one. When we change the nexus among
will increase one. When we change the nexus among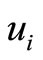 ,
, 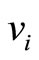 ,
, 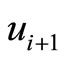 and
and 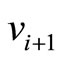 by
by 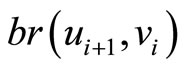 as well where
as well where  and rematch the pairs of unmatched captains and copilots who have the same optimal training month, we will get a new graph
and rematch the pairs of unmatched captains and copilots who have the same optimal training month, we will get a new graph 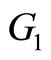 with the largest
with the largest 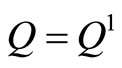 where
where 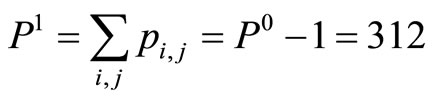 and
and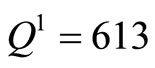 . Then we get a new non-inferior solution described in Table 3.
. Then we get a new non-inferior solution described in Table 3.
Now we paired up 312 pairs of captains and copilots. 613 pilots will attend FFS training in their optimal training months. There are 14 pilots who have to attend the training in the previous month or the succeeding month of their optimal training months. And there are 3 pilots in month 5 and month 1 who cannot be matched with other pilots.
Repeating above steps, we will get the following solutions shown in Tables 4-6.
Now we get all non-inferior solutions.
4. Conclusions
The air transportation developed rapidly in China and it becomes crucially important for airline companies to

Table 3. P1 = 312 and Q1 = 613.

Table 4. P1 = 311 and Q1 = 617.
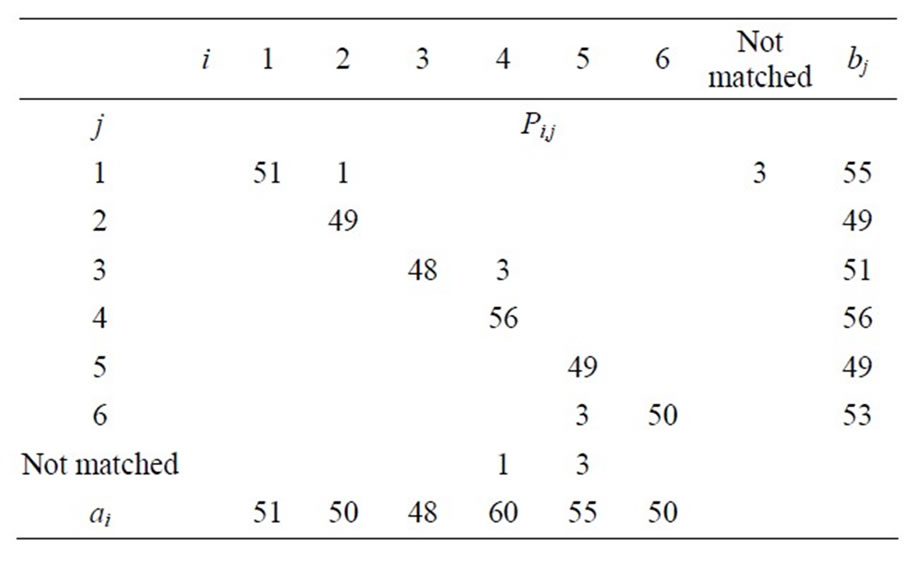
Table 5. P1 = 310 and Q1 = 620.
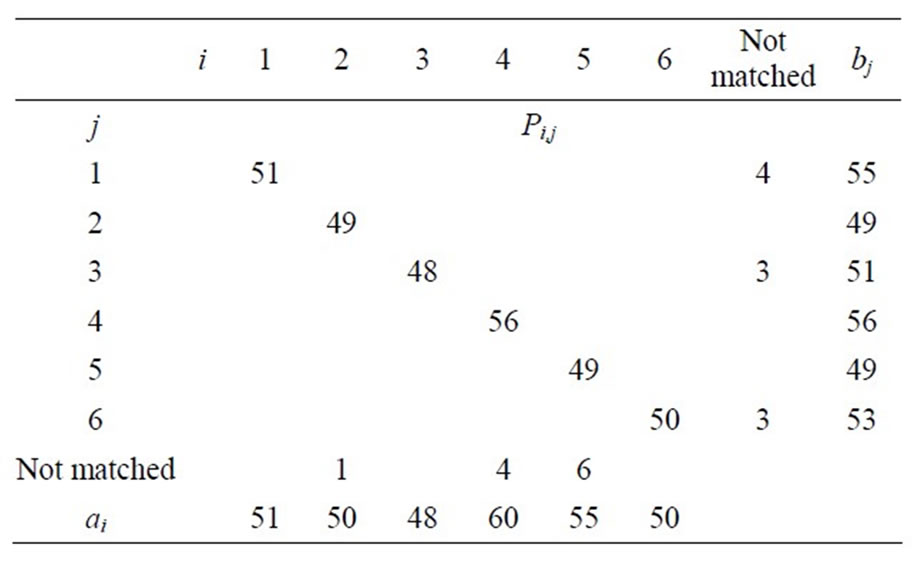
Table 6. P1 = 310 and Q1 = 627.
training pilots so as to ensure the aviation safety.
PFRT problem is a multi-objective pilots training problem. Mathematic models and graph models about it are built. According to the characteristics of the problem, we convert it into a longest-route problem with weighted paths and design an algorithm to solve it.
This method can effectively generate pilots’ FFS training plans with two kinds of personnel.
Due to the method in this study cannot solve the similar problem involving more than two kinds of personnel yet, further research should be done on it.
5. Acknowledgements
I thank members of the Research Center of Overall Planning Safety and Security Management, Institute of Policy and Management, Chinese Academy of Sciences, for their help in this study. We are also very grateful to the reviewers for their invaluable suggestions to improve the quality of the manuscript.
REFERENCES
- B. C. Pan, Z. Y. Song, et al., “The Research on Optimization Model for Recurrent Training Plan of Aviator Full Flight Simulators,” Chinese Journal of Management Science, Vol. 16, No. 2, 2008, pp. 69-75.
- W. B. Liu, S. Z. Zhang and B. L. Shi, “Solution of Pilot Simulator Timetable Problem Based on Genetic Algorithm,” Computer Engineering, Vol. 37, No. 15, 2011, pp. 140-142.
- I. H. Toroslu and Y. Arslanoglu, “Genetic Algorithm for the Personnel Assignment Problem with Multiple Objectives,” Information Sciences, Vol. 177, No. 3, 2007, pp. 787-803. doi:10.1016/j.ins.2006.07.032
- A. M. Geoffrion, “Proper Efficiency and the Theory of Vector Maximization,” Journal of Mathematical Analysis and Applications, Vol. 22, No. 3, 1968, pp. 618-630. doi:10.1016/0022-247X(68)90201-1
- J. F. Cordeau and M. Maischberger, “A Parallel Iterated Tabu Search Heuristic for Vehicle Routing Problems,” Computers & Operations Research, Vol. 39, No. 9, 2012, pp. 2033-2050. doi:10.1016/j.cor.2011.09.021
- Q. H. Wu, J. K. Hao, et al., “Multi-Neighborhood Tabu Search for the Maximum Weight Clique Problem,” Annals of Operations Research, Vol. 196, No 1, 2012, pp. 611-634. doi:10.1007/s10479-012-1124-3
- R. Kia, A. Baboli, et al., “Solving a Group Layout Design Model of a Dynamic Cellular Manufacturing System with Alternative Process Routings, Lot Splitting and Flexible Reconfiguration by Simulated Annealing,” Computers & Operations Research, Vol. 39, No. 11, 2012, pp. 2642- 2658. doi:10.1016/j.cor.2012.01.012
- K. Deb, “Multi-Objective Optimization Using Evolutionary Algorithms,” New York, 2001.
- M. Cruz-Ramirez, C. Hervas-Martinez, et al., “MultiObjective Evolutionary Algorithm for Donor-Recipient Decision System in Liver Transplants,” European Journal of Operational Research, Vol. 222, No. 2, 2012, pp. 317-327. doi:10.1016/j.ejor.2012.05.013
- A. Thapar, D. Pandey, et al., “Satisficing Solutions of Multi-Objective Fuzzy Optimization Problems Using Genetic Algorithm,” Applied Soft Computing, Vol. 12, No. 8, 2012, pp. 2178-2187. doi:10.1016/j.asoc.2012.03.002
- E. G. Talbi, M. Basseur, et al., “Multi-Objective Optimization Using Metaheuristics: Non-Standard Algorithms,” International Transactions in Operational Research, Vol. 19, No. 1-2, 2012, pp. 283-305.


 G1
G1 G2
G2