Engineering
Vol. 3 No. 12 (2011) , Article ID: 9212 , 6 pages DOI:10.4236/eng.2011.312150
Decay of Vortices in an Electrically Conducting Fluid in the Presence of a Magnetic Field
1Department of Mathematics, National Institute of Science & Technology, Berhampur, India
2Department of Mathematics, Indian Institute of Technology, Kharagpur, India
E-mail: reza@nist.edu, asg@maths.iikgp.ernet.in
Received August 16, 2011; revised October 17, 2011; accepted October 25, 2011
Keywords: Decay of Vortices, Magnetohydrodynamics
ABSTRACT
The decay of vortices in flows of an electrically conducting fluid in the presence of a magnetic field is studied. Two flow configurations are considered: 1) flow in a double array of vortices; 2) flow behind a two-dimensional grid. It is found that in the presence of a uniform transverse magnetic field, the vortices decay much faster than those in a viscous fluid in the absence of magnetic field. It is observed that in the steady flow behind a two-dimensional grid in the presence of a uniform transverse magnetic field, a pair of bound eddies appear behind the single elements of the grid. The scale of these eddies depends on the strength of the magnetic field. It is also found that the distance from the stagnation point over which the vortices decay to zero decreases with increase in the magnetic field. At large distance, however, the streamlines become parallel as in the case of a viscous fluid.
1. Introduction
The manner in which vortices decay in flows of an incompressible viscous fluid is of particular importance in studying the phenomenon of turbulence in a fluid. In particular, in grid-generated turbulence vortices decay in the flow behind the grid. Taylor [1] discussed the flow in a double array of vortices in an incompressible viscous fluid and found that such vortices decay exponentially with time. This decay is essentially due to viscous action. The fact that in this type of flow the nonlinear terms in the vorticity equation are self-canceling led Taylor to obtain an exact solution of the problem. It is noteworthy that in this type of flow, vorticity is constant along streamlines. A similar situation arises in steady flow of an incompressible viscous fluid behind a two-dimensional grid which was investigated by Kovasznay [2]. Assuming periodicity of the flow in one direction, he obtained an exact solution of the Navier-Stokes equations, which reveals the existence of a pair of bound eddies behind the single element of the grid with streamlines that become parallel at a large distance downstream. Lugt and Schwiderski [3] constructed a class of separable solutions of Stokes equations which give valuable information on the mechanism of growth and decay of vortices in an incompressible viscous fluid. For example it was shown that a decaying discontinuity line is a process which involves the progressive obliteration of a discrete spectrum of vortices in such a way that little vortices with large damping coefficients dominate in the beginning and the bigger vortices of few number replace them later on. The motion and decay of circular vortex rings with an inner viscous core was investigated by Gunzburger [4]. He reduced Navier-Stokes equations to a coupled integro-differential system. The analysis was then applied to the motion and decay of pair of coaxial vortex rings.
Smith et al. [5] reported on observations of turbulent behaviour without requiring the use of Taylor “frozen turbulence” hypothesis in a towed grid-generated homogeneous turbulence of grid Reynolds number of order 105 within a stationary channel filled with helium II. The subsequent decay in time t of the line density of quantum vortices was measured by them by second sound attenuation and associated vorticity 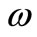 follows the expected behaviour of an incompressible viscous fluid with
follows the expected behaviour of an incompressible viscous fluid with  consistent with the motion of a turbulent state of helium II.
consistent with the motion of a turbulent state of helium II.
Gupta [6] investigated the decay of double array of vortices in the flow of a viscoelastic fluid. It is found that vortices decay much faster in this fluid than those in a viscous fluid. However such a result is shown to be true for a second-order fluid (see Markovitz and Coleman [7]) which is a viscoelastic fluid (with small memory) provided the time scale which characterizes the memory of the fluid and the size of the vortices obey certain restricttions. On the other hand Rajagopal [8] showed that the results of Taylor [1] on the decay of vortices as mentioned above hold unconditionally regardless of the time scale characterizing the fluid or the size of vortices in the case of incompressible second-grade fluids (Fosdick and Rajagopal [9]) which are also viscoelastic provided these fluids are thermodynamically compatible. As a further extension of this work, Prusa and Rajagopal [10] found a new exact solution to the above problem studied by Taylor [1] in the case when the nonlinear inertial term in the momentum equation is not identically zero. They also showed that in this case the streamlines for an incompressible viscous flow are also streamlines for a second grade fluid (viscoelastic fluid). The only difference lies in the fact that the decay rate of vortices for the second grade fluid is slower than that for an incomepressible viscous fluid.
On the other hand in a two-dimensional flow of an incompressible viscous electrically conducting fluid where the vorticity is perpendicular to the plane of the flow, a magnetic field in the plane of the flow leads to suppression (or decay) of vorticity. Such suppression of vorticity is found in Hartmann flow (Shercliff [11]) between two parallel plates in the presence of a uniform transverse magnetic field. The suppression of turbulence or vorticity by a uniform magnetic field was investigated by Moffatt [12]. It is important to note that a magnetic field tends to make the flow field anisotropic in the sense that it becomes independent of the coordinate parallel to the field. An experimental study of the large-time decay of an initially three-dimensional turbulent flow structure in the presence of a steady magnetic field for large and moderate value of the magnetic interaction parameter was made by Sreenivasan and Alboussiere [13].
The aim of the present paper is to investigate decay of vortices in an electrically conducting fluid in the presence of a magnetic field. When an electrically conducting fluid flows in the presence of a magnetic field, an electromotive force is generated in a direction at right angles to the direction of both the fluid velocity and the magnetic field. Since the fluid is electrically conducting, a current flows in the direction of the electromotive force, which modifies the imposed magnetic field. This current in the presence of the resultant magnetic field gives rise to a body force known as Lorentz force which affects the fluid flow. The effect of a magnetic field on the decay of vortices is studied in this paper.
2. Flow in a Double Array of Vortices
Let us consider a double array of vortices in the flow of an incompressible viscous and electrically conducting fluid in the presence of a magnetic field. The alignment of the vortices is shown in Figure 1 where a uniform magnetic field B0 acts along y-direction.
The Navier-Stokes equation of motion including the Lorentz forceis
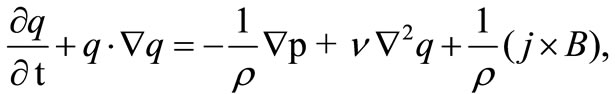 (1)
(1)
where q,  ,
,  , p, j and B denote the fluid velocity, density, the kinematic viscosity of the fluid, pressure, electric current density and the magnetic field, respectively. The equation of continuity is
, p, j and B denote the fluid velocity, density, the kinematic viscosity of the fluid, pressure, electric current density and the magnetic field, respectively. The equation of continuity is
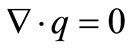 (2)
(2)
Maxwell’s equations are
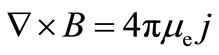 (3)
(3)
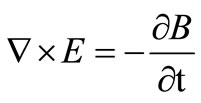 (4)
(4)
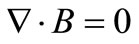 (5)
(5)
where μe is the magnetic permeability. Ohm’s law is.
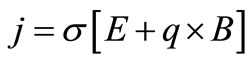 (6)
(6)
where 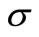 the electrical conductivity of the fluid (assumed constant) and E is the electric field.
the electrical conductivity of the fluid (assumed constant) and E is the electric field.
The flow is two-dimensional. Let u and v denote the velocity components along x and y-directions, respecttively, so that . We shall assume that the induced magnetic field in the flow is negligible. Such an assumption is justified in the flow of a conducting fluid of very small electrical conductivity so that the magnetic Reynolds number RM is very small in the flow. In flow of liquid metals such as mercury or liquid sodium whose electrical conductivity is very low, RM is indeed very small. Thus we take
. We shall assume that the induced magnetic field in the flow is negligible. Such an assumption is justified in the flow of a conducting fluid of very small electrical conductivity so that the magnetic Reynolds number RM is very small in the flow. In flow of liquid metals such as mercury or liquid sodium whose electrical conductivity is very low, RM is indeed very small. Thus we take
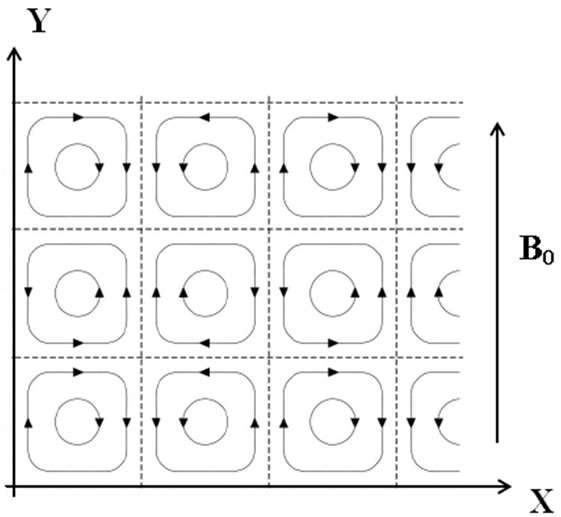
Figure 1. Streamlines for double array of vortices.
 (7)
(7)
where B0 is the imposed magnetic field mentioned earlier. Clearly the electric current and the electric field act along the z-direction (i.e., normal to the xy-plane) and so from (6), we get
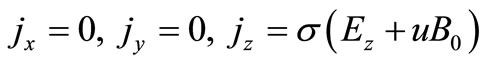 (8)
(8)
Since the induced magnetic field is neglected, it follows from (4) that 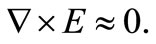 Further the electric field acts in the z-direction which is the direction of electric current. This gives
Further the electric field acts in the z-direction which is the direction of electric current. This gives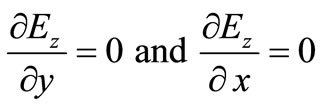 . Thus Ez is a function of z and t only. The electric current is now determined from (6) and not from (3). But as pointed out by Shercliff [11], the consequence of (3) viz,
. Thus Ez is a function of z and t only. The electric current is now determined from (6) and not from (3). But as pointed out by Shercliff [11], the consequence of (3) viz,
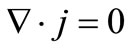 (9)
(9)
must be satisfied. Equation (8) then give  since u is a function of x, y and t. Hence from (9) it follows that Ez is a function of t only and we take Ez = 0, which will correspond to the electrically short-circuited condition. Thus from (8), we have
since u is a function of x, y and t. Hence from (9) it follows that Ez is a function of t only and we take Ez = 0, which will correspond to the electrically short-circuited condition. Thus from (8), we have
 (10)
(10)
Using (7) and (10) the momentum Equation (1) gives
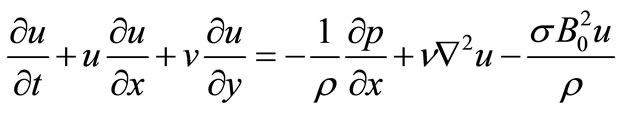 (11)
(11)
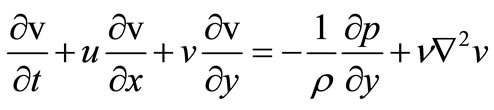 (12)
(12)
The equation of continuity (2) gives
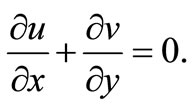 (13)
(13)
Eliminating p from (11) and (12), the equation for vorticity  is
is
 (14)
(14)
where
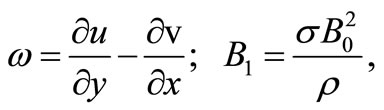 (15)
(15)
Equation (13) enables us to define a stream function 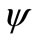 such that
such that
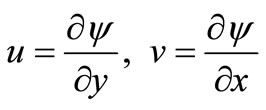 (16)
(16)
This gives from (15)
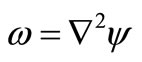 (17)
(17)
Following Taylor [1], we now assume
 (18)
(18)
for the flow representing the double array of vortices (see Figure 1) with assumed periodicity in both x and y directions, A,  and d being constants. Using (17), this leads to
and d being constants. Using (17), this leads to
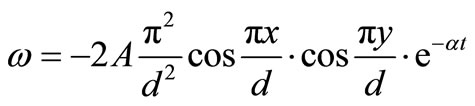 (19)
(19)
so that
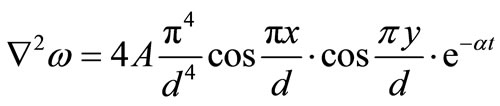 (20)
(20)
Substitution from (16), (19) and (20) in (14) yields
 (21)
(21)
To validate this result, we may note that in the absence of magnetic field (B1 = 0), Equation (21) gives the decay time  of vortices as
of vortices as 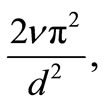 which agrees with the result of Taylor [1]. It may also be noted that a further validation of the results of decay of vortices in the a second-order (viscoelastic) fluid is that the decay rate
which agrees with the result of Taylor [1]. It may also be noted that a further validation of the results of decay of vortices in the a second-order (viscoelastic) fluid is that the decay rate 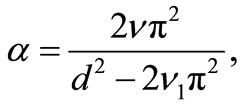 where
where 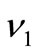 is the viscoelastic parameter reduces to
is the viscoelastic parameter reduces to 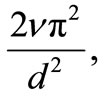 of Taylor [1] for a viscous fluid when
of Taylor [1] for a viscous fluid when 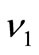 = 0. We thus find that in the case of an electrically conducting fluid in the presence of a magnetic field (B1 > 0), vortices decay much faster than those in a viscous fluid.
= 0. We thus find that in the case of an electrically conducting fluid in the presence of a magnetic field (B1 > 0), vortices decay much faster than those in a viscous fluid.
3. Flow behind a Two-Dimensional Grid
We consider the laminar flow of an incompressible, viscous and electrically conducting fluid in the presence of a uniform transverse magnetic field behind a two-dimensional grid with x-axis normal to the grid (Figure 2). Here the average velocity along this axis is u0. The flow is permeated by a uniform magnetic field B0 along y-axis.
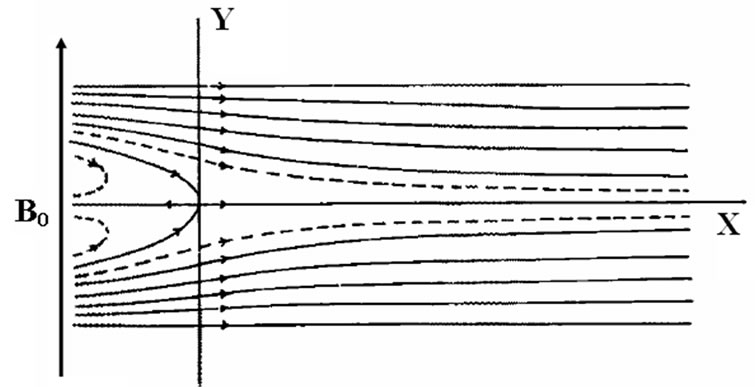
Figure 2. Streamlines behind a two-dimensional grid.
Denoting local velocity components along the x and y directions by u0+u'(x, y) and v'(x, y), the vorticity Equation (14) becomes
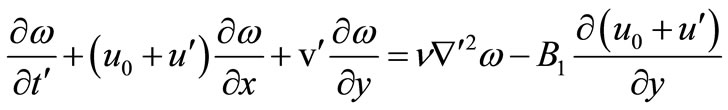 (22)
(22)
where t' is time and
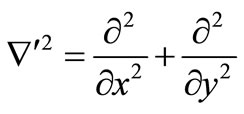 (23)
(23)
Let us introduce the following dimensionless quantities
 (24)
(24)
where M is the grid-spacing. Equation (22) then becomes
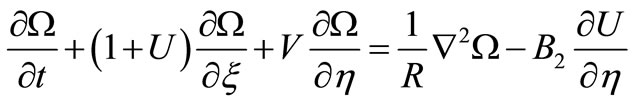 (25)
(25)
where
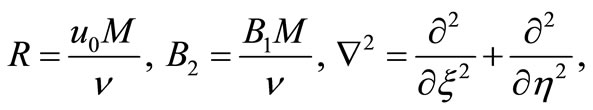 (26)
(26)
In the steady state, Equation (25) reduces to
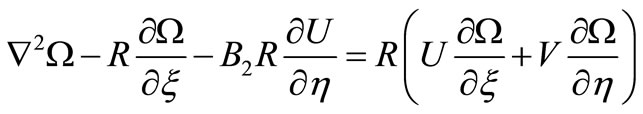 (27)
(27)
The equation of continuity (13) in dimensionless form is given by
 (28)
(28)
This enables us to define a dimensionless stream function 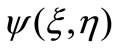 such that
such that
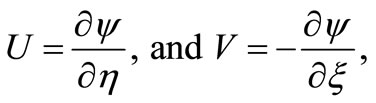 (29)
(29)
which gives
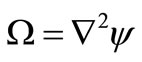 (30)
(30)
Assuming periodicity of the solution in the y-direction, we take following Kovasznay [2]
 (31)
(31)
This gives from (30)
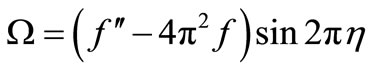 (32)
(32)
where a prime denotes differentiation with respect to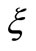 .
.
Hence the terms 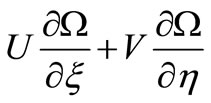 in (27) will vanish if
in (27) will vanish if
 (33)
(33)
and its solution is
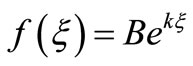 (34)
(34)
B and k being constants. In this case Equation (27) reduces to a linear equation given by
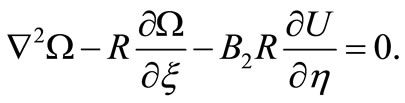 (35)
(35)
To solve (35) we set
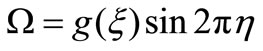 (36)
(36)
Using (29), (31), (34) and (36) we obtain from (35)
 (37)
(37)
The solution of (37) is
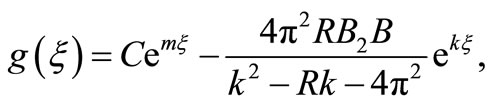 (38)
(38)
where C is a constant and  with
with
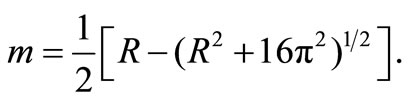 (39)
(39)
The solution (38) is consistent with the boundary condition that the vorticity  given by (36) vanishes at large distance downstream so that
given by (36) vanishes at large distance downstream so that  provided that k < 0. Equation (36) now gives
provided that k < 0. Equation (36) now gives
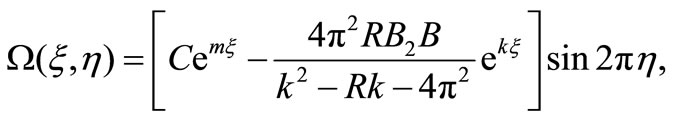 (40)
(40)
Further from (30), (31) and (34), we have
 (41)
(41)
Comparing (40) with (41) and remembering that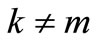 , we get
, we get
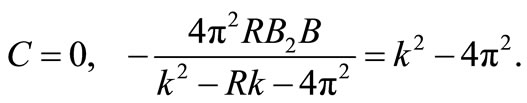 (42)
(42)
Hence the vorticity is given by
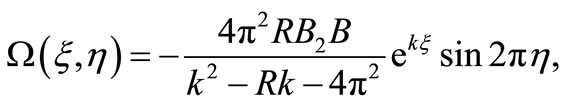 (43)
(43)
where k satisfies the biquadratic Equation (42), which is
 (44)
(44)
Now the stream function for the average flow is given by 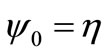 and so the stream function for the flow behind the grid is given by
and so the stream function for the flow behind the grid is given by
 (45)
(45)
where use is made of (31) and (34). If we choose the stagnation point at 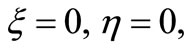 then
then
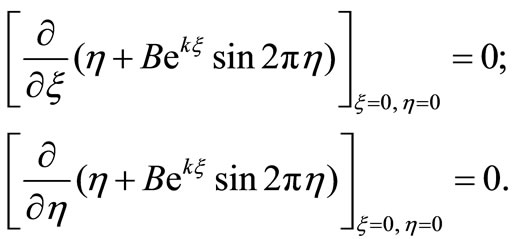 (46)
(46)
These give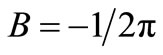 . Hence the flow behind the grid is given by
. Hence the flow behind the grid is given by
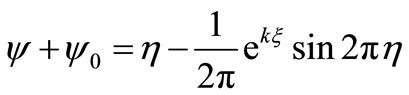 (47)
(47)
so that the velocity components are
 (48)
(48)
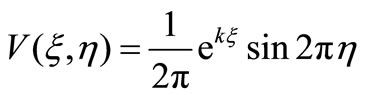 (49)
(49)
and the vorticity 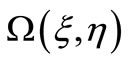 is given by (43). The structures of the Equations (47)-(49) are similar to those for flow of a viscous fluid by Kovasznay [2]. Thus the pattern of streamlines found by this author will also hold in the present problem and we should, therefore, expect the appearance of a pair of bound eddies behind the single elements of the grid as in Figures 3-5. However the scale of such eddies depends on k which satisfies Equation (44) and is of order
is given by (43). The structures of the Equations (47)-(49) are similar to those for flow of a viscous fluid by Kovasznay [2]. Thus the pattern of streamlines found by this author will also hold in the present problem and we should, therefore, expect the appearance of a pair of bound eddies behind the single elements of the grid as in Figures 3-5. However the scale of such eddies depends on k which satisfies Equation (44) and is of order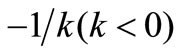 . Table 1 gives the negative root k of Equation (44) for different values of the magnetic parameter B2 and the Reynolds number R.
. Table 1 gives the negative root k of Equation (44) for different values of the magnetic parameter B2 and the Reynolds number R.
It is observed that for a fixed value of R, −k increases with increase in the magnetic parameter B2, so that the distance from the stagnation point over which the vortices decay to zero decreases with increase in the magnetic field (Figures 3-5). At large distance downstream, however, the streamlines become parallel as in the case of a viscous fluid.
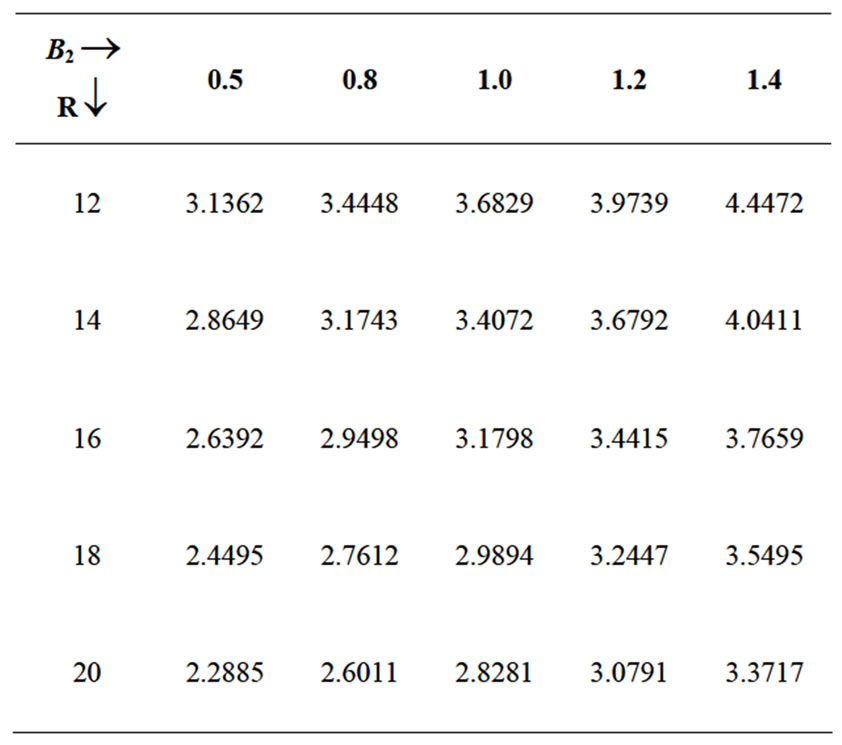
Table 1. Values of –k.

Figure 3. Streamlines behind a two-dimensional grid when R = 20 and B2 = 0.5.
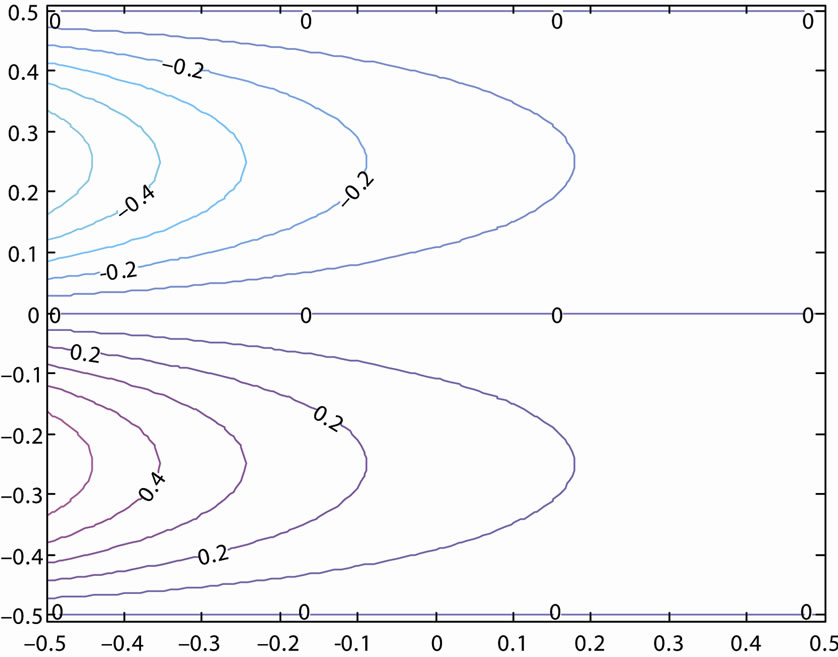
Figure 4. Streamlines behind a two-dimensional grid when R = 20 and B2 = 0.8.
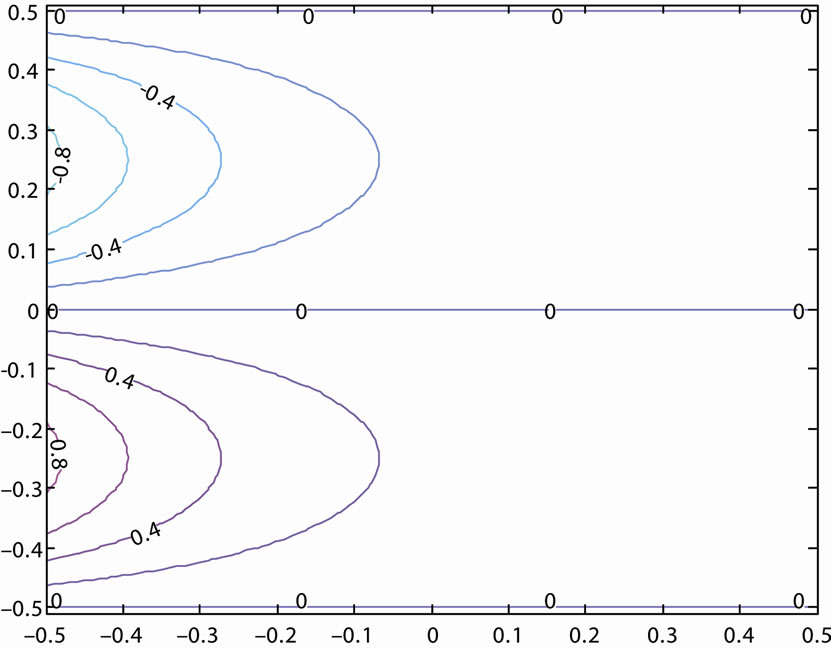
Figure 5. Streamlines behind a two-dimensional grid when R = 20 and B2 = 1.4.
4. Conclusions
An analysis is made of the decay of vortices in flows of electrically conducting fluid in the presence of a uniform magnetic field. It is found that in the flow in a double array of vortices permeated by a uniform transverse magnetic field, the vortices decay much faster than those in a viscous fluid in the absence of magnetic field. It is observed that in the steady flow behind a two-dimensional grid in the presence of a uniform transverse magnetic field, a pair of bound eddies appear behind the single elements of the grid. The scale of these eddies depends on the strength of the magnetic field. It is also found that the distance from the stagnation point over which the vortices decay to zero decreases with increase in the magnetic field. At large distance, however, the streamlines become parallel as in the case of a viscous fluid.
5. Acknowledgements
One of the authors (A. S. G.) acknowledges the financial assistance of Indian National Science Academy, New Delhi for carrying out this work. Authors would also like to acknowledge the use of the facilities and technical assistance of the Center for Theoretical Studies at Indian Institute of Technology, Kharagpur.
6. REFERENCES
- G. I. Taylor, “On the Decay of Vortices in a Viscous Fluid,” Philosophical Magazine, Vol. 46, 1923, pp. 671- 674.
- L. I. G. Kovasznay, “Laminar Flow behind a Two Dimensional Grid,” Proceedings of Cambridge Philosophical Society, Vol. 44, No. 1, 1948, pp. 58-62. doi:10.1017/S0305004100023999
- H. J. Lugt and E. W. Schwiderski, “Birth and Decay Vortices,” The Physics of Fluids, Vol. 9, 1966, pp. 851-859. doi:10.1063/1.1761785
- M. D. Gunzburger, “Motion of Decaying Vortex Ring with Non-Similar Vorticity Distribution,” Journal of Engineering Mathematics, Vol. 6, No. 1, 1972, pp. 53-61. doi:10.1007/BF01535239
- M. R. Smith, R. J. Donnelly, N. Goldenfeld and W. F. Vinen, “Decay of Vorticity in Homogeneous Turbulence,” Physical Review Letters, Vol. 71, No. 16, 1993, pp. 2583- 2586. doi:10.1103/PhysRevLett.71.2583
- A. S. Gupta, “Decay of Vortices in a Visco-Elastic Liquid,” Meccanica, Vol. 7, No. 4, 1972, pp. 232-235. doi:10.1007/BF02133721
- H. M. Markovitz and B. D. Coleman, “Advances in Applied Mechanics,” Academic Press, New York, 1964.
- K. R. Rajagopal, “On the Decay of Vortices in a Second Grade Fluid,” Meccanica, Vol. 15, 1980, pp. 185-186. doi:10.1007/BF02128929
- R. L. Fosdick and K. R. Rajagopal, “Uniqueness and Drag for Fluids of Second Grade in Steady Motion,” International Journal of Non-Linear Mechanics, Vol. 13, No. 5-6, 1978, pp. 131-137.
- V. Prusa and K. R. Rajagopal, “A Note on the Decay of Vortices in a Viscous Fluid,” Meccanica, Vol. 46, No. 6, 2010, pp. 875-880.
- J. A. Shercliff, “A Textbook of Magnetohydrodynamics,” Pergamon Press, Oxford, 1965
- H. K. Moffatt, “On the Suppression of Turbulence by a Uniform Magnetic Field,” Journal of Fluid Mechanics, Vol. 28, No. 3, 1967, pp. 571-592. doi:10.1017/S0022112067002307
- B. Sreenivasan and T. Alboussière, “Experimental Study of a Vortex in a Magnetic Field,” Journal of Fluid Mechanics, Vol. 464, No. 1, 2002, pp. 287-309.


