Engineering
Vol. 3 No. 10 (2011) , Article ID: 8085 , 11 pages DOI:10.4236/eng.2011.310128
Evaluation of the Performance of Infrared Thermography for on-Line Condition Monitoring of Rotating Machines
1Gembloux Agro-Bio Tech, Université de Liège, Gembloux, Belgium
2Mechanical Engineering, University Mons, Mons, Belgium
E-mail: Vincent.Leemans@ulg.ac.be
Received June 7, 2011; revised July 6, 2011; accepted July 22, 2011
Keywords: Infra-Red Thermography, Conditional Monitoring, ARX
ABSTRACT
This study evaluated the possibility of infrared thermography to measure accurately the temperature of elements of a rotating device, within the scope of condition monitoring. The tested machine was a blower coupled to a 500 kW electric motor, that operated in multiples regimes. The thermograms were acquired by a fixed thermographic camera and were processed and recorded every 15 minutes. Because the normal temperature variat-ions could easily mask a drift caused by a failure, a corrected temperature was computed using autorecursive models. It was shown that an efficient temperature correction should compensate for the variations of the process, and for the ambient temperatures variations, either daily or seasonal. The standard deviation of the corrected temperature was of a few tenth of degree, making possible the detection of a drift of less than one degree and the prediction of potential failure.
1. Introduction
Infrared thermography measure the surface temperature of a body without contact. Currently it is used in different industrial sectors for on-line quality control of products and thermal inspection of industrial structures [1]. The use for building thermal audits is also well known [2]. For condition monitoring and maintenance purpose, infrared thermography finds applications where phenomenon producing a temperature rise (or rarely a drop) is expected. Such is the case for control of electrical utilities, kiln insulation, piping for examples. Overloads of electric motors, insulation defect in motor windings, cloging of blower girds are also cited [3]. In the mechanical sector, applications where friction, wear and fatigue are expected could be involved [1].
Different sensing techniques have been reported to monitor on-line bearing wear, including vibr-ation and acoustic measurements, electrostatic wear charge and analysis of debris size [4-6]. Infrared thermography was cited as a complementary method or for particular applications. Shaft alignment default, bearing wear and lack of lubrification were reported [7]. Dedicated applications of infrared thermography have also been described to diagnose diesel engine injection faults [8], to detect alteration in the coating of gas turbine blades [9] or for condition monitoring of exhaust system blowers in nuclear plots [10]. The use of trackside hot-box detector to identify railroad wheels bearings presenting a temperature greater than 105.5˚C are also shown [11]. All the bearings were monitored while the train passes beside the detectors and the temperature of every bearing was compared to the mean temperature of all the bearings.
Different origins are cited for the temperature rise during the wear process, mainly the thermal process involved during fatigue plastic deformation of metal and the increase of friction. High temperatures were reported during bearing wear, when fatigue crack propagation and spallation process were involved [6,12]. During a fatigue test at very high fatigue cycle regime, the temperature may grow locally and significantly before fracture [13]. At the moment of the formation of the fatigue crack, an increase of 0.07˚C was observed. Afterwards, the temperature evolved rapidly with a temperature rise exceeding 100˚C. The increase in temperature occurring during a fatigue test was linked to the fatigue life of the specimens as shown in study of the temperature evolution during fatigue damage by using infrared thermography [14].
Authors studying the service life of bearing reported temperature during and at the end of bearing live, whether using thermography or thermocouples [6,15-17]. A study of machine tool spindle to obtain an assembly presenting a good stiffness at low speed and a limited temperature increase at high speed monitored the fatigue life of bearings [15]. It showed by model and by experiment that a temperature rise between 16˚C and 34˚C was to be expected in normal working conditions. In a study of bearing load for high speed spindle, it was clearly showed that the temperature of the bearing depend on the charge and on the rotational speed [16]. The bearing temperature were of 30˚C, 42˚C and 48˚C for rotational speed of respectively 2600, 5500 and 9000 rpm and for a room temperature of 26˚C. Author also showed that these temperature changes modified the pre-load of the bearings. Incidentally for our concern, authors also showed that by using an active bearing pre-load control, they could stabilise the bearing load. In that case, the temperatures were respectively of 31˚C and 39˚C for rotational speed of respectively 2600 and 5600 rpm. A study of the wear of tapered roller bearings was carried out on a proof bank consisting in two support bearings and two test bearing [6]. The vibration acceleration, the temperatures and electrostatic wear charges were monitored on-line during an experiment that lasted nearly 63 hours. The measured temperatures were those of the tested couple bearings, the inlet and outlet oil temperature and the room temperature. Results showed higher values of the different in-line parameters during the first 4 hours and a steady state afterwards. The temperature was then around 70˚C, fifty degrees above the room temperature. At 53.5 hours, a wear pike was observed at a support bearing, immediately followed by an increase in acceleration and temperature. The temperature augmented of 4˚C during the hour after the event the presented a plateau of 4.5 h and then an increase up to the end of the test with a maximal value around 85˚C. The acceleration followed the same pattern. It is important to note that the first distress occurred on a support bearing, which were not monitored in temperature. In another study, ball bearings were monitored by measuring vibrations and temperature by using infrared thermography [17]. Authors reported a temperature grow of 15˚C for a rms vibration speed of 0.5 m/s (corresponding to normal conditions) and of 25˚C for 2.4 m/s (corresponding to degraded conditions).
From these experiments in controlled conditions, it can be noted that the reported normal service temperatures of bearings vary widely from one application to another and within an application with the charge applied to the bearing. The temperature rise at the beginning of a degradation was lesser than 10˚C, but evolves rapidly at the end of live. This value is in the same range as the usual day and night variations and lesser than seasonal variations. To detect early the degradation, it appears that those temperature variations should be compensated. The aim of this study is to develop methods to compensate for the temperature variations due to the process characteristics and to the ambient conditions. In the framework of a research program intending to monitor on-line the vibration and temperature of rotating machines, a blower powered by an electric motor (500 kW) was used.
2. Material and Method
The whole machine is composed by following elements: a 500 kW electric motor, a coupling, two main bearings and the blower. The couple and speed vary by level according to the production needs, as shown in Figure 1. The studied period lasted from the 15th of September 2009 up to the 26th of January 2010.
Early measurements showed that the equipment temperature varied in a wide range (more than 30˚C), following the day/night or the summer/winter ambient temperatures. The variable transmitted power was also hypothesised to be a variation source. If small temperature drift due to wear had to be detected, the effect of these variations should be compensated. The simplest compensation seems to subtract the ambient temperature from the temperature of the element. The result of such a method is presented hereafter but a residual variability remained. To take into account the thermal inertia and the different heat inputs and outputs, a physical model of the elements temperature was build and adjusted using a least square recursive method. To detect a temperature drift caused by wear two ways were compared, the first one using a model adjusted during a given period, the other using a model adjusted continuously.
The method proposed in the present paper requires a fixed thermal camera as well as sensors or acquisition devices to measure the transmitted power, which involve costs. It seems thus interesting to know which of these
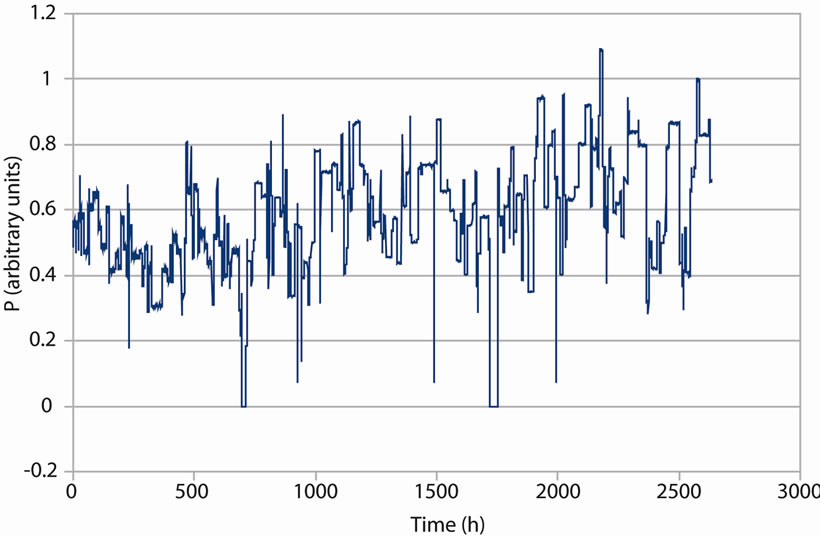
Figure 1. Evolution of the power transformed by the electric motor during time.
sensors are required for accurate object temperature estimation. Different models requiring more or less data have been proposed. The minimal “model” refers to the measure of the ambient temperature and of the temperature of the element at regular but distant interval which could be carried out by inspections using a mobile camera.
Another model included the same data but acquired on-line, at short interval, which gives the possibility to take into account the thermal inertia of the element. The two last models also include the power transmitted by the element (or converted for the motor).
2.1. The Measurements
A thermographic camera (FLIR A320, using microbolometers) was placed at the roof of the industrial hall (7 m high), observing the studied equipment from above (Figure 2). The camera was placed into a protective casing, with a “glass” presenting a transparency of 0.95 in the wavelength range of the camera. The thermograms were acquired and preprocessed at five Hertz (for a contingent visual control by an operator) and were processed and recorded every 15 minutes.
The main preprocessing was a recursive filtering to reduce measurement noises:
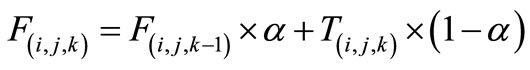 (1)
(1)

Figure 2. View of the studied equipment. The casing of the blower is visible far left; the two main bearings are visible left (one black, one blue); the motor is at the right; above is the casing of the thermographic camera.
with F the filtered thermogram, T the measured thermogram in kelvin, i and j pixels coordinates and k time step was an arbitrary parameter fixed at 0.975. The acquisition noise was reduced below half a kelvin and the time constant was of 8 sec, which was sufficient for the application.
Into the thermograms, several regions of interest (noted ROI) were defined, encompassing each element, as detailed into Table 1 and presented in Figure 3. The motor fan cover and the ground were considered as possible areas into which the ambient temperature could be measured. The ground being subjected to moisture and having its own thermal inertia, was rejected. On contrary, the fan cover being in contact with turbulent ambient air presented little thermal inertia. Several parameters were computed on these ROIs, the most important in this context being the maximal and mean temperatures. The ROI 5 was not used in this application.

Figure 3. A thermogram and the regions of interest in green and blue. From top left to right, ROI 2, the fan cover; ROI 0, the motor; ROI 1, the drive bearing of the motor, ROI 3 the main bearing (coupling-side); ROI 4, the main bearing (blower-side); ROI 5, the blower; bottom left, ROI 6, the ground. The red spots are the position of local maxima, not used in this study.

Table 1. Denomination of the area of interest.
The data were acquired on a period of four months, representing 10,530 records. The first 1500 were used as training set to adjust the models. The remaining records were used for validation.
The radiation measured by a thermographic camera comes in part from the emission of the body of which the temperature should be assessed and in part from the reflection of the environment radiations (Maldague, 2001). The emissivities of the body and the environment temperature are influence factors which had to be known before hand and had to be given to the camera. The temperatures returned by camera were compensated according to those factors. The values were adjusted in summer based on theoretical values and contact temperatures measurements, before the period considered in this study and using Equation (2) here after. Eventually, occasional contact temperature measurement confirmed that the emissivity remained constant. But the ambient temperature varied in a wide range, from 303 K (30˚C) in summer to 273 K (0˚C) in winter and the measurements made in autumn and in winter were no longer correct. The temperatures were then compensated according to the following equation:
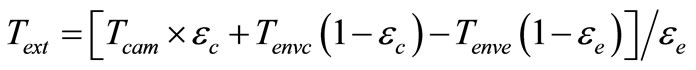 (2)
(2)
where Test is the temperature after correction, Tcam the value returned by the camera (after internal correction), εc the emissivity given to the camera, εe the estimated value of the emissivity, Tenvc the environment temperature given to the camera, Tenve the estimated environment temperature. As no drift was observed for the emissivity, the values of εc and εe are equal (0.92). Tenvc was of 300 K, which was correct at that the beginning of the measurements. The value of Tenve varying continuously and was chosen as the mean value of Tcam computed for the motor fan cover (ROI 2, before correction). Strictly speaking, this is not correct because the measure of Tenve should itself be corrected. The maximum correction was observed to be 2.6 K. But it should be noted that as both the temperature of the element and the estimation of the environment temperature were corrected. The effect of the ambient temperature variations on the estimation of a temperature drift of an element was in fact much less. For these reasons the correction was deemed sufficient.
The rotational speed and the current used by the motor are acquired thanks to a CompactRIO device (National Instruments, Austin, USA). The product of the speed in krpm by the current in kA was used as a measure of the transmitted power.
2.2. On-Line Inspection
An analytical model of the elements was used to compensate the influences of the environment temperature and of the process on the element temperature. This model was based on some hypothesis. The temperature of the body was supposed homogeneous, the body received an energy flux qi from the process, exchanged a flux qx with a source at fixed but unknown temperature (for example to the soil, by conduction) and lost a flux qo into the ambient air. The derivative of the temperature was proportional to the difference between the input and the output:
 (3)
(3)
where T is the temperature of the element, t is the time and k0 is a constant. For the rotating elements, the friction coefficient were supposed being constant, which implied that the lost energy (the input) was proportional to the transmitted power P:
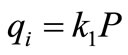 (4)
(4)
where k1 is a constant. The power was expressed as the product of the rotational speed and of the current used by the motor. The temperature exchange terms were given by:
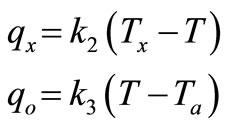 (5)
(5)
where Tx is the temperature of the unknown source, Ta is the ambient temperature, k2 and k3 are constants. If Tx was lesser than T, the body loosed heat this way and qx is negative, which is in accordance with Equation (3). Equation (3) may be rewritten :
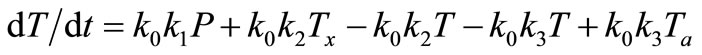 (6)
(6)
The equivalent discrete time model is given by
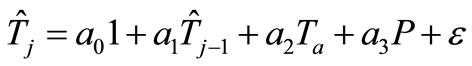 (7)
(7)
where  is the estimated temperature of the considered organ at time step j and :
is the estimated temperature of the considered organ at time step j and :
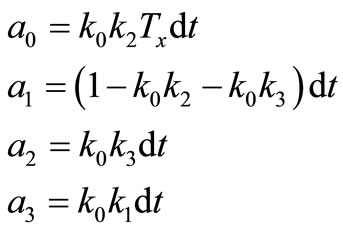 (8)
(8)
Tx being unknown, it is included into the coefficient which left an independent term. This can be written under a vectorial form:
 (9)
(9)
or
 (10)
(10)
The model was of auto-recursive with exogenous type (ARX, Ljung [18]) and θ was adjusted using recursive least square method, by minimising the cost function J given by :
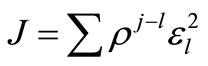 (11)
(11)
where ρ is a forgetting factor adjusted to 0.999.
Three models have been tested, the first one including the independent term and both ambient and element temperatures. This model took into account the thermal inertia of the element and a fixed temperature source, but not the process power (and thus did not require these sensors). It was noted 1TT (in reference to the composition of the parameter vector φ). The second model included both temperature and the Power, but not the independent term (noted TTP). The third model was complete and was noted 1TTP.
Two ways were explored to detect temperature drift. The classical one consisted in adjusting θ during a given period. It was observed that for this application a period of 1500 measurements was required and sufficient for model 1TTP (less for the other models). Taking into account that the mean period for a given process P level was about height hours, which correspond to 32 measurements it can be notice that 1500 measurements made around 45 process changes. After the adjustment period, θ was fixed while the error of the model ε kept evolving. As the temperature is expected to raise in presence of a degradation, to detect a drift, an upper limit of a confidence interval of ε, noted ε2, was computed. Considering that ε should have a null mean it was ε2 given by
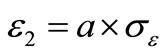 (12)
(12)
where a was a coefficient chosen equal to three and σε was the standard deviation computed on the 1500 first data. If ε grew and stood above that limit, a temperature drift was said to be detected.
For the other way, the model was updated after each measurement. After the update, the result of the model was computed for fixed values of the variable Ta and P. This response gave the temperature that the organ would have presented in standard conditions, that is to say if the ambient temperature and the transmitted power remained constant. This temperature should have remained constant and independent of the operating conditions (included in the model) but should have been sensible to a temperature rise due to degradation because this would mean changes in the parameters k1 or a3. To detect this drift, the mean and the standard deviation of Tj, noted Tm and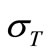 , were estimated during a given period. This period was chosen to 1500 data, equal to the learning period of the fixed model and is called, by analogy with the fixed model, the training data set, the remaining of the data being hereafter called the validation data set. An upper limit of a confidence interval for Tj was given by
, were estimated during a given period. This period was chosen to 1500 data, equal to the learning period of the fixed model and is called, by analogy with the fixed model, the training data set, the remaining of the data being hereafter called the validation data set. An upper limit of a confidence interval for Tj was given by
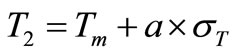 (13)
(13)
The value of aσT, in itself an evaluation of the quality of the method, was also recorded to compare the fixed and the variable methods.
As a lower threshold might also drive to more false alert, the ratio alert, that is to say the ratio of error ε or temperatures Tj above their respective thresholds, was also recorded. If the distribution of the errors or the temperatures were of Gaussian type, a value of a equal to three should show a ratio alert of 0.14%.
2.3. Regular Mobile Inspection
If regular visits were to be considered instead of on-line inspection, the same kind of image may be expected and the ROI may also be defined. But the only way to reduce the temperature variations is to compute the difference ΔTn between elements (maximal temperature of ROI 0,1,3,4) and the ambient temperature (mean temperature of ROI 2):
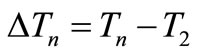 (14)
(14)
where n is the ROI number. An upper bound to the variations of ΔTn can be computed as for the previous case, by computing the mean difference and the standard deviation of the difference and using those values in (13). It should however be noted that the considered equipment is actually monitored every six weeks, so that only 8 point are recorded in a year. Even if temperature is not expected to rise before the end of live of the element, more frequent visits of the equipment should be considered while computing the statistical parameters. The data acquired with the fixed equipment were sub-sampled to obtain a data set which could be equivalent to a mobile inspection data set. One data was picked out of 96 (equivalent to an inspection a day). The first 15 data were used to compute the statistics and the rest to validate the method. This method was hereafter noted DT.
3. Results
In order to correctly interpret the results of the detection, the evolution of the temperature have to be presented first. The results are presented after.
3.1. Evolution of the Temperatures
Figure 4 shows the evolution of the measured temperature during the period (the first data was acquired on the 26th of September). On this graph and on the following

Figure 4. Temperature evolution four the four main ROIs and for the ambient temperature.
ones, several dramatic changes in the element temperatures are observed. These were caused by the regular stops of the machines for maintenance (every six weeks) or when the thermogram acquisition program was restarted (after an upgrade usually).
The motor and motor bearing (ROIs 0 and 1 respectively) have shown an unexpected temperature evolution. The motor presented an important temperature drift caused by the motor ventilation grid becoming clogged. The management of the factory was aware of the clogging and proceeded to cleaning based on visual inspection, but was unaware of the consequences on the temperature of the motor. This increase in temperature influenced directly the motor bearing and marginally, by radiation, the main bearings. This temperature drift should have been detected by the different models, but complicated the interpretation of the data. The ideal ratio alert was much higher than the theoretical value of 0.14% and was evaluated empirically to 22%.
The day-night ambient temperature variations may be larger than ten degrees and similar variations were observed for the different elements. The ambient temperature also varied with the seasons and decreased from September to January. The temperature of the element followed this trend, but with a lesser amplitude. The difference between the elements and the ambient temperature was of 20 K in September, but was of around 30 K in January (hours 4000 - 5000). This is hereafter called the seasonal drift. The reason of why the temperature of the element followed the day/night variation but not the seasonal variation was searched. It was first observed that as this drift concerned the four elements it was very probably not due to wear and should thus be compensated by the model. A drift in thermographic measurements was controlled and ruled out by using occasional contact temperature measures. Another explanation came from the results interpretation of the different model and is presented later in this text.
3.2. Result of the Detection
Table 2 gives the main results for the different tested methods. A maximum of five data is given for each element and each model. On the first line, the standard deviation of the error (for the model DT and for fixed training) or of the corrected temperature (for continuous training) are given for the training and for the validation data sets. On the second line, the value of the threshold T2 is given for the fixed models. For the variable model, asT and T2 are given. The last data is the alert rate for the given threshold. All the temperatures are given in Celcius.
The results concerning the main bearings will be presented and discussed first, because the considered temperature did not present the drift due to the clogging and were thus simpler to interpret.
For the mobile inspection, the results for DT showed that the method is susceptible to the seasonal drift, which explain why the standard deviation is higher for the validation than for the learning period. Both bearing presented similar behaviour. The difference in the alert ratios was because the seasonal drift was close to the threshold, above for the blower-side bearing, below for the coupling-side bearing. These data shows that temperature deviations around 10 degree could be detected. Compared with the temperatures given in the bibliography, this would mean that the degradation could not be easily detected in at an early stage.
The evolution of the 1TT models is presented in Figure 5. The variable 1TT model did not present seasonal drift but an important non Gaussian error was observed and the standard deviations of the learning and validation data sets were alike. As the transmitted power was not taken into account in the model, the temperature change with each process adjustment and the model have to adjust its coefficient, particularly the independent term.
The TTP models (presented in Figure 6) present less noise but is susceptible to the seasonal drift. As for DT,
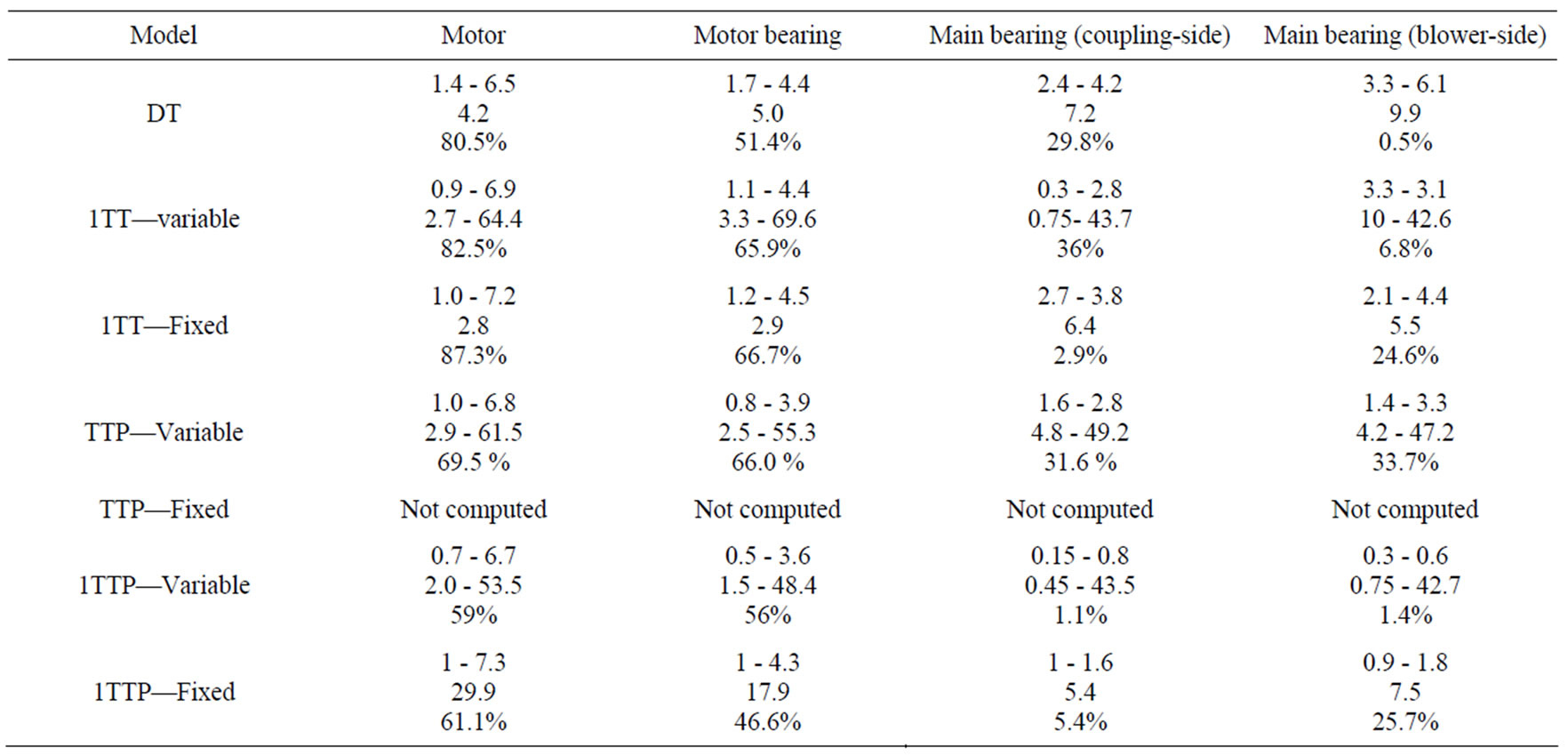
Table 2. Results for the different models, training methods and elements. For each combination and for the fixed models, the first line gives the standard deviation of the error for the learning and validation periods; the second line gives the corresponding threshold; the third line gives the ratio of errors above the threshold. For the models trained continuously, the first line gives the standard deviation of the corrected temperatures for the learning and validation periods; the second line gives the corresponding half interval above the mean temperature and the threshold; the third line gives the ratio of errors above the threshold.
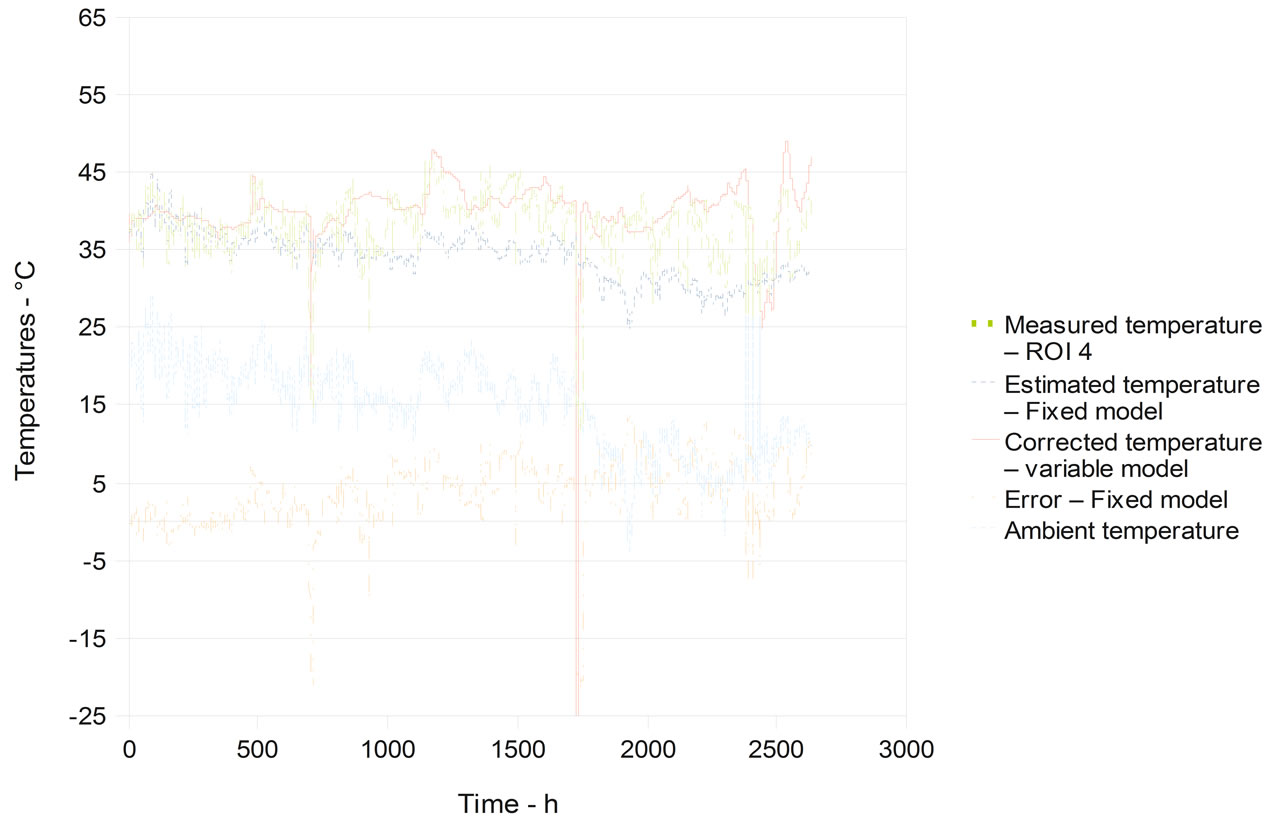
Figure 5. Temperatures for models 1TT, ROI 4.

Figure 6. Temperatures for models TTP, ROI 4.
this is the reason why the standard deviation was higher for the validation than during the training period. This also explains the unacceptable alert rate.
The 1TTP model with variable training (Figure 7) shows the lowest variability and thus the lowest threshold. It also presented the lowest alert rate though it was ten time the theoretical value. This seems to show that the error presented probability distribution more flat than the Gaussian distribution, that is to say presenting high errors with a frequency higher than the Gaussian distribution. As the threshold were found to be less than one degree above the mean temperature, it seems reasonable to consider a higher threshold to reduce the alert rate. By considering a threshold of 1.5˚C above the mean temperature, the error rate dropped to 10−4 which is a false alert every three month, which is acceptable and which should permit and early detection of degradation.
The same model with fixed training did not show the same performance. The fact that the indep-endent term was necessary for an accurate model showed that the two heat sinks should be considered, the first one being the immediate environment at ambient temperature, the other being at a fixed temperature. The soil could be a good candidate as fixed temperature heat sink. In this case, the heat transfer would not be the same in summer and winter.
On the other hand, the continuous training took into account recursively the whole set of data and the coefficient could thus be adjusted. The corrected temperature was thus independent of the seasonal drift.
The fixed models were trained during two weeks in September which is too short compared with the duration of the seasonal changes and these models could hardly respond correctly in January. The results for the motor and the motor bearing, presenting a drift caused by clogging, showed that all the models detected the drift, but all exceeded the alert rate evaluated at 22%. The reason varied from model to model. For DT and 1TT, the seasonal drift was in cause. For the 1TTP model, the cause was the time needed by the model to readjust its coefficients after the cleaning of the grid (Figure 8). The cleaning is a brutal change in the thermal behaviour of the engine. After cleaning, the engine being better ventilated and the true values of coefficients k3 and thus a1 and a2 changed between two measures. This kind of model is not suited for such dramatic changes and needed time to readjust the parameters after the cleaning. More frequent cleaning, for example each time the drift is detected, could solve this problem. Nevertheless the behaviour of the motor temperature showed that temperature drifts were detected.
4. Conclusions
This paper presented a method to use on-line temperature measurement of rotating machine elements to detect abnormal temperature evolution, which could be used to detect wear or other defects. The case study was an industrial blower and the element which were considered were a motor, the drive motor bearing and the two bearings supporting the blower.
Quantities such as the ambient temperature or the transmitted power affected the temperature of the elements. Autorecursive models with exogenous input of the temperature in function of these quantities were built and trained. Two ways were used to detect a temperature
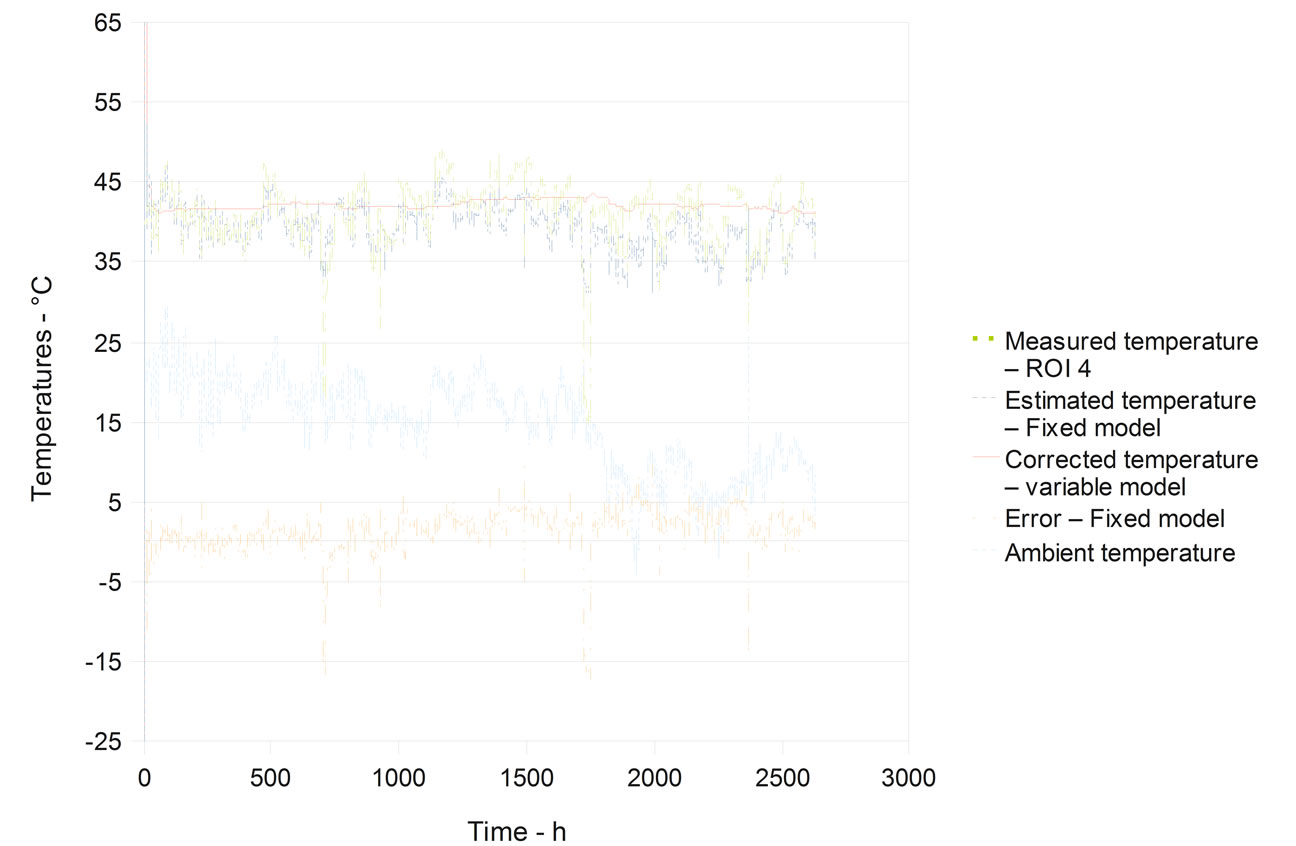
Figure 7. Temperatures for models 1TTP, ROI 4.
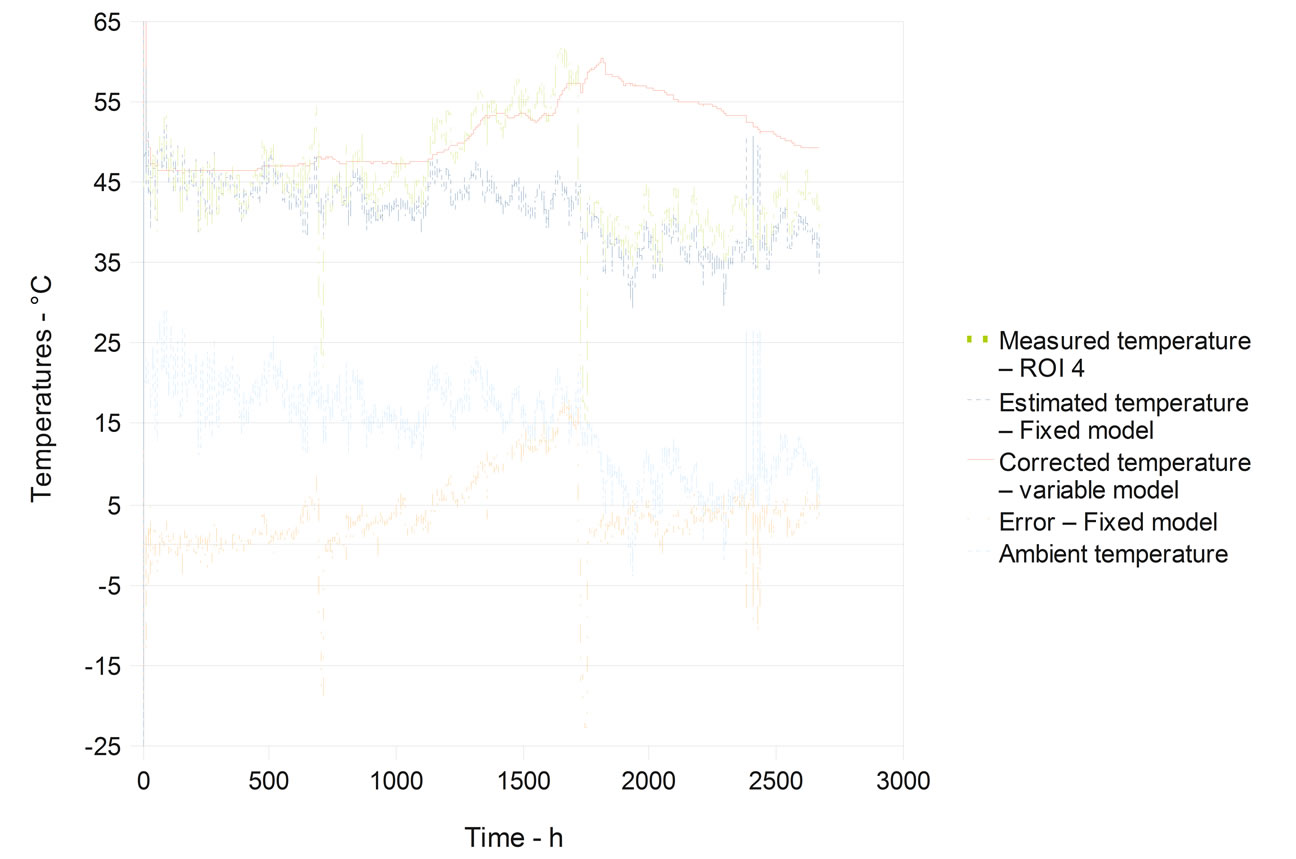
Figure 8. Temperatures for models 1TTP, ROI 0.
drift. For the first way the model was trained during a given period and next the error of the model was monitored. Any drift would be inducting an increase of the error. When the error exceeded a thresholds based on three standard deviation of the error, a drift was said to be detected. The second way considered a continuous training, the model being adapted after each measurement. A drift was detected by feeding the model with fixed input, thus giving the temperature of the element in standard conditions. The threshold was here the mean temperature plus three standard deviation of this temperature.
Several models were tested, each with different number of inputs, corresponding to different hardware requirement and thus to different costs of the system. It was shown that the simplest model taking into account only the ambient temperature effect and was able to detect temperature drift around ten degrees which is not enough for an early detection of the element’s end of live. The model taking into account also the thermal inertia of the element was not found more precise. Adding the influence of the transmitted power was an improvement. The best model took into account the ambient temperature, thermal inertia, the transmitted power and heat exchanges with a fixed temperature sink. This model had to be trained continuously in order to be able to compensate for the temperature variations due to the process, variations between day and night and the seasonal variations. The corrected temperature was, in normal condition, stable over the studied period of four month and was able to detect a temperature drift of around one degree. A threshold of 1.5˚C above the mean temperature generated false alarms in less than one case per three month.
By measuring precisely the element temperature and by detecting an early temperature drift, it should be possible to monitor the temperature evolution and thus to predict the remaining live of the element. This information is crucial for an advanced maintenance program.
5. Acknowledgements
This research was funded by the MecaTech Cluster of the Walloon Region, in the framework of the research group FiaMa.
6. REFERENCES
- X. P. V. Maldague, “Theory and Practice of Infrared Technology for Nondestructive Testing,” John Wiley & Son, New York, 2001.
- D. J. Titman, “Applications of Thermography in NonDestructive Testing of Structures,” NDT & E International, Vol. 34, No. 2, 2001, pp. 149-154. doi:10.1016/S0963-8695(00)00039-6
- O. Maletic, “Infrared Thermography in Balkans Cartonesboard Mill—Starting from Scratch,” Proceedings of Inframation, Las Vegas, 11-14 December 2005.
- J. Sun, R. J. K. Wood, L. Wang, I. Care and H. E. G. Powire, “Wear Monitoring of Bearing Steel Using Electrostatic and Acoustic Emission Techniques,” Wear, Vol. 259, No. 7-12, 2005, pp. 1482-1489.
- T. J. Harvey, R. J. K. Wood and H. E. G. Powire, “Electrostatic Wear Monitoring of Rolling Element Bearings,” Wear, Vol. 263, No. 7-12, 2007, pp. 1492-1491.
- M. Craig, T. J. Harvey, R. J. K. Wood, K. Masuda, M. Kawabata and H. E. G. Powrie, “Advanced Condition Monitoring of Tapered Roller Bearings, Part1,” Tribology International, Vol. 42, No. 11-12, 2009, pp. 1846-1856. doi:10.1016/j.triboint.2009.04.033
- A. Brown, “Thermographic Predictive Maintenance for Enhanced Productivity,” South East Asia Iron & Steel Institute Japan Conference and Exhibition, Tokyo, April 2002.
- V. Martinez, B. T. Martinez, P. O. Gonzalez and R. W. P. Uria, “Fault Detection in Diesel Engines Using Infrared Thermography,” Insight, Vol. 44, No. 4, 2002, pp. 228- 232.
- D. J. Yang and C. J. Choi, “Evaluation Method of Gaz Turbines Blades Covering Integrity by IR Camera,” International Journal of Modern Physics, Vol. 20, 2006, pp. 4329-4334.
- S. Bagavathiappan, T. Saravanan, N. P. George, J. Philip, T. Jayakurnar and B. Raj, “Condition Monitoring of Exhaust System Blowers Using Infrared Thermography,” Insight, Vol. 50, No. 9, 2008, pp. 512-515. doi:10.1784/insi.2008.50.9.512
- K. D. Cole, C. M. Tarawneh, A. A. Fuentes, B. M. Wilson and L. Navarro, “Thermal Models of Railroad Wheels and Bearings,” International Journal of Heat and Mass Transfert, Vol. 53, No. 9-10, 2010, pp. 1636-1645. doi:10.1016/j.ijheatmasstransfer.2010.01.031
- I. Kleis, U. Muiste, U. Pilvre, H. Uuemois and H. Uetz, “The Physical Mechanism of the Formation of Metal Microsphere in the Wear Process,” Wear, Vol. 53, 1979, pp. 79-85. doi:10.1016/0043-1648(79)90218-7
- N. Ranc, D. Wagner and P. C. Paris, “Study of Thermal Effect Associated with Crack Propagation during Very High Cycle Fatigue Test,” Acta Materialia, Vol. 50, No. 15, 2008, pp. 4012-4021. doi:10.1016/j.actamat.2008.04.023
- B. Yang, P. K. Liaw, M. Morrison, C. T. Liu, R. A. Buchanan, J. Y. Huang, R. C. Kuo, J. G. Huang and D. E. Fielden, “Temperature Evolution during Fatigue Damage,” Intermetallics, Vol. 13, No. 3-4, 2005, pp. 419-428. doi:10.1016/j.intermet.2004.07.032
- A. Jiang and H. Mao, “Investigation of Variable Optimum Preload for a Machine Tool Spindle,” International Journal of Machine Tools & Manufacture, Vol. 50, No. 1, 2010, pp. 19-28. doi:10.1016/j.ijmachtools.2009.10.001
- J.-S. Chen and K.-W. Chen, “Bearing Load Analysis and Control of a Motorized High Speed Spindle,” Machine tools & Manufacture, Vol. 45, No. 12-13, 2005, pp. 1487-1493.
- A. Mazioud, J.-F. Durastanti, L. Ibos and E. Surugue, “Detection of Rolling Bearing Degradation Using Infrared Thermography,” Proceedings of the 8th International Conference on Quantitative Infrared Thermography (QIRT 2006), Padoue, 27-30 June 2006.
- L. Ljung, “System Indentification. Theory for the User,” 2nd Edition, Prentice Hall, Upper Saddle River, 1999.

