Engineering
Vol. 2 No. 10 (2010) , Article ID: 3182 , 12 pages DOI:10.4236/eng.2010.210105
A Fast Predicating of Nutrient Removal Efficiency in Five Steps Sequencing Batch Reactor System Using Fuzzy Logic Control Model
1Department of Environmental Science and Engineering, Southeast University, Nanjing, China
2Department of Chemical Engineering, Faculty of Engineering, Basrah, Iraq
3Department of Civil Engineering, Faculty of Engineering, Basrah, Iraq
E-mail: saad.arab@yahoo.com
Received June 10, 2010; revised August 4, 2010; accepted August 6, 2010
Keywords: Fuzzy Logic Control, Hydraulic Retention Time and SBR System
ABSTRACT
Removal efficiency of COD, NH4-N and PO4-P and NO3-N in five step SBR processes is widely influenced by hydraulic retention time of Anaerobic/Anoxic/Aerobic/Anoxic/Aero-bic step of this system where the hydraulic retention time in each step is influence directly on removal efficiency of this system therefore the operator of this system cannot control on this system without experience or a control model. The major objective of this paper is develop a control model (Fuzzy Logic Control Model) based on fuzzy logic rule to predict the maximum removal efficiency of COD,NH4-N,PO4-P and NO3-N and minimize hydraulic retention time in each step of SBR process where the controlled variables was the hydraulic retention times in the Anaerobic/Anoxic/Aerobic/Anoxic/Aerobic step respec-tively and the output variables was the COD, NH4-N, PO4-P and NO3-N removal efficiency at constant ratio of C/N/P and sludge age. As a results Fuzzy logic if-then rules were used and MIMO Model was built to control COD, NH4-Nand PO4-P and NO3-N removal efficiency based on hydraulic retention time in each tank of five step SBR process where the three dimension results show that the influence of hydraulic residence time at each step of SBR system on removal efficiency COD, NH4-N, PO4-P and NO3-N. Fuzzy control model provide a suitable tool for control and fast predict of Hydraulic residence time effects on biological nutrient removal efficiency in five-step sequencing batch reactor.
1. Introduction
Conventional control methods are powerful when good analytical mathematical models are available to support their development and operation. This situation is uncommon in real processes. Particularly, the real-time control of wastewater treatment plants (WWTP) is a difficult but essential task, due to the lack of accurate dynamical models describing the process and reliable on -line instrumentation (Olsson and Newell, 1999). However, WWTP can be properly operated by specialized people, having knowledge about the process, though in practice, this know-how is essentially qualitative, empirical, and incomplete. The operation of a WWTP represents therefore a knowledge intensive task. In this regard, a system capable of giving all the possible information about the state of the process must be available in order to establish the basis of a diagnosis system integrating all the possible knowledge. This requirement is an important step to have successful control.
Decisions(Patry and Chapman, 1989). Applications of knowledge-based systems to activated sludge processes are being widely studied (Chapman et al., 1989, Barnett et al., 1992). Most of systems are off-line KnowledgeBased Expert Systems (KBES) mainly diagnostic and advising tools to help process Operators. An activated sludge wastewater treatment plant can be classified as a complex system due to its nonlinear dynamics, large uncertainty in uncontrolled inputs and in the model parameters and structure, multiple time scale of the dynamics, and multi input-output structure. Some KBES have been designed with the main purpose of online supervision, though the emphasis on real-time supervisor control is usually absent. Many researchers have studied the Operation characteristics and parameters of step feeding process by theoretical analysis and computer simulation S. Fujii, 1996. L. Larrea, A. Larrea, 2001. G. Zhu 2006. Some practical experiences were also drawn from extended; renewed or retrofitted Conventional activated sludge process, J. Fillos, 1996. S. Schlegel, 1992. E. Gorgun, 1996. S. Wang, 2006. During the last two decades, there were a variety of applications of fuzzy logic control in wastewater treatment plants to optimize operation and performance of bioprocesses. Fuzzy logic provides a language with a syntax and semantics to translate qualitative knowledge into numerical reasoning. In most engineering problems, information about the probabilities of various risk items is only vaguely known. The term computing with words has been introduced by Zadeh (1996) to explain the notion of reasoning linguistically rather than with numerical quantities. Fuzzy rule -based modeling is one of techniques that make use of human knowledge and deductive processes where the experience of operator is assisted to manage and operate biological wastewater treatment plant satisfactorily using operational observations. It is important to develop computer operational decision support systems that are able to play a similar role to the expert in daily operation in minimizing cost and increase performance of wastewater treatment processes. The control objective and parameters ranged from aeration T. J. Ferrer, 1998. T. Kalker, 1999. M. Fiter, 2005. Effluent suspended solid Y. Tsai, 1996. External carbon addition M. Yong, 2006 [17], and loading rate E. Murnleitner, 2002, to nitrification in Sequencing Batch Reactor (SBR) process Y. Peng, 2003, and dissolved oxygen concentration A. Traoré, 2004. A fuzzy control strategy was applied by Meyer et al. (2003) for the control of aeration in wastewater treatment plants with pre-denitrfication. The implementation of expert systems based on fuzzy logic rules are described elsewhere (Carrasco et al., 2002; Puñal et al., 2002). Recently, especially attention to the expert supervision and control of anaerobic digestion processes is reported (Flores et al., 2000; Polit et al., 2002). Fuzzy control algorithms have been widely applied to pursue better effluent quality and higher economic efficiency on aerobic biological treatment processes (Irene et al., 2008; Wu et al., 2007; Murnleitner et al., 2002. Marsili-Libelli (2006) developed fuzzy pattern recognition to control SBR switching. The switching strategy was from the indirect observation of process state through simple physicochemical measurements and the use of an inferential engine to determine the most appropriate switching schedule. In this study, fuzzy rule based model is developed to predict the maximum removal efficiency of COD, NH4-N, PO4-P and NO3-N and minimize hydraulic retention time in each stage, Anaerobic-Anoxic (1)-Aerobic (1)-Anoxic (2)-Aerobic (2), of SBR system whereas the hydraulic retention time have direct influence on energy and operation cost of wastewater treatment plant. The fuzzy model is built based on if-then rules for hydraulic retention time and removal efficiency of COD, NH4-N, PO4-P and NO3-N based on experimental data that collected from the literature.
Fuzzy control law: The features of the fuzzy logic toolbox of MATLAB® constitute a support for the easy implementation of the set of rules, these being the main part of the control law developed in this study. The fuzzy methodology applied was Mamdani’s fuzzy inference method (Mamdani and Assilian, 1975). In this method, the first and the second part of the fuzzy inference process consist in the fuzzification of the inputs and application of fuzzy operators. Based on acquired knowledge on the process, a set of rules handling the regulation of the COD, NH4-N, PO4-P and NO3-N removal efficiency in dependence on the hydraulic retention times of the reactors was set up. The output of the control law was the COD, NH4-N, PO4-P and NO3-N removal efficiency. The first step to build the control law was the translation of possible values of the different inputs and output variables into linguistic labels given by membership functions. The system configuration of RsFLC is shown in Figure 1.
2. Material and Methods
The experimental set up was fermenter (Bioflo IIC, New Brunswick) with a 5 L working volume was used as the SBR. The fermenter was microprocessor controlled for aeration, agitation, pH and dissolved oxygen (DO).
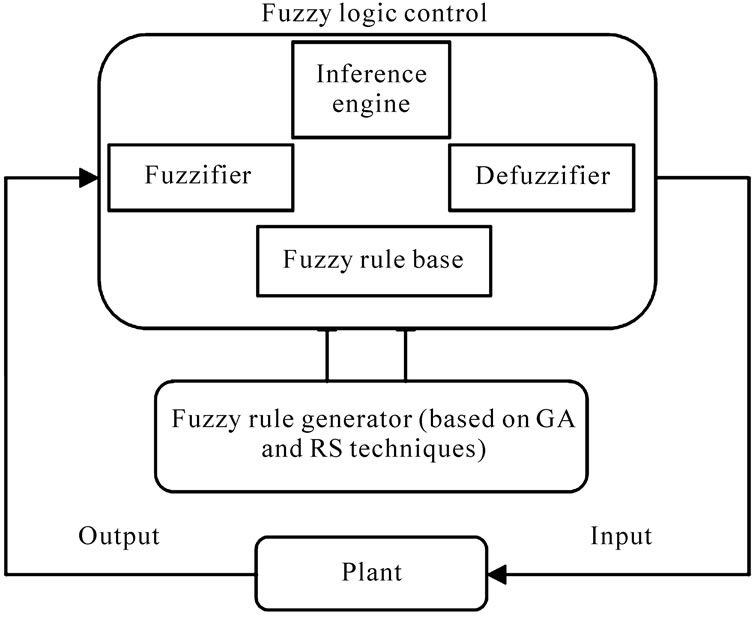
Figure 1. System configuration of RsFLC.
Aeration was provided by using an air pump and a sparger. Agitation speed was varied between 25 and 300 rpm. The pH, DO and ORP of the nutrient medium were continuously monitored by the relevant probes. The fermenter was used to investigate the effectiveness of Hydraulic retention time on the removal efficiency of COD, NH4-N, PO4-P and NO3-N. The effect of Hydraulic retention time on removal efficiency at constant sludge age (10 days) is shown in Table 1.
2.1. Fuzzy Rule Based Modeling
In fuzzy rule-based modeling, the relationships between variables are represented by means of fuzzy if-then rules of the form “If antecedent proposition then consequent proposition”. The antecedent proposition is always a fuzzy proposition of the type “x is A” where x is a linguistic variable and A is a linguistic constant term. The proposition’s truth-value (a real number between 0 and 1) depends of degree of similarity between x and A.
Depending on the form of the consequent proposition, two main types of rule-based fuzzy models are commonly used:
• Linguistic fuzzy model: Both antecedent and the consequent are fuzzy propositions (e.g., Mamdani model).
• Takagi-Sugeno (TS) fuzzy model: the antecedent is a fuzzy proposition; the consequent is a crisp function.
The linguistic model (Zadeh, 1973; Mamdani, 1977) has the capacity to capture qualitative and highly uncertain knowledge in the form of if–then rules:
Ri: If x is Ai then y is Bi; i = 1, 2, …, K (1)
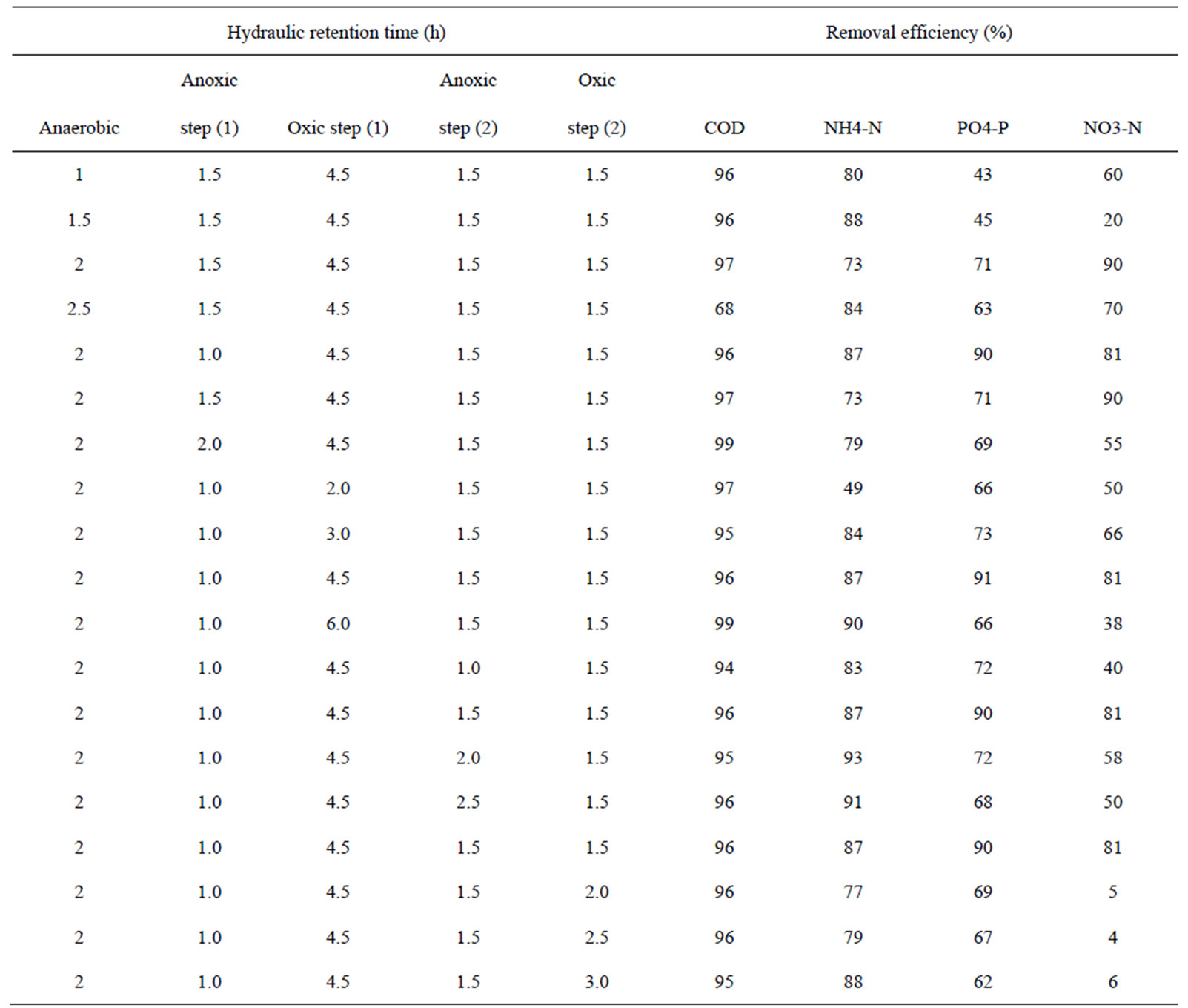
Table 1. Expeimental data of removal efficiency and hydraulic retention time of five step SBR system at (COD/N/P = 100/5/1.5).
where, x is the input (antecedent) linguistic variable and Ai is the antecedent linguistic constants (the qualitatively defined functions). Similarly, y is the output (consequent) linguistic variable and Bi is the consequent linguistic constants. The values of x and y and Ai and Bi are fuzzy sets defined in the domains of their respective base variables. The linguistic terms Ai and Bi are usually selected from sets of predefined terms, such as small, medium, large. The rule base R = {Ri/i = 1, 2, …, K} and the sets A and B constitute the knowledge base of the linguistic model. Each rule is regarded as a fuzzy relation (fuzzy restriction on the simultaneous occurrences of values x and y): Ri (X × Y) → [0,1]. This relation can be computed in two basic ways-by using:
• Fuzzy implications or
• Fuzzy conjunctions (Mamdani method). In this study, the Mamdani method was used, in which conjunction AΛB is computed by a minimum operator (a t-norm):
Ri = Ai × Bi
i.e.,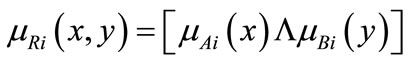 (2)
(2)
The minimum operator is computed on the Cartesian product space of X and Y, i.e., for all possible pairs of x and y. The fuzzy relation R represents the entire model Equation (1) and is given by the disjunction (union or maximum, i.e., s-norms) of the K individual rule’s relations, Ri:
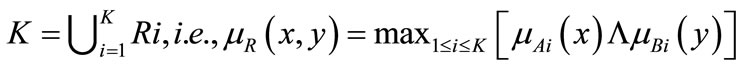 (3)
(3)
Now the entire base is encoded in the fuzzy relation R and the output of the linguistic model can be computed.
By the max-min composition (°):
y = xoR (4)
Suppose an input fuzzy value x = A¢, which has the output value B¢ given by the relational composition:
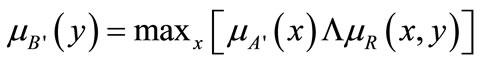 (5)
(5)
By substituting Equation (2) into Equation (5), get:
 (6)
(6)
Equation (6) can be written as follow:
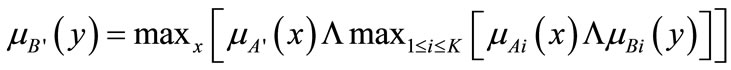 (7)
(7)
Equation (7) represents the output fuzzy Set of the linguistic model.
The most common methods used for defuzzification are: Yager (1980) centroidal method, is always used for defuzzification due to its simplicity, that can be determined as:
• Yager (1980) centroidal method, is always used for defuzzification due to its simplicity, that can be determined as:
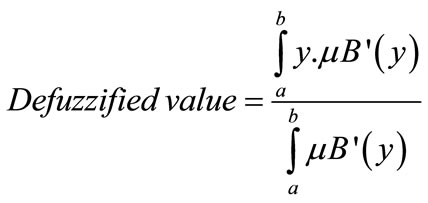 (8)
(8)
where:
a and b = The lower and upper limits of the integral which determines the validity domain of the membership function
y = The centroidal distance from the origin;
• Chen (1985) ranking method
• Bertoluzza et al. (1995) method and
• Tran and Duckstein (2002) method
The above algorithm is the Mamdani inference that used as (SISO) single input and single output. It can be extended to Multiple Inputs and Single Output (MISO) and Multiple Outputs (MIMO). The MIMO model is a set of MISO models.
In the case of MIMO model Ri becomes as follow:
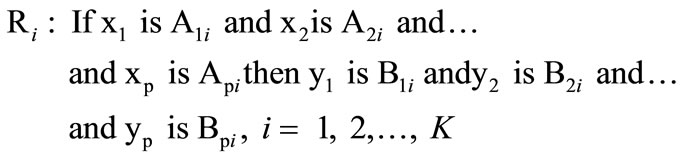 (9)
(9)
The above model is the special case of Equation (1), as the set Ai and Bi is obtained by the Cartesian product of fuzzy sets:
Aij = Ai1 × Ai2 × Ai3 × …… × Aip (10)
Bik = Bi1 × Bi2 × Bi3 × ….... × Bip (11)
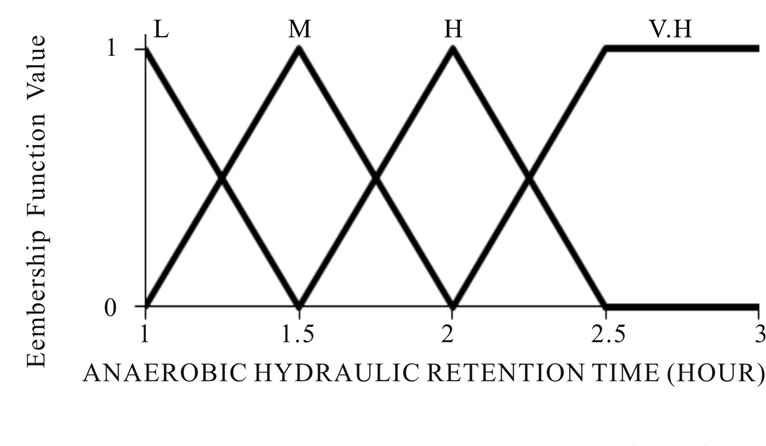
Hydraulic retention time modeling: The data collected for 17 operating conditions as shown in Table 1 were used for developing a fuzzy rule-based model. The efficiency of multi-tank was assessed based on COD, NH4-Nand PO4-P and NO3-N removal efficiency. The control parameters of MIMO model are Anaerobic HRT, Anoxic step one HRT, Aerobic step one HRT, Anoxic step two HRT and Aerobic step two HRT were defined by qualitative scales as shown in Figure 2.
The variability in the input control parameters was used for fuzzification. A Hydraulic retention time were expressed by low, small medium, medium, high and very high scale in each tank (anaerobic, anoxic, aerobic, anoxic and aerobic).
The response of the model is the removal efficiency of COD, NH4-N, PO4-P and NO3-N and for COD and NO3-N output, a six granularity scale (very low (V.L),
 (a)
(a)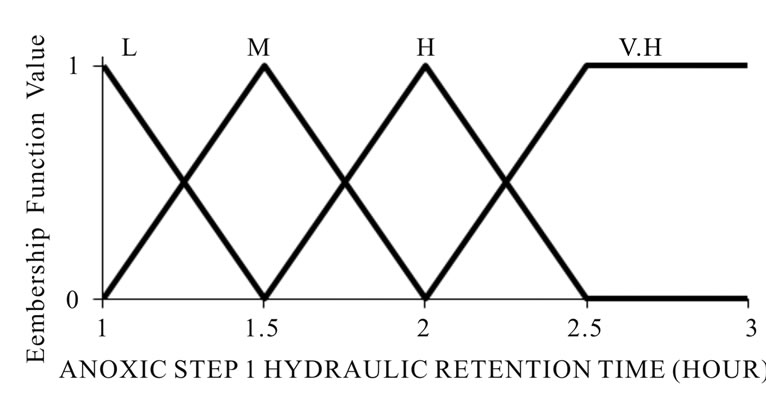 (b)
(b)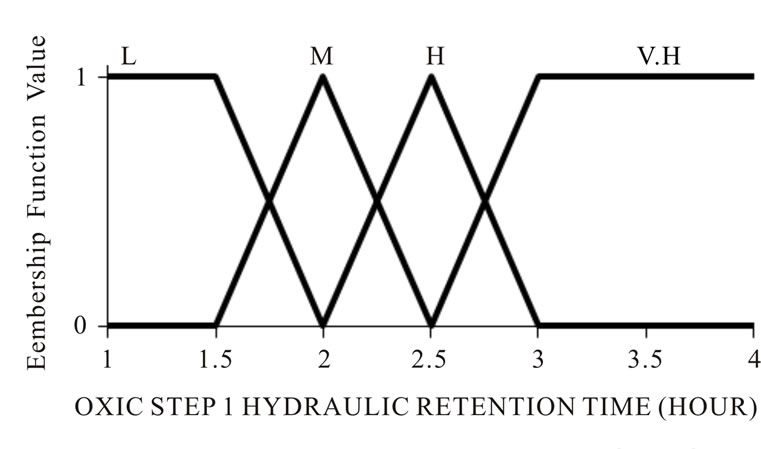 (c)
(c) (d)
(d) (e)
(e) (f)
(f)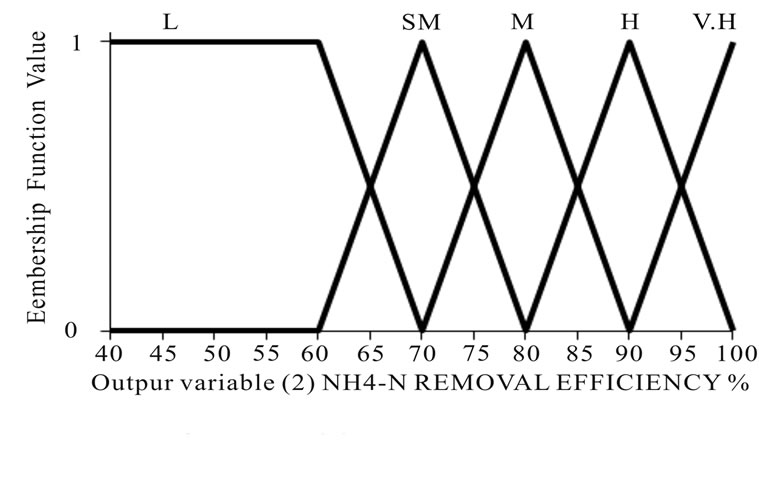 (g)
(g) (h)
(h) (i)
(i)
Figure 2. The input and output of MIMO model in Mamdani inference fuzzy logic model.
low(L), small medium (S.M), medium(M), high (H), very high(V.H)) while for NH4-N and PO4-P output, a five granularity scale (low(L), small medium (SM), medium(M), high (H), very high(V.H)) were used as shown in Figure 2. The fuzzy rule based model was developed with seventeen rules based on the collected data under each operating condition and expert judgment as shown in Table 2.
3. Results and Discussion
3.1. Fuzzy Control Application
The Mamdani inference was established based on 17 fuzzy linguistic rules as shown in Figure 3(b). The defuzzified results and graphical outputs can be derived as shown in Figures 3(a)-(c) whereas Figure 3 illustrates an example of the surface viewer screen obtained from the fuzzy logic toolbox. Twoor three-dimensional graphic results of variables can be plotted and compared. The relationships between the nutrient concentrations of five step SBR system and the hydraulic retention time inputs of the model can be obtained as shown in Figure 4. Figure 4 is shows that COD, NH4-N, PO4-P and NO3-N
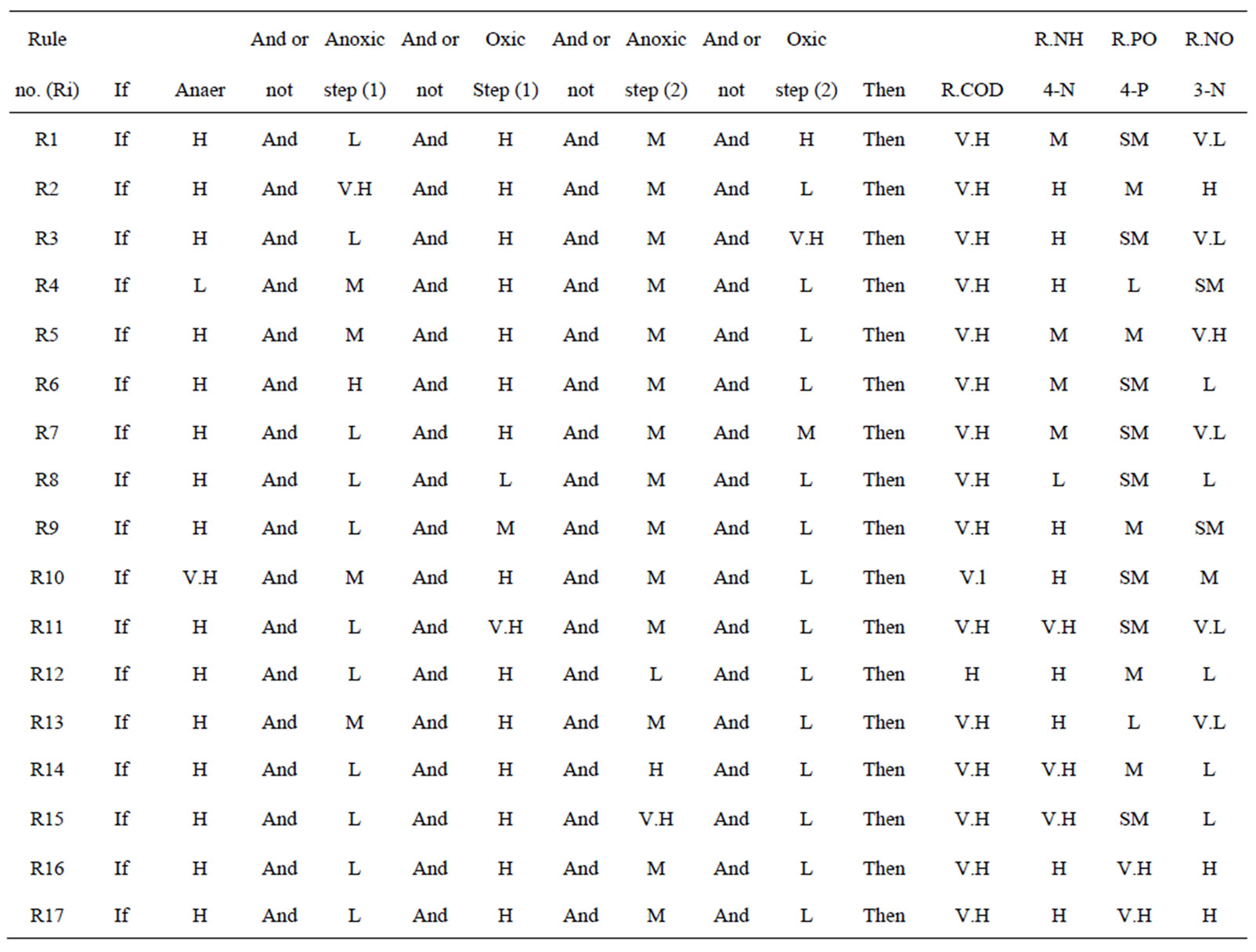
Table 2. Fuzzy rule based model for hydraulic retention time and removal efficiency in SBR system at constant sludge age (MIMO model).
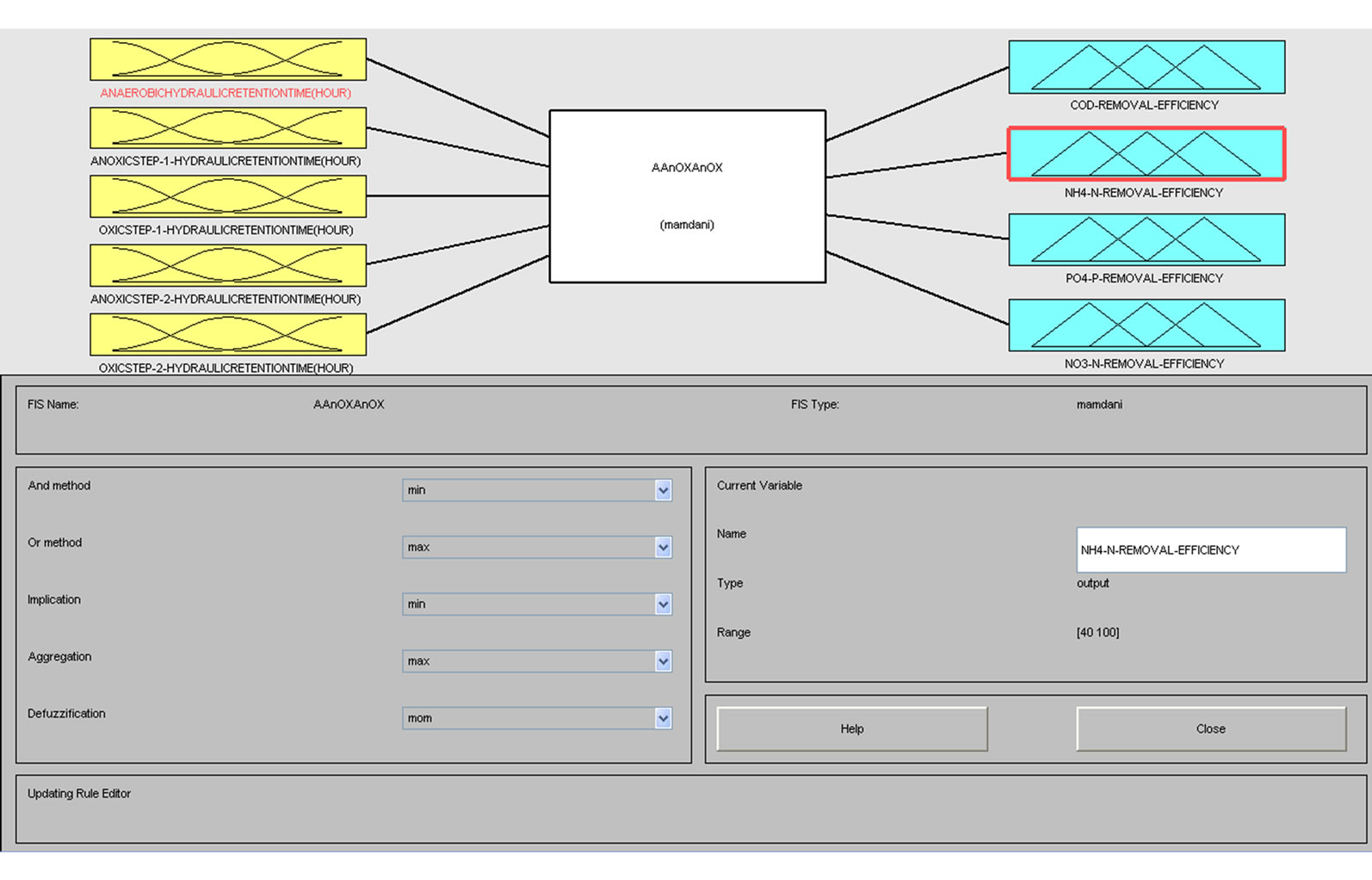 (a)
(a) (b)
(b)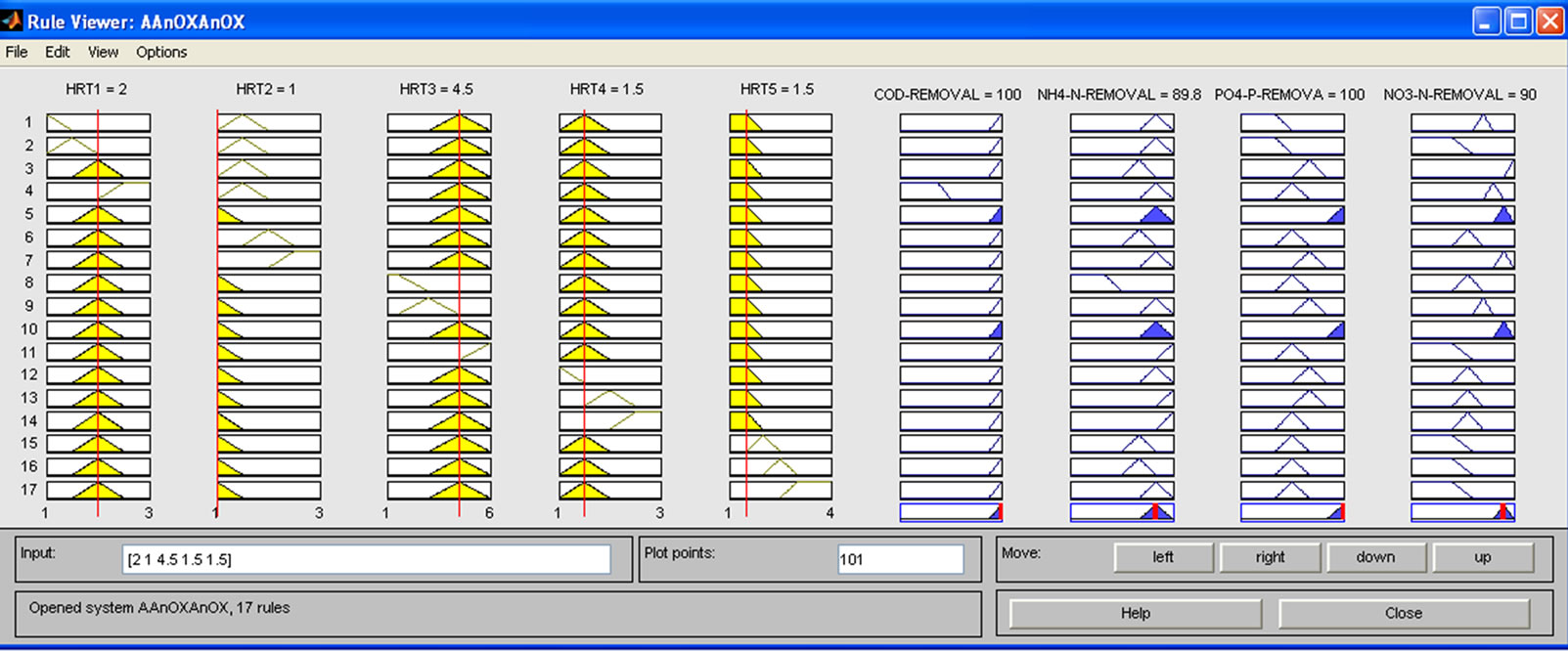 (c)
(c)
Figure 3. Fuzzy inference system (a) FIS editor screen; (b) Rule editor of matlab-fuzzy and (c) Rule viewer screen to obtain defuzzified results.
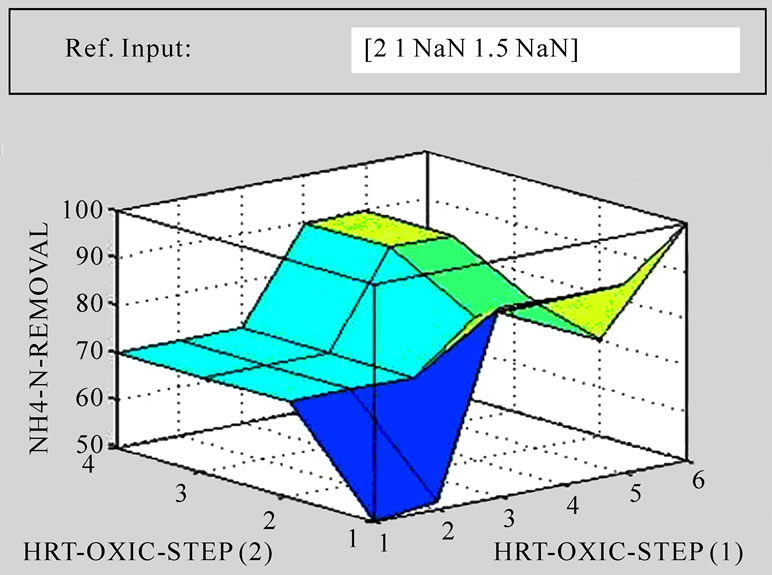 (a)
(a) (b)
(b) (c)
(c)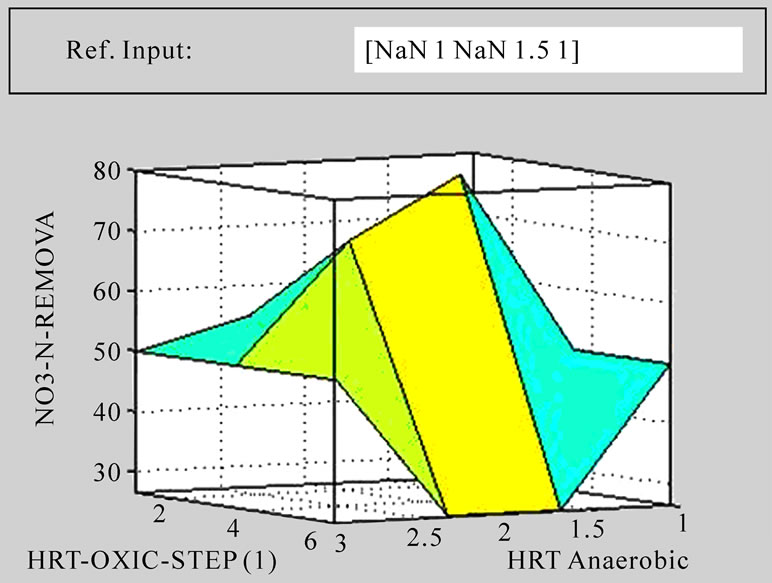 (d)
(d)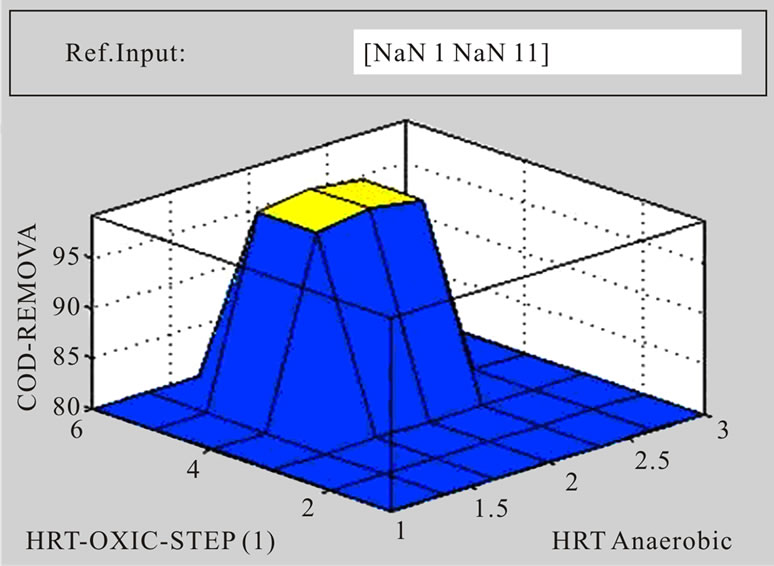 (e)
(e)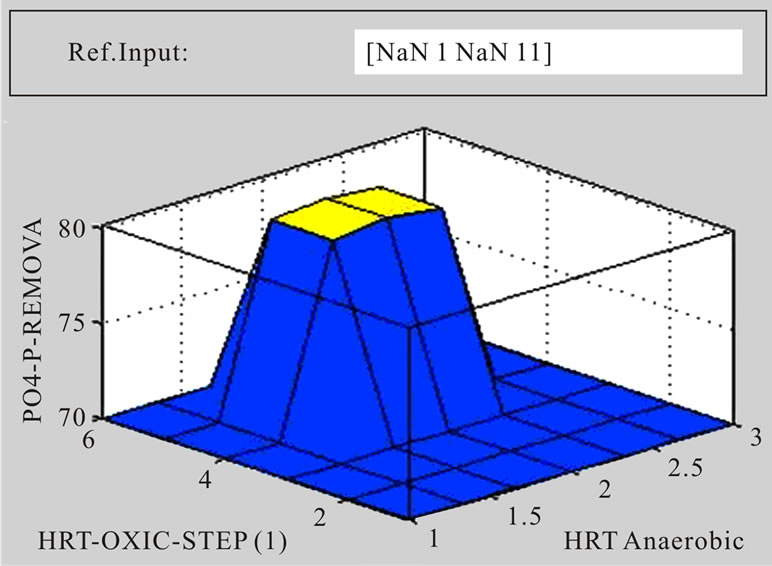 (f)
(f)
Figure 4. 3D response surface graph for output value under different hydraulic retention time (C/N/P = 100/5/1.5, sludge age (10) days).
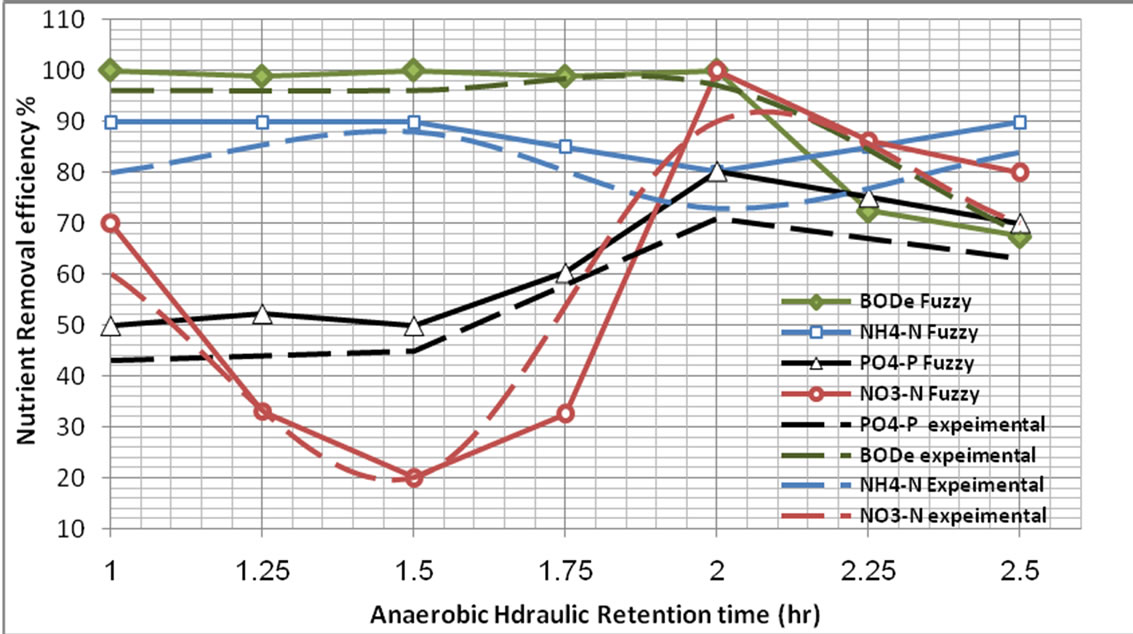
Figure 5. Overall nutrient percent removal at different hydraulic retention time of the anaerobic step.
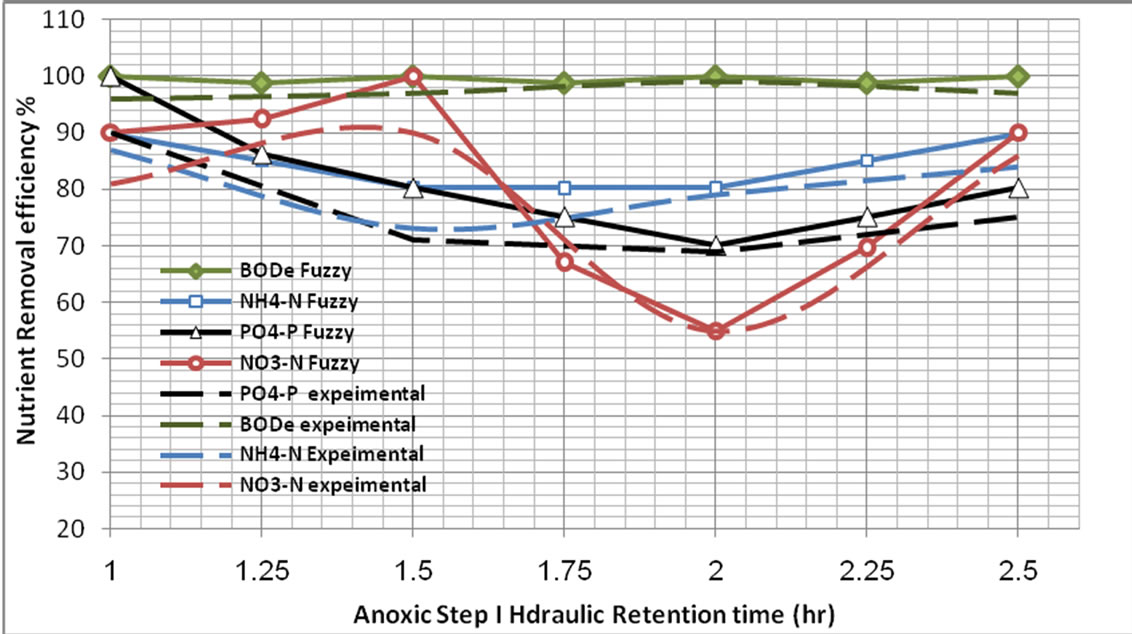
Figure 6. Overall nutrient percent removal at different hydraulic retention time of the anoxic step I.
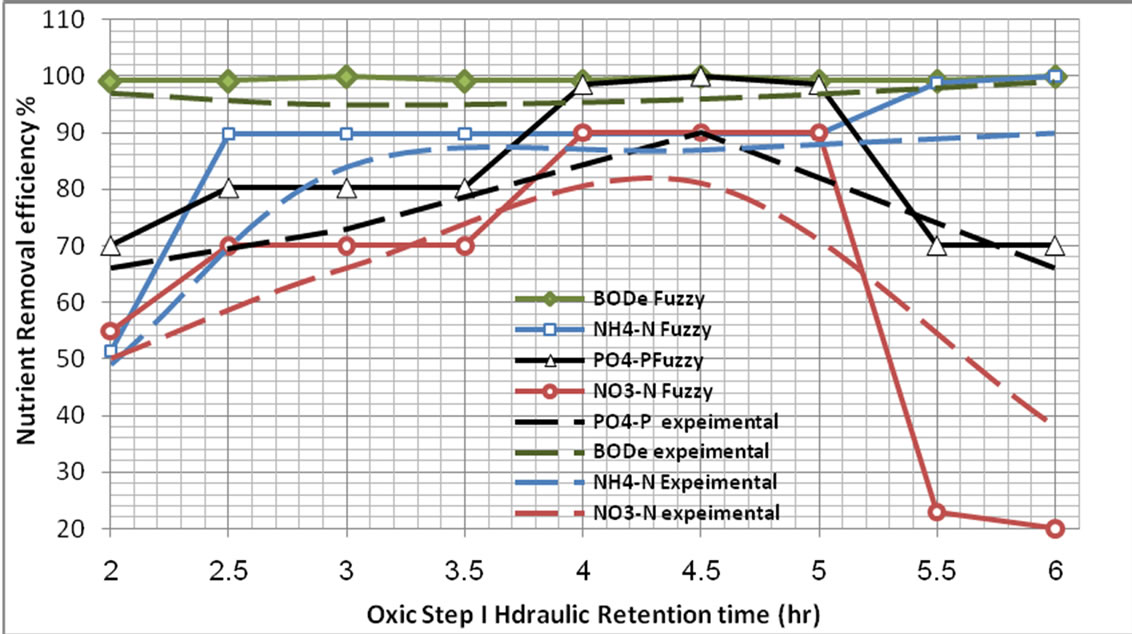
Figure 7. Overall nutrient percent removal at different hydraulic retention time of the oxic step I.
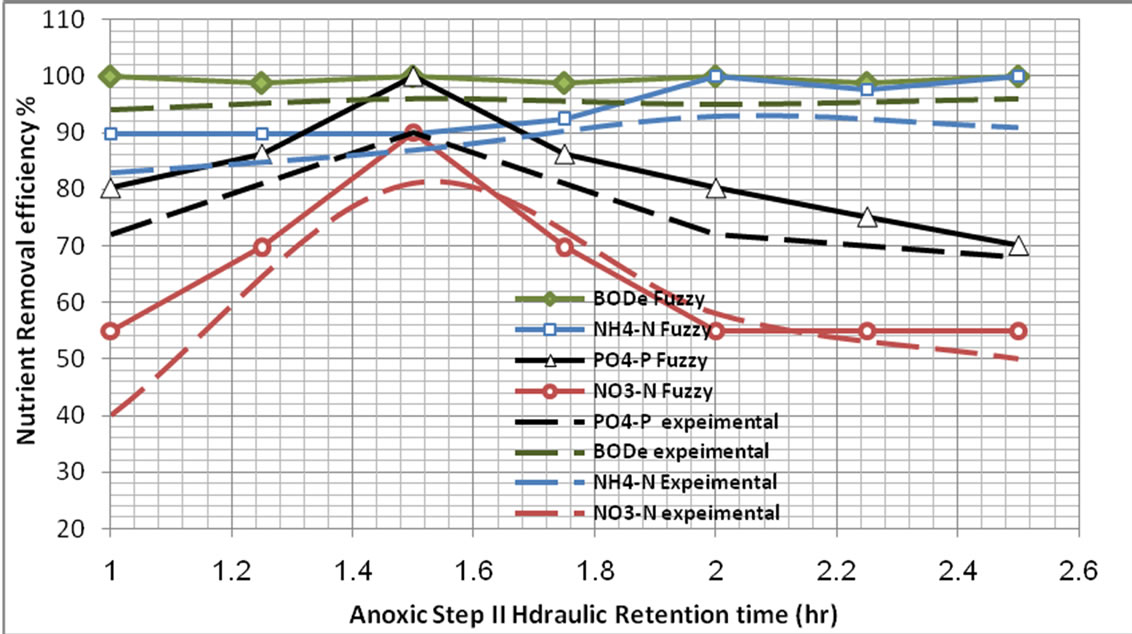
Figure 8. Overall nutrient percent removal at different hydraulic retention time of the anoxic step II.
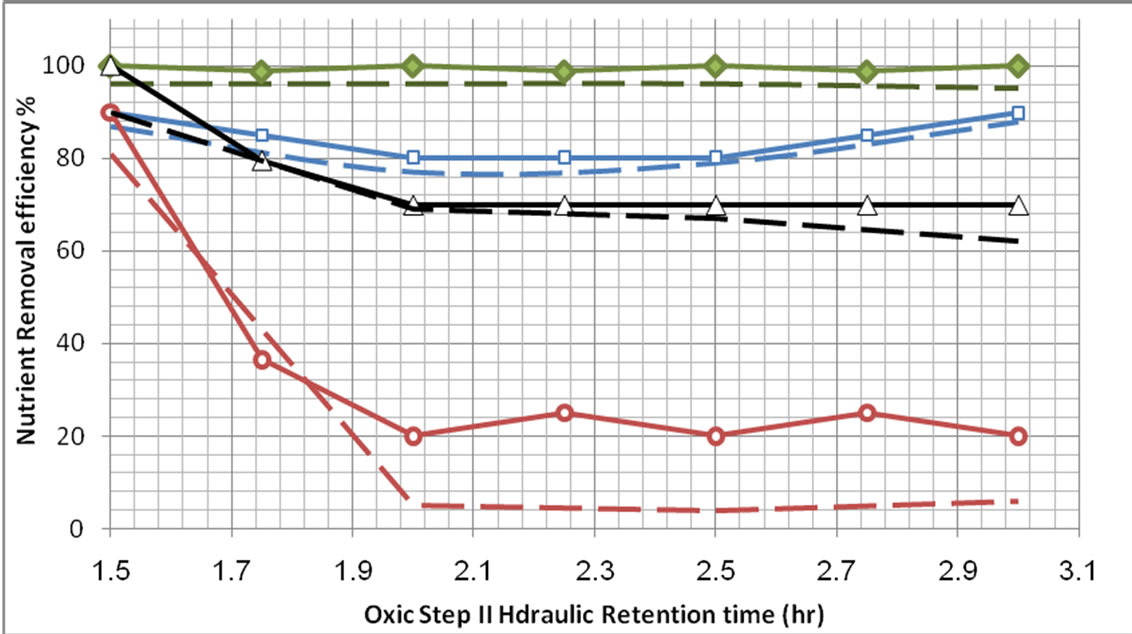
Figure 9. Overall nutrient percent removal at different hydraulic retention time of the oxic step II.
removal efficiency of the system with the inputs Anaerobic, Anoxic, Aerobic, Anoxic and Aerobic hydraulic retention time of the model. Figure 3(c) shows the results of applied rules and their corresponding outputs according to the mass center of variables. Using the interface, defuzzified values for output variables can be derived changing input values manually. Different output values can be obtained through the rule viewer according to the given input values.
It is not flexible to get defuzzified output values for all the real input values using the interface. For that reason, a program is written using MATLAB codes to drive defuzzified output results in accordance with real input values.
3.2. Comparison with Experimental Data
The comparison results of Fuzzy logic model with Experimental data are shown in Figures 5-9. The results show that Fuzzy logic Control model is a good tool that can be used in Prediction Removal efficiency of five step SBR system whereas the comparison results indicated that the FLC model have a good convergence performance and the predictions of outflow nutrient removal efficiency coincided well with the experimental values.
4. Conclusions
Fuzzy logic model was built based on if-then rules (from collection data) for COD, NH4-Nand PO4-P and NO3-N removal efficiency and hydraulic retention time in each step of five step SBR process. A control law based on fuzzy logic features was developed and validated for Hydraulic retention time in Anaerobic/Anoxic/Aerobic/ Anoxic/Aerobic tank of SBR wastewater process. The controlled variables was the Hydraulic retention times in the Anaerobic/Anoxic/Aerobic/Anoxic/Aerobic tank respectively and the output variables was the COD, NH4-N, PO4-P and NO3-N removal efficiency. The model provides a new tool for control hydraulic residence time effects on biological nutrient removal efficiency in five -step sequencing batch reactor.
5. REFERENCES
- A. Uygur and F. Kargi, “Hydraulic Residence Time Effects in Biological Nutrient Removal Using Five-Step Sequencing Batch Reactor,” Enzyme and Microbial Technology, Vol. 35, No. 2-3, 2004, pp. 167-172.
- S. Fujii, “Theoretical Analysis on Nitrogen Removal of the Step-Feed Anoxic-Oxic Activated Sludge Process and Its Application for the Optimal Operation,” Water Science and Technology, Vol. 34, No. 1-2, 1996, pp. 459 -466.
- L. Larrea, A. Larrea, E. Ayesa, J. Rodrigo, M. LopezCarrasco and J. Cortacans, “Development and Verification of Design and Operation Criteria for the Step Feed Process with Nitrogen Removal,” Water Science and Technology, Vol. 43, No. 1, 2001, pp. 261-268.
- G. Zhu and Y. Peng, “Theoretical Evaluation on Nitrogen Removal of Step-Feed Anoxic/Oxic Activated Sludge Process,” Journal of Harbin Institute of Technology, Vol. 13, No. 3, 2006, pp. 99-102.
- J. Fillos, V. Diyamandoglu, L. Carrio and L. Robinson, “Full-Scale Evaluation of Biological Nitrogen Removal in the Step-Feed Activated Sludge Process,” Water Environment Research, Vol. 68, No. 2, 1996, pp. 132-142.
- S. Schlegel, “Operational Results of wastewater Treatment Plants with Biological N and P Elimination,” Water Science and Technology, Vol. 25, No. 4-5, 1992, pp. 241 -247.
- E. Gorgun, N. Artan, D. Orhon and S. Sozen, “Evaluation of Nitrogen Removal by Step Feeding in Large Treatment Plants,” Water Science and Technology, Vol. 34, No. 1-2, 1996, pp. 253-260.
- S. Wang, L. Yu, G. Man, H. Zhu, D. Peng and X. Wang, “A Pilot Study on a Step-Feeding Anoxic/Oxic Activated Sludge System,” Water Science and Technology, Vol. 53, No. 9, 2006, pp. 95-101.
- T. Kalker, C. Van Goor, P. Roeleveld, M. Ruland and R. Babuska, “Fuzzy Control of Aeration in an Activated Sludge Wastewater Treatment Plant: Design, Simulation and Evaluation,” Water Science and Technology, Vol. 39, No. 4, 1999, pp. 71-78.
- M. Fiter, D. Guell, J. Comas, J. Colprim, M. Poch and I. Rodriguez-Roda, “Energy Saving in a Wastewater Treatment Process: An Application of Fuzzy Logic Control,” Environmental Technology, Vol. 26, No. 11, 2005, pp. 1263-1270.
- J. Ferrer, M. Rodrigo, A. Seco and J. Penya-Roja, “Energy Saving in the Aeration Process by Fuzzy Logic Control,” Water Science and Technology, Vol. 38, No. 3, 1998, pp. 209-217.
- Y. Tsai, C. Ouyang, M. Wu and W. Chiang, “Effluent Suspended Solid Control of Activated Sludge Process by Fuzzy Control Approach,” Water Environment Research, Vol. 68, No. 6, 1996, pp. 1045-1053.
- M. Yong, P. Yong-Zhen, W. Xiao-Lian, W. Shu-Ying, “Intelligent Control Aeration and External Carbon Addition for Improving Nitrogen Removal,” Environmental Modelling and Software, Vol. 21, 2006, pp. 821-828.
- E. Murnleitner, T. Becker and A. Delgado, “State Detection and Control of Overloads in the Anaerobic Wastewater Treatment Using Fuzzy Logic,” Water Research, Vol. 36, No. 1, 2002, pp. 201-211.
- Y. Peng, J. Gao, S. Wang and M. Sui, “Use of pH as Fuzzy Control Parameter for Nitrification under Different Alkalinity in SBR Process,” Water Science and Technology, Vol. 47, No. 11, 2003, pp. 77-84.
- A. Traoré, S. Grieu, S. Puig, L. Corominas, F. Thiery, M. Polit and J. Colprim, “Fuzzy Control of Dissolved Oxygen in a Sequencing Batch Reactor Pilot Plant,” Chemical Engineering Journal, Vol. 111, No. 1, 2005, pp. 13-19.
- U. Meyer and H. J. Pöpel, “Fuzzy-Control for Improved Nitrogen Removal and Energy Saving in WWWT-Plants with Pre-Denitrification,” Water Science and Technology, Vol. 47, No. 11, 2003, pp. 69-76.
- E. F. Carrasco, J. Rodríguez, A. Puñal, E. C. Roca and J. M. Lema, “Rule-Based Diagnosis and Supervision of a Pilotscale Wastewater Treatment Plant Using Fuzzy Logic Techniques,” Expert Systems with Applications, Vol. 22, No. 1, 2002, pp. 11-20.
- A. Puñal, J. Rodríguez, E. F. Carrasco, E. Roca and J. M. Lema, “An Expert System for Monitoring and Diagnosis of Anaerobic Wastewater Treatment Plants,” Water Research, Vol. 36, No. 10, 2002, pp. 2656-2666.
- J. Flores, B. Arcay and J. Arias, “An Intelligent System for Distributed Control of an Anaerobic Wastewater Treatment Process,” Artificial Intelligence, Vol. 13, No. 4, 2000, pp. 485-494.
- M. Polit, M. Estaben and P. Labat, “A Fuzzy Model for an Anaerobic Digester, Comparison with Experimental Results,” Artificial Intelligence, Vol. 15, No. 5, 2002, pp. 385-390.
- L. A. Zadeh, “Fuzzy Logic Computing with Words,” IEEE Transactions—Fuzzy Systems, Vol. 4, No. 2, 1996, pp. 103-111.
- B. Olsson and B. Newell, “Wastewater Treatment Systems—Modelling, Diagnosis and Control,” IWA Publishing, London, 1999.
- G. G. Patry and D. Chapman, “Dynamic Modeling and Expert Systems in Wastewater Engineering,” Lewis Publishers, Chelsea, 1989.
- M. W. Barnett, G. G. Patry and M. Hiraoka, “Knowledge-Based (Expert) Systems for the Activated Sludge Process,” In: J. F. Andrews, Ed., Dynamics and Control of the Activated Sludge Process, Technomic Publishing Company, Lancaster, 1992, pp. 231-243.
- J. Irene, C. Julián, L. Javier and A. B. Juan, “Start-Up of a Nitrification System with Automatic Control to Treat Highly Concentrated Ammonium Wastewater: Experimental Results and Modeling,” Chemical Engineering Journal, Vol. 144, No. 3, 2008, pp. 407-419.
- C. Y. Wu, Z. Q. Chen, X. H. Liu and Y. Z. Peng, “Nitrification-Denitrification via Nitrite in SBR Using Real -Time Control Strategy when Treating Domestic Wastewater,” Biochemical Engineering Journal, Vol. 36, No. 2, 2007, pp. 87-92.
- E. Murnleitner, T. M. Becker and A. Delgado, “State Detection and Control of Overloads in the Anaerobic Wastewater Treatment Using Fuzzy Logic,” Water Research, Vol. 36, No. 1, 2002, pp. 201-211.
- S. Marsili-Libelli, “Control of SBR Switching by Fuzzy Pattern Recognition,” Water Research, Vol. 40, No. 5, 2006, pp. 1095-1107.
- E. H .Mamdani, “Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Systems,” Fuzzy Sets and Systems, Vol. 26, No. 1, 1977, pp. 1182-1191.
- L. A. Zadeh, “Outline of a New Approach to the Analysis of Complex Systems and Decision Process,” IEEE Transactions of Systems, Man and Cybernetics, No. 1, 1973, pp. 28-44.
- R. R. Yager, “A General Class of Fuzzy Connectives,” Fuzzy Sets and Systems, Vol. 4, No. 3, 1980, pp. 235-242.
- C. Betroluzza, N. Corral and A. Salas, “On a New Class of Distances between Fuzzy Numbers,” Mathware and Soft Computing, Vol. 2, No. 2, 1995, pp. 71-84.
- L. T. Tran and L. Duckstein, “Comparison of Fuzzy Numbers Using a Fuzzy Distance Measure,” Fuzzy Sets and Systems, Vol. 130, No. 3, 2002, pp. 331-341.
Nomenclature
a: The lower limits of the integral of the membership function
b: The upper limits of the integral of the membership function
COD: Chemical oxygen demand Concentration
FIS: Fuzzy Inference system
FLC: Fuzzy Logic Control
i,j,k: subscript symbols
H: High Value
HRT: Hydraulic Retention time
L: Low value
M: Medium
MIMO: Multi Input Multi Output model
MISO: Multi Input Single Output Model
NH4-N: Ammonia Nitrogen Concentration
NO3-N: Nitrate Nitrogen Concentration
PO4-P: Poly Phosphate concentration
SM: Small medium value
V.H: Very High Value
VL: very low value
y: The centroidal distance from the origin in output membership function.
NOTES
*Corresponding Author: Xi-Wu Lu, Southeast University

