Intelligent Control and Automation
Vol.04 No.03(2013), Article ID:35646,14 pages
10.4236/ica.2013.43037
Attitude Control of a Flexible Satellite by Using Robust Control Design Methods
Reza Mohsenipour1, Hossein Nemati2, Mehrzad Nasirian1, Abdolreza Kashani Nia1
1Malekashtar University of Technology, Tehran, Iran
2East Tehran (QiamDasht) Branch, Islamic Azad University, Tehran, Iran
Email: mohsenipour.r@tescooil.com, c.nemati@gmail.com, nasirian@mut.ac.ir, akashaninia@aut.ac.ir
Copyright © 2013 Reza Mohsenipour et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.



Received April 1, 2013; revised May 1, 2013; accepted May 8, 2013;
ABSTRACT
The increase of satellite’s dimensions has caused flexibility and formation of uncertainty in their model. This is because of space missions being more complex and using light moving structures in satellites. Satellites are also encountered with various circumferential disturbance torques. This uncertainty in model and disturbance torques will cause undesir- able performance of satellites’ attitude control system. So, for attitude control of these satellites, those methods should be used which are robust to uncertainty of the plant’s model and can reject the effects of disturbances and the measure- ment noise. One of these methods is the robust control design method. But, because of pole’s place of these satellite’s dynamics equations, the designing procedure of robust control will face difficulties. In this paper, by using an internal feedback as a novel idea, the satellite’s dynamics equations are changed in such a way that the poles will be placed in proper locations. Then, for these new equations, by regarding the effects of flexibility as uncertainty and considering the uncertainty in inertia matrix of satellite, an H∞ controller has been designed and for better performance, a μ-controller has been improved. Afterwards, these two controllers are analyzed and compared for the original dynamic equations, not for the modified ones. Also, for comparison, a classic controller has been also designed for the original plant and eventually all these three controllers are compared with each other.
Keywords:
Attitude Control of Satellite; Robust Control; Flexible Satellite; Uncertainty

1. Introduction
Designing satellites with various missions such as cli- matic, military, geology and astrological missions will cause the payloads being increased and as a result, the increase of their dimensions, weight and consumed power. So, for more energy absorption, the effective sec- tion surface of satellite should be increased to installing more solar panels. On the other side, the existent limita- tions on satellites’ launch will cause the restriction on their volume and weight. To decrease the volume of sat- ellites, they are designed as a concentrated structure with some supplemental parts which are fastened before launch and are opened after settlement in orbit, and to decrease the weight of satellites, the light materials are used in designing structures. The whole of these factors; means light weight, low volume and large section surface will cause the flexibility of satellites’ structure. In this case, preserving correct direction of main body and flexi- ble parts encounter with many challenges. According to these realities, many theoretical researches have been
done to identify and control flexible structures [1,2].
In the past three decades, the flexible satellites which are known as big spatial structures in some articles are considered a lot. In some NASA reports, the effect of satellites’ flexibility in attitude control system, as un- usual acts, has been mentioned [3]. More researches on this issue have specified that the reason of this strange act is the flexibility of the structure which will be inten- sified in some cases by attitude control system [4].
Before 70’s decade, the attitude control and stabiliza- tion systems of satellites were designed according to dy- namic modeling of rigid bodies and Single-Input Single- Output (SISO) controllers. Along with the development of spatial sciences in the late 70’s, big satellites which have flexible parts and include many sensors and actua- tors were considered. So, the need for using complex control laws and Multi-Input Multi-Output (MIMO) con- trol systems for satellites were found to be essential [5]. For high-accuracy performance in pointing, three-axis attitude control will be used for satellites which lead to a MIMO control system. Generally, satellites are exposed to various circumferential disturbances such as solar pre- ssure torques, magnetic torques, aerodynamic torques and celestial dust. Moreover, in most cases the inertia matrix of satellite isn’t specified exactly. So, designing the control system for flexible satellites will be encoun- tered with a lot of problems [6]. Three main issues in designing attitude control of satellite are the space envi- ronmental disturbance, uncertainty in flexible structure and inertia matrix of satellite as well as control input constraints [7].
A review of using robust control for satellites is as fol- lows. In [8], designing of an optimal low-order robust control with alpha-shift for attitude control of a space- craft with solar electric propulsion has been discussed. In this article, a new method of block-shift for replacing different sets of closed-loop eigenvalues by different values has been introduced. In [9], a mixed controller is designed which considers both stability ro- bustness and root-mean-square performance and is of particular interest for attitude control of microsatellites. The mixed controller shows a remarkable ca- pability of achieving a balanced tradeoff between and performances. The authors in [10] describe modeling of a flexible structure and three-axis controller design process. Also, they demonstrate the suitable per- formance of this design in maneuverability by applying it to a large flexible spacecraft model. In [7], a mixed output-feedback controller has been proposed for microsatellite attitude control with pole placement constraints against the internal uncertainty of moment- of-inertia variation and space environmental disturbances. The simulation results demonstrate that the presented mixed control system is robust stable and op- timal in the sense of norm, and has good steady- state and dynamic performance against parameter uncer- tainties and various disturbances for the microsatellite attitude control system. In [11], an optimization-based approach is proposed for the robustness analysis of an attitude and orbit control system (AOCS) for flexible satellites.
In this paper, it is intended to design robust attitude control for a flexible satellite with a desirable accuracy and performance against the uncertainty in the satellite’s model and inertia matrix and with the existence of con- trol input constraints and in the presence of environ- mental disturbances and measurement noise. The rest of this paper is as follows. In Section 2, the dynamic equa- tions of a flexible satellite’s attitude and the actuator of reaction wheel has been derived and the disturbances of space environment are discussed. Since the desirable attitude of satellite’ tracking has small angles around zero, the extracted equations of the satellite will be lin- earized and combined with the equations of reaction wheel. In Section 3, it is shown that the original lin-
earized equations of the satellite causes some problem in the robust control design procedure. So by using two unit feedbacks, its poles will be placed in a more proper place and new equations will be obtained. Also, in this section a nominal model for the satellite and needed weight functions for designing robust controller will be selected. In Section 4, a classical controller, based on Euler angels errors, for the original equations and an controller, by using the new idea of internal feedback, for the modi- fied equations will be designed. But, neither will achieve the desired robust performance for the original plant. Afterwards, to improve the performance of attitude con- trol, a μ-controller for the modified equations will be designed to ensure the robust performance for the origin- nal plant. Using the obtained results for all three control- lers, the paper will be concluded in Section 5.
2. System and Disturbances Modeling
2.1. Satellite’s Attitude and Reaction Wheel Modeling
The kinematic equations of satellite’s attitude are as be- low,
(1)
in which , and are roll, pitch and yaw and is the angular velocity vector of orbital reference frame with respect to body frame stated in body frame. According to the definition, the orbit refer- ence frame’s center conforms to satellite’s center of mass, axis is towards the earth center, axis is in di- rection of satellite’s velocity and axis is vertical to plane of orbit so that transform the frame to a right-hand orthogonal frame. The body frame will be selected in a way that its axes conform to main axes of inertia. Vector satisfies the equation
(2)
in which ω0 is the angular velocity of orbit, and are accordingly for and and
is the angular velocity of body frame
with respect to inertial frame which will be obtained from Euler’s moment equations. Assuming that body frame axes conforming to main inertial axes, Euler’s moment equations is as
(3)
in which is disturbance moment, is angular momentum vector of satellite’s rigid body, is the angular momentum vector of reaction wheel and is the gravity gradient moment which will be obtained by Equation (4).
(4)
Equations (1) to (4) form the dynamic nonlinear equa- tions of satellite’s attitude [12].
Here, to produce the moment, three reaction wheels will be used in direction of body axes. The block diagram of reaction wheel to control the attitude of satellite is as Figure 1. In this figure u is the output of controller and is the exerted torque to satellite in direction of re-
lated axis [12].
Transfer function of Figure 1 is approximately as fol- lows [12].
(5)
So, the combination of the satellite’s equations and the actuators is approximately the same satellite’s equations, and the controller for satellite’s equations will be de- signed apart from reaction wheel equations. Since the desirable angle which the satellite should track is around the zero angles and also to use the concepts of linear control and simplifying the analysis, the Equations (1)- (4) can be linearized. By linearizing these equations around zero point, linear state space form of dynamic equations of satellite’s attitude will be obtained as
(6)
in which ,
and
Figure 1. The block diagram of reaction wheel to control the attitude of satellite [12].
Satellite’s configuration is as Figure 2. The system response of satellite’ attitude with given specifications in Table 1, to one step with amplitude has been shown in Figure 3. As it could be seen, the system is unstable in each three channels of roll, pitch and yaw.
2.2. Disturbances Modeling
One of the key issues in attitude control of satellites is the environment disturbances which deflect the attitude of satellite from its desirable state and ignoring these disturbances make the designed controller completely use- less.
Magnetic torque: a magnetic torque will affect on sat- ellite’s configure because of earth’s magnetic field and satellite’s magnetic materials. This torque will be ob- tained by
(7)
in which is the residual magnetic moments of the satellite caused by permanent and induced magnetism and the satellite-generated current loops and B is the geo- centric magnetic flux density. Vector B will be obtained, in orbit reference system, by
(8)
in which and is the beam of satellite’s orbit and is the angle of satellite’s orbit with respect to geomagnetic equator [13].
Aerodynamic torque: because of satellite’s move- ment in upper atmosphere of earth, an aerodynamic tor- que will affect on satellite. This torque can be obtained as
(9)
in which is the atmospheric density, is the ve- locity of satellite, is the drag coefficient, is the
Figure 2. The satellite’s configuration.
Table 1. Satellite physical and orbital characteristics.
unit vector along velocity direction, is the area of vertical surface on and is a vector from satel- lite’ center of mass to center of pressure [9].
Solar torque: because of the contact of solar radiation particles with satellite, a disturbance force will exert on satellite. This force can be obtained approximately by
(10)
in which is the velocity of light, is the area op- posed to sun radiation, is the reaction coefficient, is the radiation angle, is the unit vector along sun radiation direction and is the distance from the sat- ellite’s center of mass to the solar pressure center [12].
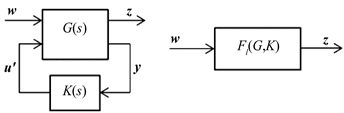
Now, by considering the dynamic equations of satel- lite’s attitude and reaction wheel, the object is to design an attitude control system as shown in Figure 4.
Figure 3. Response of open-loop system.
Figure 4. The block diagram of satellite attitude control system.
3. Selection of Nominal Model and Needed Weight Functions
The modeling of flexible satellite will be done in a way that a nominal model will be selected and flexi- bility effects will be considered as uncertainty around the nominal model. These uncertainties lead to the perturbed models . Equations (6) with nominal amounts of Table 1 will be considered as nominal model. To con- sider flexibility effects, it is assumed that the inertia moments of satellite have 30 percentage of uncertainty. Since the system has unmodelled flexible parts, the un- certainty will be considered as multiplicative unstruc- tured. For a SISO system, the perturbed model structure of based on nominal model of , multipli- cative unstructured uncertainty block of and un- certainty weight function of is as
(11)
which its block diagram is shown in Figure 5.
The weight function of should be selected in a way that relation
(12)
by condition will be established for all per- turbed models of [14]. The transfer function ma- trix of linearized system is obtained as follows
Figure 5. Block diagram of the perturbed model of P with multiplicative unstructured uncertainty.
(13)
The satellite’ attitude is a MIMO system, so for each element of this matrix, a weight function of should be selected in such a way that, it satisfies the rela- tion (12) for i, j = 1, 2, 3. For elements with zero value, the uncertainty weight function could be equal to 1. Bode diagram of for the non-zero elements of Equation (13) has been shown in Figure 6. It could be seen that except for the , other fig- ures have big overshoots because of placement of some poles on imaginary axis. So, the weight functions of corresponding to those which should satisfy the relation (12), have also same overshoots and this will cause the issue of robust controller design face difficul- ties [14]. The poles of non-zero elements of Equation (13) are as
One of the ways for elimination of this problem is dis-
Figure 6. Bode diagram of for the non-zero elements of Equation (13).
placement of poles slightly [8]. But, here the amounts of inertia moments of satellite are so that the system’s poles which are on imaginary axis are very close to the origin and the problem won’t be solved by this displacement, too.
For overcoming this problem, equations should be changed in a way that poles go sufficiently away from imaginary axis. With a new idea, according to Figure 7,
two unit internal feedbacks in the main nonlinear plant will be made from roll and yaw outputs to first and third inputs respectively. So, the state space’s form of the modified linearized plant will be obtained as
(14)
where
and Figure 4 will change to Figure 8.
The matrix of transfer function of the modified plant is as Equation (15).
(15)
The poles of non-zero elements of Equation (15) are
.
Bode diagram of for the non-zero elements of Equation (15) are shown in Figure 9. It can be seen that overshoots are eliminated. Now, weight functions of will be selected in a way that satis- fies the Equation (12) for the modified plant. This is done and shown in Figure 9.
The condition of robust stability for a SISO system is
(16)
in which is the transfer function of desirable closed-loop system and is the weight function of uncertainty [15]. Since the elements of Equation (15) are not reachable separately, the matrix of weight function will be selected as
(17)
where
(18)
So, weight functions will be obtained as Equations (19).
The condition of nominal performance for a SISO sys-
Figure 7. To make internal feedback in the main system.
Figure 8. Block diagram of satellite attitude control with internal feedback.
tem is as
(20)
in which is transfer function of the error to refer- ence input and is the sensitivity weight function [15]. Here, it’s desirable that the output of closed-loop system track a sinus route with minimum control effort and error less than 2˚. So, the matrix of sensitivity weight function for the discussed system with trial and error will be selected as
(21)
where
(22)
For limiting the controller output, beside the weight functions of uncertainty and sensitivity, a related weight function will be selected as .
4. Controller Design
In this part, for the Equations of original plant (6), a clas- sical controller, based on Euler angles errors, and for the Equations of the modified plant (14), two robust control- lers and will be designed. Eventually, the ori- ginal nonlinear system, described by Equations (1)-(4), will be simulated with each of three controllers in closed- loop form. In simulations, the inertia moments of satel- lites have 30 percent of uncertainty as shown in Figure 10. The simulation of the closed-loop system has done in two cases. In one case, the closed-loop system response is obtained to zero reference input and with equal to disturbance pulse, which is shown in Figure 11. In the other case, the closed-loop system response to a refer- ence sinus input with the amplitude of 15 degree in roll channel, 10 degree in pitch channel and 5 degree in yaw channel and 20 Hz frequency in the presence of space physical disturbances and measurement noise, is obtained to examine the performance of system in tracking. The RMS amount of attitude sensors’ noise of and their error are considered equal to 0.01˚.
4.1. Classical Controller
When a classical controller is designed for the equations of rigid body of a satellite, although it can be robust somehow against the uncertainty, but there isn’t any gua- rantee to have a desirable performance for a practical plant. Here, for the original plant with Equations (6), a classical controller has been designed based on Euler angles’ errors and the control laws are as Equations (23) with coefficients , , , , and [12].
(23)
The closed-loop system response to disturbance pulse for this controller has drawn in Figure 12. Its perform- ance in tracking and control effort has also been shown in Figures 13 and 14 respectively. Tracking error’s norm is about 5˚.
4.2. H∞ Suboptimal Controller
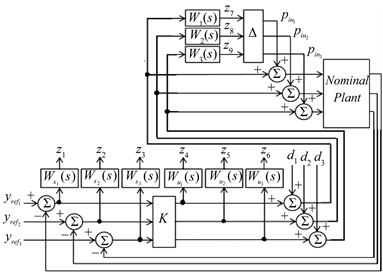
Interconnections of system for designing subopti- mal controller, regarding to selected weight functions, are as Figure 15. In this figure, is the disturbance and and are the input and output of uncer- tainty block, respectively. By considering Figure 16, the object is to find the controller which satisfies Equation (24). In this equation, is the generalized system [14].
(24)
Designing suboptimal controller could be done in MATLAB by using the hinsyn command. This com- mand will design an suboptimal controller for the open-loop system in Figure 15 [16]. Here, by using this command, an suboptimal controller with the degree of 22 is obtained.
For the closed-loop system analysis with the H∞ sub- optimal controller, from the aspect of robust stability, no- minal performance and robust performance, the structure shown in Figure 17, will be used. In this figure, the un- certainty has been gathered in Δ block which is con- sidered as Equation (25).
Figure 9. Bode diagram of for the non-zero elements of Equation (15).
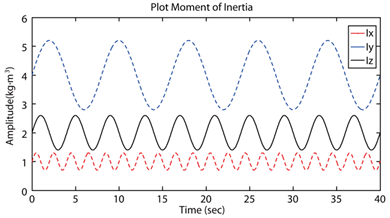
Figure 10. Changes of satellite inertia moments with 30 per- centage of uncertainty.
Figure 11. Disturbance pulse input in simulation of the closed-loop system response to disturbance.
Closed-Loop System to Disturbance with Kclassic
Figure 12. The closed-loop system response with Kclassic to the disturbance pulse of Figure 11.
Closed-Loop System to Tracking with Kclassic
Figure 13. The closed-loop system performance in tracking with Kclassic.
Control Effort with Kclassic
Figure 14. The control effort of closed-loop system with Kclassic in tracking.
Figure 15. The standard H∞ configuration.
Figure 16. Closed-loop LFT structure in H∞ design.
Figure 17. Structure of closed-loop system for μ analysis.
(25)
The upper bound and low bound frequency response of for controller is shown in Figure 18. Re- garding that for robust stability, the condition
(26)
should be established [14], it could be seen clearly that the closed-loop system with has guaranteed the ro- bust stability.
For nominal and robust performances, the Equations (27) and (28) should be established, respectively [14].
(27)
(28)
The frequency response of nominal and robust per- formances is shown in Figure 19. It’s shown that the system with has the nominal performance but hasn’t guaranteed the robust performance.
The closed-loop system’s response with to dis- turbance pulse is drawn in Figure 20. As it can be considered, the system in each three channels has eli- minated the disturbance with lower overshoot than the classical controller. Its performance in tracking has been also shown in Figure 21. In each three channels, the controller has better performance than the classical controller. The control effort in tracking, has been also drawn in Figure 22. This control signal is smaller than the corresponding signal for classical controller.
4.2. μ-Synthesis: D-K Iteration Method
The block diagram of the closed-loop system which is used in -synthesis is as Figure 17. In D-K iteration method, a controller will be obtained from Equation (29).
Robust Stability with Khin
Figure 18. Robust stability of Khin.
Normal Performance and Robust Performance with Khin
Figure 19. Nominal and robust performance of Khin.
Closed-Loop System Response to Disturbance with Khin
Figure 20. The closed-loop system response with Khin to disturbance pulse in Figure 11.
Closed-Loop System Response to Disturbance with Khin
Figure 21. The closed-loop system performance in tracking with Khin.
Control Effort with Khin
Figure 22. The control effort of closed-loop system with Khin in tracking.
(29)
The object of μ-synthesis is to find a stabilizing con- troller of so that the condition (30), is established [14].
(30)
By using MATLAB [16], after 6 repetitions, the - controller has been obtained with . But, the obtained controller is with the degree of 52, which its implementation can be problematic. Usually, a reduced- order controller is preferred. Here for reducing the degree of controller, Hanckel-norm approximation is used [14]. The reduced order controller from the main controller is with the degree of 19. The frequency response of main -controller and reduced controller has been shown in Figure 23. It can be seen that the frequency response of both controllers are completely on each other.
The robust stability and robust performance analysis of controller are shown in Figures 24 and 25, respec- tively. It could be considered that contrary to the controller, this controller has guaranteed the robust per- formance, in addition to robust stability.
The response of the closed-loop system with to disturbance pulse is drawn in Figure 26. According to this figure, the system has eliminated the disturbance in each three channels, well. Its performance in tracking and the control effort are shown in Figures 27 and 28, respectively, which are approximately the same as closed- loop system with .
Figure 23. Frequency responses of full- and reduced-order controllers.
Robust stability with Kmu
Figure 24. Robust stability of Kmu.
Nominal Performance and Robust Performance with Kmu
Figure 25. Nominal and robust performance of Kmu.
Closed-Loop System Response to Disturbance with Kmu
Figure 26. The closed-loop system response with Kmu to disturbance pulse in Figure11.
Closed-Loop System Tracking with Kmu
Figure 27. The closed-loop system performance in tracking with Kmu.
Control Effort with Kmu
Figure 28. The control effort of closed-loop system with Khin in tracking.
In Figure 29, the performance of two controllers, and , are compared with increasing of uncertainty norm. This figure shows that -controller will guaran- tee the robust performance for uncertainties with the magnitude of 1.012. For controller, the perform- ance of closed-loop will degrade more rapidly with the increase of uncertainty amplitude and won’t guarantee the robust performance for uncertainties more than the magnitude 0.9335.
Three designed controllers have been compared with each other in Table 2. According to this table, the and robust controllers have better performance than the classical controller. Although and control- lers performance are approximately the same, but the most important criteria is to guarantee the robust perfor- mance. According to Figure 29 and Table 2, only the -controller satisfies this criteria; and also the degree of this controller is lower than the controller. So, it can be concluded that the -controller is the best option for this system comparing to the other controllers.
5. Conclusion
The aim of this paper is attitude control of a flexible sat- ellite by using robust controllers. To do so, a classical controller based on Euler degrees’ errors and two robust controllers of and μ, by using the new idea of inter- nal feedback to resolve robust controller design problem, were designed. The simulation results show that the and μ robust controllers are better than classical control- ler, both in elimination of disturbance and in tracking. The two and μ controllers have approximately the same performance regarding the disturbance elimination
Performance Degradation Curve for Khin and with Kmu
Figure 29. Performance degradation for two controllers.
Table 2. Comparing three designed controllers.
and tracking error. But, the μ-controller guarantees the robust performance for the original plant, contrary to the controller and has a better performance regarding the robustness against uncertainty of flexible structure of satellite. Furthermore, it has the best performance to sat- isfy control effort limitations. It has also of lower order in comparison to controller. Therefore, it could be concluded that the μ-controller is the best choice among the other controllers.
References
- 1. D. C. Hyland, J. L. Junkins and R. W. Longman, “Active Control Technology for Large Space Structures,” Journal of Guidance, Control and Dynamics, Vol. 16, No. 5, 1993, pp. 801-821. doi:10.2514/3.21087
- 2. O. Morgul, “Control and Stabilization of a Flexible Beam Attached to a Rigid Body,” International Journal of Control, Vol. 51, No. 1, 1990, pp. 11-31. doi:10.1080/00207179008934048
- 3. R. B. Noll, J. Zvava and J. J. Deyst, “Effect of Structural Flexibility on Spacecraft Control Systems,” Journal of Spacecraft and Rockets, 1969.
- 4. T. siamak, “On Attitude Recovery of Spacecraft Using Nonlinear Control,” Ph.D. Thesis, Concordia University, Montreal, 2005.
- 5. O. Z. Hayrani, “Dynamics and Control in Modal-Space of Flexible Spacecraft,” Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, 1979.
- 6. G.-X. Li, J. Zhou and F.-Q. Zhou, “Variable Structure Control for Flexible Spacecraft,” Proceedings of the 25th Chinese Control Conference, Harbin, 7-11 August 2006, pp. 943-946.
- 7. B. Wu, X. Cao and Z. Li, “Multi-Objective OutputFeedback Control for Microsatellite Attitude Control: An LMI Approach,” Acta Astronautica, Vol. 64, No. 11-12, 2009, pp. 1021-1031. doi:10.1016/j.actaastro.2008.12.012
- 8. M. SeetharamaBhat, A. G. Sreenatha and S. K. Shrivastava, “Robust Low Order Dynamic Controller for Flexible Spacecraft,” IEE Proceedings-D, Vol. 138, No. 5, 1991, pp. 460-468.
- 9. C. D. Yang and Y. P. Sun, “Mixed H2/H∞ State-Feedback Design for Microsatellite Attitude Control,” Control Engineering Practice, Vol. 10, No. 9, 2002, pp. 951-970. doi:10.1016/S0967-0661(02)00049-7
- 10. J. S. Chae and T. W. Park, “Dynamic Modeling and Control of Flexible Space Structures,” KSME International Journal, Vol. 17, No. 12, 2003, pp. 1912-1921.
- 11. W. Wang, P. P. Menon, D. G. Bates and S. Bennani, “Robustness Analysis of Attitude and Orbit Control Systems for Flexible Satellites,” IET Control Theory & Applications, Vol. 4, No. 12, 2010, pp. 2958-2970. doi:10.1049/iet-cta.2009.0531
- 12. M. J. Sidi, “Spacecraft Dynamics and Control a Practical Engineering Approach,” Cambridge University Press, New York, 1997.
- 13. J. Kulkarni and M. Campbell, “An Approach to Magnetic Torque Attitude Control of Satellites via H∞ Control for LTV Systems,” 43rd IEEE Conference on Decision and Control, Bahamas, 14-17 December 2004, pp. 273-277.
- 14. S. Skogestad and I. Postlethwaite, “Multivariable Feedback Control Analysis and Design,” John Wiley & Sons, Hoboken, 2001.
- 15. K. Zuou and J. Doyle, “Essentials of Robust Control,” Prentice Hall, Upper Saddle River, 1998.
- 16. D.-W. Gu, P. Hr. Petkov and M. M. Konstantinov, “Robust Control Design with Matlab,” Springer, Berlin, 2005.