Intelligent Control and Automation
Vol.4 No.2(2013), Article ID:31745,7 pages DOI:10.4236/ica.2013.42024
Optimal Seat and Suspension Design for a Half-Car with Driver Model Using Genetic Algorithm
1Engineering Physics and Mathematics Department, Faculty of Engineering (Mataria), Helwan University, Cairo, Egypt
2Automotive and Tractors Engineering Department, Faculty of Engineering (Mataria), Helwan University, Cairo, Egypt
3Electrical Engineering Department, Faculty of Engineering, Al-Baha University, Al-Baha, KSA
4Mechanical Design Department, Faculty of Engineering (Mataria), Helwan University, Cairo, Egypt
5Mechanical Engineering Department, Faculty of Engineering, Al-Baha University, Al-Baha, KSA 6Engineering and Mechanical Design Department, Faculty of Engineering, Mansoura University, Mansoura, Egypt
Email: abouelatta@mans.edu.eg
Copyright © 2013 Wael Abbas et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 27, 2012; revised January 27, 2013; accepted February 6, 2013
Keywords: Biodynamic Response; Genetic Algorithms; Multi-Objective Optimization; Mathematical Model
ABSTRACT
This paper presents an optimal vehicle and seat suspension design for a half-car vehicle model to reduce human-body vibration (whole-body vibration). A genetic algorithm is applied to search for the optimal parameters of the seat and vehicle suspension. The desired objective is proposed as the minimization of a multi-objective function formed by the combination of seat suspension working space (seat suspension deflection), head acceleration, and seat mass acceleration to achieve the best comfort of the driver. With the aid of Matlab/Simulink software, a simulation model is achieved. In solving this problem, the genetic algorithms have consistently found near-optimal solutions within specified parameters ranges for several independent runs. For validation, the solution obtained by GA was compared to the ones of the passive suspensions through sinusoidal excitation of the seat suspension system for the currently used suspension systems.
1. Introduction
Recently, many people have focused their attention on the ride quality of vehicle which is directly related to driver fatigue, discomfort, and safety. As traveling increases, the driver is more exposed to vibration mostly originating from the interaction between the road and vehicle. Vibration will make them feel discomfort and fatigue sometimes along with injury [1]. Safety in transport is associated most often with solutions which help prevent accidents or minimize their effects. However, safety in case of people working professionally means also minimizing all those factors which can adversely affect the psychomotor state of the driver during the ride, as well as their subsequent health. Many researchers studies conducted in different regions of the world have shown a convincing relationship between driver health and whole-body vibration (WBV) [2].
The vibration of vehicle causes the operator’s whole body to vibrate, as opposed to just one part of their body, says their hand or foot. Harmful effects of whole-body vibration are experienced when the exposure time is longer than the recommended standard set by ISO (ISO 2631-1, 1997) [3]. For example, vibrations between 2.5 and 5.5 Hz generate strong resonance in the vertebra of the neck and lumbar region. These situations can cause chronic musculoskeletal stress or even permanent damage to the effected regions. Therefore, employers should make adjustments in the light of technical progress and scientific knowledge regarding risks related to exposure to vibration, with a view to improving the safety and health protection of workers. In the case of transport, WBV controls may include the use of suspended seats, suspended cabs, vehicle suspension systems, proper tire inflation [2]. One solution to this problem is to develop an active seat and suspension systems capable of canceling the vibrations felt by the operator. Several passive, semi-active, active, and fully active seats have been designed and built to address this problem.
The use of automotive seat and suspension systems are a common way to isolate the vehicle operator from the adverse effects of vibration exposure to improve the ride comfort but also it has to control the dynamic tyre load with acceptable suspension working space to enhance the vehicle stability and safety. Thus, many researchers studies passive, active and semi-active vehicle seat and suspension design [4-11]. Some lumped-parameter models were further modified to represent seated human vehicle’s driver with seat integrated with a vehicle model to assess the biodynamic responses of seated human-body expose to vertical vibrations in driving conditions [12- 15]. On the other hand, genetic algorithms (GA) method increases the probability of finding the global optimal solution and avoids convergence to a local minimum which is a drawback of gradient-based methods [16,17]. Therefore, genetic algorithms optimization is used to determine both the active control and passive mechanical parameters of a vehicle suspension system and to minimize the extreme acceleration of the passenger’s seat, subjected to constraints representing the required roadholding ability and suspension working space.
This paper presents a 4-DOF human-body model developed by authors [15], with linear seat suspension coupled with half car model. In this model, a genetic algorithm was applied to search for the optimal parameters of the seat and vehicle suspension to reduce human vibration (whole-body vibration) and to achieve the best comfort of the driver.
2. Mathematical Model Formulations
2.1. Proposal Model
This section is devoted to the mathematical modeling of proposed model, including the biodynamic lumped human linear seat model coupled with half-car model of ground vehicles as illustrated in Figure 1.
A half-car model with 4-DOF is considered, taking into account pitch motion of the vehicle’s body. The degrees of freedom are; vertical body displacement xb, vehicle body pitch angle θ, front wheel displacement xwf and rear wheel displacement xwr. The front wheel of the vehicle is represented by the mass mwf, the damping coefficient Ctf and the spring coefficient Ktf. Similarly the rear wheel is represented by the mass mwr, the damping coefficient Ctr and the spring coefficient Ktr. The suspensions of the front and rear wheels are described by the damper’s coefficients Csf and Csr and the spring’s coefficients Ksf and Ksr, respectively. The mass mb and the inertia I represent the vehicle body sprung mass. The location of the centre of gravity is given by L1 and L2. Typical design parameters for the half-car and seat suspension are listed in Table 1.
The human-body, has a 4-DOF that proposed by Abbas et al. [15]. In this model, the seated human-body was constructed with four separate mass segments interconnected by five sets of springs and dampers, with a total human mass of 60.67 kg. The four masses represent

Figure 1. Schematic diagram of biodynamic lumped humanseat coupled with a half-car model.
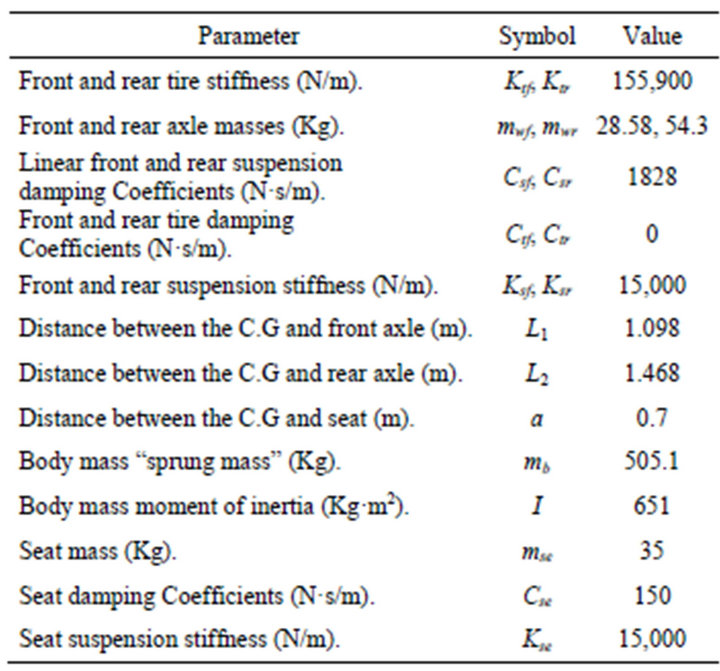
Table 1. Half-car and seat suspension model parameters.
the following body segments: head and neck (m1), upper torso (m2), lower torso (m3), and thighs and pelvis (m4). The arms and legs are combined with the upper torso and thigh, respectively. The stiffness and damping properties of thighs and pelvis are (k5) and (c5), the lower torso are (k4) and (c4), upper torso are (k2, k3) and (c2, c3), and head are (k1) and (c1). The schematic of the model is shown in Figure 1, and biomechanical parameters of the model are listed in Table 2.
2.2. Equations of Motion
The different motions of a nine degree-of-freedom of the resulting half-car and seat suspension modelare governed by Equations (1)-(9).
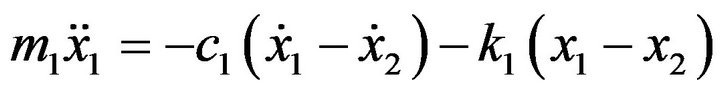 (1)
(1)
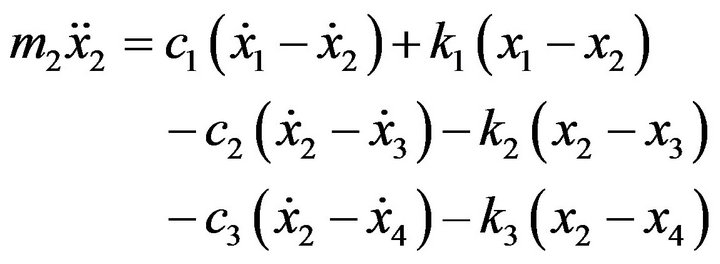 (2)
(2)
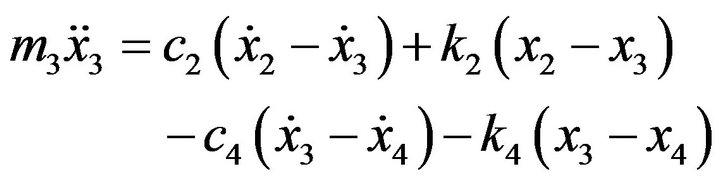 (3)
(3)
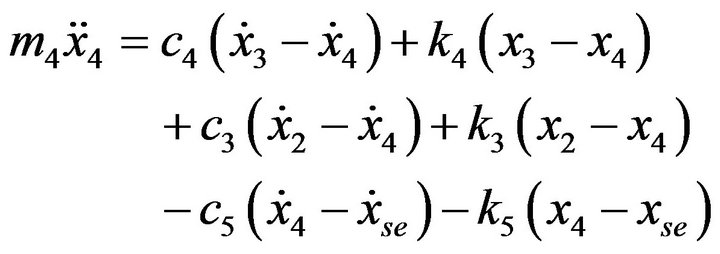 (4)
(4)
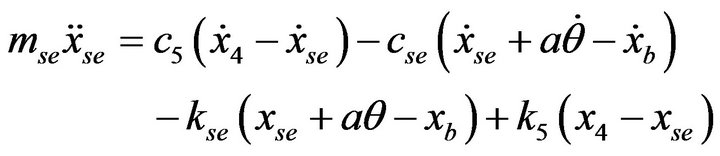 (5)
(5)
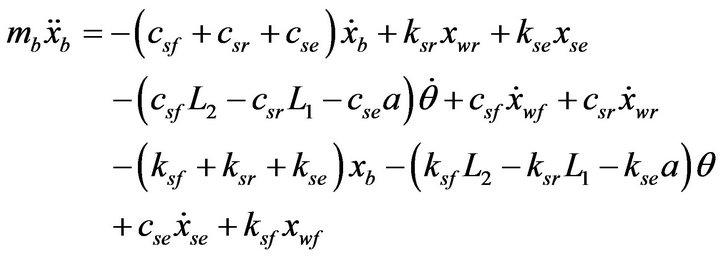 (6)
(6)
 (7)
(7)
 (8)
(8)
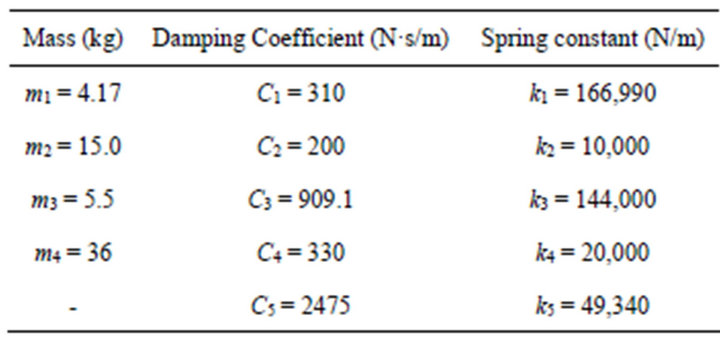
Table 2. Biomechanical parameters of Abbas model.
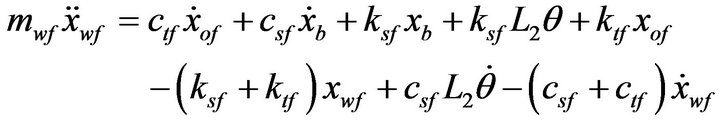 (9)
(9)
2.3. Input Profile Excitations
In this work, the sinusoidal road profiles excitation is adopted to evaluate the proposed system. The sinusoidal road equations are listed below:
 (10)
(10)
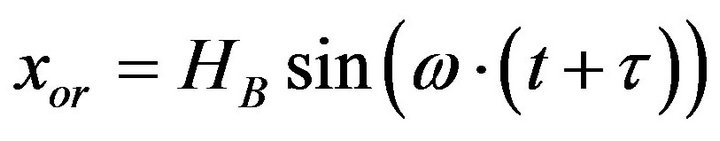 (11)
(11)
where, ω is the radian frequency of the road and is equal to .
.
Mathematical model of road profile can be derived as the follows: vehicle with wheelbase Lw passing over each hump with speed V will have front ground displacement xof. The rear ground xor follows the same track as the front with a given time delay t, (wheelbase correlation) and that is equal to the wheelbase divided by vehicle speed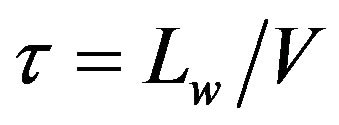 . This study assumed that the vehicle model travels with the constant velocity of 20 km/h (5.5 m/s), HB (0.035 m) is the hump height, and LB (1 m) is the width of the hump.
. This study assumed that the vehicle model travels with the constant velocity of 20 km/h (5.5 m/s), HB (0.035 m) is the hump height, and LB (1 m) is the width of the hump.
3. Optimal Linear Seat Suspension Design
3.1. Numerical Simulations
The displacement, velocity, and acceleration for the model in terms of time domain are obtained by solving equations of motion represented by Equations (1)-(9), using Matlab/SimulinkTM software (R2012b). The initial conditions are assumed at equilibrium position. In this assumption, the driver is seated, where the input excitation has not been provided to the seat. Therefore, the initial velocity and displacement for each mass are equal to zero.
3.2. Optimization via Genetic Algorithms
Genetic algorithm is a stochastic global search method which is based on the metaphors of natural biological evolution, according to Darwin (1809-1882) evolution theory. Genetic algorithm has abilities that differ substantially from more traditional search and optimization methods. Genetic Algorithms (GAs) are employed to search for the optimal linear parameters of the seat and vehicle suspension to achieve the best comfort of the driver. The upper and lower boundaries of seat and vehicle suspension parameters are selected based on previous studies. Table 3 shows the genetic algorithm parameters and its values.
3.2.1. Objective Function
Since the health of the driver is as important as the stability of the car, the desired objective is proposed as the minimization of a multi-objective function formed by the combination of not only seat suspension working space (seat suspension deflection “ssws”) but also the head acceleration , and seat mass acceleration
, and seat mass acceleration . The classical weighted sum approaches has been used to solve a multi-objective optimization problem as shown in Equation (12).
. The classical weighted sum approaches has been used to solve a multi-objective optimization problem as shown in Equation (12).
 (12)
(12)
where, w1, w2 and w3 are weighting factors to emphasize the relative importance of the terms. Table 4 shows weighting factors that used in excitation inputs.
3.2.2. Optimization Procedure
Genetic algorithms initialize seat and suspension design variables ksf ,ksr, kse, csf, csr and cse (Initial Population). The initial populations are passed into the proposal model to solve the dynamic responses (displacement and acceleration) of the system. The population is then coded into chromosomes, a binary representation of a solution. An evaluation function rates solutions in terms of their fitness. Here, fitness is a numerical value describing the probability for a solution (genome) to survive and reproduce. Only a portion of the population (survivors or solutions with higher fitness values) is selected for creating a new population. This new population is created by using a crossover operator. Crossover is a procedure for exchanging pieces of chromosome data with one another. Crossover allows genes that generate good fitness to be preserved and enlarged in a new generation of the popu-

Table 3. Genetic algorithm parameters.

Table 4. Weighting factors.
lation. Mutation is a genetic operator and it randomly flips the bits of an offspring’s genotype. This is equivalent to perturbing the mated population stochastically. Mutation prevents the population from homogenizing in a particular set of genes such that any gene in a generation has a certain probability of being mutated in future generations. The new population is being mixed up to bring some new information into this set of genes, and this needs to happen in a well-balanced way.
Once the new generation is created, the aforementioned steps are repeated until some convergence criteria are satisfied, such as running time or fitness. The overall technique is summarized in the flowchart as illustrated in Figure 2.
4. Results and Discussion
The optimal seat and vehicle suspension parameters of the present model are determined by genetic algorithms, compared with current passive parameters, andlisted in Table 5.
Figures 3 and 4 present the history of the some selected response components of the human model in case of

Figure 2. Design process using GA.
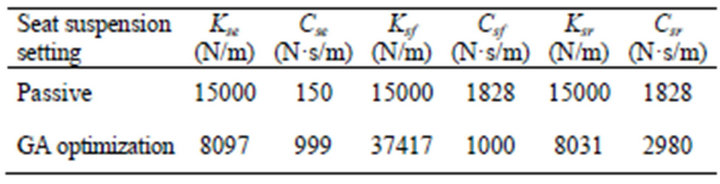
Table 5. The design results from the GA program.
 (a)
(a)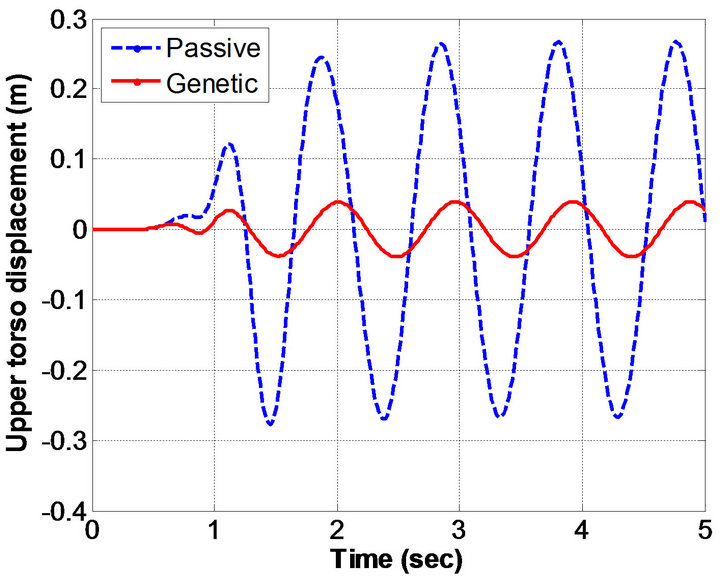 (b)
(b)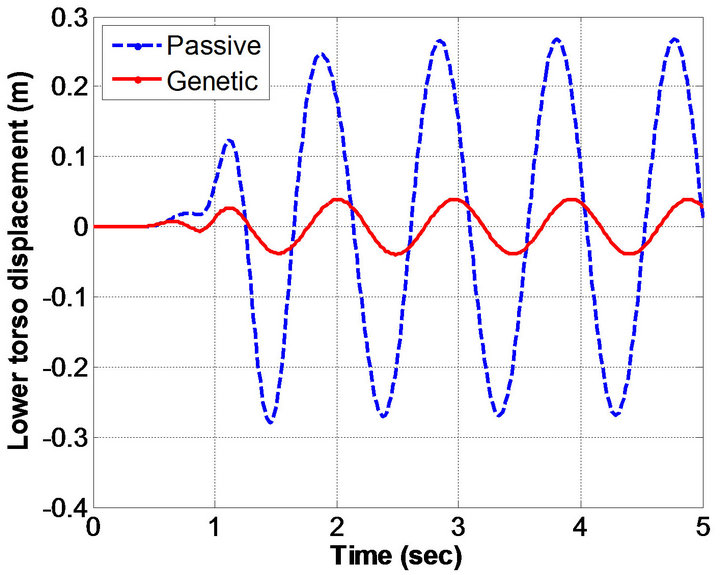 (c)
(c)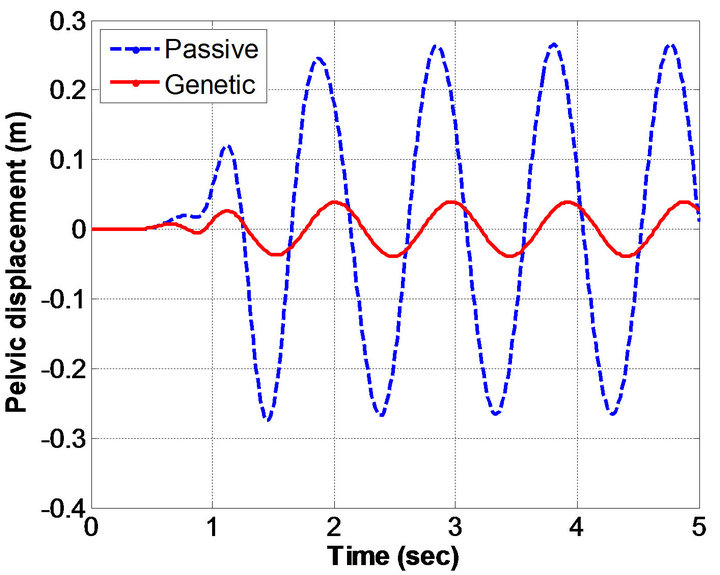 (d)
(d)
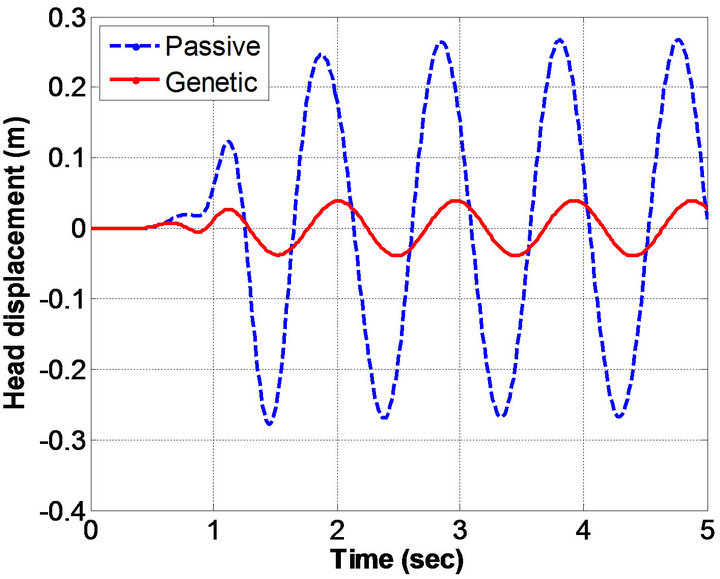
Figure 3. Human displacement histories obtained: (a) Head; (b) Upper torso; (c) Lower torso; and (d) Pelvic.
 (a)
(a)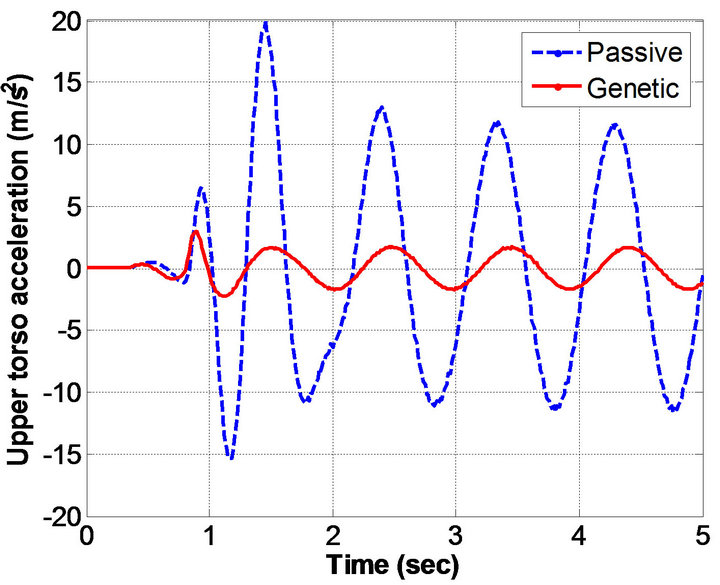 (b)
(b)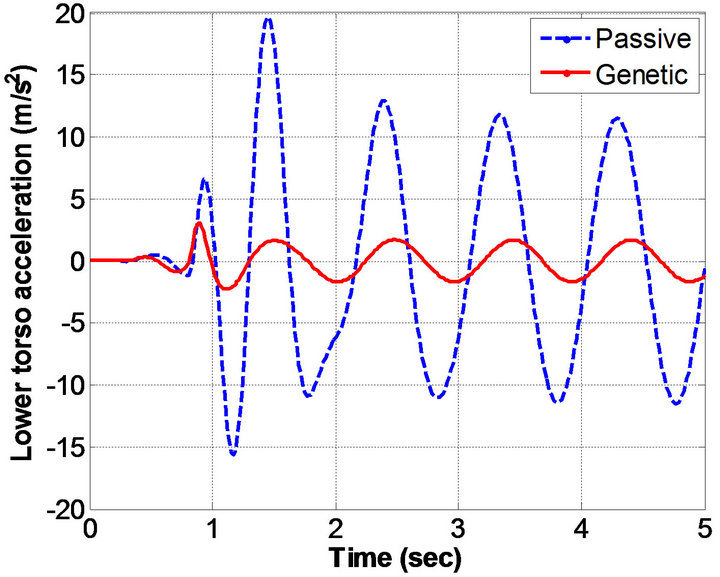 (c)
(c)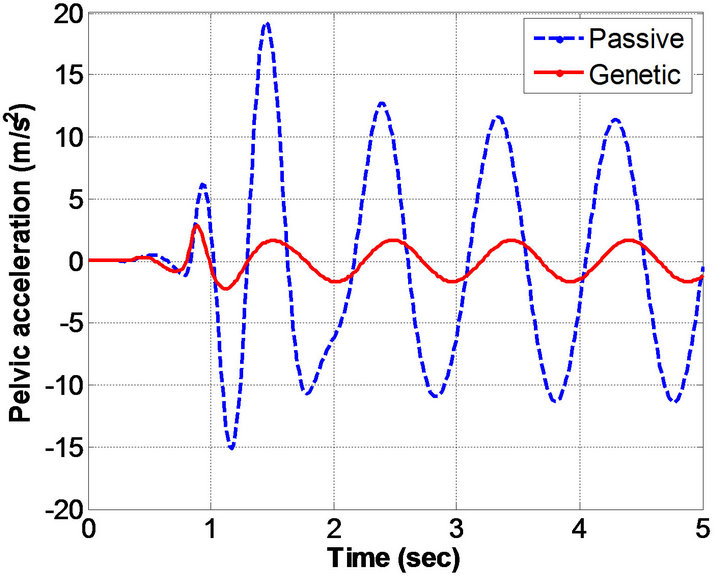 (d)
(d)
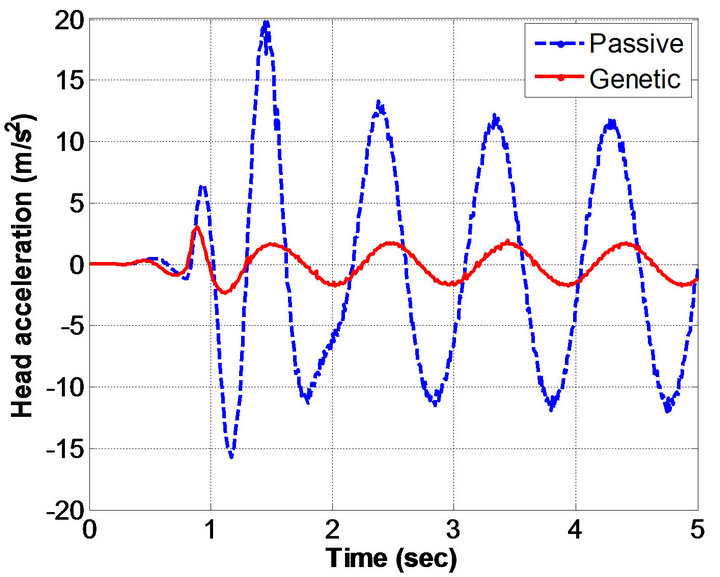
Figure 4. Human acceleration histories obtained: (a) Head; (b) Upper torso; (c) Lower torso; and (d) Pelvic.
sinusoidal excitation. In particular, the results in Figure 3 shows the displacement histories obtained for head, upper torso, lower torso, and pelvis respectively. Figure 4 depicts the acceleration histories obtained from the human-body model. The obtained results by genetic algorithms method were compared with passive model.
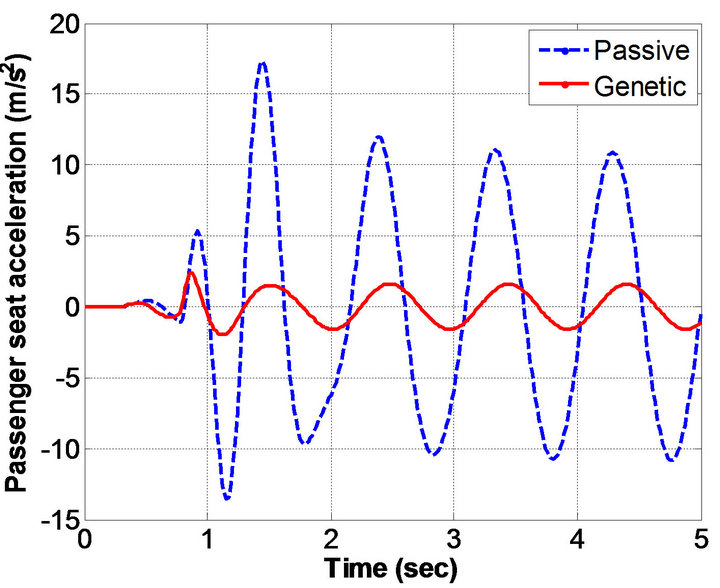
On the other hand, Figure 5 presents seat acceleration, seat displacement and vehicle body acceleration. Table 6 lists the reduction of the human’s vertical acceleration and displacement peaks. It can be observed that the reduction of the human’s vertical peak acceleration is about85% in case of GA suspension as compared with passive suspension. The reduction of the human’s vertical displacement peak is about85% in case of GA suspension
 (a)
(a) (b)
(b) (c)
(c)
Figure 5. (a) Seat acceleration; (b) Seat displacement; and (c) Vehicle body acceleration.
as compared with passive suspension. Also, the reduction of the seat vertical peak acceleration is 86.22% and the reduction of the seat vertical displacement peak is 85.32% of GA suspension as compared with passive suspension.
Table 7 shows a comparison between the RMS results obtained from GA compared to those passive results in terms. From this table, the percentage improvement for head acceleration is 85.24%, for upper torso acceleration is 85.18%, for lower torso acceleration is 85.19%, and for pelvic acceleration is 85.23%. On the other hand, the percentage improvement for seat acceleration is 85.27%.
5. Conclusions
Genetic algorithm optimization is a global optimization technique, searching for a design that minimizes an objective function subject to constraints. Genetic algorithm was used to design the seat and vehicle suspension system via a half-car suspension model. The desired objective is proposed as the minimization of a multi-objective function formed by the combination of seat suspension working space, head acceleration, and seat mass for the best reduction of human vibration (whole-body vibration) and to achieve the best comfort of the driver. In all simulation runs, it can be observed that:
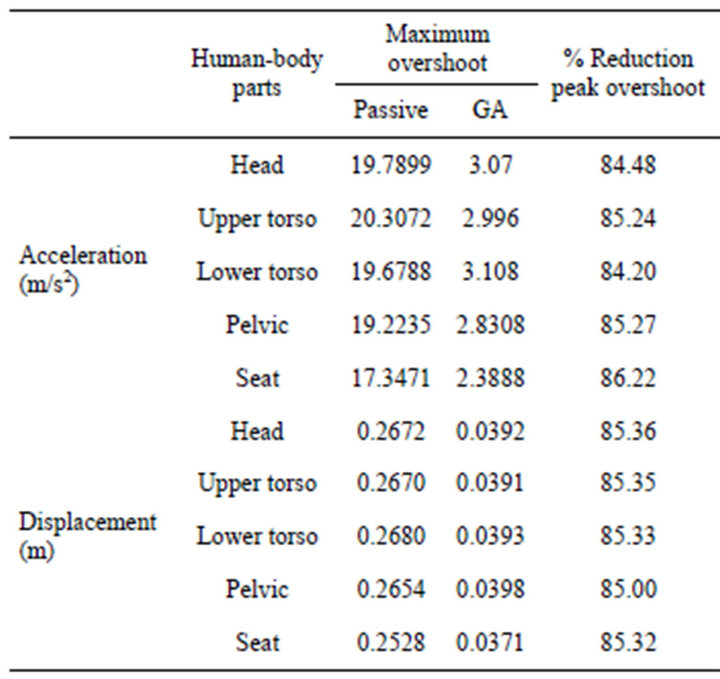
Table 6. Reduction in peak values for half-car model.
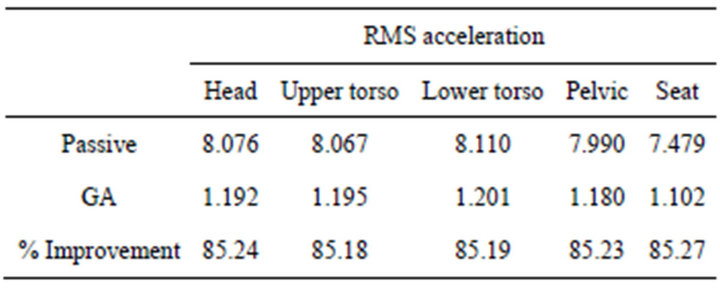
Table 7. RMS improvement results for half-car model.
• The genetic algorithm has been able to find optimal suspension systems which are similar to those found with local optimization search methods.
• The results of optimal seat and vehicle suspensions system by using genetic algorithms has successfully managed improving for all the dynamic performance parameters.
• The numerical results and the plots indicate that optimal system is less oscillatory, and have lower values of maximum over shoots than passive suspension system. This is directly related to driver fatigue, discomfort, and safety.
These results are encouraging and suggest that genetic algorithm can be easily used in other complex and realistic designs often encountered in the engineering.
7. Acknowledgements
This research is a part of a project titled “Optimal seat suspension design for a quarter-car with human-body model using genetic algorithms”. This project was supported by the Deanship of Scientific Research, Al-Baha University, KSA (Grant No. 3/1433).The assistance of Faculty Deanship of Scientific Research is gratefully acknowledged.
REFERENCES
- W. Abbas, O. B. Abouelatta, M. El-Azab, M. Elsaidy and A. A. Megahed, “Optimal Seat Suspension Design Using Genetic Algorithms,” Journal of Mechanics Engineering and Automation, Vol. 1, No. 1, 2011, pp. 44-52.
- A. Gągorowski, “Simulation Study on Stiffness of Suspension Seat in the Aspect of the Vibration Assessment Affecting a Vehicle Driver,” Logistics and Transport, Vol. 11, No. 2, 2010, pp. 55-62.
- ISO 2631-1, “Mechanical Vibration and Shock Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements,” International Organization for Standardization, 1997.
- L. Sun, “Optimum Design of ‘Road-Friendly’ Vehicle Suspension Systems Subjected to Rough Pavement Surfaces,” Applied Mathematical Modelling, Vol. 26, No. 5, 2002, pp. 635-652. doi:10.1016/S0307-904X(01)00079-8
- M. Bouazara, M. J. Richard and S. Rakheja, “Safety and Comfort Analysis of a 3-D Vehicle Model with Optimal Non-Linear Active Seat Suspension,” Journal of Terramechanics, Vol. 43, No. 2, 2006, pp. 97-118. doi:10.1016/j.jterra.2004.10.003
- L. Sun, X. Cai and J. Yang, “Genetic Algorithm-Based Optimum Vehicle Suspension Design Using Minimum Dynamic Pavement Load as a Design Criterion,” Journal of Sound and Vibration, Vol. 301, No. 1-2, 2007, pp. 18-27. doi:10.1016/j.jsv.2006.08.040
- Ö. Gündoğdu, “Optimal Seat and Suspension Design for a Quarter Car with Driver Model Using Genetic Algorithms,” International Journal of Industrial Ergonomics, Vol. 37, No. 4, 2007, pp. 327-332. doi:10.1016/j.ergon.2006.11.005
- H. S. Hassanin, A. M. Rabeih, S. M. El-Demerdash and K. Y. Younes, “Active Suspension of Highway Truck Seat Using Genetic Algorithms,” SAE International, Paper No. -01-1458, 2008. doi:10.4271/2008-01-1458
- M. Brogioli, M. Gobbi, G. Mastinu and M. Pennati, “Parameter Sensitivity Analysis of a Passenger/Seat Model for Ride Comfort Assessment,” Experimental Mechanics, Vol. 51, No. 8, 2011, pp. 1237-1249. doi:10.1007/s11340-010-9460-1 http://link.springer.com/content/pdf/10.1007%2Fs11340-010-9460-1
- M. El-Kafafy, S. M. El-Demerdash and A. M. Rabeih, “Automotive Ride Comfort Control Using MR Fluid Damper,” SCIRP Journal of Engineering, Vol. 4, 2012, pp. 179-187. www.scirp.org/journal/PaperDownload.aspx?paperID=18818
- J. J. Zhang, R. Z. Gao, Z. Y. Zhao and W. S. Han, “Fuzzy Logic Controller Based Genetic Algorithm for Semi-Active Suspension,” Journal of Scientific and Industrial Research, Vol. 71, 2012, pp. 521-527. http://nopr.niscair.res.in/bitstream/123456789/14520/1/JSIR%2071%288%29%20521-527.pdf
- M. K. Patil, M. S. Palanichamy and N. G. Dhanjoo, “Minimization of the Vertical Vibrations Sustained by a Tractor Operator, by Provision of a Standard-Type Tractor Seat Suspension,” Annals of Biomedical Engineering, Vol. 6, No. 2, 1978, pp. 138-153. doi:10.1007/BF02584540 http://link.springer.com/content/pdf/10.1007%2FBF02584540
- F. Amirouche, L. Palkovics and J. Woodrooffe, “Optimal Driver Seat Suspension Design for Heavy Trucks,” International Journal of Heavy Vehicle Systems, Vol. 2, No. 1, 1995, pp. 18-45.
- C. Papalukopoulos and S. Natsiavas, “Nonlinear Biodynamics of Passengers Coupled with Quarter Car Models,” Journal of Sound and Vibration, Vol. 304, No. 1-2, 2007, pp. 50-71. doi:10.1016/j.jsv.2007.01.042
- W. Abbas, O. B. Abouelatta, M. El-Azab, M. Elsaidy and A. A. Megahed, “Optimization of Biodynamic Seated Human Models Using Genetic Algorithms,” SCIRP Journal of Engineering, Vol. 2, 2010, pp. 710-719. www.scirp.org/journal/PaperDownload.aspx?paperID=2796
- A. E. Baumal, J. J. McPhee and P. H. Calamai, “Application of Genetic Algorithms to the Design Optimization of an Active Vehicle Suspension System,” Computer Methods in Applied Mechanics and Engineering, Vol. 163, No. 1, 1998, pp. 87-94. doi:10.1016/S0045-7825(98)00004-8
- R. Alkhatib, G. N. Jazar and M. F. Golnaraghi, “Optimal Design of Passive Linear Suspension Using Genetic Algorithm,” Journal of Sound and Vibration, Vol. 275, No. 3-4, 2004, pp. 665-691. doi:10.1016/j.jsv.2003.07.007

