Intelligent Control and Automation
Vol.05 No.03(2014), Article ID:48606,13 pages
10.4236/ica.2014.53018
A Parameter Varying PD Control for Fuzzy Servo Mechanism
Nader Jamali Soufi1, Mohsen Kabiri Moghaddam2, Saeed Sfandiarpour Boroujeni3, Alireza Vahidifar1
1Sama Technical and Vocational Training College, Islamic Azad University, Islamshahr Branch, Tehran, Iran
2Department of Electrical and Electronic Engineering, K. N. Toosi University of Technology, Tehran, Iran
3Department of Electrical and Electronic Engineering, University of Shiraz, Shiraz, Iran
Email: Jamali.tabrizu@yahoo.com, m.kabiri77@yahoo.com, saeed.controleng@gmail.com, alireza.vahidifar@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 May 2014; revised 27 June 2014; accepted 11 July 2014
ABSTRACT
This paper presents the formulation of novel implementation method based on parameter varying PD controller for fuzzy servo controllers. This formulation uses the approximation of fuzzy nonlinear function including error and error derivation in operation point. Obtained fuzzy control law has been employed to control angular position of servo using digital control technique applied to a typical microcontroller like AVR. The performance and robustness of modified fuzzy controller in comparison with PID controller evaluated in no load, applied external disturbance with different magnitude conditions has been studied. The simulation results showed that the proposed fuzzy controller has a considerable advantage in rise time, settling time and overshoot respect to PID controller when the servo system encounters with nonlinear features like saturation and friction.
Keywords:
Parameter Varying PD Controller, Fuzzy Position Control (FPC) System, FLC, Servo Motor

1. Introduction
All control systems suffer from problems related to undesirable overshoot, longer settling times, vibrations and stability while going from one state to another state. Real-world systems are nonlinear, accurate modeling is difficult, costly and even impossible in most cases. On other side, a servo control system is one of the most important and widely used in control systems. The role of the control system may include: maintaining the position of a motor within certain limits, even when the load on the output of the motor might vary that this is called regulation or varying the position of the motor and load according to an externally set program of values that this called set point tracking [1] .
Today, applications of servomechanisms include their use in automatic machine tools, satellite-tracking antennas, celestial-tracking systems on telescopes, automatic navigation systems, manufacturing industry, transportation, computers, communication networks and antiaircraft-gun control systems. In many applications, servomechanisms allow high-powered devices to be controlled by signals from devices of much lower power.
The operation of the high-powered device results from a signal (called the error, or difference, signal) generated from a comparison of the desired position of the high-powered device with its actual position. A servomotor is a specific type of motor and rotary encoder combination, usually with a dedicated, that forms a servomechanism. This assembly may in turn form part of another servomechanism. The encoder provides position and usually speed feedback, which by the use of a PID controller allow more precise control of position and thus faster achievement of a stable position (for a given motor power). However, the conventional digital control systems like classic PID solve the above problems approximately and generally do not work well for non-linear systems, and particularly complex and vague systems that have no precise mathematical models [2] . Therefore, we need to intelligent and precise control systems to acquiring desired response. Moreover, it has been known that mentioned controllers produce more noise. Therefore, more advanced control techniques need to be used, which will minimize the noise effects [3] . To overcome these difficulties, various types of modified conventional PID controllers such as auto-tuning and adaptive controllers have been developed lately [4] - [6] .
Here we suggest intelligent control approach. There are three basic approaches to intelligent control: knowledge-based expert systems, fuzzy logic, and neural networks. All three approaches are interesting and very promising areas of research and development. In this paper, we present only the fuzzy logic approach. Fuzzy logic proposed by Lotfi A. Zadeh in 1973. Zadeh introduced the concept of linguistic variables [7] that can be described simply as “computing with words rather than numbers” or “control with sentences rather than equations” [8] .
Fuzzy Logic is a multivalued logic that allows intermediate values to be defined between conventional evaluations like true/false, yes/no, high/low and emerged as a tool to deal with uncertain, imprecise, or qualitative decision-making problems. Fuzzy logic control (FLC) is a control method based on fuzzy logic. Today, fuzzy control applications cover a variety of practical systems, such as the control of cement kilns [9] , train operation [10] , parking control of a car [11] , heat exchanger, robots, and also in many other systems, such as home appliances, video cameras, elevators, aerospace and etc.
Many different approaches are used for fuzzy controller implementation which they can be cited to hybrid- methods such as neuro-fuzzy [12] [13] , PI-like fuzzy [14] , multivariate regression [15] , non-linear bond graphs (BG) [16] . In neuro-fuzzy approach, controller learns fuzzy rules incrementally or decrementally and the learning algorithm uses a linguistic error measure that is expressed by fuzzy rules.
In PI-like fuzzy approach, first, the proposed fuzzy controller adopts the step response of phase trajectories to derive the corresponding linguistic control rules of such a system, and then applies the relationship between input and output signals in a proportional integral controller to convert the relationship of linguistic control rules to a decision table. Multivariate regression analysis attempts to determine a formula that can describe how elements in a vector of variables respond simultaneously to changes in others. For linear relations, regression analyses here are based on forms of the general linear model. Also, a bond graph is a graphical representation of a physical dynamic system. It is similar to the better-known block diagram and signal-flow graph, with the major difference that the arcs in bond graphs represent the bi-directional exchange of physical energy, while those in block diagrams and signal-flow graphs represent uni-directional flow of information. Furthermore, bond graphs are multi domain and domain neutral. This means a bond graph can incorporate multiple domains seamlessly.
In particular, for servo system, fuzzy logic PID [17] , Taguchi-method [18] , DSP-based fuzzy logic [19] and neuro-fuzzy controller [20] are used in literatures. In this paper, we proposed a novel method based on parameter varying PD controller for fuzzy servo controllers that uses the approximation of fuzzy nonlinear function including error and its derivation in operation point.
This paper is organized as follows: firstly, the overall framework of the theory of fuzzy control and its defuzzification methods are presented. Then fuzzy control algorithm based on PD controller has been approximated. Then the dynamic modeling of servo motor system and its experimental implementation using the proposed algorithm is done. Finally, simulation results of the proposed controller are compared with PID controller.
2. Motivation for Fuzzy Control
Classical mathematics and conventional control theory are quite limited in modeling and controlling complex nonlinear dynamical systems, particularly ill-formulated and partially described physical systems. The motivation for using fuzzy logic technology in control systems stems from the fact that it allows designers to build a controller even when their understanding of the system is still in a vague, incomplete, and developing phase.
Moreover, it can be noted that the servo controller design does not require to explicit knowledge of the motor and load characteristics [21] . Since the fuzzy controllers are designed directly from the properties of the process, the development time is often shorter than for conventional controllers [22] .
The overall procedure for developing a fuzzy control system for a model servo system is shown in Figure 1. The system uses measured variables as inputs to describe the error or derivation of error from the servo. These inputs are then “fuzzified” using membership functions supplied by an expert operator to determine the degree of membership in each input class. The resulting “fuzzy inputs” are evaluated using a linguistic rule base and fuzzy logic operations to yield an appropriate output and an associated degree of membership. This “fuzzy output” is then defuzzified to give a crisp output response that can be applied to the drive servo.
According to real-world requirements, the linguistic variables have to be transformed to crisp output. There are many defuzzification methods (e.g. Center of gravity, bisector of area, mean of area and center of average) that are in following [23] [24] .
2.1. Center of Gravity (COG)
For discrete sets, COG is called center of gravity for singletons (COGS) where the crisp control value is the abscissa of the center of gravity of the fuzzy set, where 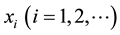 is a point in the universe of the conclusion and
is a point in the universe of the conclusion and 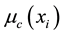 is the membership value of the resulting conclusion set. For continuous sets, summations are replaced by integrals.
is the membership value of the resulting conclusion set. For continuous sets, summations are replaced by integrals.
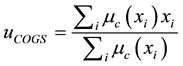 (1)
(1)
2.2. Bisector of Area (BOA)
Where 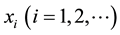 is a point in the universe (U) of the conclusion. There may be several solutions
is a point in the universe (U) of the conclusion. There may be several solutions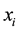 , thus this method is a complex method computationally. For discrete sets,
, thus this method is a complex method computationally. For discrete sets, 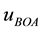 is the abscissa
is the abscissa 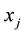 that minimizes the presented formula. Here
that minimizes the presented formula. Here 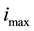 is the index of the largest abscissa
is the index of the largest abscissa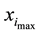 . Moreover
. Moreover 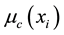 is membership value of the resulting conclusion set.
is membership value of the resulting conclusion set.
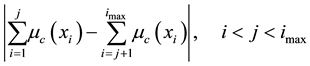 (2)
(2)
Figure 1. General structure of the fuzzy part.
2.3. Mean of Maximum (MOM)
In this method the crisp value is chosen by point with the highest membership. There may be several points in the overall implied fuzzy set which have maximum membership value. Therefore, it is a common practice to calculate the mean value of these points. Here 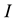 is the (crisp) set of indices
is the (crisp) set of indices 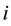 where
where 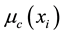 reaches its maximum
reaches its maximum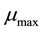 .
.

2.4. Center of Average (COA)
Where 



in this paper, the chosen defuzzification method for implementation is COA.

3. Problem Description and Methodology
3.1. Fuzzy Controller Based on PD Controller
A fuzzy logic controller has four main components as shown in Figure 1: fuzzification, inference, rule base and defuzzification. Implementation of an FLC requires the choice of four key factors [25] : number of fuzzy sets that constitute linguistic variables, mapping of the measurements onto the support sets, control protocol that determines the controller behavior and shape of membership functions. Thus, FLCs can be tuned not just by adjusting controller parameters but also by changing control rules, membership functions.
Rule bases, inference mechanism and defuzzification methods are the sources of nonlinearities in FLCs but it is possible to construct a rule base with linear input-output characteristic for FLC to become a linear controller with a control signal [26] . It is constructive to apply a similar analysis to Fuzzy PID control in order to accommodate integral action but the integrator creates problems by increasing the order of the closed loop system. Here, output signal is a function with two variables: error and derivation of error. Control signal U(n) is a nonlinear function of “error” and “derivation of error” as shown in Figure 2.
The simplest membership functions are formed using straight lines. In most literatures, because of the simplicity of the theory and implementation of triangular membership functions in design of fuzzy controller, these functions are used. In this study, the triangular membership function is chosen for each fuzzy linguistic value of the error and the derivation of error as shown in Figure 3 and Figure 4, respectively.
When

Figure 2. Fuzzy PD controller.
Figure 3. Membership function for error (e).
Figure 4. Membership function forderivation

When discussing it, considering the Equation (4) there are eight conditions as mentioned in [24] .
For design FPC, we consider to the fifth condition, arbitrary:
Thus

In later equation, 


We denote the input-output relation of the controller 

For sufficiently small



where
Note. The operating point (OP) that we consider it for linearization here is

Also

Considering Equation (8), we have:

Then after some algebra operations the Equation (12) become
Thus
We can see that the above controller behaves like a parameter varying PD controller thus the FLC performs like PID controller when we have not any external load or disturbance. Takagi-Sugeno or Mamdani [27] fuzzy inference system can be used to design the fuzzy controller.
In this paper, Mamdani fuzzy inference system is used. The inputs of FPD are “Error (E)” and “Derivate of Error (DE)” while the output is “control”. Input and output variables of FPD consist of three fuzzy sets namely N (negative), Z (zero), P (positive) as shown in Figures 5-7, respectively.
The fuzzy rule bases used in design of controller for the servo system are following:
Figure 5. Fuzzy input variable “error”.
Figure 6. Fuzzy input variable “derivation of error”.
Figure 7. Fuzzy output variable “control”.
3.2. Flowchart for Real-Time Implementation of FPC
Figure 8 shows the flow chart for the hierarchical fuzzy control algorithm, where 

3.3. PID Controller
When the digital controller is used, one could replace the derivative term with a backward difference and the integral term may be replaced with a sum. For a small constant sampling time, 

PID controllers can be set using the rules of Ziegler Nichols (ZN) or manually. Hand-tuning is generally used by experienced control engineers based on the special rules but these rules are not always valid. In recent years, many studies have been performed for optimization of PID coefficients which can be pointed to an extremum seeking [4] , stochastic algorithm [5] , genetic algorithm [6] and so on. Then the derivative gain 




4. Modelling and Implementation
The heart of the system that integrates the system components, control operations and defines features functionality using related techniques and methods is software. The total schematic diagram of this system including controller, actuator, process, and position sensor is shown in Figure 9. Designed printed circuit board (PCB) in Altium Designer Summer (ADS) environment and photograph of the implemented position tracking control system using fuzzy Logic are shown in Figure 10 and Figure 11 respectively. The system dynamics are represented as follows: The state space equations for a typical servo motor as follows:
Figure 8. Flow chart for the position fuzzy control system.
Figure 9. Schematic diagram of control system.
Figure 10. Circuit of FLC in ADS environment.
Figure 11. A view of the implemented system in lab.

where 



where 






Remark. For applications where the load is to be rapidly accelerated or decelerated frequently, the electrical and mechanical time constants of the motor play an important role. The mechanical time constants in these motors are reduced by reducing the rotor inertia. In this study, a DC motor with these specifications was used: (moment of inertia of the rotor: 1e-3 j, rated motor voltage: 6 v DC, armature inductance: 0.01 H, armature resistance: 0.005 Ω, Electromotive force constant: 0.22, Back E.M.F. Constant: 1.5, Damping ratio: 1.91 N×s/m).
5. Simulation Results
In this paper, first PID classic controller is designed for system control of servo mechanism using Section 3.3. Note that chosen gains for PID controller are given in this section. Then fuzzy controller using nine rules and triangular membership functions designed in Matlab/Simulink environment by Mamdani approach in Section 3.1.
The output response of both the PID and fuzzy logic controllers were presented. Figure 12 shows the result of the comparison between the output response (i.e. Position of servo) for the PID and Fuzzy logic controller under
Figure 12. Output response in no load condition.
no-load condition. Figure 13 and Figure 14 show the obtained result from comparison between PID controller and FLC for applied external disturbance (η) with different amplitudes η = 0.1 + sin(t) , η = 0.9 + 0.9sin(t), respectively.
Simulation results shows that the FLC performs like PID controller when we have not any load or changed parameters or disturbance [23] but when comparing both controllers under injected load or changed parameters or disturbance, the FLC performs better than PID controller [28] . However, the performance of PID controllers depends heavily on the operating parameters of the system. Also, if there is any change in the system, a significant amount of time is required to reset the controllers.
Considering proposed method, output responses using different defuzzification methods such as center of gravity (COG), bisector of area (BOA), mean of maximum (MOM), center of average (COA) under no load condition, load and external disturbance (η) conditions were shown in Figures 15-17, respectively. One can result that center of average (COA) method has an acceptable result than other methods (i.e. COG, BOA and MOM).
PID controller is designed on operating point and when it encountered with uncertainty or unmodeled dynamics in the system, it cannot compensate these changes enough effectively. Besides, fuzzy controller can cover these changes and handles them.
Figure 13. Output with external disturbance η = 0.1 + sin(t).
Figure 14. Output with external disturbance η = 0.9 + 0.9 sin(t).
Figure 15. Output response in no load condition.
Figure 16. Output response with constant load.
Figure 17. Output response with external disturbance.
6. Conclusion
The formulation of a novel implementation method based on parameter varying PD controller for the fuzzy logic servo controller is presented. Then obtained results from the comparison between PID controller and FLC with proposed method are presented. Simulation results show that FLC performs like PID controller for when we have not any load or changed parameters or disturbance but when comparing both controllers with considering injected load or changed parameters or disturbance, the fuzzy logic controller performs better.
References
- Heidari, Y., Noee, A.R., Shayanfar, H.A. and Salehi, S. (2010) Robust Control of DC Motor Using Fuzzy Sliding Mode Control with Fractional PID Compensator. The Journal of Mathematics and Computer Science, 1, 238-246.
- Vikas, S.W., Mithun, M.B., Tulasi, R.D. and Kumar, A.D. (2010) A New Fuzzy Logic Based Modelling and Simulation of a Switched Reluctance Motor. Journal of Electrical Engineering & Technology, 5, 276-281. http://dx.doi.org/10.5370/JEET.2010.5.2.276
- Killingsworth, N.J. and Krstic, M. (2006) PID Tuning Using Extremum Seeking. IEEE Control Systems Magazine, 26, 70-79. http://dx.doi.org/10.1109/MCS.2006.1580155
- Karthikraja, A. (2009) Stochastic Algorithm for PID Tuning of Bus Suspension System. International Conference on Control Automation Communication and Energy Conservation, Perundurai, 4-6 June 2009, 1-6.
- Altinten, A., Karakurt, S., Erdogan, S. and Alpbaz, M. (2010) Application of Self-Tuning PID Control with Genetic Algorithm to a Semi-Batch Polystyrene Reactor. Indian Journal of Chemical Technology (IJCT), 17, 356-365.
- Zadeh, L.A. (1973) Outline of a New Approach to the Analysis of Complex Systems and Decision Processes. IEEE Transactions Systems Man and Cybernetics, SMC-3, 28-44. http://dx.doi.org/10.1109/TSMC.1973.5408575
- Natsheh, E. and Buragga, K.A. (2010) Comparison between Conventional and Fuzzy Logic PID Controllers for Controlling DC Motors. International Journal of Computer Science Issues (IJCSI), 7, 128-134.
- Wang, X., Meng, Q., Yu, H., Yuan, Z. and Xu, X. (2005) Distributed Control for Cement Production of Vertical Shaft Kiln. International Journal for Information & Systems Sciences (IJISS), 1, 264-274.
- Bing, G., Hairong, D. and Yanxin, Z. (2009) Speed Adjustment Braking of Automatic Train Operation System Based on Fuzzy-PID Switching Control. Sixth International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, 14-16 August 2009, 577-580.
- Hanafy, M., Gomaa, M.M., Taher, M. and Wahba, A. (2011) Path Generation and Tracking for Car Automatic Parking Employing Swarm Algorithm. IEEE International Conference on Computer Engineering Systems, Cairo, 29 November 2011-1 December 2011, 99-104.
- Mudi, R.K., Dey, C. and Lee, T.T. (2006) Neuro-Fuzzy Implementation of a Self-Tuning Fuzzy Controller. IEEE International Conference on Systems, Man and Cybernetics, 6, 5065-5070.
- Akcayol, M.A. and Sagiroglu, S. (2007) Neuro Fuzzy Controller Implementation for an Adaptive Cathodic Protection on Iraq-Turkey Crude Oil Pipeline. Applied Artificial Intelligence: An International Journal, 21, 241-256. http://dx.doi.org/10.1080/08839510701196345
- Azzouna, A., Sakly, A., Trimeche, A., Mtibaa, A. and Benrejeb, M. (2010) PI-Like Fuzzy Control Implementation Using FPGA Technology. 5th International Conference on Design and Technology of Integrated Systems in Nanoscale Era (DTIS), Hammamet, 23-25 March 2010, 1-6. http://dx.doi.org/10.1109/DTIS.2010.5487595
- Baleghy, A.N. and Mashhadi, M.S.K. (2012) Design and Implementation Fuzzy Controller in the Frost-Free Refrigerator by Using Multivariate Regression. 20th Iranian Conference on Electrical Engineering (ICEE), Tehran, 15-17 May 2012, 840-844. http://dx.doi.org/10.1109/IranianCEE.2012.6292470
- Linkens, D.A., Wang, H., Bennett, S. and Xia, S. (1992) Using Qualitative Bond Graph Reasoning to Derive Look-Up Tables for Fuzzy Logic Controllers. First International Conference on Intelligent Systems Engineering, Edinburgh, 19-21 August 1992, 226-231.
- Yu, J.Z., Hu, X.L. and Ding, R. (2009) Fuzzy Logic PID Based Control Design for Permanent Magnet Synchronous Motor Servo System. Second International Conference on Intelligent Computation Technology and Automation, 2, 728-731.
- Tzeng, C.B., Liu, Y.C. and Young, M.S. (1995) A Preliminary Study of Fuzzy Control Parameters and Taguchi- Method on DC Servo Motor Control. IEEE/IAS International Conference on Industrial Automation and Control: Emerging Technologies, Taipei, 22-27 May 1995, 170-174.
- Hao, Y. (2012) DSP-Based Fuzzy Logic Servo Motor Control. International Conference on Control Engineering and Communication Technology (ICCECT), Liaoning, 7-9 December 2012, 556-559.
- Sang, H.K. and Lark, K.K. (2001) Design of a Neuro-Fuzzy Controller for Speed Control Applied to AC Servo Motor. IEEE Proceedings International Symposium on Industrial Electronics (ISIE), 1, 435-440.
- Kumar, N.S. and Kumar, C.S. (2010) Design and Implementation of Adaptive Fuzzy Controller for Speed Control of Brushless DC Motors. International Journal of Computer Applications, 1, 36-41.
- Claudia, P. and Miguel, S. (2008) Speed Control of a DC Motor by Using Fuzzy Variable Structure Controller. Proceedings of the 27th Chinese Control Conference, Kunming, 16-18 July 2008, 311-315.
- Namazov, M. and Basturk, O. (2010) DC Motor Position Control Using Fuzzy Proportional-Derivative Controllers with Different Defuzzification Methods. Turkish Journal of Fuzzy Systems, 1, 36-54.
- Huang, T.T., Chung, H.Y. and Lin, J.J. (1999) A Fuzzy PID Controller Being Like Parameter Varying PID. IEEE International Fuzzy Systems Conference Proceedings, 1, 269-276.
- Jantzen, J. (2007) Foundations of Fuzzy Control. WS: John Wiley & Sons, Ltd. http://dx.doi.org/10.1002/9780470061176
- Pahuja, R., Verma, H.K. and Uddin, M. (2011) Design and Implementation of Fuzzy Temperature Control System for WSN Applications. IJCSNS International Journal of Computer Science and Network Security, 11, 1-10.
- Mamdani, E.H. (1977) Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Synthesis. IEEE Transactions on Computers, C-26, 1182-1191. http://dx.doi.org/10.1109/TC.1977.1674779
- Alassar, A.Z., Abuhadrous, I.M. and Elaydi, H.A. (2010) Comparison between FLC and PID Controller for 5DOF Robot Arm. International Conference on Advanced Computer Control (ICACC), 5, 277-281.
- Aslam, F. and Kaur, G. (2011) Comparative Analysis of Conventional, P, PI, PID and Fuzzy Logic Controllers for the Efficient Control of Concentration in CSTR. IJCA, 17, 12-16.

























