Intelligent Control and Automation
Vol. 3 No. 3 (2012) , Article ID: 22052 , 4 pages DOI:10.4236/ica.2012.33031
Feedback Linearization Optimal Control Approach for Bilinear Systems in CSTR Chemical Reactor*
1College of Automation and Electronic Engineer, Qingdao University of Science & Technology, Qingdao, China
2Department of Computer Engineering, Qingdao Technological University Qingdao College, Qingdao, China
Email: gaodexin@qust.edu.cn
Received June 27, 2012; revised July 25, 2012; accepted August 3, 2012
Keywords: Bilinear System; Feedback Linearization; Optimal Control
ABSTRACT
This paper considers the optimal control problem for the bilinear system based on state feedback. Based on the concept of relative order of the output with respect to the input, first we change a bilinear system to a pseudo linear system model through the coordinate transformation. Then based on the theory of linear quadratic optimal control, the optimal controller is designed by solving the Riccati equation and introducing state feedback with state prediction. At last, the simulation results in CSTR Chemical reactor show the effectiveness of the method.
1. Introduction
Bilinear system is a special nonlinear system, during the processes of the engineering, social economy and ecology, there are so many objects can be described by bilinear systems. Bilinear system is close to linear system in the aspects of form, so some theory of linear systems can be used for bilinear systems. Meanwhile, because of bilinear systems can be approximated as many nonlinear systems, it is more accurate than the traditional linear approximation. Therefore, the study of bilinear systems is becoming particularly important. At present, some research results about the bilinear systems have been obtained. For example, Aganovic proposed a method of global successive approximation about bilinear system [1,2]; DISOPE approximate algorithm based on bilinear model is presented by Li [3]; Tang has studied the optimal control of the discrete bilinear system [4-6]. Hofer and Tibken obtained the optimal solutions in terms of a sequence of the differential Riccati equation [7]. The optimal iterative algorithm based on quadratic performance index about bilinear system is given in the reference [8], etc.
This paper concentrates on the solution of the optimal control problem for bilinear systems with a quadratic criterion based on state feedback. Firstly, the model of the bilinear system is given in this paper and changed to the nonlinear system model; Secondly, a complex nonlinear system model is changed to an easy pseudo linear system model by the differential homeomorphism; Then the optimal control law is designed by solving the Riccati equation; Finally, performance of the obtained optimalcontrol for bilinear systems with a quadratic criterion is verified in the CSTR Chemical reactor example.
The paper is organized as follows. Section 2 states the optimal control problem for bilinear systems. The solution to the optimal control problem and the proof of the obtained results, based on the maximum principle are given in Section 3. Section 4 presents an example illustrating the efficiency of control provided by the obtained optimal regulator for bilinear systems. Simulation graphs demonstrating better performance of the obtained optimal regulator are included.
2. Problem Statement
Consider bilinear systems described by the following difference equations
 (1)
(1)
where, 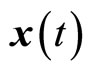 is the state vector;
is the state vector; 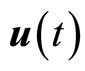 is the control vector;
is the control vector;  is the output vector;
is the output vector; ,
, 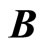 ,
, 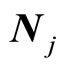 are scalar matrixes of appropriate dimensions;
are scalar matrixes of appropriate dimensions; 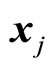 is the j-th component of state vector;
is the j-th component of state vector; 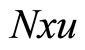 is the bilinear term;
is the bilinear term; 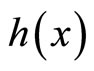 is the scalar function of
is the scalar function of![]() .
.
Assumption 1. The relative degree of the output![]() with respect to the input
with respect to the input 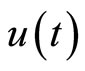 is
is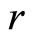 , that is
, that is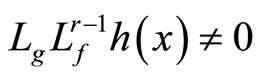 .
.
Through exact linearization, we can change the bilinear system (1) to an easy pseudo linear system (2).
 (2)
(2)
where, 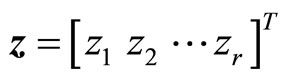 is the new state vector,
is the new state vector,
 ,
, 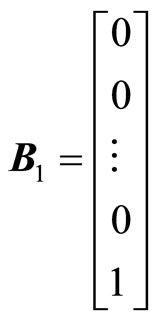
Then we can get the optimal control law base on the pseudo linear system (2).
3. State Feedback Exact Linearization
Transform bilinear system (1) into the general expression of nonlinear system as follow
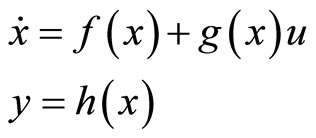 (3)
(3)
where,  ,
, 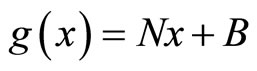 ,
, 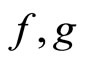 are continuously differentiable functions.
are continuously differentiable functions.
Consider the nonlinear systems described by the difference equation, according to Assumption 1, then get
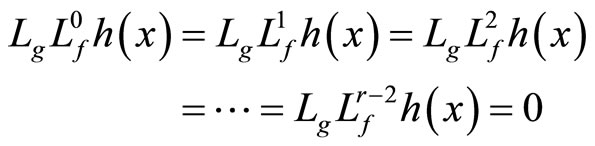 (4)
(4)
 (5)
(5)
Let:
 (6)
(6)
where  is the partial differential homeomorphism. We can change system (3) to a new standard form as follow
is the partial differential homeomorphism. We can change system (3) to a new standard form as follow
 (7)
(7)
In the expression (7),  and
and 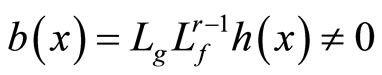 are the nonlinear scalar functions. From the first to the
are the nonlinear scalar functions. From the first to the 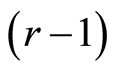 expressions are linear equations, only an equation which contains the control vector
expressions are linear equations, only an equation which contains the control vector 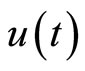 is nonlinear. In order to make expression (7) linearizing, let
is nonlinear. In order to make expression (7) linearizing, let
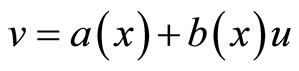 (8)
(8)
Expression (9) can be obtained
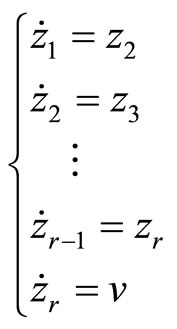 (9)
(9)
Expression (8) can be written as: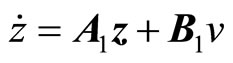 , where,
, where,
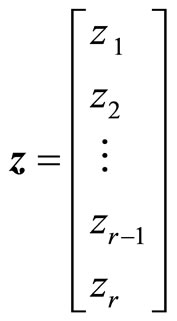 ,
,  ,
, 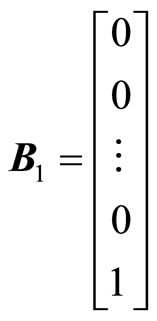
Then the expression of control variable u is obtained.
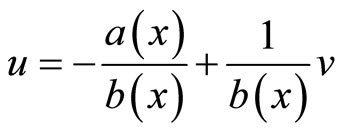 (10)
(10)
4. Optimal Controller Design
Nonlinear system (3) is transformed into equivalent pseudo linear system (2), where v is the control variable of the  standard form, the linear systems described by the following difference equation
standard form, the linear systems described by the following difference equation
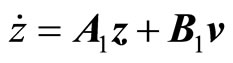
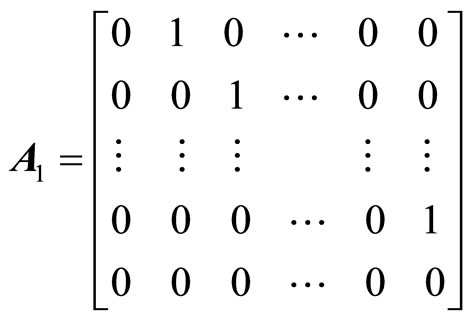
where, z is the new state vector; v is the new control vector; 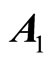 is the state coefficient matrix:
is the state coefficient matrix: 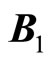 is the control coefficient matrix; system (2) is completely controllable.
is the control coefficient matrix; system (2) is completely controllable.
Select the quadratic performance index of system (2) as
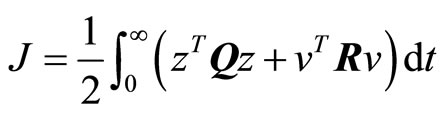 (11)
(11)
where, Q is a positive-semi definite matrix; R is a positive definite matrix.
Lemma 1. The optimal control problem of system (2) with the quadratic performance index (11) is unique existence if the system is completely controllable and observable. It can be expressed as
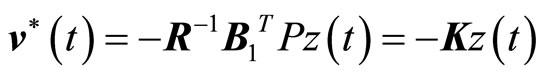 (12)
(12)
where 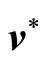 is the optimal control vector, K is the optimal feedback gain matrix, that is
is the optimal control vector, K is the optimal feedback gain matrix, that is
 (13)
(13)
P is the unique positive semi-definite solution of the  matrix equation
matrix equation
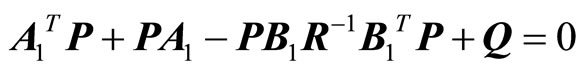 (14)
(14)
The optimal control law of the system (2) can be found from the following equation
 (15)
(15)
where,  can be obtained by Equation (13).
can be obtained by Equation (13).
Take Equation (6) into Equation (15), get
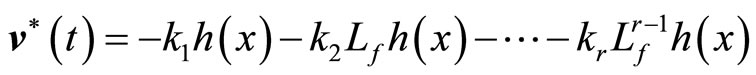 (16)
(16)
Compare (10) with expression (16), the optimal control law of the nonlinear system (3) is obtained as follow
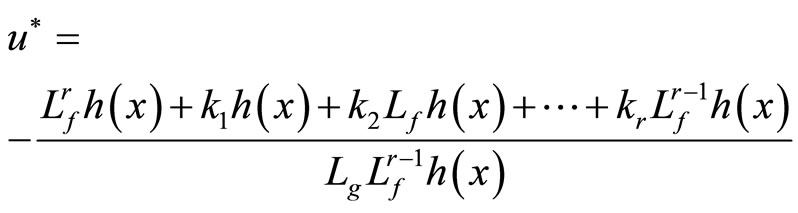 (17)
(17)
Then the optimal control law of the bilinear system (1) is
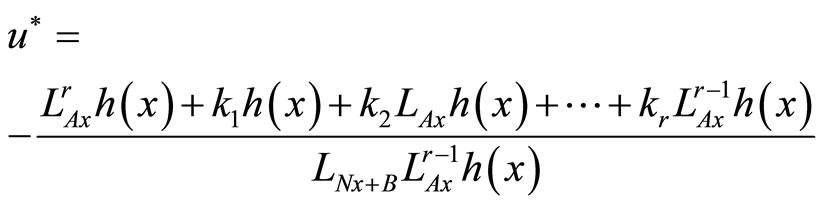 (18)
(18)
The structure diagram is shown as Figure 1.
5. A Simulation Example
In order to illustrate the effectiveness and feasibility of this method, consider Continuous-Stirred Tank Reactor (CSTR) model [9]
 ,
, 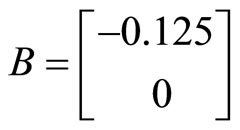 ,
,
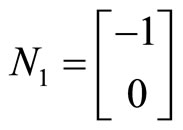 ,
, 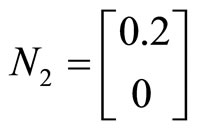
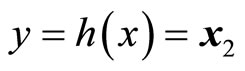 ,
, 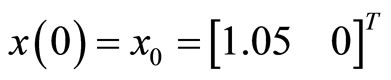
where, the state vector 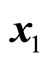 and
and 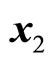 represent the temperature and density of initial production in the chemical reactor respectively. The control vector u represents the flow rate of cooling in the chemical reactor.
represent the temperature and density of initial production in the chemical reactor respectively. The control vector u represents the flow rate of cooling in the chemical reactor.
Through computing, we have
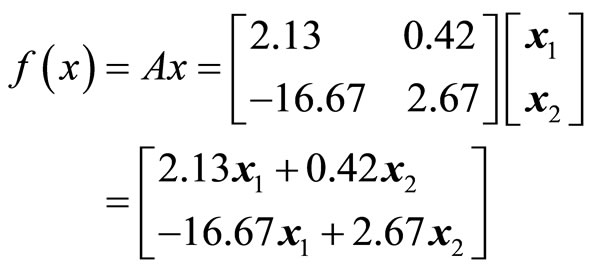 (19)
(19)
 (20)
(20)
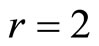 ,
,
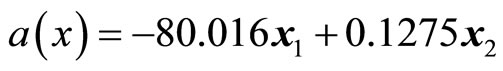

According to the state feedback exact linearization approach of optimal control for bilinear systems, we can get:
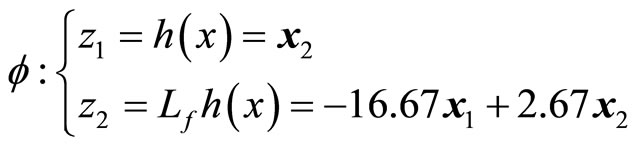 (21)
(21)
Select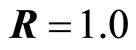 ,
, 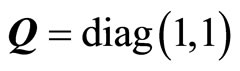 , then
, then

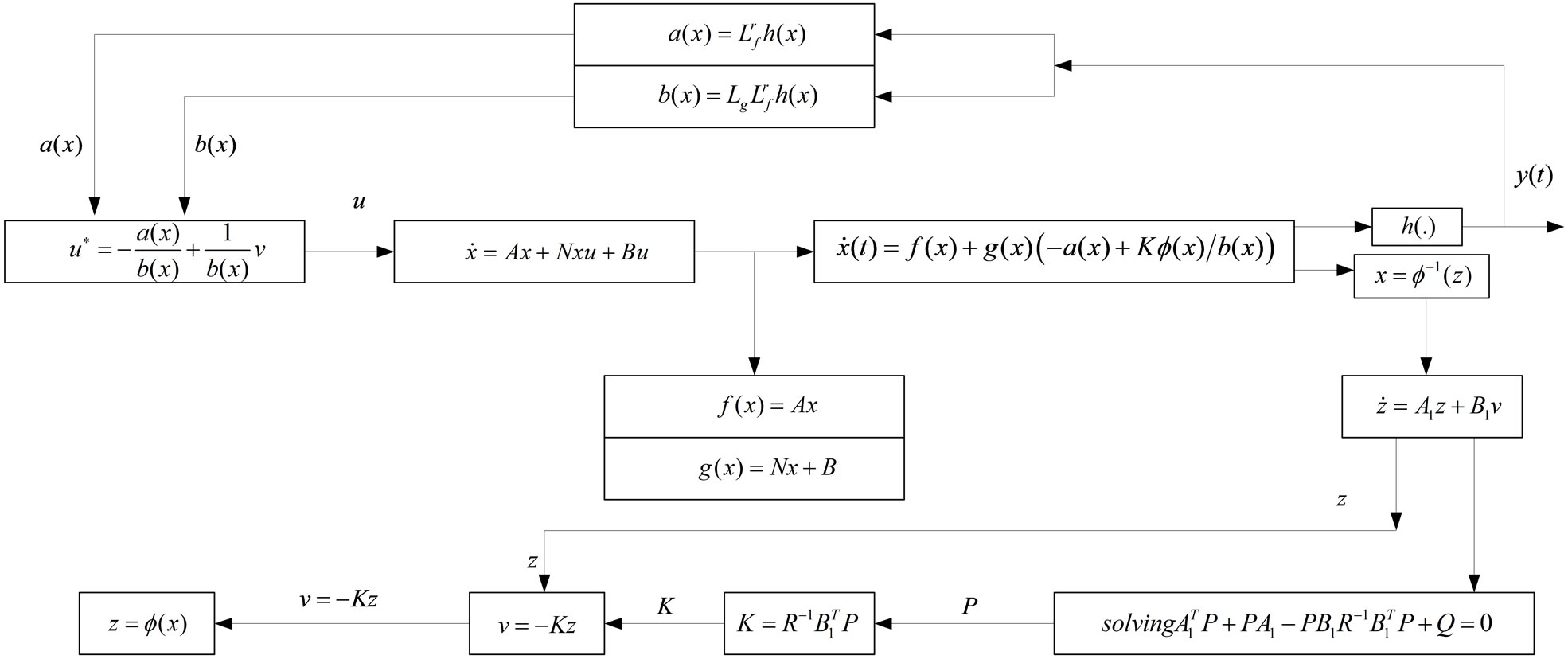
Figure 1. The structure diagram of bilinear system.

Figure 2. The simulation curve of state vector x1(t).
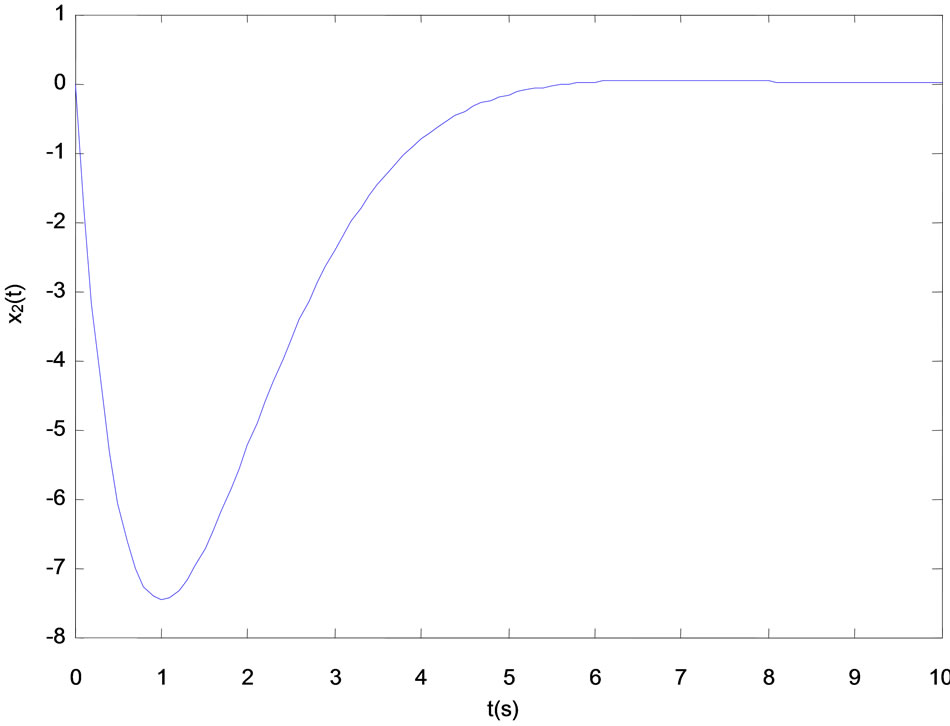
Figure 3. The simulation curve of the state vector x2(t).
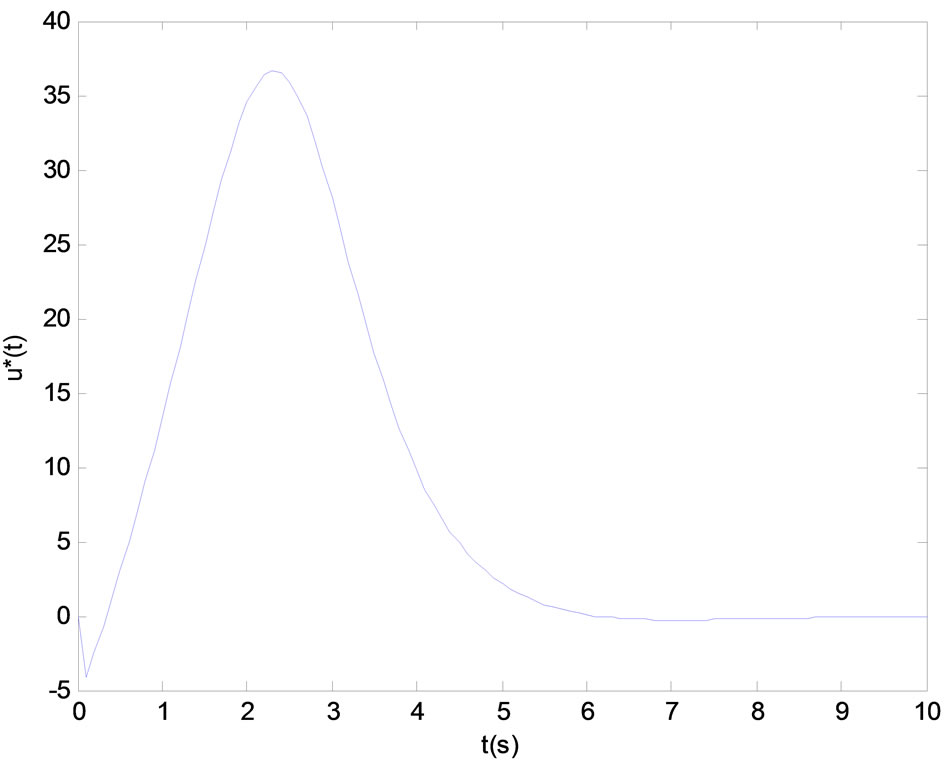
Figure 4. The simulation curve of the control vector u(t).
Simulation results are presented in Figures 2-4.
6. Conclusion
We have presented a state feedback exact linearization approach of optimal control for bilinear systems. The precise optimal controller is designed by solving the Riccati equation and introducing state feedback with state prediction. At last, the simulation results in chemical reactor show that the proposed approach is valid and easy to implement, the controller has a good convergence effect.
REFERENCES
- Z. Aganovic and Z. Gajic, “The Successive Approximation Procedure for Finite-Time Optimal Control of Bilinear Systems,” IEEE Transactions Automatic Control, Vol. 39, No. 9, 1994, pp. 1932-1935. doi:10.1109/9.317128
- Z. Aganovic and Z. Gajic, “The Successive Approximation Procedure for Stead State Optimal Control of Bilinear Systems,” Journal of Optimization Theory and Application, Vol. 84, No. 2, 1995, pp. 273-291.
- J.-M. Li, K.-Y. Xing and B.-W. Wang, “DISOPE Algorithm of Optimal Control Based on Bilinear Model for Nonlinear Continuous Time Systems,” Control and Decision, Vol. 15, No. 4, 2000, pp. 461-464.
- G.-Y. Tang, H. Ma and B.-L. Zhang, “Successive Approximation Approach of Optimal Control for Bilinear Discrete-Time Systems,” IEEE Proceedings of Control Theory & Applications, Vol. 152, No. 6, 2005, pp. 639- 644.
- G.-Y. Tang, Y.-D. Zhao and H. Ma, “Optimal Output Tracking Control for Bilinear Systems,” Transactions of the Institute of Measurement and Control, Vol. 28, No. 4, 2006, pp. 387-397. doi:10.1177/0142331206073065
- G.-Y. Tang, “Feedforward and Feedback Optimal Control for Linear Systems with Sinusoidal Disturbances,” High Technology Letters, Vol. 7, No. 4, 2001, pp. 16-19. doi:10.1109/68.903206
- E. Hofer and B. Tibken, “An Iterative Method for the Finite-Time Bilinear Quadratic Control Problem,” Journal of Optimization Theory and Applications, Vol. 57, No. 3, 1988, pp. 411-427. doi:10.1007/BF02346161
- D.-X. Gao, G.-Y. Tang and Q. Yang, “Feedback Linearization Optimal Control of Nonlinear Systems with External Disturbance,” Control and Instruments in Chemical Industry, Vol. 34, No. 2, 2007, pp. 20-24.
- S.-H. Lee and K. Lee, “Bilinear Systems Controller Design with Approximation Techniques,” Journal of the Chungcheong Mathematical Society, Vol. 8, No. 1, 2005, pp. 101-116.
NOTES
*This work was supported in part by the National Natural Science Foundation of China (60804005), and by the Natural Science Foundation of Shan Dong Province (ZR2011FQ006), by the Natural Science Foundation of Qingdao City (12-1-4-3-(17)-jch).

