Journal of Information Security
Vol.06 No.03(2015), Article ID:58387,14 pages
10.4236/jis.2015.63025
Evaluation of Modified Vector Space Representation Using ADFA-LD and ADFA-WD Datasets
Bhavesh Borisaniya, Dhiren Patel
Computer Engineering Department, NIT Surat, India
Email: borisaniyabhavesh@gmail.com, dhiren29p@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2015; accepted 25 July 2015; published 28 July 2015
ABSTRACT
Predicting anomalous behaviour of a running process using system call trace is a common practice among security community and it is still an active research area. It is a typical pattern recognition problem and can be dealt with machine learning algorithms. Standard system call datasets were employed to train these algorithms. However, advancements in operating systems made these datasets outdated and un-relevant. Australian Defence Force Academy Linux Dataset (ADFA-LD) and Australian Defence Force Academy Windows Dataset (ADFA-WD) are new generation system calls datasets that contain labelled system call traces for modern exploits and attacks on various applications. In this paper, we evaluate performance of Modified Vector Space Representation technique on ADFA-LD and ADFA-WD datasets using various classification algorithms. Our experimental results show that our method performs well and it helps accurately distinguishing process behaviour through system calls.
Keywords:
System Call Trace, Vector Space Model, Modified Vector Space Representation, ADFA-LD, ADFA-WD

1. Introduction
System call is a request for a service that program makes to the kernel. Sequence of the system calls can describe the behaviour of the process. System call traces are used in Host based Intrusion Detection System (HIDS) to distinguish normal and malicious processes. There are a number of data representation techniques found in literature (e.g, n-gram model and lookahead pairs [1] [2] , sequencegram [3] , pairgram [4] , etc.) used to extract the features from the system call trace for process behaviour classification.
By considering collected system call traces as set of document and system calls as words, we can apply classical data representation and classification techniques used in the area of natural language processing (NLP) and information retrieval (IR). Document representation techniques such as Boolean model and vector space model were reported in literature for extracting features from system call traces. X. Wang et al. [5] used n-gram with Boolean model for feature extraction and Support Vector Machine (SVM) with Gaussian Radial Basis Function (GRBF) kernel function for classification. K. Rieck et al. [6] used vector space model and considered frequency of system call in a trace as a weight of system call. They utilized polynomial kernel function for classifying the vectors storing weight of each system call. Y. Liao and V. R. Vermuri [7] have used vector space model for system call trace representation and applied k-nearest neighbour (kNN) classifier, where nearness was calculated using cosine similarity. However, these approaches are not considering system call sequence infor- mation, which would help in better describing the system call behaviour.
Researchers were utilizing the well-known system call trace datasets like University of New Maxico (UNM) intrusion detection dataset [8] , and DARPA intrusion detection dataset [9] to train the machine learning algo- rithms for process behaviour prediction. However, these datasets were compiled decades ago and are not very relevant for modern operating systems [10] . Recently (in 2013), new system call trace datasets released by G. Creech et al. known as ADFA datasets [10] [11] . ADFA datasets are considered as new benchmark for evaluating system call based intrusion detection systems. It has a wide collection of system call traces representing modern vulnerability exploits and attacks.
G. Creech et al. [12] have proposed semantic model for anomaly detection using short sequences of ADFA- LD Dataset. They have prepared the dictionary of word and phrase from the dataset and evaluated it with the Hidden Markov Model (HMM), Extreme Learning Machine (ELM) and one-class SVM algorithms. They achieve accuracy of 90% for ELM and 80% for SVM with 15% false positive rate (FPR) [12] [13] . For ADFA- WD evaluation also, G. Creech et al. [11] have used HMM, ELM and SVM. They noted 100% accuracy with 25.1% FPR for HMM, 91.7% accuracy with 0.23% FP rate with ELM and 99.58% accuracy with 1.78% FP rate for SVM. However, learning a dictionary of all possible short sequences is a time consuming task [14] [15] . Miao Xie et al. [15] have applied k-nearest neighbour (kNN) and k-means clustering (kMC) algorithms on ADFA-LD dataset. They considered frequency based model for data representation and used principal com- ponent analysis (PCA) to reduce the dimension of feature vector. With combination of kNN and kMC they achieve accuracy of 60% with 20% of FPR. In another attempt Miao Xie et al. [13] have applied one-class SVM with short sequence based technique on ADFA-LD. With one-class SVM, they achieved maximum accuracy of 70% with around 20% of FPR.
We modified the X. Wang et al. [5] approach given for Boolean model and proposed Modified Vector Space Representation in [16] to represent process system call trace in terms of feature vector. It is system call frequency based approach and utilizes the Vector Space Model with n-gram. In [16] , we have evaluated the pro- posed method on system call trace datasets used in [17] . In this paper, we apply modified vector space repre- sentation approach on ADFA-LD and ADFA-WD dataset and discuss results obtained with the help of different classification techniques chosen for evaluation.
Rest of the paper is organized as follows: Section 2 describes classic data representation techniques in context of system call trace with their limitations. Section 3 discusses modified vector space representation. Section 4 details the datasets, algorithms selected, chosen evaluation metrics and experiments methodology used for evaluation. Section 5 discusses the performance results followed by conclusion and references at the end.
2. System Call Trace Representation
In order to classify the process behaviour using system call trace, one needs to extract the features from it. Data representation techniques can be used to convert the system call trace into feature vector. Common data repre- sentation techniques used for system call representation are as follows:
2.1. Trivial Representation
The basic representation of system call trace is to consider it as a string (sequence) of system calls. Let us consider an operating system with total m number of unique system calls, then set of system calls can be re- presented by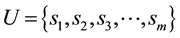 . Let
. Let 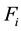 be finite sequence of system calls and
be finite sequence of system calls and 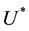 represents the set of all possible finite sequences of system calls then
represents the set of all possible finite sequences of system calls then 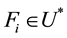 and
and 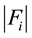 represents the length of the sequence. N is the total number of applications (normal and malware) used in training and testing for analysis. D is the dataset
represents the length of the sequence. N is the total number of applications (normal and malware) used in training and testing for analysis. D is the dataset
containing system call traces of selected applications and formally defined as 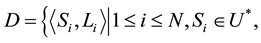
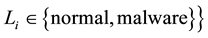 , where
, where 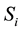 is a system call trace of
is a system call trace of 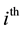 application and
application and 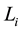 is its label (i.e. normal or
is its label (i.e. normal or
malware). The memory complexity for such representation is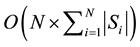 . Here
. Here 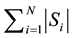 represents the
represents the
total length of sequences. If length of system call sequences is large, this could be a big number.
2.2. Boolean Model
Simple representation technique can be found in the area of information retrieval is Boolean Model [18] . It is an exact match model, which can represent a system call trace as a vector having all possible system call number as its index. The value of index is 1 if system call is present in given trace and 0 otherwise.
Consider total number of system calls in an operating system is m. A system call trace 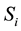 can be represented using boolean model as a feature vector
can be represented using boolean model as a feature vector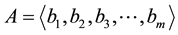 , where,
, where, 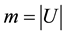 and
and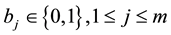 . The memory complexity of Boolean model is
. The memory complexity of Boolean model is
2.3. Vector Space Model
Vector Space Model is another common and powerful technique used in information retrieval field to represent document as set of words [18] . It is also known as “bag of words” technique as it assigns weight to each word in the given document in order to determine how much the document is relevant to specific words. Here the weight is assigned to a word as number of times the word appear in the document. In the context of system call repre- sentation, system call trace is considered as document and each system call as one word. Then we can apply vector space model to represent given system call trace as a feature vector.
To represent the system call traces using vector space model (bag of words) representation, let us con- sider a feature set B, as a set of vectors corresponds to applications’ system call traces. System call trace for an application i with this model can be represented as, vector










3. Modified Vector Space Representation
Vector space model cannot preserve the relative order of system calls. e.g. Feature vector for system call traces 


In order to represent the system call traces using this approach, let us consider 









Representation created using n-gram model is more costly than normal vector space model as
If we consider only those unique terms that appear in training data, the memory requirement would be less compared to considering all possible unique terms generated from U. This can be represented by set of all unique terms of length l occurring in training data. The set can be defined as





The feature vector built by considering only those terms that appeared in training data is much compact than other system call representations. However, it requires prior knowledge of unique terms in system call traces, which is not always possible. We can easily find the unique terms from the training data. However, during training, we might not have explored all possible usages of application. It is quite possible that, terms that were not present in the training data may appear in testing data.
Modified Vector Space Representation [16] extends the previous representation (which considers unique terms from training data only) by incorporating mechanism to handle any unforeseen terms during testing. We deliberately add a system call number (we refer it as unknown (unk)) in list, whose value is higher than any system call number present in system call list for OS. We form terms of length l comprising this unknown system call number including one term having all unknown system call number. Let E be the set of unknown terms comprising unk system call number. unk is a number deliberately added in the list of system call numbers to map terms, which are not seen during training but found in testing. Hence, the new feature set can be defined as



call trace sequences in training, memory complexity of this representation would be


4. Evaluation
In this section we provide details of datasets, classification algorithms selected, evaluation metrics and experi- ments methodology used for evaluation.
4.1. Datasets
We have evaluated modified vector space representation with two datasets namely ADFA-LD (Linux Dataset) and ADFA-WD (Windows Dataset) constructed by G. Creech et al. [10] -[12] . Table 1 describes the number of traces collected from [21] for each category for ADFA-LD and ADFA-WD dataset. For ADFA-LD system call traces for specific process were generated using auditd [22] Unix program, an auditing utility for collecting security relevant events. These traces were then filtered for undersize and oversize limit, which is 300 Bytes to 6 kB for training data and 300 Bytes to 10 kB for validation data [11] [12] . ADFA-LD dataset was collected under Ubuntu 11.04 fully patched operating system with kernel 2.6.38. The operating system was running different services like webserver, database server, SSH server, FTP server etc. ADFA-LD also incorporates system call traces of different types of attacks. Table 2 describes details of each attack class in ADFA-LD dataset [11] [12] .
Table 1. Number of system call traces in different category of ADFA-LD and ADFA-WD dataset.
Table 2. Attack vectors used to generate ADFA-LD attack dataset.
ADFA-WD (Windows Dataset) represents the high-quality collection of DLL access requests and system calls for a variety of hacking attacks [11] . Dataset was collected in Windows XP SP2 host with the help of Procmon [23] program. Default firewall was enabled and Norton AV 2013 was installed to filter only sophisticated attacks and ignore the low level attacks. The OS environment enabled file sharing and configured network printer. It was running applications like, webserver, database server, FTP server, streaming media server, PDF reader, etc. Total 12 known vulnerabilities for installed applications were exploited with the help of Metasploit framework and other custom methods. Table 3 describes the details of each attack class in ADFA-WD dataset [11] .
4.2. Algorithms Selected for Experiments
We selected Weka workbench [24] [25] for evaluation of modified vector space representation on ADFA-LD and ADFA-WD datasets. Weka hosts number of machine learning algorithms which can be easily applied on our prepared datasets of varying term-size. We selected nine well-known classification algorithms from six different categories given in Weka. The list of selected algorithms, selected options for individual algorithm and their respective category in Weka are shown in Table 4.
4.3. Experiments Methodology
Datasets were collected from [21] and then converted into modified vector space representation for various term-size. For these experiments we selected the term-size 1, 2, 3 and 5. For each dataset (i.e. ADFA-LD and ADFA-WD) we ran experiments for binary class as well as for multiclass label classification. For binary class we considered one of two labels for each trace - normal and attack. For multiclass classification, number of classes and class labels are different for both datasets. In ADFA-LD we have total 7 class labels viz. normal, adduser, hydra-ftp, hydra-ssh, java-meterpreter, meterpreter and webshell. While in ADFA-WD we have total 13 class labels viz. normal and V1 to V12. We ran each chosen algorithms with selected options on converted data in Weka through 10-fold cross-validation method. Table 5 describes the number of features extracted from ADFA-LD and ADFA-WD dataset for varying term-size using modified vector space representation.
4.4. Evaluation Metrics
We have used the following common evaluation metrics that are widely used in information retrieval area [18] :
True Positive (TP): Number of attack traces detected as attack traces.
False Positive (FP): Number of attack traces detected as normal traces.
True Negative (TN): Number of normal traces detected as normal traces.
False Negative (FN): Number of normal traces detected as attack traces.
Figure 1 shows the confusion matrix, which can be used to derive other measures.
Precision: It is the ratio of how many attack traces predicted as attack traces out of total number of traces predicted as attack traces.
Table 3. Vulnerabilities considered to generate ADFA-WD attack dataset.
Table 4. List of selected algorithms with their options.
Table 5. Number of features extracted from ADFA-LD and ADFA-WD dataset for term-size 1, 2, 3 and 5.
Figure 1. Confusion matrix.
Recall: Recall also known as the True Positive Rate (TPR). It is the ratio of how many attack traces pre- dicted as attack traces out of total number of actual attack traces.
Accuracy: Accuracy is the proportion of true results (number of attack traces and normal traces detected correctly) in the total number of samples.
FP Rate: False Positive Rate (FPR) is a measure of how many normal trace are labelled as attack trace by classifier.
F-Measure: It is a measure that combines precision and recall into a single measure. It is calculated as harmonic mean of precision and recall.
Receiver Operating Characteristics (ROC) Curve: It is a graph of true positive rate against false positive rate. It represents the performance of binary classifier as its discrimination threshold is varied.
Area Under the ROC Curve (AUC): It is the area covered by ROC curve. It is equivalent to the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one [26] .
5. Results and Analysis
Figure 2 shows the performance results in terms of accuracy and false positive rate of selected algorithms with varying term-size on both datasets. The results shown here are the weighted average of results derived for individual class labels. Detailed experiment (weighted average) results on ADFA-LD and ADFA-WD are given in Appendix (Tables A1-A4).
From Figure 2, we can observe that using modified vector space representation all algorithms perform reasonably well. However, IBk and J48 performed best in all experiments.
With IBk algorithm we can notice that as we increase the term-size, its performance starts degrading (i.e. accuracy decreases and FP Rate increases). These changes are clearly visible in case of ADFA-LD dataset. Similar performance results are achieved by J48 in all experiments. However, IBk have higher FP Rate compare to J48 for term-size 3 and 5 on ADFA-LD dataset.
Comparing IBk and J48 with application perspective, J48 requires more time in building the decision tree model during training but it is faster during testing phase. On contrary, IBk does not have any difference between training and testing phase. It finds distance between test instance and all other training instances during testing phase. Due to this IBk seeks high amount of memory space to store all training instances during testing phase compare to J48, whereas storing J48 model is merely a tree to be stored. So, with J48 in testing phase classifying a test instance is as simple as traversing limited number of branches (based on feature values) of a decision tree from root to leaf.
On ADFA-WD dataset, all algorithms perform well for binary class classification, but perform poorly for multiclass classification. Similar facts can be observed from Figure 3 and Figure 4. Figure 3 shows ROC curves of IBk (k = 1) and J48 with all term-size on ADFA-LD and ADFA-WD datasets for binary class classi- fication. Figure 4 shows ROC curves of IBk (k = 1) and J48 with term-size 3 on ADFA-LD and ADFA-WD datasets for multiclass classification. From Figure 4(c), Figure 4(d) and Table A4 we can observe that IBk and J48 achieves high accuracy for normal class on ADFA-WD, but fails to distinguish among attack classes. The
Figure 2. Performance results (FP rate and accuracy) of selected algorithms on ADFA-LD and ADFAWD dataset with binary class and multiclass classification for varying term-size. (a) FP rate―ADFA-LD (binary class); (b) Accuracy― ADFA-LD (binary class); (c) FP rate―ADFA-LD (multiclass); (d) Accuracy―ADFA-LD (multiclass); (e) FP rate― ADFA-WD (binary class); (f) Accuracy―ADFA-WD (binary class); (g) FP rate―ADFA-WD (multiclass); (h) Accuracy―ADFA-WD (multiclass).
Figure 3. ROC curves of IBk (k = 1) and J48 on ADFA-LD and ADFA-WD with various term-size for binary class classification. (a) IBk (k = 1) on ADFA-LD; (b) J48 on ADFA-LD; (c) IBk (k = 1) on ADFA-WD; (d) J48 on ADFA-WD.
possible cause for this could be, similarity among system call traces of vulnerabilities exploits launched through metasploit.
6. Conclusion
In this work, we have evaluated our proposed modified vector space representation using ADFA-LD and ADFA-WD system call trace datasets. We extracted features from both datasets using our proposed method for varying term-size. We also considered binary class and multiclass classification for evaluation on both datasets. Modified vector space representation (term-size 2, 3 and 5) performs as well as standard vector space model (term-size 1) if not better in terms of accuracy, FP rate and F-measure. There is no significant difference in results for varying term-size. However, higher term-size preserves more system call sequence information, which provides resistance against mimicry attacks. From the evaluation results, we conclude that IBk and J48 perform better on both datasets compare with other selected algorithms.
Figure 4. ROC curves of IBk (k = 1) and J48 with term-size 3 on ADFA-LD and ADFA-WD for multiclass classification. (a) IBk (k = 1) on ADFA-LD; (b) J48 on ADFA-LD; (c) IBk (k = 1) on ADFA-WD; (d) J48 on ADFA-WD.
Cite this paper
BhaveshBorisaniya,DhirenPatel, (2015) Evaluation of Modified Vector Space Representation Using ADFA-LD and ADFA-WD Datasets. Journal of Information Security,06,250-264. doi: 10.4236/jis.2015.63025
References
- 1. Forrest, S., Hofmeyr, S.A., Somayaji, A. and Longstaff, T.A. (1996) Sense of Self for Unix Processes. Proceedings of the 1996 IEEE Symposium on Security and Privacy, Oakland, 6-8 May 1996, 120-128. http://dx.doi.org/10.1109/SECPRI.1996.502675
- 2. Hofmeyr, S.A., Forrest, S. and Somayaji, A. (1998) Intrusion Detection Using Sequences of System Calls. Journal of Computer Security, 6, 151-180. http://dl.acm.org/citation.cfm?id=1298081.1298084
- 3. Hubballi, N., Biswas, S. and Nandi, S. (2011) Sequencegram: n-Gram Modeling of System Calls for Program Based Anomaly Detection. 2011 Third International Conference on Communication Systems and Networks (COMSNETS 2011), Bangalore, 4-8 January 2011, 1-10. http://dx.doi.org/10.1109/COMSNETS.2011.5716416
- 4. Hubballi, N. (2012) Pairgram: Modeling Frequency Information of Lookahead Pairs for System Call Based Anomaly Detection. Fourth International Conference on Communication Systems and Networks (COMSNETS 2012), Bangalore, 3-7 January 2012, 1-10. http://dx.doi.org/10.1109/COMSNETS.2012.6151337
- 5. Wang, X., Yu, W., Champion, A., Fu, X. and Xuan, D. (2007) Detecting Worms via Mining Dynamic Program Execution. Proceedings of Third International Conference on Security and Privacy in Communications Networks and the Workshops (SecureComm 2007), Nice, 17-21 September 2007, 412-421.
http://dx.doi.org/10.1109/SECCOM.2007.4550362 - 6. Rieck, K., Holz, T., Willems, C., Düssel, P. and Laskov, P. (2008) Learning and Classification of Malware Behavior. Detection of Intrusions and Malware, and Vulnerability Assessment, LNCS, 5137, 108-125. http://dx.doi.org/10.1007/978-3-540-70542-0_6
- 7. Liao, Y. and Vemuri, V.R. (2002) Using Text Categorization Techniques for Intrusion Detection.
USENIX Security Symposium, USENIX Association, Berkeley, 51-59.
https://www.usenix.org/legacy/events/sec02/full_papers/liao/liao.pdf - 8. Forrest, S. University of New Mexico (UNM) Intrusion Detection Dataset. http://www.cs.unm.edu/~immsec/systemcalls.htm
- 9. DARPA Intrusion Detection Dataset. http://www.ll.mit.edu/ideval/data/
- 10. Creech, G. and Hu, J. (2013) Generation of a New IDS Test Dataset: Time to Retire the KDD Collection. Wireless Communications and Networking Conference (WCNC 2013), Shanghai, 7-10 April 2013, 4487-4492. http://dx.doi.org/10.1109/WCNC.2013.6555301
- 11. Creech, G. (2014) Developing a High-Accuracy Cross Platform Host-Based Intrusion Detection System Capable of Reliably Detecting Zero-Day Attacks. Ph.D. Dissertation, University of New South Wales, Sydney. http://handle.unsw.edu.au/1959.4/53218
- 12. Creech, G. and Hu, J. (2014) A Semantic Approach to Host-Based Intrusion Detection Systems Using Contiguous and Discontiguous System Call Patterns. IEEE Transactions on Computers, 63, 807-819. http://dx.doi.org/10.1109/TC.2013.13
- 13. Xie, M., Hu, J. and Slay, J. (2014) Evaluating Host-Based Anomaly Detection Systems: Application of the One-Class SVM Algorithm to ADFA-LD. Proceedings of the 11th IEEE International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2014), Xiamen, 19-21 August 2014, 978-982. http://dx.doi.org/10.1109/fskd.2014.6980972
- 14. Xie, M. and Hu J. (2013) Evaluating Host-Based Anomaly Detection Systems: A Preliminary Analysis of ADFA-LD. Proceedings of the 6th IEEE International Congress on Image and Signal Processing (CISP 2013), Hangzhou, 16-18 December 2013, 1711-1716. http://dx.doi.org/10.1109/CISP.2013.6743952
- 15. Xie, M., Hu, J., Yu, X. and Chang, E. (2014) Evaluating Host-Based Anomaly Detection Systems: Application of the Frequency-Based Algorithms to ADFA-LD. Proceedings of 8th International Conference on Network and System Security (NSS 2014), Lecture Notes in Computer Science, 8792, 542-549. http://dx.doi.org/10.1007/978-3-319-11698-3_44
- 16. Borisaniya, B., Patel, K. and Patel, D. (2014) Evaluation of Applicability of Modified Vector Space Representation for in-VM Malicious Activity Detection in Cloud. Proceedings of the 11th Annual IEEE India Conference (INDICON 2014), Pune, 11-13 December 2014, 1-6. http://dx.doi.org/10.1109/INDICON.2014.7030588
- 17. Canali, D., Lanzi, A., Balzarotti, D., Kruegel, C., Christodorescu, M. and Kirda, E. (2012) A Quantitative Study of Accuracy in System Call-Based Malware Detection. Proceedings of the 2012 International Symposium on Software Testing and Analysis (ISSTA 2012), Minneapolis, 15-20 July 2012, 122-132. http://dx.doi.org/10.1145/2338965.2336768
- 18. Manning, C., Raghavan, P. and Schütze, H. (2008) Introduction to Information Retrieval. Cambridge University Press, Cambridge. >http://www-nlp.stanford.edu/IR-book
http://dx.doi.org/10.1017/CBO9780511809071 - 19. Wagner, D. and Dean, D. (2001) Intrusion Detection via Static Analysis. Proceedings of the 2001 IEEE Symposium on Security and Privacy, Oakland, 14-16 May 2001, 156-168. http://dx.doi.org/10.1109/secpri.2001.924296
- 20. Wagner, D. and Soto, P. (2002) Mimicry Attacks on Host-Based Intrusion Detection Systems. Proceedings of the 9th ACM Conference on Computer and Communications Security (CCS 2002), Washington DC, 18-22 November 2002, 255-264. http://dx.doi.org/10.1145/586110.586145
- 21. The ADFA Intrusion Detection Datasets. http://www.cybersecurity.unsw.adfa.edu.au/ADFA IDS Datasets/
- 22. Auditd. http://linux.die.net/man/8/auditd
- 23. Process Monitor (Procmon). https://technet.microsoft.com/en-us/library/bb896645.aspx
- 24. Holmes, G., Donkin, A. and Witten, I.H. (1994) WEKA: A Machine Learning Workbench. Proceedings of the 1994 Second Australian and New Zealand Conference on Intelligent Information
Systems, Brisbane, 29 November-2 December 1994, 357-361.
http://www.cs.waikato.ac.nz/ihw/papers/94GH-AD-IHW-WEKA.pdf
http://dx.doi.org/10.1109/ANZIIS.1994.396988 - 25. Weka. http://www.cs.waikato.ac.nz/ml/weka/
- 26. Fawcett, T. (2006) An Introduction to ROC Analysis. Pattern Recognition Letters, 27, 861-874. http://dx.doi.org/10.1016/j.patrec.2005.10.010
Appendix: Experiment Results
In this section we provide detailed experiment results on ADFA-LD and ADFA-WD with binary class and multiclass class labels. Results shown here are weighted average results of individual class results.
Table A1. Experiment results for various term-size on ADFA-LD dataset with binary class labels.
Table A2. Experiment results for various term size on ADFA-WD dataset with binary class labels.
Table A3. Experiment results for various term size on ADFA-LD dataset with multiclass class labels.
Table A4. Experiment results for various term-size on ADFA-WD dataset with multiclass class label.











