Materials Sciences and Applications
Vol.5 No.8(2014), Article
ID:47498,13
pages
DOI:10.4236/msa.2014.58060
Some Practical Aspects of the Oxidative Stability of Polypropylene Pipes
A. A. Apostolov1*, S. Djoumaliisky2
1Laboratory on Structure and Properties of Polymers, Faculty of Chemistry and Pharmacy, Sofia University, Sofia, Bulgaria
2Institute of Mechanics, Bulgarian Academy of Sciences, Sofia, Bulgaria
Email: *apostolov@chem.uni-sofia.bg
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2014; revised 11 May 2014; accepted 2 June 2014
ABSTRACT
The oxidation time and oxidation temperature of a total of 20 specimens with unknown pre-history from various manufacturers of polyethylene and poly(ethylene-co-propylene) are determined. The specimens are in the form of fittings used in piping. The specimens are divided into two groups corresponding to their melting temperature and polyethylene content in the copolymer, respectively. The oxidation activation energy for the two groups is calculated. Reasonable relationship between the measured oxidation time and the time, calculated on the base of the measured oxidative temperature, is obtained. The scattering of experimental data is thoroughly examined and some recommendations aiming at improving the results are suggested. Specific recommendations are given for the cases of technological and post consummative piping waste. The paper critically estimates the accuracy in the measured oxidation time and temperature as well as their mutual relation.
Keywords:Polypropylene, Material Testing, Oxidation Induction Time, Oxidation Induction Temperature

1. Introduction
The present work is addressed to the degradation of polypropylene (PP) and poly(ethylene-co-propylene) tubes and fittings, used in piping. PP degrades due to various factors as temperature, oxidation, pressure, uvand γ-radiation, etc. The temperature of thermal degradation is often cited in the certificate of tubes (see e.g. [1] ) and is usually between 300˚C - 350˚C. For this reason no thermal degradation is expected in domestic piping where the highest temperature is 95˚C. On the other hand, oxygen dissolved in water attacks the inner side of the tubes and oxygen from the air attacks the outer side of the tubes. Hence, the thermo-oxidative degradation (i.e. oxidative degradation enhanced by temperature) is the main factor that substantially decreases the service life of the tubes and fittings.
According to the widely used standard ASTM 3895 [2] the products, made of polyolefins should contain antioxidants assuring minimum oxidation induction time of 20 min. The German DIN EN728 [3] is generally similar to the American standard. The oxidation time allows prediction of the so-called “indicative life time” at certain temperature, e.g. 20˚C for cold water. This prediction, though, calls for long lasting experiments of isothermal annealing of PP samples for a year [4] . The oxidation induction time (OIt) can be measured by conventional differential scanning calorimetry (DSC) (see e.g. [5] ) or by pressure differential scanning calorimetry [6] at somewhat elevated temperature (in the vicinity of 200˚C) to shorten the antioxidant depletion. In brief, the DSC procedure is as follows: a small PP sample is put in an open aluminum pan; an open empty pan is used as a reference. The pans are heated into the DSC cell in N2 atmosphere up to 200˚C and kept isothermally for 1 min. Then the atmosphere is switched to O2 and the sample is kept in an isothermal mode for a certain time that is reasonable for the antioxidant depletion. A certain time after switching the gas the base line declines exotermally indicating the start of the degradation process. The oxidation induction time is the time lag between the onset of the constant temperature (after 1 min for equilibrating) and the beginning of degradation. It is normally considered that higher oxidation induction time corresponds to longer piping lifetime. This method is used for both fresh and used PP products. In the latter case the measured oxidation time determines whether the PP product usage should be ceased.
Another simple method for characterizing the material’s resistance to oxidative degradation uses the so-called oxidation induction temperature (OIT) [3] [7] . For this purpose a thermogram in oxygen atmosphere is taken from room temperature up to 300˚C. During the temperature increase the PP melting peak is seen first, while further on the base line declines exothermally due to thermal degradation, hence the degradation temperature is determined. Generally the higher the degradation temperature, the longer the expected tube lifetime.
The thermal oxidation stability of PP depends directly on the type and quantity of antioxidants used. The OItvalue generally follows a linear relationship with the antioxidant concentration, which makes the OIt test a useful quality control procedure for tracking the concentration of the antioxidant [8] . Generally, the OIt based conclusions depend on the type of oxidants used that is usually not given in the certificates. Some of the antioxidants like thiosynergists and especially hindered amines are not very effective processing stabilizers at 200˚C [8] (at which temperature OIt is determined) and in this paper we accept that such antioxidants have not been used in our specimens. Also, antioxidant efficiency varies with temperature [8] . These are other reasons to accomplish additional tests by measuring the OIT. Schmid et al. claim that it is more appropriate to use OIT than OIt at low temperatures whereas the use of OIt at higher temperatures helps to better differentiate the samples [9] .
According to Ilie and Senetscu [10] there are some general features of the polymer thermo-oxidation process. In our case of polypropylene and poly(ethylene-copropylene) some specific parameters and conditions may vary:
• The induction time depends on the polymer nature, structure and density, etc. The stereo regular polymers are less prone to oxidation as compared to the atactic ones [10] . In our case every fitting could comprise attactic, isoand syndiotactic-PP as well as PE in various ratios. Osawa and coworkers proved the higher stability to thermooxidation of syndiotactic polypropylene as compared to isotactic polypropylene and highdensity polyethylene and assigned this high stability to the helicoidal structure of s-PP [11] .
• The oxygen absorption is proportional to the polymer open surface [10] . This could really be responsible for the unconsistence of some data for one and the same fitting.
• The oxygen absorption rate depends on the diffusion coefficient of oxygen [10] . Thus, due to the difference of these coefficients: 4.6 × 10−7 for LDPE [10] and 2.9 × 10−8 cm2/s for PP [12] might be another reason for a difference between the fittings of the two groups.
• The absorbed oxygen mass in the thermal oxidation process is inversely proportional to the crystallinity degree of the polymer. The oxidation process starts within its amorphous phase or interfibrilar areas [10] . It seems obvious that the fittings differ in crystallinity thus affecting the oxidation in a different way. In addition, the degree of crystallinity also depends on the PP molecular weight. For instance, it drops from 90% to 68% for molecular weight 70 to 175 kg/mol, respectively [13] .
It is the aim of this work to shed more light on the use of the above mentioned OIt and OIT and their mutual relation as main characteristics for characterizing the tubes and fittings. Some remarks on the antioxidant distribution and other factors affecting the scattering of OIt for one and the same sample are given.
2. Experimental
2.1. Specimens
In this work a specimen represents a (pipe) fitting. A total of 20 commercial specimens of polypropylene and/or poly(ethylene-co-propylene) fittings for pipes were investigated by DSC. Every sample was taken “as is” from the respective fitting that was believed to be representative of manufacture typical production run. Generally, the type and quantity of the antioxidants used were not given in the specs. The DSC method was used in different modes, as described above, and OIt and OIT were obtained. Minimum three (in case of large inhomogeneity 4 - 6) samples from every specimen were tested and the mean value of IOIt was taken. The variables measured are given in Table 1 together with their abbreviation and a brief explanation of the measuring mode.
The samples were cut from the outer side of the fittings in form of flakes weighing between 4.5 and 5.5 mg to assure better reproducibility [14] . This limited this work to only oxidation from the oxygen in the air, eventually facilitated by irradiation by light, uvand irradiation). Before starting the experiments, the surface layer was removed in order to avoid an eventual surface-core effect. All specimens were randomly numerated and DSCruns were executed with a couple of samples taken from each specimen. Next, the specimens were arranged in the order of their increasing melting temperature and the abbreviations below for the specimens and corresponding samples will be used further on (Figure 1).
Table 1. DSC-modes of measuring and their brief explanation.
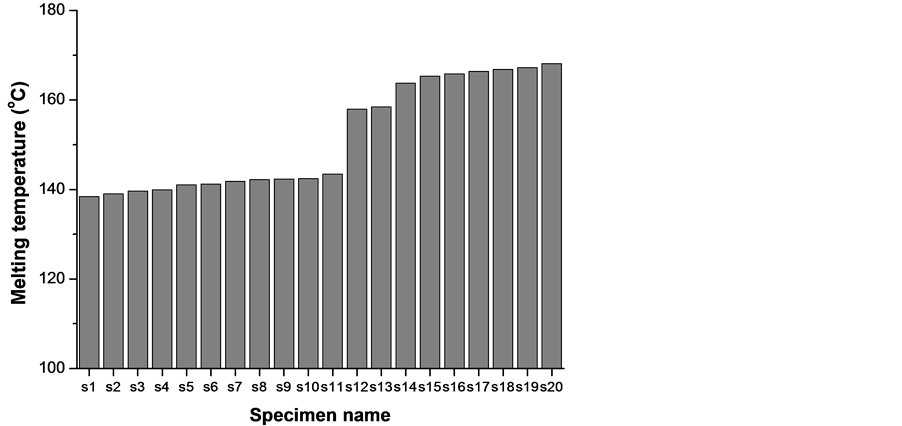
Figure 1. Melting temperature in increasing order of samples s1 to s20: lower melting temperature group s1 to s11; higher melting temperature group s12 to s20.
The specimens can be divided in two groups, according to Figure 1. Every fitting comes from a different producer. The lower melting temperature group includes samples from s1 to s11 and their melting temperatures are in the range from 138.4˚C to 143.4˚C or 140.9˚C ± 2.5˚C. The higher melting temperature group includes samples from s12 to s20 and their melting temperatures are in the range from 157.9˚C to 168.1˚C or 163.0˚C ± 5.1˚C. The two temperature intervals are clearly separated. The isotactic PP melting temperature is 171˚C [16] -[18] . Various producers of PP pipes and fittings do not use neat PP but poly(ethylene-co-propylene) and that is why the measured melting temperatures of all samples are lower. Polypropylene and polyethylene form two types of copolymers [19] . When the ethylene content is up to 6% by mass, random copolymer is formed. Relatively long oligopropylene blocks are separated by 1 - 2 repeat units of ethylene. Their melting temperature is slightly lower than that of isotactic polypropylene. These are the higher melting temperature samples s12 - s20, showing small temperature depression of an average of 6˚C. There are also random copolymers that melt in this interval, see e.g. [20] , for a polypropylene random co-polymer (PP type 3) that melts at 150˚C - 154˚C or [1] where poly(propylene-co-ethylene) melts at 165˚C. When the ethylene content is between 5% and 15% by mass, block copolymer is formed [19] . Due to the large difference in the content of propylene and ethylene, the oligopropylene blocks are much longer than the oligoethylene ones. There is a significant depression of an average of 20˚C of the iso-PP melting temperature due to its relatively short blocks.
The lower melting temperature samples s1 - s11 form this group and their diffractograms are given in Figure 2. They all are typical for the PP-homopolymer. The diffractograms of the samples from the second group are very similar to these of the first group and are not given here for the sake of simplicity. Since the two main PE reflexes at 20.5 and 22.5 deg 2q are missing in all twenty diffractograms the PE blocks are too short to crystallize separately.
2.2. Apparatuses and Methods
DSC calorimeter Q200 of TA instruments (USA) was used in heating mode with 10˚C/min heating rate or in isothermal mode at 200˚C; in both cases in a constant flow of N2 (during heating) or O2 (during oxidation) of 50 ml/min. Aluminum pans were used in order to avoid any catalytic effect [21] . Sample size was between 4.5 - 5.5 mg.
A Labsys apparatus of SETARAM, France, was used for simultaneous DSC and thermogravimetric analysis (TGA).
Wide-angle X-ray diffraction patterns were recorded using a Siemens Kristalloflex diffractometer, operated in reflection, utilising a CuKα-radiation. Slices of the fittings were used and since they were not flat the angular position of the PP reflexes varies a little from sample to sample (Figure 2). Since the melting temperature is slightly lower than the melting temperature of isotactic PP and the main reflexes of PE are missing (Figure 2) the PE blocks are too short for PE to crystallize separately. On the other hand PP prevails in the copolymer and its blocks make own crystallites that give reflexes on the diffractograms (Figure 2). Yet these blocks are limited in length hence they built up imperfect crystallites that melt at slightly lower temperature. All crystallites belong to the alpha-form of PP. Thus, although the thermal oxidative stability of β-PP is higher than that of neat PP [22] it cannot affect our results (see Figure 2).
3. Results and Discussion
Some specimens were consistent, i.e., few samples taken from one and the same specimen had close oxidation times/temperatures. Other specimens, though, exhibited large data scattering of the corresponding samples. In this case more samples (up to six) from one and the same specimen were measured. Table 2 represents an example of scattering of experimental data of IOIt (in increasing order) for three selected specimens.
Assuming all possible precautions for good reproducibility were taken we refer this scattering to inhomogeneously distributed antioxidant. Such tubes or fittings should be used in practice with care. One can conclude that their stability will be determined by the least oxidation time between all times characterizing one and the same fitting.
Next step was to establish if the oxidation temperature and oxidation time were mutually related. Figure 3 shows the dependences of the mean IOIT and mean OIT on the mean OIt. Both dependencies were fitted with straight lines according to the least square method.
The parameters of linear fits of the data from Figure 3 are given in Table3 The data for the correlation coef-
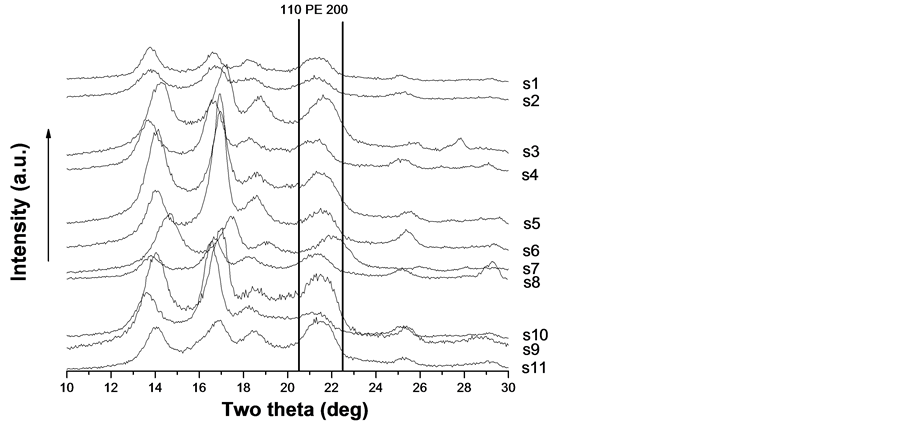
Figure 2. Wide-angle diffractograms of the lower melting group samples s1 - s11. The position of the expected two strongest PE reflexes is shown.

Figure 3. Dependence of the mean initial oxidation induction temperature (○) and mean oxidation induction temperature (·) on the mean initial oxidation induction time for the set of 20 specimens. The points of both groups were fitted with straight lines.
Table 2. Example of scattering of experimental data of IOIt (in increasing order) for three selected specimens.
Table 3. Intercept А, standard deviation DA, slope В, standard deviation DВ, correlation coefficient R, and significance level p as obtained from the linear fits of the data in Figure 3.
ficient R and significance level p show strong correlation between the mean IOIT and mean OIT on one side, and mean IOIt, on another. There are largely scattered times for some specimens (see Table 2). The dependencies shown in Figure 3 do not reflect any physical relation between the parameters; at this stage purely formal relationship was sought.
Additionally, the relation between IOIT and OIT was obtained (Figure 4). The goal was to give priority to one of these temperatures for characterization of the fittings. The parameters of this linear fit are given in Table4
As expected, Table 4 shows strong correlation between the two temperatures. It can be easily calculated from the slope of the fit in Figure 3 that 1˚C change in IOIT leads to 0.8˚C change in OIT. Hence the IOIT is a little bit more sensitive to the inhomogeneity and/or level of the antioxidant in the specimens than OIT and for this reason it should be preferred for their characterization.
Let us now elaborate the relation between the variables that characterize the specimens. We will seek a relationship between the measured time and the time, calculated on the base of the measured temperature. In particular we will use the time and temperature obtained by extrapolation, i.e., OIt and OIT. Schmid et al. [9] investigated six PE samples and obtained an exponential increase of OIt on OIT. This does not correspond to our case, Figure 4, where a straight line seems good enough to fit the data. We tried to clarify the relation between of OIt and OIT. First, we found the activation energy E using the described by Starink [23] so-called direct p(x)-isoconversion method, where p(x) is the so-called temperature integral that in our case was calculated after substituting x = Ea/R as suggested by Madhusudanan et al. [24] .
![]() (1)
(1)
The values of the constants in the above relation a = 0.37773896, b = 1.00145033 and c = 1.89466100 were taken from Tang et al. [25] . The relationship between the heating rate β and OIT, here designated simply as T, is given by Focke and van der Westhuizen [26] ; R = 8,314 J/K×mol is the universal gas constant:
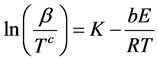 (2)
(2)
with intercept
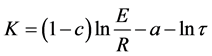 (3)
(3)
and slope
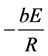 (4)
(4)
where τ is a characteristic time constant of the ersatz chemical reaction determining the length of the induction time period [26] .
Further on we use these equations together with the Gimzewski’s postulate that OIT and OIt correspond to the same level of antioxidant depletion. Also, the values of the activation energy E are specific for each antioxidant but assumed independent on concentration [26] . Since our specimens are commercial almost no data are given to characterize them, in particular the nature and quantity of the antioxidant are not given. That is why as first approximation we assumed that all 20 specimens contain the same antioxidant hence the activation energy does not depend on the antioxidant nature.
In order to calculate the activation energy by Equations (1)-(3) OIt was measured for various heating rates β between 1.25 and 20˚C/min twice for every heating rate and the mean of the two was taken. A relatively homogeneous with respect to the antioxidant specimen s15 (i.e. characterized by close values of OIt) was chosen. The mass of the samples was relatively small (in order to avoid overshooting) and approximately constant (between 2.0 and 2.3 mg). The obtained relation between β and OIT is shown in Figure 5 in appropriate coordinates. Further on these data were fitted with a straight line and an activation energy 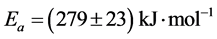 or
or ![]() using the slope and Equation (4) was calculated. Several authors have reported for polypropylene activation energy between 220 and 270 kJ/mol [27] -[29] . Our value of 279 kJ/mol is close to these values. In addition some or all specimens are made of poly(ethylene-co-propylene) copolymer, its activation energy unknown (see below).
using the slope and Equation (4) was calculated. Several authors have reported for polypropylene activation energy between 220 and 270 kJ/mol [27] -[29] . Our value of 279 kJ/mol is close to these values. In addition some or all specimens are made of poly(ethylene-co-propylene) copolymer, its activation energy unknown (see below).
Further on, we applied Gimzewski’s relationship between induction temperatures and induction times [30]
Table 4. Intercept А, standard deviation DA, slope В, standard deviation DВ, correlation coefficient R, and significance level p as obtained from the linear fits of the data in Figure 5.

Figure 4. Relation between the mean oxidation induction temperature and mean initial oxidation induction temperature for the set of 20 specimens.
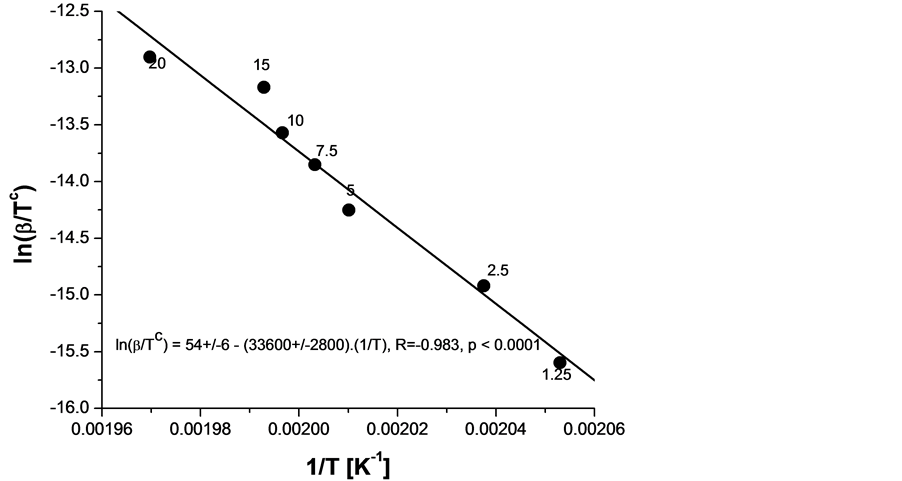
Figure 5. Graphical presentation of Equation (2) as a straight line, fitting the experimental points, differing in the heating rate β (fixed as a parameter in K/min) and the measured T ≡ OIT. The higher melting temperature sample s15 was used as very homogeneous for all heating rates β (marked in K/min next to every data point).
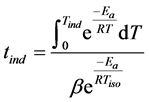 (5)
(5)
where the induction period tind ≡ OIt, Tiso is the temperature of the isothermal DSC run, Tind ≡ OIT and T is the temperature (variable). To apply this equation the sample should contain an oxidation inhibitor. Knowing the activation energy (see Figure 5), the integration was executed numerically as the lower temperature limit was set to 100˚C below Tiso rather than zero because there wоuld be no significant reaction at this temperature [30] . In our case Tiso equals 200˚C. Mark that this temperature is suitable for PE, too, hence it will be suitable for the copolymer samples. Next we put Ea = 279 kJ/mol as obtained from Figure 5 and took log from both sides of Equation (5). The graphical presentation obtained is shown in Figure 6.
In the ideal case the experimental time equals the calculated one hence the slope of the linear fit (Figure 6) will be 1. In our case this slope equals 1.132 ± 0.019, i.e., it is significantly different from 1. For this reason we allowed the activation energy in Equation (5) to vary until the slope of the linear fit becomes 1. The result is shown in Figure 7 and the corresponding Ea = 204 kJ/mol.
Figure 5 represents Equation (2) for all specimens and Ea = 279 kJ/mol as obtained from the higher melting temperature sample s15. By plotting the same figure for lower melting temperature sample s4, activation energy Ea = 197 kJ/mol was obtained (Figure 8).
To shed more light on the mechanism of the processes, taking place in the samples from both groups, simultaneous DSC and TGA were taken. The results are presented in Figure 9 for both lower s4 and higher s15 melting temperature samples, respectively, each one representative for the respective group, see Figure 1.
From Figure 9 it is clearly seen that: 1) the two samples melts in the expected regions; 2) they are stable up to 300˚C in argon atmosphere but start to degrade oxidatively in the vicinity of 210˚C in oxygen; 3) the degradation is accompanied by a severe mass loss of 70% up to 300˚C; 4) a single well-defined weight loss event is obtained at temperature approx. 15˚C higher than the oxidation start. This can be explained by the initial scission of the polypropylene chains, followed by formation of volatile products; 5) the decomposition of PP and poly(ethylene-co-propylene) is expected to be the same since he thermo-oxidative degradation of PP is quite similar to that of PE except that the exothermic reaction is steady [31] , and 6) TGA data for both samples show a small increase in sample mass, which occurs prior to degradation. As Peterson et al. pointed out, this increase is likely to be caused by the formation of a small amount of the polymer oxide [31] .
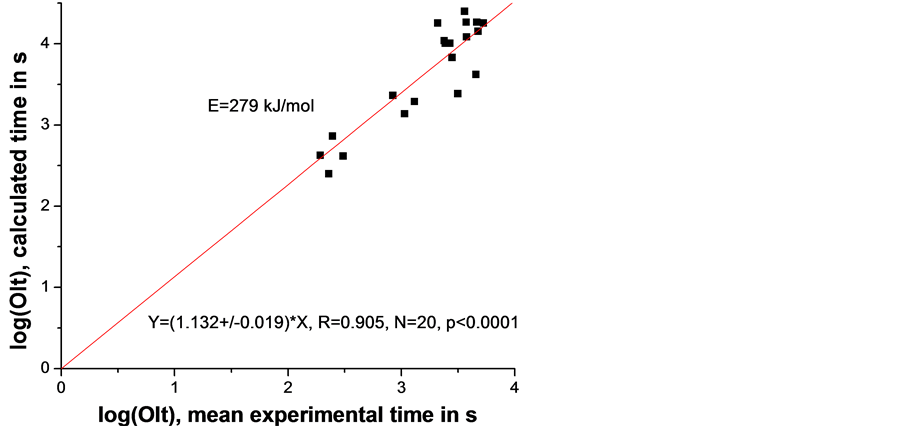
Figure 6. Graphical presentation of Equation (5), i.e. relation between mean experimental time and calculated time (both in logarithmic scale). The activation energy Ea was obtained from Figure 5 and Equation (4).
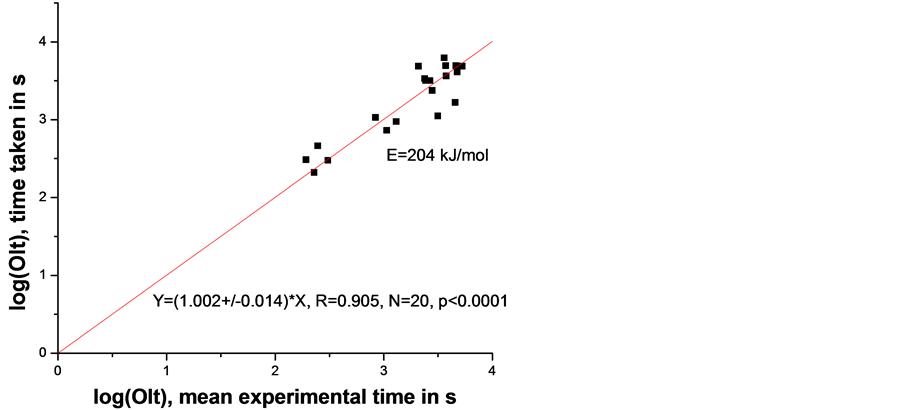
Figure 7. Graphical presentation of Equation (5), i.e., relation between mean experimental time and calculated time (both in logarithmic scale) where the activation energy was adjusted by putting the experimental time equal to the calculated time.
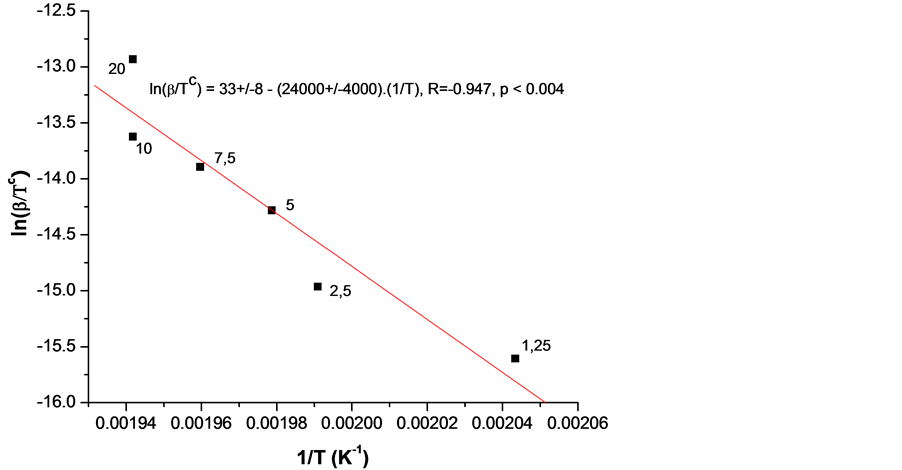
Figure 8. Graphical presentation of Equation (2) as a straight line, fitting the experimental points, differing in heating rate β (fixed as a parameter in K/min) and the measured T ≡ OIT. As very homogeneous, the lower melting temperature sample s4 was used for all heating rates (marked next to every data point).
We now focus on the two activation energies, obtained for the lowerand higher melting temperature samples. Having in mind the relatively large standard errors (see Figure 5 and Figure 8) it is obvious that the difference between the two activation energies of 279 and 197 kJ/mol is not significant hence they are practically equal; thus the rounded mean (Ea = 240 kJ/mol) is the best estimate of the activation energy.
Now let us comment on the scattering of the experimental data points in Figure 3, Figure 4, Figure 6 and Figure 7. There is a thorough review of the experimental effects due to the usage of DSC by Blaine et al. [14] . According to them the main effects that determine the precision are the test temperature, end point selection, oxygen flow rate, specimen size, specimen pan type, and catalyst effects.
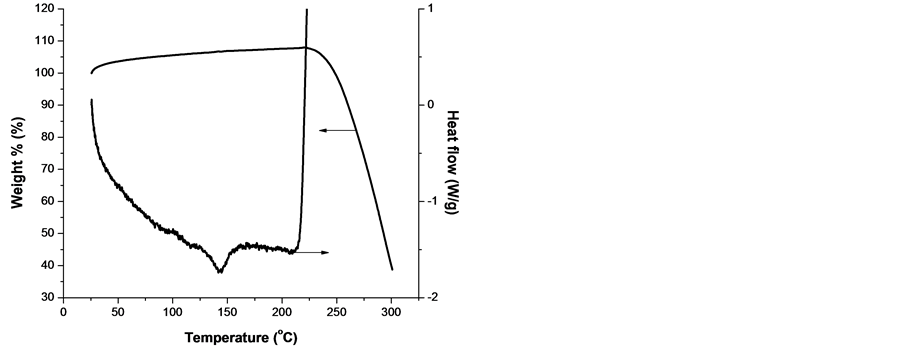 (a)
(a)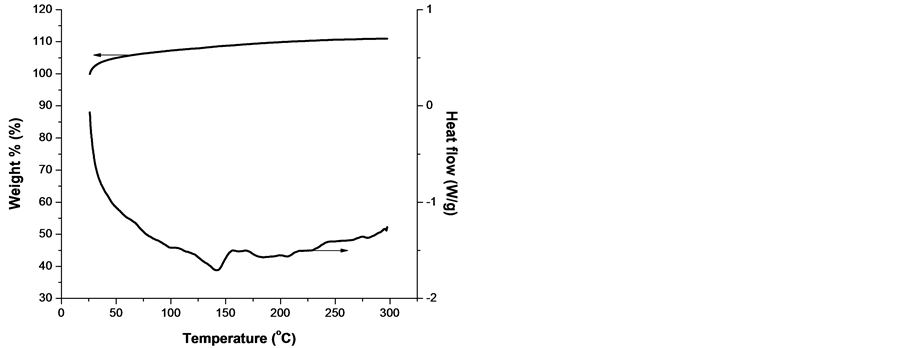 (b)
(b)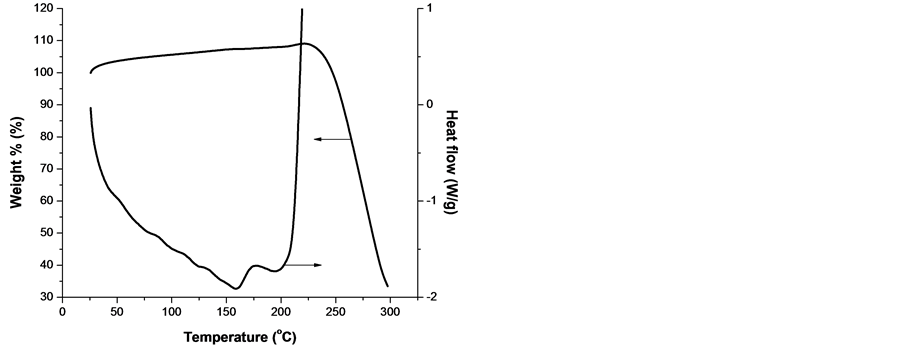 (c)
(c) (d)
(d)
Figure 9. Curves of DSC and TGA of lower melting temperature sample s4 (a, b) and higher melting temperature sample s15 (c, d) obtained with a linear heating rate of 10 K/min in oxygen (left) and argon atmosphere (right).
o The test temperature chosen is appropriate for both PP and PE (Yet, in some cases 190˚C is preferable for PE).
o End point selection. The onset of the oxidation is taken as the end-point of the induction period. Two means of determining the oxidation onset are in use. The more common is the extrapolation onset. The second method for establishment of the end point is the first deviation from the baseline. Some threshold is set, usually 50 mW/g. The endpoint is taken at the point where the exothermic event crosses that threshold [14] .
o If the standard error of both OIT and IOIT is the same (say 1˚C) OIT is a little more sensitive than IOIT since the slope of the linear fit in Figure 4 is lower than unity (0.8). This could be pointed out as a humble reason to prefer measuring of IOIT rather than OIT.
o Effect of temperature. By default this is the temperature of isothermal mode when determining OIt (usually 200˚C for PP [2] ; this is also our case.). According to Blaine et al. [15] for polyethylene specimens the effect of the 200˚C test temperature on the OIt is 2.9 min/˚C. After careful temperature calibration according to the standard procedure for DSC Q200 we set the temperature to 200˚C and followed its value for two hours. We found it stable with time within ±0.03˚C that corresponded to a negligible error of 0.09 min in OIt.
o Effect of oxygen flow rate. The results of Blaine et al. [14] show that OItime value may change by 3.5 min for each 10 ml/min change in purge gas flow rate. We followed the oxygen flow rate for two hours and found it stable within ±0.05 ml/min that corresponded to a negligible error of 0.02 min in OIt.
o Regardless of the longer induction period in aluminum pans in comparison to cupper, stainless steel, nickel and platinum pans, the former were preferred since they lead to better reproducibility [15] . Remark: Strictly speaking the above given conclusions are valid for PE samples but we adopted these conclusions for PP due to the similarity in the oxidative degradation.
o Effect of sample mass and form. Due to low heat conductivity in general it is better to use samples with similar mass (Blaine claimed for less than 5 mg sample mass [14] ). Similar sample area for all samples is also recommended. In the ideal case in order to get highly reproducible results for OIt test, constant and thin disk sample geometry is favorable. Samples in a form of few small pieces may present a better option, but the thermal contact and the heat transfer within the sample are poor. In addition, the surface-to-volume ratio of small pieces is very irreproducible [14] . We used sample mass between 4.5 and 5.5 mg and by a naked eye tried to always cut samples with the same thickness.
o The major factor affecting reproducibility in our case of PP (homoor co-polymer) specimens turned out to be the inhomogeneity of the antioxidant. This conclusion is based on the fact that some specimens give samples with reasonably close to each other OIt and other—do not. Some specimens reveal somewhat larger values of times/temperatures. Finally, there are specimens giving very scattered values of the measured OIt. Representatives of these three groups are specimens 11, 4 and 7, respectively (Table 2). Specimen 15 also shows homogenous distribution of the antioxidant and was used to construct Figure 5 for evaluation of the activation energy. Let us also remind that all specimens are “as received” from the manufacturer and the type of the antioxidant, its concentration and especially whether it is homogenously distributed or not, are not given in the specs. The latter is really very significant and good homogeneity can be obtained by using thorough and continuous mixing of the highly viscous polymer melt with the antioxidant (in the tube and fitting production), but this of course overprices them.
o The sample selection is another reason for scattering of the OIt data. As pointed out by Ye and Tan, the sampling location on the part also has an impact on the OIt result because various locations of the sample may have different concentration of antioxidant additives [21] . For example, in the case of water pipe, the sample taken from the outside of the pipe may have a higher OIt than the sample taken from the inside of the pipe because the antioxidant additive at the surface can be extracted by water [9] . For this reason when taking a sample we firstly removed the surface layer (thus in addition we evaded the so called “Surface-core” effect).
o Let us also not forget that some specimens could have been stabilized with a different antioxidant. This will affect the scattering of the points in Figure 3, Figure 4, Figure 6 and Figure 7, but cannot affect the scattering of the points in Figure 5 and Figure 8 since each one of them is obtained using one and the same specimen.
4. Conclusions
1) On the basis of 20 specimens from various manufacturers correlation between the oxidation induction temperature and oxidation induction time was found.
2) The use of initial oxidation induction temperature instead of oxidation induction temperature leads to a moderate improvement of the correlations.
3) For characterization of PP samples, especially inhomogeneous, use of the initial oxidation induction time instead of oxidation induction temperature (both initial and extrapolated) is recommended.
4) Generally, the inhomogeneous distribution of the antioxidant is the main reason for scattering of the experimental data for one and the same fitting. On the other hand, all samples we cut from a specific fitting weight approx. 5 mg in the hope that better reproducibility will be achieved. It may be concluded from the widths of the X-ray peaks that the crystallites are several tens of micrometers large. Thus, the amount of the amorphous PP part may vary from sample to sample regardless the fact that they weigh equally. Then, as Shibryareva pointed out, morphological irregularity of polymer results from the presence of crystalline and amorphous regions in the same polymer. This type of irregularity affects the regularities and rates of polymer oxidation [32] .
5) In contrast to some authors, we found the OIt more reliable than the OIT. Yet, in case of large inhomogeneity, oxidation induction temperature can be added additionally to the oxidation induction times to more confidently characterize the specimens. This approach resembles the one of Lugao et al. [33] , who suggest that every sample is characterized by a set of two parameters (time and temperature). Although these authors also use DSC, they do not use it in an isothermal mode and call the time obtained “temperature oxidative induction time” [33] .
6) One last remark connected specifically to the recycling of PP and poly(ethylene-co-propylene) products: If we use technological waste, there is no need to investigate a large number of samples from one and the same batch, whereas post consummative waste should be characterized either separately, or the whole mass should be ground, homogenized and then characterized by “overall” oxidation induction time.
This work deals mainly with OIt and OIT as readily obtainable by DSC parameters for assessment of the fitting’s life. For this reason no other techniques (FTIR, etc.) were employed.
Acknowledgements
The authors are grateful for the financial support of the Bulgarian Ministry of Education and Science—National Science Fund (Project No DTK 02/7-2010).
References
- Zdravotny ustav se sidlem v Ostrave, protokolu o zkousce evid, C1411/2003.
- ASTM D 3895-07, Test Method for Oxidative Induction Time of Polyolefins by DSC.
- DIN (ISO 11357-6:2008).
- Beaumier, D and Blond, E. (2008) Durability of Polypropylene Tubes “Draintube”. SAGEOS, File S006-159.
- Viebke, J. and Gedde, U.W. (1998) Assessment of Lifetime of Hot-water Polyethylene Pipes Based on Oxidation Induction Time Data, Polymer Engineering and Science, 38, 1244-1250. http://dx.doi.org/10.1002/pen.10293
- Marcus, S.M. and Blaine, R.L. (1997) Estimation of Bias in the Oxidative Induction Time Measurement by Pressure DSC, TA Instruments. Inc., New Castle, DE 19720.
- Ezrin, M., Zepke, A., Helwig, J., Lavigne, G. and Dudley, M. (2001) Plastic Failure Due to Oxidative Degradation in Processing and Service. In: Moalli, J., Ed., Plastic Failure Analysis and Prevention, Plastics Design Library, Norwich.
- Jakoby, P. (2003) The Effect of Hindered Phenol Stabilizers on Oxygen Induction Time (OIT) Measurements, and the Use of OIT Measurements to Predict Long Term Thermal Stability. http://www.pstc.org/files/public/Jacoby.pdf
- Schmid, M., Ritter, A. and Affolter, S. (2006) Determination of Oxidation Induction Time and Temperature by DSC, Journal of Thermal Analysis and Calorimetry, 83, 367-371. http://dx.doi.org/10.1007/s10973-005-7142-5
- Sorin I.E. and Radu S. (2009) TE-VSC, Polymeric Materials Review on Oxidation, Stabilization and Evaluation Using CL and DSC Methods, TE Technical Note. Sorin.Ilie@cern.ch
- Kato M. and Osawa Z. (1999) Effect of Stereoregularity on the Thermo-Oxidative Degradation of Polypropylenes. Polymer Degradation and Stability, 65, 457-461.
- Dibelo, P.M., Manganaro, J.L. and Aguinaldo, E.R. (1991) Encyclopedia of Chemical Technology. 4th Edition, John Wiley, New York, 938.
- Bruno, F., Richaud, E., Verdu, J. and Farcas, F. (2008) Embrittlement of Polypropylene Fibre during Thermal Oxidation, Journal of Material Science, 43, 1026-1032. http://dx.doi.org/10.1007/s10853-007-2242-1
- Blaine, R.L., Lundgren, C.J. and Harris, M.B. (1997) Oxidative Induction Time—A Review of DSC Experimental Effects. In: Riga, A.T. and Patterson, G.H., Eds., Oxidative Behavior of Materials by Thermal Analytical Techniques, ASTM STP 1326, ASTM.
- Patterson, G.H. and Riga, A.T. (1993) Factors Affecting Oxidation Properties in Differential Scanning Calorimetric Studies. Thermochimica Acta, 226, 201-210. http://dx.doi.org/10.1016/0040-6031(93)80221-U
- Wunderlich, B. (1976) Macromolecular Physics, Volume 2: Crystal Nucleation, Growth, Annealing. Academic Press, New York.
- Boor Jr., J. (1979) Ziegler-Natta Catalysts and Polymerization. Academic Press, New York.
- Keith, H.D. and Padden Jr., F.J. (1964) Spherulitic Crystallization from the Melt. II. Influence of Fractionation and Impurity Segregation on the Kinetics of Crystallization. Journal of Applied Physics, 35, 1286-1296. http://dx.doi.org/10.1063/1.1713607
- Essential Chemical Industry, CIEC Promoting Science. http://www.essentialchemicalindustry.org
- Suitall Catalog Data of PP-R Pipes & Fittings, Suitall Polypro Limited. http://www.indiamart.com/suitall-polypro-limited/products.html
- Ye, P., Tan, B.C. (2012) How to Optimize OIT Tests? Application Note. www.perkinelmer.com
- Lv, Y.D., Huang, Y.J., Kong, M.Q. and Li, G.X. (2013) Improved Thermal Oxidation Stability of Polypropylene Films in the Presence of β-Nucleating Agent. Polymer Testing, 32, 179-186. http://dx.doi.org/10.1016/j.polymertesting.2012.10.008
- Starink, M.J. (2003) The Determination of Activation Energy from Linear Heating Rate Experiments: A Comparison of the Accuracy of Isoconversion Methods. Thermochimica Acta, 404, 163-176. http://dx.doi.org/10.1016/S0040-6031(03)00144-8
- Madhusudanan, P.M., Krishnam, K. and Ninan, K.N. (1986) New Approximation for the p(x) Function in the Evaluation of Non-isothermal Kinetic Data. Thermochimica Acta, 97, 189-201. http://dx.doi.org/10.1016/0040-6031(86)87019-8
- Tang, W., Liu, Y., Zhang, H. and Wang, C. (2003) New Approximate Formula for Arrehenius Temperature Integral. Thermochimica Acta, 408, 39-43. http://dx.doi.org/10.1016/S0040-6031(03)00310-1
- Focke, W.W. and van der Westhuizen, I. (2010) Oxidation Induction Time and Oxidation Onset Temperature of Polyethylene in Air. Journal of Thermal Analysis and Calorimetry, 99, 285-293. http://dx.doi.org/10.1007/s10973-009-0097-1
- Marshall, D.I., George, E.J., Turnipseed, J.N. and Glenn, J.L. (1973) Measurement of Oxidation Stability of Polyolefins by Thermal Analysis. Polymer Engineering and Science, 13, 415-421. http://dx.doi.org/10.1002/pen.760130604
- Bockhorn, H.A., Hornung, A., Hornung, U. and Schawaller, D. (1999) Kinetic Study on the Thermal Degradation of Polypropylene and Polyethylene, Journal of Analytical and Applied Pyrolysis, 48, 93-109. http://dx.doi.org/10.1016/S0165-2370(98)00131-4
- Ballice, L. and Reimert, R. (2002) Classification of Volatile Products from the Temperature-Programmed Pyrolysis of Polypropylene (PP), Atactic-Polypropylene (APP) and Thermogravimetrically Derived Kinetics of Pyrolysis. Chemical Engineering and Processing, 41, 289-296. http://dx.doi.org/10.1016/S0255-2701(01)00144-1
- Gimzewski, E. (1992) The Relationship between Oxidation Induction Temperatures and Times for Petroleum Products. Thermochimica Acta, 198, 133-140. http://dx.doi.org/10.1016/0040-6031(92)85067-6
- Peterson, J.D., Vyazovkin, S. and Wight, C.A. (2001) Kinetics of the Thermal and Thermo-Oxidative Degradation of Polystyrene, Polyethylene and Poly (Propylene). Macromolar Chemistry and Physics, 202, 775-784.
- Shibryaeva, L. (2012) Thermal Oxidation of Polypropylene and Modified Polypropylene-Structure Effects.http://www.intechopen.com/books/polypropylene/thermal-oxidation-of-polypropylene-and-modified-polypropylene-structure-effects
- Lugao, A.B., Cardoso, C.L., Hutzler, B., Machado, L.D.B. and Conceicao, R.N. (2002) Temperature Dependent Oxidative-Induction Time (TOIT) of Irradiated and Non-Irradiated Polypropylene—A New Method. Radiation Physics and Chemistry, 63, 489-492. http://dx.doi.org/10.1016/S0969-806X(01)00544-8
NOTES

*Corresponding author.


