ABSTRACT

Application of Maxwell’s equations and the theory of relativity on the processes in atoms with real oscillator leads to the structural constant of atoms s₀ = 8.278692517. Measurements show that the ratio of energy of the photon and its frequency is not constant which means that Planck’s h is not constant. The theory which is consistent with these measurements, has been found. This theory covers processes in electron configuration and also at the core of atoms. Based on the structural constant s₀ the maximum possible atomic number Z is determined. In order to encompass all atoms and all nuclides a new measurement unit has been proposed. That is the measurement unit for the order of substance. The introduction of structural constant s₀ makes 11 fundamental constants redundant, including Planck’s h. The structural constant of atoms s₀ stands up as the most stable constant in a very wide range of measurement, so it may replace variable Planck’s h well. Continuity of the bremsstrahlung is explained.

Keywords:

Boscovich, Bremsstrahlung, Hyperon, Neutron, Order of Substance, Planck, Redundant Constants, Soddy, Structural Constant

1. Introduction

In addition to general interest reaching scientific truth, another motive for publishing this article is finding the answer to Millikan’s question about the linearity of frequency ν and voltage V in the famous Einstein’s formula of the photoelectric effect, 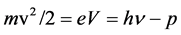, in which 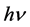is the energy absorbed by the electron from the light wave, p is the work necessary to get the electron out of the metal, 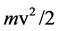is the energy with which it leaves the surface, h is known quantity introduced by Planck in 1900 [1] . It is shown here that the answer to this question can only be made in a wide range of measurement, at voltages up to several tens kV, and that these ranges at that time (from just a few volts) were too small, as for other researchers (E. Ladenburg, Verh. d. D. Phys. Ges. 9, 504, 1907), thus also for Millikan’s experiments. Finally, this paper shows that there is no linearity between ν and V. In fact, it can be taken as this linearity exists at low energies (of several eV), and certainly not at high energies (of tens keV). This issue deals with, among others, also several contemporary researchers [2] - [9] .

Planck’s h relates to the energy 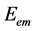of a photon to its frequency (ν) through the equation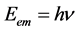. This means that Planck’s h is defined as the ratio

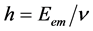. The American physicists William Duane and Franklin L. Hunt (1915), in the article “On X-Ray Wave-Lengths”, Physical Review [10] , give the maximum frequency 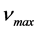at the edge of the continuous spectrum of X-rays that can be emitted by bremsstrahlung in an X-ray tube by accelerating electrons through an excitation voltage V into a metal target. Afterwards the numerous experiments of other physicists [11] - [16] pointed to the conclusion that the ratios 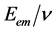of energy and frequency of photon are constant. Thus was declared Duane-Hunt law, 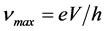, where 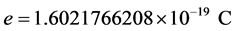is the elementary charge. This law is used to accurately determine Planck’s h. The three atomic constants, e, m and h are possible to measure with any real precision only in certain combinations, and the three simplest quantities that can thus be determined experimentally are e, e/m and h/e. R. T. Birge (1935) and J. W. M. DuMond (1939) have shown that there is an intolerable discrepancy of about 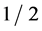to 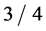of a percent between measuring and calculating the Rydberg constant determined according to Bohr’s formula,

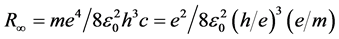, where 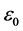is electric constant. Because of that DuMond even concludes: “the possibility of revealing an important modification of theory in this way is also present” [17] . My statistical analysis of the results of said experiments has shown that the ratio is not constant, i.e., Planck’s h is not constant [18] - [24] . Harmonious results between theory and measurements are obtained using relativity and one alternative law. The said law is found and used with the help of structural constant of atoms s₀ = 8.278692517066260, [20] [24] . This law gives (let’s call it so) an extended Duane-Hunt’s law [24] , Equation (55):

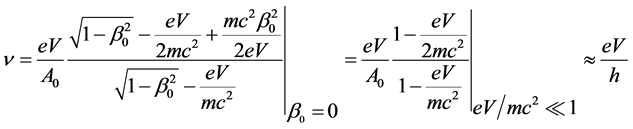, (1)

where 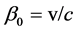is the ratio of initial velocity 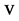of the electron in the atom which is located in the target; the speed of light in vacuum is

; is electron mass, and

(2)

stand for the action constant [24] , Equation (48), where is magnetic constant. The aforementioned alternative law we checked here using the form which provides access to NIST critically evaluated data on ground states and ionization energies of atoms and atomic ions [25] .

The continuous spectrum of bremsstrahlung can be explained from Equation (1) as a result of the continuity of the initial velocity of the electron in the atoms on the target, because any initial speed can completely continuously produce any of the frequencies in the spectrum within the specified power limits. More continuous distribution of frequencies we can get with the inclusion of the angle of incident rays (or electrons) and the position of the electrons in the target at the moment of collision, but this is not in detail analyzed here.

2. Energy Relations in the Atoms

The total mechanical energy E of an electron in an atom is the sum of its kinetic energy K, and its potential energy U [26] [27] :

. (3)

The kinetic energy of the electron, with mass m, moving at an arbitrary velocity is given by [27] :

. (4)

In [24] was found

, (5)

where Z is atomic number; is the maximum amount of the atomic number (theoretically it does not have to be an integer). Furthermore, in accordance with [22] represents electromagnetic properties of an atom (Z represents electrical properties and represents properties of the transmission (Lecher) line, which is a model of electromagnetic processes in an atom, with a detailed description in [22] . The most accurate account of, [24] , Equation (82), is from the expression:

, (6)

where eV is electrical or (by an amount equal to it) electromagnetic energy E_em required for ionization of atom.

Using Equations (4) and (5) we record the kinetic energy:

. (7)

We assume that the electron in an atom moves in a circular orbit. There is acceleration perpendicular to the direction of motion. With the Coulomb’s law applies [27] :

, (8)

or

, (9)

where r is the radius of curvature of the trajectory (in this particular case it is the radius of the circular orbit of the electron in atom), q = −e is electron charge, Q = Ze is the core charge,. Using Equation (9) and noting that an electron is of opposite charge of the nucleus, the potential energy of electron is [22] :

. (10)

Because of the law of conservation of energy, the part of it that is dissipated from the atom is electromagnetic energy E_em, which, on the other hand, is the amount equal to the total mechanical energy E of an electron, but with a negative sign [22] , which also represents the energy required for ionization of atoms eV:

. (11)

With Equation (5), Equation (11) gives (see Figure 1):

. (12)

3. Application of Structural Constant

Previous theoretical considerations and knowledge can be used for several different purposes. Here are three applications that are specifically enabled by the new findings, which enabled the discovery of structural constants of atoms and the existence of discrete states within the atom based on the existence of two separate periodic phenomenon in the atom, i.e., the circular motion of the electron around the nucleus and the formation of oscillating electromagnetic energy in the atom; (1), connection with neutrons and hyperons, (2), then enabling the determination of the new unit of measurement for the order of substance and finally, (3), shows the redundancy of several fundamental constants.

3.1. Connections of with the Neutrons and Hyperons

Stable states and discretization appear in the atom as a result of the harmonization of two different periodical processes; electromagnetic oscillations and the circular motion of electrons [18] [19] and [24] . Equation (13) extended to other states of atoms (not just to the first state, i.e., not just); read [24] , Equation (83):

, (13)

where stands for or for depending on whether the orbits are far or near to the atomic nucleus, respectively. On the first orbit (ground state, for) of the hydrogen atom is the greatest. Also in the second case, on the same first orbit (for) of the hydrogen atom is the lowest. On the first orbit (for) of the last hydrogen-like atoms, because of the impossibility of exceeding the

speed of light, is 1. This means that

. (14)

On the smallest orbit (for) of the hydrogen atom, for the same reason, i.e., because of the impossibility of exceeding the speed of light, is also 1. This means that

. (15)

From Equations (13) and (14) results:

. (16)

For example, by choosing discrete state we get

, (17)

. (18)

The mass M of hydrogen atom in the state of n = 1/126 is equal to the sum of the mass of the proton and the electron mass:

. (19)

This mass correspond to the mass of neutron (the difference is <0.0005%). Furthermore, according to Equations (9) and (13):

, (20)

where

(21)

stands as a mathematical abbreviation for the length L₀ of the world of atoms. For and Z = 1 L₀ is approximately equal to a Bohr radius a₀. If we take it as a unit of measurement of length and as a unit of measurement of speed, then the unit of measurement of time is

. (22)

Now is from Equation (20) and with Z = 1:

. (23)

According to the classical concept, Equation (23) is the orbital radius of the electron in the hydrogen, but this hydrogen due to the increased mass of the electron has a mass of neutron. As we see, in addition to well-known stable states there are those, previously unknown, that are below the ground state n = 1 (i.e.,). The stable states of atoms, that are below n = 1, seems to reveal and describe properties of other particles, for example neutron n⁰ and hyperons and, [20] , see Table 1 and Figure 1.

3.2. Order of Substance as the New Physical Quantity

There are currently 118 known elements with more than 3100 nuclides,

a. The mass corresponds to the mass of hydrogen (m_P + m = 938.272 + 0.511 = 938.783 MeV), 2014 CODATA, http://physics.nist.gov/constants. b. The mass corresponds to the mass of the neutron, 939.5654133 MeV, 2014 CODATA. http://physics.nist.gov/constants, [29] . c. The masses correspond to the masses of hyperon, 1115.683 MeV, and hyperon, 1314.83 MeV. https://en.wikipedia.org/wiki/Hyperon, [29] .

https://en.wikipedia.org/wiki/Table_of_nuclides. A nuclide is an atomic species characterized by the specific constitution of its nucleus, i.e., by its number of proton Z, its number of neutrons N, and its nuclear energy state. The number of protons Z within the atom’s nucleus is called atomic number and is equal to the number of electrons in the neutral (non-ionized) atom. Each atomic number Z identifies a specific element, but not the isotope; an atom of a given element may have a wide range in its number N of neutrons. The number of nucleons (both protons Z and neutrons N) in the nucleus is the atom’s mass number A = Z + N, and each isotope of a given element has a different mass number.

With such a large number of nuclides or isotopes, there is a need for their sorting, classification and marking with the use of today’s knowledge. There are also disputes between nuclide concept and isotope concept. Nuclide refers to a nucleus rather than to an atom, because identical nuclei belong to one nuclide, for example each nucleus of the carbon-15 nuclide is composed of 6 protons and 9 neutrons. The nuclide concept (referring to individual nuclear species) emphasizes nuclear properties over chemical properties, whereas the isotope concept (grouping all atoms of each element) emphasizes chemical over nuclear.

No arbitration between the two concepts, it is best to make a clean substrate, with that later these concepts can any self-build further its goals. The existence of isotopes was first suggested in 1913 by the radiochemist Frederick Soddy, who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions.

Since Frederick Soddy deal and chemistry and a nucleus of atoms, just his name connects both of these areas, isotopes and nuclides. So my suggestion is to recognize and accept the existence of a new physical quantity, named the order of substance, that is signified with Soddy’s name, S, so-called Soddy’s number, covering the whole substances with properties of atoms and their nuclei. Any physical quantity has its own unit of measurement. Because this is not only about counting, but it is a combination of different properties of atoms, as new quality, this current quantitative measurement unit (mole) is not suitable for expression of Soddy’s number. Soddy’s number requires a new unit of measurement. The idea is that each nuclide gets its own unique and easily definable number.

In this sense, can be used the knowledge of the maximum possible number of different atoms,. My proposal for the formation of Soddy’s number is as follows:

, (24)

where is the expected or projected maximum number of neutrons in the nucleus of each atom, and B is a new measurement unit of a physical quantity the order of substance, for which I propose the name “boscovich”, with the symbol “B”, in honor of Rogerio Boscovich, which 250 years ago was a forerunner of atomic physicists [28] . Soddy’s number, on one hand, must include all possible atoms and their nuclei. On the other hand, has to demonstrate that it can’t be exceeded (i.e., “one”, or 100%, in other words there is nothing outside of it). It means:

, (25)

this gives:

.(26)

It is estimated that number of neutrons in a nucleus certainly not exceeds one thousandth (and therefore we put). Thus, Equation (24) becomes:

. (27)

The Soddy’s number for the carbon, with Z = 6 and N = 7, for example, is:

. (28)

The Soddy’s number for vacuum (Z = 0, N = 0) is S_(0,0) = 0.000 B, for neutron, for hydrogen (protium), for hydrogen (deuterium), for mercury and for the last now known atom, Oganesson,. In this way we classified all existing atoms and associated nuclides, as well as those that will be discovered. This was achieved by introducing a new basic unit of measurement for physical size order of substance (see Table 2).

3.3. The Redundant Constants

After the discovery of structural constant of atoms and determining its amount (8.278692517066260), we can determine its relation to other physical quantities and constants. According to the amount we see immediately that

a. “boscovich” is a unit of order of substance amount B = 1/(2s₀² + 1) = 1/138.073499584258 = 0.0072425194046.

is associated with the fine-structure constant through the relation

. The difference in the amount of 0.027% with respect to 2014 CODATA (137.035999) is explicable by the fact that our data relates to a zero speed of the electron, and 2014 CODATA relates to the speed of electron on the Bohr radius. Also other such differences, in the same amount or multiples thereof, which will appear later on, refer to the same cause. But if h is equal to A₀ all these differences disappear.

If we share the action constant, expressed by Equation (2), with e², we get another constant, which is in amount equal to the von Klitzing constant h/e², with the same error 0.027% as in the previous case:

. (29)

Action constant has already been determined [24] , and we see that it can also be calculated in the following way:

. (30)

A point charge Q created at a distance r from the charge (relative to the potential at infinity, where this potential is calculated as a Zero) the electric potential difference:

, (31)

so that the potential energy U of the charge q, according to Equation (10), is

. (32)

When moving charge q (masses m) is on the potential then for its removal to infinity must be spent the work, where is different from V (i.e.,). Using Equations (20) and (31) we write

:

, (33)

whereas according to Equations (11) and (13) applies:

. (34)

From Equations (1), (5), (11) and (33) results [24] :

. (35)

If we divide Equation (35) with potential get the ratio of the two constants, that ratio is, of course, again a constant-let’s call them conversion constant, K₀, because it converts electrical potential (voltage) to frequency:

. (36)

The Equation (35) we can now write with the help of Equation (36):

. (37)

The Equation (37) has the same shape as the equation of the frequencies in the alternating-current Josephson effect, () U_DC,

https://en.wikipedia.org/wiki/Josephson_effect, where is the Josephson’s constant, while U_DC is the potential difference at the superconducting junction, analogous to the above-mentioned potential difference within the atom. Therefore, using Equation (36) we find:

. (38)

From [18] , Equation (70), comes

, (39)

where is Rydberg constant. This constant, with

, and the use of Equation (2), takes the form:

. (40)

Using Equations (13) and (20) the magnetic dipole moment [26] associated with an electron orbit is given by

, (41)

where I is the electric current and A is the area of the loop, and T is the time required for one orbit (see Table 3).

a. Difference value in relation to the Committee on Data for Science and Technology, 2014 CODATA. b. Here σ is the structural coefficient of transmission (Lecher) lines representing the electromagnetic oscillator in an atom [19] and Z is atomic number. c. This formula is derived in [30] . d. The difference disappears if true.

4. Conclusions

With the current measurement results and with the appropriate theory, Duane- Hunt law which includes Planck’s h has been tested. Using 120 measurements in the range of 13.6 eV to 204.4 keV, i.e., in the range 1:15000, we conclude that Planck’s h is not constant. The results presented here confirm that Planck’s h is approximately constant in the energy range from a few eV, but for energy over a dozen keV h becomes significantly smaller and decreases to zero. That conclusion has been confirmed by statistical analysis of old measurement results from a century ago as well. So far, there was no suitable theory that could explain it, but now this theory exists and it is in accordance with both the old and the new measurements. With this theory it is possible to determine some phenomena in the nucleus of the atom. This theory also shows that the maximum possible atomic number Z is equal to the integer of 2, i.e., 137. Also, the proposal for a new measurement unit for the order of substance, “boscovich”, B, has been introduced. At the end, it can be shown that by using structural constants s₀ 11 different previous fundamental constants are redundant, including Planck’s h. Interrelationships among all these constants exist, and therefore it is possible to unite the manner described.

Further work in this area should include the study of possible stable states of atoms in states below the ground state with the expectation, in addition to the neutron and hyperons, some other particles could be found.

In this article, the voltage to 204.4 kV (Z = 110, darmstadtium) has been covered. The future research should broaden that range to 511 kV. In that process not only the voltage, but also corresponding frequency should be measured.

This article explains the continuous spectrum of bremsstrahlung. The formula for calculating the frequency of this radiation has been shown.

The work is based on the use of Maxwell’s equations and Einstein’s theory of relativity and the use of real oscillators, instead of Planck’s virtual oscillators. The quantization is only a consequence of harmonizing two continuous processes in the atom: the propagation of electromagnetic energy and the circular motion of electrons [18] [24] .

Acknowledgements

The author thanks to Ms. Srebrenka Ursić and Mr. Damir Vuk,

www.systemcom.hr, for useful discussions, to Mr. Branko Balon for the useful discussions, too, to Mr. Velibor Ravlić and Mr. Zlatko A. Voloder for encouragement in the writing this article and for expressing great expectations in benefits of using structural constants s₀ instead of Planck’s h, then to Prvomajska TZR, Ltd., Zagreb, Croatia, www.prvomajska-tzr.hr, and to Drives-Control, Ltd., Zagreb, Croatia, www.drivesc.com, for logistic support.

Cite this paper

Perkovac, M. (2017) Planck’s h and Structural Constant s₀. Journal of Modern Physics, 8, 425-438. https://doi.org/10.4236/jmp.2017.83027

References