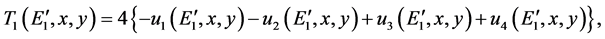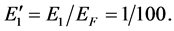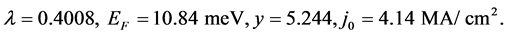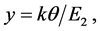Journal of Modern Physics
Vol.08 No.01(2017), Article ID:73753,11 pages
10.4236/jmp.2017.81009
A Detailed Study of the Role of Fermi Energy in Determining Properties of Superconducting NbN
G. P. Malik1,2
1School of Environmental Sciences, Jawaharlal Nehru University, New Delhi, India
2Present Address: B 208 Sushant Lok 1, Gurgaon, Haryana, India

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 27, 2016; Accepted: January 20, 2017; Published: January 23, 2017
ABSTRACT
The recent concern with the role of Fermi energy (EF) as a determinant of the properties of a superconductor (SC) led us to present new EF-dependent equations for the effective mass (m*) of superconducting electrons, their critical velocity, number density, and critical current density, and also the results of the calculations of these parameters for six SCs the Tcs of which vary between 3.72 and 110 K. While this work was based on, besides an idea due to Pines, equations for Tc and the gap at T = 0 that are explicitly EF-dependent, it employed an equation for the dimensionless construct 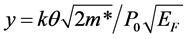 that depends on EF only implicitly; k in this equation is the Boltzmann constant, θ is the Debye temperature, and P0 is the critical momentum of Cooper pairs. To meet the demand of consistency, we give here derivation of an equation for y that is also explicitly EF-dependent. The resulting framework is employed to (a) review the previous results for the six SCs noted above and (b) carry out a study of NbN which is the simplest composite SC that can shed further light on our approach. The study of NbN is woven around the primary data of Semenov et al. For the additional required inputs, we appeal to the empirical data of Roedhammer et al. and of Antonova et al.
that depends on EF only implicitly; k in this equation is the Boltzmann constant, θ is the Debye temperature, and P0 is the critical momentum of Cooper pairs. To meet the demand of consistency, we give here derivation of an equation for y that is also explicitly EF-dependent. The resulting framework is employed to (a) review the previous results for the six SCs noted above and (b) carry out a study of NbN which is the simplest composite SC that can shed further light on our approach. The study of NbN is woven around the primary data of Semenov et al. For the additional required inputs, we appeal to the empirical data of Roedhammer et al. and of Antonova et al.
Keywords:
EF-Incorporated Equations for Tc, 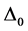 , and
, and  of a Superconductor, NbN
of a Superconductor, NbN

1. Introduction
Some of the recent studies [1] - [7] concerned with high-Tc superconductors (SCs) have been motivated by the belief that Fermi energy (EF) plays an important role in determining their Tcs and gap-structures. These studies make it natural to ask: why not incorporate EF (equivalently, chemical potential μ) into the equations for the Tc and the gap 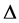 of an SC, and then treat it as an independent variable? This is a departure from the usual practice because these parameters are conventionally calculated via equations sans EF because of the assumption
of an SC, and then treat it as an independent variable? This is a departure from the usual practice because these parameters are conventionally calculated via equations sans EF because of the assumption
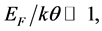 (1)
(1)
where k is the Boltzmann constant and 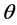 is the Debye temperature.
is the Debye temperature.
The proposed approach requires, besides the values of Tc and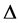 , another property of the SC in order to determine EF. Upon choosing critical current density
, another property of the SC in order to determine EF. Upon choosing critical current density 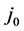 of the SC, new equations for both elemental and composite SCs valid at T = 0 were recently presented in [8] for j0 and the following of their properties: m*,
of the SC, new equations for both elemental and composite SCs valid at T = 0 were recently presented in [8] for j0 and the following of their properties: m*, 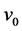 , and ns, which denote, respectively, the effective mass of superconducting electrons, their critical velocity at which
, and ns, which denote, respectively, the effective mass of superconducting electrons, their critical velocity at which 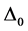 vanishes, and the density of superconducting electrons. While the results of such a study for Sn, Pb, MgB2, YBCO, Bi-2212, and Tl-2212 were also reported in [8] , it was based on, unlike the equations for
vanishes, and the density of superconducting electrons. While the results of such a study for Sn, Pb, MgB2, YBCO, Bi-2212, and Tl-2212 were also reported in [8] , it was based on, unlike the equations for 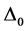 and Tc, an equation for the dimensionless construct
and Tc, an equation for the dimensionless construct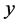 , defined below, that is dependent on EF only implicitly.
, defined below, that is dependent on EF only implicitly.
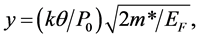 (2)
(2)
where m*, P0, and EF are in units of electron volts.
To meet the demand of consistency, we present here the derivation of a new equation for 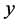 that also contains EF explicitly―to put it on par with the equations for Tc and
that also contains EF explicitly―to put it on par with the equations for Tc and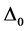 . While this leads us to review our earlier results, we also undertake here a detailed study of the superconducting properties of NbN because:
. While this leads us to review our earlier results, we also undertake here a detailed study of the superconducting properties of NbN because:
(i) It is the simplest composite SC different samples of which (a) have been fabricated by the same method of preparation, (b) are geometrically similar, but (c) differ in size (e.g., film thickness), and for which (d) data in the form 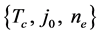 are available, where ne is the density of conduction electrons. This is unlike the composite SCs dealt with earlier, which were not necessarily fabricated by the same method of preparation and for which the values of
are available, where ne is the density of conduction electrons. This is unlike the composite SCs dealt with earlier, which were not necessarily fabricated by the same method of preparation and for which the values of 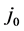 and ne were not available. We were then led to estimate the values of
and ne were not available. We were then led to estimate the values of 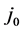 for these SCs from the data at T = 4.2 K. Given the values of Tc and ne for NbN, we can now also shed light on the ratio
for these SCs from the data at T = 4.2 K. Given the values of Tc and ne for NbN, we can now also shed light on the ratio 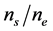
(ii) Since the value of the highest Tc reported for it in [9] is 15.25 K, it is the simplest composite SC for which we believe one-phonon exchange mechanism (OPEM) to be operative. This is unlike, e.g., MgB2 for which, given its Tc, we need to invoke the two- phonon exchange mechanism (TPEM).
(iii) The above features make NbN the simplest testing ground for some key steps of our approach, such as the procedure followed for resolving θNbN into θNb and θN.
The paper is organized as follows. In Section 2 are reproduced from [8] those equations that constitute our framework in the OPEM scenario, which may be defined as one in which the Tc of an SC can be accounted for by a value of the interaction parameter 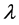

2. EF-Incorporated Equations for Various Properties of an SC
Recalled below from [8] are some of the equations that we need for NbN. In these equations 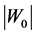
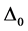


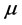
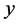
Equation for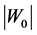
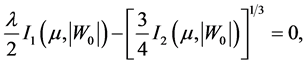
where

and
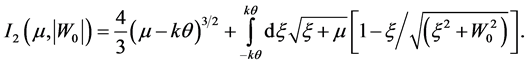
Equation for Tc:

where
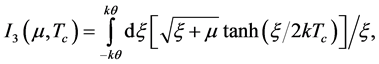
and

In the above equations

After 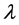
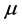
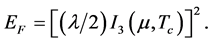
Equation for y:
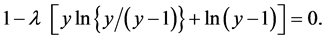
This equation has been obtained by assuming that

where
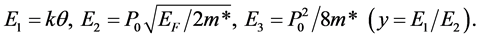
Equation for j0(EF):
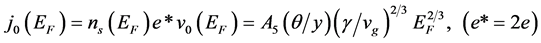
where
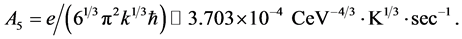
3. The Modified Equation for y in the OPEM Scenario
Equation (11) has been derived in [10] (pp. 115-120) by assuming Inequality (1). In order to do away with this inequality, we begin here with the following equation for moving CPs because the present derivation differs from the earlier one only beyond it.
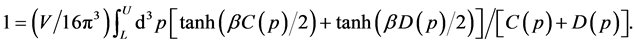
In this equation
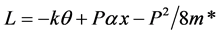

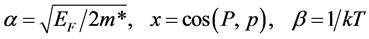


Equation (16) was obtained via a Bethe-Salpeter equation. It seems interesting to point out that when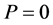
The equation for the critical momentum 
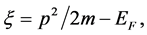

where

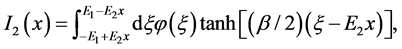

and we have used (9), (13) and (19). Besides, justification to follow, we have dropped E3 everywhere except in the denominator of (25) in order to avoid the singularity at

In order to obtain the 



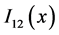










Because the constituents of both 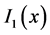
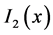
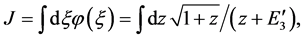
where we have used (25), put 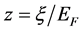
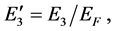
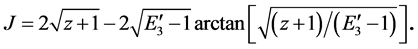
Therefore, for 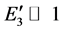

Taking into account the overall sign of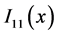

where 


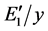


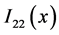
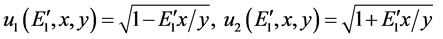

Then substituting 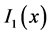
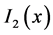
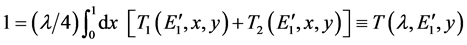
where
and 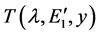
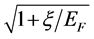
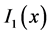
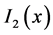
obtain. It generalizes (11) which was obtained without this factor. While we could earlier solve (11) in the OPEM scenario with the input of 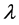
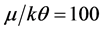
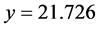
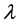
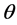
4. Study of NbN Based on EF-Incorporated Equations
4.1. Outline of Procedure
Working in the OPEM scenario, we
(A) Solve. (6) with the input of θ and Tc to determine 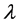

(B) Solve (32) to obtain the values of 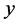
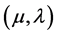
(C) Calculate 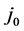
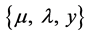
As predictions, this process also yields the values of m*, ns, and 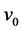



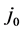
Before we can proceed as above, we need to fix the Debye temperature of the ions that cause pairing in NbN, i.e., θNb.
4.2. Debye Temperature of Nb Ions in NbN
θNbN is not quoted in [9] . The reported values for it vary in the range 250 - 335 K [13] [14] [15] [16] . We begin by adopting [13]
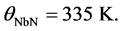
We now need to resolve θNbN into θNb and θN, which must be different because masses of Nb and N ions are different. As in [8] , we do so via the following equations
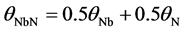
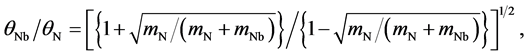
where 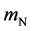

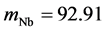
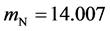
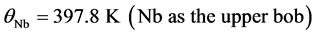

the corresponding values for θN being 272.2 and 564.3 K (which we do not need). In the following we shall perform all calculations with both the above values of θNb.
4.3. Choosing the Values of Tc for Which the Data in [9] Are Addressed
In [9] , while values of Tc varying between 9.87 and 15.25 K have been reported for 13 samples of NbN for which the values of 
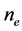
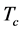

4.4. A Consistency Check of (6)
If we solve the usual BCS equation for Tc (i.e., the equation sans EF) with θ = 105.7 (397.8 K) and Tc = 10.72 K, we obtain λ = 0.4142 (0.2682). These are precisely the values we obtain via (6) for the same values of Tc and θ and the additional input of μ (or EF) = 100 kθ for each value of θ being considered. Note that 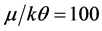

4.5. Fixing Additional Required Inputs
Having fixed the values of θNb and Tc, we can carry out steps (A) and (B) spelled out in Section 4.1; to carry out step (C) we additionally need the values of γ and the cell parameters of different samples of NbN, which are not given in [9] . We fix these by appealing to the data in [13] . A summary of all the inputs required for this study is given in Table 1. Based on the data in [17] , this table includes the estimated values of 
4.6. Results
For each of the three values of Tc and both the values of θNb noted above, we carried out steps (A)-(C) noted in Section (4.1) for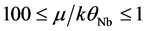
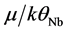

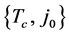

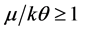

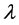
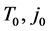
Table 1. Experimental values of 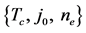
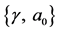
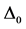
Table 2. Results of calculations for θNb = 105.7 K. The value of 
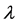



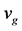
We now take up the results following from θNb = 397.8 K. The least permissible value of μ corresponding to it, i.e., 

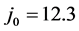
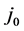



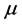
Since this value of 
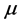
Our considerations so far have been based on the derived values of θNb from θNbN = 335 K. In order to find if there is a lower limit on the value of θNb, we now report our findings based on the values of θNb derived from the lowest value of θNbN that was noted above, i.e., 250 K. This value leads via (34) and (35) to θNb = 296.8 (Nb as the upper bob) and θNb = 78.9 K (Nb as the lower bob). Since the former of these values exceeds the upper limit noted above, we did not pursue it any further. For the latter value, we obtained for any assumed value of
Because both these values of 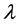
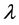
Above considerations raise the question: Could 
Given in Table 3 are the predicted values of various parameters concomitant with
Table 3. With θNb = 105.7 K, predicted values of various parameters of NbN that are concomitant with the calculated values of 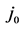
Notes: (i) The equations employed for the calculation of the above parameters have been derived in [8] and are as follows: 
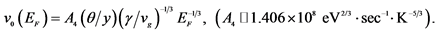
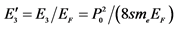
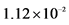

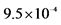
the experimental values of Tc and 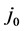
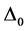
5. A Review of the Results Obtained in [8] in View of the Modified Equation for y
For Sn and Pb, all our earlier results remain unchanged because solution of (32) for these elements yields the same values for 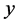
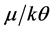

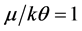

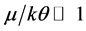
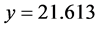
For each of the high-Tc SCs dealt with in [8] , there are two


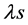

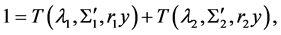
where 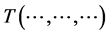


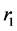


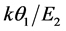
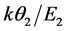
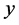
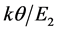
Equation (38) generalizes (32) to the TPEM scenario; because it explicitly contains EF as a variable, it is also a generalized version of equation (30) in [8] . Upon solving (38) with the input of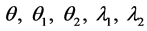
6. Discussion
In connection with fixing θNb, we recall that Debye temperature is just another way to specify Debye frequency; it is not to be confused with thermodynamic temperature. We now note that, based on neutron powder diffraction experiments, different values of Debye temperature for the constituents of anisotropic LCO have been reported [19] . This lends support to the idea that the Debye temperature of a composite SC needs to be “resolved.” The results reported here depend only on the value of θNb, for the identification of which we have simply employed (34) and (35) as a vehicle.
Among the five variables that determine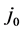
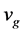
7. Conclusions
The main results of this paper are: (i) a new EF-dependent equation for the dimensionless construct 

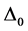

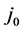
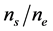
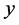

The work reported here is continuation of an attempt to find via theory tangible clues about raising the Tcs of composite SCs. The role of experiment in this quest can hardly be over-emphasized. While huge amounts of such data about hundreds of SCs are now available, we have not come across a single composite SC for which all the relevant parameters identified here, i.e., θ, Tc, 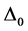
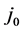
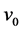
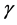

We conclude by noting that the derivations of most of the equations employed in this paper and the concepts on which they are based, e.g., multiple Debye temperatures, superpropagator, and the Bogoliubov constraint, can be found at one place in [10] .
Acknowledgements
The author thanks Dr. A. Semenov for kindly responding to his queries concerned with the experimental data reported in [9] , and Professor D.C. Mattis for encouragement.
Cite this paper
Malik, G.P. (2017) A Detailed Study of the Role of Fermi Energy in Determining Properties of Superconducting NbN. Journal of Modern Physics, 8, 99-109. http://dx.doi.org/10.4236/jmp.2017.81009
References
- 1. Lee, D. (2012) Nature Physics, 8, 364-365.
- 2. Zhang, Y., et al. (2012) Nature Physics, 8, 371-375.
- 3. Allan, M.P., et al. (2012) Science, 336, 563-567.
https://doi.org/10.1126/science.1218726 - 4. Lin, X, Zhu, Z., Fauqué, B. and Behnia, K. (2013) Physical Review X, 3, 021002.
https://doi.org/10.1103/PhysRevX.3.021002 - 5. Alexandrov, A.S. (2001) Physica C: Superconductivity, 363, 231-236.
https://doi.org/10.1016/S0921-4534(01)01095-4 - 6. Jarlborg, T. and Bianconi, A. (2013) Physical Review B, 87, 054514.
https://doi.org/10.1103/PhysRevB.87.054514 - 7. van der Marel, D., van Mechelen, J.L.M. and Mazin, I.I. (2011) Physical Review B, 84, 205111.
https://doi.org/10.1103/PhysRevB.84.205111 - 8. Malik, G.P. (2016) Journal of Superconductivity and Novel Magnetism, 29, 2755-2764.
- 9. Semenov, A., et al. (2009) Physical Review B, 80, 054510.
https://doi.org/10.1103/PhysRevB.80.054510 - 10. Malik, G.P. (2016) Superconductivity: A New Approach Based on the Bethe-Salpeter Equation in the Mean Field Approach. World Scientific, Singapore.
https://doi.org/10.1142/9868 - 11. Thouless, D.J. (1960) Perturbation Theory in Statistical Mechanics and the Theory of Superconductivity. Annals of Physics, 10, 553-588.
https://doi.org/10.1016/0003-4916(60)90122-6 - 12. Nozières, P. and Schmitt-Rink, S. (1985) Bose Condensation in an Attractive Fermion Gas: From Weak to Strong Coupling Superconductivity. Journal of Low Temperature Physics, 59, 195-211.
https://doi.org/10.1007/BF00683774 - 13. Roedhammer, P., Gmelin, E., Weber, W. and Remeika, J.P. (1977) Observation of Phonon Anomalies in NbCxN1-x Alloys. Physical Review B, 15, 711-717.
https://doi.org/10.1103/PhysRevB.15.711 - 14. Geballe, T.H., et al. (1966) High-Temperature SP-Band Superconductors. Physics, 2, 293-310.
- 15. Pellan, Y., Dousselin G., Pinel, J. and Sohn, Y.U. (1990) Temperature and Magnetic Field Dependence of NbN Film Resistivity: 3D Weak Localization Effects. Journal of Low Temperature Physics, 78, 63-77.
https://doi.org/10.1007/BF00682110 - 16. Geibel, C., Rietschel, H., Junod, A., Pelizzone M. and Muller, J. (1985) Electronic Properties, Phonon Densities of States and Superconductivity in Nb1-xVxN. Journal of Physics F: Metal Physics, 15, 405-416.
https://doi.org/10.1088/0305-4608/15/2/014 - 17. Antonova, E.A., Dzhuraev, D.R., Motulevich, G.P. and Sukhov, V.A. (1981) Superconducting Energy Gap of Niobium Nitride. Journal of Experimental and Theoretical Physics, 53, 1270-1271.
- 18. Malik, G.P. (2015) A Study of Heavy-Fermion Superconductors via BCS Equations Incorporating Chemical Potential. Journal of Modern Physics, 6, 1233-1241.
https://doi.org/10.4236/jmp.2015.69128 - 19. Kwei, G.H., Lawson, A.C. and Mostoller, M. (1991) Vibrational Properties and Atomic Debye Temperature for La2CuO4 from Neutron Powder Diffraction. Physica C: Superconductivity, 175, 135-142.
https://doi.org/10.1016/0921-4534(91)90244-S