ABSTRACT

In view of the properties of mesons in hot strongly interacting matter, the properties of the solutions of the truncated Dyson-Schwinger equation for the quark propagator at finite temperatures within the rainbow-ladder approximation are analysed in some detail. In Euclidean space within the Matsubara imaginary time formalism, the quark propagator is not longer a O(4) symmetric function and possesses a discrete spectrum of the fourth component of the momentum. This makes the treatment of the Dyson-Schwinger and Bethe-Salpeter equations conceptually different from the vacuum and technically much more involved. The question whether the interaction kernel known from vacuum calculations can be applied at finite temperatures remains still open. We find that, at low temperatures, the model interaction with vacuum parameters provides a reasonable description of the quark propagator, while at temperatures higher than a certain critical value 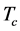the interaction requires stringent modifications. The general properties of the quark propagator at finite temperatures can be inferred from lattice QCD (LQCD) calculations. We argue that, to achieve a reasonable agreement of the model calculations with that from LQCD, the kernel is to be modified in such a way as to screen the infra-red part of the interaction at temperatures larger than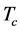. For this, we analyse the solutions of the truncated Dyson-Schwinger equation with existing interaction kernels in a large temperature range with particular attention on high temperatures in order to find hints to an adequate temperature dependence of the interaction kernel to be further implemented in the Bethe-Salpeter equation for mesons. This will allow investigating the possible in medium modifications of the meson properties as well as the conditions of quark deconfinement in hot matter.

Keywords:

Dyson-Schwinger, Bethe-Salpeter Equations, Rainbow Ladder Truncation, Quark Propagator, Chiral Symmetry

1. Introduction

The description of mesons as quark-antiquark bound states within the framework of the Bethe-Salpeter (BS) equation with momentum dependent quark mass functions, determined by the Dyson-Schwinger (DS) equation, is able to explain successfully many spectroscopic data, such as meson masses [1] - [7] , electromagnetic properties of pseudoscalar mesons and their radial excitations [8] [9] [10] and other observables [10] - [17] . Contrary to purely phenomenological models, like the quark bag model, such a formalism maintains important features of QCD, such as dynamical chiral symmetry breaking, dynamical quark dressing, requirements of the renormalization group theory etc., cf. Ref. [18] . The main ingredients here are the full quark-gluon vertex function and the dressed gluon propagator, which are entirely determined by the running coupling and the bare quark mass parameters. In principle, if one were able to solve the Dyson-Schwinger equation, the approach would not depend on any additional parameters.

However, due to known technical problems, one restricts oneself to calculations within effective models which specify the dressed vertex function 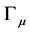and interaction kernel. The rainbow-ladder approximation [2] is a model with rainbow truncation of the vertex function in the quark DS equation and a specification of the dressed quark-quark interaction kernel as. (Here, 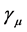is a Dirac gamma matrix and 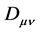stands for the gluon propagator; g is the coupling strength and k denotes a momentum.)

The model is completely specified once a form is chosen for the effective coupling. The ultraviolet behavior is chosen to be that of the QCD running coupling; the ladder-rainbow truncation then generates the correct perturbative QCD structure of the DS and BS equations. Moreover, the ladder-rainbow truncation preserves such an important feature of the theory as the maintenance of the Nambu- Goldstone theorem in the chiral limit, according to which the spontaneous chiral symmetry breaking results in an appearance of a (otherwise absent) scalar term in the quark propagator of the DS equation. As a consequence, in the BS equation a massless pseudoscalar bound state should appear. By using the Ward identities, it has been proven (see, e.g. Refs. [19] [20] [21] ) that in the chiral limit the DS equation for the quark propagator and the BS equation for a massless pseudo-scalar in ladder approximation are completely equivalent. It implies that such a massless bound state (pion) can be interpreted as a Goldstone boson. This results in a straightforward understanding of the pion as both a Goldstone boson and quark-antiquark bound state.

Another important property of the DS and BS equations is their explicit Poincaré invariance. This frame-independency of the approach provides a useful tool in studying processes when a rest frame for mesons cannot or needs not be defined.

The merit of the approach is that, once the effective parameters are fixed (usually the effective parameters of the kernel are chosen, cf. Ref. [22] [23] , to reproduce the known data from lattice calculations, such as the quark mass function and/or quark condensate), the whole spectrum of known mesons is supposed to be described, on the same footing, including also excited states. The achieved amazingly good description of the mass spectrum with only few effective parameters encourages one to employ the same approximations to the truncated Dyson-Schwinger (tDS) and truncated Bethe-Salpeter (tBS) equations also at finite temperatures with the hope that, once an adequate description of the quark propagators at non-zero temperature (T) is accomplished, the corresponding solution can be implemented in to the BS equation for mesons to investigate the meson properties in hot and dense matter.

At low temperatures the properties of hadrons in nuclear matter are expected to change in comparison with the vacuum ones, however the main quantum numbers, such as spin and orbital momenta, space and inner parities etc. are maintained. The hot environment may modify the hadron masses, life time (decay constant) etc. Contrarily, at sufficiently large temperature in hot and dense strongly interacting matter, phase transitions may occur, related to quark deconfinement phenomena, as e.g. dissociation of hadrons in to quark degrees of freedom. Therefore, these temperature regions are of great interest, both from a theoretical and experimental point of view. Hitherto, the truncated DS and BS formalism has been mostly used at large temperatures to investigate the critical phenomena near and above the pseudo-critical and (phase) transition values predicted by lattice simulation data (cf. Refs. [24] [25] [26] [27] and and references therein quoted). It has been found that, in order to achieve an agreement of the model results with lattice data, a modification of the vacuum interaction kernel is required. Namely, the infra-red term has to vanish abruptly in this region. Accordingly, it has been suggested [24] [25] to employ a kernel with a Heavyside step-like behaviour in the vicinity of the (pseudo-)critical temperature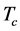. Then, it becomes possible to achieve a rather reliable description of such quantities as the quark spectral function, plasmino modes, thermal masses etc., see also Ref. [28] . However, a use of such a discontinuously modified interaction in the BS equation in the whole temperature range becomes hindered. Another strategy of solving the DS equation in a larger interval of temperatures is to utilize directly the available LQCD results to fit, point by point, the interaction kernel at given temperatures. In such a way one achieves a good description of the quark mass function and condensate for different temperatures, including the region beyond [29] [30] . The success of such approaches demonstrates that the rainbow approximation to the DS equation with a proper choice of the interaction kernel is quite adequate in understanding the properties of quarks in hot environment. Nevertheless, for systematic studies of quarks and hadrons within the BS equation, on needs a smooth parametrization of the kernel in the whole interval of the considered temperatures. In view of still scarce LQCD data, such a direct parametrization from “experimental” data is problematic. An alternative method is to solve simultaneously a (truncated) set of Dyson-Schwinger equations for the quark and gluon propagators within some additional approximations [31] . This approach also provides good description of quarks in vicinity of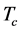, however it becomes too cumbersome in attempts to solve the BS equation, since in this case one should solve a too large system of equations. It should also be noted that there are other investigations of the quark propagator within the rainbow truncated DS equation, which employ solely the vacuum parameters in calculations of T-dependencies of quarks [32] without further attempts to accommodate the kernel to LQCD results. As a result one finds that the critical behaviour of the propagators (e.g. chiral symmetry restoration) starts at temperatures much smaller than the ones expected from LQCD.

In the present paper we are interested in a detailed investigation of the quark propagator in the whole range of temperatures, from zero temperatures up to above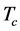, and find a reliable smooth parametrization of the kernel. We start with the interaction kernel known at and extend it, step by step, to larger temperatures by finding the prerequisites to meet the requirements of the LQCD and to be able to implement the kernel into the BS equation in subsequent studies of the hadron bound states at finite temperatures.

In quantum field theory, a system embedded in a heat bath can be described within the imaginary-time formalism, known also as the Matsubara approach [33] [34] [35] . Due to finiteness of the heat bath temperature T the Fourier transform to Euclidean momentum space becomes discrete, resulting in a discrete spectrum of the energy, known as the Matsubara frequencies. Consequently, the interaction kernel and the DS solution become also discrete with respect to these frequencies. Moreover, since the heat bath already fixes a particular frame, the corresponding DS and BS equations are not longer symmetric. This requires a separate treatment of the transversal and longitudinal parts of the kernel with the need of an additional function in parametrizing the quark propagators. All this makes the consideration of the DS equation different from the vacuum case. However, here is the hope that the phenomenological interaction kernel defined at 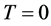can be, to some extent, applied for finite temperatures as well.

In the present paper we investigate the prerequisites to the interaction kernel of the DS formalism at finite temperatures to be able to investigate, in a subsequent step, different processes with the challenging problem of changes of meson characteristics at finite temperatures. Our goal is to determine with what extend the rainbow truncation of the DS equation is applicable in a large interval of temperature, starting from low values, with the effective parameters, known to accomplish an excellent description of the hadron properties in vacuum, towards temperatures above the critical values predicted by lattice calculations. We try to find a proper modification of the kernel at higher temperatures to be able to describe the properties of the quark propagator in the whole temperature range. A reliable parametrization of the T-dependence will allow to implemented it directly into the BS equation in the same manner as at 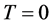and to investigate, e.g. in-medium changes of mesons in hot environment. This is crucial, e.g. in understanding the di-lepton yields in nucleus-nucleus collisions. Our future goal is to investigate to what extend the effective parameters, known to accomplish an excellent description of the hadron properties in vacuum, can be utilized in the BS equation to investigate the hadron modifications in hot and dense matter below and above the critical or cross-over temperature. For this we consider the quark propagators from the DS equation in a large temperature range and investigate their properties and compare qualitatively with other approaches, such as the LQCD calculations.

Our paper is organized as follows. In Section 2, we recall the truncated BS and DS equations in vacuum and at finite temperatures. The rainbow approximation for the DS equation kernel in vacuum is introduced and the system of equations for the quark propagator, to be solved at finite temperature, is presented. Numerical solution for the chirally symmetric case is discussed in Section 3, where the chiral quark condensate and spectral representation for the quark propagator are introduced. It is found that, to achieve a reasonable behaviour of the spectral functions above the critical temperature, a modification of the interaction kernel is needed. In Section 4, we consider the solution of the truncated DS equation for finite bare masses. The inflection points of the quark condensate and the mass function are considered as a definition of the pseudo-critical temperature at finite quark masses. The procedure of regularization of integrals in calculating the quark condensate from the solution of the DS equation is discussed in some detail. It is shown that, for finite quark masses, the inflection method determines the pseudo critical temperatures by ~50% smaller than the ones obtained by other approaches, e.g. by lattice QCD calculations. The possibility to reconcile the model and lattice QCD results is considered too. The impact of the infrared term in the interaction kernel in the vicinity and above the critical temperature is also briefly discussed. Summary and conclusions are collected in Section 6. A brief explanation of the meaning of the rainbow-ladder approxiamtion is presented in the Appendix.

2. Basic Formulae

2.1. Dyson-Schwinger and Bethe-Salpeter Equations in Vacuum

¹Usually, for quarks of masses the partitioning parameters are chosen as. However, in general the BS solution is independent of the choice of.

To determine the bound-state mass of a quark-antiquark pair one needs to solve the DS and the homogeneous BS equations, which in the rainbow ladder approximation and in Euclidean space read

(1)

(2)

where and are the partitioning parameters defining the quark momenta as with P and k denoting the total and relative momenta of the bound system, respectively;¹ stands for the BS vertex function being a matrix, and are the propagators of bare and dressed quarks, respectively with mass parameter m and the dressing functions and. In Euclidean space we use the Hermitian matrices which obey the anti-commutation relation; for the four-product one has. The masses M of mesons as bound states of a m₁-quark and m₂-antiquark follow from the solution of BS equation, , in specific channels, with the solution of the DS Equation (1) as input into the calculations in Equation (2). The interaction between quarks in the pair is encoded in imagined as gluon exchange. For consistency, the same interaction is to be employed in the DS Equation (1) for the inverse dressed quark propagator.

Often, the coupled equations of the quark propagator S, the gluon propagator and the quark-gluon vertex function, all with full dressing (and, if needed, supplemented by ghosts and their respective vertices), are considered as an integral formulation being equivalent to QCD. In practice, due to numerical problems, the finding of the exact solution of the system of coupled equations for can hardly be accomplished and therefore some approximations [5] [17] [18] are appropriate. Note that we must know the form of and, not only in the ultraviolet range, where perturbation theory is applicable, but also in the infra-red range, where perturbation theory fails and lattice simulations are to be corrected for finite-volume effects. and satisfy DS equations. However, studies of these equations in QCD are rudimentary and are presently used only to suggest qualitatively reliable ansätze for these functions. That is why the quantitative studies of the quark DS equation to date have employed model forms of the gluon propagator and quark-gluon vertex. Leaving a detailed discussion of the variety of approaches in dressing of the gluon propagator and vertex function in DS equations (see e.g. Refs. [40] [41] and references therein quoted) we mention only that in solving the DS equation for the quark propagator one usually employs truncations of the exact interactions and replaces the gluon propagator combined with the vertex function by an effective interaction kernel. This leads to the truncated Dyson-Schwinger equation for the quark propagator which may be referred to as the gap equation. In explorative calculations, the choice of the form of the effective interaction is inspired by results from calculations of Feynman diagrams within pQCD maintaining requirements of symmetry and asymptotic behaviour already implemented, cf. Refs. [5] [10] [18] [41] . The results of such calculations, even in the simplest case of accounting only for one-loop diagrams with proper regularization and renormalization procedures, are rather cumbersome for further use in numerical calculations, e.g. in the framework of BS or Faddeev equations. Consequently, for practical purposes, the wanted exact results are replaced by suitable parametrizations of the vertex and the gluon propagator. Often, one employs an approximation which corresponds to one-loop calculations of diagrams with the full vertex function, substituted by the free one, (we suppress the color structure and account cumulatively for the strong coupling later on). To emphasize the replacement of combined gluon propagator and vertex we use the notation, where an additional power of g from the second undressed vertex is included.

2.2. Choosing an Interaction Kernel

Note that the nonperturbative behaviour of the kernel at small momenta, i.e. in the infra-red (IR) region, nowadays is not uniquely determined and, consequently, suitable models are needed. In principle, constraints on the infra-red form of the kernel can be sought from studies of the DS equations with the fully dressed gluon propagator, , and the dressed gluon-quark vertex. However, there is almost no information available from DS equation studies; the gluon propagator itself has been often studied via the gap equation, and from such studies one can merely qualitatively conclude that the gluon propagator is enhanced in the infra-red. There are several ansätze in the literature for the IR kernel, which can be formally classified in the two groups: i) the IR part is parametrized by two terms―a delta distribution at zero momenta and an exponential, i.e. Gaussian term, and ii) only the Gaussian term is considered. In principle, the IR term must be supplemented by a ultraviolet (UV) one, which assures the correct asymptotics at large momenta. A detailed investigation [7] [42] of the interplay of these two terms has shown that, for bound states, the IR part is dominant for light (u, d and s) quarks with a decreasing role for heavier (c and b) quark masses for which the UV part may be quite important in forming mesons with masses as bound states. In the vacuum, if one is interested in an analysis of light mesons with, the UV term can be omitted. This is not the case for finite temperatures (T) where one can expect that at sufficiently large T some phase transition can occur and/or quark dissociation of mesons into quark degrees of freedom in hot matter. In such a temperature range, the IR term is expected to be screened [24] [25] and, consequently, the perturbative UV behaviour can become important even for light mesons.

Following examples in the literature [2] [5] [9] [10] [12] [16] the interaction kernel in the rainbow approximation in the Landau gauge is chosen as

(3)

where the first term originates from the effective IR part of the interaction determined by soft, non-perturbative effects, while the second one ensures the correct UV asymptotic behaviour of the QCD running coupling. In what follows we restrict ourselves to two models. i) The interaction consists of both the IR and UV terms: Such an interaction is known as the Maris-Tandy (MT) model [2] . ii) The UV term is ignored at all: This interaction is known as Alkofer-Watson-Weigel [16] kernel, referred to as the AWW model. It should be noted that at zero temperatures these models, with only a few adjustable parameters―the IR strength D, the slope parameter and quark mass parameter m in the AWW model and additionally, , and in the formfactor in the MT model―provide a good description of the pseudoscalar, vector and tensor meson mass spectra [3] [4] [6] [7] . Therefore, at finite temperatures a tempting choice of the interactions is to keep them the same as in vacuum.

2.3. Finite Temperatures

The theoretical treatment of systems at non-zero temperatures differs from the case of zero temperatures. In this case, a preferred frame is determined by the local rest system of the thermal bath. This means that the symmetry is broken and, consequently, the dependence of the quark propagator on and requires a separate treatment. To describe the propagator in this case a third function C is needed, besides the functions A and B introduced above for vacuum. Yet, the theoretical formulation of the field theory at finite temperatures can be performed in at least two, quite different, frameworks which treat fields either with ordinary time variable, e.g. the termo-field dynamics (cf. [37] ) and path-integral formalism (cf. [38] [39] ), or with imaginary time () which is known as the Matsubara formalism [33] [34] [35] [36] . In this paper we utilize the imaginary-time formalism within which the partition function is defined and all calculations are performed in Euclidean space. Since at the (imaginary) time evolution is restricted to the interval, the quark fields become anti-periodic in time with the period. In such a case the Fourier transform is not longer continuous and the energies of particles become discrete [33] [34] [35] which are known as the Matsubara frequencies, i.e. for Fermions (n is an integer, running from minus to plus infinity). The inverse quark propagator is now parametrized as

(4)

Accordingly, the interaction kernel is decomposed in to a transversal and longitudinal part

(5)

where and the gluon screening (Debye) mass is introduced in the longitudinal part of the propagator, where enters. The scalar coefficients are defined below. The projection operators can be written as

(6)

The gap equation has the same form as in case of, Equation (1), except that within the Matsubara formalism the integration over is replaced by the summation over the corresponding frequencies, formally

(7)

Then the system of equations for A, B and C to be solved reads (cf. also Ref. [29] )

(8)

(9)

(10)

where and the propagator functions are defined by

(11)

for and. The form of the interaction kernel is taken the same as at, i.e. both the transversal and longitudinal parts consisting of two terms―the infra-red and ultraviolet ones. The information on these kernels is even more sparse than in the case of. While the effective parameters of the kernel in vacuum can be adjusted to some known experimental data, e.g. the meson mass spectrum from the BS equation, at finite temperature one can rely on results of QCD calculations, e.g. by using results of the nonperturbative lattice calculations. There are some indications, cf. [43] , that at low temperatures the gluon propagator is insensitive to the temperature impact, and the interaction can be chosen as at with [24] . However, in a hot and/or dense medium the gluon is also subject to medium effects and thereby becomes effectively massive with finite transversal (known also as the Meissner mass) and longitudinal (Debye or electric) masses. Generally, these masses appear as independent parameters with contributions depending on the considered process [44] . The role of the Meissner masses in the tDS equation at zero chemical potential is not yet well established and requires separate investigations. This is beyond the goal of the present paper where only the Debye mass, , is considered. It should be noted that, independently of the value of the chemical potential, in most approaches based on the tDS equation within the rainbow approximation it is also common practice to ignore the effects of Meissner masses. This is inspired by the results of a tDS equation analysis in the high temperature and density region [45] which report that the Meissner mass is of no importance in tDS equation. At this level the Debye mass is the only T depending part of the kernel. The Debye mass is well defined in the weak-coupling regime. In [30] [46] [47] [48] it was found that the T-dependence of the Debye mass is in leading order

(12)

where and denote the number of active color and flavor degrees of freedom, respectively; the running coupling in the one-loop approximation is

(13)

with E being the energy scale. For the temperature range considered in the present paper we adopt, which often employed [30] [46] [47] [48] choice for the Debye mass in the tDS equation. It should be noted, however, that such a choice of is not unique. It may vary in some interval, in dependence on the employed method of infra-red regularization [34] [47] . Since the Debye mass enters as an additional energy parameter in, which determines the Gaussian form of the IR part of the interaction (3), an increase of results in a shift of the tDS solution towards lower temperatures leaving, at the same time, the shape of the solution practically unchanged. Accordingly, smaller values of shift the solution towards larger temperatures. Our numerical calculations show that a decrease of by a factor of 2 results in a ~15% shift of the solution to larger temperatures. The transversal and longitudinal parts of the interaction kernel (5) can be cast in the form

(14)

(15)

In the present paper we use several sets of parameters for the interaction kernel (3):

1), , ,; results with these parameters are denoted as AWW (IR term only) [16] and MT1 (IR+UV terms) [2] .

2) and, ,; MT2 [2] .

3) AWW, MT1 and MT2 with a modified parameter D making it dependent on temperature; at low T it remains constant, equal to the values used in the AWW, MT1 and MT2 sets, while at large temperatures, where the IR contribution is expected to be screened, the parameter D becomes a decreasing function of T. In this case, since the IR term vanishes, the AWW model is not applicable. It should be noted that all these models provide values for the vacuum quark condensate in a narrow corridor, , and the correct and meson masses as quark- antiquark bound states [7] .

3. Solutions of the tDS Equation in the Chiral Limit

3.1. Order Parameters

As seen from Equation (9) in the chiral limit, i.e. at, the trivial solution is possible, known as the Wigner-Weyl mode. It is of separate interest since this is the case where the dynamical chiral symmetry breaking is completely disabled. In the present paper, however, we are interested in solutions with finite dynamical quark masses given by the ratio, which enter the BS equation and determine accordingly the hadron bound states in a heat bath. Therefore, we will not consider the Wigner-Weyl mode solution and focus instead on (Nambu-Goldstone mode). It should be also noted that even for the sign of B is not defined. Equation (9) is invariant under. The sign of the solution can be fixed only by fixing the sign of the initial conditions for B. Here we consider positive values of B.

We solve numerically the system of Equations (8)-(10) by an iteration procedure. Since the UV term in the MT1 and MT2 models is logarithmically divergent, a regularization of the integral over the internal momentum and summation over is required. Usually, at one employs an invariant cutoff. The dependence of the solution on is removed by choosing a subtraction scheme defined at a renormalization point such that. In an analogous way one performs the renormalization procedure at finite temperature T [26] [29] . The only difference is that the internal momentum is restricted by the condition. At each iteration step this requires an interpolation of the previous solution to define the new Gaussian mesh for. In our calculations we employ a cubic spline interpolation procedure and a mapping

(16)

for the Gaussian integration with for a mesh of 64 nodes. This provides a rather large cutoff. The summation over is truncated at a large value of, where in our calculations for low temperatures and at temperatures are utilized. In Figure 1 and Figure 2 we exhibit the solution of the system (8)-(10) for the lowest Matsubara frequency in dependence on the momentum at low temperature (, Figure 1) and higher temperature (, Figure 2). A comparison with the vacuum solution [49] shows that qualitatively there is no difference of the solutions at finite T. To emphasize the dependence on the effective parameters D and, in Figure 1 and Figure 2 we present results of calculations for the two different sets. In Figure 1, left panel, the solutions are represented by solid and dashed curves, while the solutions by dotted and dash-dotted curves for MT1 and MT2 sets, respectively. The solutions, left panel, are for MT1 (solid curve) and NT2 (dashed curve). The dependence on the values of the effective parameters is seen only at low momenta. In this region, the dependence is mainly determined by the slope parameter, cf. Equation (3), which is quite different for the two employed parameter sets. At larger momenta (cf. Figure 2), the common asymptotics is approached already at.

The dependence of the solution on the temperature is of particular interest. It is known that in dense and hot matter there may occur different kind of phase transitions.

In SU(3) gauge theory, the deconfinement transition is of first order at related to the center symmetry, while in 2 + 1 flavor QCD with physical quark masses it is a cross-over at, see [50] [51] [52] . At non-zero baryon density, the liquid-gas phase transition at matters, and a critical end point of an additional first-order phase transition curve is still hypothetical. According to the Columbia plot [53] , two-flavor QCD in the chiral limit displays a first-order deconfinement and chiral restoration transition. The corresponding quantity which characterises such transitions is known as order parameter of the considered media. Natural candidates to be considered as order parameters or elements thereof are the mass function and the quark condensate, being an integral characteristics of the mass too. Order parameters determine the so-called critical temperature or the cross-over region which will serve as an indicator for a possible (phase) transition.

At high enough temperatures one expects a chiral restoration. This means that at a certain high value of the temperature the mass function B should vanish, indicating a possible phase transition in the hot matter. The lowest temperature at which holds is called the critical temperature, i.e. for the mass function the critical temperature can be defined as that value of T at which the solution vanishes. Analogously, for the chiral condensate, can be determined also as the temperature above which vanishes. In principle, these two critical temperatures can be slightly different.

The chiral condensate is defined by

(17)

where the trace is performed in spinor space. In Figure 3 we present results of calculations of the T-dependence of the mass solution B (left panel), and the normalized chiral condensate (right panel) in the chiral limit.

One infers from this figure that in a large range of T the solution is a smoothly decreasing function of T, except for a narrow interval where sharply decreases towards zero, as seen in Figure 4 where, for the sake of better determination of T for which, the solution is presented in a log-scale. It should be stressed that for very small values of B () the convergence of the iteration procedure for Equation (9) becomes rather poor. One needs to increase essentially the number of iterations in order to achieve the same accuracy in the whole range of considered temperatures. In addition, the actual accurate calculations in the neighbourhood of are restricted by numerical manipulations with quantities close to the machine zero. These numerical effects hinder a precise determination of in the chiral limit,. In our calculations, we analyse the values of B below 10⁻⁶⁰ to determine the interval for. An inspection of the numerical results shows that, for the MT1 model, the critical temperature is about 130 MeV, while for the MT2 model one has about 110 MeV. An analogous determination of from the chiral condensate provides slightly different values, e.g. for MT1 and for the MT2 model. The AWW set provides values close to the MT1 model. The obtained values are by 20% smaller than that obtained from QCD calculations [54] , which report a cross-over temperature in the range which is now narrowed to (154 ± 9) MeV [55] , however, for 2 + 1 flavor QCD with physical masses. It should be also noted that the general feature of the quark condensate, as a function of the temperature below the chiral transition limit, is established in a model independent way [56] [57] by the low-temperature expansion where is the pion decay constant in the chiral limit (). Our results in Figure 3 are in a qualitative agreement with that. It should be emphasized that the above quoted values for stem from the inspection of the numerical results of B and

at small values. On the linear scale in Figure 3 however, one infer instead values of about 120 MeV or even less.

3.2. Spectral Representation above T_c

Another important quantity characterizing the hot matter is the spectral representation of the retarded quark propagator. The Euclidean propagator can be transferred to Min- kowski space by an analytical continuation of the solution of the gap equation to real energies,

(18)

In Minkowski space, the dispersion relation for the quark propagator determines the spectral representation which is directly related to the imaginary part of the propagator,. It means that in Euclidean space the same spectral density can be associated to the retarded quark propagator

(19)

From this the importance of studying can be inferred. Note that, since the spectral density characterises the propagation of a particle, the dispersion relations in our case are meaningful only in the (deconfinement) region, where quarks can be treated to some extent as quasi-particles. Recall that in Minkowski space the propagator of a free particle can be written as

(20)

where is the energy of the particle and are the projection operators on positive and negative energy solutions, respectively, obeying. Therefore, for a free quark

(21)

i.e. the spectral functions characterize the propagation of quasi-particles with positive (normal) and negative (abnormal) energies. This can serve as a hint in parametrizing the spectral density in Euclidean space. Owing to parity and rotation symmetries, the Dirac structure of the quark spectral function at finite temperature is in general decomposed as

(22)

In the present paper we focus to two particular cases.

i) Chiral limit, where the scalar, or “mass”, part vanishes. In this case, the spectral function at negative energies describes the so-called plasmino mode [28] . In the chiral limit the projection operators are of a particularly simple form and the spectral density can be written as

(23)

where.

ii) Zero momenta: The projection operators are and

(24)

Note that at zero momenta the energy E of the quark can be associated to a mass which in literature is referred to as the thermal mass, a subject of many investigations within lattice QCD, cf. [28] . Results of such calculations are often considered as “experimental” data for the corresponding quantity. This is an important issue, since the model calculations of can be related to “experimental” data and to serve as a guide in fixing the phenomenological parameters and to estimate the applicability of the model which is based directly on parametrisations and scale settings by vacuum meson physics. It can be shown that the quark propagator can be written in the same form (23). So, in the chiral limit one can note

(25)

where

(26)

If one writes the dispersion relations for the model propagators (26)

(27)

then by inverting (27) one can obtain the (model) spectral density. Note that in model calculations the problem of inverting expressions like (27) is ill posed. Nevertheless, instead of inverting the equation (27), one can suggest a reliable parametrization for which allows an analytical calculation of the integral over and then to minimize the quantity

(28)

where the integral in Equation (28) must be preliminarily carried out analytically to leave the dependence only on and effective parameters. In such a way one can find the effective parameters and estimate the behaviour of.

The simplest parametrization for the spectral function at finite T is suggested by the case of a free quark propagator (21), i.e. one can expect that exhibits two maxima. For the two-pole parametrization the spectral function reads

(29)

With such a parametrization the spectral function describes the propagation of quasi-particles with the positive energy and aniti-particles with negative energy; the second term in (29) is known also as the plasmino mode [28] . The weights of the normal and plasmino modes play an important role in estimating the phase transitions in hot matter. At zero momenta, one has and. In this case the energy parameters determine the thermal masses, , which are predicted [28] in lattice QCD to be an increasing function of T and at to be. This important “experimental” result may be used in choosing the model kernels of the tDS equation. As the momentum increases one expects that the plasmino mode vanishes and.

In our calculations we use the Levenberg-Marquardt algorithm for minimization of in Equation (28). Results of calculations are exhibited in Figure 5.

It can be seen that both, MT1 and MT2 models (solid and dashed curves in Figure 5), provide increasing functions of T. However, the absolute values at are far from that predicted by QCD [54] . It implies that, while at low temperatures the two models with vacuum parameters, maintain a satisfactory description of the quark

propagators at, the interaction kernel requires modifications, cf. Ref. [24] [25] . Such modifications are inspired by the fact that, at sufficiently large temperatures, thermodynamics should be describable in terms of a weakly interacting quark-gluon gas, and at asymptotically large temperatures all thermodynamic quantities should converge to the ideal gas limit (for a discussion of the lattice QCD approaching to the perturbative limit see, e.g. Ref. [50] ). It means that, at large temperatures, the IR term in the interaction kernel must diminish or even vanish. A first attempt to modify the interaction kernel was done in Ref. [24] , where the weight D of the IR term above is abruptly (via a step function) replaced by a phenomenological, T-dependent decreasing function. In the present paper we suggest another modification of the IR term which smoothly decreases at large T and, at the same time, does not affect the IR term at low T. To do so, we introduce a suppression function which has a Heavyside step-like behavior at temperatures,

(30)

where the additional adjustable parameters are and as some diffuseness of the IR interaction. With such a parametrization, at the weight D of the IR part is as in the vacuum, , and at,. In our calculations we adopt and, which assures for both, MT1 and MT2 models, a reasonable behaviour of the thermal masses at, see Figure 5 (cf. also Ref. [54] ).

Another important characteristic is the behaviour of the plasmino mode as a function of the momentum. We find, cf. also [24] , that, while the energy of the normal mode monotonously increases with (as it should be), the plasmino mode decreases up to a minimum value, than sharply increases approaching the normal mode at large, see Figure 6-left panel. This does not mean at all that the role of plasmino mode is increasing too and becomes of the same importance as the normal one. Instead, the weight sharply decreases with increasing, vanishing at large, cf. Figure 6-right panel. The local minimum of the plasmino mode is related to the Van Hove singularity.

4. Solution of the tDS Equation at Finite Bare Masses

At finite quark masses the solution of the tDS equation differs from the chiral limit in at least two aspects. First, the Wigner-Weyl mode is not longer a solution. Second, the integrals over are logarithmically divergent in the UV region. This means that a regularization and renormalization procedure is required. To make the results finite one usually uses the Feynman method by introducing a cut-off parameter for the integrals, followed by a subsequent reliable subtraction procedure [1] [29] [58] . In approximate models after performing the necessary regularizations and renormalizations have been performed, the effective phenomenological parameters are fixed in such a way that a bulk of the effects is already included. Numerically it implies that by choosing a large enough cutoff there is no need for further normalizations to solve the tDS equation. In our calculations, the integral over is performed up to which assures an asymptotic behaviour of the solution, and with an accuracy better than ~0.1%. However, in further calculations involving one shall bear in mind that additional divergences may become apparent for another kind of calculations, and regularization procedures may be still required, as e.g. in calculations of the chiral condensate. At finite quark masses the chiral condensate is in fact quadratically divergent, cf. Equation (17). This is manifestly seen if one considers the quark condensate at but,

(31)

where. At large values of the momenta the asymptotic solution of the tDS equation becomes, and the integral (31) is quadratically divergent. On can regularize it by subtracting at large momenta the asymptotic quark mass. Denote, where at large enough momenta the quantity

goes to zero which implies that at the dynamical chiral symmetry breaking vanishes, i.e. the mass function receives its asymptotic value. Now, if the cut off parameter is chosen large enough, , then

(32)

where, and the regularized condensate does not depend on.

In obtaining (32) we put and in the second integral. Equation (32) illustrates the quadratic divergence of the integral and, at the same time, hints to how the subtraction procedure is to be chosen to eliminate this divergence. With this in mind, one can define a renormalized (subtracted) quark condensate as

(33)

where and denote the mass of light, e.g. u, and heavy, e.g. s, quarks, respectively. At, Equation (33) determines the required renormalized, cut-off inde-

pendent light-quark condensate. Exactly the same procedure is applied to determine the quark condensate at finite T, see also Ref. [30] . The remaining multiplicative divergences can be removed by normalizing to quark condensate at zero temperature.

In Figure 7 we present the dependence of the mass function and the chiral condensate on the temperature at finite bare masses, and. From the figure one infers that, since and the chiral condensate do not exactly vanish at large T, their asymptotic values cannot serve for a clear-cut definition of the critical temperature. Instead, one can use the method of the maximum of the chiral susceptibility, i.e. the maxima of the derivatives of B and/or with respect to the quark bar mass, as well as the inflection point of the mass function or of the condensate, i.e. the maxima of the corresponding derivatives with respect to the temperature [30] :

(34)

The (pseudo-)critical temperature is fixed by the condition and/or.

Figure 7 and Figure 8 clearly demonstrate that the inflection points at finite quark bare masses provide much smaller (pseudo-)critical temperatures; for all T-inde- pendent interactions one has, cf. also Ref. [32] . With the modified interaction, Equation (30), for which the IR term is screened at large temperatures, , the positions of the inflection points, which occur below , remain the same. This implies, for a better agreement with the lattice QCD [29] [54] , the interaction kernel, for finite bare quark masses, must acquire an appropriate dependence on the temperature also below. Another important issue of our analysis of the T-dependence of the IR term is that, starting from a relatively large temperature of, the dependence of the IR term is basically governed by the Debye mass which suppresses at large T. This is a hint that in the considered models the Debye mass has to be included only in the perturbative part of the interaction, i.e. in the UV term only.

5. Impact of the IR term

Analysing the relative contributions of the IR and UV terms in the interaction we find that, while at the UV term can be ignored in considering the hadron ground states [3] , at finite temperatures the ultraviolet behavior can become important.

In Figure 9, left panel, we present the separate contributions of the IR (dashed curve) and UV (dash-dot-dot curve) terms to the tDS solution. It is clearly seen that the absolute contribution of the UV term becomes sizeably only at large temperatures. However, in the full kernel (solid curve, with both UV and IR term), the influence of UV part is visible already at low T. This is because of interference effects and effects of higher Matsubara frequencies in the tDS Equation (1). Nevertheless, the overall shape of and, consequently the inflection point, is entirely governed by the IR interaction term. As mentioned above, all the considered interactions provide a critical temperature significantly lower than the one in lattice QCD calculations. Obviously, modifications of the kernel in the region above similar to Equation (30) do not affect the behaviour of and below such temperatures. Thus, a modification of the IR term in the whole range of T is required. A possible modification of the kernel is as follows: (i) in the IR term the Debye mass is omitted, (ii) the parameter D receives a T-dependence similar to Equation (30), and (iii) the UV term, being inspired by perturbative QCD calculations, remains unchanged, i.e.

(35)

The new effective parameters of the modified kernel should smoothly approach their vacuum values as T approaches zero and must provide a suppression of the IR interaction term above the (pseudo-)critical temperature. As in the previous case above, a simple expression simulating such a behaviour may be written by utilizing two suppression functions with a Heavyside step function-like behaviour, one acting below and, the second one acting above, for example

(36)

where and are new adjustable parameters. In Figure 10 we present an illustration of the change, according to Equation (36), of the IR parameter D, computed with a particular choice of the effective parameters, , , , , , and. At low temperatures, D is practically equal to its vacuum value, smoothly increases with temperature (making the interference with the UV term more pronounced), up to a maximum value (~6%) around the critical temperature, then it is screened at larger temperatures, see also [24] [25] .

The resulting solution, as well as the quark condensate for the modified interaction are exhibited in Figure 11, where the solid and dashed curves are for the T-dependent solution for the MT1 and AWW models, respectively. It is clearly seen that the inflection points are shifted towards larger values of temperature, providing critical temperatures for AWW and for MT1, which now are better compatible with the above quoted lattice values. This persuades us that

the MT1 and AWW models with proper modifications of the interaction kernel can provide a reasonable description of the quark propagators and quark condensate at finite temperatures. Such a modified interaction can be used then in the BS equation to analyse the behaviour of mesons embedded in a hot environment.

Obviously, the effective parameters in Equation (36) can be tuned further to obtain an improved agreement with lattice calculations. This is not the goal of the present paper. We reiterate that we are interested in choosing an effective interaction suitable for solving the BS equation at finite temperature in a large interval of T, which can allow for performing qualitative analyses of the behaviour of mesons in hot (and dense) matter as well as to infer from this the relevant order parameters and other conditions for a possible phase transition at large temperature.

6. Summary

We have investigated the impact of various choices of the effective quark-gluon interaction within the truncated rainbow approximations on the solution of the truncated Dy- son-Schwinger (tDS) equation at finite temperature. The ultimate goal is to establish a reliable interaction kernel adequate in a large range of temperatures which, being used in the Bethe-Salpeter equation, allows for an analysis of the behaviour of hadrons in hot matter, including possible phase transitions and dissociation effects. For this we investigate to what extent the models, which provide an excellent description of mesons at zero temperatures, can be applied to the truncated tDS equation at finite temperatures. We find that in the chiral limit at temperatures below a critical value both models, with and without the ultraviolet term, describe fairly well the quark propagators. The critical temperature obtained from the condition of a zero of the mass function B and/or of the quark condensate is in agreement with calculations within the lattice or unquenched QCD. However, at temperatures above the considered models with vacuum parameters fail to describe such important characteristics of the quark propagators as the quark spectral functions, thermal masses, plasmino mode etc. To achieve agreement of the model calculations with QCD lattice results, a modification of the interaction kernels is required. A simple change of the interaction is to suppress the contribution of the IR term at large temperatures, thus making the interaction dependent on the temperature. At finite quark masses, the considered models seems to provide too small values for the (pseudo-) critical temperature which are by smaller than the ones found in lattice QCD. Modifications of the interaction in the same manner as for the chiral case, i.e. suppressing the IR term above, do not affect the values of the (pseudo-)critical temperatures defined by the maximum of the susceptibility of the function B or as the inflection point for the quark condensate. To obtain a larger value of the critical temperature the interaction kernel has to be modified also for smaller temperatures, even below. The Debye mass plays a crucial role in parametrizing the IR term. An inclusion of as a Gaussian exponential, cf. Equation (3), results in an essential suppression of the solution of the tDS equation at, making problematic the attempts of obtaining larger, close to the lattice values. It seems that the Debye mass ought to be included only in the perturbative part of the interaction. The T-dependence of the IR term must be re-parametrized. The results of lattice calculations for the T-dependence of the quark condensate suggest that the T-dependence has to be chosen in such a way that at small temperatures the IR term approaches its vacuum value remaining constant or smoothly changing up to; then it must be completely screened at larger temperatures.

A more detailed parametrization of the IR term requires a separate and meticulous analysis of the tDS equation at finite T and will be done elsewhere.

Acknowledgements

This work was supported in part by the Heisenberg-Landau program of the JINR-FRG collaboration, GSI-FE and BMBF. DSM and LPK appreciate the warm hospitality at the Helmholtz Centre Dresden-Rossendorf.

Cite this paper

Dorkin, S.M., Viebach, M., Kaptari, L.P. and Kämpfer, B. (2016) Extending the Truncated Dyson-Schwinger Equation to Finite Temperatures. Journal of Modern Physics, 7, 2071-2097. http://dx.doi.org/10.4236/jmp.2016.715182

References

Appendix

Rainbow Truncation

The gap equation can be written as [2]

(37)

where is the dressed gluon propagator;, the quark-gluon vertex; represents a Poincaré invariant regularization of the four-dimensional integral, with the regularization mass-scale; denotes the current-quark bare massand stand for the corresponding renormalisation constants, with the renormalisation point, and is a GellMann matrix acting in color space. The solution of Equation (37) has the general form and is renormalized according to at a sufficiently large value of, with the renormalized quark mass at the scale. Since the behaviour at high momenta is fixed by perturbation theory and the renormalisation flow, in concrete calculations on needs specify the gap equation at low momenta, i.e. in the infra-red region. As mentioned above, in studies of the quark DS equation one has to employ reliable model forms of the gluon propagator and quark-gluon vertex, suitable for the whole range of momentum squared. In rainbow-ladder truncation, which is leading-order in the most widely used scheme, cf. [5] [16] [19] , this is achieved by adopting the requirements, , where m is a phenomenological mass parameter, and

(38)

where is a smooth continuation of the perturbative-QCD running coupling to all values of spacelike-k² fulfilling the constraint of being finite at the origin. The infra-red term is constrained by the condition of the consistency with Ward identities for the tDS and tBS equations and to be negligibly small in the perturbative region, i.e. at. Otherwise, is a pure phenomenological term, the form of which can be only qualitatively inferred from lattice calculations or from solution of a (truncated) set of Dyson-Schwinger equations for the quark and gluon propagators within some additional reasonable approximations. After choosing an explicit form of the interaction, the numerical values of the phenomenological parameters are determined from fitting empirical data.