Received 21 September 2015; accepted 17 November 2015; published 20 November 2015

ABSTRACT

In this work, some types of nonlinear Liouville equation (NLE) and nonlinear Master equations (NME) are studied. We found that the nonlinear terms in the equation can resist state of system damping so that an information solitonic structure appears. Furthermore, the power in the nonlinear term is independent of limitation of the solution. This characteristic offers a possibility to construct complicated information solitons from some simple solutions, which allow one to solve complicated NLE or NME. The results obtained in this work may provide an innovated channel for the quantum information transmission over far distance against dissipation and decoherence, and also open a constructive way to resist age decaying of system by designing adjusted field interaction with the system nonlinearly.

Keywords:

Quantum Information Density, Master Equation, Nonlinearity

1. Introduction

It is well known that the nonlinear Schrödinger equation (NSE) provides the solitonic solution which provokes many applications such as optical soliton communications; however it seems to be not clear what is the solution of the corresponding nonlinear Liouville equation (NLE) and the relevant physical meanings? This issue is interesting because the solitonic information communication needs to develop stable and low dissipative channel to transmit or receive singles against dissipation and decoherence. Hence understanding the corresponding NLE with solitonic structure of the density operator may allow us to innovate some methods to control dissipation and decoherence in the information transmission. On the other hand, although quantum information theory in studying transmission and processing of quantum states, entanglement of states for quantum computation, quantum cypotography or quantum teleportation has achieved great progresses [1] - [6] , the efficient proposals for controlling decoherence and dissipation of states of the quantum information are still strongly required; so that in nowadays, one of major obstacles for realizing real quantum information devices or networks is decoherence. For investigating this issue, an interesting problem is arisen. What is basic equation for quantum information? In previous works [7] [8] , we have presented that the Liouville equation still holds for quantum information density (QID). In this way, a density operator can be considered as a minimum unit of QID [9] - [15] . This reveals an essential informational character of density operator as a sort of information density. Then we proposed a nonlinear master equation and studied its asympototic solution as a sort of information soliton with invariant structure locally when time elapsed enough long [16] . In this work, we continually introduce a sort of NLE which has certain solitonic solution in the sense of the information density based on NSE. Then, as extension, a type of nonlinear Master equation (NME) is also studied. We show that the nonlinear term in NME resists state of system damping so that an asymptotic solution appears. Hence the study of the long time evolution of these structures may shed more light on the soliton dynamic of information density as the asymptotic configuration can be determined by using the technique of integration within an ordered product plus the method to solve the nonlinear differential equation. Let us start firstly to derive a NLE from a NSE.

2. Nonlinear Liouville Equation

Actually, if a NSE is defined as

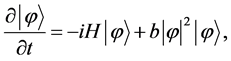(1)

and

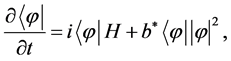(2)

then a relevant NLE can be introduced by

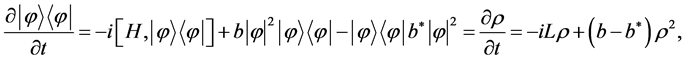(3)

where b 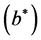is defined as a complex (conjugate) coupling number, and notice here is introduced by a sort of “direct” product which is not usually scalar product, namely

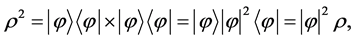(4)

which is only true if the “direct” product 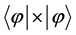of the pure state (such as a solitonic state) is defined as

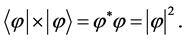(5)

Thus an interested solitonic solution of density operator, which can be defined as an information soliton based on the information meaning of density operator, can be constructed by

(6)

where 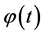may be a solitonic wave function [17] expressed as

(7)

where the amplitude is a fuction of time and space.

Then any NLE with higher order of power can be solved by using above formulation, e.g. if a NLE is ex- pressed by

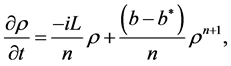(8)

where corresponding NSE is

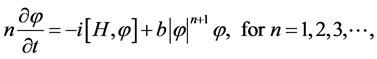(9)

then, by using to multiply into both sides of Equation (8), one can get

(10)

which allows Equation (10) to become

(11)

Now let, one can obtain a new formal NLE described by

(12)

whose solution likes Equation (6), i.e.

(13)

Therefore a general information soliton for Equation (8) can be constructed by

(14)

Furthermore, if one assuming

(15)

then using the same approach above, one can obtain

(16)

which corresponds to a general NLE with a nonlinear term,

(17)

where defining

(18)

Finally a general information solitonic solution can be achieved by

(19)

where notice again that is a soliton of wave function. One of significant meanings for this construction is that one can design an information soliton which especially satisfies our requirements. For example, if one needs an information soliton which has to be represented as a quantum entropy operator, then via choosing one can achieve

(20)

which is just a sort of entropy operator.

3. Generalization

The above mentioned NLE motivates us to consider logically to introduce a general nonlinear Liouville equation (GNLE) as

(21)

where can be chosen as an analytic function of, whose physical meaning can be understood as a type of quantum information density [16] . Then using the Baker-Hausdorf formula and the Magnus lemma [18] , a derivative of QID (or ratio of negative entropy density) can be deduced as

(22)

where, and notice is the entropy operator. So if is chosen as an analytic function of to allow rate of entropy operator to be zero (which may corresponds to certain

equilibrium or stable state of the system),

(23)

then a NLE can be achieved by

(24)

where. This is an extension of the above NLE. Notice here is not only restrict in the pure state of solitonic wave. For example, if, then

(25)

However, if or, then a GNLE can be given by

(26)

or

(27)

This type of GNLE can be used to design a channel of quantum information against dissipation and decoherence. More concretely speaking, for open system plus complicated environment, if transfers to certain terms which are related to a master equation, consequently Equations (25)-(27) can be changed to sort of nonlinear master equations. The asymptotic solutions of these equations are just type of information solitons as previously mentioned. The author wants to enphasize here that GNLE can be seen as an extension of the original NLE since there is no necessary to restrict in the definition of “direct” prodct in the process to deduce GNLE. There- fore GNLE is also true for defined in usually scalar product, such as

(28)

where is an integral measure.

4. Information Solitons

For instance, in the amplitude damping model, a master equation with nonlinear term can be described by

(29)

where is a damping number, a, is an annihilation or a creation operator, respectively. The nonlinear term can be supposed to originate from certain nonlinear interaction between the system and environment, such as a potential implying in a driven system.

Then using the coherent and entangled state as a basis developed by Fan Hongyi [19] , one can get

(30)

which approximately produces

(31)

where is defined as the creation (annihilation) operator acting on the thermostats, e.g. developed by Takahashi and Umezawa [20] [21] , and is defined by

(32)

so transformations , , and acting on the state are provoked, which guaran- tees to commute with right thermostats to produce above Equation (30), namely

(33)

For solving this nonlinear Equation (30), by left acting on the both sides of Equation (31), one gets

(34)

This yields

(35)

so that

(36)

Thus a formal solution of this equation is given by

(37)

where corresponds to time.

By using a thermo-coherent and entangled state (notice) left acting on Equation (37) one gets

(38)

where the relations, and have been used. Therefore one gets an integral form of the normal product expressed as

(39)

Then, in terms of the integral formula based on the Technique of Integration Within an Ordered Product of Operators (IWOP) [19]

(40)

one obtains

(41)

The integral term in Equation (41) is calculated as

(42)

where the relevant parameters are introduced by

(43)

So, this allows one to get

(44)

Then by means of Equation (36), Equation (44) gives an asymptotic solution for:

(45)

Furthermore, if the nonlinear term, then the above asymptotic solution can be extended by

(46)

where notice

(47)

the operator A commutes with a sort of particle number operator, so the both share common eigen- vectors, this physical condition [19] guarantees convergence of in the formal solution (38). Hence, from Equation (26) one can get

(48)

where defining

(49)

which gives an equation group described by

(50)

and the relevant sum gives,

(51)

Then based on the above formalism, a series of asymptotic solutions can be represented as

(52)

which enables one to attain

(53)

furthermore,

(54)

Therefore, when time the corresponding asymptotic solution of Equation (26) is achieved by

(55)

In the same way, from Equation (52), one can also obtain

(56)

so that one obtains

(57)

then an asymptotic solution of Equation (27) is also given by

(58)

The above asymptotic configurations can also be defined as a sort of information soliton in the sense: (1) they are invariant structure locally when time elapses enough long, and (2) these structures exist as form of density operator with meaning of QID. The study of the long time evolution of these structures may shed more light on the soliton dynamic of information density as the asymptotic configuration appear through kind of nonlinear self-interaction of the information density reduced from environment. In fact, a type of asymptotic configuration for the (non-)Markovian system with linear interaction between system and environment are found, and a wide class of nonlinear corrections of evolution equations are also found leading to superluminal effects [22] - [24] . However, here we want to emphasize that the information solitons obtained here is an asymptotic stable struc- ture of density operator (or QID) and have quantum information density meaning. The basic principle is based on the micro-representation of the second law of thermodynamics, i.e. since QID is just the negative entropy density, hence the physical meaning of Liouville equation for QID allows us to consider logically (also taking into account dissipative structure theory of Prigogine [25] [26] ) introduce a micro-representation of the second law of thermodynamics by

(59)

which gives naturally a general Liouville equation for the open system constructed by

(60)

where is assumed to be introduced by the difference of QID between the system and environment. More generally, this difference is supposed to be produced by a potential of information density, which drives the system to evolve along the direction described by the second law of thermodynamics. So, from the point of view of thermodynamical second law we can introduce a difference (or gradient) of QID to allow

(61)

where is assumed to be introduced by a difference (or gradient) of QID. This expression looks like a microscopic representation of thermodynamical second law: when the QID in the two coupled systems are not equal to each other, then there exist a difference (or gradient) of QID, which will spontaneously drive the higher QID to transmit to the lower QID until the both arriving at equilibrium.

5. Application

Generally, the above results provoke a constructive mechanism to realize a sort of self-organization from the non-equlibrium process for the open system. This may be useful, from physical justification, to construct the stable information transmission among remote space rockets or prolong life span against age decaying of systems. For example, if the original organization is expressed unfortunately by a master equation of the ampli- tude damping model,

(62)

then in terms of well known characteristic of master equation, the final asymptotic solution tends to decaying zero state,

(63)

So for prolonging life of the organization one can use a driving field F which satisfies

(64)

to enable original master equation to become

(65)

where is a coupling number to introduce a nonlinear term,. Consequently, an asymptotic solution for Equation (65) is obtained by

(66)

where notice again

(67)

This shows that the status of the system remain invariance by means of the interaction of the external field, which allows the original system to prolong life span without decaying.

More generally along this line, a master equation of the amplitude damping model described various decaying processes, after considering a nonlinear term, can be given by

(68)

where is a damping number, a, is a creation or an annihilation operator, respectively. Then utilizing the same approach as the formalism used above, one can let

(69)

so, one obtains

(70)

Thus a formal solution of this equation is given by

(71)

where corresponds to time.

By using a coherent and entangled state left acting on both sides of Equation (37), the equation becomes

(72)

then one gets an integral form of the normal product as

(73)

where the integral part is given by

(74)

Then an asymptotic solution of Equation (68) can be achieved

(75)

which gives an integral representation as

(76)

This allows one to find that the power of is independent on the limitation of (75), so one can use this character to find asymptotic solution for the extended equation

(77)

where if giving, then one has

(78)

hence one obtains

(79)

All of these are processed in the open system through a sort of nonlinear interaction expressed as a functional of. Therefore the above information soliton can also be used in quantum information channel to carry infor- mation over far distance for long time. The transmission of signals in this channel is not only dissipative, but also possibly decoherence-free when time past long. In this sense, previously proposed integration of squeezing coherent state, e.g. Equation (79), may provide an efficient way to transmit information by preserving coherence against decaying. The advantage of this sort of transmission comparing with the optic soliton transmission in the optic fiber is that this transmission channel may be applied into free space. For instance, it may be used in communication among basis, satellites and spacecrafts in remote space. However, the author want to stress again that the relevant carriers in the channel are information density whose solitonic structure is orientation from the nonlinear self-interaction term or. These terms transfer the original decaying result,

, to an asymptotic configuration, as expression of Equation (75). It is this

nonlinearity to eliminate the dissipation by producing a sort of self-organization, i.e. information soliton.

6. Conclusions and Remarks

The nonlinear kinetic equations included NLE and NME based on the micro-representation of the second law of thermodynamics are studied. The nonlinear terms in the equation can resist state of system damping so that an information solitonic structure appears. While the power in the nonlinear term is independent of the limitation of the solution, which permits one to construct more complicated structures of information soliton in the solution of complicated equations. The information soliton can be understood as some invariant structure of information density locally as a self-organization created from nonlinearity. So, these results can provide an innovated channel for the quantum information transmission over far distance against decoherence or damping, and also offer a constructive way to prolong life span of the original system by designing adjusted field interacting with the system nonlinearly.

Cite this paper

Bi Qiao, (2015) Nonlinear Liouville Equation and Information Soliton. Journal of Modern Physics,06,2058-2069. doi: 10.4236/jmp.2015.614212

References