Journal of Modern Physics
Vol.06 No.11(2015), Article ID:59708,6 pages
10.4236/jmp.2015.611156
A Study of Neutron and Gamma-Ray Interaction Properties with Cobalt-Free Highly Chromium Maraging Steel
M. M. Kassab1, S. U. El-Kameesy2, M. M. Eissa3, A. Abdel-Latif M1*
1Department of Physics, Faculty of Engineering, Fayoum University, Fayoum, Egypt
2Department of Physics, Faculty of Science, Ain Shams University, Cairo, Egypt
3Department of Steel and Ferroalloys, CMRDI, Helwan, Egypt
Email: *ahmed@fayoum.edu.eg
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 August 2015; accepted 15 September 2015; published 18 September 2015
ABSTRACT
Cobalt-free maraging steels of different compositions have been prepared by electro-slag remelting technique using titanium and chromium instead of cobalt. Neutron removal cross-sections have been calculated, also mass attenuation coefficients and effective electron densities have been determined for the prepared samples in the photon energy range up to 2.8 MeV. Other steel alloys and lead samples have also been investigated for the sake of comparison. The results prove the superiority of cobalt-free maraging steels compared with the other steel types to be used as a proper shielding material in the nuclear field. Among the investigated steels, the steel “0.045%C- 13.35%Ni-2.05%Cr-4.5%Mo-0.06%Ti” has the best attenuation properties.
Keywords:
Maraging Steel, Cobalt-Free, Mass Attenuation Coefficients, Effective Electron Density, Fast Neutron Removal Cross-Section

1. Introduction
Researchers have focused on studying the neutron and photon interactions with matter (attenuation coefficients) as radiation is a part of our life. This is attributed to increasing the use of radioactive sources in different fields such as tomography, nuclear research applications, and medicine. The attenuation coefficient is an important parameter that characterizes the penetration and diffusion of neutrons and gamma rays with matter; it depends on the chemical compositions of the alloy and the incident energy. The absorbed and scattered radiations are related to the effective electron density and density of the material.
Maraging steels comprise a special class of high strength steels that differ from conventional steels in that they are hardened by a metallurgical reaction that doesn’t involve carbon. Indeed, these steels are strengthened by the precipitation of intermetallic compounds at temperatures about 480˚C. The term maraging is coming from martensite age hardening of low-carbon, iron-nickel lath martensite matrix [1] [2] .
The standard maraging steel contains “18% Ni, 8% Co, 5% Mo and 0.4% Ti”, but Ni, Co and Mo are expensive elements, this keeps the steels rather expensive, preventing wider selection and application [3] [4] . Therefore, developing cobalt-free maraging steel with reduced quantities of expensive alloying elements to lower the production cost has been an important direction of maraging steels research [5] .
Another serious point to remove cobalt is that, it has radioactive isotopes (60Co) resulted from irradiation with high energy neutron flux and this is dangerous to be used as a shielding material. 60Co nucleus emits two gamma rays with energies of 1.17 and 1.33 MeV.
To overcome this problem, titanium and chromium were used as the primary strengthening elements replacing Co in steels, also for enhancing toughness and improving corrosion resistance, the nickel content is reduced to about 12% [6] . In addition to that highly chromium steels lead to advanced nuclear applications, as pressure vessels and the first wall in fusion reactor; this is due to their excellent thermal properties and swelling resistance.
Irradiation with neutron can change the microstructure and microchemistry of the steel materials, and this lead to bad mechanical properties of these steels such as embrittlement and hardening.
So, the purpose of the present work is to study the interactions of the neutron and gamma rays with the new investigated cobalt-free maraging alloys. These alloys have highly chromium (martensitic and ferritic) in which chromium concentration ranges from 2.0% to 18.0% of the weight. This study has to be undertaken via determining the neutron attenuation coefficients and measuring the mass attenuation coefficients at different γ-ray energies ranged up to 2.7 MeV by using different point radioactive sources (60Co, 232Th ,133Ba and 137Cs). In addition, a comparison with other steel types is also outlined.
Also special concern has been devoted to study the effect of chromium contents on some physical parameters of the produced new alloys.
2. Theoretical Calculations
2.1. Total Mass Attenuation Coefficient
In this work we summarize some theoretical relations that are used. A parallel beam of mono-energetic gamma ray photons are attenuated in the matter according to Lambert-Beer law [7] :
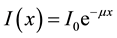 (1)
(1)
where I0 is the initial photon density, I(x) is the photons that penetrates the alloy distance x and µ is the total linear attenuation coefficient. We can write it as:
 (2)
(2)
The mass attenuation coefficient µ/ρ for any mixtures of elements is calculated by [8] [9] :
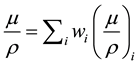 (3)
(3)
where 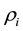 and
and 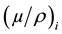 are the partial density and the mass attenuation of the ith constituent, respectively and wi is the weight fraction of ith constituent.
are the partial density and the mass attenuation of the ith constituent, respectively and wi is the weight fraction of ith constituent.
2.2. Effective Electron Density
The effective atomic number Zeff of the steel alloys consisting of different elements is based on the determination of total attenuation cross section for γ rays interactions and it can be obtained by the following formula [10] - [13] :
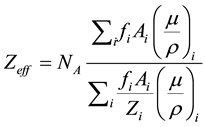 (4)
(4)
where NA is the Avogadro’s constant, (µ/ρ)i is the mass attenuation coefficient in the ith element, Zi is the atomic number of the ith element; Ai and fi are atomic weights (in gram) and number of atoms of element i relative to total number of atoms in the alloy respectively.
The effective electron density, Neff expressed in number of electrons per unit mass, is closely related to the effective atomic number and given by
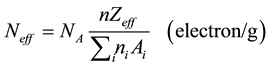 (5)
(5)
2.3. Effective Removal Cross-Section for Fast Neutron (ΣR cm−1)
The removal cross-sections, or the neutron attenuation coefficients, ΣR for compounds and homogenous mixtures may be calculated from the value ΣR/ρ or ΣR for various elements in the compounds or mixtures using the following equation Kaplan 1989 [10] .
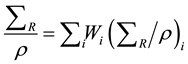 (6)
(6)
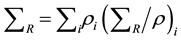 (7)
(7)
where Wi is the weight percentage, ρi and (ΣR/ρ)i are the partial density and the fast neutron mass attenuation coefficient of the ith constituent, respectively.
3. Materials and Methods
3.1. Preparation of the Shielding Material
The cobalt-free maraging steel samples were prepared, using pilot plant induction furnace electro-slag remelting technique (ESR). Titanium and chromium were used instead of cobalt and to overcome the problem of retained austenitic; the nickel content was reduced to about 12%. The steels were subjected to solution treatment (at 820˚C for 1 hour), with the aging process (at 480˚C for 2 hours).
3.2. The Mass Attenuation Coefficient
The mass attenuation coefficient of gamma radiation was measured with a narrow collimated beam using the gamma transmission method; which consists of hyper pure germanium (HPGe) detector with relative efficiency ~25%. The sample was placed between the standard gamma point source and the detector. The experiment was repeated with and without the sample for 5 min. The samples were irradiated by photons emitted from (60Co, 232Th, 133Ba and 137Cs) radioactive point sources in the range from 0.2 to 2.8 MeV.
4. Results and Discussions
The constituents of the highly chromium cobalt-free maraging alloys (S1, S2, S3, S4 and S5) are presented in Table 1. The table also includes a high-nitrogen free nickel steel (SN) and a carbon steel (SC) for the sake of comparison.
The total mass attenuation coefficients for different steel samples that have been measured at photon energies range from 0.2 to 3 MeV are shown in Figure 1. Figure 1 illustrates clearly the superiority of the new cobalt-free alloy than the other steel types, as a γ-ray shielding material. The attenuation coefficient of lead is also presented in the same figure for the sake of comparison.
Figure 1. Mass attenuation coefficients of the investigated alloys at different photon-energies.
Table 1. Chemical composition of the investigated alloys.
The effective electron densities Neff at photon energy range in the aforementioned γ-ray energy range have been calculated for different concentrations of steel alloys and the results have been displayed in Figure 2. It can be seen from this figure that the effective electron densities decreases with the energy increase in the energy region below 1.0 MeV, then it reaches a nearly stable value for higher energies. Moreover, the value of the effective electron densities for S3 is the highest one in the high-energy region (>1.0 MeV), followed by that of S2 and at last that of nitrogen steel SN. These results go parallel with the mass attenuation coefficient. Neff of the high-nitrogen steel drops to lower values below the other steels (in the high energy region) and this may be attributed to the lower atomic number of nitrogen (14N).
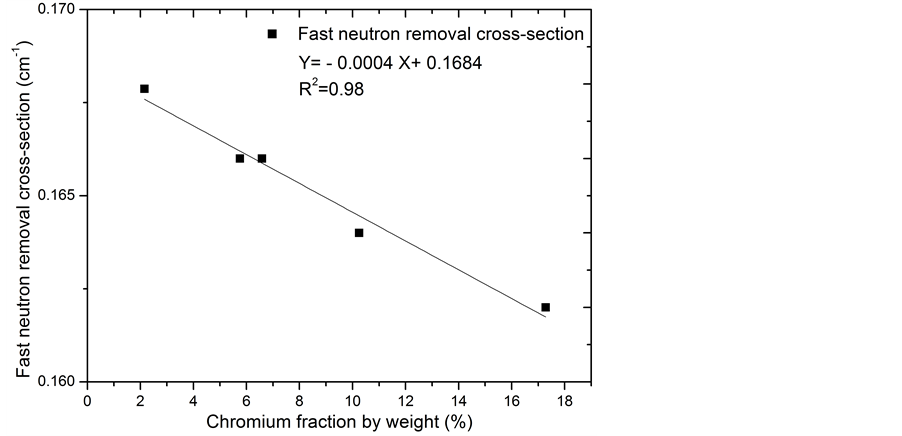
Table 2 lists the calculations of the effective removal cross-section for cobalt-free steels; containing different chromium concentrations. It was found that the neutron attenuation coefficient is inversely proportional to the chromium content on the expense of iron as shown in Figure 3. Furthermore, the results show that S3 has the best neutron attenuation coefficient, and this can be attributed to its high iron content, compared with the other investigated samples in the present work.
The relation between the γ-ray attenuation coefficients and chromium contents is given in Figure 4; the equation for the fitting function and the linear regression coefficient, R2, is given in each graph. It is clearly seen from Figure 3 and Figure 4 that, mass attenuation coefficients and removal cross section are inversely proportional to the chromium contents. This result shows that there are some sorts of analogy between the fast neutron removal cross section and the γ-ray attenuation coefficients.
Figure 2. The effective electron density for selected three investigated alloys as a function of gamma ray energies.
Figure 3. Fast neutron removal cross-section with chromium contents.
Table 2. Calculations of the fast removal cross-section for the samples.
Figure 4. Gamma-ray attenuation coefficient with chromium contents.
5. Conclusions
New shielding cobalt-free maraging steels were developed by electro-slag remelting technique using titanium and chromium instead of cobalt and reducing nickel content to about 12%.
Mass attenuation coefficients, effective electron densities, and fast neutrons removal cross-section for the five investigated alloys have been evaluated. A comparison of mass attenuation coefficients for cobalt-free, lead, carbon-steel and high-nitrogen steel has been undertaken. The achieved results reveal the superiority of S3 cobalt-free alloy (0.045%C-13.35%Ni-2.05%Cr-4.5%Mo-0.06%Ti) than the other investigated alloys as a proper shielding material in the industrial and nuclear domain.
Acknowledgements
Special thanks are due to research groups of the nuclear physics lab, faculty of science, Ain shams university. Also, special thanks are due to members of metallurgical lab, CMRDI for their help.
Cite this paper
M. M.Kassab,S. U.El-Kameesy,M. M.Eissa,A.Abdel-Latif M, (2015) A Study of Neutron and Gamma-Ray Interaction Properties with Cobalt-Free Highly Chromium Maraging Steel. Journal of Modern Physics,06,1526-1532. doi: 10.4236/jmp.2015.611156
References
- 1. Kim, Y.G., et al. (1986) Materials Science and Engineering, 79, 133-140.
http://dx.doi.org/10.1016/0025-5416(86)90396-4 - 2. Leslie, W.C. and Hornbogen, E. (1996) Chapter 17—Physical Metallurgy of Steels. Physical Metallurgy. 4th Edition, R. W. Cahn and P. Haasen, Oxford, 1555-1620.
- 3. Prokoshkina, V.G. and Kaputkina, L.M. (2006) Materials Science and Engineering, 438-440, 222-227.
http://dx.doi.org/10.1016/j.msea.2006.02.075 - 4. He, Y., et al. (2006) Metallurgical & Materials Transactions, 37, 1107-1116.
http://dx.doi.org/10.1007/s11661-006-1089-4 - 5. Sha, W., et al. (2012) Materials Science and Engineering, A536, 129-135.
http://dx.doi.org/10.1016/j.msea.2011.12.086 - 6. Dautovich, D.P. (1976) Corrosion, 3, 64-76.
- 7. Wood, J.I. (1982) Computational Methods in Reactor Shielding. Pergamon Press, New York.
- 8. El-Khayatt, A.M. and Akkurt, I. (2013) Annals of Nuclear Energy, 60, 8-14.
http://dx.doi.org/10.1016/j.anucene.2013.04.021 - 9. Kurudirek, M., et al. (2011) Radiation Physics and Chemistry, 80, 855-862.
http://dx.doi.org/10.1016/j.radphyschem.2011.03.015 - 10. Gong, J., et al. (2001) Journal of Non-Crystalline Solids, 282, 325-328.
http://dx.doi.org/10.1016/S0022-3093(01)00341-6 - 11. Akkurt, I. and El-Khayatt, A.M. (2013) Journal of Radioanalytical and Nuclear Chemistry, 295, 633-638.
http://dx.doi.org/10.1007/s10967-012-2111-5 - 12. Erdem, M., et al. (2010) Radiation Physics and Chemistry, 79, 917-922.
http://dx.doi.org/10.1016/j.radphyschem.2010.04.009 - 13. Yilmaz, E., et al. (2011) Annals of Nuclear Energy, 38, 2204-2212.
http://dx.doi.org/10.1016/j.anucene.2011.06.011
NOTES

*Corresponding author.