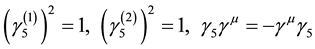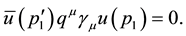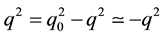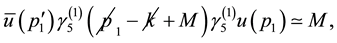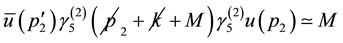Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57410,9 pages
10.4236/jmp.2015.67097
Two Pion versus σ-Meson Exchange Potentials
Sachiko Oshima1, Takehisa Fujita2, Naohiro Kanda2, Akihiro Yoshimi3
1College of Industrial Technology, Nihon University, Chiba, Japan
2Department of Physics, Faculty of Science and Technology, Nihon University, Tokyo, Japan
3Research Core for Extreme Quantum World, Okayama University, Okayama, Japan
Email: oshima.sachiko@nihon-u.ac.jp, fffujita@phys.cst.nihon-u.ac.jp, nkanda@phys.cst.nihon-u.ac.jp, yoshimi@okayama-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 April 2015; accepted 21 June 2015; published 25 June 2015
ABSTRACT
The two pion exchange potentials are evaluated by carrying out the numerical integrations of three Feynman parameters in the corresponding Feynman diagrams. The two pion exchange potentials give rise to the attractive force which is quite similar to the effective scalar meson with its mass of 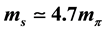 and its strength of
and its strength of 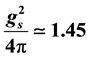 at T = 0 channel. However, there is a strong isospin dependence of
at T = 0 channel. However, there is a strong isospin dependence of 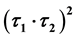 which should be different from the phenomenological σ-meson exchange calculations. Therefore, the medium range attraction of the T = 0 nuclear interaction should be due to the two pion exchange processes, but the T = 1 channel is still an open problem.
which should be different from the phenomenological σ-meson exchange calculations. Therefore, the medium range attraction of the T = 0 nuclear interaction should be due to the two pion exchange processes, but the T = 1 channel is still an open problem.
Keywords:
Nucleon-Nucleon Interactions, Nuclear Forces

1. Introduction
The nuclear potential is first described by Yukawa [1] who introduces one meson (pion) exchange process, and this is reasonable since pion is the lightest meson in nature. However, one pion exchange potential (OPEP) alone cannot bind deuteron since it is not sufficiently strong. In this respect, one should consider a potential which gives rise to the leading nucleon-nucleon attractive potential which can bind deuteron. There should be basically two directions in understanding the leading potential, one which is due to the two pion exchange potentials [2] - [4] and the other which introduces many bosons that may presumably exist in nature [5] - [7] .
The two pion exchange approaches, however, cannot be very successful for describing the nucleon-nucleon scattering data. This is basically because the calculated potential is not necessarily written clearly in its shape, and therefore it is not very easy to understand what the real effect of the two pion exchange potentials is. On the other hand, the nucleon-nucleon interaction with one boson exchange potential (OBEP) is quite successful for reproducing the nucleon-nucleon scattering data. In fact, there are already sufficiently large numbers of works available for the determination of the shape of nucleon-nucleon potential with one boson exchange processes. In this case, exchanged bosons are taken from experimental observations with the exception of σ meson [8] -[11] . There, the masses and the coupling constants of the exchanged bosons are determined from various methods, partly experimentally and partly theoretically. The determination of these parameters may have some ambiguities, but one can see that the basic part of the nuclear force can be well understood until now.
However, there is one important problem which is not solved yet completely. This is related to the medium range attraction of the nucleon-nucleon potential, and this is normally simulated by the effective scalar meson exchange process. However, the quark model cannot predict the presence of the scalar meson, and therefore a massive scalar meson (σ-meson) should not be directly coupled to nucleons. People discuss that there should be a π − π resonance state with a very broad width, and this may be a candidate of the corresponding σ-meson which generates the medium attraction [12] . However, this pion must be far off the mass shell in nucleon- nucleon interactions, and therefore it should be extremely difficult to prove that the s-wave π − π resonance state may couple to nucleons and induce the nucleon-nucleon potential.
In addition, people also believe that the medium range attraction may well be simulated by the second order calculation of one pion exchange potential (OPEP) in which the intermediate Δ-resonance state is included [13] [14] . However, it is also known that this cannot give rise to the sufficiently large contributions to the medium range attractions. Also, there are many calculations of the nucleon-nucleon interaction due to the two pion exchange processes [2] -[4] , and this may indeed give rise to the medium range attraction even though until now there is no clear cut evaluation which can isolate the nuclear force contribution to the medium range attraction.
In this paper, we present a careful calculation of the two pion exchange processes, and in the evaluation, we have made no approximation. We first evaluate the corresponding Feynman diagrams which contain the integration of the four momentum k. This integration can be carried out exactly by introducing the Feynman parameters, and thus we are left with the integrations of the three Feynman parameters. This can be only carried out numerically, and we find that the corresponding T-matrix can be expressed reasonably well, at least, up to 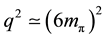 as
as
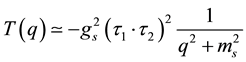 (1.1)
(1.1)
where
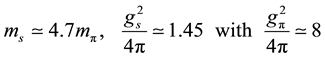 (1.2)
(1.2)
where the mass 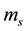 and the coupling constant
and the coupling constant 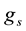 should have a small increase ( up to ~20%) as the function of
should have a small increase ( up to ~20%) as the function of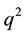 . Here,
. Here, 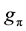 and
and 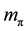 denote the
denote the  coupling constant and pion mass, respectively. Therefore, the predicted values of the mass and the coupling constant of the effective
coupling constant and pion mass, respectively. Therefore, the predicted values of the mass and the coupling constant of the effective 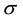 meson from the two pion exchange diagrams are given for the
meson from the two pion exchange diagrams are given for the  channel as
channel as
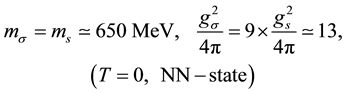 (1.3)
(1.3)
which should be compared with the phenomenological values of the 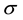 meson mass and coupling constant as determined by fitting to the nucleon-nucleon scattering data for the
meson mass and coupling constant as determined by fitting to the nucleon-nucleon scattering data for the 
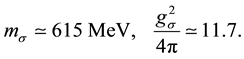
They indeed agree with each other at the quantitative level. The physical reason why the two pion exchange processes become quite large can be easily understood. The one pion exchange potential is suppressed due to the pseudo-scalar interaction with nucleon, and thus the one pion exchange process in the second order diagram is relatively weak. Indeed, one knows that the one pion exchange calculation should pick up the small component in the nucleon Dirac wave function. However, the two pion exchange diagrams have no such suppression and thus they can give rise to the largest contribution to the nucleon-nucleon potential. Since it is the fourth order process, it turns out to be an effective scalar interaction which is always attractive.
The two pion exchange potentials have a very strong isospin dependence, and, in fact, T = 1 force is very weak. This may not be consistent with the σ meson exchange potential determined in OBEP, and the potential with the T = 1 channel may well be connected to the interaction with the intermediate Δ-resonance state.
2. Nuclear Potential with σ-Meson
It is well-known that the quark model cannot predict the existence of the σ-meson in nature since a quark and an
anti-quark with spin 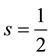
there is a possible resonance state which may correspond to the σ-meson, that is, the s-wave π − π resonance which should be 0++ state. Here, we briefly discuss the physical effect of the σ-meson.
2.1. Paris Potential
The effect of the s-wave π − π resonance on nucleon-nucleon potential is first employed by the Paris potential, and in fact, they consider the medium range interaction in terms of the s-wave π − π resonance effect. However, the difficulty is concerned with the two pions which must be far off the mass shell state since they are exchanged mesons. In this respect, this is beyond the perturbation theory and thus any theoretical description must be very difficult. In fact, they make use of the dispersion relation in constructing the two pion resonance states in the Paris potential. As a result, the Paris potential has made a great success for the description of the realistic nucleon-nucleon potential, without explicitly using the σ-meson state.
2.2. Real σ-Meson Exchange
An existence of the σ-meson state in nature has been extensively discussed, but there is no clear cut explanation of experimental observation of the σ-meson state [12] [15] -[17] . This is mainly because this resonance should have, at least, a very broad width, and therefore it should be difficult to be identified as a particle.
In addition, even if it is found as a particle, one should clarify how it can couple to nucleon. In this case, we find a T-matrix as
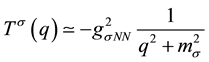
where 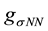

However, if one starts from the 2π state, then the effect of the σ-meson should be quite similar to the Paris potential description, even though we cannot prove anything because it is beyond the perturbation theory.
3. Two Pion Exchange Processes
Now, we should consider the two pion exchange diagrams in order to obtain a proper nucleon-nucleon interaction. There are, of course, many calculations of the two pion exchange diagrams [2] -[4] [18] , but until now there is no solid calculation of the two pion exchange potentials which are compared to the observed data in a clear way. However, one can easily convince oneself that the fourth order process involving the four γ5 interactions is not suppressed at all, in contrast to the one pion exchange diagram where the γ5 coupling is indeed suppressed by the
factor of 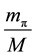
should be very important to calculate the two pion exchange processes properly in order to understand the medium range attraction of the nucleon-nucleon interaction.
3.1. T-Matrix Evaluation
Now, the evaluation of the two pion exchange Feynman diagrams is done in a straight forward way [18] [19] , and we find the corresponding T-matrix as
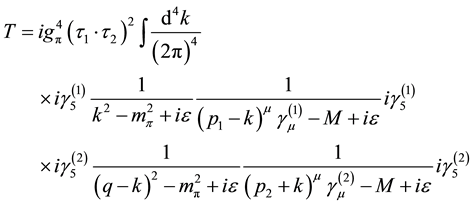
where 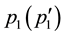
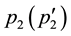
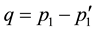
we can rewrite Equation (3.1) as
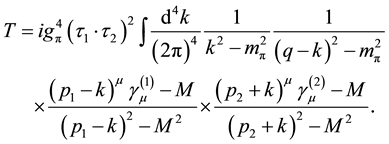
Now, we introduce the integration trick in terms of Feynman parameters x, y, z as
Further, we assume that the nucleons at the initial state are on the mass shell
and therefore we also find
In addition, we take the non-relativistic limit for the nucleon motion and thus obtain

where s is defined as
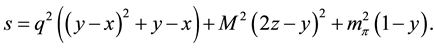
The momentum integration of k can be easily done, and we find
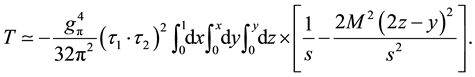
3.2. Dependence of Momentum Transfer q
This three dimensional integration of x, y, z can be done only numerically, and the calculated result can be well fit by the following shape
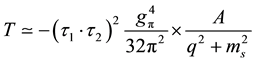
where A and ms are found to be weakly dependent on the momentum transfer q. Here, we replace the four momentum transfer of q as
since we may use the static approximation to a good accuracy

If we take the value of the πNN coupling constant as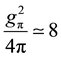
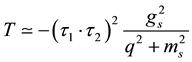
where
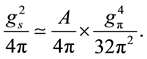
Here, we discuss the q dependence of the numerical calculations of ms and
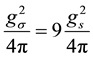
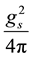
As can be seen from Table 1, we see that the mass mσ and 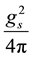
q. These values of ms and the coupling constant should be compared with the phenomenological values of the σ
meson mass mσ and coupling constant 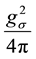
the T = 0 channel [8] [9]
Table 1. The q dependence of the σ mass and the coupling constant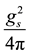
They indeed agree with each other at the quantitative level. The physical reason why the two pion exchange processes become quite large can be easily understood. The one pion exchange potential is suppressed that the one pion exchange calculation should pick up the small component in the nucleon Dirac wave function. However, the two pion exchange diagrams have no such suppression and thus it can give rise to the largest contribution to the nucleon-nucleon potential. Since it is the fourth order process, it turns out to be an effective scalar interaction which is always attractive.
3.3. Comparison with Reid Potential at T = 0 Channel
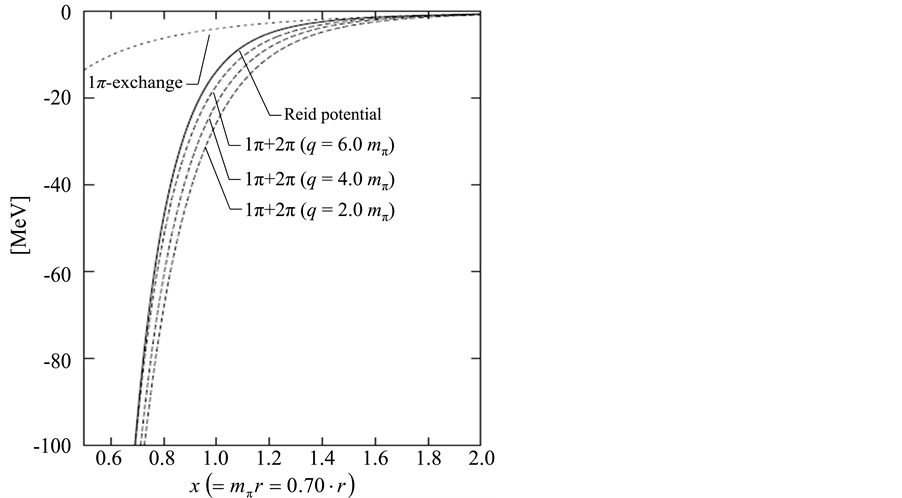
In order to see more explicitly what is the behavior of the two pion exchange potentials, we show the strength of the two pion exchange potentials as a function of r at the T = 0 channel and compare them with the behavior of the Reid potential [20] . As can be seen from Figure 1, we can say that the behaivior of the two pion exchange potentials together with the one pion exchange potential at the T = 0 channel is quite similar to the one obtained from the Reid potential. It should be very important to stress that the two pion exchange potentials obtained here does not have any free parameters to adjust, and still it is consistent with the Reid potential even though it is only for the T = 0 channel.
In Figure 1, we show the comparison between the calculated potential due to the two pion exchange processes and the Reid potential. They agree with each other in a quantitative level.
4. Double Counting Problem
In general, the evaluation of the two boson exchange potential should be carefully made due to the double counting problem. This is clear since the solution of the Schrödinger equation with the one boson exchange potential should contain the repeat of the one boson exchange process in some way or the other, and therefore the inclusion of the two pion exchange diagrams in the field theory evaluation should be examined to what extent it should be considered for the nucleon-nucleon interaction. In this section, we clarify that the double counting effect concerning the two pion exchange potentials is not very large, and it is indeed well justified that we do not have to worry about the double counting problem in a practical sense.
Figure 1. Potential curves of one-pion plus two-pion, in which the two-pion contributions are calculated from the presented T- matrices for q = 2.0 mπ, 4.0 mπ, 6.0 mπ (dashed lines). The Reid potential (solid line) and one-pion potential (dotted line) also shown for comparison.
4.1. Ladder Diagrams
In order to understand the double counting problem, we should first start from the Lippmann-Schwinger equation for the T-matrix, and the T-matrix equation for the nucleon-nucleon scattering case can be written as
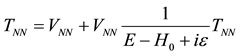
where VNN and H0 denote the nucleon-nucleon potential and the two nucleon Hamiltonian in the free state, respectively. Suppose this VNN should be one pion potential Vπ, and we insert it into Equation (4.1) and expand it into the ladder type contributions
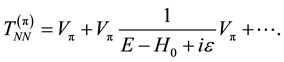
Here, it is claimed that the second term should correspond to the contributions from the two pion exchange potentials. Indeed, it indicates that some part of the two pion exchange processes should be taken into account in this T-matrix equation. However, this is not necessarily correct for the pion exchange process since the one pion exchange potential is suppressed a great deal due to the γ5 interaction which picks up the product of the large and small components of the Dirac wave function. On the other hand, the second order ladder calculation can take into account only the large components of the Dirac wave functions. This is clear since the Lippmann- Schwinger equation is solved only for the non-relativistic wave function. In addition, the OPE potential is obtained already by making the approximation of the non-relativistic reduction, and thus the two pion exchange processes are completely different from the second order ladder contribution of OPE potential. Below we will discuss it more explicitly.
4.2. One Pion Exchange Potential
Here, we see that the T-matrix of the one pion exchange process is written as
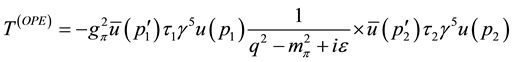
and after some static and non-relativistic approximations, we obtain the OPE potential

where
Here, one finds the suppression factor of
obtained only after one takes the expectation value of the γ5 matrix with free Dirac wave functions, and the suppression factor comes from this point of the expectation value 
4.3. Two Pion Exchange Potentials
On the other hand, the two pion exchange diagrams do not have any such suppressions because one considers all the intermediate states which pick up the states strongly coupled to the γ5 vertex with the initial nucleon state. We can write it more explicitly

Here, one can see that the dominant contributions of the numerator become
and thus there is no suppression any more, in contrast to the one pion exchange potential case. In addition, one sees that the ladder contribution of Equation (4.2) can only take into account the intermediate states which are always described in terms of the non-relativistic wave functions in the Lippmann-Schwinger equation, and the OPEP is obtained only after one has taken the expectation value of the γ5 with the free Dirac states.
4.4. Schematic Explanation of Double Counting
Here, we present the schematic expression of the double counting problem. In field theory, we can write the T- matrix of one pion and two pion exchange processes as
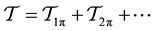
and as we see from above evaluation, the typical strength can be written if we reduce them to the non-relativistic reduction as

where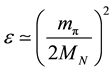
T-matrix for one pion exchange potential as
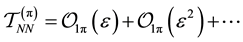
Therefore, the second order ladder contribution from the one pion exchange potential must be of the order of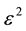
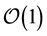
In summary, the second order ladder type calculation of the small potential like one pion potential cannot give rise to such a large contribution of the potential obtained in Equation (3.8), and therefore, there is no sizable double counting problem in this calculation, apart from the very small part of the two pion exchange potentials,
which should be a correction of the order of 
4.5. Validity of Perturbation Theory
The two pion exchange potentials are larger than the one pion exchange potential, and this may give rise to a question as to what should be a validity of the perturbation theory in strong interactions. This is indeed quite an important question, and we should answer for this basic problem.
In fact, the perturbation theory in strong interaction is generally rather bad. In this sense, it is quite possible that the six order calculation of three pion exchange process may not necessarily be smaller than one pion exchange potential, and thus we should take this effect into account. This is the reason why we should solve the Lippmann-Schwinger equation which is not based on the perturbation theory. By this Lippmann-Schwinger equation, we can sum up all of the higher order effects in the strong interaction. In this case, however, we have to employ the non-relativistic equation, and this is indeed an approximation we have made in the nucleon-nucleon scattering process. But the problelm of the perturbation theory is nicely avoided in the nucleon-nucleon scattering case.
π − N Scattering
Here, we should make a comment on the π − N scattering problem. In the case of π − N scattering, it is well- known that the simple-minded calculation of the perturbation theory should give some overestimation of the scattering cross section in comparison with experiments. This is, however, clear that the fourth and higher order calculation should make a large contribution to the T-matrix since the perturbation theory may not necessarily be justified. Therefore, in the π − N scattering process, we have to consider some kind of Lippmann-Schwinger type equation which can take into account the contributions of the higher order effects.
5. Chiral Perturbation Model
Here, we should discuss the nucleon-nucleon potential which is calculated by the chiral perturbation model. This is somewhat difficult to follow what is indeed a new aspect beyond the standard calculation due to one boson exchange mode calculations.
5.1. Chiral Symmetry Breaking
People still believe that the chiral symmetry in some of the field theory model can be spontaneously broken as Nambu and Jona-Lasinio claimed a long time ago [21] . However, if one examines their paper carefully, then one can easily see that the chiral symmetry is never broken spontaneously [22] [23] . In their paper, they use the Bogoliubov transformation which is, of course, an approximation scheme. In this case, due to the approximation, an apparent mass term appears after the Bogoliubov transformation, even though its mass has infinitely large. In nuclear physics application of this wrong theory, people make use of the cut-off as the nucleon mass, and thus the infinite mass is avoided by hand.
In terms of mathematics, we explain what is the symmetry breaking story [22] .
5.2. Goldstone Boson
In this sense, a question may arise as to why people make use of the chiral symmetry breaking. One possible answer may be that they want to consider that pion should be a Goldstone boson. This is connected to the fact that there is no way to solve QCD, and, in particular, pion is special in that it is very light. However, quarks have finite mass, and therefore there is no chiral symmetry, and thus there is no point of the spontaneous symmetry breaking before the wrong claim of Nambu and Jona-Lasinio.
6. Conclusions
We have presented a new calculation of the old type Feynman diagram in the two pion exchange processes. The result is quite interesting since the corresponding T-matrix of the two pion exchange diagrams turns out to be just similar to the T-matrix of the effective σ meson exchange case where we obtain the corresponding effective
σ meson mass 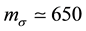
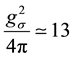
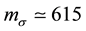
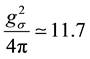
are determined from the OBEP analysis of the nucleon-nucleon scattering experiments. However, this is only the T = 0 channel since the two pion exchange potentials have a strong isospin dependence. In this respect, the result of the present study may invoke some further investigations of the nucleon-nucleon potential.
In this calculation, we have employed the value of the πNN coupling constant gπ which is determined from the
pion decay process into two photons, 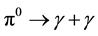

hand, people use the πNN coupling constant 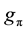
References
- Yukawa, H. (1935) Proceedings of the Physico-Mathematical Society of Japan, 17, 48.
- Wortman, W.R. (1968) Physical Review Letters, 176, 1762. http://dx.doi.org/10.1103/PhysRev.176.1762
- Haracz, R.D. and Sharma, R.D. (1968) Physical Review Letters, 176, 2013. http://dx.doi.org/10.1103/PhysRev.176.2013
- Partovi, M.H. and Lomon, E.L. (1970) Physical Review D, 2, 1999. http://dx.doi.org/10.1103/PhysRevD.2.1999
- Kiang, D., Preston, M.A. and Tip, P. (1968) Physical Review Letters, 170, 907. http://dx.doi.org/10.1103/PhysRev.170.907
- Sakurai, J.J. (1967) Advanced Quantum Mechanics. Addison-Wesley, Boston.
- Bohr, A. and Mottelson, B.R. (1998) Nuclear Structure. Vol. 1, World Scientific, Singapore City. http://dx.doi.org/10.1142/3530-vol1
- Machleidt R., Holinde, K. and Elster, Ch. (1987) Physics Reports, 149, 1-89. http://dx.doi.org/10.1016/S0370-1573(87)80002-9
- Machleidt, R. (1989) Advances in Nuclear Physics, 19, 189.
- Lacombe, M., Loiseau, B., Richard, J.M., Vinh Mau, R., Cote J., Pires, P. and de Tourreil, R. (1980) Physical Review C, 21, 861. http://dx.doi.org/10.1103/PhysRevC.21.861
- Lacombe, M., Loiseau, B., Richard, J.M., Vinh Mau, R., Cote, J., Pires, P. and de Tourreil, R. (1981) Physics Letters B, 101, 139-140. http://dx.doi.org/10.1016/0370-2693(81)90659-6
- Törnqvist, N.A. and Roos, M. (1996) Physical Review Letters, 76, 1575-1578. http://dx.doi.org/10.1103/PhysRevLett.76.1575
- Holinde, K. (1981) Physics Reports, 68, 121-188. http://dx.doi.org/10.1016/0370-1573(81)90188-5
- Valderrama, M.P. and Ariola, E.R. (2011) Physical Review C, 83, Article ID: 044002. http://dx.doi.org/10.1103/PhysRevC.83.044002
- Particle Data Group, Roos, M., et al. (1970) Physics Letters, B33, 125.
- Particle Data Group, Söding, P., Bartels, J., Barbaro-Galtieri, A., Enstrom, J.E., Lasinski, T.A., Rittenberg, A., Rosenfeld, A.H., Trippe, T.G., Barash-Schmidt, N., Bricman, C., Chaloupka, V. and Roos, M. (1972) Physics Letters B, 39, 25- 145.
- Trippe, T.G., Barbaro-Galtieri, A., Kelly, R.L., Rittenberg, A., Rosenfeld, A.H., Yost, G.P., et al. (1976) Reviews of Modern Physics, 48, S1-S245. http://dx.doi.org/10.1103/RevModPhys.48.S1
- Gross, F. (1993) Relativistic Quantum Mechanics and Field Theory. John Wiley & Sons, New York.
- Bjorken, J.D. and Drell, S.D. (1964) Relativistic Quantum Mechanics. McGraw-Hill Book Company, New York.
- Reid, R.V. (1968) Annals of Physics, 50, 411-448. http://dx.doi.org/10.1016/0003-4916(68)90126-7
- Nambu, Y. and Jona-Lasinio, G. (1961) Physical Review, 122, 345-358. http://dx.doi.org/10.1103/PhysRev.122.345
- Fujita, T. (2011) Symmetry and Its Breaking in Quantum Field Theory. 2nd Edition, Nova Science Publishers, New York.
- Fujita, T. and Kanda, N. (2013) Fundamental Problems in Quantum Field Theory. Bentham Publishers, Emirate of Sharjah. http://dx.doi.org/10.2174/97816080575591130101
- Nishijima, K. (1969) Fields and Particles. W. A. Benjamin, Inc., New York.
- Kanda, N., Abe, R., Fujita, T., Kato, H. and Tsuda, K. (2011) T-Matrix of Z0 Decay into Two Photons. http://arxiv.org/abs/1109.0926