Received 27 January 2015; accepted 13 February 2015; published 25 February 2015

ABSTRACT

This paper studies the problem of isochronal synchronization of chaotic systems with time-de- layed mutual coupling. Based on the invariance principle of differential equations, an adaptive feedback scheme is proposed for the stability of isochronal synchronization between two identical chaotic systems. Unlike the usual linear feedback, the variable feedback strength is automatically adapted to isochronally synchronize two identical chaotic systems with delay-coupled, so this scheme is analytical, and simple to implement in practice. Simulation results show that the isochronal synchronization behavior is determined by time delay.

Keywords:

Isochronal Synchronization, Mutual Coupling, Adaptive Control

1. Introduction

Synchronization of nonlinear systems, particularly chaotic systems, has attracted the attention of many researchers [1] [2] . Many control techniques have been devised for chaos synchronization [3] - [7] . In practice, control systems frequently present time delays due to i) finite time necessary for sensing state information, ii) finite time needed for information processing and transmission and iii) finite time necessary for the control actuator to respond to a given command. It is worth noting that the general idea of synchronization of chaotic systems with coupling delay seems to follow the idea of simple stabilization of a slave chaotic system in the delayed trajectory of its master. As such, given a master system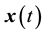, a slave system 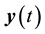and coupling delay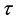, it is understood that the system achieve complete synchronization when 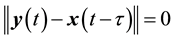as, as assumed in [8] . This form of synchronization is referred to in the literature as achronal synchronization [9] .

Isochronal synchronization has been considered in numerical simulations [9] - [13] and experimental setups [11] [14] - [16] . In this case, somewhat counter intuitively, chaotic units synchronize without any relative time delay, although the transmitted signal is received with a large time lag. In most of the rigorous results based on the Lyapunov-Krasovskii stability or Lyapunov-Razumikhin stability, the proposed scheme is very specific, but also the added controller is sometimes too big to be physically practical. One practical scheme is the linear feed- back. However, in such a technique it is very difficult to find the suitable feedback constant, and thus numerical calculation has to be used, e.g., the calculation of the conditional Lyapunov exponents. Due to numerical calculation, such a scheme is not regular since it can be applied only to particular models. More unfortunately, it has been reported that the negativity of the conditional Lyapunov exponents is not a sufficient condition for complete chaos synchronization, see [17] . Therefore, the synchronization based on these numerical schemes cannot be strict (i.e., high-qualitative), and is generally not robust against the effect of noise. Especially, in these schemes a very weak noise or a small parameter mismatch can trigger the desynchronization problem due to a sequence of bifurcations [18] .

Actually, this open problem, although significant for complete chaos synchronization, is very difficult and cannot admit the optimization solution [3] . For example, in [13] , rigorous criteria are presented to guarantee isochronal synchronization motion, but the criteria are so complicated that specific numerical calculation is necessary for particular examples in practice.

In this paper, we give a novel answer to the above open problem. We prove rigorously by using the invariance principle of differential equations [19] that a simple feedback coupling with updated feedback strength, i.e., an adaptive feedback scheme, can strictly isochronally synchronize two identical chaotic systems with time-delayed mutual coupling. Furthermore, we research the relationship between isochronal synchronization behavior and time delay.

2. Adaptive Feedback Controller

Consider an n-dimensional chaotic system governed by ODE,

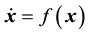, (1)

where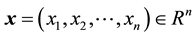, is a nonlinear vector function. And let 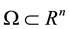be a chaotic bounded set of Equation (1) which is globally attractive. For the vector function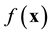, we give a general assumption.

For any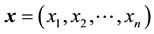, , 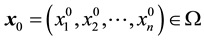there exists a constant 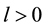satisfying

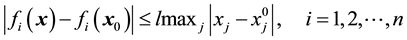. (2)

We call the above condition as the uniform Lipschitz condition, and l refers to the uniform Lipschitz constant. Note this condition is very loose, for example, the condition (2) holds as long as 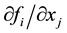are bounded. Therefore the class of systems in the form of Equations (1) and (2) include all well-known chaotic and hyperchotic systems.

Now, consider a pair of identical chaotic systems with bidirectional delay coupling in the form

, (3)

, (4)

where the feedback coupling diagonal matrix, and its diagonal elements are k_i, i = 1, 2, , n; denote the coupling delay. The problem is to design a feedback matrix such that isochronal synchronization is guaranteed to occur for coupling delay. Let, denote the synchronization error of Equations (3) and (4). Instead of the usual linear feedback, the feedback strength, here will be duly adapted according to the following update law:

, (5)

where, are arbitrary constants, and is a design parameter such that

,. Thus, , are arbitrary constants due

to, are arbitrary constants. For this reason, one can choose proper constants as the values of, , and do not consider the value of. Now, we introduce an important lemma, i.e., the well-known Lasalle invariance principle [19] .

Lemma 1: Consider the n-dimensional vector differential equation

. (6)

Let be a scalar function with continuous first partials for all. Assume that

(1) for all,

(2) for all.

Let E be the set of all points where and let M be the largest invariant set of Equation (6) contained in E (A set is said to be invariant if each solution starting in M remains in M for all t). Then every solution of Equation (6) bounded for approaches M as.

Theorem 1: Suppose that the uniform Lipschitz condition (2) holds, then the bounded solutions starting from arbitrary initial values of systems (3), (4) and (5) possess asymptotic behavior: and as, where and is a constant vector depending on the initial values.

Proof: For the 3n-dimensional systems (3), (4) and (5), we construct the following scalar function:

, (7)

where is a constant bigger than, i.e.,. Obviously, , for all. By differentiating the function along the trajectories of systems (3), (4) and (5), we obtain

(8)

Namely, for systems (3), (4) and (5), the constructed scalar function satisfies the conditions (1) and (2) in Lemma 1. In the other side, from the above deduction it is easy to find that the set as in Lemma 1 is given by. Moreover, in conjunction with systems (3), (4) and (5) the largest invariant set contained in is. Then Theorem 1 follows from Lemma 1, where is a constant vector depending on the initial values (and the parameter, as well).

Obviously, such isochronal synchronization motion is strict (i.e., high-qualitative), global (as long as the chaotic attractor is globally attractive), and nonlinear stable. In particular, the nonlinear global stability implies that such isochronal synchronization is quite robust against the effect of noise, namely under the case of presenting a small noise, the synchronization error eventually approaches zero and ultimately fluctuates around zero wherever the initial values start.

3. Simulation Results

This section illustrates the applications of the results obtained in this paper through the isochronal synchronization of Lorenz chaotic system. The Lorenz system [20] is described by, where

, (9)

such that the coupled systems are given in the form

, (10)

, (11)

with the update law (5). The parameters considered are, ,. The initial conditions are ar-

bitrary and the transients are disregarded, so that when the feedback control functions are activated, the systems are in the chaotic regime. The systems (10) and (11) are solved using fourth Runge-Kutta method, and time step is set as 0.01. Let,. The initial feedback strength is chosen to be,. The corresponding numerical results are shown in Figure 1 and Figure 2. Here, we choose two different time delay values of and as simulation parameters for the data shown in Figure 1 and Figure 2, respectively. To explicitly show the control effect of the proposed method, the time interval is divided into two parts: At the first stage of the simulation, no control input is applied; the control input is then activated at 10 seconds.

To further verify the robust against the effect of noise and parameter mismatch, an additive uniformly distributed noise in the range (i.e., a noise of the strength 0.5) is present in the coupling signals and, and parameter mismatches are slowly random time-varying in the range. The initial

conditions are arbitrary and the transients are disregarded, so that when the feedback control functions are activated, the systems are in the chaotic regime. The systems (10) and (11) are solved using fourth Runge-Kutta method, and time step is set as 0.01. Let,. The initial feedback strength is chosen to be,. The corresponding numerical results are shown in Figure 3. Here, we choose the time delay value of as simulation parameter for the data shown in Figure 3. To explicitly show the control effect of the proposed method, the time interval is divided into two parts: At the first stage of the simulation, no control input is applied; the control input is then activated at 10 seconds.

Form Figure 1, we can see that isochronal synchronization can be quickly achieved by the present control scheme (i.e., the transient time to synchronization is very short). From Figure 2, we can see that the steady states are achieved at, and isochronal synchronization is vanished. Simulation results show that isochronal synchronization of Lorenz system occurs when. So, isochronal synchronization sensitively depends on the time delay. And the critical time delay may be different in different chaotic systems. In practice, the critical time delay can be obtained from simulation results. From Figure 3, we can see that such isochronal synchronization is robust against the effect of noise and parameter mismatch.

4. Conclusions

In this study, we have given a novel answer to an open problem in the field of isochronal synchronization. In comparison with previous methods, the proposed scheme supplies a simple, analytical, and (systematic) uniform

controller to isochronal synchronization strictly two arbitrary identical chaotic systems satisfying a very loose condition. The technique is simple to implement in practice, and quite robust against the effect of noise and parameter mismatch. Simulation results show that the isochronal synchronization behavior sensitively depends on the time delay. There exists a critical time delay such that the isochronal synchronization occurs otherwise the steady states are achieved.

Acknowledgements

The research is supported by the Talents Project of Sichuan University of Science and Engineering (No. 2011RC07), the Key project of Artificial Intelligence Key Laboratory of Sichuan Province (No. 2011RZJ02), the Science and Technology Key Project of Zigong (No. 2012D09), the Cultivation Project of Sichuan University of Science and Engineering (No. 2012PY19), the High-level Innovative Talents Plan of Sichuan University of Science and Engineering (2014), the National Natural Science Foundation of China (Grant No: 11426047), the Basic and Advanced Research Project of CQCSTC (Grant No: cstc2014jcyjA00040) and the Research Fund of Chongqing Technology and Business University (Grant No: 2014-56-11).

References