Journal of Modern Physics
Vol.05 No.18(2014), Article ID:52545,11 pages
10.4236/jmp.2014.518202
Effect of Projectile Break-Up Threshold Energy on Incomplete Fusion at Energy ≈ 4 - 7 MeV/Nucleon
Sabir Ali1*, Tauseef Ahmad1, Kamal Kumar1, Isar Ahmad Rizvi1, Avinash Agarwal2, Sandeep S. Ghugre3, Ajit Kumar Sinha3, Ashok Kumar Chaubey4
1Department of Physics, Aligarh Muslim University, Aligarh, India
2Department of Physics, Bareilly College, Bareilly, India
3UGC-DAE Consortium for Scientific Research, Kolkata, India
4Department of Physics, Addis Ababa University, Addis Ababa, Ethiopia
Email: *sabirjhk@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 October 2014; revised 12 November 2014; accepted 7 December 2014
ABSTRACT
Complete and incomplete fusion cross sections have been measured for the 20Ne + 51V system to investigate the influence of projectile break-up at or above the barrier energies. The excitation function of the individual reaction channel measured using off-line γ-ray spectroscopy has been compared with those estimated theoretically using the statistical model code PACE4. A significant fraction of incomplete fusion has been found in the production of residues involving α-particle in the exit channel. In order to understand the energy dependence of incomplete fusion reactions, incomplete fusion fraction has been deduced, which has also been compared with the earlier data available for 12C and 16O projectiles to look for the projectile structure dependence.
Keywords:
Heavy Ion Induced Reaction, Complete Fusion, Incomplete Fusion, Break-Up Reaction

1. Introduction
Recent experimental studies of nuclear reactions, involving heavy ion as projectiles, indicate that complete fusion (CF) and incomplete fusion (ICF) processes are the dominant and competing mode of reactions at energies near and above the Coulomb barrier [1] -[4] . The fusion reaction proceeds for the energetic projectiles capable of overcoming the fusion barrier, resulting from the sum of repulsive Coulomb and attractive nuclear potentials. A model calculation was proposed by Gasques et al. [5] suggesting the suppression of CF due to the break-up of incident projectile under the influence of the target’s field. Since then, the study of projectile break-up and its effect on CF suppression has become an active topic of research [6] -[8] . In recent years, it has been observed that for low Z-projectiles (Z ≤ 10), e.g., 12C, 16O and 20Ne, with incident energies slightly above the Coulomb barrier, interacting with medium and heavy mass targets, both the CF and ICF processes may be considered as the dominant reaction mechanism [9] - [14] . CF has been experimentally defined as the capture of total charge or mass of the incident projectile by the target nucleus. In order to explain the dynamics of ICF reactions, several models were proposed. Among these theoretical models, the most effective and comprehensive one is the model proposed by Udagawa and Tamura [15] . According to break-up fusion model of Udagawa and Tamura [15] , ICF is usually understood as a two-step process: break-up of the incident projectile in the vicinity of the target, followed by fusion of one of the projectile fragment with the target nucleus, while the other escapes. It is now established that ICF reaction starts competing with CF at bombarding energies just above the Coulomb barrier and is characterized by an incomplete transfer of momentum from projectile to target i.e., fusion products carry only a part of the incident projectile’s momentum [4] . The break-up of projectiles 12C, 14N and 16O into α-cluster in an interaction with the target nuclei was first observed by Britt and Quinton [16] . However, Inamura et al. [17] have modified the understanding about the ICF reactions by performing the particle-γ coincidence experiment. Recently, Singh et al. [18] have shown that ICF reactions can also be used as a promising tool to populate the high spin states. Till now several theories and models have been proposed to understand the break-up process [15] [19] , but still there are various issues to be addressed. Morgenstern et al. [20] proposed the mass-asymme- try systematic, which was later on supplemented by Singh et al. [21] by introducing the projectile structure de- pendency of ICF, i.e., the ICF depended on mass-asymmetry as well as on the projectile structure. Further, Yadav et al. [6] proposed the α-Q (Qα) value systematic according to which ICF was dictated by the Qα value of the projectile, i.e., more negative Qα value translated into less ICF fraction. Extensive experimental studies, using the loosely bound projectiles, have been carried out to understand the mechanism of the break-up process [22] [23] , but the experimental data involving strongly bound projectiles are very scarce. In recent years, Singh et al. [11] and Ali et al. [24] have studied the ICF reactions and its dependence on mass-asymmetry using 20Ne projectile on different targets. Similar studies were also carried away by other groups using 12C [25] [26] and 16O [21] [27] [28] projectiles. Light heavy α-cluster projectiles (5 ≤ Z ≤ 10) like 12C, 16O and 20Ne, covering a wide range of break-up threshold energy (EB.U) [4.73 MeV (20Ne) - 7.36 MeV (12C)], seem to be the good candidates for the study of ICF reaction and its dependence on EB.U value of the projectile. Moreover, as suggested in recent studies [6] [22] , the projectile structure also plays an important role in ICF reactions. Hence, a comparison of the experimental data involving different light heavy α-cluster projectiles, straddle over a range of EB.U, on a single target will provide a better understanding about the effects of projectile structure on ICF reactions. With this motivation, the present work is carried out using 20Ne ion beam on 51V target. The observed results were merged with the results obtained by Ismail et al. from the study of 12C [29] and 16O [30] induced reactions on 51V target, to acquire a clear understanding about the systematic of ICF reaction with the EB.U of the α-cluster projectiles. In the present work excitation functions (EFs) of 10 radionuclides, namely 67Ge(p3n), 66Ge(p4n), 66Ga(αn), 61Cu(2α2n), 60Cu(2α3n), 61Co(2α2p), 56Mn(3α2pn), 55Co(3α4n), 62Zn(αp4n) and 63Zn(αp3n), populated through CF and/or ICF processes in the reaction of 20Ne + 51V, have been measured in the energy range of ≈82 - 145 MeV using activation technique. Experimentally measured EFs are then compared with the theoretical values calculated using the statistical model code PACE4 [31] . In the next section, details of the experimental setup are discussed. The analysis and interpretation of the EFs of evaporation residues (ERs) populated through CF and/or ICF processes, and the ICF strength function are presented in Section 3. Final section contains the summary and conclusion of the work presented here.
2. Experimental Details
2.1. Target Preparation and Irradiation
In order to carry out the experiment, first the self-supporting target foils of isotopically pure (99.97%) 51V of thicknesses ranging from ≈1.19 - 1.50 mg/cm2 and Al-degrader foils of thicknesses ranging from ≈1.47 - 1.64 mg/cm2 were prepared at Target Lab of VECC, Kolkata. The thickness of each target and degrader foil was measured separately by two methods. Firstly, by weighing the 51V target and Al-degrader foils, and secondly, by measuring the energy loss suffered by 5.485 MeV α-particles from the 241Am source while traversing the target and degrader medium. The measured thicknesses of 51V target and Al-degrader foils using these two methods were quite in agreement with each other. The prepared target foils were cut into square pieces of 1.5 ´ 1.5 cm2 and placed into the Aluminum holders of standard size having concentric holes of 10 mm in diameter. Each target foil was backed by an Al foil of appropriate thickness (hereafter called the target catcher foil assembly) to trap the heavy recoiling products produced in the reaction. The use of stack-foil activation technique, i.e., by using a set of successive target-catcher foil arrangement, helps in reducing the energy of the beam on the subsequent targets and ensured a relatively wide energy range for measuring the excitation function (the energy dependence of cross section). The stack-foil activation technique has this considerable advantage of allowing the simultaneous determination, in a single irradiation, of the excitation functions of a large number of exit channel products. This technique has been extensively utilized in the study of nuclear reactions using the stable ion beams and the results were found to be quite satisfactory and in agreement with the predictions of theoretical models [26] [27] [32] .
The stack was placed normal to the beam direction with 51V target facing the beam and it was irradiated with 20Ne6+ ion beam at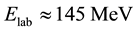 . Keeping in view the half-lives of interest, irradiation has been carried out for ≈11 hrs. The weighted average beam current of about ≈40 nA behind the target assembly was measured with an electron suppressed Faraday cup, using a current integrator device, for every 2 min, so as to correct for the variation, if any, in the beam intensity during the irradiation, which are particularly important for short lived radionuclides. Despite of precautionary measures to keep the beam current constant, there exist some fluctuation in the beam current and the error arising due to the beam current fluctuation was found to be less than 6%. The incident energy of 20Ne6+ ion beam on each target foil, present in the stack, was calculated from the energy degradation of the initial beam energy using stopping power software SRIM [33] . The incident energy on each target foil has been taken as the energy at half of the target thickness. Beam flux was measured by two methods. Firstly, by measuring the time-weighted beam current, and secondly, by measuring the total charge collected in Faraday cup. The beam flux calculated using these two methods were found to agree well with each other.
. Keeping in view the half-lives of interest, irradiation has been carried out for ≈11 hrs. The weighted average beam current of about ≈40 nA behind the target assembly was measured with an electron suppressed Faraday cup, using a current integrator device, for every 2 min, so as to correct for the variation, if any, in the beam intensity during the irradiation, which are particularly important for short lived radionuclides. Despite of precautionary measures to keep the beam current constant, there exist some fluctuation in the beam current and the error arising due to the beam current fluctuation was found to be less than 6%. The incident energy of 20Ne6+ ion beam on each target foil, present in the stack, was calculated from the energy degradation of the initial beam energy using stopping power software SRIM [33] . The incident energy on each target foil has been taken as the energy at half of the target thickness. Beam flux was measured by two methods. Firstly, by measuring the time-weighted beam current, and secondly, by measuring the total charge collected in Faraday cup. The beam flux calculated using these two methods were found to agree well with each other.
2.2. Post Irradiation Analysis and Identification of Residues
After irradiation, the γ-ray activities produced in each target foil of the stack was recorded using 60 cm3 HPGe detector coupled to a PC based data acquisition system at VECC, Kolkata. The resolution of HPGe detector was found to be 1.9 keV for 1.33 MeV γ-ray from 60Co source. The geometry dependent photo-peak detection efficiency of the HPGe detector at various source-detector separations were measured using the 152Eu source of known strength. The γ-ray spectroscopy software package RADWARE [34] has been used for analyzing the γ-ray spectrum. A typical γ-ray energy spectrum obtained from the irradiation of 51V target by 20Ne6+ ion beam at 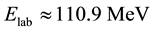 is shown in Figure 1. Various peaks in the observed γ-ray spectra were assigned to different ERs on the basis of their characteristic γ-radiation as well as by their measured half-lives. The measured half-lives of the observed ERs were found to be in good agreement with their literature values. The nuclear spectroscopic data used in the evaluation and measurement of the cross sections were taken from the Radioactive Isotopes Data Table of Brown and Firestone [35] and are listed in Table 1 for ready reference.
is shown in Figure 1. Various peaks in the observed γ-ray spectra were assigned to different ERs on the basis of their characteristic γ-radiation as well as by their measured half-lives. The measured half-lives of the observed ERs were found to be in good agreement with their literature values. The nuclear spectroscopic data used in the evaluation and measurement of the cross sections were taken from the Radioactive Isotopes Data Table of Brown and Firestone [35] and are listed in Table 1 for ready reference.
The reaction cross section of identified ERs populated via different possible channels were estimated using standard formulation [8] , given by
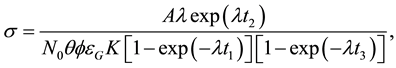 (1)
(1)
where A is the total number of counts recorded under the peak in time t3, λ is the decay constant of the product nucleus, N0 is the total number of nuclei present in the target foil, μ is the branching ratio of identified γ-ray, A is the incident beam flux, εG is the geometry-dependent efficiency of the HPGe detector, t1 is the irradiation time of the stack, t2 is the time elapsed between the termination of the irradiation and start of the counting, t3 is the
counting time and  is the self-absorption correction factor for the target material of thickness
is the self-absorption correction factor for the target material of thickness
“d” with the absorption coefficient “μ”. The correction factor for the decay of the induced activity due to the delay time t2 between the stop of irradiation and the start of the counting is taken as  and the correction factor due to decay of the irradiated sample during the data accumulation time t3 is taken as
and the correction factor due to decay of the irradiated sample during the data accumulation time t3 is taken as
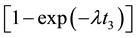 . During the irradiation, a factor
. During the irradiation, a factor 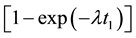 takes care of the decay of ERs and is known
takes care of the decay of ERs and is known
Figure 1. Typical γ-ray spectrum of 20Ne + 51V system obtained from irradiation at .
.
Table 1. List of observed reaction channels in the 20Ne + 51V reaction are given in first column along with the half-life in column 2 and other columns have spectroscopic properties.
as the saturation correction factor.
Various factors are likely to introduce error and uncertainty in the measured reaction cross sections. Some of the potential sources of error in the present work are as follows: 1) Fluctuation in the beam current lead to variation in the flux. Proper care has been taken to keep the beam current constant. However, error arising due to this factor was found to be less than 6%. 2) Non-uniformity of the target thickness leads to an uncertainty in determining the number of target nuclei. In order to check the uniformity of the target, the thickness of each target foil has been measured at different position by α-transmission method as well as by weighing the individual foils using a microbalance. Error due to the uncertainty in target thickness was found to be less than 3%. 3) Errors arising due to the geometry-dependent detector efficiency, caused by the statistical uncertainty in the counts under the peak, were estimated to be less than 5%. 4) Error contributed due to the dead time of the spectrometer was kept below 8% by suitably adjusting the sample-detector separation. Efforts were made to minimize the uncertainty and the overall error estimated in the present work does not exceed 22%.
3. Analysis and Interpretation of the Results
In order to understand that up to what extent the decay of various radionuclide can be justified by equilibrated compound nucleus decay, experimentally measured EFs are analyzed using the code PACE4 [31] . This code is based on the Hauser-Feshbach theory of compound nucleus (CN) decay, and uses statistical approach of CN de- excitation by Monte Carlo procedure. The code calculates at each stage of de-excitation, the angular momentum projection which enables the determination of angular distributions of the emitted particles. PACE4 uses the BASS model to calculate the fusion cross sections 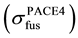 [36] . The nuclear parameters like Q-value, fission cross section, optical model parameters and γ-ray strength function required for the calculations are inbuilt in the code. The optical model potentials of Becchetti and Greenlees [37] are used for calculating the transmission coefficients for neutrons and protons, and the optical model potential of Satchler [38] is used for α-particle emissions. In the description of γ-ray competitions, emissions of E1, E2, M1, and M2 γ-rays are included and the strengths for these transitions are taken from the tables of Endt [39] . The decay intensities of these γ-rays in Weisskopf unit are E1 = 0.00008, M1 = 0.025, E2 = 4.80, and M2 = 0.0195 for the 20Ne + 51V system. The dif-
[36] . The nuclear parameters like Q-value, fission cross section, optical model parameters and γ-ray strength function required for the calculations are inbuilt in the code. The optical model potentials of Becchetti and Greenlees [37] are used for calculating the transmission coefficients for neutrons and protons, and the optical model potential of Satchler [38] is used for α-particle emissions. In the description of γ-ray competitions, emissions of E1, E2, M1, and M2 γ-rays are included and the strengths for these transitions are taken from the tables of Endt [39] . The decay intensities of these γ-rays in Weisskopf unit are E1 = 0.00008, M1 = 0.025, E2 = 4.80, and M2 = 0.0195 for the 20Ne + 51V system. The dif-
fuseness parameter 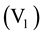 in the transmission coefficient,
in the transmission coefficient, 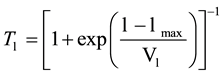 , is taken as 4ħ, and the
, is taken as 4ħ, and the
value of fusion barrier, from PACE4 calculation for the entire energy range, was found to be 32.33 MeV. The level density parameter “a” (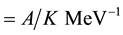 , where A is the mass number of the composite system and K is a free parameter) is one of the important parameter in PACE4 calculation. The level density parameter a is often described by
, where A is the mass number of the composite system and K is a free parameter) is one of the important parameter in PACE4 calculation. The level density parameter a is often described by
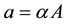 (2)
(2)
where α is a constant obtained from fitting of the available known data. However, there are models which suggest that level density parameter may have more complicated form than what was stated in Equation (2). Kataria et al. [40] , on the basis of the results of earlier investigation of the thermodynamic properties of nuclei, presented a semi empirical nuclear level density formula. On the basis of prescription of Kataria’s model of level density parameter and some previous results [1] [2] [4] , in the present work the value of K is varied from 8 to 12 in step of 2 (K = 8, 10, 12) to reproduce the experimentally measured EFs of ERs populated through pxn channel, within the physically justified limits. The values of some important parameters used in PACE4 calculations of the present system are listed in Table 2. It may be pointed out that any enhancement in EFs, above the values predicted by PACE4, may be attributed to some physical processes not included in the code PACE4.
3.1. Evaporation Residues Populated through pxn Channels
Complete fusion of 20Ne projectile with 51V target lead to the formation of excited compound nucleus 71As*. The dominant decay mode of 71As* through the emission of neutron and proton lead to the formation of isotope 66,67Ge via pxn (x = 3, 4) channel. The remaining ERs have too short/long half-lives and difficult to extract from the measured gamma lines. The experimentally measured fusion cross sections of the pxn channel residues were given in Table 3 and plotted in Figure 2(a) and Figure 2(b). As can be seen from Figure 2(a) and Figure 2(b), the experimental EFs of the residues populated through pxn channel were in good agreement with their theoretical values calculated using the code PACE4 for level density parameter K = 8. The values of K = 10, 12 also reproduces the experimental EFs of pxn channel residues as is evident from Figure 2 but K = 8 gives a slightly better fit. A good agreement between the theoretical and experimental EFs confirms the production of these
Table 2. List of some important parameters used to perform the PACE4 calculations.
Table 3. Experimentally measured reaction cross section of pxn (x = 3, 4) ERs produced in 20Ne + 51V reaction are given in column 2 - 3 for the energy listed in column 1. The sum total of measured cross section of residues populated through pxn channels are listed in column 4 where as column 5 gives the corresponding PACE4 values. Column 6 gives the experimental fusion cross sections where as column 7 represents R. See text for details.
Figure 2. Experimentally measured EFs of ERs (a) 67Ge(p3n) and (b) 66Ge (p4n) are compared with the PACE4 predictions for different values of level density parameter (K = 8, 10, 12).
residues through the de-excitation of fully equilibrated compound nucleus formed through the CF reaction. The pxn (x = 3, 4) channel ERs observed in the present work have very little contribution to CF cross sections. The remaining CF residues could not be detected due to their too short/long half-lives. The unaccounted CF cross section due to the formation of stable/unstable ERs in the present reaction, were accounted using the statistical model code PACE4 as it was done earlier in Ref. [41] [42] . By using the code PACE4, ratio
(x = 3, 4) is calculated and using this ratio experimental fusion cross section is calculated as
The values of experimental fusion cross sections 
3.2. Evaporation Products via α-Emitting Channels
In order to understand the formation mechanism of low Z-residues, experimentally measured EFs of α-channel residues along with their PACE4 values are plotted and as a representative case the EFs of 63Zn(αp3n) and 60Cu(2α3n) are shown in Figure 3(a) and Figure 3(b). α-channel residues were expected to be populated via CF and/or ICF processes. As can be seen from Figure 3, there is a significant enhancement in the experimentally measured reaction cross sections over the theoretically calculated values. This enhancement in experimental reaction cross section over the predicted PACE4 values is attributed to the contribution of ICF in the formation of α-channels residues. It is also observed that degree of ICF contributions, in the formation of ERs populated through α-emitting channels, are varying from residue to residue. For example, the trend of EF measured for 66Ga(αn) residue reflects the interplay between the contributions of CF and ICF processes through two different decay channels:
Figure 3. Experimentally measured EFs of ERs (a) 63Zn(αp3n) and (b) 60Cu(2α3n), expected to be populated via CF and/or ICF processes, are compared with their the theoretical prediction (PACE4).
1) CF: The excited 71As* nucleus formed through CF reaction may decay via the emission of an α-particle and a neutron (αn channel) as
Here Ethr. is the threshold energy for the given reaction.
2) ICF: Only a part of the incident projectile (i.e., 16O) fuses with the 51V target to form an incompletely fused composite system 67Ga*, while the α-particle moves in the forward direction as a spectator. The excited 67Ga* nucleus further decay via the emission of a neutron (n) as
(α-particle as a spectator),
Furthermore, in order to have a better representation, the sum of experimentally measured reaction cross sections of all identified α-emitting channel residues (i.e., the sum of experimentally measured reaction cross sections of 66Ga, 60,61Cu, 61,55Co, 56Mn and 62,63Zn residues), have been compared with those estimated theoretically using the statistical model code PACE4 in Figure 4(a). As can be seen from this figure, the sum of experimentally measured reaction cross sections of α-emitting channel residues 

3.3. ICF Strength Function
Experimentally measured reaction cross sections of the individual ERs populated through α-emitting channel in 20Ne + 51V reaction are listed in column 2 - 9 of Table 4. In Table 4, column 10 gives the sum of ICF cross sections



Figure 4. (a) Sum total of experimentally measured (dashed line) and theoretically predicted (solid line) EFs of the observed α-emitting channel residues are compared; (b) Total fusion cross section (σTF), sum of all CF 

Table 4. Experimentally measured reaction cross section of individual α-channel ERs populated in 20Ne + 51V reaction along with the
last column of Table 4 gives the percentage fraction of ICF (FICF) calculated as











Moreover, in order to have a better insight into the onset and influence of ICF, FICF has been deduced from the analysis of the given data. To have an idea about the projectile structure effect on the underlying reaction dynamics, the values of FICF (%) are plotted in Figure 5(a) as a function of reduced projectile energy (Ec.m/Vb) for the present system along with those of 16O + 51V and 12C + 51V systems from Ref. [29] [30] . The ICF strength function FICF, is taken as an empirical definition of the probability of ICF at different projectile energies. As
Figure 5. (a) FICF (%) for the 20Ne + 51V system along with those of 16O + 51V and 12C + 51V system as a function of reduced projectile energy (Ec.m/Vb); (b) FICF (%) as a function of break-up threshold projectile energy (EB.U) for the three different projectiles on 51V target at a constant Vrel = 0.0863c.
shown in Figure 5(a), the value of FICF was found to be 2.97% at 1.84Vb and increases smoothly up to 22.13% at 3.22Vb for 20Ne + 51V system whereas for 16O + 51V system it rises from 3.15% at 1.99Vb to 11.13% at 2.65Vb and in the case of 12C + 51V system it was 3.65% at 2.23Vb and reaches a maximum value of 11.88% at 3.33Vb. The observed increasing trend of FICF (%) with Ec.m/Vb suggests that break-up probability of incident projectile increases under the influence of increasing input angular momenta. The incident projectile, under the influence of target’s field, may break-up into energetically favored α-fragments to pave the path for the ICF reactions. 20Ne projectile is likely to break-up into α + 16O whereas 16O projectile is expected to break-up into α + 12C and 12C projectile into α + 8Be. Moreover, the effect of EB.U values of these α-cluster projectiles on their break-up probability was quite evident from the observed trend of FICF (%). As can be seen from Figure 5(a), the values of FICF (%) for the 20Ne + 51V reaction was maximum, followed by 16O + 51V reaction, and minimum in the case of 12C + 51V reaction throughout the energy range. This particular trend of FICF (%) is associated with the magnitude of EB.U value of the incident projectile. Lower EB.U value of a projectile makes it more susceptible to the break-up process and hence leading to a higher value of FICF.
3.4. Systematics of ICF for Different α-Cluster Projectile System
The α-cluster projectiles with lower EB.U value, as in the present case, may break-up before undergoing fusion with the target and in turn give rise to ICF. Similar results were also observed for strongly bound α-cluster projectiles, having relatively higher EB.U values, e.g., 16O and 12C, but at slightly higher incident energies [43] [44] . In order to elaborate the observed trend of FICF (%) with Ec.m/Vb (Figure 5(a)) in a better way, the three most energetically favorable break-up channels for the 20Ne, 16O and 12C induced reactions on 51V target have been calculated and listed in Table 5. The other break-up channels, not shown in Table 5, require energy ≥ 20 MeV. For these three projectiles, break-up into α-fragments are energetically most favorable as evident from Table 5. Experiments with 6Li and 7Li projectiles incident on 208Pb [45] [46] target also supports the break-up of incident projectiles into energetically favored partitions of α + 2H and α + 3H, respectively. Similar results were also reported from the study of reactions using 12C on 208Pb, 13C on 207Pb [47] , 12,13C on 159Tb [6] [48] and 10,11B on 209Bi [5] . The FICF (%) for 20Ne, 16O and 12C induced reactions on 51V target are shown in Figure 5(b) as a function of EB.U value of the projectiles. As it can be inferred from this figure, FICF (%) decreases linearly with increase in EB.U value of the incident projectiles, suggesting a major role played by EB.U value of the projectiles on ICF. The break-up probability of incident projectile is expected to be influenced by its EB.U value. The larger FICF (%) for 20Ne as compared to 16O and 12C is related to lower EB.U value of 4.73 MeV for 20Ne as compared to 7.16 MeV and 7.36 MeV for 16O and 12C, respectively.
Moreover, a systematic variation of FICF with mass asymmetry 
Table 5. In column 3, Q values for the most energetically favorable break-up channels of projectiles 20Ne, 16O and 12C given in column 1, and in the last column, the product following the capture of each of the fragments of the 51V target.
of projectile structure dependence. Morgenstern et al. suggested that for a fixed relative velocity (Vrel/c), given by

where m is the reduced mass of the projectile-target system and Vb is the fusion barrier, the fraction of incomplete fusion increases almost linearly with increasing mass asymmetry.
4. Summary and Conclusion
In the present work, EFs of 10 evaporation residues populated via CF and/or ICF processes in 20Ne + 51V system have been measured at energies ≈ 4 - 7 MeV/nucleon. The experimentally measured EFs of pxn (x = 3, 4) channel residues were found to agree reasonably well with the predictions of PACE4, indicating their production via CF only. However, in the case of ERs populated through α-emitting channels, a significant enhancement in the experimental reaction cross section has been observed as compared to the PACE4 calculations. This enhancement in experimental reaction cross section over the PACE4 value was attributed to the ICF of 20Ne with 51V. It has been observed that ICF fraction of the total fusion cross section FICF, increases with the increase in projectile energy. The present observation thus supports the systematic of Morgenstern et al. [20] . The present result along with the previously studied systems shows a dependency of FICF on EB.U value of the incident projectile. Obviously, a further experimental investigation on ICF as a function of the break-up threshold energy, which may perhaps be target specific, is required. As a future outlook, one can attempt similar experiments with the same projectile on a series of heavy targets (e.g., Pb, Bi and others) in order to investigate the extent of CF and ICF. In particular, a systematic study of this kind can test the recently published three-dimensional classical dynamical model [49] , which relates the below barrier no capture break-up yield to above barrier CF and ICF cross sections.
Acknowledgements
The authors thank the Variable Energy Cyclotron Centre (VECC), Kolkata and Department of Physics, AMU, Aligarh for extending necessary facilities to perform this work. Authors are also thankful to Prof. M. Shoeb and A. Yadav for their valuable suggestions. Authors (S.A and K.K) thank the University Grants Commission (UGC) of the Government of India for financial assistance.
References
- Kumar, K., et al. (2013) Physical Review C, 88, Article ID: 064613. http://dx.doi.org/10.1103/PhysRevC.88.064613
- Kumar, K., et al. (2013) Physical Review C, 87, Article ID: 044608.
- Amanuel, F.K., et al. (2011) Physical Review C, 84, Article ID: 024614. http://dx.doi.org/10.1103/PhysRevC.84.024614
- Yadav, A., et al. (2012) Physical Review C, 85, Article ID: 034614.
- Gasques, L.R., Hinde, D.J., Dasgupta, M., Mukherje, A. and Thomas, R.G. (2009) Physical Review C, 79, Article ID: 034605. http://dx.doi.org/10.1103/PhysRevC.79.034605
- Yadav, A., et al. (2012) Physical Review C, 86, Article ID: 014603.
- Gomes, P.R.S., et al. (2011) Physical Review C, 84, Article ID: 014615. http://dx.doi.org/10.1103/PhysRevC.84.014615
- Amanuel, F.K., et al. (2011) European Physical Journal A, 47, 156. http://dx.doi.org/10.1140/epja/i2011-11156-6
- Agarwal, A., et al. (2012) EPJ Web of Conferences, 38, Article ID: 17001.
- Singh, D., et al. (2012) Nuclear Physics A, 879, 107. http://dx.doi.org/10.1016/j.nuclphysa.2012.01.020
- Singh, D., Ali, R., Afzal Ansari, M., Tomar, B.S., Rashid, M.H., Guin, R. and Das, S.K. (2011) Physical Review C, 83, Article ID: 054604. http://dx.doi.org/10.1103/PhysRevC.83.054604
- Singh, D., Afzal Ansari, M., Ali, R., Sathik, N.P.M. and Ismail, M. (2006) Journal of the Physical Society of Japan, 75, Article ID: 104201. http://dx.doi.org/10.1143/JPSJ.75.104201
- Sharma, M.K., Singh, B.P., Gupta, S., Musthafa, M.M., Bhardwaj, H.D., Prasad, R. and Sinha, A.K. (2003) Journal of the Physical Society of Japan, 72, 1917-1925. http://dx.doi.org/10.1143/JPSJ.72.1917
- Ahmad, T., Rizvi, I.A., Agarwal, A., Kumar, R., Golda, K.S. and Chaubey, A.K. (2011) International Journal of Modern Physics E, 20, 645. http://dx.doi.org/10.1142/S0218301311018137
- Udagawa, T. and Tamura, T. (1980) Physical Review Letters, 45, 1311. http://dx.doi.org/10.1103/PhysRevLett.45.1311
- Britt, H.C. and Quinton, A.R. (1961) Physical Review, 124, 877. http://dx.doi.org/10.1103/PhysRev.124.877
- Inamura, T., Ishihara, M., Fakuda, T., Shimoda, T. and Hiruta, H. (1977) Physics Letters B, 68, 51-54. http://dx.doi.org/10.1016/0370-2693(77)90032-6
- Singh, P.P., Singh, B.P., Sharma, M.K., Gupta, U., Kumar, R., Singh, D., et al. (2009) Physics Letters B, 671, 20-24. http://dx.doi.org/10.1016/j.physletb.2008.11.035
- Bondrof, J.P., De, J.N., Fai, G., Karvinen, A.O.T., Jakobsson, B. and Randrup, J. (1980) Nuclear Physics A, 333, 285- 301. http://dx.doi.org/10.1016/0375-9474(80)90234-1
- Morgenstern, H., Bohne, W., Galster, W., Grabisch, K. and Kyanowski, A. (1984) Physical Review Letters, 52, 1104. http://dx.doi.org/10.1103/PhysRevLett.52.1104
- Singh, P.P., Singh, B.P., Sharma, M.K., Unnati, Singh, D.P., Prasad, R., et al. (2008) Physical Review C, 77, Article ID: 014607. http://dx.doi.org/10.1103/PhysRevC.77.014607
- Dasgupta, M., Hinde, D.J., Butt, R.D., Anjos, R.M., Berriman, A.C., Carlin, N., et al. (1999) Physical Review Letters, 82, 1395. http://dx.doi.org/10.1103/PhysRevLett.82.1395
- Dasgupta, M., Hinde, D.J., Hagino, K., Moraes, S.B., Gomes, P.R.S., Anjos, R.M., et al. (2002) Physical Review C, 66, Article ID: 041602(R). http://dx.doi.org/10.1103/PhysRevC.66.041602
- Ali, R., Singh, D., Afzal Ansari, M., Rashid, M.H., Guin, R. and Das, S.K. (2010) Journal of Physics G: Nuclear and Particle Physics, 37, Article ID: 115101. http://dx.doi.org/10.1088/0954-3899/37/11/115101
- Mukherjee, S., Sharma, A., Sodaye, S., Goswami, A. and Tomar, B.S. (2006) International Journal of Modern Physics E, 15, 237. http://dx.doi.org/10.1142/S0218301306003886
- Chakarbarty, S., Tomar, B.S., Goswami, A., Gubbi, G.K., Manohar, S.B., Sharma, A., Bindukumar, B. and Mukherjee, S. (2000) Nuclear Physics A, 678, 355-366. http://dx.doi.org/10.1016/S0375-9474(00)00339-0
- Chowdhury, D.P., Guin, R., Saha, S.K. and Sudersanan, M. (2003) Nuclear Instruments and Methods in Physics Research B, 211, 288.
- Gupta, U., Singh, D.P., Sharma, M.K., Yadav, A., Kumar, R., Singh, B.P., et al. (2008) Nuclear Physics A, 811, 77-92. http://dx.doi.org/10.1016/j.nuclphysa.2008.07.013
- Ismail, M. and Sharma, R.P. (1999) Parmana Journal of Physics, 52, 609.
- Ismail, M., Sharma, R.P. and Rashid, M.H. (1997) Parmana Journal of Physics, 49, 623.
- Gavron, A. (1980) Physical Review C, 21, 230. http://dx.doi.org/10.1103/PhysRevC.21.230
- Penionzhkevich, Yu.E., Lukyanov, S.M., Astabatyan, R.A., Demekhina, N.A., Ivanov, M.P., Kalpakchieva, R., et al. (2009) Journal of Physics G: Nuclear and Particle Physics, 36, Article ID: 025104. http://dx.doi.org/10.1088/0954-3899/36/2/025104
- Ziegler, J.F. (2006) SRIM-2006. The Stopping Power and Range of Ions in Matter. http://www.srim.org/SRIM/SRIMLEGL.htm
- Radford, D. (1995) Software Package for Interactive Graphical Analysis of Gamma-Ray Coincidence Data. http://radware.phy.ornl.gov/
- Browne, E. and Firestone, R.B. (1986) Table of Radioactive Isotopes. Wiley, New York.
- Bass, R. (1974) Nuclear Physics A, 231, 45-63. http://dx.doi.org/10.1016/0375-9474(74)90292-9
- Becchetti, F.D. and Greenlees, G.W. (1969) Physical Review, 182, 1190. http://dx.doi.org/10.1103/PhysRev.182.1190
- Satchler, G.R. (1965) Nuclear Physics, 70, 177-195. http://dx.doi.org/10.1016/0029-5582(65)90233-6
- Endt, P.M. (1981) Atomic Data and Nuclear Data Tables, 26, 47-91. http://dx.doi.org/10.1016/0092-640X(81)90011-5
- Kataria, S.K., Ramamurthy, V.S. and Kapoor, S.S. (1978) Physical Review C, 18, 549. http://dx.doi.org/10.1103/PhysRevC.18.549
- Parkar, V.V., Palit, R., Sharma, S.K., Naidu, B.S., Santra, S., Joshi, P.K., et al. (2010) Physical Review C, 82, Article ID: 054601. http://dx.doi.org/10.1103/PhysRevC.82.054601
- Palshetkar, C.S., Santra, S., Chatterjee, A., Ramachandran, K., Thakur, S., Pandit, S.K., et al. (2010) Physical Review C, 82, Article ID: 044608. http://dx.doi.org/10.1103/PhysRevC.82.044608
- Gutbrod, H.H., Winn, W.G. and Blann, M. (1973) Physical Review Letters, 30, 1259. http://dx.doi.org/10.1103/PhysRevLett.30.1259
- Zolnowski, D.R., Yamada, H., Cala, S.E., Kahler, A.C. and Sugihara, T.T. (1978) Physical Review Letters, 41, 92. http://dx.doi.org/10.1103/PhysRevLett.41.92
- Scholz, D., Gemmeke, H., Lassen, L., Ost, R. and Bethge, K. (1977) Nuclear Physics A, 288, 351-364. http://dx.doi.org/10.1016/0375-9474(77)90140-3
- Shotter, A.C., Bice, A.N., Wouters, J.M., Rae, W.D. and Cerny, J. (1981) Physical Review Letters, 46, 12. http://dx.doi.org/10.1103/PhysRevLett.46.12
- Kalita, K. (2011) Journal of Physics G: Nuclear and Particle Physics, 38, Article ID: 095104. http://dx.doi.org/10.1088/0954-3899/38/9/095104
- Yadav, A., et al. (2012) EPJ Web of Conferences, 21, Article ID: 08005.
- Diaz-Torres, A., Hinde, D.J., Tostevin, J.A., Dasgupta, M. and Gasques, L.R. (2007) Physical Review Letters, 98, Article ID: 152701. http://dx.doi.org/10.1103/PhysRevLett.98.152701
NOTES
*Corresponding author.

















