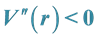Journal of Modern Physics
Vol.05 No.17(2014), Article ID:51901,6 pages
10.4236/jmp.2014.517187
Revisiting Galactic Rotation Curves Given a Noncommutative-Geometry Background
Peter K. F. Kuhfittig, Vance D. Gladney
Department of Mathematics, Milwaukee School of Engineering, Milwaukee, USA
Email: kuhfitti@msoe.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 September 2014; revised 2 October 2014; accepted 21 October 2014
ABSTRACT
It was shown earlier by Rahaman et al. that a noncommutative-geometry background can account for galactic rotation curves without the need for dark matter. The smearing effect that characterizes noncommutative geometry is described by means of a Gaussian distribution intended to replace the Dirac delta function. The purpose of this paper is two-fold: 1) to account for the galactic rotation curves in a more transparent and intuitively more appealing way by replacing the Gaussian function by the simpler Lorentzian distribution proposed by Nozari and Mehdipour and 2) to show that the smearing effect is both a necessary and sufficient condition for meeting the stability criterion.
Keywords:
Galactic Rotation Curves, Noncommutative Geometry

1. Introduction
That noncommutative geometry can account for galactic rotation curves without the need for dark matter has already been shown in Ref. [1] . The effect in question is a small effect, not only difficult to determine but also difficult to present in an intuitively appealing way. This paper uses a slightly different approach that may provide a clearer picture. This approach is introduced in Section 2 followed by the analysis in Section 3. It is shown in Section 4 that the noncommutative-geometry background is needed for stability.
2. Noncommutative Geometry and Galactic Rotation Curves
An important outcome of string theory is the realization that coordinates may become noncommuting operators on a 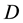 -brane [2] [3] . The commutator is
-brane [2] [3] . The commutator is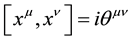 , where
, where 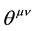 is an antisymmetric matrix. As discussed in Refs. [4] [5] , noncommutativity replaces point-like structures by smeared objects. The smearing effect is accomplished by using a Gaussian distribution of minimal length
is an antisymmetric matrix. As discussed in Refs. [4] [5] , noncommutativity replaces point-like structures by smeared objects. The smearing effect is accomplished by using a Gaussian distribution of minimal length  instead of the Dirac delta function [6] [7] . A simpler but equally effective way is to assume that the energy density of the static and spherically symmetric and particle-like gravitational source has the form [8] [9]
instead of the Dirac delta function [6] [7] . A simpler but equally effective way is to assume that the energy density of the static and spherically symmetric and particle-like gravitational source has the form [8] [9]
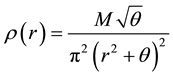 (1)
(1)
Here the mass  of the particle is diffused throughout the region of linear dimension
of the particle is diffused throughout the region of linear dimension 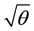 due to the uncertainty. The noncommutative geometry is an intrinsic property of spacetime and does not depend on any particular feature such as curvature.
due to the uncertainty. The noncommutative geometry is an intrinsic property of spacetime and does not depend on any particular feature such as curvature.
To connect the noncommutative geometry to dark matter and hence to galactic rotation curves, we need to introduce the metric for a static spherically symmetric spacetime:
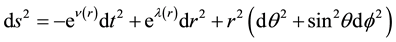 (2)
(2)
For this metric, the Einstein field equations are
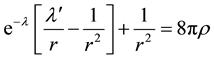 (3)
(3)
 (4)
(4)
and
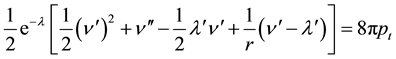 (5)
(5)
One goal of any modified gravitational theory is to explain the peculiar behavior of galactic rotation curves without postulating the existence of dark matter: test particles move with constant tangential velocity 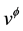 in a circular path. It is noted in Ref. [10] that galactic rotation curves generally show much more complicated dynamics. For present purposes, however, the analysis can be restricted to the region in which the velocity is indeed constant. So taking the observed flat rotation curves as input, it is well known that, as a result,
in a circular path. It is noted in Ref. [10] that galactic rotation curves generally show much more complicated dynamics. For present purposes, however, the analysis can be restricted to the region in which the velocity is indeed constant. So taking the observed flat rotation curves as input, it is well known that, as a result,
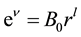 (6)
(6)
where 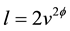 and
and  is an integration constant [11] . Moreover, it is shown in Ref. [12] that in the presumed dark matter dominated region,
is an integration constant [11] . Moreover, it is shown in Ref. [12] that in the presumed dark matter dominated region, 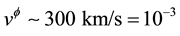 for a typical galaxy. So
for a typical galaxy. So 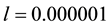
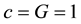
To address the issue of stable orbits, we first note that given the four-velocity 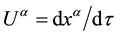

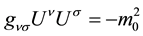
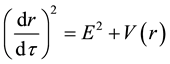
which results in

Here the constants 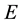


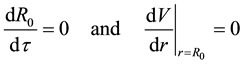
From these conditions, we obtain [1]
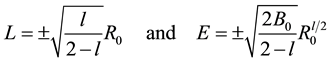
The orbits are stable if
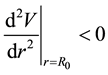
and unstable if
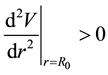
3. The Solution
The smeared gravitational source in Equation (1) leads to a smeared mass. More precisely, the Schwarzschild solution of the Einstein field equations associated with the smeared source leads to the line element

The smeared mass is implicitly given by
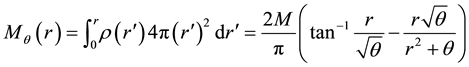
which can also be obtained from Equation (3) (Equations (4) and (5) also yield 
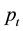
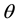

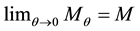
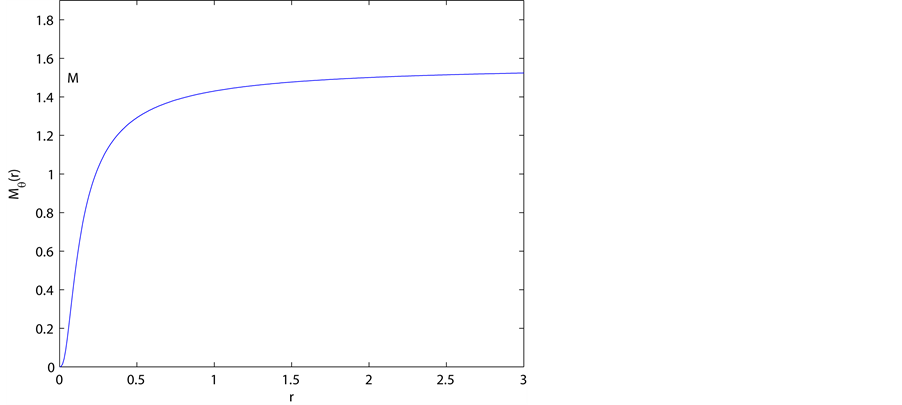
so that the modified Schwarzschild solution reduces to the ordinary Schwarzschild solution (see Figure 1).
Figure 1. The graph of the smeared mass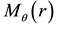
The mass 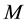
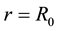

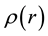

Observe that the mass of the shell becomes
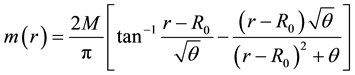
again dependent on 

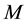
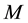
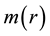
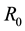
At this point we can finally address the question of stability by examining the potential 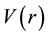
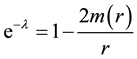
So from Equation (8),

To see the effect of the smearing, we first compute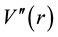

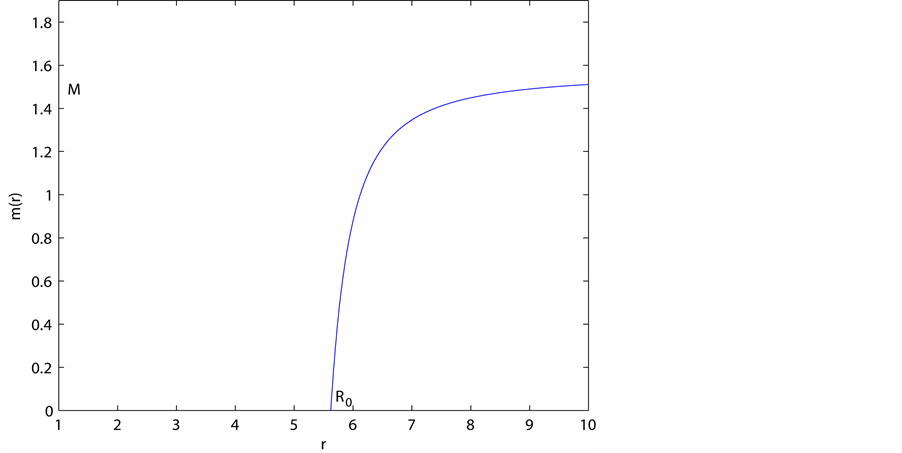
Figure 2. The graph of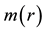
From Equation (17),

and

It now follows directly that at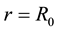
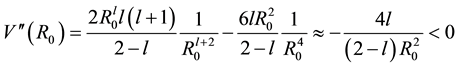
We therefore have a stable orbit at 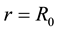
4. The Need for Noncommutative Geometry
We saw in the previous section that the smearing effect in noncommutative geometry is responsible for the stable orbit at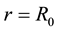
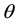
To this end, we return to Equation (20) and observe that the third term,

strongly dominates near 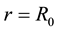
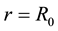
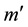
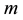

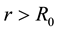
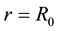
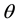


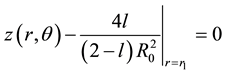
Hence 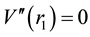
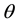

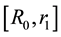

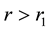
4.1.
As noted above, for
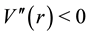
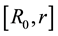
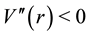
To this end, we obtain from Equation (25),

and hence from Equations (21) and (22),
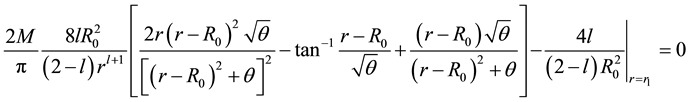
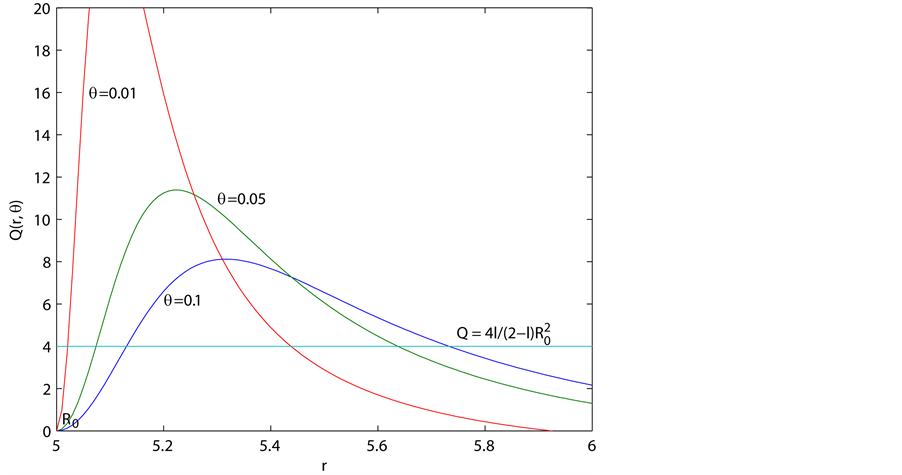
Figure 3. Plot showing that if
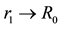
for every fixed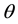


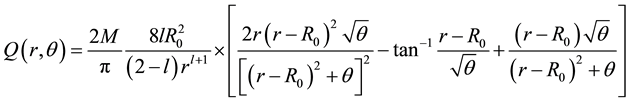
as a function of 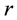
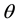


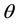


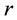
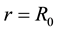
So, as a next step, we plot 

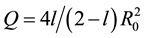


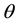
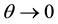
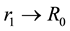


4.2.
Recall that 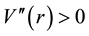
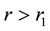
5. Conclusions
It is shown in Ref. [1] that a noncommutative-geometry background can account for galactic rotation curves without the need for dark matter. The smearing effect that characterizes noncommutative geometry is described by means of a Gaussian distribution of minimal length
That noncommutative geometry, which has all the appearances of a small effect and can account for the galactic rotation curves, is consistent with the corresponding situation in 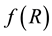
References
- Rahaman, F., Kuhfittig, P.K.F., Chakraborty, K., Usmani, A.A. and Ray, S. (2012) General Relativity and Gravitation, 44, 905-916. http://dx.doi.org/10.1007/s10714-011-1320-5
- Witten, E. (1996) Nuclear Physics B, 460, 335-350. http://dx.doi.org/10.1016/0550-3213(95)00610-9
- Seiberg, N. and Witten, E. (1999) Journal of High Energy Physics, 9909, Article ID: 032.
- Smailagic, A. and Spalluci, E. (2003) Journal of Physics A, 36, L-467-L-471. http://dx.doi.org/10.1088/0305-4470/36/33/101
- Smailagic, A. and Spalluci, E. (2003) Journal of Physics A, 36, L-517-L-521. http://dx.doi.org/10.1088/0305-4470/36/39/103
- Nicollini, P., Smailagic, A. and Spalluci, E. (2006) Physics Letters B, 632, 547-551. http://dx.doi.org/10.1016/j.physletb.2005.11.004
- Kuhfittig, P.K.F. (2013) International Journal of Pure and Applied Mathematics, 89, 401-408. http://dx.doi.org/10.12732/ijpam.v89i3.11
- Nozari, K. and Mehdipour, S.H. (2008) Classical and Quantum Gravity, 25, Article ID: 175015. http://dx.doi.org/10.1088/0264-9381/25/17/175015
- Kuhfittig, P.K.F. (Submitted) Macroscopic Traversable Wormholes with Zero Tidal Forces Inspired by Noncommutative Geometry.
- Böhmer, C.G., Harko, T. and Lobo, F.S.N. (2008) Astroparticle Physics, 29, 386-392. http://dx.doi.org/10.1016/j.astropartphys.2008.04.003
- Nandi, K.K., Valitov, I. and Migranov, N.G. (2009) Physical Review D, 80, Article ID: 047301.
- Matos, T., Guzman, F.S. and Nunez, D. (2000) Physical Review D, 62, Article ID: 061301R.
- Nandi, K.K., Filippov, A.I., Rahaman, F., Ray, S., Usmani, A.A., Kalam, M. and De Benedictis, A. (2009) Monthly Notices of the Royal Astronomical Society, 399, 2079-2087. http://dx.doi.org/10.1111/j.1365-2966.2009.15399.x