Received 18 June 2014; revised 15 July 2014; accepted 8 August 2014

ABSTRACT

This paper posits the discovery of the new elementary particles from the energy spectrum for the knees-ankles-toe of cosmic rays. The energy spectrum from 10⁹ eV to 10²⁰ eV appears to follow a single power law except few breaks at the knees-ankles-toe. The power index increases at the first knee and the second knee, and decreases at the ankle. Above 4 × 10¹⁹ eV, the power index increases as the “toe”. The fine structure of the cosmic ray spectrum shows that an ankle with decrease in power index is in between the first knee and the second knee, resulting in two knees, two ankles, and one toe. This paper posits that the knees-ankles-toe are explained by the very high-energy fermions and bosons in the periodic table of elementary particles that places all known leptons, quarks, gauge bosons, and the Higgs boson in the table with the calculated masses in good agreement with observed values. In the periodic table, some high-energy dimensional fermions (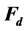where dimensional orbital number from 5 to 11) and bosons 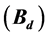are involved in the knees-ankles-toe. At the knees and the toe, some parts of the energies from the energy sources of cosmic rays are spent to generate 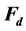and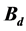, resulting in the increase of power index. The ankles are the the middle points (midpoints) between the adjacent dimensional fermions and bosons. At a midpoint, the energy is too high to keep the thermally unstable high-energy dimensional particle,resulting in the decay and the decrease of power index. The calculated masses of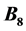, the midpoint, 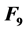, the midpoint, and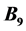, are 1.7 × 10¹⁵, 2 × 10¹⁶, 2.4 × 10¹⁷, 2.8 × 10¹⁸, and 3.2 × 10¹⁹ eV, respectively, which are in good agreement with observed 3 × 10¹⁵, 2 × 10¹⁶, 3 × 10¹⁷, 3 × 10¹⁸, and 4 × 10¹⁹ eV for the first knee, the first ankle, the second knee, the second ankle, and the toe, respectively. The mass of 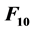is 4.4 × 10²¹ eV beyond the GZK limit, so 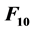and above are not observed.

Keywords:

Cosmic Rays, Knee, Ankle, Toe, the Periodic Table of Elementary Particles, New Elementary Particles

1. Introduction

The study of cosmic rays has been important for the study of elementary particles. Before the advent of particle accelerators, subatomic particles such as muon and mesons were first discovered from cosmic rays. Currently, high-energy cosmic rays have much higher energies than the energy of particles accelerated by the Large Hadron Collider. Cosmic rays again attract great interest in the study of elementary particles beyond the capacity of particle accelerators. This paper posits the discovery of the new elementary particles from the energy spectrum for the knees-ankles-toe of cosmic rays.

The energy spectrum from 10⁹ eV to 10²⁰ eV appears to follow a single power law 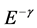except few breaks [1] . The power index, 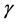, increases at 3 × 10¹⁵ eV known as the “first knee”, For energies above 3 × 10¹⁷ eV, the spectrum is even steeper at the second knee. The power index decreases at 3 × 10¹⁸ eV known as the “ankle”. The power index increases above 4 × 10¹⁹ eV as the “toe” [2] . The standard model for the origins of galactic cosmic rays is galactic supernova remnant (SNR). According to the SNR cosmic-ray hypothesis, charged particles are accelerated by the shock front created in a supernova and then further accelerated by the magnetic fields created in a supernova until they gain enough energy to escape this process and become newly formed cosmic rays. In the conventional theory, the knee marks the point where the magnetic fields as galactic accelerators reach their energetic limits, while the ankle marks the point where the galactic cosmic ray intensity falls below the intensity of cosmic rays from extragalactic sources of ultra-high-energy cosmic rays (UHECR) [3] . The exact reason for their presence is still an open question.

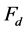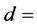This paper posits that the knees-ankles-toe are explained by the very high energy fermions and bosons in the periodic table of elementary particles [4] [5] that places all known leptons, quarks, gauge bosons, and the Higgs boson in the table with the calculated masses in good agreement with observed values. In the periodic table, some high-energy dimensional fermions (where dimensional orbital number from 5 to 11) and bosons 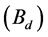are involved in the knees-ankles-toe. At the knees and the toe, some parts of the energies from the energy sources of cosmic rays are spent to generate 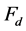and, resulting in the increase of power index. The ankles are the middle points (midpoints) between the adjacent dimensional fermions and bosons. At a midpoint, the energy is too high to keep the thermally unstable high-energy dimensional particle, resulting in the decay and the decrease of power index. The calculated masses of the dimensional bosons, fermions, and the midpoints are in good agreement with the observed knees, ankles, and toe. The mass of is 4.4 × 10²¹ eV beyondthe GZK limit, so and above are not observed.

In Section 2, the cosmic rays for the knees-ankle-toe are discussed. Section 3 describes the periodic table of elementary particles. Section 4 deals with the knees-ankles-toe in the periodic table of elementary particles.

2. The Cosmic Rays for the Knees-Ankles-Toe

The fine structure of the cosmic ray spectrum measured in Tunka-133 [6] and KASCADE Grande [7] [8] experiments shows that the spectrum in the energy range of 10¹⁶ to 10¹⁸ eV cannot be fitted with single power index. The power index decreases around 2 × 10¹⁶ eV for spectrum hardening and increases around 3 × 10¹⁷ eV for spectrum steepening. The decrease in power index at 2 × 10¹⁶ eV indicates the appearance of the “first ankle” before the “second ankle” at 3 × 10¹⁸ eV that also has a decrease in power index, and is usually considered as “the ankle”. As a result, there are two knees, two ankles, and one toe. The first knee, the first knee, the first ankle, the second knee, the second ankle, and the toe are at3 × 10¹⁵ eV, 2 × 10¹⁶ eV, 3 × 10¹⁷ eV, 3 × 10¹⁸ eV, and 4 × 10¹⁹ eV, respectively. Such spectrum signifies that the ankles with decrease in power index are the transition points between the two knees and between the second knee and the toe with increase in power index.

In terms of the sources of cosmic rays, cosmic rays below 10¹⁰ eV are solar cosmic rays, and cosmic rays from 10¹⁰ eV to 10¹⁸ eV are galactic cosmic rays within the Milky Way. One viable explanation for the ultrahigh energy cosmic rays above 3 × 10¹⁸ eV with different chemical composition from the second knee is an extragalactic origin. The high energy extragalactic cosmic rays are derived from the diffusion of low energy protons (<10¹⁷ eV) on extragalactic magnetic fields [6] .

3. The Periodic Table of Elementary Particles

In this paper, the knees-ankles-toe are explained by the very high energy fermions and bosons in the periodic table of elementary particles [4] [5] that places all known leptons, quarks, gauge bosons, and the Higgs boson in the table with the calculated masses in good agreement with observed values by using only four known constants: the number of the extra spatial dimensions in the eleven-dimensional membrane, the mass of electron, the mass of boson, and the fine structure constant of electromagnetism. As the periodic table of elements based on the atomic orbitals, the periodic table of elementary particles is based on the seven mass dimensions as the seven dimensional orbitals from to derived from the extra space dimensions of eleven dimensional membrane as in Figure 1.

The seven dimensional orbitals are arranged as, where and are dimensional fermion and dimensional boson. The dimensional fermions below are leptons and quarks. To distinguish leptons and quarks, another set of seven dimensional orbitals is needed as the auxiliary dimensional orbitals between to in addition to the original principal dimensional orbitals. The principal dimensional orbitals are mainly for leptons, while the auxiliary dimensional orbitals are mainly for quarks as in Figure 2.

The previous communications [4] shows that the masses of fundamental particles are related to each other with three simple formulae, and that the use of accepted mass data allows calculation of masses of many other particles. The formulae are

, (1a)

(1b)

, (1c)

where d is the dimensional orbital number from 6 to 11. Each dimension has its own, and all’s except of the seventh dimension (weak interaction) are equal to, the fine structure constant of electromagnetism. In the Standard Model, coupling constant as running coupling constant is based on the perturbative beta function where coupling constant changes logarithmically with energies. In Equation (1), different fermions and bosons with different d’s have different starting masses and coupling constants based on the non-perturba- tive calculation for the starting masses and coupling constants from Equation (1). Each starting mass orcoupling constant then has its own running mass orcoupling constant based on the perturbative beta function. The Standard Model does not provide the starting masses of leptons, quarks, and gauge bosons, while the periodic table of elementary particles provides the starting masses of leptons, quarks, and gauge bosons by using Equation (1) and some other equations [4] [5] . Therefore, the periodic table of elementary particles is consistent with and supplementary to the Standard Model.

The periodic table with leptons, quarks, and gauge bosons is described in Reference [4] [5] . The periodic table of elementary particles without leptons and quarks is as Table 1.

In Table 1, (the fine structure constant for electromagnetic field), , and [9] . is not same as because there is a mixing between and as the symmetry mixing between U(1) and SU(2) in the standard theory of the electroweak interaction, and is not equal to 1. The calculated value for is 0.02973, and is 0.2454 in good agreement with 0.2312 for the observed value of [10] .

The lowest energy boson at is the Coulomb field for electromagnetism. The second lowest boson at is (a spin 1 boson as a half of the spin 0 pion) for the strong interaction. The pion theory [11] where pions mediate the strong interaction works well at long enough distances (longer than the nucleon radius) or low enough energies. At short enough distances (shorter than the nucleon radius) or high enough energies, gluons emerge. In this paper, gluons are derived from the need to hide the auxiliary dimensional orbitals. As mentioned previously, leptons are derived mostly from the seven principal dimensional orbitals, while quarks are derived mostly from the seven auxiliary dimensional orbitals. Only the seven principal dimensional orbitals for leptons are revealed, while the seven auxiliary dimensional orbitals for quarks are hidden to preserve the seven apparent total dimensional orbitals instead of the fourteen apparent total dimensional orbitals. As a result, gluons emerge at the short distances to mediate the strong interaction among quarks in order to confine or hide isolated quarks (the auxiliary dimensional orbitals) within nucleons, while at the long distances without isolated quarks outside of nucleon at low energies, pions emerge to mediate the residual strong interaction for the nucleon-nucleon interaction or the nuclear force. (At low energies or long distances, gluons based on the negative perturbative beta function in QCD do not work due to the infrared divergence [12] .) Although all of the gauge bosons in the Standard Model are originated from the local gauge symmetry, only gluon results in the confinement, while all other gauge bosons do not result in confinement. The confinement is not automatic for all gauge bosons, and only gluon results in the confinement.

The third lowest boson at is for the weak interaction. In the Standard Model, bosons and boson are related. The mass of bosons is equal to the mass of boson times. Like photon at, is neutral, so instead of is the dimensional boson at. The highest energy boson is has the mass of the Planck mass for gravity. The calculated energy for is 1.1 × 10²⁸ eV in good agreement with the Planck mass, 1.2 × 10²⁸ eV. The knees-ankles-toe in cosmic rays involves_, , and.

4. The Knees-Ankles-Toe in the Periodic Table of Elementary Particles

The paper posits that at knees and the toe, some parts of the energies from the energy sources of cosmic rays are

spent to generate and, resulting in the increase of power index. The energy spectrum of cosmic rays is like the energy spectrum of a molecule. A slope change or peak in the curve of the spectrum of a molecule indicates the presence of a specific chemical bond, while aslope change or peak in the curve of the spectrum of cosmic rays indicates the presence of a specific dimensional particle. The ankles are the middle points (midpoints) between the adjacent dimensional fermions and bosons.

(2)

At a midpoint, the energy is too high to keep the thermally unstable high-energy dimensional particle, resulting in the decay and the decrease of power index. Unlike the thermally stable elementary particles for gravity and the Standard Model (the electroweak and the strong interactions), the high-energy dimensional particles outside of gravity and the Standard Model are not thermally stable. As a result, at the extremely high temperature in the beginning of the universe, only the thermally stable elementary particles for gravity and the Standard Model (the electroweak and the strong interactions) existed. The masses of leptons, quarks, and gauge bosons are too close together to be distinctive knees and ankles, so the knees-ankles-toe involves, , and whose masses are far apart to be detected as the knees-ankles-toe.

The calculated masses of, the midpoint, , the midpoint, and, are 1.7 × 10¹⁵, 2 × 10¹⁶, 2.4 × 10¹⁷, 2.8 × 10¹⁸, and 3.2 × 10¹⁹ eV, respectively, which are in good agreement with observed 3 × 10¹⁵, 2 × 10¹⁶, 3 × 10¹⁷, 3 × 10¹⁸, and 4 × 10¹⁹ eV for the first knee, the first ankle, the second knee, the second ankle, and the toe, respectively as in Table 2.

The mass of is 4.4 × 10²¹ eV beyondthe GZK (Greisen-Zatsepin-Kuzmin) limit, which occurs at about 5 × 10¹⁹ eV, as the maximum energy of cosmic ray particles that have traveled long distances (about 160 million light years), due to the theoretical energy losses of higher-energy ray particles and to scattering from photons in the cosmic microwave background. Therefore, and above are not observed.

5. Summary

This paper posits the discovery of the new elementary particles from the energy spectrum for the knees-ankles-toe of cosmic rays. The energy spectrum from 10⁹ eV to 10²⁰ eV appears to follow a single power law except few breaks at the knees-ankles-toe. The power index increases at the first knee and the second knee, and decreases at the ankle. Above 4 × 10¹⁹ eV, the power index increases as the “toe”. The fine structure of the cosmic ray spectrum shows that an ankle with decrease in power index is in between the first knee and the second knee, resulting in two knees, two ankles, and one toe. This paper posits that the knees-ankles-toe are explained by the very high-energy fermions and bosons in the periodic table of elementary particles that places all known leptons, quarks, gauge bosons, and the Higgs boson in the table with the calculated masses in good agreement with observed values. In the periodic table, some high-energy dimensional fermions (where dimensional orbital number from 5 to 11) and bosons are involved in the knees-ankles-toe. At the knees and the toe, some parts of the energies from the energy sources of cosmic rays are spent to generate and, resulting in the increase of power index. The ankles are the middle points (midpoints) between the adjacent dimensional fermions and bosons. At a midpoint, the energy is too high to keep the thermally unstable high- energy dimensional particle, resulting in the decay and the decrease of power index. The calculated masses

of, the midpoint, , the midpoint, and, are 1.7 × 10¹⁵, 2 × 10¹⁶, 2.4 × 10¹⁷, 2.8 × 10¹⁸, and 3.2 × 10¹⁹ eV, respectively, which are in good agreement with observed 3 × 10¹⁵, 2 × 10¹⁶, 3 × 10¹⁷, 3 × 10¹⁸, and 4 × 10¹⁹ eV for the first knee, the first ankle, the second knee, the second ankle, and the toe, respectively. The mass of is 4.4 × 10²¹ eV beyond the GZK limit, so and above are not observed.

References