Journal of Modern Physics
Vol.5 No.6(2014), Article ID:45033,4 pages DOI:10.4236/jmp.2014.56049
Self-Contradictions from the Excessive Use of Natural Units
Allen D. Allen
Physics Division, New Terra Enterprises, Los Angles, USA
Email: allend.allen@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 6 January 2014; revised 8 February 2014; accepted 5 March 2014
ABSTRACT
The hypothesis c = h = G = 1 implies that unit mass is not a single-valued function but rather has two widely varying values, such as 7.4 × 10−51 kg and 4.0 × 1035 kg. Hence, the considerable body of work in theoretical physics that uses this common convention must be deemed suspect. In order to avoid this problem, theoreticians must limit themselves to c = h = 1 or, exclusively, c = G = 1 depending upon whether they are chiefly concerned with atomic physics or with gravity, respectively.
Keywords:Primitive Dimensions, Measurement Systems, Natural Units

1. Introduction
The primitive dimensions of mechanics are space, mass and time. We can experience these dimensions intuitively through our senses. When we walk across a room we experience moving through an extent of physical space. When we do unaided manual labor we become familiar with mass or at least weight. When we celebrate an anniversary we acknowledge an interval of time lasting one year. But to make scientific measurements we need a measurement system.
Definition 1: A physical measurement system is an ordered 3-tupple containing three distinct literal words chosen from a natural language, such as English, that designate the unit of measurement for an interval of space, the unit of measurement for a quantity of mass, and the unit of measurement for an interval of time, in that order. Each element of a physical measurement system is independent of the other two.
The MKS system [meter, kilogram, second] is an example of a physical measurement system and the one that will be used in this paper. Note that the meter is not an intrinsic function of the kilogram or of the second, and the kilogram is not an intrinsic function of the second. Rather, each element of the MKS system was chosen by historical serendipity. For clarity, this paper will abbreviate kilogram as kg, and second as sec, but will not abbreviate meter.
There is a more historically recent type of measurement system.
Definition 2: A natural measurement system is an ordered 3-tuple [Ux, Um, Ut] of three distinct word variables that designate the unit of measurement for an interval of space, the unit of measurement for a quantity of mass, and the unit of measurement for an interval of time, in that order. The elements of a natural measurement system are not all independent of one another.
In theoretical physics it is a common practice to simplify calculations by using a natural measurement system to give one or more constants a magnitude of unity [1] -[13] . This is done without much thought or analysis, an oversight the present paper serves to correct.
2. Common Conventions
Begin with a simple but important observation.
Lemma: The ratio of two units of measurement for the same primitive dimension raised to the same power is a dimensionless real number.
Proof (by example): It is convenient to use an example that will be helpful in the sequel.
 . (1)
. (1)
Now consider a simple and common natural unit by adopting the convention,
 , (2)
, (2)
where c is the vacuum speed of light. Equation (2) means
 . (3)
. (3)
Equation (3) has simple solutions since it follows from (2) and (3) that
 , (4)
, (4)
 . (5)
. (5)
It then follows by lemma that
 , (6)
, (6)
where (meters·light-Ut−1) and (sec·Ut−1) are dimensionless but variable real numbers that depend upon the value for Ut in seconds.
Let k be a physical constant that must be expressed using all three primitive dimensions: space, mass and time. If we have c = 1, then it is obvious from (4)-(5) that in order to have c = k = 1, unit mass Um must be a single-valued function of unit time Ut. As a common example, suppose we have
 , (7)
, (7)
where h is Planck’s constant,
 . (8)
. (8)
Equations (7)-(8) mean that
 . (9)
. (9)
It follows from (9) that
 , (10)
, (10)
where by lemma (meters2·light-Ut−2) and (sec·Ut−1) are dimensionless real numbers. Without loss of generalization, assume Ut = “second”. Then from (1), (10) becomes
 . (11)
. (11)
But now suppose we want
 , (12)
, (12)
where
 (13)
(13)
is the gravitational constant. Then (12) becomes
 , (14)
, (14)
such that
 , (15)
, (15)
where by lemma, (meters3 light-Ut−3) and (Ut2 sec−2) are dimensionless real numbers. Again assume without loss of generalization that Ut = “second”. Then from (1) and 15,
 , (16)
, (16)
and
 . (17)
. (17)
Comparing (11) and (17), we see that the hypothesis
 (18)
(18)
implies
 (19)
(19)
Equation (19) is obviously false and by 86 orders of magnitude! Yet many theoreticians make use of (18) or natural units in the same form that substitute ℏ for h or 8πG for G [9] -[13] . This merely changes the values in (11) and (17) without making them equal. In order to confirm this, suppose we multiply h by a literal real number r±1, where r ≠ 1. Then (11) becomes
 . (20)
. (20)
We could also multiply G by a literal real number u±1, where u ≠ 1. Then (17) becomes
 . (21)
. (21)
Hence, 19 becomes
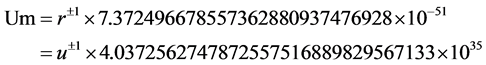 (22)
(22)
and
 . (23)
. (23)
Thus, literal numbers such as 1/2π or 8π or anything similar cannot begin to account for the magnitude of the error shown by (19).
3. Conclusions
It has been demonstrated that the excessive use of natural units due to a hypothesis in the form of h = c = G = 1 implies a grossly false assumption, such as 7.4 × 10−51 = 4.0 × 1035. Since anything can be proven if we start with a false hypothesis, the considerable body of theoretical research that relies on this false assumption [9] -[13] must be deemed suspect.
In order to avoid this problem, theoreticians must choose between c = h = 1 or, exclusively, c = G = 1 depending upon whether they are chiefly concerned with atomic physics or with gravity, respectively. As a reviewer was astute enough to point out, the hypothesis c = h = G = 1 has no physical meaning whatsoever. It is merely used to simplify calculations. But the constants h and G have very different physical meanings and to equate them is to wind up with a mathematical self-contradiction.
References
- Baumann, D. and Green, D. (2011) Journal of Cosmology and Astroparticle Physics, 2011. (IOP Journal)
- Li, M. and Wang, Y. (2010) Physics Letters B, 687, 243-247. http://dx.doi.org/10.1016/j.physletb.2010.03.042
- Longair, M.S. (2003) Planck and Natural Units. In: Theoretical Concepts in Physics: An Alternative View of Theoretical Reasoning in Physics, 2nd Edition, Cambridge University Press, New York, 336. http://dx.doi.org/10.1017/CBO9780511840173
- Perkins, D.H. (2000) Introduction to High Energy Physics. 4th Edition, Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511809040
- Artru, X. and Rullhusen, P. (1998) Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 145, 1-7. http://dx.doi.org/10.1016/S0168-583X(98)00241-9
- Barton, G. (1990) Physics Letters B, 237, 559-562. http://dx.doi.org/10.1016/0370-2693(90)91224-Y
- Boffi, S., Giusti, C. and Pacati, F.D. (1979) Nuclear Physics A, 319, 461-476. http://dx.doi.org/10.1016/0375-9474(79)90526-8
- Kolbenstvedt, H. (1967) Journal of Applied Physics, 38, 4785-4787. http://dx.doi.org/10.1063/1.1709220
- Tsyba, P.Y., Kulnazarov, I.I., Yerzhanov, K.K. and Myrzakulov, R. (2011) International Journal of Theoretical Physics, 50, 1876-1886. http://dx.doi.org/10.1007/s10773-011-0703-4
- Corda, C. (2009) International Journal of Modern Physics D, 18, 2275. http://dx.doi.org/10.1142/S0218271809015904
- Kothawala, D., Sarkar, S. and Padmanabhan, T. (2007) Physics Letters B, 652, 338-342. http://dx.doi.org/10.1016/j.physletb.2007.07.021
- Mirza, B. and Zamaninasab, M. (2007) Journal of High Energy Physics, 2007. (IOP Journal)
- Witten, E. (1986) Physics and Geometry. In: Proceedings of the International Congress of Mathematicians, Berkeley, 3-11 August 1986.

