Journal of Modern Physics
Vol.5 No.1(2014), Article ID:42260,6 pages DOI:10.4236/jmp.2014.51009
Diamond as a Solid State Quantum Computer with a Linear Chain of Nuclear Spins System
Departamento de Fsica de la Universidad de Guadalajara, Guadalajara, México
Email: gulopez@cencar.udg.mx
Received November 1, 2013; revised December 1, 2013; accepted January 2, 2014
ABSTRACT
By removing a 12C atom from the tetrahedral configuration of the diamond, replacing it by a 13C atom, and repeating this in a linear direction, it is possible to have a linear chain of nuclear spins one half and to build a solid state quantum computer. One qubit rotation, controlled-not (CNOT) and controlled-controlled-not (CCNOT) quantum gates are obtained immediately from this configuration. CNOT and CCNOT quantum gates are used to determined the design parameters of this quantum computer.
Keywords:Quantum Computer; Controlled-Not Gate; Diamond
1. Introduction
So far, the idea of having a working quantum computer with enough number of qubits (at least 1000) has faced two main problems: the decoherence [1-8] due the interaction of the environment with the quantum system, and technological limitations (pick up signal from NMR quantum computer [9,10], laser control capability in ion trap quantum computer [11,12], physical build up for more than two qubits like in photons cavities [13], atoms traps [14,15], Josephson’s joint ions [16], Aronov-Bhom devices [17], diamond NV device [18], or high field and high field gradients in linear chain of paramagnetic atoms with spin one half [19]). In particular, the linear chain of paramagnetic atoms of spin one half became a good mathematical model to make studies of quantum gates [20], quantum algorithms [21], and decoherence [22] which could be applied to other quantum computers. In this paper, one put together the ideas of using the diamond stable structure and the linear chain of spin one half nucleus. To do this, on the tetrahedral 12C (with nuclear spin zero) configuration of the diamond main structure, one removes a 12C element of this configuration and replace it by a 13C (with nuclear spin one half) atom, and one repeats this replacement along a linear direction of the crystal. By doing this replacement, one obtains a linear chain of atoms of nuclear spin one half which is protected from the environment by the crystal structure and the electrons cloud. Therefore, one could have a quantum computer highly tolerant to environment interaction and maybe not so difficult to build it, from the technological point of view.
2. 12C-13C Diamond and Spin-Spin Interaction
The above idea is represented in Figure 1, where the 13C atoms are place on the position of some 12C atoms. This replacement could be done using the same technics used to construct the diamond NV structure [23], or using ion implantation technics [24] and neutralization of 13C in the diamond [25]. It is assumed in this paper that this configuration can be built somehow.
Now, as one can see, the important interaction on this configuration is the spin-spin interaction between the nucleus of the 13C atoms. This interaction is well known [26] and is given by
 (1)
(1)
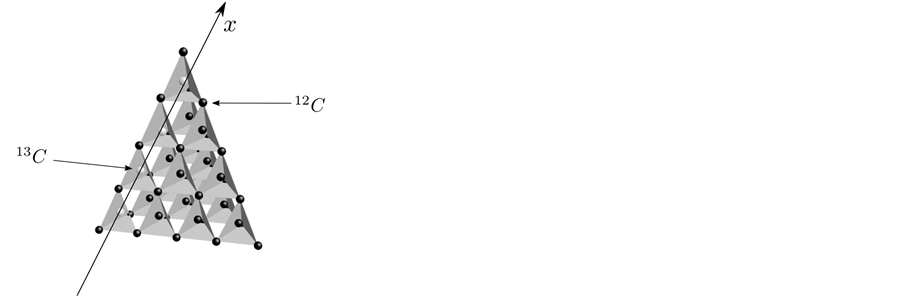
Figure 1. Diamond 12C -13C.
where the magnetic moment  of 13C’s is related with the nuclear spin as
of 13C’s is related with the nuclear spin as
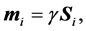 (2)
(2)
being ![]() the proton gyromagnetic ratio
the proton gyromagnetic ratio 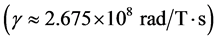 . Without loosing the main idea, it will be assumed here that 13C magnetic moment is due to proton. The variable
. Without loosing the main idea, it will be assumed here that 13C magnetic moment is due to proton. The variable  indicates the separation vector between two 13C nucleus, which has magnitude
indicates the separation vector between two 13C nucleus, which has magnitude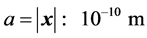 . Aligning the chain of 13C nucleus along the x-axis of the reference system and assuming Ising interaction between 13C nucleus, this energy can be written as
. Aligning the chain of 13C nucleus along the x-axis of the reference system and assuming Ising interaction between 13C nucleus, this energy can be written as
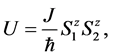 (3)
(3)
where the coupling constant ![]() has been defined as
has been defined as
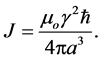 (4)
(4)
3. Hamiltonian of the System
Consider a magnetic field of the form
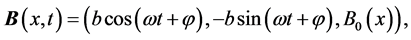 (5)
(5)
where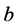 ,
, ![]() , and
, and 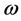 are the magnitude, the phase, and the frequency of the transverse rf-field. The z-component of the magnetic field has a gradient on the x-axis, determined by the difference on Larmore’s frequencies of the 13C’s nuclear magnetic moments,
are the magnitude, the phase, and the frequency of the transverse rf-field. The z-component of the magnetic field has a gradient on the x-axis, determined by the difference on Larmore’s frequencies of the 13C’s nuclear magnetic moments,
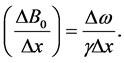 (6)
(6)
The magnetic field at the location of the ith-13C atom is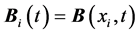 , and the interaction energy of the magnetic moments of the 13C atoms with the magnetic field is
, and the interaction energy of the magnetic moments of the 13C atoms with the magnetic field is
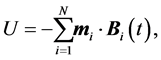 (7)
(7)
where ![]() is the number of 13C atoms aligned along the x-axis. This energy can be written as
is the number of 13C atoms aligned along the x-axis. This energy can be written as
 (8)
(8)
where  is the Larmore’s frequency of the ith-13C,
is the Larmore’s frequency of the ith-13C,
 (9)
(9)
![]() is the Rabi’s frequency,
is the Rabi’s frequency,
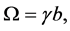 (10)
(10)
![]() and
and ![]() are the ascent and descent spin operators,
are the ascent and descent spin operators, 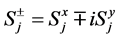 , and
, and ![]() has been defined as
has been defined as
![]() (11)
(11)
Let us consider first and second neighbor interactions among 13C nuclear spins, and assuming equidistant separation between any pair of spins, the Hamiltonian of the system is
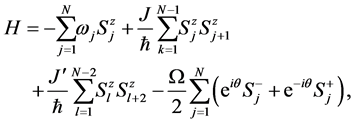 (12)
(12)
where ![]() is the coupling constant of first neighbor 13C atoms, and
is the coupling constant of first neighbor 13C atoms, and ![]() is the coupling constant of second neighbor 13C atoms which must be about one order of magnitude lower than
is the coupling constant of second neighbor 13C atoms which must be about one order of magnitude lower than![]() . One can write this Hamiltonian as
. One can write this Hamiltonian as , where
, where 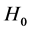 and
and ![]() are defined as
are defined as
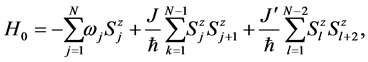 (13)
(13)
and
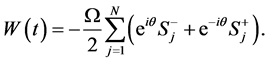 (14)
(14)
The operator 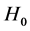 is diagonal on the basis
is diagonal on the basis 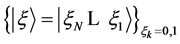 of the Hilbert space of
of the Hilbert space of ![]() dimensionality. Its eigenvalues defines the spectrum of the system,
dimensionality. Its eigenvalues defines the spectrum of the system,
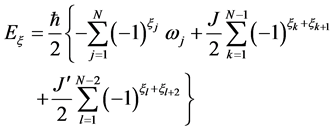 (15)
(15)
Since 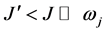 for
for![]() , this spectrum is not degenerated with
, this spectrum is not degenerated with 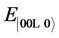 as the energy of ground state, and
as the energy of ground state, and 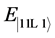 as the energy of the most exited state. To calculate the spectrum, one has used the following action of
as the energy of the most exited state. To calculate the spectrum, one has used the following action of 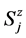 operator
operator
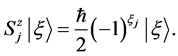 (16)
(16)
The Schrödinger’s equation,
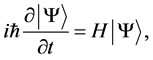 (17)
(17)
is solved by proposing a solution of the form
 (18)
(18)
which brings about the following system of first order differential equations on the interaction representation
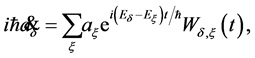 (19)
(19)
where 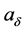 and
and 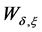 are defined as
are defined as
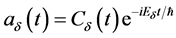 (20)
(20)
and
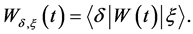 (21)
(21)
This is very well known procedure to solve time dependent Schrödinger’s equation, and the solution of Equation (19) brings about he unitary evolution of the system (given the initial condition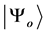 ).
).
Defining the evolution parameter 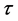 through the change of variable
through the change of variable 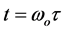
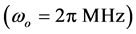 , the parameters
, the parameters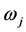 ,
, ![]() ,
, ![]() and
and ![]() are real numbers given in units of
are real numbers given in units of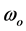 . This evolution parameter will be used below in the analysis of the CNOT quantum gate.
. This evolution parameter will be used below in the analysis of the CNOT quantum gate.
4. Analysis of the System
In order to get an operating quantum computer, one needs to show that, at least, one qubit rotation gate  and two qubits CNOT gate
and two qubits CNOT gate  or three qubits controlled-controlled-not (CCNOT) gate
or three qubits controlled-controlled-not (CCNOT) gate 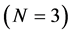 can be constructed from this quantum system. Because this quantum system is homeomorphic [27] to the linear chain of paramagnetic atoms with spin one half system [28], it is clear from the point of view of mathematical models that the above gates can be constructed with this 12C-13C diamond system. However, one needs to assign realistic workable parameters for the real design of a 12C-13C diamond quantum computer. To do this, one studies in this section the behavior of a quantum CNOT and CCNOT gates as a function of several parameters. One neglect one qubit rotation
can be constructed from this quantum system. Because this quantum system is homeomorphic [27] to the linear chain of paramagnetic atoms with spin one half system [28], it is clear from the point of view of mathematical models that the above gates can be constructed with this 12C-13C diamond system. However, one needs to assign realistic workable parameters for the real design of a 12C-13C diamond quantum computer. To do this, one studies in this section the behavior of a quantum CNOT and CCNOT gates as a function of several parameters. One neglect one qubit rotation 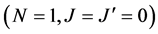 because it is obvious that one can get it through an arbitrary pulse on the rf-field with the frequency given by the Larmore's frequency of the qubit
because it is obvious that one can get it through an arbitrary pulse on the rf-field with the frequency given by the Larmore's frequency of the qubit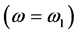 , for a single 13C atom in the diamond structure. In particular, the NOT quantum gate is obtained using a
, for a single 13C atom in the diamond structure. In particular, the NOT quantum gate is obtained using a  -pulse duration
-pulse duration 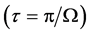 with this frequency. Therefore, the study of the CNOT
with this frequency. Therefore, the study of the CNOT  and CCNOT
and CCNOT 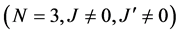 quantum gates is of the most interest. The equations for the two and three qubits dynamics are shown on the appendix. CNOT quantum gate corresponds to the transition
quantum gates is of the most interest. The equations for the two and three qubits dynamics are shown on the appendix. CNOT quantum gate corresponds to the transition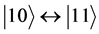 , and CCNOT quantum gate corresponds to the transition
, and CCNOT quantum gate corresponds to the transition . The first and second transitions are obtained through the resonant frequencies
. The first and second transitions are obtained through the resonant frequencies
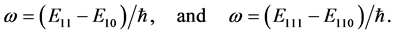 (22)
(22)
Larmore’s frequencies are denoted by ![]() and
and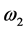 , and
, and 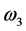 is parametrized as
is parametrized as
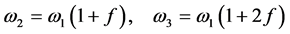 (23)
(23)
where  measures the relative change of the frequencies of qubits. The separation of the 13C nucleus,
measures the relative change of the frequencies of qubits. The separation of the 13C nucleus, 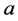 , is parametrized as
, is parametrized as
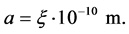 (24)
(24)
For the CNOT quantum gate, one has the initial conditions 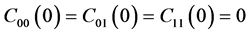 and
and 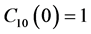 . The time is allowed to last a
. The time is allowed to last a  -pulse
-pulse , and one takes the coupling constant as a fixed paramenter,
, and one takes the coupling constant as a fixed paramenter,
![]() (25)
(25)
Figure 2 shows the fidelity parameter,
 (26)
(26)
at the end of the 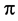 -pulse, as a function of the Rabi's frequency, where
-pulse, as a function of the Rabi's frequency, where 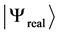 is the state obtained with the simulation, and
is the state obtained with the simulation, and 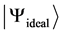 is the expected state
is the expected state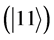 . The simulation was done for two different weak magnetic fields and for
. The simulation was done for two different weak magnetic fields and for 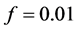 (1),
(1), 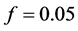 (2),
(2), 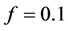 (3), and
(3), and 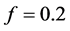 (4). The oscillations seen on this picture are due to the low and high contribution of the non resonant states (
(4). The oscillations seen on this picture are due to the low and high contribution of the non resonant states (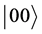 and
and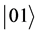 ) to the dynamics of the system, which depends on Rabi’s frequency and they are explained by the
) to the dynamics of the system, which depends on Rabi’s frequency and they are explained by the  -method [19]. As one can see from this picture , the CNOT gate is very well produced either with
-method [19]. As one can see from this picture , the CNOT gate is very well produced either with 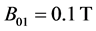 and
and 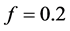 or with
or with 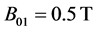 and
and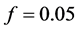 .
.
Figure 3 shows the gradient of magnetic field along the x-axis, the coupling constant![]() , and the fidelity
, and the fidelity 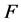 of the CNOT quantum gate as a function of the two qubits separation (characterized by the parameter
of the CNOT quantum gate as a function of the two qubits separation (characterized by the parameter![]() , Equation (24)), having
, Equation (24)), having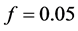 . As one can see, the fidelity is not sensitive for relatively wide variation of
. As one can see, the fidelity is not sensitive for relatively wide variation of![]() , meanwhile the gradient and coupling constant have the strong variation deduce from Equation (6) and Equation (4). Considering the separation of the two 13C atoms about the the length of the diamond unit cell, one can select
, meanwhile the gradient and coupling constant have the strong variation deduce from Equation (6) and Equation (4). Considering the separation of the two 13C atoms about the the length of the diamond unit cell, one can select![]() , corresponding to a coupling constant of
, corresponding to a coupling constant of![]() , and a magnetic field gradient of
, and a magnetic field gradient of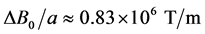 .
.
One needs to mention that in the case the alignment of the 13C atoms be along the z-axis (the same direction of
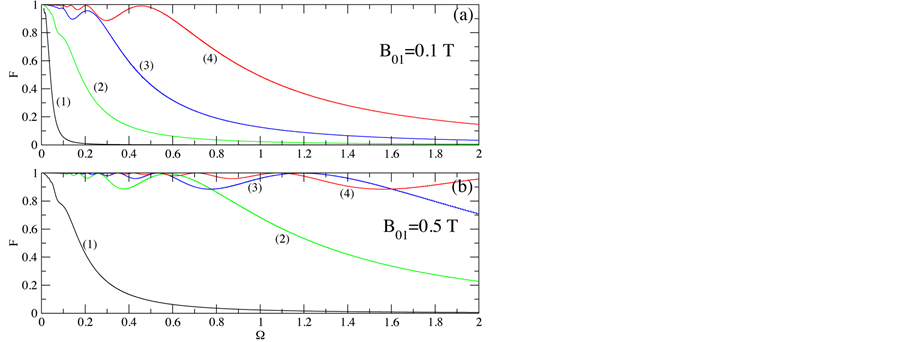
Figure 2. Fidelity at the end of the π-pulse for CNOT.
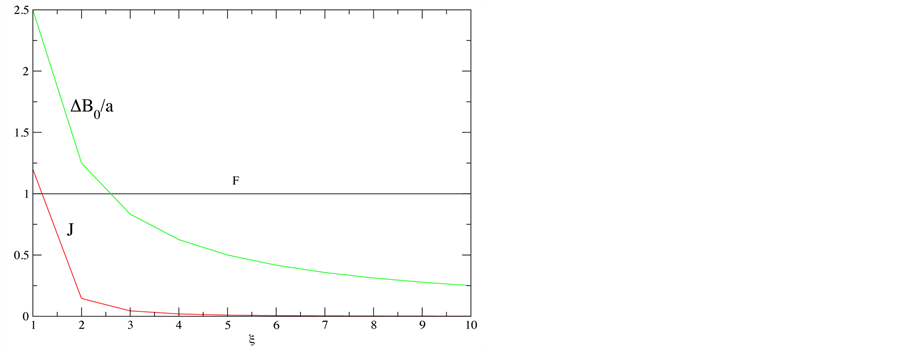
Figure 3. Effect of 13C-13C separation.
the longitudinal magnetic field), the coupling constant deduced from Equation (1) would be given by![]() , with
, with ![]() given by Equation (4), and basically the results are the same as the presented here.
given by Equation (4), and basically the results are the same as the presented here.
According to these results, one has now an idea of the value of the parameters for the design of a quantum computer with the 12C - 13C diamond quantum system: (a) Separation between 13C atoms is  which can be aligned along the x-axis, (b) coupling constant is
which can be aligned along the x-axis, (b) coupling constant is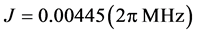 , (c) longitudinal magnetic field is
, (c) longitudinal magnetic field is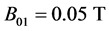 , (d) gradient of this longitudinal magnetic field along the x-axis is
, (d) gradient of this longitudinal magnetic field along the x-axis is  , and (e) magnitude of the rf-magnetic field on the plane x-y is
, and (e) magnitude of the rf-magnetic field on the plane x-y is 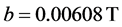 (Rabi's frequency
(Rabi's frequency ).
).
For the CCNOT quantum gate, one has the initial conditions 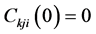 for
for  and
and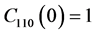 . The time is allowed to last a
. The time is allowed to last a 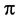 -pulse
-pulse . The coupling parameter
. The coupling parameter ![]() is taken as before, and second neighbor coupling parameter
is taken as before, and second neighbor coupling parameter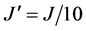 . Figure 4 shows the fidelity parameter as a function of Rabi’s frequency for magnetic field intensities (1)
. Figure 4 shows the fidelity parameter as a function of Rabi’s frequency for magnetic field intensities (1)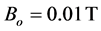 , (2)
, (2)
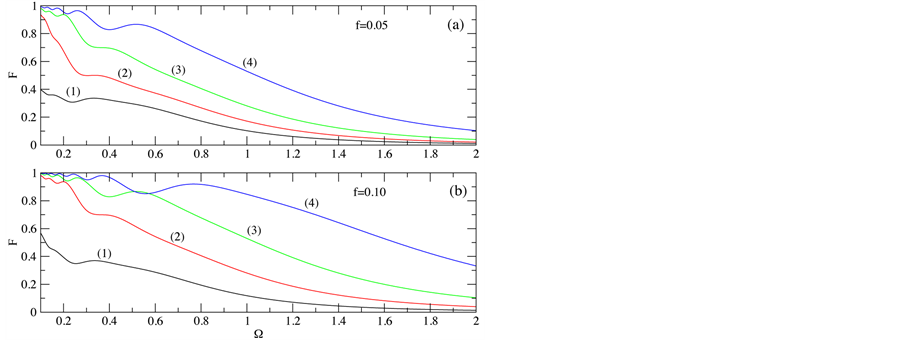
Figure 4. Fidelity at the end of the π-pulse for CCNOT.
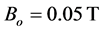 , (3)
, (3)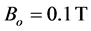 , and (4)
, and (4)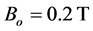 , for
, for 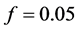 (a), and for
(a), and for 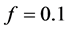 (b). As one can see fro these plots, a good CCNOT quantum gate can be obtained by choosing
(b). As one can see fro these plots, a good CCNOT quantum gate can be obtained by choosing 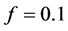 (implying and encresing of the gradient of the magnetic field by a factor of two), and with the other parameters given as defined with the CNOT quantum gate.
(implying and encresing of the gradient of the magnetic field by a factor of two), and with the other parameters given as defined with the CNOT quantum gate.
Although the gradient of the magnetic field might be a concern, the magnitude of the longitudinal magnetic field is low enough to think that this gradient can be achieved. The scalability of the system is clear, the read out system could be based on single spin measurement technics [29], and studies on decoherence remains to be done on this system. This quantum computer resembles a solid state NMR system [30].
5. Conclusion and Discussion
It was shown that by removing a 12C atom, replacing it by a 13C atom in the tetrahedral configuration of the diamond, and doing this process periodically in a linear direction, one could get a linear chain of nuclear spins one half which can work as a quantum computer. The interaction between 13C atoms is governed by the magnetic dipole-dipole interaction, and the parameters of a possible quantum computer design were determined by studying the quantum CNOT and CCNOT gates with two and three qubits respectively. Although there might be a concern about the gradient of the magnetic field along the lines of 13C atoms, it must not be so difficult to get this gradient since the magnitude of this magnetic field is relatively low (0.5 T). In principle, it is possible to replace a 12C atom by any other spin one half atom. However, an unclose configuration of electrons in the lattice makes necessarily to take into account the interaction of electrons with this atom (as it is the case of diamond NV configuration) which makes the analysis and the quantum computer much more complicated and sensitive to environment interaction. The misplacement of the 13C atom along the x-axis produces different coupling constant in the interaction, but according to Figure 4, the fidelity of the CNOT quantum gate does not change, and one would expect the same result for quantum algorithms. The displacement of 13C atoms off x-axis changes the coupling constant and the interaction itself, which has to be studied. In addition, it still remains to study the decoherence on this system. Finally, one recalls that the carbon isotopesatoms 12C, 13C and 14C occur naturally on Earth with a percent of about 99%, 1% and 10−4%, 14C being a radioactive isotope with a half life of about 5730 years and having spin zero. Therefore, 14C is not an important composition at all in the diamond structure.
REFERENCES
- H.-P. Breuer and F. Petruccione, “The Theory of Open Quantum Systems,” Oxford University Press, Oxford, 2006.
- A. O. Caldeira and A. T. Legget, Physica A: Statistical Mechanics and its Applications, Vol. 121, 1983, pp. 587- 616. http://dx.doi.org/10.1016/0378-4371(83)90013-4
- W. G. Unruh and W. H. Zurek, Physical Review D, 1989, Vol. 40, pp. 1071-1094 http://dx.doi.org/10.1103/PhysRevD.40.1071
- B. L. Hu, J. P. Paz and Y. Zhang, Physical Review D, Vol. 45, 1992, pp. 2843-2861. http://dx.doi.org/10.1103/PhysRevD.45.2843
- A. Venugopalan, Physical Review A, Vol. 56, 1997, pp. 4307-4310. http://dx.doi.org/10.1103/PhysRevA.56.4307
- H. D. Zeh, Foundations of Physics, Vol. 3, 1973, pp. 109- 116. http://dx.doi.org/10.1007/BF00708603
- J. P. Paz and W. H. Zurek, Proc. Les Houches, Vol. 111A, 1997, p. 409.
- G. Lindblad, Communications in Mathematical Physics, Vol. 48, 1976, pp. 119-130. http://dx.doi.org/10.1007/BF01608499
- W. S. Warren, Science, Vol. 277, 1997, pp. 1688-1690. http://dx.doi.org/10.1126/science.277.5332.1688
- L. M. L. Vandersypen, M. Steffen, G. Breyta, C. S. Yannoni, M. H. Sherwood and I. L. Chuang, Nature, Vol. 414, 2001, p. 883. http://dx.doi.org/10.1038/414883a
- M. H. Holzschelter, Los Alamos Science, Vol. 27, 2002, p. 264.
- C. Monroe and J. Kim, Science, 2013, Vol. 339, p. 1164. http://dx.doi.org/10.1126/science.1231298
- H. Walter, B. T. H. Varcoe, B. G. Englert and T. Becker, Reports on Progress in Physics, Vol. 69, 2006, p. 1325. http://dx.doi.org/10.1088/0034-4885/69/5/R02
- D. Jaksch, J. I. Cirac, P. Zoller, S. L. Rolston, R. Côté and M. D. Lukin, Physical Review Letters, Vol. 85, 2000, pp. 2208-2211. http://dx.doi.org/10.1103/PhysRevLett.85.2208
- K. C. Younge, B. Knuffman, S. E. Anderson and G. Raithel, Physical Review Letters, Vol. 104, 2010, Article ID: 173001. http://dx.doi.org/10.1103/PhysRevLett.104.173001
- I. Chiorescu, Y. Nakamura, C. J. P. M. Harmans and J. E. Mooij, Science, Vol. 299, 2003, pp. 1869-1871. http://dx.doi.org/10.1126/science.1081045
- A. Yu. Kitaev, Annals of Physics, Vol. 303, 2003, pp. 2-30. http://dx.doi.org/10.1016/S0003-4916(02)00018-0
- L. Childress and R. Hanson, MRS Bulletin, Vol. 38, 2013, pp. 134-138. http://dx.doi.org/10.1557/mrs.2013.20
- G. P. Berman, D. I. Kamenev, D. D. Doolen, G. V. López and V. I. Tsifrinovich, Contemporary Mathematics, Vol. 305, 2002, p. 13. http://dx.doi.org/10.1090/conm/305/05213
- G. V. López and L. Lara, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 39, 2006, p. 3897. http://dx.doi.org/10.1088/0953-4075/39/18/019
- G. V. López, T. Gorin and L. Lara, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 41, 2008, Article ID: 055504. http://dx.doi.org/10.1088/0953-4075/41/5/055504
- G. V. López and P. López, Journal of Modern Physics, Vol. 3, 2012, pp. 85-101. http://dx.doi.org/10.4236/jmp.2012.31013
- K. Lakoubovskii and G. J. Adriaenssens, Journal of Physics: Condensed Matter, Vol. 13, 2001, p. 6015.
- R. W. Hamm and M. E. Hamm, “Industrial Acceleretors and Their Applications,” World Scientific, Singapore, 2012.
- M. A. Cazalilla, N. Lorente, R. D. Muño, J. P. Gauyacq, D. Teillet-Billy and P. M. Echenique, Physical Review B, Vol. 58, 1998, pp. 13991-14006. http://dx.doi.org/10.1103/PhysRevB.58.13991
- J. D. Jackson, “Classical Electrodynamics,” 3rd Edition, Chapter 5.6, John Wiley and Sons, Inc., Hoboken, 1999.
- A. N. Kolmogorov and S. V. Fomin, “Introductory Real Analysis,” Dover Publications, Inc., Mineola, 1970.
- M. A. Nielsen and I. L. Chuang, “Quantum Computation and Quantum Information,” Cambridge University Press, Cambridge, 2000.
- D. Rugar, R. Budakian, H. J. Mamin and B. W. Chui, Nature, Vol. 430, 2004, p. 329. http://dx.doi.org/10.1038/nature02658
- M. J. Duer, “Introduction to Solid-State NMR Spectroscopy,” Blackwell, Oxford, 2004.
Appendix
Two qubits dynamics is obtained from Equations (13), (14), and (19), resulting the equations
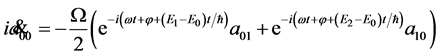 (27)
(27)
 (28)
(28)
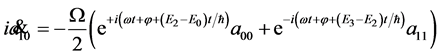 (29)
(29)
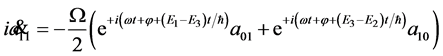 (30)
(30)
where the complex variables ![]() for
for ![]() correspond to the amplitude of probability to find the system on the states
correspond to the amplitude of probability to find the system on the states 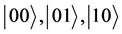 and
and , and one has
, and one has 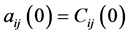 and
and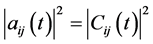 . Decimal notation on the energies
. Decimal notation on the energies ![]() corresponds to its binary elements
corresponds to its binary elements 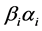 for
for .
.
As before, three qubits dynamics is described by the equations
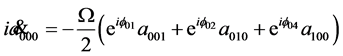 (31)
(31)
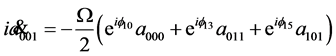 (32)
(32)
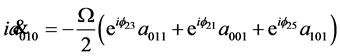 (33)
(33)
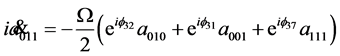 (34)
(34)
 (35)
(35)
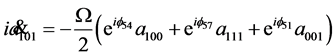 (36)
(36)
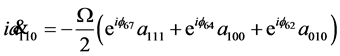 (37)
(37)
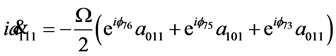 (38)
(38)
with 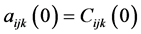 and
and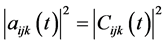 ,
,
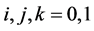 . The phases
. The phases ![]() are defined as
are defined as
 , where decimal
, where decimal ![]() corresponds to its binary elements
corresponds to its binary elements  for
for .
.
For both cases, the energies ![]() are deduced from Equation (15).
are deduced from Equation (15).

