Journal of Modern Physics
Vol.4 No.12(2013), Article ID:41151,6 pages DOI:10.4236/jmp.2013.412199
Discretization and Interaction of Fields via the Classical Kaluza-Klein Theory
Département de Mathématiques et de Statistique, Université de Moncton, Moncton, Canada
Email: claude.gauthier@umoncton.ca
Copyright © 2013 Doris LaChance, Claude Gauthier. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 2, 2013; revised November 1, 2013; accepted November 25, 2013
Keywords: Kaluza-Klein Theories; Geometric Quantization; Interaction of Fields
ABSTRACT
We show how the metric of a five-dimensional hyperspace-time can be used to model the quantum nature of electromagnetic interactions. The space-time neighborhood of the point where such an interaction takes place bends according to the curl and the derivative of the local electromagnetic four-potential, both calculated in the direction of the latter. In this geometric setting, the presence of a non-gravitational field is needed to induce the discretization of any gravitational field. We also exploit two variants of the classical Kaluza-Klein five-dimensional theory to obtain coupled generalizations of Einstein’s and Maxwell’s equations. The first variant involves an unspecified scalar field that may be related to the inflaton. The equations of the second variant show a direct interdependency of gravitation and electromagnetism that would emerge or be activated through the production of electromagnetic waves.
1. Introduction
In Kaluza’s [1] and Klein’s [2] original formulations, the mathematical modeling of gravitation through general relativity is based on the space-time section of the metric of a five-dimensional hyperspace-time, and that of electromagnetism uses the first four components of its fifth line, or column. The fact that the equations of electromagnetism are invariant under the gauge group U(1) implies that the fifth dimension must have a cyclic character. The usual interpretation of this is that the fifth dimension winds upon itself according to a circle, whose radius is very small in order to explain why this dimension is unobservable. These fifth dimension characteristics were postulated by Kaluza and Klein and taken up by almost all their followers. In practice, the smallness of the fifth dimension radius of curvature means that the hyperspace-time metric is independent of this dimension.
With the above properties assumed to apply to the fifth dimension, Kaluza and Klein were able to obtain a formal unification of gravitation and electromagnetism. However, this unification is unsatisfactory because it does not show how gravitational and electromagnetic fields interact. A deeper unification of gravitation and electromagnetism requires a revision of the postulate applying to the geometric structure of the fifth dimension. As it is, the postulate concerns only local symmetries of the group U(1) used to characterize the continuous functions describing classical electromagnetism. A more complete geometric modeling of electromagnetism must also allow expressing the discontinuity of certain functions associated with an electrically charged particle, such as its energy when it is involved in an interaction. To model this discontinuous variation, we shall postulate that the geometric structure of the fifth dimension has a global symmetry making it multiconnected [3-5]. The fifth dimension then decomposes into equal length intervals, each topologically equivalent to the circle S1. This multiconnectivity generates a structure with a discrete group of symmetry G over the fifth dimension. The group G establishes an order into the set of these intervals and renders homologous points of the fifth dimension. The multiconnectivity of the fifth dimension reduces its metric measure to that of only one of its finite intervals. Thus it is no longer necessary for the fifth dimension to have a strong curvature to be unobservable. The flexibility to choose one of these intervals as the geometric framework necessary to describe the continuous properties of electromagnetism is a degree of freedom similar to those of continuous gauges in standard field theories: here it corresponds to a discontinuous gauge.
This five-dimensional hyperspace-time can be seen as a fibre bundle whose base is space-time and fibres are copies of the fifth dimension. Above each point of the trajectory of a charged particle in space-time, a finite interval of the fifth dimension must be chosen to describe the properties of the continuous symmetries related to a possible interaction with an exterior electromagnetic field. Without such a field, the particle is free and the finite interval can be arbitrarily chosen above each point of its trajectory: this choice determines a horizontal section in the hyperspace-time fibre bundle. When the particle undergoes an electromagnetic interaction at a given point in space-time, the quantum effect on the particle generates a modification, over this point and with respect to the horizontal section, of the finite interval needed to describe the continuous properties related to the interaction. Since neighborhoods of homologous points belonging to different finite intervals have the same local geometry, the continuous properties of electromagnetism are invariant under changes of this interval. At the point of space-time where the interaction takes place, this change of interval implies a discontinuous variation of the hyperspace-time metric along the fifth dimension. Outside this point, the hyperspace-time metric stays independent of the fifth dimension, in accordance with the original Kaluza-Klein postulate. Our postulate thus differs from that of Kaluza and Klein only at the interaction point. Relying on this new postulate, the present paper first aims to show how the metric of a five-dimensional hyperspace-time can be used to unify gravitational and electromagnetic theories, and simultaneously explain qualitatively the quantum nature of electromagnetic interactions. In its second part, we shall reconsider the field interaction aspect of the original Kaluza-Klein theory and obtain coupled generalizations of Einstein’s and Maxwell’s equations.
In this paper, Latin indices are for space-time and run from 1 to 4. Greek letters are hyperspace-time indices and run from 1 to 5. The signatures of space-time and hyperspace-time metrics are respectively (−1,1,1,1) and (−1,1,1,1,1). A line over a space-time symbol will indicate that we consider its hyperspace-time version. The electromagnetic tensor is defined by Fmn=An,m-Am,n where Am designates the covariant components of the electromagnetic four-potential.
2. Hyperspace-Time Metric and Scalar Curvature
In a completely geometric unified field theory, the hyperspace-time metric  should allow to describe all properties of fields. To express the fact that physics seems to depend only on space-time coordinates, Kaluza and Klein postulated that the components
should allow to describe all properties of fields. To express the fact that physics seems to depend only on space-time coordinates, Kaluza and Klein postulated that the components 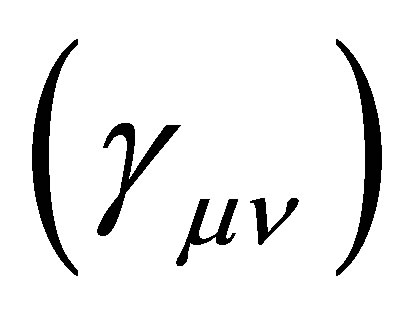 are independent of x5. They also postulated that under the coordinate transformation
are independent of x5. They also postulated that under the coordinate transformation  the new space-time coordinates
the new space-time coordinates  are independent of x5. Therefore, the original Kaluza-Klein postulate concerning the fifth dimension is
are independent of x5. Therefore, the original Kaluza-Klein postulate concerning the fifth dimension is
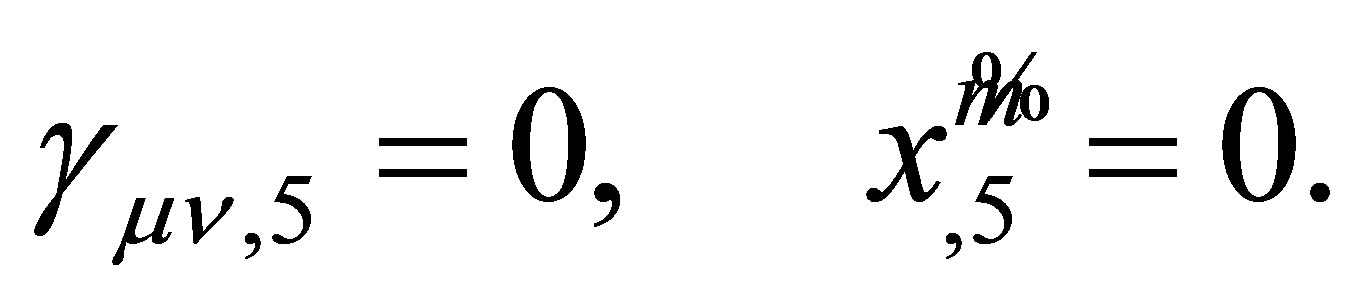
Taking into account these equations, it is easily shown that the most general expression for such a metric is
 (1)
(1)
where (gmn) is the space-time metric, Am is the electromagnetic four-potential and k is an arbitrary constant.
To express mathematically the discrete nature of an electromagnetic interaction occurring at a point x0 of hyperspace-time, we assume that the mathematical mechanism modeling the electromagnetic interaction is related only to the hyperspace-time metric components which are independent of the space-time metric. Inspired by the way how electrons change their orbit around a nucleus, we postulate that if 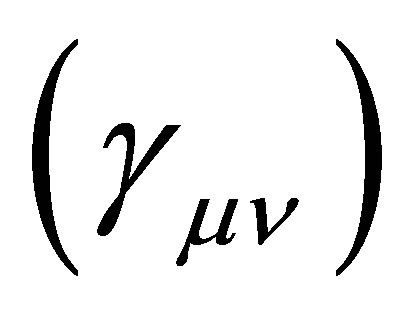 varies with respect to x5, then
varies with respect to x5, then
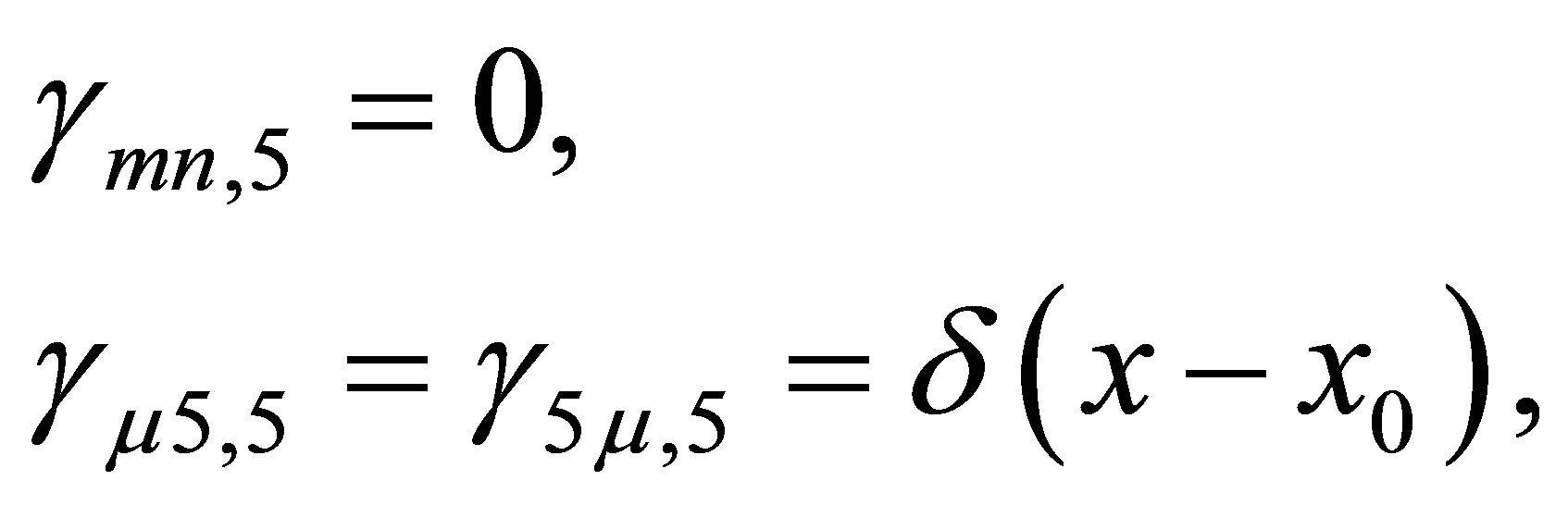 (2)
(2)
where 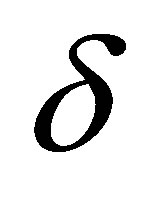 designates the Dirac distribution. This new postulate will be said of discretization due to the fifth dimension. To simplify the presentation, we shall set
designates the Dirac distribution. This new postulate will be said of discretization due to the fifth dimension. To simplify the presentation, we shall set  until Section 5. It is then straightforward to deduce the hyperspace-time scalar curvature:
until Section 5. It is then straightforward to deduce the hyperspace-time scalar curvature:
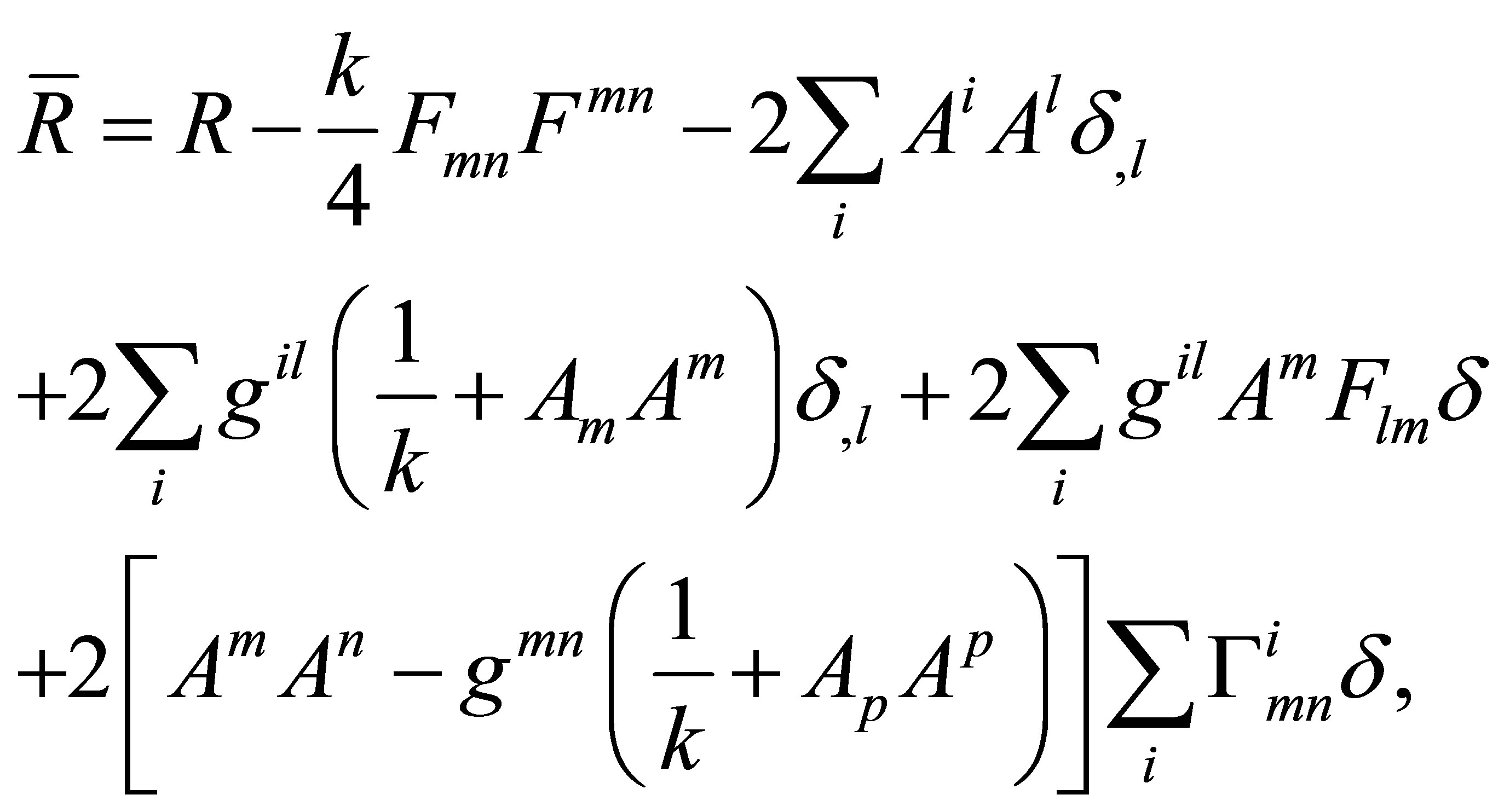 (3)
(3)
where R is the space-time scalar curvature.
3. Field and Interaction Equations
Let S denotes the action associated with Equation (3). We designate by g the determinant of the space-time metric and by  the four-dimensional space of coordinates x2, x3, x4 and x5 between two given values of time x1. Then
the four-dimensional space of coordinates x2, x3, x4 and x5 between two given values of time x1. Then
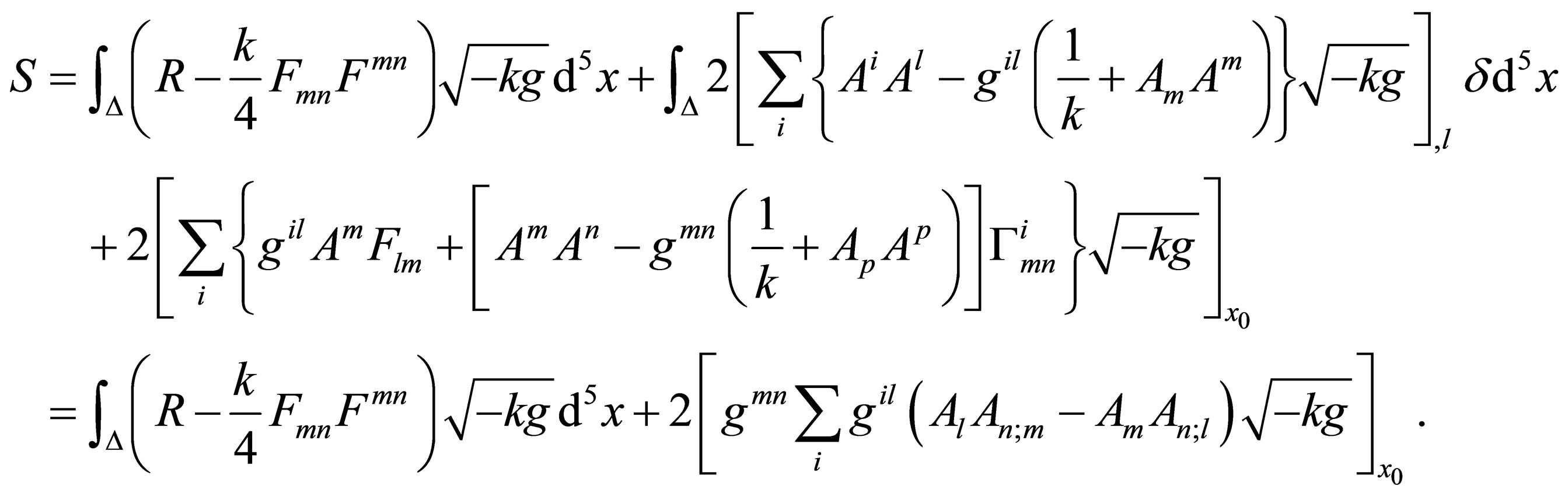 (4)
(4)
By successively varying the space-time metric and the electromagnetic four-potential, the first term on the right-hand side of Equation (4) yields the Einstein and Maxwell equations deduced by Klein. Its second term is an expression of the electromagnetic interaction at x0. Bringing in the Lorenz gauge, Equation (4) becomes
 (5)
(5)
The second term of the right-hand side of Equation (5) shows that the interaction can be described as a multiple of the sum of partial variations of the electromagnetic four-potential’s squared norm evaluated at x0 in the direction of its largest variation. This expression can also be written
 (6)
(6)
According to [5], the second term on the right hand side of Equation (5) corresponds to a point of space-time where a change of horizontal section occurs in the hyperspace-time fibre bundle. This change thus takes place optimally in the sense that it is carried out in the direction of a gradient. Moreover, Equation (6) shows that the way this change is realized involves the curl and the derivative of the electromagnetic four-potential, both calculated at x0 in the direction of this four-potential. Depending on the space-time curvature, and on the value of the electromagnetic four-potential in the neighborhood of x0, the change of horizontal section will thus occur more or less rapidly, and with a rotation more or less pronounced. These effects should emerge physically as contributions to the 4-momentum and angular momentum of the particle subject to this interaction.
Observe that since

The space-time metric, i.e. the gravitational field, thus varies discontinuously at x = x0 and depends on the value of the electromagnetic 4-vector at this point. If this four-potential is identically zero, the postulate of discretization due to the fifth dimension then reduces to Klein’s original postulate and there is no discretization. The presence of a non-zero electromagnetic four-potential is thus necessary to induce the discretization of the gravitational field.
4. Quantization Due to Hyperspace-Time
Let us now try to extend the mathematical mechanism modeling the electromagnetic interaction to all components of the hyperspace-time metric, i.e. to replace Equations (2) with
 (7)
(7)
A straightforward calculation shows that the hyperspace-time scalar curvature then becomes:
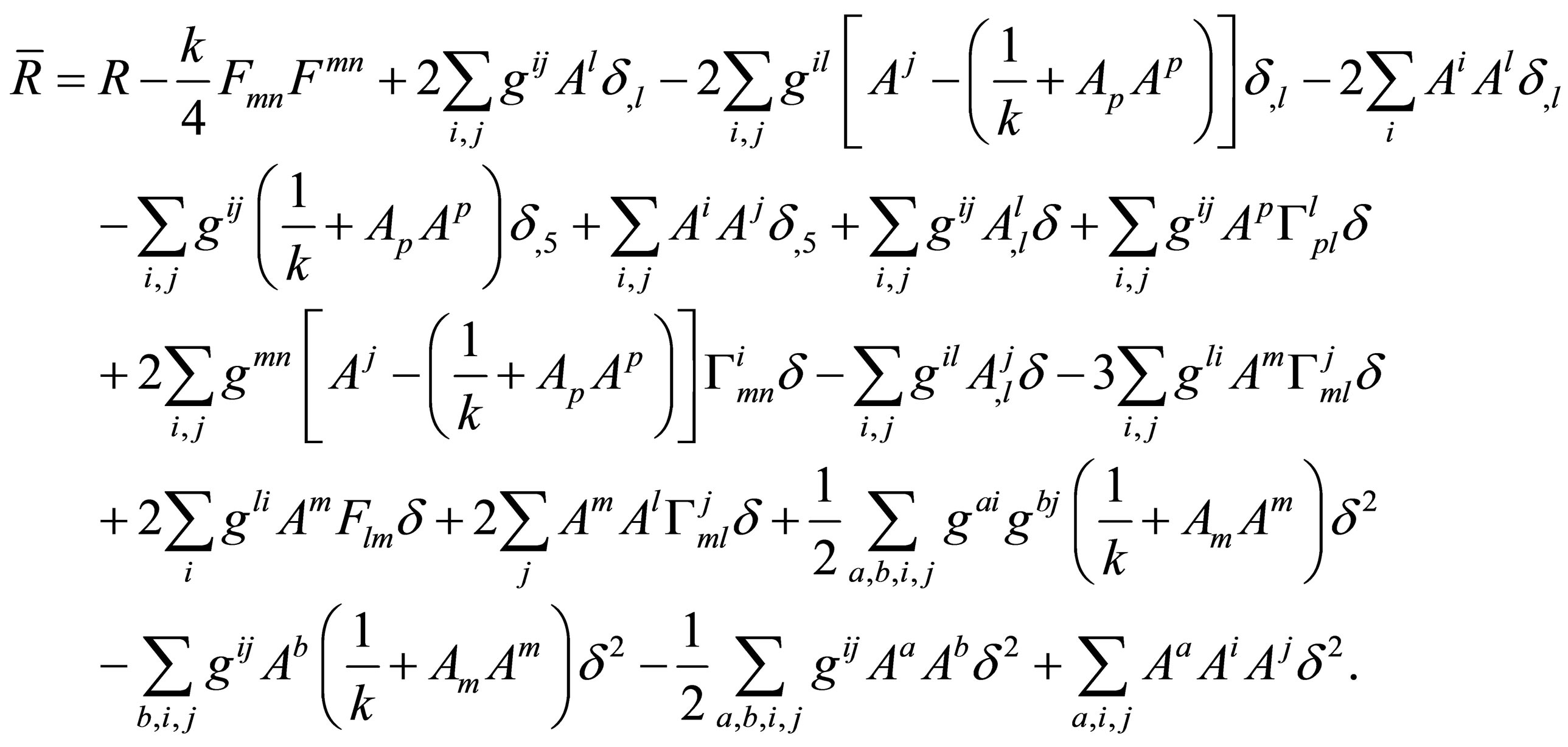
This expression involves products of the Dirac distribution, which is impossible within the framework of the theory [6]. The same observation applies even if the electromagnetic four-potential is identically zero, because the hyperspace-time scalar curvature is then

Therefore, the postulate based on Equations (7) does not allow deducing the equations of a discretized gravitational field.
5. Interaction through Unification
Even if Klein was aware that 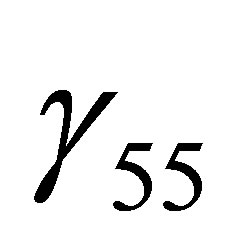 can be any differentiable scalar function of space-time coordinates, he chose to replace it with the proportionality constant k between
can be any differentiable scalar function of space-time coordinates, he chose to replace it with the proportionality constant k between 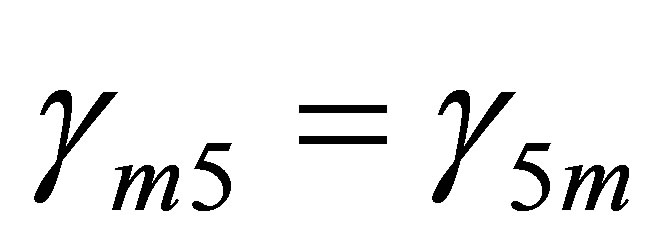 and
and 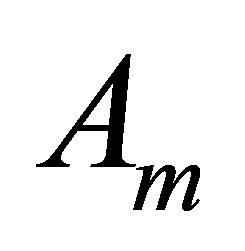 in order to facilitate his calculations. However, this choice led him to the well known unsatisfactory unification of gravitation and electromagnetism. Since Kaluza’s and Klein’s works, several hundred papers were written trying to improve this situation (see e.g. [7]). Many paths were explored but none have yielded a satisfactory unified field theory. We shall now reconsider the field interaction aspect of the original Kaluza-Klein theory by returning to the starting point of Klein’s development, i.e. to the metric of Equation (1) and replace
in order to facilitate his calculations. However, this choice led him to the well known unsatisfactory unification of gravitation and electromagnetism. Since Kaluza’s and Klein’s works, several hundred papers were written trying to improve this situation (see e.g. [7]). Many paths were explored but none have yielded a satisfactory unified field theory. We shall now reconsider the field interaction aspect of the original Kaluza-Klein theory by returning to the starting point of Klein’s development, i.e. to the metric of Equation (1) and replace  with a differentiable function α of the space-time coordinates. Following the approach of Hilbert to get the equations of general relativity and of Klein to obtain his formal geometric unification of gravitation and electromagnetism, we shall derive new unified fields equations from a variational principle based on the scalar curvature
with a differentiable function α of the space-time coordinates. Following the approach of Hilbert to get the equations of general relativity and of Klein to obtain his formal geometric unification of gravitation and electromagnetism, we shall derive new unified fields equations from a variational principle based on the scalar curvature  deduced from this modified expression of
deduced from this modified expression of . A straightforward calculation first yields
. A straightforward calculation first yields
 (8)
(8)
The equations of motion in space-time are then obtained by varying the action built up with Equation (8) separately with respect to the three sets of independent dynamical variables gmn, Am and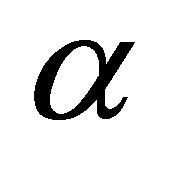 . Direct calculations give, respectively,
. Direct calculations give, respectively,
 (9)
(9)
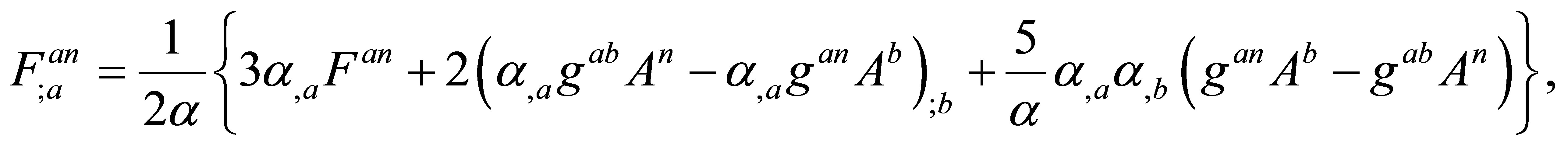 (10)
(10)
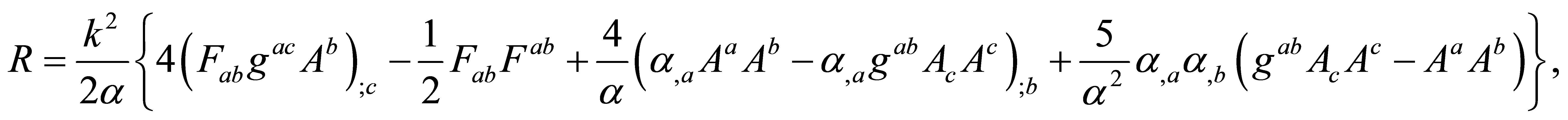 (11)
(11)
where
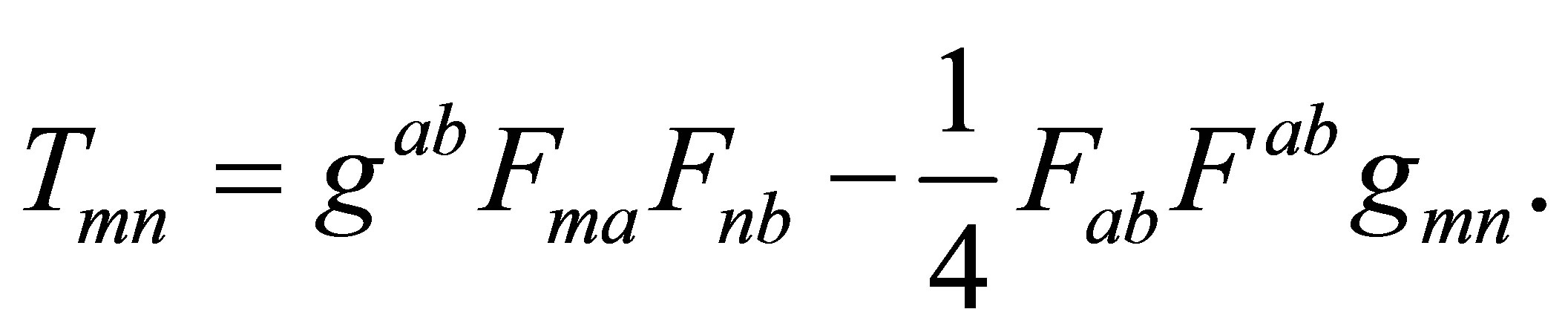
In this unified fields theory, the Equations (9), (10) and (11) correspond to three different laws of nature. If the function α is constant, then Equations (9) and (10) respectively reduce to the Einstein equations for a spacetime with Tmn as energy-momentum tensor, and the Maxwell equations for a free space-time. Since Equation (11) results from the variations of α, this equation does not exist if α is a constant.
Considering a situation where the three laws describe by Equations (9)-(11) apply, we can substitute Equations (10) into Equation (11), and the resulting expression into Equations (9). The space-time where this situation occurs is then described by
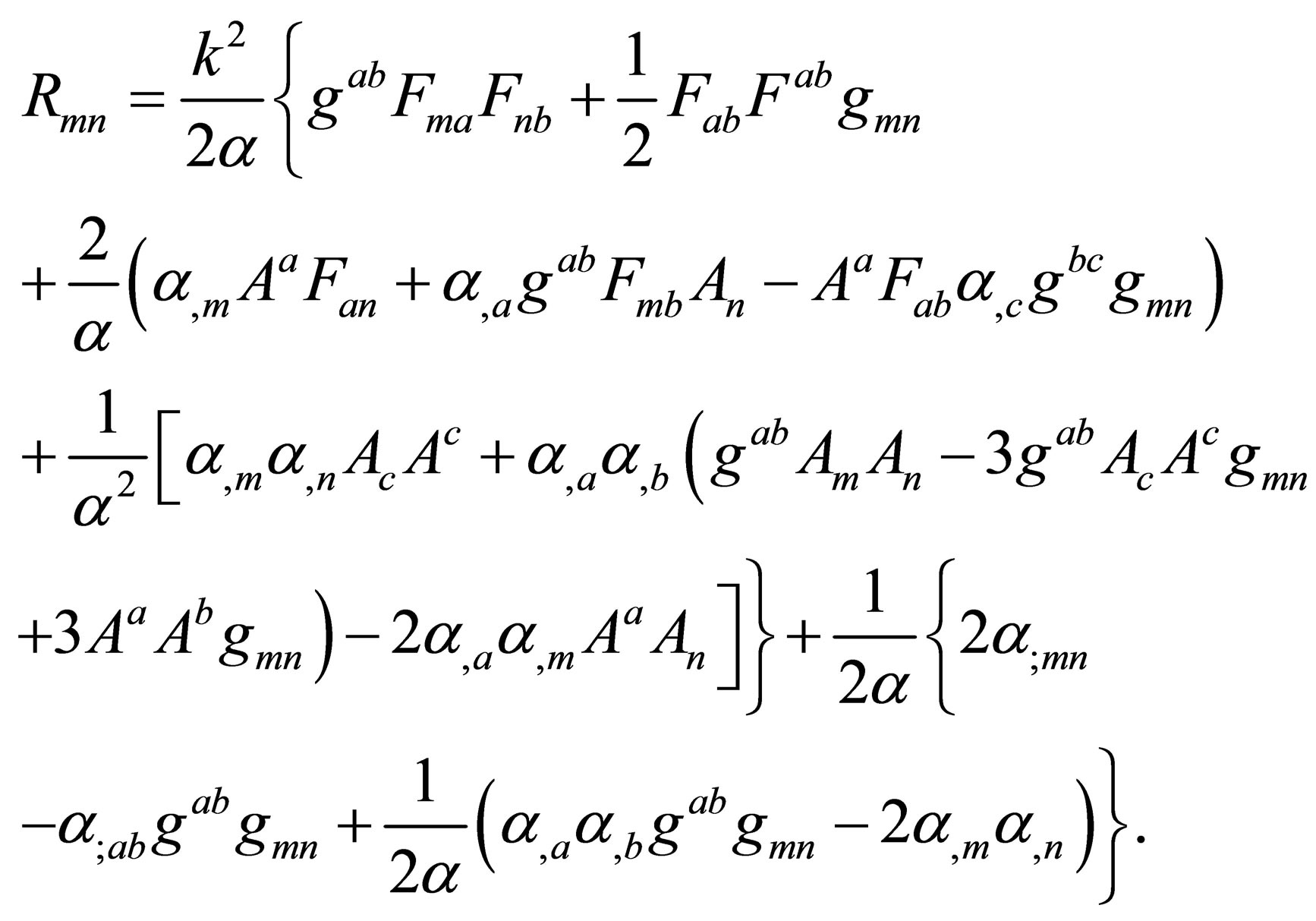
(12)
Observe that if k = 0, or if the electromagnetic fourpotential is identically zero, then Equations (12) reduce to
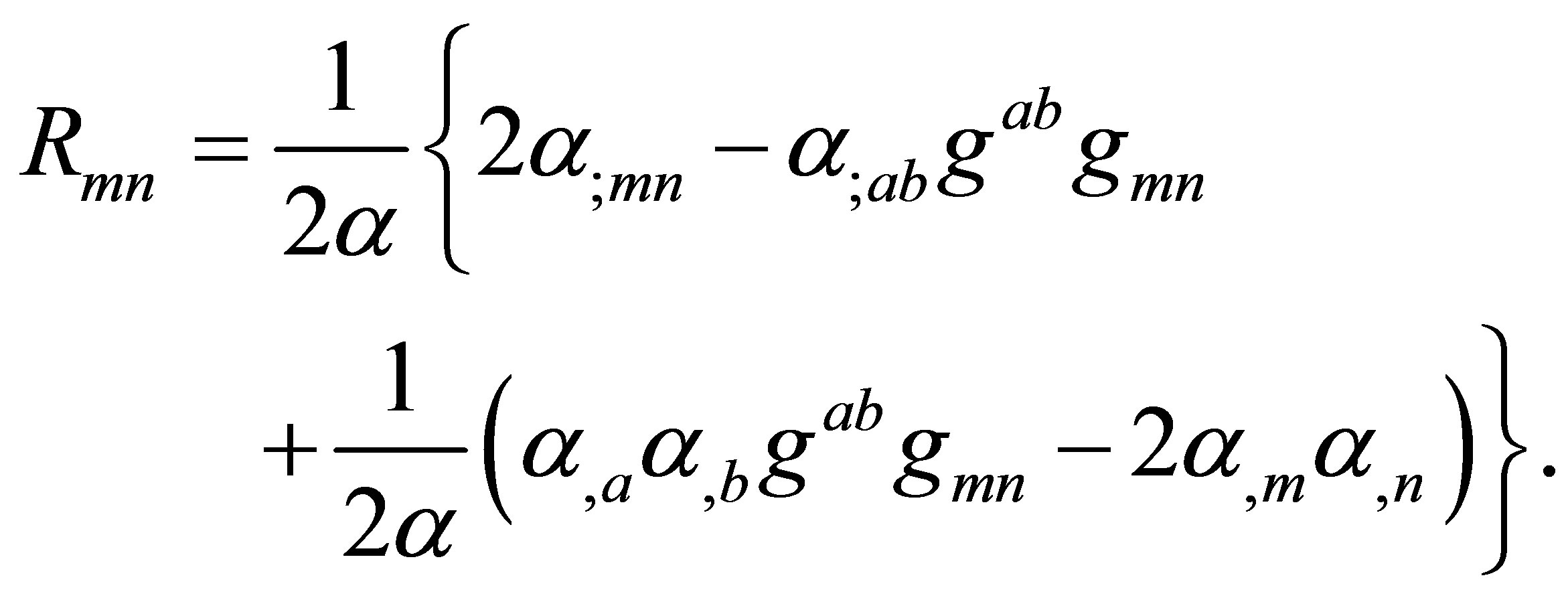
Such an equation may be used to model a universe whose expansion is regulated by the scalar field α.
6. Electromagnetic Energy Density
In the preceding Section, the independence of the scalar field α with respect to the variables gmn and Am was assumed to simplify the calculations. But such a scalar field is hard to find. We shall now consider an easily reachable scalar field by observing that it was arbitrary at the starting point of Klein’s development. If we allow it to depend on the variables gmn and Am, then we can use the electromagnetic energy density of space-time given by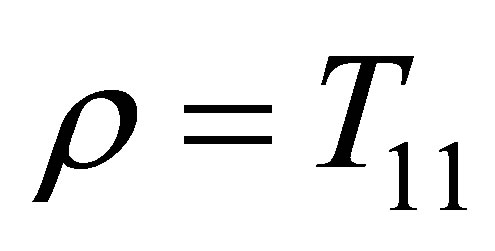 . For this scalar field, the equations of motion in space-time are found by varying the action determined by Equation (8) separately with respect to gmn and Am. Straightforward calculations yield, respectively,
. For this scalar field, the equations of motion in space-time are found by varying the action determined by Equation (8) separately with respect to gmn and Am. Straightforward calculations yield, respectively,
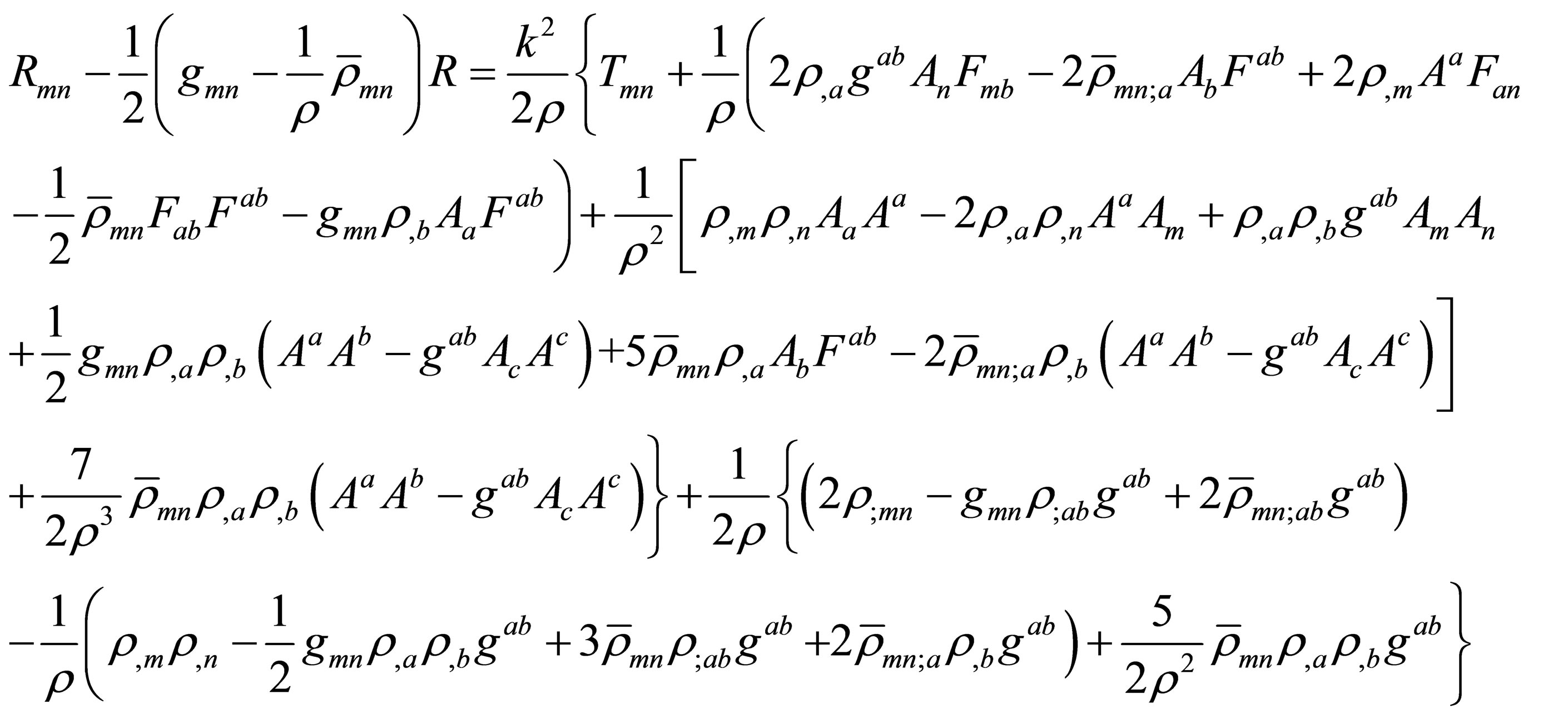 (13)
(13)
 (14)
(14)
where  and
and  are the partial derivatives of
are the partial derivatives of  with respect to
with respect to  and
and  respectively.
respectively.
One way to solve the system of Equations (13) and (14) is first to rewrite Equations (14) as four partial differential equations of order one for R. The common solution of these equations is an expression of R in terms of the electromagnetic four-potential and of an arbitrary scalar function of the space-time coordinates. By substituting this expression of R into Equations (13), we obtain equations for Rmn analogous to Equations (12), but with a more complex expression and an arbitrary function on its right-hand side. This arbitrary function here plays a role similar to that of α in Section 5.
7. Conclusions
In the first part of this paper, we have shown how the metric of a five-dimensional hyperspace-time can be used to model the quantum nature of electromagnetic interactions. In this framework, the neighborhood of the point where an interaction takes place bends according to the curl and the derivative of the local electromagnetic four-potential, both calculated in the direction of the latter. We have also seen that a non-gravitational field is required to induce the discretization of any gravitational field.
In its second part, we have reconsidered the field interaction aspect of the original Klein’s unifying scheme which led to two independent laws of nature. With the method of Section 5, we have obtained a system of three coupled groups of equations for gmn, Am and α. These groups of equations correspond to three different laws of nature. Due to the coupling between the groups of equations, these laws are not independent: each one will depend on gmn, Am and α. Observe that this unifying scheme calls in a scalar function acting at a middle scale and which must not be of gravitational nor of electromagnetic origin. It is hard to find such a scalar field; at very large scale it could be identified with the field describing the inflationary phase in the early universe.
Envisaging the possibility of controlling the unspecified scalar field of Section 5, we have replaced it in Section 6 with the space-time local density of electromagnetic energy. Other choices are possible. This has led us to a system of two groups of equations corresponding to two interdependent laws of nature. If we consider Equations (13) and (14) as generalizations of Einstein’s equations in the presence of an electromagnetic field and of Maxwell’s equations, respectively, these groups of equations show that it would be possible to influence the gravitational field in a region of space-time by locally changing the electromagnetic field. Reciprocally, a variation of the gravitational field would cause a variation of the electromagnetic field. Since any variation of the electromagnetic field generates electromagnetic waves, the two above predictions could be tested through phenomena involving a large and sudden emission of electromagnetic waves.
REFERENCES
- T. Kaluza, “Zum Unitätsproblem in der Physik,” Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 1921, pp. 966-972.
- O. Klein, Zeitschrift für Physik, Vol. 37, 1926, pp. 895- 906. http://dx.doi.org/10.1007/BF01397481
- C. Gauthier and P. Gravel, Canadian Journal of Physics, Vol. 68, 1990, pp. 385-387. http://dx.doi.org/10.1139/p90-061
- C. Gauthier and P. Gravel, Nuovo Cimento A, Vol. 104, 1991, pp. 325-336. http://dx.doi.org/10.1007/BF02799141
- O. Ben Khalifa and C. Gauthier, Central European Journal of Physics, Vol. 5, 2007, pp. 151-164. http://dx.doi.org/10.2478/s11534-007-0002-0
- L. Schwartz, “Théorie des Distributions,” Hermann, Paris, 1978.
- J. Overduin and P. Wesson, Physics Reports, Vol. 283, 1997, pp. 303-380. http://dx.doi.org/10.1016/S0370-1573(96)00046-4

